Next Article in Journal
Integration of Hydrate-Based Desalination (HBD) into Multistage Flash (MSF) Desalination as a Precursor: An Alternative Solution to Enhance MSF Performance and Distillate Production
Next Article in Special Issue
Detection of Water Hyacinth (Eichhornia crassipes) in Lake Tana, Ethiopia, Using Machine Learning Algorithms
Previous Article in Journal
Community Agricultural Reservoir Construction and Water Supply Network Design in Ubon Ratchathani, Thailand, Using Adjusted Variable Neighborhood Strategy Adaptive Search
Previous Article in Special Issue
Geomatics-Based Modeling and Hydrochemical Analysis for Groundwater Quality Mapping in the Egyptian Western Desert: A Case Study of El-Dakhla Oasis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 15
Issue 3
10.3390/w15030595
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review of Numerical Modelling of Morphodynamics in Braided Rivers: Mechanisms, Insights and Challenges

by
Youfei Hu
,
Haiyan Yang
*,
Haolan Zhou
and
Qianwen Lv
Department of Hydraulic Engineering, College of Water Conservancy and Civil Engineering, South China Agricultural University, Guangzhou 510642, China
*
Author to whom correspondence should be addressed.
Water 2023, 15(3), 595; https://doi.org/10.3390/w15030595
Submission received: 19 October 2022 / Revised: 2 December 2022 / Accepted: 28 December 2022 / Published: 2 February 2023
(This article belongs to the Special Issue Research on Applications of Remote Sensing and Geographic Information Systems (GIS) in Water Resources)
Browse Figures
Versions Notes

Abstract

:
In the past decade, the numerical modelling of braided river morphodynamics has experienced a significant advance due to the increasing computer power and the development of numerical techniques. Numerical models are quite efficient in exploring scenarios with different settings, and they can be applied to investigate the complicated physics laws of natural braided rivers and manage complex river engineering problems. However, braided river models are far from fully developed, e.g., the representation of flow and sediment transport, model sensitivity, essential effects of sediment transport, bank erosion and vegetation, and require intensive refinement and validation to enhance their prediction accuracy. The recent application of advanced field measurement techniques offers model development a new chance by providing abundant measurement data of a high quality. The present study reviews the essential mechanisms and applications of typical braided river models; compares their accuracy; discusses the recent progress, advantages and shortcomings; and illustrates the challenges and future research trends.

1. Introduction

Braided rivers are widely distributed in mountainous regions under a variety of climatic regions, characterized by multiple unstable channels and ephemeral bars formed by intense bed load transport and a set of very active channel processes [1]. Figure 1 shows some examples of typical braided reaches in nature. The first five from the Sunwapta River, Canada to the Tuotuo River, China, are located in mountainous areas (Figure 1a–e), and the last two of the Yellow River, China and the Brahamputra River, Bangladesh are located on plains (Figure 1f,g). The understanding of braided river morphodynamics is largely restricted by the fact that they are characterized by unstable networks and highly active channel processes [2].
Numerical models, which are complementary to field observations, can provide a large dataset of sufficient spatial resolution and time series to analyze the morphodynamics in rivers, and have shown their potential to produce morphological elements, braiding phenomena and statistical characteristics similar to natural braided rivers [3,4,5,6,7]. They have been applied to explain some poorly understood phenomena in natural braided rivers, such as avulsions [8,9]; discuss the essential factors controlling the complex processes in braided rivers; and test hypotheses that are difficult to be verified in natural rivers [10,11]. Previous studies have reviewed the existing numerical models for braided river simulation [3,5,12,13,14,15,16,17].
Despite the progress made so far, braided river models are still in their early stage, with many problems far from being solved, e.g., the representation of flow and sediment transport, sediment sorting effect, bank erosion, vegetation and model sensitivity. The complicated and frequently changing nature of braided rivers determines that an exact simulation of their braided patterns is nearly impossible [12]. Recently, the simulation of braided rivers has transferred from idealized simulation with schematic boundary conditions to natural braided reaches with measured topography and flow and sediment conditions [5,18]. Fortunately, the recent advances in measurement techniques, such as multi-spectral imaging, LiDAR and unmanned aerial vehicles (UVAs) [19,20,21,22,23,24,25,26,27], provide a new opportunity for the development of numerical models. Based on the high-quality field data of digital elevation model (DEM) and real-time monitoring data of flow and sediment, the accurate simulation and evolution prediction of specific natural braided rivers will become expected in the future.
The objectives of the present study are the following: (1) review the recent numerical models for braided river simulation and model application fruits in natural rivers; (2) analyze the recent progress of models and discuss their advantages and shortcomings; and (3) propose the challenges and future research trends.

2. Braided River Models

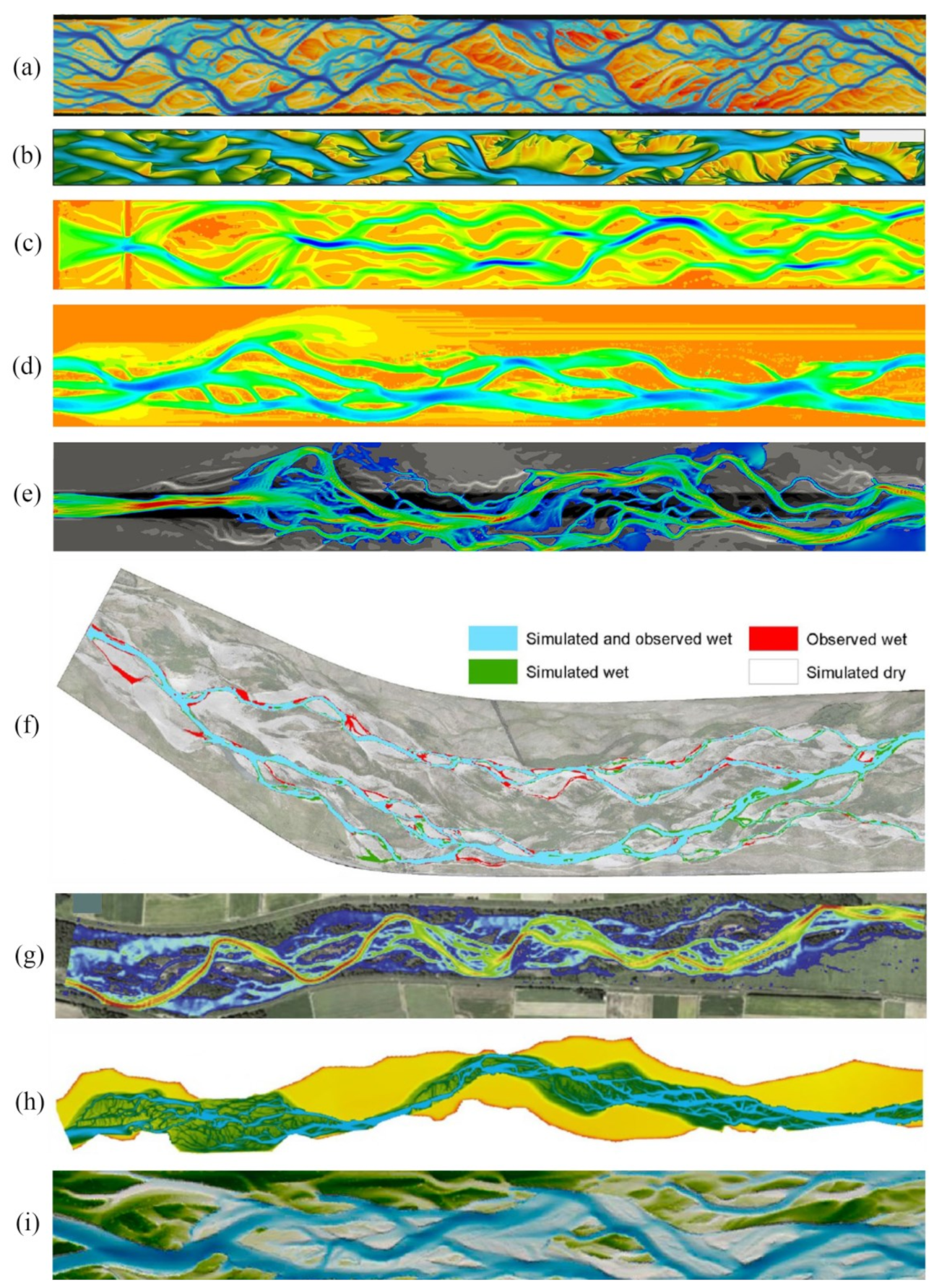
2.1. Braided River Model Evolution

Braided river modelling has experienced an advancement from reduced-complexity approaches to physics-based models [3,28,29]. For the former, cellular model is most prevalent, which does not include the calculation of water depth, flow velocity or flow momentum, but routes discharge downstream by allowing water to flow to lower neighboring cells referring to local variations in topography [30]. The cellular model cannot be applied to study the interactions between flow, sediment and bed deformation [31], and thus plays poorly in simulating flow routines in natural braided rivers [32]. Other models were also developed, such as the linear models for investigating the number of migrating alternate bars, and random walk models for predicting the geometry of braided channel systems [33,34].
Physics-based models provide more detailed process information for understanding natural braided rivers due to their better representation of hydraulic and morphodynamic processes [15]. Physics-based numerical models, ranging from one-dimensional (1D) to three-dimensional (3D), can near-completely represent the complicated processes in natural braided rivers. A 1D model cannot adequately simulate the lateral flow necessary for braiding, whereas a two-dimensional (2D) model can make spatially explicit predictions of flow depth, velocity and bed shear stress, incorporating the influence of topography in steering flow and allowing lateral variation in water surface elevation [35,36,37]. Studies also show that, a depth-integrated edition of Delft 3D with parameterized spiral motion provides large-scale bar pattern statistics that are comparable with those of a fully 3D model [38]. Therefore, a 2D physics-based model offers the greatest potential for simulating braided river morphodynamics at temporal and spatial scales that are of interest to investigations related to river mechanisms and management [15].

2.2. Model Theories and Solutions

Physics-based models usually simplify morphodynamic problems by decoupling the processes of flow and sediment transport, typically including predicting flow, predicting sediment transport and deposition and updating the bathymetric grid [36]. A few models have reproduced well the details of the braided patterns and evolution processes in real braided rivers, as summarized in Table 1.
Braided river models are normally two-dimensional (except for SSIIM (3D) in Table 1), in that they are simpler than three-dimensional, but can produce braided channel patterns that are comparable with those by a full three-dimensional model [38]. These models often solve the depth-averaged shallow water form of the Navier–Stokes equations that are based on the principles of continuity of mass and conservation of momentum, while they can also consider the secondary flow by introducing a helical flow component. For sediment transport, the current braided river models often consider suspended load and bed load, which can be simulated separately or jointly. The governing equation of suspended load transport is usually presented by a two-dimensional advection–diffusion equation for solute transport, while the governing equation of bed load is usually described by a two-dimensional advection equation. The total rate of change in bed elevation is determined by the source items of the suspended load and bed load.
Hydrodynamic modules solve flow dynamics by simplifying the Navier–Stokes equations and introducing discrete timesteps and grid cells in space and time into the model. Shallow water equations are often solved using an alternating direction implicit (ADI) scheme or other explicit schemes such as the cubic-interpolated propagation (CIP) scheme without time-splitting technique and the total variation diminishing (TVD) MacCormack scheme [29,56,57,58]. The ADI scheme works well for slow flow when the Froude number is much less than unity. Equations of shallow water with the Froude number approaching or exceeding unity are calculated using either the CIP or the TVD scheme. The TVD scheme is a shock-capturing scheme, and thus is powerful in describing rapidly varying flows [59,60,61], enabling its efficiency in simulating the local fast flow in braided rivers. Advanced grid generation techniques are key to simulating the evolution of river channels especially near the bank zone. Numerical models such as Mike and Delft3D apply a mixture of structured and unstructured grids, such as an orthogonal curvilinear grid [62,63].
Many equations have been proposed for describing the transport of sediment particles in natural flows, yet few have been applied in existing physics-based braided river models. As summarized in Table 1, the equations of Meyer-Peter and Müller (1948) and Engelund and Hansen (1967) are most often adopted, followed by that of van Rijn (1984, 1993) [39,40,44,51]. These models consider both suspended load and bed load, whereas uniform sediment particles are usually adopted, indicating the roughness of the models. Furthermore, no comparisons among these equations have been made with specific case studies, mainly because sediment transport conditions often significantly differ in individual river reaches. Scenarios with different equations could help to find suitable conditions for various equations and might provide ways to enhance the simulation ability of the existing models.
For bed deformation, many researchers adopted a multiple bed layer method [6,8,64], whereby the riverbed is divided into several layers, and the deposition and erosion related to the suspended load and bed load are incorporated into bed morphologic change equations. The upper active layer is renewed by the erosion and deposition mass, and then the exchange between the upper and second layer is calculated.

2.3. Essential Effects for Braided Pattern Modelling

Studies found that essential effects are necessary for braided river models to generate typical braided patterns with phenomena and processes similar to natural rivers. The effect of secondary flow is considered in several ways (Table 1): (1) included in shallow water equations with a function of spiral flow intensity [3,38], (2) included in the sediment transport rate equation by a curvature component [29,58], or (3) combined in the calculation of dispersion stresses [65]. Secondary flow plays an important role in sediment transport and bank retraction, which has been evaluated by Yang et al. [6]. Without secondary flow, a braided river still forms, while it generates fewer but wider channels with a slower development rate.
The effect of bank erosion in braided river models is often considered by simplified rule-based parameterizations of the bank erosion process. Normally, it is either calculated based on the repose slope where bank erosion is parameterized on the excess slope with respect to a critical value [29,66], or based on the product of transport capacity at the toe and transverse bank slope [3]. For braided river models, it still lacks a detailed description and validation of accurate prediction. Models can accurately reproduce observed morphological changes if bank erosion is correctly predicted [67].
Non-uniform sediment transport is essential in influencing the coarsening and fining processes in local units, i.e., the transport of each fraction is calculated separately incorporating the “hiding” effect between large and small particles, and then the active bed layer is updated with new composition and elevation [68]. Nicholas proposed that the inclusion of at least two sediment size fractions is one essential factor for providing the transformation from single-thread to multi-thread channels [3]. Previous studies have shown the important role of non-uniform sediments, but few works have considered it. This could be investigated in future work, especially for Delft3D that contains a sediment division module [6,8,57,66].
Several models have considered the effect of channel bed slope and sediment gravity on sediment transport, usually coupled in the sediment transport rate (Table 1). When the channel slope is gentle, the effect of gravity on sediment transport is usually ignored; when the riverbed slope is steep, gravity may change the sediment transport capacity and significantly influence bed deformation [69]. The driven effect of gravity in sediment sorting and segregation in flows has been analyzed using the most recent theories of granular fluid mechanics [70].

2.4. Typical Physics-Based Models

A few physics-based models have been developed and produced essential phenomena and processes of natural braided rivers, including (1) Delft 3D [5,10,71] and depth-integrated Delft 3D [4,49], (2) HSTAR [3,72], (3) FaSTMECH [55] and (4) other 2D morphodynamic models [6,8,18], as summarized in Figure 2. The first five cases focus on idealized or conceptual braided rivers (Figure 2a–e), whereas the last four demonstrate simulations of natural rivers based on exact boundary conditions (Figure 2f–i). These models successfully predicted the typical processes and characteristics in natural braided rivers, such as the classical braided pattern, channel bifurcation and closure and bar migration, and showed their ability in promoting our understanding of the complicated morphodynamic processes in natural braided rivers [18].
In the past decade, models have often been applied to simulate idealized scenarios, to determine their capability to reproduce morphology and dynamics characteristics of braided rivers and to determine model sensitivity to generally used equations for flow and sediment transport (Figure 2a–e). Recently, researchers have started to apply those models to investigate braiding activities under a changing environment based on the initial boundary conditions of natural rivers, and tried to give predictions and suggestions for engineering work [18] (Figure 2f–i). Advanced field measurement technologies and computational techniques will largely promote model application in morphodynamic process simulation and real scenario prediction in natural rivers.
For braided river simulation, Delft 3D is the most widely used physics-based model, and it is usually applied in 2D, yet sometimes in 3D. As shown in Table 1, this model integrates the equations of Meyer-Peter and Müller (1948), Engelund and Hansen (1967) and van Rijn (1984) [39,40,51]. Although Delft 3D includes non-uniform sediment transport, it is often applied considering uniform sediment particles. Schuurman determined the capability of Delft3D in producing the key characteristics of idealized braided sand-bed rivers, investigated the initiation and evolution of bars and bifurcations in braided networks and discussed their relationship to channel migration and the dynamic braided pattern [4] (Figure 2b). These authors recently applied the model to the upper braided reach of the Yellow River, and found the effects of annual peak discharges on the larger-scale channel pattern and on the smaller-scale bars [5] (Figure 2h). Delft3D has also been applied to assess the influence of spatial variations in channel width on bar evolution [50]. Javernick evaluated the ability of Delft3D in simulating the flow path of a braided reach of the Ahuriri River in New Zealand [48] (Figure 2g), and assessed its ability in predicting the bed load transport observed in braided river experiments [49]. Williams et al. (2016a) evaluated the ability of Delft3D in predicting the location and volume of sediment erosion and deposition in a braided reach of the Rees River, New Zealand during a flood, and suggested further improving the realism of bank erosion processes and testing the sensitivity of the model to the upstream sediment boundary condition [32]. Comparing the results of Delft3D with field observations, Singh et al. (2017) proposed the essential effects of sediment heterogeneity on the simulation of long-term morphological evolution in gravel-bed braided systems [74].
Other physics-based models are also applied to simulate braided river morphodynamics. Jang and Shimizu (2005) incorporated a moving boundary-fitted coordinate system to simulate a laboratory braided river, and produced similar bar and channel evolution processes [29]. Nicholas (2013) applied HSTAR to simulate very similar braided patterns with those of large sand-bed natural rivers, and identified the key elements for a model to simulate a wide range of river styles [3] (Figure 2a). Iwasaki et al. (2016) applied a 2D model to simulate the Otofuke River in Japan, and concluded that a cyclical process of meandering channel development with moderate sinuosity and a subsequent chute cutoff was a fundamental morphodynamic process in braided rivers [18] (Figure 2f). Yang et al. (2015; 2017; 2018; 2020) developed a 2D physics-based model that considered non-uniform sediments for both suspended and bed load transport, and produced morphologic processes and geomorphic features that compared well with those of real rivers [6,8,9,53] (Figure 2c,d). Davy et al. (2017) adopted a physics-based precipitant model that directly transferred water and matter between flow and bed, and reproduced both straight and braided patterns [75]. Olsen (2021) applied a sediment transport model SSIIM to simulate idealized alluvial channel and explain avulsion processes in large, braided rivers (Figure 2e). Sarker (2022a) studied the channel migrations in the upper Meghna River using MIKE 21C [11]. Stecca et al. (2022) devised a hydrograph-splitting technique to solve the morphological model GIAMT2D-veg, and reproduced the previous vegetation encroachment and morphological changes in an idealized reach of the lower Waitaki River [7] (Figure 2i).
The key technological advances of braided river models, that are essential in producing the braiding features and complicated braided processes, can be summarized as follows: (1) incorporation of the effect of secondary flow; (2) multiple-fractional method, representing coarsening and fining effects of graded sediments; (3) treatment of vegetation simulation that represents active channel conversion to floodplain by vegetation colonization [3]; (4) multiple-layer arrangement for vertical sorting process; (5) numerical solution scheme efficient in describing the trans-critical flow common in natural braided rivers, e.g., the TVD MacCormack scheme [9], hydrograph-splitting technique for model solution during floods [7], etc.

3. Challenges and Future Work

3.1. Model Assessment and Accuracy

Models are usually validated before they are applied in specific cases, to assess their representation for flow, sediment transport and bed deformation. The primary challenge in evaluating model performance is the availability of natural experiment datasets that quantify topographic change at a suitable frequency, and quantify bed load transport rates at model boundaries [15]. In an early stage, braided river models are often assessed based on field research and laboratory experiments in a qualitative way, sometimes with a few data from field measurements [29,76].
Braided river models are also validated by comparing their statistical characteristics with those of real rivers, focusing on channel planform features and morphologic properties, which can be described by braiding indices, sinuosity indices, total or average width, average confluence–confluence distance and so on [77]. Braided rivers also show scale-invariant properties that result from the same underlying mechanical processes inherent in all braided rivers [78], and can be described by methods of state-space plots, transect topographic properties and scaling. The calculation of these properties of simulated braided rivers could test the model representation ability in geomorphic and morphologic characteristics for natural rivers [4,6], but ignore their ability in simulation details, such as flow field and sediment transport rate.
Within the last decade, advanced measurement techniques, such as multi-spectral imaging, aerial and terrestrial LiDAR, terrestrial laser scanning (TLS) and terrestrial photogrammetry, have begun to be applied in field surveys and laboratory experiments [79]. These techniques enable the accurate measurement of channel geometry, flow field, sediment transport and bed elevation, providing abundant datasets with high spatial and temporal resolutions [19,20,21]. Recent studies have begun to focus on numerical model calibration and verification using these techniques. Williams et al. (2016a) identified the ability of Delft3D in simulating the bed level change by successfully predicting the total volume of erosion and deposition in the braided Rees River [32]. Dixon et al. (2017) validated HSTAR by comparing erosional and depositional shapes with those obtained in field observations [80]. Javernick et al. (2018) demonstrated that Delft3D could provide channel morphology comparable to that of the braided Ahuriri River using structure-from-motion photogrammetry [49].

3.2. Advantages and Challenges

Although existing models have produced braided rivers with many phenomena and properties similar to natural rivers, the development of numerical models of river morphodynamics is far from being a solved issue. Numerical models require intensive refinement and validation to enhance their prediction accuracy. The representation of flow and sediment transport remains to be improved, with empirical equations and parameters remaining to be tested and validated. Effects essential for bed morphodynamic evolution, e.g., numerical solution schemes, bank erosion, sediment gradation and vegetation, still need to be investigated to find more appropriate and accurate descriptions. In addition, there is a lack of quantitative discussion on essential processes in natural braided rivers, e.g., braiding mechanisms, morphologic changes, sediment fining and coarsening and responses to floods.
Even braided river models are based on physics; they have to be solved by simplification because Navier–Stokes equations that describe fluid flow cannot be solved analytically. Thus, one cannot be certain that a mismatch between model results and observations is not due to the simplifications and numerical techniques or the initial and boundary conditions used in the model [81]. Therefore, models are not very useful for simulating the details of a concrete existing case.
Bank erosion in braided river models remains a challenge, which is often considered by a simplification of the rule-based parameterizations of the bank erosion process. Depth-averaged 2D models for braided rivers cannot well-represent the near-bank flow due to the adoption of depth-averaged flow equations and to the need of relatively large grid-cells with shapes that often do not follow the bank line properly [14]. Bank erosion is essential for accurately predicting the frequent channel migrations and river geometry changes in natural braided rivers, so reliable bank erosion models still need to be embedded into existing 2D physics-based models, and their accuracy needs to be validated and enhanced.
Sediment gradation plays an essential role in the calculation of sand erosion and deposition, yet few simulation works consider the size sorting of sediments. Singh et al. (2017) demonstrated that Delft3D considering uniform sediment transport produced an unrealistic bed topography in the long-term response of natural gravel-bed braided rivers [74]. The inclusion of at least two sediment size fractions is proposed as one essential factor for providing a continuous transition of the river channel pattern [3]. The “hiding” effect of small particles by large particles is widely acknowledged, yet its influence on the evolution of the braided river pattern is far from fully discussed.
In the past decade, many of the new remote-sensed platforms have allowed accurate spatial data to be collected cheaply and efficiently, and the use of remote sensing in investigating river environments has experienced a significant increase [79]. However, many studies are still restricted to confirm the accuracy of remotely sensed data, other than generate new insights and ideas on fluvial form and function. Satellite images from Google Earth have been used to study the in-channel avulsion activities in large sand-bed braided rivers [8,9]. The adequate use of these data will largely promote new insights into braided river morphodynamics and the advance of numerical models.

3.3. Future Work

Under the great advances of braided river models, the variables essential for braiding dynamics that were once hidden in empirical coefficients, regarding flow and sedimentation, bank erosion, bar dynamics and vegetation, can be addressed in future work by refining the existing models. Consequently, braided river models can increasingly consider effects that are essential for braiding processes and river pattern evolution in natural braided rivers and enhance the efficiency of modelling work.
Since sediment transport equations in braided river models contain empirical elements and play quite differently in distinct rivers [14], it is meaningful to evaluate their performance by comparing them in individual natural braided rivers. Scenarios with models adopting different sediment transport equations could help to test and find their suitable conditions and might provide ways to enhance the model simulation ability.
Benefiting from the recent advances in measurement techniques—remote sensing, LiDAR, TLS and UVA—it is easy to obtain abundant data of high quality in natural braided rivers, including accurate DEM data and real-time monitoring data of flow and sediment. Consequently, case studies of natural rivers can be conducted with numerical models, and the following questions can be put forward: (1) How does a natural braided reach evolve in response to changes in the discharge, sediment load fluctuation, manmade projects and further global climate change? (2) What are the necessary conditions for transitions in river patterns to occur in response to these changes?
Braided rivers can be divided into types with high and low braiding intensity. The influence of flow discharge on braiding intensity was investigated with laboratory experiments [73,77]. However, the planform geometry of natural braided rivers has rarely been investigated. Remote-sensing images of increasing resolution can be obtained from satellites, e.g., historical images from Google Earth, or terrestrial images by UVAs. They provide opportunities for further understanding of the braiding characteristics in natural braided rivers.
In addition, despite the excellent ability of braided river models in comparing scenarios with different boundary conditions, they are far from widely used in river management [5]. These models have great potential in promoting the understanding necessary for creating more diverse and reliable management schemes in large braided rivers, and can provide useful predictions and suggestions for managing complex river engineering problems, such as flood control facilities and the reconstruction of riparian ecosystems [17].

4. Conclusions

Numerical models are very useful tools for exploring complicated physics laws and managing the complex engineering problems in natural braided rivers. Despite the great progress made in the last decade, these models still require intensive refinement and validation, and consequent application in natural braided reaches with boundary details. Extensive studies should be conducted to find more efficient numerical solution schemes and suitable application conditions for various sediment transport equations that contain many empirical elements. The effects essential for braided pattern evolution, e.g., bank erosion, non-uniform sediment and vegetation, can be tested and evaluated to identify the key ingredients necessary for efficient and accurate computations. The advanced field measurement techniques can easily provide abundant high-quality data. These data enable simulation research with accurate DEM data and fully detailed boundaries, and will largely promote the development of numerical models and enrich the morphodynamic theories of braided rivers.

Author Contributions

Conceptualization, H.Y.; resources, Y.H.; data curation, Y.H.; writing—original draft preparation, H.Y.; writing—review and editing, Y.H.; visualization, Q.L.; supervision, H.Z.; funding acquisition, H.Y. and H.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (grant number 42271011), the Guangzhou Municipal Science and Technology Bureau (grant number 202201010753) and the Guangdong Science and Technology Department (grant number 2020A1515010914).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are openly available in Google Earth.

Acknowledgments

We thank Binliang Lin from Tsinghua University for his kind suggestions on the current research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ashmore, P.E. Morphology and dynamics of braided rivers. In Treatise on Geomorphology; Shroder, J., Wohl, E., Eds.; Academic Press: San Diego, CA, USA, 2013; Volume 9, pp. 289–312. [Google Scholar]
  2. Surian, N. Fluvial processes in braided rivers. In Rivers–Physical, Fluvial and Environmental Processes; Rowiński, P., Radecki-Pawlik, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 403–425. [Google Scholar]
  3. Nicholas, A.P. Modelling the continuum of river channel patterns. Earth Surf. Process. Landf. 2013, 38, 1187–1196. [Google Scholar] [CrossRef]
  4. Schuurman, F.; Marra, W.A.; Kleinhans, M.G. Physics-based modeling of large braided sand-bed rivers: Bar pattern formation, dynamics, and sensitivity. J. Geophys. Res.-Earth Surf. 2013, 118, 2509–2527. [Google Scholar] [CrossRef]
  5. Schuurman, F.; Ta, W.Q.; Post, S.; Sokolewicz, M.; Busnelli, M.; Kleinhans, M. Response of braiding channel morphodynamics to peak discharge changes in the Upper Yellow River. Earth Surf. Process. Landf. 2018, 43, 1648–1662. [Google Scholar] [CrossRef]
  6. Yang, H.Y.; Lin, B.L.; Zhou, J.J. Physics-based numerical modelling of large braided rivers dominated by suspended sediment. Hydrol. Process. 2015, 29, 1925–1941. [Google Scholar] [CrossRef]
  7. Stecca, G.; Fedrizzi, D.; Measures, R.; Hicks, D.M.; Hoyle, J.; Zolezzi, G. Development of a numerical model for braided river morphology and vegetation evolution with application to the Lower Waitaki River (Aotearoa—New Zealand). Adv. Water Resour. 2022, 166, 104236. [Google Scholar] [CrossRef]
  8. Yang, H.Y. Numerical investigation of avulsions in gravel-bed braided rivers. Hydrol. Process. 2020, 34, 3702–3717. [Google Scholar] [CrossRef]
  9. Yang, H.Y.; Lin, B.L.; Zhou, J.J. Avulsions in a Simulated Large Lowland Braided River. Water Resour. Manag. 2018, 32, 2301–2314. [Google Scholar] [CrossRef]
  10. Schuurman, F.; Kleinhans, M.G. Bar dynamics and bifurcation evolution in a modelled braided sand-bed river. Earth Surf. Process. Landf. 2015, 40, 1318–1333. [Google Scholar] [CrossRef]
  11. Sarker, S. Essence of MIKE 21C (FDM Numerical Scheme): Application on the River Morphology of Bangladesh. Open J. Model. Simul. 2022, 10, 88–117. [Google Scholar] [CrossRef]
  12. Kleinhans, M.G. Sorting out river channel patterns. Prog. Phys. Geogr. -Earth Environ. 2010, 34, 287–326. [Google Scholar] [CrossRef]
  13. Lotsari, E.; Thorndycraft, V.; Alho, P. Prospects and challenges of simulating river channel response to future climate change. Prog. Phys. Geogr.-Earth Environ. 2015, 39, 483–513. [Google Scholar] [CrossRef]
  14. Siviglia, A.; Crosato, A. Numerical modelling of river morphodynamics: Latest developments and remaining challenges. Adv. Water Resour. 2016, 93, 1–3. [Google Scholar] [CrossRef]
  15. Williams, R.D.; Brasington, J.; Hicks, D.M. Numerical modelling of braided river morphodynamics: Review and future challenges. Geogr. Compass. 2016, 10, 102–127. [Google Scholar] [CrossRef]
  16. Olsen, N.R.B. 3D numerical modelling of braided channel formation. Geomorphology 2021, 375, 107528. [Google Scholar] [CrossRef]
  17. Busnelli, M.; Schuurman, F. Hydro-morphological management to improve navigation and ecological functions on the ‘Canal del Dique’Colombia. In River Flow 2020; CRC Press: London, UK, 2020; pp. 2135–2143. [Google Scholar]
  18. Iwasaki, T.; Shimizu, Y.; Kimura, I. Numerical simulation of bar and bank erosion in a vegetated floodplain: A case study in the Otofuke River. Adv. Water Resour. 2016, 93, 118–134. [Google Scholar] [CrossRef]
  19. Brasington, J.; Vericat, D.; Rychkov, I. Modeling river bed morphology, roughness, and surface sedimentology using high resolution terrestrial laser scanning. Water Resour. Res. 2012, 48, W11519. [Google Scholar] [CrossRef]
  20. Javernick, L.; Brasington, J.; Caruso, B. Modeling the topography of shallow braided rivers using Structure-from-Motion photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
  21. Kasprak, A.; Wheaton, J.M.; Ashmore, P.E.; Hensleigh, J.W.; Peirce, S. The relationship between particle travel distance and channel morphology: Results from physical models of braided rivers. J. Geophys. Res.-Earth Surf. 2015, 120, 55–74. [Google Scholar] [CrossRef]
  22. Kidová, A.; Lehotský, M.; Rusnák, M. Geomorphic diversity in the braided-wandering Belá River, Slovak Carpathians, as a response to flood variability and environmental changes. Geomorphology 2016, 272, 137–149. [Google Scholar] [CrossRef]
  23. Lallias-Tacon, S.; Liebault, F.; Piegay, H. Use of airborne LiDAR and historical aerial photos for characterising the history of braided river floodplain morphology and vegetation responses. Catena 2017, 149, 742–759. [Google Scholar] [CrossRef]
  24. Connor-Streich, G.; Henshaw, A.J.; Brasington, J.; Bertoldi, W.; Harvey, G.L. Let’s get connected: A new graph theory-based approach and toolbox for understanding braided river morphodynamics. Wiley Interdiscip. Rev. Water 2018, 5, e1296. [Google Scholar] [CrossRef]
  25. Middleton, L.; Ashmore, P.; Leduc, P.; Sjogren, D. Rates of planimetric change in a proglacial gravel-bed braided river: Field measurement and physical modelling. Earth Surf. Process. Landf. 2019, 44, 752–765. [Google Scholar] [CrossRef]
  26. Acharya, B.S.; Bhandari, M.; Bandini, F.; Pizarro, A.; Perks, M.; Joshi, D.R.; Wang, S.; Dogwiler, T.; Ray, R.L.; Kharel, G.; et al. Unmanned Aerial Vehicles in Hydrology and Water Management: Applications, Challenges, and Perspectives. Water Resour. Res. 2021, 57, e2021WR029925. [Google Scholar] [CrossRef]
  27. Guo, W.; Dong, C.M.; Lin, C.Y.; Zhang, T.; Zhao, Z.X.; Li, J. 3D Sedimentary Architecture of Sandy Braided River, Based on Outcrop, Unmanned Aerial Vehicle and Ground Penetrating Radar Data. Minerals 2022, 12, 739. [Google Scholar] [CrossRef]
  28. Murray, A.B.; Paola, C. A cellular model of braided rivers. Nature 1994, 371, 54–57. [Google Scholar] [CrossRef]
  29. Jang, C.L.; Shimizu, Y. Numerical simulation of relatively wide, shallow channels with erodible banks. J. Hydraul. Eng. 2005, 131, 565–575. [Google Scholar] [CrossRef]
  30. Coulthard, T.J.; Hicks, D.M.; Van De Wiel, M.J. Cellular modelling of river catchments and reaches: Advantages, limitations and prospects. Geomorphology 2007, 90, 192–207. [Google Scholar] [CrossRef]
  31. Doeschl, A.B.; Ashmore, P.E.; Davison, M. Methods for assessing exploratory computational models of braided rivers. In Braided Rivers: Process, Deposits, Ecology and Management; Sambrook-Smith, G.H., Best, J.L., Bristow, C.S., Petts, G.E., Jarvis, I., Eds.; Special publication number 36 of the International Association of Sedimentologists (IAS); Blackwell Publishing: Oxford, UK, 2006; pp. 177–197. [Google Scholar]
  32. Williams, R.D.; Measures, R.; Hicks, D.M.; Brasington, J. Assessment of a numerical model to reproduce event-scale erosion and deposition distributions in a braided river. Water Resour. Res. 2016, 52, 6621–6642. [Google Scholar] [CrossRef]
  33. Crosato, A.; Desta, F.B.; Cornelisse, J.; Schuurman, F.; Uijttewaal, W.S.J. Experimental and numerical findings on the long-term evolution of migrating alternate bars in alluvial channels. Water Resour. Res. 2012, 48, 1–14. [Google Scholar] [CrossRef]
  34. Webb, E.K. Simulation of braided channel topology and topography. Water Resour. Res. 1995, 31, 2603–2611. [Google Scholar] [CrossRef]
  35. Nelson, J.M.; Bennett, J.P.; Wiele, S.M. Flow and sediment-transport modeling. In Tools in Fluvial Geomorphology; Kondolf, G.M., Piégay, H., Eds.; Wiley: Chichester, UK, 2005; pp. 539–576. [Google Scholar]
  36. Spasojevic, M.; Holly, F.M. Two-and three-dimensional numerical simulation of mobile-bed hydrodynamics and sedimentation. In Sedimentation Engineering: Processes, Measurements, Modeling, and Practice; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 683–761. [Google Scholar]
  37. Bürgler, M.; Vetsch, D.F.; Boes, R.; Vanzo, D. Systematic comparison of 1D and 2D hydrodynamic models for the assessment of hydropeaking alterations. River Res. Appl. 2022, 1–18. [Google Scholar] [CrossRef]
  38. Schuurman, F.; Kleinhans, M.G. Self-formed braid bars in a numerical model. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 5–9 December 2011; p. 0672. [Google Scholar]
  39. Engelund, F.; Hansen, E. A Monograph on Sediment Transport in Alluvial Channels; Teknik Forlag: Copenhagen, Denmark, 1967. [Google Scholar]
  40. Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, Stockholm, Sweden, 7 June 1948; pp. 39–64. [Google Scholar]
  41. Harten, A.; Lax, P.D.; Leer, B.v. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. J. Siam Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
  42. Ikeda, S.; Parker, G.; Sawai, K. Bend theory of river meanders, part 1: Linear development. J. Fluid Mech. 1981, 112, 363–377. [Google Scholar] [CrossRef]
  43. Ashida, K.; Michiue, M. Study on hydraulic resistance and bed-load transport rate in alluvial streams. In Proceedings of the Japan Society of Civil Engineers, Tokyo, Japan, 10 October 1972; pp. 59–69. [Google Scholar]
  44. van Rijn, L.C. Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas; Aqua publications: Amsterdam, The Netherlands, 1993. [Google Scholar]
  45. Engelund, F. Flow and bed topography in channel bends. J. Hydraul. Div. 1974, 100, 1631–1648. [Google Scholar] [CrossRef]
  46. Sarker, S. A short review on computational hydraulics in the context of water resources engineering. Open J. Model. Simul. 2022, 10, 1–31. [Google Scholar] [CrossRef]
  47. Bagnold, R.A. An approach to the sediment transport problem from general physics. US Geol. Surv. Prof. Pap. 1966, 422-I, 231–291. [Google Scholar]
  48. Javernick, L.; Hicks, D.M.; Measures, R.; Caruso, B.; Brasington, J. Numerical Modelling of Braided Rivers with Structure-from-Motion-Derived Terrain Models. River Res. Appl. 2016, 32, 1071–1081. [Google Scholar] [CrossRef]
  49. Javernick, L.; Redolfi, M.; Bertoldi, W. Evaluation of a numerical model’s ability to predict bed load transport observed in braided river experiments. Adv. Water Resour. 2018, 115, 207–218. [Google Scholar] [CrossRef]
  50. Duró, G.; Crosato, A.; Tassi, P. Numerical study on river bar response to spatial variations of channel width. Adv. Water Resour. 2016, 93, 21–38. [Google Scholar] [CrossRef]
  51. van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
  52. Zhou, J.; Lin, B. Flow and Sediment Modelling; China Hydropower Press: Beijing, China, 2006; pp. 173–278. (In Chinese) [Google Scholar]
  53. Yang, H.Y.; Lin, B.L.; Sun, J.; Huang, G.X. Simulating Laboratory Braided Rivers with Bed-Load Sediment Transport. Water 2017, 9, 686. [Google Scholar] [CrossRef] [Green Version]
  54. Parker, G. Surface-based bedload transport relation for gravel rivers. J. Hydraul. Res. 1990, 28, 417–436. [Google Scholar] [CrossRef]
  55. Harrison, L.R.; Dunne, T.; Fisher, G.B. Hydraulic and geomorphic processes in an overbank flood along a meandering, gravel-bed river: Implications for chute formation. Earth Surf. Process. Landf. 2015, 40, 1239–1253. [Google Scholar] [CrossRef]
  56. Williams, R.D.; Brasington, J.; Hicks, M.; Rennie, C.D.; Vericat, D. Hydraulic validation of two-dimensional simulations of braided river flow with spatially continuous a Dcp data. Water Resour. Res. 2013, 49, 5183–5205. [Google Scholar] [CrossRef]
  57. Wang, H.; Zhou, G.; Shao, X.J. Numerical simulation of channel pattern changes Part II: Application in a conceptual channel. Int. J. Sediment Res. 2010, 25, 380–390. [Google Scholar] [CrossRef]
  58. Takebayashi, H.; Okabe, T. Numerical modelling of braided streams in unsteady flow. Proc. Inst. Civ. Eng.-Water Manag. 2009, 162, 189–198. [Google Scholar] [CrossRef]
  59. Wang, J.; Ni, H.; He, Y. Finite-difference TVD scheme for computation of dam-break problems. J. Hydraul. Eng. 2000, 126, 253–262. [Google Scholar] [CrossRef]
  60. Ming, H.T.; Chu, C.R. Two-dimensional shallow water flows simulation using TVD-MacCormack scheme. J. Hydraul. Res. 2000, 38, 123–131. [Google Scholar] [CrossRef]
  61. Liang, D.F.; Lin, B.L.; Falconer, R.A. Simulation of rapidly varying flow using an efficient TVD-MacCormack scheme. Int. J. Numer. Methods Fluids. 2007, 53, 811–826. [Google Scholar] [CrossRef]
  62. Morianou, G.G.; Kourgialas, N.N.; Karatzas, G.P.; Nikolaidis, N.P. River flow and sediment transport simulation based on a curvilinear and rectilinear grid modelling approach—A comparison study. J. Water Sci. Technol. Water Supply 2017, 17, 1325–1334. [Google Scholar] [CrossRef]
  63. Morianou, G.G.; Kourgialas, N.N.; Karatzas, G.P.; Nikolaidis, N.P. Assessing hydro-morphological changes in Mediterranean stream using curvilinear grid modeling approach—Climate change impacts. Earth Sci. Inform. 2018, 11, 205–216. [Google Scholar] [CrossRef]
  64. Wu, W. Computational River Dynamics; Taylor & Francis Group: London, UK, 2007; p. 499. [Google Scholar]
  65. Lien, H.; Hsieh, T.; Yang, J.; Yeh, K. Bend-flow simulation using 2D depth-averaged model. J. Hydraul. Eng. 1999, 125, 1097–1108. [Google Scholar] [CrossRef]
  66. Sun, J.; Lin, B.L.; Kuang, H.W. Numerical modelling of channel migration with application to laboratory rivers. Int. J. Sediment Res. 2015, 30, 13–27. [Google Scholar] [CrossRef]
  67. Stecca, G.; Measures, R.; Hicks, D.M. A framework for the analysis of noncohesive bank erosion algorithms in morphodynamic modeling. Water Resour. Res. 2017, 53, 6663–6686. [Google Scholar] [CrossRef]
  68. Mosselman, E. Modelling sediment transport and morphodynamics of gravel-bed rivers. In Gravel-Bed Rivers: Processes, Tools, Environments; Church, M., Biron, P.M., Roy, A.G., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 101–115. [Google Scholar]
  69. Guan, M.F.; Wright, N.G.; Sleigh, P.A. 2D Process-Based Morphodynamic Model for Flooding by Noncohesive Dyke Breach. J. Hydraul. Eng. 2014, 140, 04014022. [Google Scholar] [CrossRef]
  70. Armanini, A. Granular flows driven by gravity. J. Hydraul. Res. 2013, 51, 111–120. [Google Scholar] [CrossRef]
  71. Paudel, S.; Singh, U.; Crosato, A.; Franca, M.J. Effects of initial and boundary conditions on gravel-bed river morphology. Adv. Water Resour. 2022, 166, 104256. [Google Scholar] [CrossRef]
  72. Sambrook Smith, G.H.; Nicholas, A.P.; Best, J.L.; Bull, J.M.; Dixon, S.J.; Goodbred, S.; Sarker, M.H.; Vardy, M.E.; Bristow, C. The sedimentology of river confluences. Sedimentology 2019, 66, 391–407. [Google Scholar] [CrossRef]
  73. Egozi, R.; Ashmore, P. Experimental Analysis of Braided Channel Pattern Response to Increased Discharge. J. Geophys. Res.-Earth Surf. 2009, 114, F02012-1–F02012-15. [Google Scholar] [CrossRef]
  74. Singh, U.; Crosato, A.; Giri, S.; Hicks, M. Sediment Heterogeneity and Mobility in the Morphodynamic Modelling of Gravel-Bed Braided Rivers. Adv. Water Resour. 2017, 104, 127–144. [Google Scholar] [CrossRef]
  75. Davy, P.; Croissant, T.; Lague, D. A precipiton method to calculate river hydrodynamics, with applications to flood prediction, landscape evolution models, and braiding instabilities. J. Geophys. Res.-Earth Surf. 2017, 122, 1491–1512. [Google Scholar] [CrossRef] [Green Version]
  76. Wu, W.; Altinakar, M.; Wang, S. Depth-average analysis of hysteresis between flow and sediment transport under unsteady conditions. Int. J. Sediment Res. 2006, 21, 101. [Google Scholar]
  77. Egozi, R.; Ashmore, P. Defining and measuring braiding intensity. Earth Surf. Process. Landf. 2008, 33, 2121–2138. [Google Scholar] [CrossRef]
  78. Sapozhnikov, V.B.; Foufoula-Georgiou, E. Self-affinity in braided rivers. Water Resour. Res. 1996, 32, 1429–1439. [Google Scholar] [CrossRef]
  79. Entwistle, N.; Heritage, G.; Milan, D. Recent remote sensing applications for hydro and morphodynamic monitoring and modelling. Earth Surf. Process. Landf. 2018, 43, 2283–2291. [Google Scholar] [CrossRef]
  80. Dixon, S.; Nicholas, A.; Sambrook Smith, G. Morphodynamic model validation for tropical river junctions. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 12–17 April 2015. [Google Scholar]
  81. Oreskes, N.; Shrader-Frechette, K.; Belitz, K. Verification, validation, and confirmation of numerical models in the Earth sciences. Science 1994, 263, 641–646. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Water 15 00595 g001 550
Figure 1. Examples of typical braided reaches in nature (from Google Earth): (a) Sunwapta River, Canada; (b) Waimakariri River, New Zealand; (c) Ahuriri River, New Zealand; (d) Tagliamento River, Italy; (e) Tuotuo River, China; (f) middle reach of the Yellow River, China; and (g) Brahamputra River, Bangladesh.
Figure 1. Examples of typical braided reaches in nature (from Google Earth): (a) Sunwapta River, Canada; (b) Waimakariri River, New Zealand; (c) Ahuriri River, New Zealand; (d) Tagliamento River, Italy; (e) Tuotuo River, China; (f) middle reach of the Yellow River, China; and (g) Brahamputra River, Bangladesh.
Water 15 00595 g001
Water 15 00595 g002 550
Figure 2. Summary of typical simulated braided rivers with numerical models: (a) a conceptual simulation of the Waimakariri River, New Zealand [3]; (b) an idealized large sand-bed braided river, with data from the Brahamputra River, Bangladesh [10]; (c) an idealized large alluvial braided river, with data from the lower reach of the Yellow River, China [6]; (d) a laboratory river by Egozi and Ashmore [73]; (e) an idealized large braided river, with data from the physical model study [16]; (f) the Otofuke River, Japan [18]; (g) the Ahuriri River, New Zealand [48]; (h) the upper Yellow River, China [5]; and (i) the lower Waitaki River, New Zealand [7].
Figure 2. Summary of typical simulated braided rivers with numerical models: (a) a conceptual simulation of the Waimakariri River, New Zealand [3]; (b) an idealized large sand-bed braided river, with data from the Brahamputra River, Bangladesh [10]; (c) an idealized large alluvial braided river, with data from the lower reach of the Yellow River, China [6]; (d) a laboratory river by Egozi and Ashmore [73]; (e) an idealized large braided river, with data from the physical model study [16]; (f) the Otofuke River, Japan [18]; (g) the Ahuriri River, New Zealand [48]; (h) the upper Yellow River, China [5]; and (i) the lower Waitaki River, New Zealand [7].
Water 15 00595 g002
Table
Table 1. Summary of typical physics-based numerical models for braided river simulation.
Table 1. Summary of typical physics-based numerical models for braided river simulation.
ModelsSediment Transport Equations (qs)Numerical Solution
Techniques		Sediment CompositionBed Slope and
Gravity (to qs)		Secondary FlowResearchers
HSTAREngelund and Hansen (1967) [39]; Meyer-Peter and Müller (1948) [40]Godunov-type
finite volume scheme [41]		uniform (for sand)Ikeda (1981) [42]included in the Navier–Stokes equation[3]
Individual modelAshida and Michiue (1972) [43]finite difference schemeuniformincluded in qbn with equation of van Rijn (1993) [44]included in near bed flow velocity [45][18,46]
Delft 3DMeyer-Peter and Müller (1948) [40]alternating direction implicit (ADI scheme, cyclic method of Stelling and Leendertse)uniformBagnold (1966) [47]& Ikeda (1981) [42]included in qbn[48,49]
Meyer-Peter and Müller (1948) [40][50]
Engelund and Hansen (1967) [39]; Meyer-Peter and Mueller (1948) [40]; van Rijn (1984) [51][4,5,10]
Individual2D advection diffusion equation [52]; van Rijn (1993) [44]ADI scheme,
total variational diminishing (TVD) scheme		non-
uniform		included in qbn with formula of van Rijn (1993) [44]included in qbn [45][6,53]
FaSTMECHParker (1990) [54]ADI schemeuniformnoneincluded in a streamline-based vertical structure
submodel		[55]
SSIIMEngelund and Hansen (1967) [39]finite volume methoduniformincluded in qbn with formula of van Rijn (1993) [44]included in qbn[16]
GIAMT2D-vegMeyer-Peter and Müller (1948) [40]finite volume methoduniformnoneincluded in qbn[7]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Hu, Y.; Yang, H.; Zhou, H.; Lv, Q. A Review of Numerical Modelling of Morphodynamics in Braided Rivers: Mechanisms, Insights and Challenges. Water 2023, 15, 595. https://doi.org/10.3390/w15030595

AMA Style

Hu Y, Yang H, Zhou H, Lv Q. A Review of Numerical Modelling of Morphodynamics in Braided Rivers: Mechanisms, Insights and Challenges. Water. 2023; 15(3):595. https://doi.org/10.3390/w15030595

Chicago/Turabian Style

Hu, Youfei, Haiyan Yang, Haolan Zhou, and Qianwen Lv. 2023. "A Review of Numerical Modelling of Morphodynamics in Braided Rivers: Mechanisms, Insights and Challenges" Water 15, no. 3: 595. https://doi.org/10.3390/w15030595

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop