Threshold Recognition of Water Turbidity for Clogging Prevention during Groundwater Recharge Using Secondary Effluent from Wastewater Treatment Plant
Abstract
:1. Introduction
2. Materials and Methods
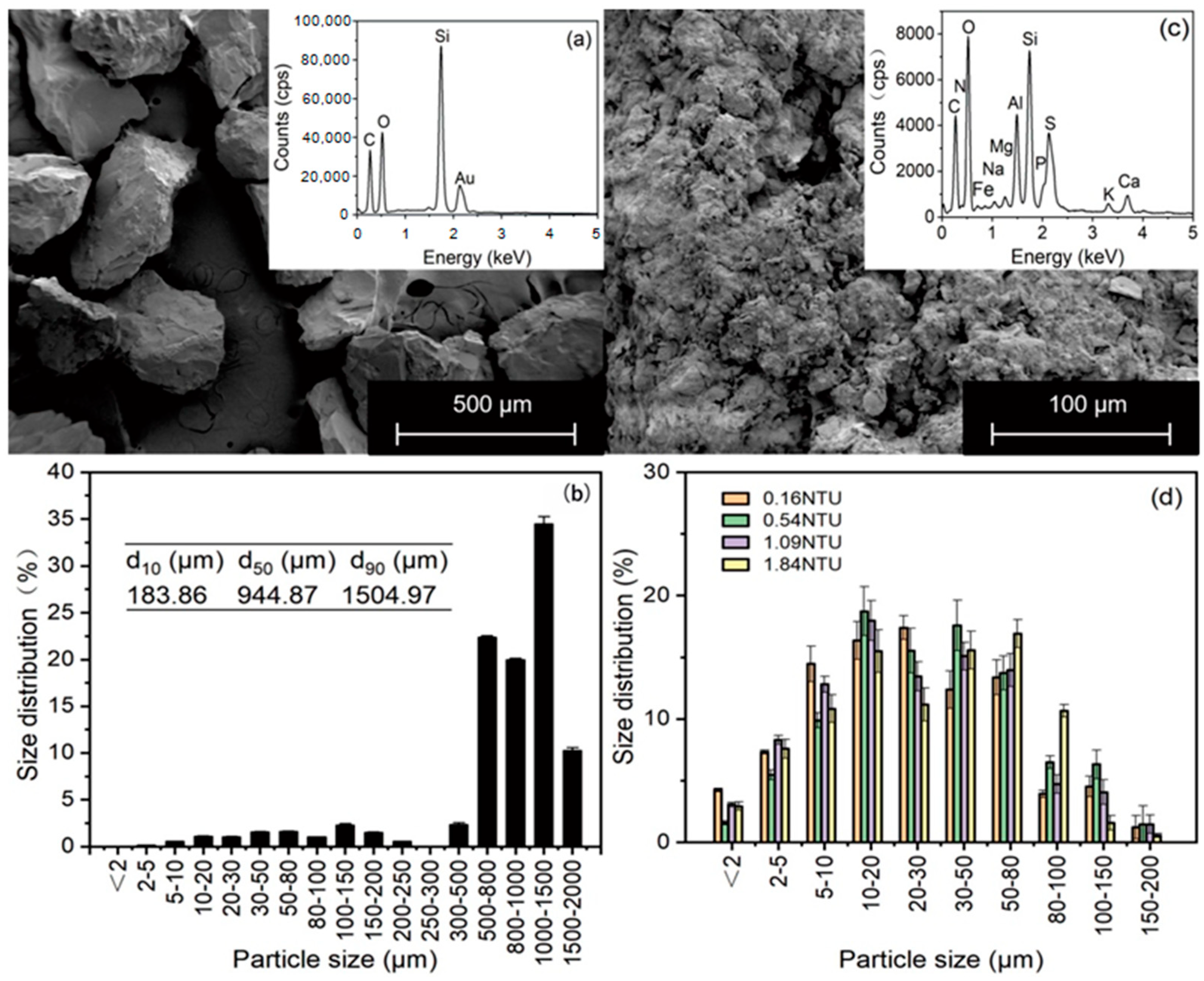
2.1. Porous Medium
2.2. Suspension
2.3. Column Experiments
2.4. Physical Clogging Model
- The porous medium should be homogeneous and saturated.
- Darcy’s law governs water migration.
- Dispersion effects are absent during the transport of suspended particles.
- No biochemical reaction occurs to change the characteristics of porous media or suspended particles.
2.5. Contact Efficiency and DLVO Theory
3. Results and Discussion
3.1. Breakthrough Curves and Particle Retention
3.2. Particle Transport and Deposition
3.2.1. Calculation of Contact Efficiency
3.2.2. Effect of Attachment Efficiency
3.3. Variations in Hydraulic Conductivity
3.4. Comparison of Simulation and Experimental Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, B.; Long, F.; Rao, D.; Xu, T. The effect of temperature on the seepage transport of suspended particles in a porous medium. Hydrol. Process. 2017, 31, 382–393. [Google Scholar] [CrossRef]
- Liu, S.; Persson, K.M. Situations of water reuse in China. Water Policy 2013, 15, 705–727. [Google Scholar] [CrossRef]
- Yuan, J.; Van Dyke, M.I.; Huck, P.M. Water reuse through managed aquifer recharge (MAR): Assessment of regulations/guidelines and case studies. Water Qual. Res. J. Can. 2016, 51, 357–376. [Google Scholar] [CrossRef]
- Sultana, S.; Ahmed, K.M. Assessing risk of clogging in community scale managed aquifer recharge sites for drinking water in the coastal plain of south-west Bangladesh. Bangladesh J. Sci. Res. 2016, 27, 75–86. [Google Scholar] [CrossRef]
- Ye, X.Y.; Cui, R.J.; Du, X.N.A.; Ma, S.J.; Zhao, J.T.; Lu, Y.; Wan, Y.Y. Mechanism of Suspended Kaolinite Particle Clogging in Porous Media During Managed Aquifer Recharge. Groundwater 2019, 57, 764–771. [Google Scholar] [CrossRef] [PubMed]
- Dillon, P.; Pavelic, P.; Massmann, G.; Barry, K.; Correll, R. Enhancement of the membrane filtration index (MR) method for determining the clogging potential of turbid urban stormwater and reclaimed water used for aquifer storage and recovery. Desalination 2001, 140, 153–165. [Google Scholar] [CrossRef]
- Dillon, P.J.; Hickinbotham, M.R.; Pavelic, P. Review of International Experience in Injecting Water into Aquifers for Storage and Reuse. In Water Down under 94: Groundwater Papers; Institution of Engineers: Barton, Australia, 1994. [Google Scholar]
- Rinck-Pfeiffer, S.; Ragusa, S.; Sztajnbok, P.; Vandevelde, T. Interrelationships between biological, chemical, and physical processes as an analog to clogging in aquifer storage and recovery (ASR) wells. Water Res. 2000, 34, 2110–2118. [Google Scholar] [CrossRef]
- Ahfir, N.-D.; Benamar, A.; Alem, A.; Wang, H. Influence of Internal Structure and Medium Length on Transport and Deposition of Suspended Particles: A Laboratory Study. Transp. Porous Media 2009, 76, 289–307. [Google Scholar] [CrossRef]
- Mesticou, Z.; Kacem, M.; Dubujet, P. Influence of Ionic Strength and Flow Rate on Silt Particle Deposition and Release in Saturated Porous Medium: Experiment and Modeling. Transp. Porous Media 2014, 103, 1–24. [Google Scholar] [CrossRef]
- Liu, Q.; Cui, X.; Zhang, C.; Zhan, T. Effects of particle size on characteristics of transportation and deposition of suspended particles in porous media. Chin. J. Geotech. Eng. 2014, 36, 1777–1783. [Google Scholar] [CrossRef]
- Alem, A.; Ahfir, N.D.; Elkawafi, A.; Wang, H.Q. Hydraulic Operating Conditions and Particle Concentration Effects on Physical Clogging of a Porous Medium. Transp. Porous Media 2015, 106, 303–321. [Google Scholar] [CrossRef]
- Du, X.; Song, Y.; Ye, X.; Luo, R. Colloid clogging of saturated porous media under varying ionic strength and roughness during managed aquifer recharge. J. Water Reuse Desalination 2019, 9, 225–231. [Google Scholar] [CrossRef]
- Porubcan, A.A.; Xu, S. Colloid straining within saturated heterogeneous porous media. Water Res. 2011, 45, 1796–1806. [Google Scholar] [CrossRef]
- Fan, W.; Yang, X.; Wang, Y.; Huo, M. Loopholes in the current reclaimed water quality standards for clogging control during aquifer storage and recovery in China. Water Cycle 2020, 1, 13–18. [Google Scholar] [CrossRef]
- US EPA. Guidelines for Water Reuse; US Environmental Protection Agency: Washington, DC, USA, 2004.
- Okubo, T.; Matsumoto, J. Biological clogging of sand and changes of organic constituents during artificial recharge. Water Res. 1983, 17, 813–821. [Google Scholar] [CrossRef]
- Pavelic, P.; Dillon, P.J.; Barry, K.E.; Vanderzalm, J.L.; Correll, R.L.; Rinck-Pfeiffer, S.M. Water quality effects on clogging rates during reclaimed water ASR in a carbonate aquifer. J. Hydrol. 2007, 334, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Huo, M.X.; Li, Q.; Fan, W.; Yang, J.K.; Cui, X.C. Comparison of clogging induced by organic and inorganic suspended particles in a porous medium: Implications for choosing physical clogging indicators. J. Soils Sediments 2018, 18, 2980–2994. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, X.Y.; Wheatley, A. Characterizing activated sludge process effluent by particle size distribution, respirometry and modelling. Desalination 2009, 249, 969–975. [Google Scholar] [CrossRef]
- Xu, S.P.; Gao, B.; Saiers, J.E. Straining of colloidal particles in saturated porous media. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Krauss, E.D.; Mays, D.C. Modification of the Kozeny-Carman Equation to Quantify Formation Damage by Fines in Clean, Unconsolidated Porous Media. SPE Reserv. Eval. Eng. 2014, 17, 466–472. [Google Scholar] [CrossRef] [Green Version]
- Lu, Y.; Du, X.Q.; Chi, B.M.; Yang, Y.S.; Fan, W. Numerical modelling of physical clogging during groundwater artificial recharge. In Proceedings of the 7th International Conference on Calibration and Reliability in Groundwater Modeling, Wuhan, China, 20–23 September 2009; pp. 121–126. [Google Scholar]
- Tufenkji, N.; Elimelech, M. Correlation equation for predicting single-collector efficiency in physicochemical filtration in saturated porous media. Environ. Sci. Technol. 2004, 38, 529–536. [Google Scholar] [CrossRef]
- Redman, J.A.; Walker, S.L.; Elimelech, M. Bacterial adhesion and transport in porous media: Role of the secondary energy minimum. Environ. Sci. Technol. 2004, 38, 1777–1785. [Google Scholar] [CrossRef]
- Mesticou, Z.; Kacem, M.; Dubujet, P. Coupling Effects of Flow Velocity and Ionic Strength on the Clogging of a Saturated Porous Medium. Transp. Porous Media 2016, 112, 265–282. [Google Scholar] [CrossRef]
- McGechan, M.B.; Lewis, D.R. Transport of particulate and colloid-sorbed contaminants through soil, part 1: General principles. Biosyst. Eng. 2002, 83, 255–273. [Google Scholar] [CrossRef]
- Herzig, J.P.; Leclerc, D.M.; Golf, P.L. Flow of suspensions through porous media—Application to deep filtration. Ind. Eng. Chem. 1970, 62, 8–35. [Google Scholar] [CrossRef]
- Huston, D.L.; Fox, J.F. Clogging of Fine Sediment within Gravel Substrates: Dimensional Analysis and Macroanalysis of Experiments in Hydraulic Flumes. J. Hydraul. Eng. 2015, 141, 04015015. [Google Scholar] [CrossRef]
- Fan, W.; Jiang, X.H.; Yang, W.; Geng, Z.; Huo, M.X.; Liu, Z.M.; Zhou, H. Transport of graphene oxide in saturated porous media: Effect of cation composition in mixed Na-Ca electrolyte systems. Sci. Total Environ. 2015, 511, 509–515. [Google Scholar] [CrossRef] [PubMed]
- Rahman, T.; George, J.; Shipley, H.J. Transport of aluminum oxide nanoparticles in saturated sand: Effects of ionic strength, flow rate, and nanoparticle concentration. Sci. Total Environ. 2013, 463, 565–571. [Google Scholar] [CrossRef]
- Bradford, S.A.; Yates, S.R.; Bettahar, M.; Simunek, J. Physical factors affecting the transport and fate of colloids in saturated porous media. Water Resour. Res. 2002, 38, 63-1-63-12. [Google Scholar] [CrossRef]
- Camprovin, P.; Hernandez, M.; Fernandez, S.; Martin-Alonso, J.; Galofre, B.; Mesa, J. Evaluation of Clogging during Sand-Filtered Surface Water Injection for Aquifer Storage and Recovery (ASR): Pilot Experiment in the Llobregat Delta (Barcelona, Spain). Water 2017, 9, 263. [Google Scholar] [CrossRef] [Green Version]

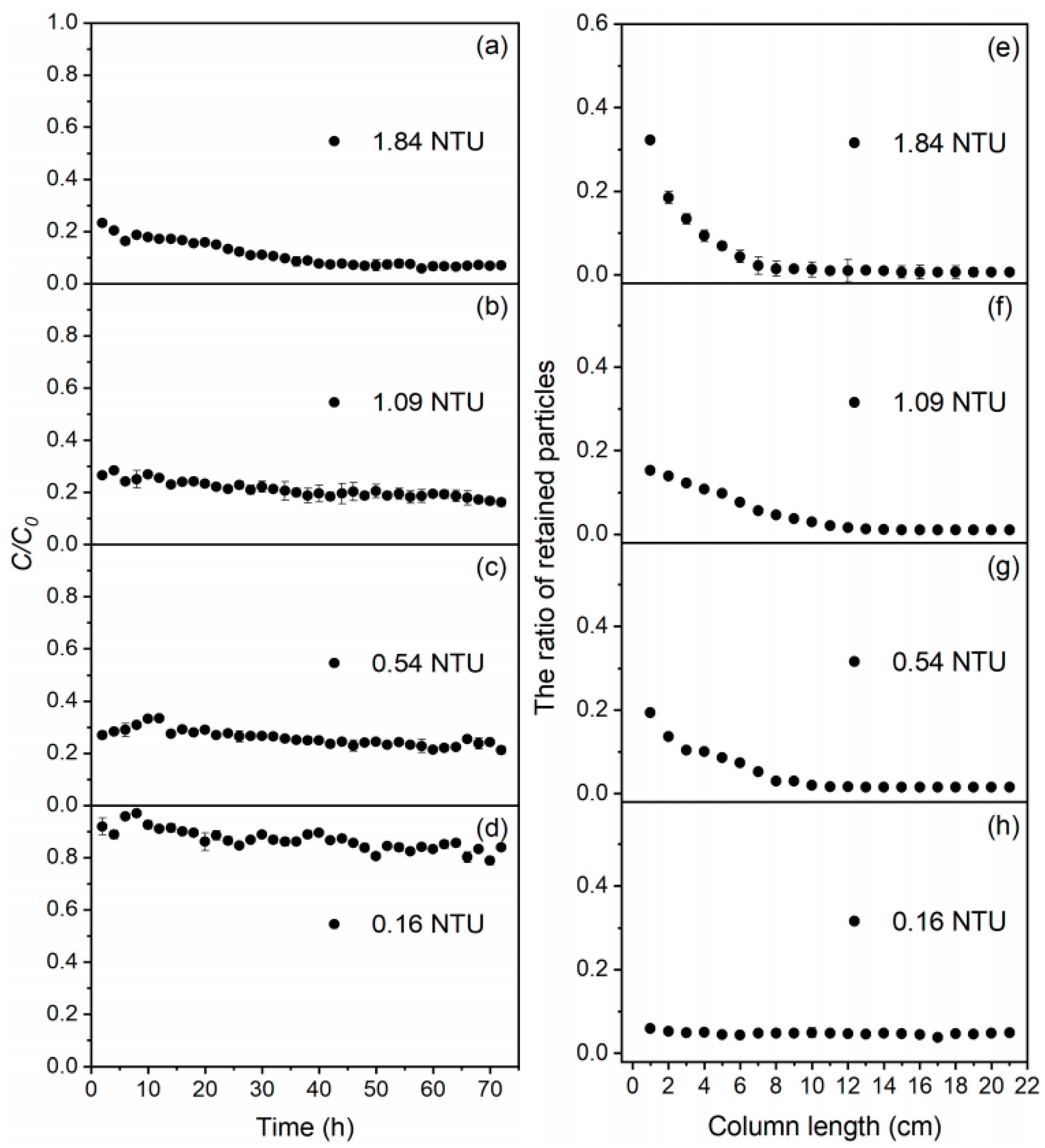


| Suspension | Mass Deposited in Each Section (%) | Md (%) | Meff (%) | Min (%) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||||
| 1.84 NTU | 55.0 | 20.9 | 4.96 | 3.17 | 1.67 | 85.7 | 11.1 | 96.8 |
| 1.09 NTU | 30.3 | 28.3 | 8.42 | 3.92 | 2.26 | 73.2 | 20.8 | 94.0 |
| 0.540 NTU | 33.8 | 30.5 | 9.79 | 7.65 | 4.53 | 86.3 | 21.3 | 108.0 |
| 0.160 NTU | 3.63 | 5.27 | 5.32 | 5.04 | 3.22 | 22.5 | 82.3 | 105.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wang, S.; Zou, S.; Wang, Y.; Fan, W.; Xiao, D. Threshold Recognition of Water Turbidity for Clogging Prevention during Groundwater Recharge Using Secondary Effluent from Wastewater Treatment Plant. Water 2023, 15, 594. https://doi.org/10.3390/w15030594
Li S, Wang S, Zou S, Wang Y, Fan W, Xiao D. Threshold Recognition of Water Turbidity for Clogging Prevention during Groundwater Recharge Using Secondary Effluent from Wastewater Treatment Plant. Water. 2023; 15(3):594. https://doi.org/10.3390/w15030594
Chicago/Turabian StyleLi, Shiwei, Siyue Wang, Shubin Zou, Yang Wang, Wei Fan, and Dan Xiao. 2023. "Threshold Recognition of Water Turbidity for Clogging Prevention during Groundwater Recharge Using Secondary Effluent from Wastewater Treatment Plant" Water 15, no. 3: 594. https://doi.org/10.3390/w15030594
APA StyleLi, S., Wang, S., Zou, S., Wang, Y., Fan, W., & Xiao, D. (2023). Threshold Recognition of Water Turbidity for Clogging Prevention during Groundwater Recharge Using Secondary Effluent from Wastewater Treatment Plant. Water, 15(3), 594. https://doi.org/10.3390/w15030594







