Research on Sustainable Scheduling of Cascade Reservoirs Based on Improved Crow Search Algorithm
Abstract
:1. Introduction
2. Multi-Objective Sustainable Scheduling Model of Cascade Reservoirs
2.1. Problem Description
2.2. Model Establishment
3. PSO-CSA Algorithm Design
3.1. Introduction to the Algorithm
- Multiple crow individuals form crow populations and live as populations.
- Each individual crow can remember where he or she hides their food.
- The crows in the crow population will find and steal each other’s food by tracking.
- When an individual crow being followed discovers that it is being followed, it takes steps to confuse the other party.
- Specifically, the specific process of the CSA algorithm is as follows:
3.2. Improvement Strategy
3.2.1. The Crow Flies at Variable Speed
3.2.2. Raven Spiral Update Location Strategy
3.2.3. Crow Memory Contraction Update Strategy
3.3. Improve the Specific Solution Steps of the Algorithm
4. Results and Discussion
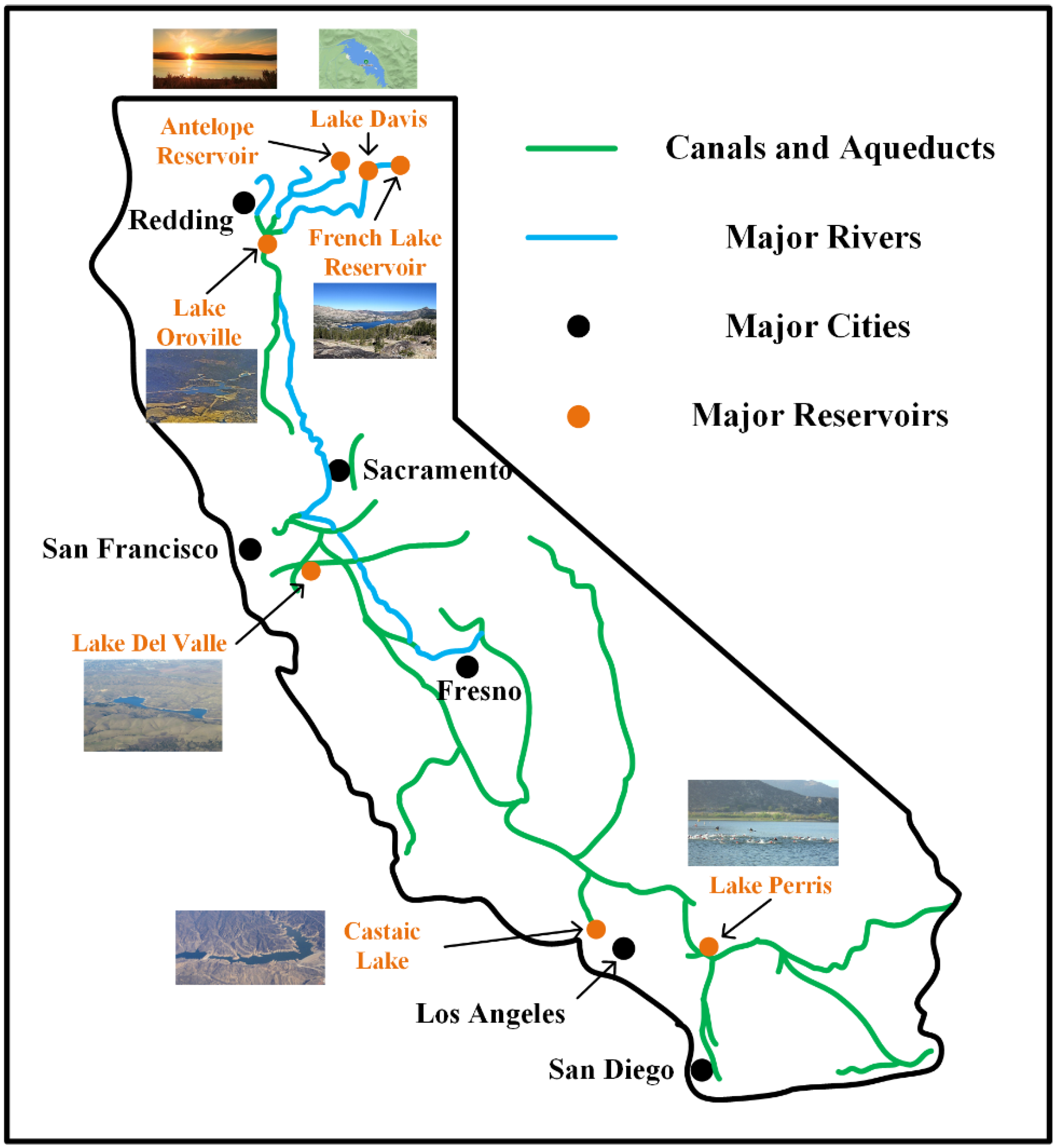
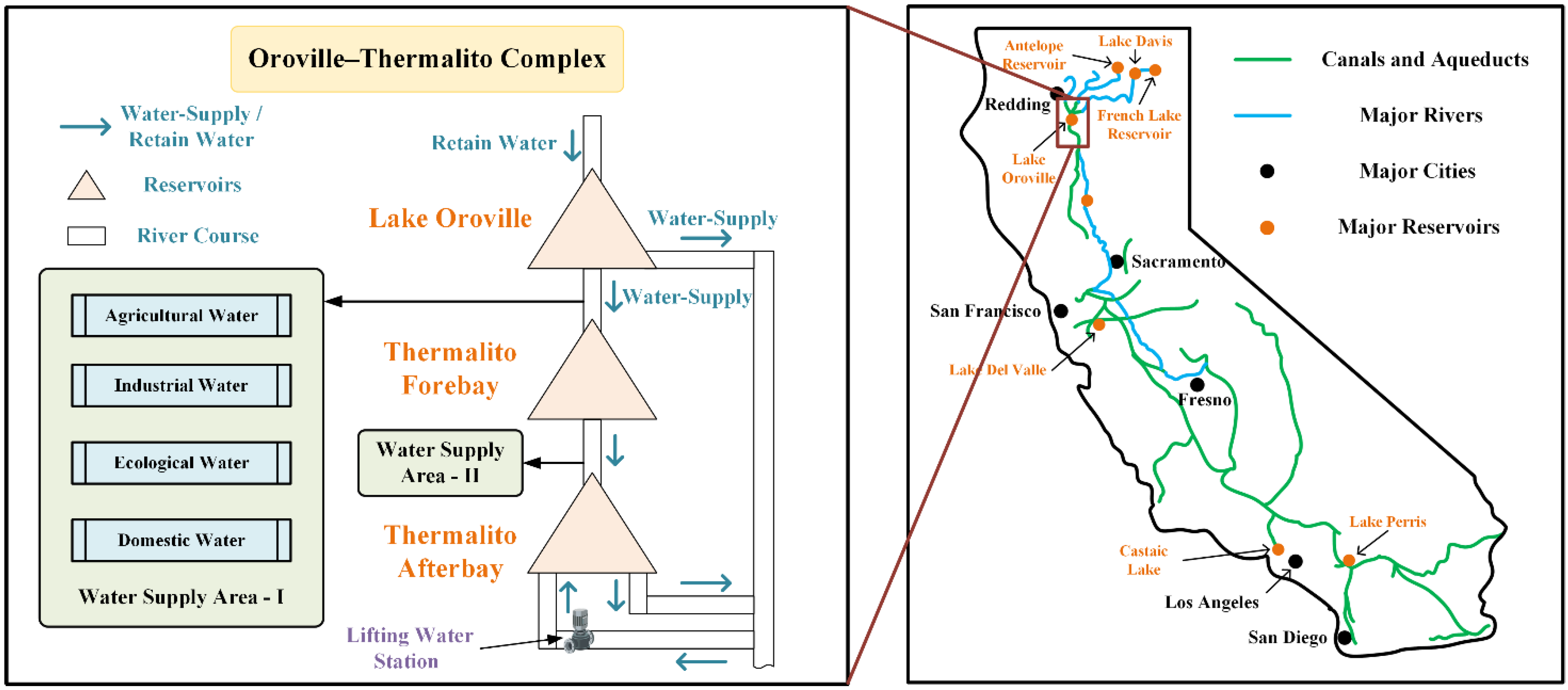
4.1. Overview of Engineering Background
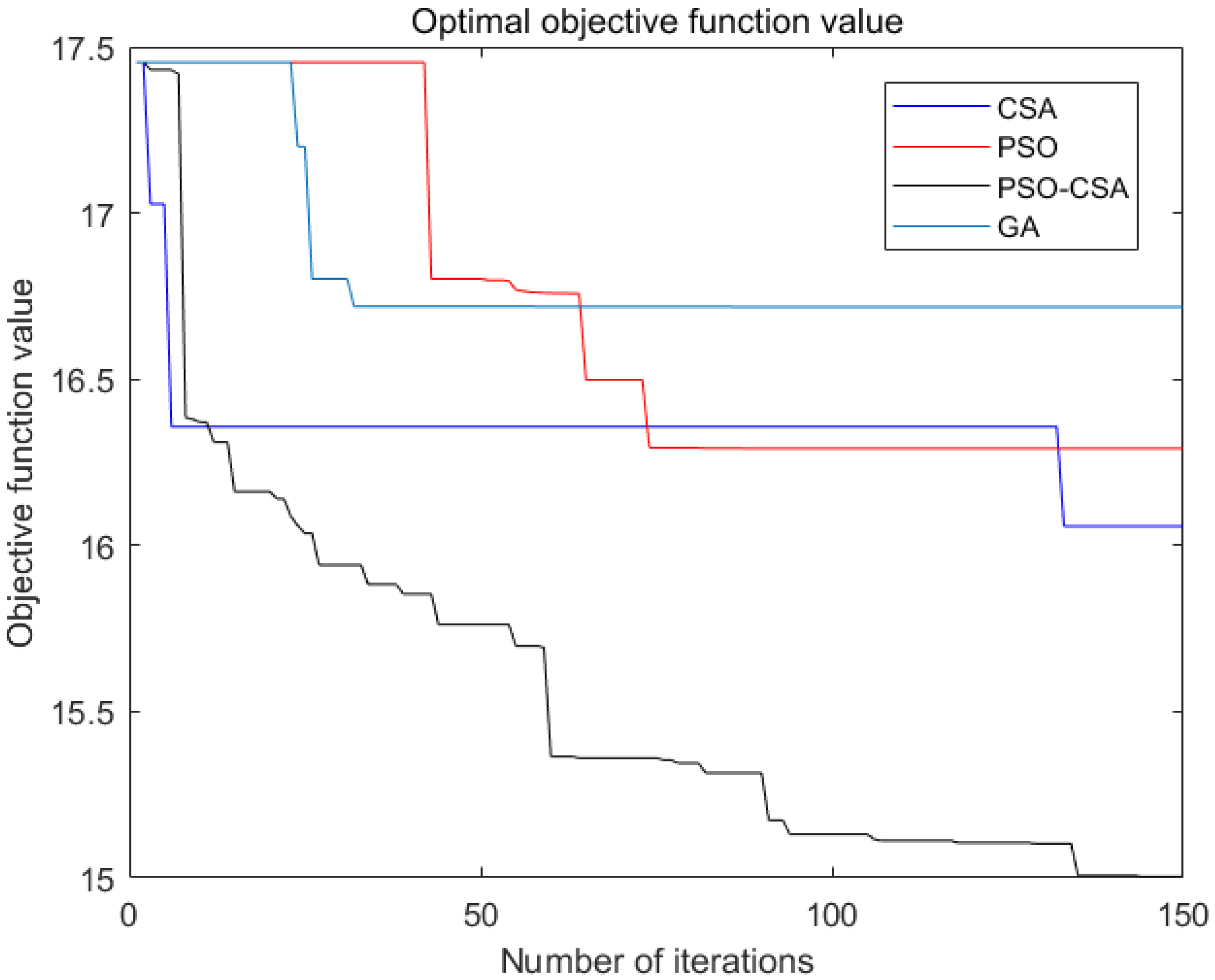
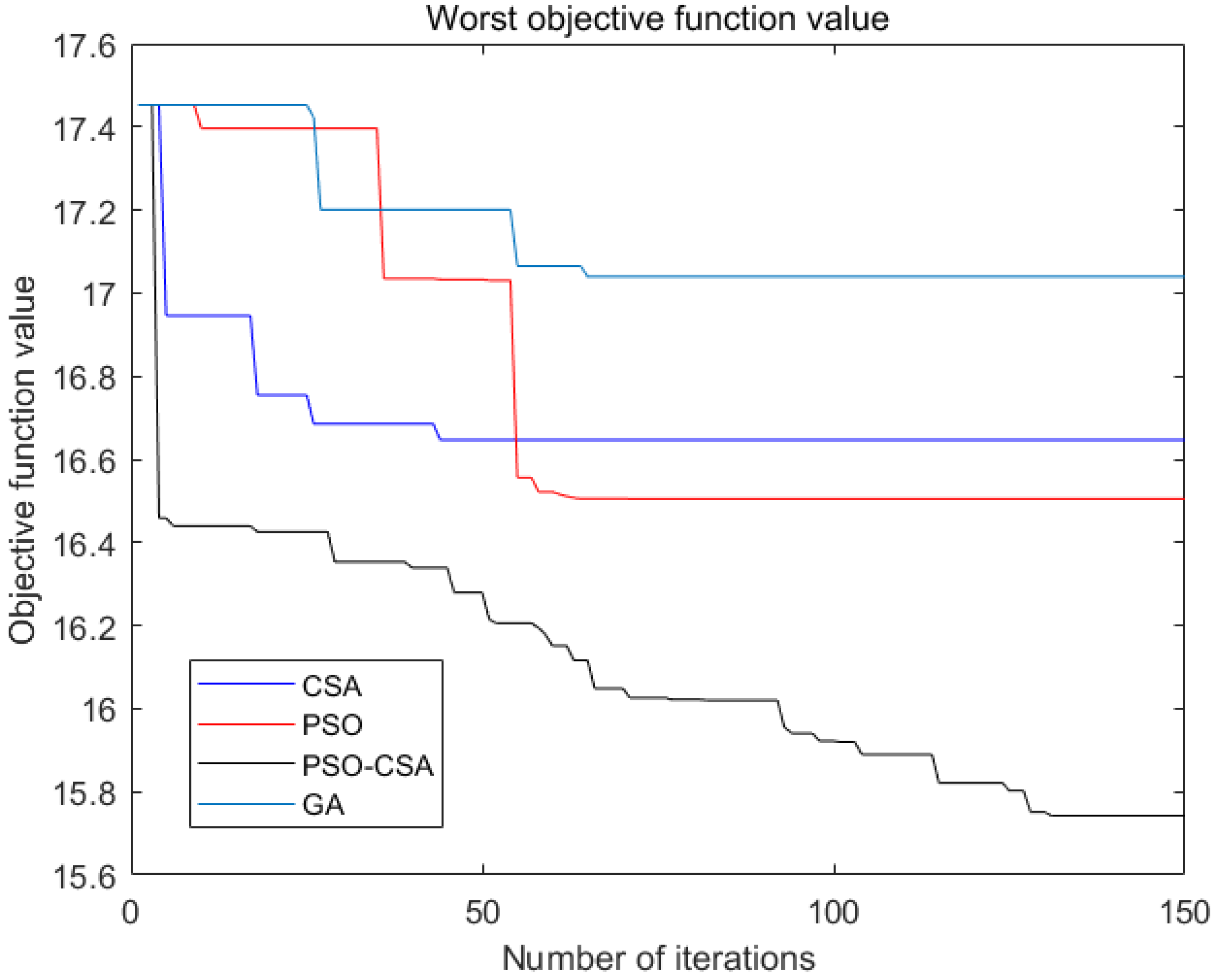
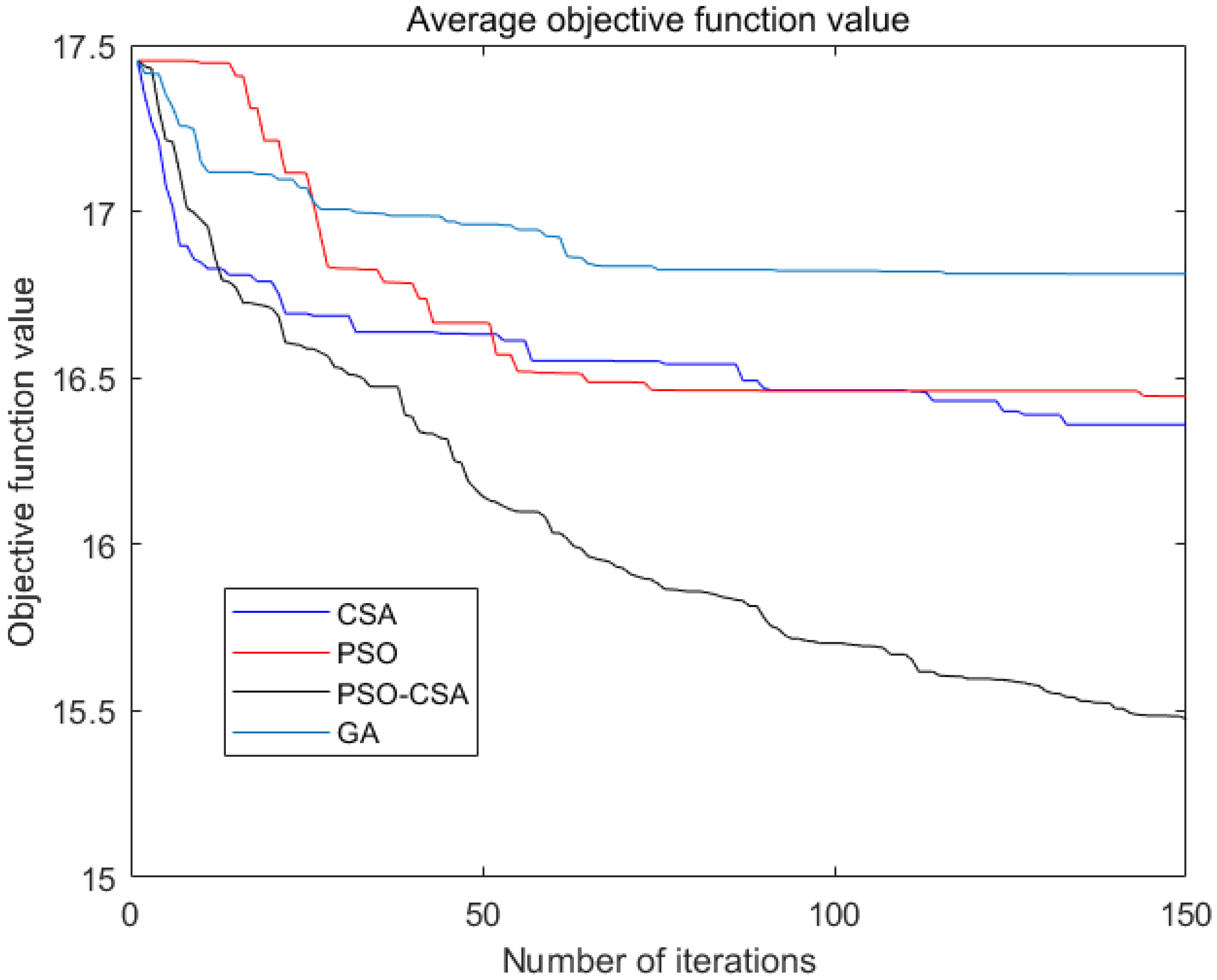
4.2. Display of Simulation Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, M.; Zhang, Q.; Yang, Y.; Wang, G.; Xu, W.; Zhao, L. Research and Application of Reservoir Flood Control Optimal Operation Based on Improved Genetic Algorithm. Water 2022, 14, 1272. [Google Scholar] [CrossRef]
- Shang, L.; Li, X.; Shi, H.; Kong, F.; Wang, Y.; Shang, Y. Long-, Medium-, and Short-Term Nested Optimized-Scheduling Model for Cascade Hydropower Plants: Development and Practical Application. Water 2022, 14, 1586. [Google Scholar] [CrossRef]
- Grigg, N.S. Large-scale water development in the United States: TVA and the California State Water Project. Int. J. Water Resour. Dev. 2021, 39, 70–88. [Google Scholar] [CrossRef]
- Yao, H.; Dong, Z.; Li, D.; Ni, X.; Chen, T.; Chen, M.; Jia, W.; Huang, X. Long-term optimal reservoir operation with tuning on large-scale multi-objective optimization: Case study of cascade reservoirs in the Upper Yellow River Basin. J. Hydrol. Reg. Stud. 2022, 40, 101000. [Google Scholar] [CrossRef]
- Dobson, B.; Wagener, T.; Pianosi, F. An argument-driven classification and comparison of reservoir operation optimization methods. Adv. Water Resour. 2019, 128, 74–86. [Google Scholar] [CrossRef]
- Seibert, S.; Skublics, D.; Ehret, U. The potential of coordinated reservoir operation for flood mitigation in large basins—A case study on the Bavarian Danube using coupled hydrological–hydrodynamic models. J. Hydrol. 2014, 517, 1128–1144. [Google Scholar] [CrossRef]
- Pan, Z.; Chen, L.; Teng, X. Research on joint flood control operation rule of parallel reservoir group based on aggregation–decomposition method. J. Hydrol. 2020, 590, 125479. [Google Scholar] [CrossRef]
- Jiao, H.; Wei, H.; Yang, Q.; Li, M. Application Research of CFD-MOEA/D Optimization Algorithm in Large-Scale Reservoir Flood Control Scheduling. Processes 2022, 10, 2318. [Google Scholar] [CrossRef]
- Ahmad, A.; Razali, S.F.M.; Mohamed, Z.S.; El-Shafie, A. The Application of Artificial Bee Colony and Gravitational Search Algorithm in Reservoir Optimization. Water Resour. Manag. 2016, 30, 2497–2516. [Google Scholar] [CrossRef]
- Bashiri, H.; Qaderi, K.; Rheinheimer, D.; Sharifi, E. Application of Harmony Search Algorithm to Reservoir Operation Optimization. Water Resour. Manag. 2015, 29, 5729–5748. [Google Scholar] [CrossRef]
- Fang, Y.; Ahmadianfar, I.; Samadi-Koucheksaraee, A.; Azarsa, R.; Scholz, M.; Yaseen, Z.M. An accelerated gradient-based optimization development for multi-reservoir hydropower systems optimization. Energy Rep. 2021, 7, 7854–7877. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Janbaz, M.; Loáiciga, H.A. Application of the gravity search algorithm to multi-reservoir operation optimization. Adv. Water Resour. 2016, 98, 173–185. [Google Scholar] [CrossRef]
- Bakanos, P.I.; Katsifarakis, K.L. Optimizing Current and Future Hydroelectric Energy Production and Water Uses of the Complex Multi-Reservoir System in the Aliakmon River, Greece. Energies 2020, 13, 6499. [Google Scholar] [CrossRef]
- Ehteram, M.; Allawi, M.F.; Karami, H.; Mousavi, S.-F.; Emami, M.; El-Shafie, A.; Farzin, S. Optimization of Chain-Reservoirs’ Operation with a New Approach in Artificial Intelligence. Water Resour. Manag. 2017, 31, 2085–2104. [Google Scholar] [CrossRef]
- Moravej, M.; Hosseini-Moghari, S.-M. Large Scale Reservoirs System Operation Optimization: The Interior Search Algorithm (ISA) Approach. Water Resour. Manag. 2016, 30, 3389–3407. [Google Scholar] [CrossRef]
- Li, Y.-B.; Liu, Y.; Nie, W.-B.; Ma, X.-Y. Inverse Modeling of Soil Hydraulic Parameters Based on a Hybrid of Vector-Evaluated Genetic Algorithm and Particle Swarm Optimization. Water 2018, 10, 84. [Google Scholar] [CrossRef]
- Recio Villa, I.; Martínez Rodríguez, J.B.; Molina, J.L.; Pino Tarragó, J.C. Multiobjective Optimization Modeling Approach for Multipurpose Single Reservoir Operation. Water 2018, 10, 427. [Google Scholar] [CrossRef]
- Liu, H.; Sun, Y.; Cao, J.; Chen, S.; Pan, N.; Dai, Y.; Pan, D. Study on UAV Parallel Planning System for Transmission Line Project Acceptance Under the Background of Industry 5.0. IEEE Trans. Ind. Inform. 2022, 18, 5537–5546. [Google Scholar] [CrossRef]
- Rashid, M.U.; Abid, I.; Latif, A. Optimization of hydropower and related benefits through Cascade Reservoirs for sustainable economic growth. Renew. Energy 2021, 185, 241–254. [Google Scholar] [CrossRef]
- Babamiri, O.; Marofi, S. A multi-objective simulation–optimization approach for water resource planning of reservoir–river systems based on a coupled quantity–quality model. Environ. Earth Sci. 2021, 80, 389. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Liu, S.; Niu, W.-J.; Li, B.-J.; Wang, W.-C.; Luo, B.; Miao, S.-M. A modified sine cosine algorithm for accurate global optimization of numerical functions and multiple hydropower reservoirs operation. Knowledge-Based Syst. 2020, 208, 106461. [Google Scholar] [CrossRef]
- Seifollahi-Aghmiuni, S.; Bozorg-Haddad, O. Simulation–Optimization Tool for Multiattribute Reservoir Systems. J. Hydrol. Eng. 2019, 24, 04019028. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Zhang, R.; Wang, S.; Cheng, C.-T. Operation rule derivation of hydropower reservoir by k-means clustering method and extreme learning machine based on particle swarm optimization. J. Hydrol. 2019, 576, 229–238. [Google Scholar] [CrossRef]
- Chen, H.-T.; Wang, W.-C.; Chen, X.-N.; Qiu, L. Multi-objective reservoir operation using particle swarm optimization with adaptive random inertia weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Ford, L.; de Queiroz, A.; DeCarolis, J.; Sankarasubramanian, A. Co-Optimization of Reservoir and Power Systems (COREGS) for seasonal planning and operation. Energy Rep. 2022, 8, 8061–8078. [Google Scholar] [CrossRef]
- Sakthivel, V.; Thirumal, K.; Sathya, P. Short term scheduling of hydrothermal power systems with photovoltaic and pumped storage plants using quasi-oppositional turbulent water flow optimization. Renew. Energy 2022, 191, 459–492. [Google Scholar] [CrossRef]
- Acuña, G.; Domínguez, R.; Arganis, M.L.; Fuentes, O. Optimal Schedule the Operation Policy of a Pumped Energy Storage Plant Case Study Zimapán, México. Electronics 2022, 11, 4139. [Google Scholar] [CrossRef]
- Zhang, X.; Deng, L.; Wu, B.; Gao, S.; Xiao, Y. Low-Impact Optimal Operation of a Cascade Sluice-Reservoir System for Water-Society-Ecology Trade-Offs. Water Resour. Manag. 2022, 36, 6131–6148. [Google Scholar] [CrossRef]
- Razavi, S.-M.; Momeni, H.-R.; Haghifam, M.-R.; Bolouki, S. Multi-Objective Optimization of Distribution Networks via Daily Reconfiguration. IEEE Trans. Power Deliv. 2021, 37, 775–785. [Google Scholar] [CrossRef]
| Symbol | Illustrate |
|---|---|
| The duration of the unit period | |
| scheduling period set, | |
| Reservoir set, | |
| The upstream water level of the reservoir during the time period | |
| The downstream level of the reservoir during the time period | |
| Loss of head of reservoirs within time | |
| The flow rate of generators in reservoir within the time period | |
| The maximum flow rate of generators in reservoir in the time period | |
| The discharge rate of the reservoir | |
| The flow rate of the reservoir | |
| The three-year average runoff within the river section | |
| The water demand of industry within the time period of the river section | |
| The water demand of agriculture within the time period of the river section | |
| The water demand of residents during the time period of the river section | |
| The water demand of the ecological environment during the time period of the river section | |
| The amount of water provided by industry in the river section during the time period of the river section | |
| The amount of water provided by agriculture in the river section during the time period of the river section | |
| The amount of water provided by residents in the river section during the time period of the river section | |
| The amount of water provided of the ecological environment during the time period in the river section | |
| Water scarcity indicator function during the time period within a river section | |
| Water shortage index function of ecological environment during the time period in the river section | |
| The output coefficient of the generator of the reservoir |
| Month | 1 | 2 | 3 | 4 | 5 | 6 | Total | |
| Reservoir | Purpose | |||||||
| A | Industry | 1000 | 1012 | 1224 | 1200 | 1200 | 1500 | |
| Agriculture | 509 | 500 | 2400 | 3972 | 4675 | 5825 | ||
| Domestic | 85 | 90 | 90 | 100 | 115 | 115 | ||
| Ecology | 75 | 88 | 90 | 115 | 167 | 199 | ||
| B | Industry | 750 | 780 | 795 | 795 | 740 | 800 | |
| Agriculture | 240 | 250 | 709 | 771 | 895 | 950 | ||
| Domestic | 600 | 590 | 580 | 625 | 707 | 794 | ||
| Ecology | 133 | 135 | 139 | 180 | 188 | 195 | ||
| Month | 7 | 8 | 9 | 10 | 11 | 12 | ||
| Reservoir | Purpose | Water Demand (Unit:m3) | ||||||
| A | Industry | 1400 | 1500 | 1224 | 1200 | 1000 | 1344 | 14,804 |
| Agriculture | 5990 | 4614 | 1200 | 1150 | 504 | 300 | 31,641 | |
| Domestic | 120 | 140 | 140 | 122 | 95 | 95 | 1307 | |
| Ecology | 204 | 207 | 200 | 188 | 152 | 107 | 1792 | |
| B | Industry | 820 | 950 | 890 | 825 | 825 | 755 | 9725 |
| Agriculture | 945 | 900 | 864 | 752 | 400 | 295 | 7972 | |
| Domestic | 790 | 787 | 746 | 690 | 605 | 610 | 8124 | |
| Ecology | 199 | 195 | 180 | 172 | 150 | 145 | 2011 | |
| Algorithm | CSA | PSO | GA | PSO-CSA |
|---|---|---|---|---|
| Index | Numerical Value | |||
| The optimal value | 16.06 | 16.29 | 16.72 | 15.00 |
| The worst value | 16.55 | 16.50 | 17.04 | 15.74 |
| The average value | 16.36 | 16.45 | 16.81 | 15.48 |
| Month | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Reservoir | ||||||
| A | 1522.7 | 1613.4 | 3559.4 | 5216.5 | 6014.5 | 7534.7 |
| B | 1591.5 | 1733.2 | 2172.0 | 2208.1 | 2420.8 | 2505.0 |
| Month | 7 | 8 | 9 | 10 | 11 | 12 |
| Reservoir | Water Demand (Unit:m3) | |||||
| A | 7063.2 | 6110.1 | 2643.3 | 2621.8 | 1732.8 | 1769.7 |
| B | 2640.0 | 2791.45 | 2614.7 | 2386.9 | 1972.3 | 1723.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Lu, J.; Zou, C.; Deng, B.; Liu, L.; Yan, S. Research on Sustainable Scheduling of Cascade Reservoirs Based on Improved Crow Search Algorithm. Water 2023, 15, 578. https://doi.org/10.3390/w15030578
Liu X, Lu J, Zou C, Deng B, Liu L, Yan S. Research on Sustainable Scheduling of Cascade Reservoirs Based on Improved Crow Search Algorithm. Water. 2023; 15(3):578. https://doi.org/10.3390/w15030578
Chicago/Turabian StyleLiu, Xiaoshan, Jinyou Lu, Chaowang Zou, Bo Deng, Lina Liu, and Shaofeng Yan. 2023. "Research on Sustainable Scheduling of Cascade Reservoirs Based on Improved Crow Search Algorithm" Water 15, no. 3: 578. https://doi.org/10.3390/w15030578






