Abstract
Accurate estimation of precipitation is critically important for a variety of fields, such as climatology, meteorology, and water resources. However, the availability of precipitation measurements has proved to be spatially inadequate for many applications. In this study, to acquire high-quality precipitation fields with enhanced accuracy and a fine-scale spatial resolution of 1 km 1 km, we developed a new data fusion method by establishing an energy function model using the downscaled Global Precipitation Measurement (GPM) Integrated Multi-satellite Retrievals (IMERG) precipitation product and high-density station observation in mainland China. Our merging approach was inspired by the interdisciplinary research framework integrating the methods in the fields of image processing, earth science, and machine learning. Cross-validation analyses were performed for the monthly precipitation over the period 2009–2018. It was found that the results of the newly developed method were more accurate than the original IMERG products in terms of root mean squared error (RMSE), mean absolute error (MAE), correlation coefficient (CC), and Kling–Gupta efficiency (KGE). The merging precipitation results exhibit consistent spatial patterns with the original IMERG products, yet have good agreement with station observations. The gauge observations were the major source of the prediction skill of precipitation for the proposed method, and the downscaled-IMERG precipitation products added additional spatial details in the final merging results. Results indicate that the proposed merging method can reproduce the spatial details of the precipitation fields as well as enhance their accuracy. In addition, the time evolution of the error index indicates that the improvement in the merged result was stable over time, with KGE improving by 14% on average. The developed approach provides a promising way of estimating precipitation with high spatial resolution and high accuracy, which will benefit hydrological and climatological studies.
1. Introduction
Precipitation plays a vital role in hydrological and climatological studies for better planning and decision-making [1,2]. Quantitative estimation of the precipitation amount and its spatial distribution with high resolution is necessary for many scientific research studies and applications, such as improving our understanding of the hydrologic cycle and investigating climatic impacts on agriculture and human society [3,4]. Traditionally, spatial distributions of precipitation have been obtained by interpolating station observations [5]. Particularly, a high density of stations is critically important to obtain the spatial details of precipitation [6]. However, meteorological stations are usually sparse and unevenly distributed; therefore, the interpolated precipitation fields that only use station observations are usually subject to large uncertainties [7,8].
Remote sensing techniques enable us to acquire the continuous precipitation fields at global and local scales [9,10]. Satellite precipitation estimates can provide the spatio-temporal distribution of precipitation in regions with complex topography and regions with sparse stations. Until now, there have been many remote precipitation products, such as the Tropical Rainfall Measuring Mission (TRMM), Multisatellite Precipitation Analysis (TMPA), Global Satellite Mapping of Precipitation (GSMaP), the Global Precipitation Measurement (GPM), Integrated Multi-satellite Retrievals (IMERG), and so on. However, compared with station observations, the satellite precipitation products tend to underestimate or overestimate precipitation [11]. Previous studies demonstrated that satellite precipitation products are subject to large uncertainties, especially in high mountain areas [12,13]. Therefore, although remote sensing can capture precipitation in a continuous way, the accuracy still needs to be enhanced. Furthermore, in spite of some available promising satellite precipitation products, their spatial resolutions are still relatively coarse, especially for regional or fine-scale studies. Therefore, there remains a need to improve the spatial details of precipitation as well as its accuracy by using multiple data sources such as satellite-based precipitation products and ground-based observations [14].
Data fusion is an efficient way to get precipitation estimates with high quality by combining multiple precipitation datasets and the auxiliary variables [11,15,16]. Previous studies have been conducted to develop methods to merge precipitation datasets in different regions [17,18,19], including conditional merging [19], weighted fusion [20], optimal interpolation techniques [21], geographically weighted regression [22], mean field bias correction method [23], Kalman filter [24], Bayesian estimation [25], neural network approach [26], co-kriging [27], and deep learning models [19]. Research has shown that, compared to the original satellite-based products, improved accuracy can be detected in the fusion results [19,26]. However, the accuracy of the fusion data varies largely among the regions and spatial scales [19]. It is still quite challenging work to generate a high-quality precipitation dataset because of its high heterogeneity.
In recent years, energy function models have made great progress in object recognition and have gradually become very attractive tools, especially in image processing, medical imaging, and computer vision [28,29]. The advantages of the energy function model are its diversity and flexibility, and different forms can be constructed according to the varied applications. Another advantage of the energy function model is that there is no assumption for the variables. Considering the characteristics of the satellite-based precipitation products and the target spatial information of precipitation, the energy function model could provide a novel way for merging precipitation information from multiple sources.
The aim of this study is to propose a new data fusion method by developing an energy functional regularization model, which is composed of a real term and a regularization term. The developed method was used to merge IMERG precipitation products and meteorological station observations over mainland China. The cross-validation method was used to demonstrate the performance of the proposed method.
2. Materials and Methods
2.1. Materials
The Chinese mainland (3°51′–53°33′ N, 73°33′–135°05′ E), located in southeast Asia along the coastline of the Pacific Ocean, was selected as the study area (Figure 1). Due to its vast territory and wide geographical span, China covers complex terrain, and the elevation ranges from less than −100 m to more than 8000 m. Significantly affected by the ocean and complex terrain, annual precipitation in China exhibits high spatial variation, decreasing from more than 2000 mm in the southeast to less than 50 mm in the northwest, with larger variations of precipitation occurring in mountainous regions than in other areas [30]. In addition, more than 60% of the annual precipitation concentrates in the wet season.
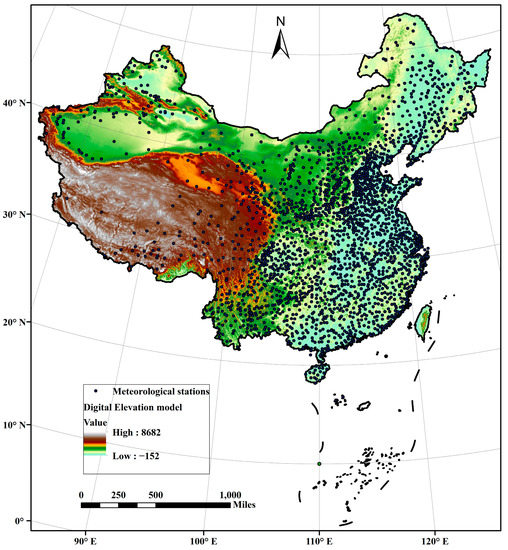
Figure 1.
The research area and the spatial distribution of 2419 national meteorological stations in China.
Monthly precipitation observations from more than 2000 meteorological stations have been used in this study. Despite the high density of this gauge network, these stations are unevenly distributed, with a high density of stations in eastern China and sparse stations in the west. Due to the availability of high-density observations, the monthly precipitation data for the period 2009–2018 were used in this study. The orography of the large mountains, especially in western China, leads to large biases in the station observations. IMERG is a new generation of multi-satellite merged precipitation retrieval product and is widely used in many fields as it potentially offers the “best” precipitation estimates [9,31,32]. It integrates the data from active and passive microwave sensors and infrared sensors by using the satellite precipitation retrieval algorithm [33]. IMERG was released in 2014 with a relatively very high spatial and temporal resolution of 0.1° and 30 min, respectively. The final run products include 3.5 months of latency following the GPM observations and provide both uncalibrated products and products calibrated using monthly gauge-based precipitation from the Global Precipitation Climatology Centre.
The elevation data with 30 m spatial resolution, downloaded from https://dwtkns.com/strm30m/, accessed on 1 May 2021, were derived from the NASA Shuttle Radar Topography Mission (STRM). The normalized difference vegetation index (NDVI) is an indicator of vegetation activity and is frequently used to estimate precipitation. The NDVI data used in this study are derived from the atmospherically corrected reflectance in the red and near-infrared wavebands of the Moderate Resolution Imaging Spectroradiometer (MODIS) sensor aboard the Terra satellite. The MOD13A3 monthly NDVI product with a spatial resolution of 1 km, obtained from http://modis-land.gsfc.nasa.gov/vi.html, accessed on 1 May 2021, was used in this study.
2.2. Methods
The satellite precipitation product can be regarded as the true precipitation field with some noise, and the true precipitation field can be seen as an image. Therefore, from this point of view, the research on acquiring high-quality precipitation can be transformed into research on image denoising. Thus, the data fusion process in this study is transformed into the process of image denoising by preserving the images’ local details as much as possible. Among the existing image-denoising approaches, the partial differential equation (PDE)-based image denoising method is the most commonly used one [34,35,36]. In addition, considerable efforts have been invested in the regularized total variation model (TV) [37,38]. The obvious advantages of the TV model include removing image noise, protecting image details, and balancing the problem between denoising and preserving details by using a regularization parameter. A classic TV model that is widely used in image denoising is as follows [39]:
where represents the true image, that is the estimated precipitation field in this study; is the image with some noises, i.e., the satellite precipitation product. is the norm of , and is the gradient operator. The first term in the right hand of Equation (1) is named the regular term, while the second term is called the data fidelity item. The regular term was used to maintain the local details of the image, and the data fidelity term was used to guarantee the accuracy of the final result. is a regularization parameter, used to balance the weight of the regular and data fidelity terms.
Given different precipitation fields and obtained from various sources with some errors, the concern here is how to combine the noisy fields into one uniformly focused precipitation filed such that the local details are clear and the error is significantly reduced.
Based upon the classic image denoising model (1), in this study we propose an energy function model for precipitation data fusion as follows:
where is the satellite precipitation product and is downscaled first by using the random forest (RF) method in this study. is another precipitation field generated by the simple inverse distance weighted (IDW) method by interpolating the high-density gauge observations over mainland China. is a positive parameter used to trade off the fidelity of the solution to the actual precipitation field and the accuracy of the result. Instead of using norm, we used norm in the first term of the right hand of Equation (2).
denotes norm, which has been demonstrated to have the capability of preserving the local details of an image.
Let , Equation (2) can be changed into:
The form of Equation (3) is similar to that of Equation (1), indicating the feasibility of the established energy function model (i.e., Equation (2)). Therefore, the famous Bregman-splitting algorithm [40,41] can be used to solve Equation (3). This method is a fast alternating directional method often used in solving regularized optimization problems [42]. To design the Bregman split algorithm for (3), we first introduce a split variable , and Equation (3) can be reformulated as:
Then, using the Bregman split algorithm, Equation (4) can be changed into:
By applying the gradient descent method, Euler–Lagrange equations corresponding to equation set (5) can be designed as:
Then, Equation (2) can be finally transformed into the following equation set:
where, , . The conjugate gradient method is then used to solve equation set (8). The parameter is obtained via sensitivity experiments, with values chosen from , , , 1, 2, 5, 10, 20, 50, 100, 500, and 1000. The regularization parameter is computed in an adaptive way by solving the Euler–Lagrange equation of Equation (3):
By multiplying and integrating over the entire study region , Equation (9) can be transformed into:
Since , then
where is the variance of the precipitation field.
The framework of the proposed data fusion method is illustrated in Figure 2. The whole process can be divided into (1) Data pre-processing, including time alignment, downscaling the calibrated IMERG data from 0.1° to 1 km and unifying the time scale to monthly. In this step, the missing data and outliers in the rain gauge observations are checked and the observations are subject to strict quality control procedures by applying the RHtest software (http://etccdi.pacificclimate.org/software.shtml, accessed on 2 May 2021). In addition, since the satellite data uses UTC time and the rain gauge observations use Beijing time, all datasets are time-matched; (2) Establishing the energy function model by developing the regular term and the data fidelity term. The regular term is established by using the RF method combined with some covariates of precipitation. The data fidelity term is established by applying the IDW method combing with the high-density gauge observations; (3) Merging different precipitation datasets and validating. The ten-fold cross-validation method was used for model evaluation. The data were randomly divided into ten non-overlapping equal subsets. Nine sets were used to train the model, while the remaining subset was used to test the performance of the methods. This process was repeated ten times. The model performance is quantified by averaging certain evaluation metrics produced from the ten tests, including the correlation coefficient (CC), mean absolute error (MAE), root mean square error (RMSE), and modified Kling–Gupta efficiency (KGE). These indicators are defined by the following Equations (12)–(15), respectively.
where is the site number. and are the estimated precipitation value and the gauge observation at the ith point. and are the mean values of and . and are the standard deviations of and , respectively. MAE is used to indicate the average error considering both systematic and random errors. RMSE is used to compare the difference between the estimations and observations and is sensitive to outliers. CC represents the degree of linear correlation between the estimations and observations. KGE is a multi-component performance defined as a combination of bias, variance, and correlation aggregate metrics, with values close to one suggesting a perfect performance.
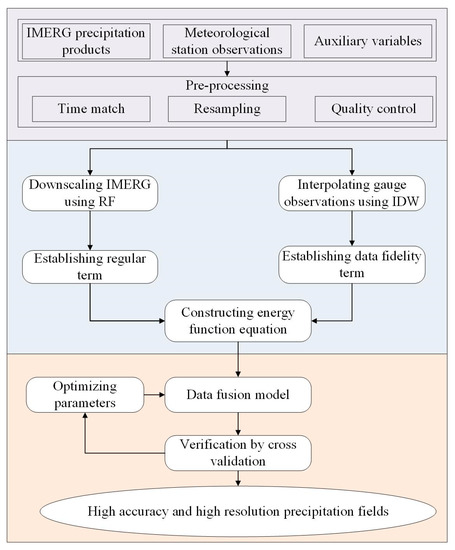
Figure 2.
Flow chart of the proposed precipitation fusion method.
3. Results
The final fusion result was first evaluated at an annual scale against the original IMERG precipitation product and the individual precipitation data obtained using the RF-based downscaling method and IDW interpolator. Figure 3 displays the spatial patterns of the precipitation fields of different methods in the year 2018. All the precipitation fields exhibited a similar spatial pattern with the annual precipitation showing an increasing trend from the northwest to the southeast of China. Compared to the original IMERG precipitation product, the downscaling result using RF (Figure 3b), the interpolation result using IDW (Figure 3c) and the final fusion result (merging the result of RF and IDW, Figure 3d) not only preserved the spatial precipitation patterns of the annual precipitation but also greatly improved their spatial details. In addition, the change range of the annual precipitation varied with the methods. The maximum value of the IMERG product was 2821.35 mm and the minimum value was 9.92 mm. By contrast, the change ranges of the results by using RF, IDW, and the merging approach were 67.6~2610.07 mm, 7.60~3182.60 mm, and 45.02~2925.07 mm, respectively. The RF method narrows the spatial dynamic range of the precipitation, while the IDW method broadens the range of the precipitation amount. After merging RF-based results with IDW-based results, the precipitation obtained from the proposed fusion method was noticeably changed, resulting in a large difference in local areas, such as in the southeast of the Tibetan plateau and the northwest of China. As indicated by other researchers [11], satellite-based precipitation products tended to underestimate precipitation in northwest China. The magnitude of underestimation of IMERG precipitation was reduced in northwestern China after downscaling and merging (Figure 3b,d). Figure 4 further shows the scatterplots between the observations and precipitation estimations by the proposed merging method and also the results of RF and IDW. It should be noted that with the high-density station network, the simple interpolation method, IDW, performed well. Although we integrated NDVI and topography information in the RF-based downscaling result, the R2 value of RF was slightly smaller than those of IDW and the original IMERG products. In other cases, with sufficient spatial constraints, the RF may perform well. In addition, there were still some underestimations and overestimations that occurred in the results of RF and IDW–based methods. The merging approach performed the best, with an R2 of 0.93, indicating that the spatial details were relatively accurate (Figure 3d). Both the magnitudes of overestimation and underestimation decreased when using the merging method (Figure 4d). In summary, compared with the IMERG precipitation product, the proposed merging method improves the spatial resolution and accuracy of the precipitation fields.
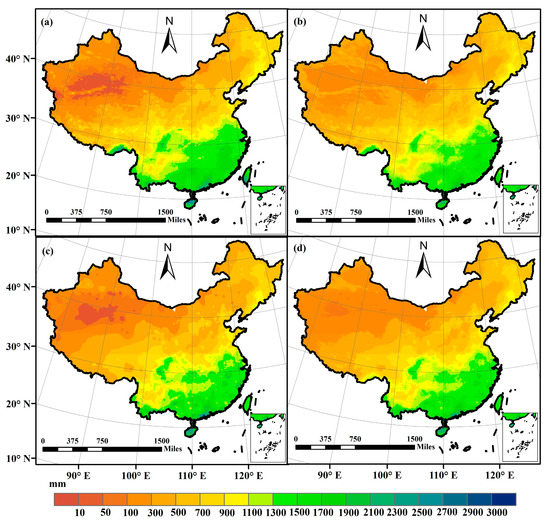
Figure 3.
Precipitation estimates in the year 2018. (a) IMERG; (b) RF; (c) IDW; (d) The merging method.
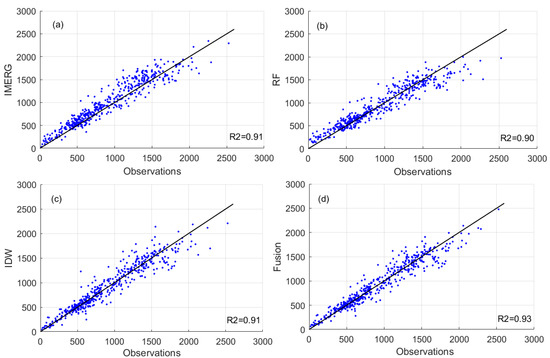
Figure 4.
Scatter plot of estimated precipitation and observations in the year 2018. (a) IMERG; (b) RF; (c) IDW; (d) The merging method.
Precipitation in January and July 2018 was selected to illustrate the monthly precipitation analysis (Figure 5 and Figure 6). All products can exhibit the precipitation difference between southeast and northwest China. Although the spatial pattern was similar among these monthly precipitation estimates, local differences can be observed by different methods, similar to the annual precipitation analysis. In January, the precipitation amount ranged from 0 to 266.22 mm for the original IMERG product, while the change ranges were 0.47~191.48 mm, 0~225.48 mm, 0~209.47 mm for RF, IDW, and the fusion methods, respectively. The maximum value of the precipitation field varied with the method. The overestimation of IMERG products was reduced by using other methods. In addition, the precipitation fields obtained from different methods showed different spatial details in some local areas. Precipitation results in July also showed similar patterns by using different methods, while different spatial change ranges existed for the methods, and large differences can be found in some local regions, such as the northwest, the southeast, and the northeast of China (Figure 6). The similar spatial pattern indicated that the proposed fusion method has the capability of capturing the spatial pattern of the precipitation field as well as improving the spatial resolution.
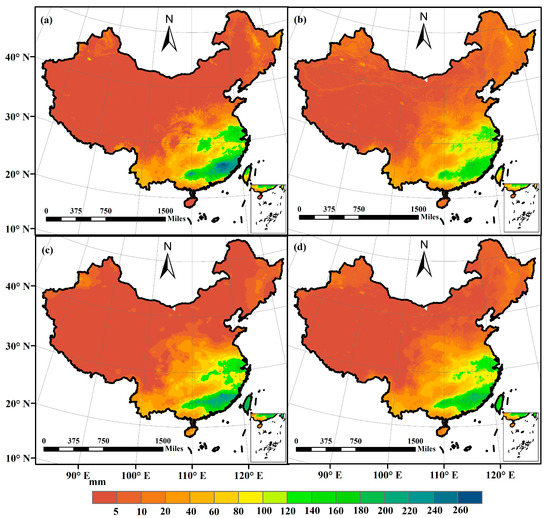
Figure 5.
Precipitation estimates in January, 2018. (a) IMERG; (b) RF; (c) IDW; (d) The merging method.
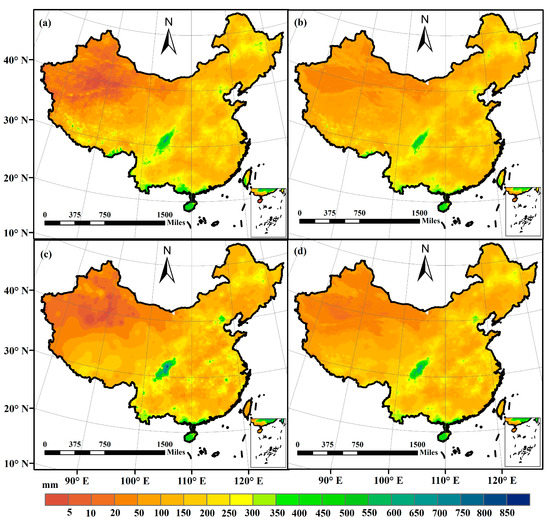
Figure 6.
Precipitation estimates in July, 2018. (a) IMERG; (b) RF; (c) IDW; (d) The merging method.
Ten years of monthly data (2009~2018) have been used to further evaluate the performance of the merging method. To calculate the error indices, we randomly selected 20% of the stations from the total number of stations. This process was repeated ten times and the average value of each index for the ten times was thus obtained. Figure 7 gives the monthly mean values of RMSE, MAE, CC, and KGE for the period 2009–2018. As can be seen, in terms of the RMSE, MAE, CC, and KGE, the merging performance was generally better than others for the monthly precipitation estimates. The RF-based downscaling results did not show large improvements compared to the original IMERG precipitation products. The added value of gauge observations was more significant for the merging process, with CC values ranging from 0.89 to 0.97, and KGE values ranging from 0.86 to 0.94 for the proposed method. Compared to the RF-based downscaling result, the RMSE and MAE of the merging method decreased by 12% and 18%, respectively, on average, and the CC and KGE values increased by 3% and 6%, respectively. The good agreement of the proposed method indicated that the accuracy of the established fusion model was mainly determined by the data fidelity term, which was constructed by using station observations. In addition, combined with the information provided in Figure 6b,d, the spatial details of the RF-based downscaling result and the merging result were similar, which was in line with the fact that the regular term established using the RF-based downscaling method in Equation (1) was used to maintain the local details of the result.
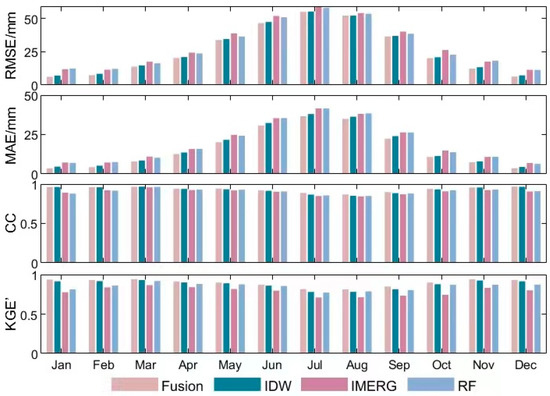
Figure 7.
Comparison of monthly mean error during 2009–2018.
The time series of KGE for the monthly precipitation estimation is displayed in Figure 8, which was calculated by cross-validation during 2009–2018 and was used to evaluate the overall performance of the proposed method. The results show that KGE exhibits high seasonal variations indicating the relatively poor performance of the proposed approach in the winter months. RF-based downscaling results had roughly the same performance as the original IMERG precipitation products, and the monthly precipitation estimates from the proposed merging method had the highest accuracy among the four datasets. Although the accuracy of the merging result was improved as compared to the precipitation estimates from RF, the improvement was less than that of the IDW method, indicating that the accuracy of the merging result was largely dependent on the gauge observations. In addition, the merging results were superior to others over the entire period, indicating that the improvement in the merging result was stable over time. Among these datasets, the fusion results exhibited the best performance, with a mean KGE value of 0.92, improved by 14% by comparing with the original IMERG precipitation products.
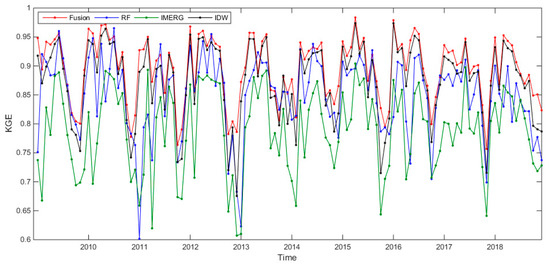
Figure 8.
Time series of KGE for the monthly precipitation estimates during 2009–2018.
4. Discussion
Precipitation data with high accuracy and high spatial resolution play significant roles in forming local and global climate models and other models in many fields. Over the past few years, satellite-based precipitation products have offered an attractive source for precipitation estimates with continuous and extensive spatial coverage, especially over large regions with diverse terrain. However, due to their retrieval algorithms and sensors, uncertainty remains regarding satellite-based products. In addition, until now, the spatial resolution of satellite-based precipitation products that are released to the public is still relatively coarse, generally ranging from 0.05° to 1° at present, which limits their wide application in local or fine-scale studies [43]. Although many previous efforts have been invested in merging precipitation information from multiple sources, they were usually restricted to some assumptions. Despite the progress, there remains a need to develop a new merging method given the high heterogeneity of the precipitation.
The aim of this study is to develop a new data fusion framework to obtain high-quality precipitation fields over mainland China. Previous studies have shown that the performance of IMERG products is better than that of some other satellite-based precipitation products [44,45]. Monthly IMERG precipitation products were thus selected to acquire precipitation with high spatial resolution and high accuracy. In addition, to guarantee the high quality of the precipitation field, other data sources were used in this study including the covariates of precipitation and, particularly, the high-density station observations in China. Inspired by the method used in the image processing field, this paper tried to introduce a new data fusion approach by combining the methods from image processing and earth science. To the best of our knowledge, this is the first attempt to apply the method of image denoising to multi-source precipitation data merging, which will guide the efforts in data fusion work for other variables.
Compared to the original IMERG precipitation products, the precipitation estimates generated by the proposed approach showed improved accuracy and higher spatial resolution. The error measurements calculated between estimations and station observations indicated that the developed method appears robust and feasible for producing accurate precipitation fields with fine spatial resolutions, which are consistent with or better than other related studies [43,46]. The accuracy of the proposed method was largely determined by the data fidelity term, while the spatial details were mainly preserved by the regular term in the proposed energy function model. The data fidelity term was established by interpolating the station observations using the simple IDW method, and the regular term was constructed by downscaling the IMERG precipitation products using the RF method. Although RF-based downscaling results had a similar performance to the original IMERG products, they retrieved the local details of the precipitation fields by using some covariates of precipitation, as shown in Figure 3, Figure 5 and Figure 6. Furthermore, the high-density station network made it possible to obtain high-quality precipitation fields. The interpolation results obtained by the simple IDW method in the data fidelity term were used to guarantee the merging results with improved accuracy (Figure 4, Figure 7 and Figure 8). The results showed that the proposed method can enhance the accuracy of the satellite-based precipitation products as well as improve spatial resolution.
The findings of this paper demonstrate the potential application of the proposed data fusion method in climatology, hydrology, and other related fields. The uncertainties associated with the proposed energy function model originate mainly from the data sources and RF downscaling process. The uncertainties in the data sources are derived primarily from the IMERG data. As previous studies indicated, underestimation and overestimation existed in the IMERG precipitation products [11,44,45]. For RF downscaling, it should be noted that the prediction range and the accuracy of the downscaling result are restricted to those covered by the training data. The capability of RF to estimate precipitation fields with fine spatial resolution is closely linked to the precipitation in the training dataset. In addition, the accuracy is significantly determined by the covariates considered in the RF-based regression. Moreover, we applied IDW in the data fidelity term due to its simplicity, which uses the locations of the known sites to determine the weight. However, IDW neglects the impacts of precipitation covariates and usually produces some “bull’s eyes”, which may limit its performance. Other interpolators, such as Kriging, could improve this situation as IDW does. Further improvement can be realized by considering more explanatory variables of precipitation and other interpolators in the data fidelity term, especially for merging precipitation data at the daily scale.
5. Conclusions
This paper proposes a new data fusion model for acquiring high-quality precipitation fields over mainland China. The developed method preserved the accuracy of the station observations and the spatial pattern and spatial details of the downscaled IMERG precipitation products. By using the cross-validation method, the results showed that the proposed method can enhance the original IMERG precipitation dataset, with the values of MAE and RMSE decreased by 15% and 19%, respectively, and the values of CC and KGE improved by 5% and 14%, respectively. The time evolution of the overall performance, indicated by KGE, showed that the improvements in the merged results were stable over time. Meanwhile, the merging results always exhibited lower MAEs and RMSEs than the RF and IDW-based results and the original IMERG precipitation products, suggesting that the proposed approach could be successfully applied to merge multisource precipitation datasets.
Funding
This study was supported by the Major Program of the National Natural Science Foundation of China (No. 42293270), the National Program of the National Natural Science Foundation of China (No. 42071374), and the Key Project of Innovation LREIS (KPI001).
Data Availability Statement
Data and additional information can be provided by directly contacting the authors.
Conflicts of Interest
The author declare no conflict of interest.
References
- Niu, J.; Chen, J.; Wang, K.; Sivakumar, B. Coherent modes in multi-scale variability of precipitation over the headwater catchments in the Pearl River basin, South China. Hydrol. Process. 2017, 31, 948–955. [Google Scholar] [CrossRef]
- Madakumbura, G.D.; Thackeray, C.W.; Norris, J.; Goldenson, N.; Hall, A. Anthropogenic influence on extreme precipitation over global land areas seen in multiple observational datasets. Nat. Commun. 2021, 12, 3944. [Google Scholar] [CrossRef] [PubMed]
- Biemans, H.; Hutjes, R.W.A.; Kabat, P.; Strengers, B.J.; Gerten, D.; Rost, S. Effects of precipitation uncertainty on discharge calculations for main river basins. J. Hydrometeorol. 2009, 10, 1011–1025. [Google Scholar] [CrossRef]
- Schoof, J.T.; Pryor, S.C.; Ford, T.W. Projected Changes in United States Regional Extreme Heat Days Derived from Bivariate Quantile Mapping of CMIP5 Simulations. J. Geophys. Res.-Atmos. 2019, 124, 5214–5232. [Google Scholar] [CrossRef]
- Asadieh, B.; Krakauer, N.Y. Global trends in extreme precipitation: Climate models versus observations. Hydrol. Earth Syst. Sci. 2015, 19, 877–891. [Google Scholar] [CrossRef]
- Charles, B.W.; Garcia, D.; Lin, K.W.; Gua, G. A revised ground-motion and intensity interpolation scheme for shakemap. Bull. Seismol. Soc. Am. 2010, 100, 3083–3096. [Google Scholar]
- Massari, C.; Crow, W.; Brocca, L. An assessment of the accuracy of global rainfall estimates without ground-based observations. Hydrol. Earth Syst. Sci. 2017, 21, 4347–4361. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Thinh, N.X. RFMEP: A novel Random Forest method for merging gridded precipitation products and ground-based measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.L.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Intergrated Multi-Satellite Retrievals for the Global Precipition Measurement (GPM) Mission (IMERG). In Satellite Precipitation Meausrement; Springer: Berlin/Heidelberg, Germany, 2020; pp. 343–353. [Google Scholar]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Sun, Q.H.; Miao, C.Y.; Duan, Q.Y.; Ashourl, H.; Sorooshian, S.; Hsu, K.L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Maggioni, V.; Massari, C. On the performance of satellite precipitation products in riverine flood modeling: A review. J. Hydrol. 2018, 558, 214–224. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.Y. A conceptual model for constructing high-resolution gaugesatellite merged precipitation analyses. J. Geophys. 2011, 116, D21106. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the triple collocation method across mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Dong, J.; Crow, W.; Reichle, R.; Liu, Q.; Lei, F.; Cosh, M.H. A global assessment of added value in the SMAP level 4 soil moisture product relative to its baseline land surface model. Geophys. Res. Lett. 2019, 46, 6604–6613. [Google Scholar] [CrossRef]
- Manz, B.; Buytaert, W.; Zulkafli, Z. High-resolution satellite-gauge merged precipittion climatologies of the tropical Andes. J. Geophys. Res. 2016, 121, 1190–1207. [Google Scholar] [CrossRef]
- Li, W.Y.; Jiang, Q.; He, X.G.; Sun, H.Q.; Sun, W.W.; Scaiono, M. Effective multi-satellite precipitation fusion procedure conditioned by gauge background fields over the Chinese mainland. J. Hydrol. 2022, 610, 127783. [Google Scholar] [CrossRef]
- Wu, H.C.; Yang, Q.L.; Liu, J.M.; Wang, G.Q. A spatiotemporal deep fusion model for merging satellite and gauge precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Shrestha, R.; Houser, P.; Anantharaj, V.G. An optimal merging technique for high resolution precipitation products. J. Adv. Model. Earth Syst. 2011, 4, 4. [Google Scholar] [CrossRef]
- Shen, J.M.; Liu, P.; Xia, J.; Zhao, Y.J.; Dong, Y. Merging multisatellite and gauge precipitation based on geographically weighted regression and long-short-term memory network. Remote Sens. 2022, 14, 3939. [Google Scholar] [CrossRef]
- Xiao, S.; Zou, L.; Xia, J.; Yang, Z.Z.; Yao, T.C. Bias correction framework for satellite precipitation products using a rain/no rain discriminative model. Sci. Total Environ. 2022, 818, 151679. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.G.; Liang, X.; Nan, Z.T. How much improvement can precipittaion data fusion achieve with a multiscale Kalman smoother-based framework? Water Resour. Res. 2011, 47, W00H12. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, Y.; Chen, Y.; Yang, Y.; Tang, G.; Yao, Y.; Long, D.; Li, C.; Han, Z.; Liu, R. Performance of optimally merged multisatellite precipitation products using the dynamic Bayesian model averaging scheme over the Tibetan Plateau. J. Geophys. Res.-Atmos. 2018, 123, 814–834. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. PERSIANN-CCS-CDR, a 3-hourly 0.04° global precipitation climate data record for heavly precipitation studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef]
- Zhang, J.M.; Xu, J.H.; Dai, X.A.; Ruan, H.H.; Liu, X.L.; Jing, W.L. Multi-source precipitation data merging for heavy rainfall events based on cokriging and machine learning methods. Remote Sens. 2022, 14, 1750. [Google Scholar] [CrossRef]
- Highnam, R.; Brady, M. Model-based image enhancement of far infrared images. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 410–415. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, Q.; Lou, S.; Hou, Y.L. Wavelet-based total variation and nonlocal similarity model for image denoising. IEEE Signal Proc. Lett. 2017, 24, 877–881. [Google Scholar] [CrossRef]
- Zhao, N.; Yue, T.X.; Zhou, X.; Zhao, M.W.; Liu, Y.; Du, Z.P.; Zhang, L.L. Statistical downscaling of precipitation using local regression and high accuracy surface modelling method. Theor. Appl. Climatol. 2017, 129, 281–292. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Jiang, L.G.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Liu, J.; Gao, F.; Liu, Z.Z. A Model of Image Denoising Based on Partial Differential Equations. In Proceedings of the 2011 International Conference on Multimedia Technology, Hangzhou, China, 26–28 July 2011; pp. 1892–1896. [Google Scholar]
- Sun, P.L.; Wang, C.X.; Li, M.; Liu, L.Q. Partial Differential Equations-Based Iterative Denoising Algorithm for Movie Images. Adv. Math. Phys. 2021, 2021, 8176746. [Google Scholar] [CrossRef]
- Ashouri, F.; Eslahchi, M.R. A new PDF learning model for image denoising. Neural Comput. Appl. 2022, 34, 8551–8574. [Google Scholar] [CrossRef]
- Jin, C.; Luan, N.L. An image denoising iterative approach based on total variation and weighting function. Multimed. Tools Appl. 2020, 79, 20947–20971. [Google Scholar] [CrossRef]
- Liu, J.J.; Ma, R.J.; Zeng, X.Y.; Liu, W.Q.; Wang, M.Y.; Chen, H. An efficient non-convex total variation approach for image deblurring and denoising. Appl. Math. Comput. 2021, 397, 125977. [Google Scholar] [CrossRef]
- Rudin, L.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Liu, X.W.; Huang, L.H. Split Bregman iteration algorithm for total bounded variation regularization based image deblurring. J. Math. Anal. Appl. 2010, 372, 486–495. [Google Scholar] [CrossRef]
- Xu, J.M.; Zhu, S.Y.; Soh, Y.C.; Xie, L.H. A Bregman Splitting Algorithm for Distributed Optimization over Networks. arXiv 2016, arXiv:1608.08031. [Google Scholar]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 2. [Google Scholar] [CrossRef]
- He, J.; Yang, K.; Tang, W.J.; Lu, H.; Qin, J.; Chen, Y.Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.W.; Zhao, N. Evaluation of eight high-resolution gridded precipitation products in the Heihe River basin, Northwest China. Remote Sens. 2022, 14, 1458. [Google Scholar] [CrossRef]
- Zhou, Z.T.; Guo, B.; Xing, W.X.; Zhou, J.; Xu, F.L.; Xu, Y. Comprehensive evaluation of the lastest GPM era IMERG and GSMaP precipitation products over mainland China. Atmos. Res. 2020, 246, 105132. [Google Scholar] [CrossRef]
- Peng, S.Z.; Ding, Y.X.; Liu, W.Z.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901–2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).