Forecasting of Rainfall across River Basins Using Soft Computing Techniques: The Case Study of the Upper Brahmani Basin (India)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area and Data Collection
2.2. Climatic Parameters
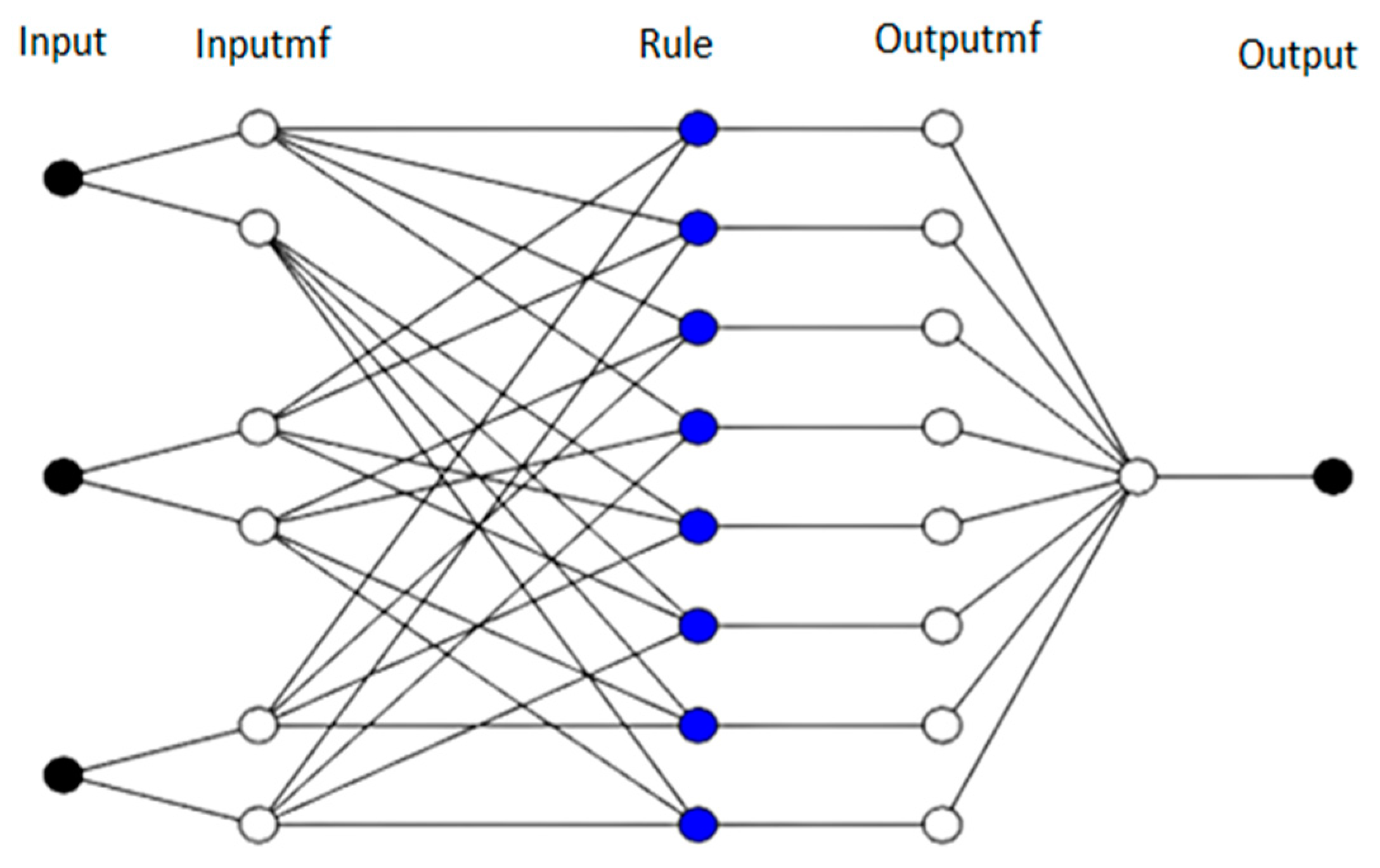
2.3. ANFIS Architecture
Development of an ANFIS Univariate Time Series Forecasting Model
3. Results and Discussion
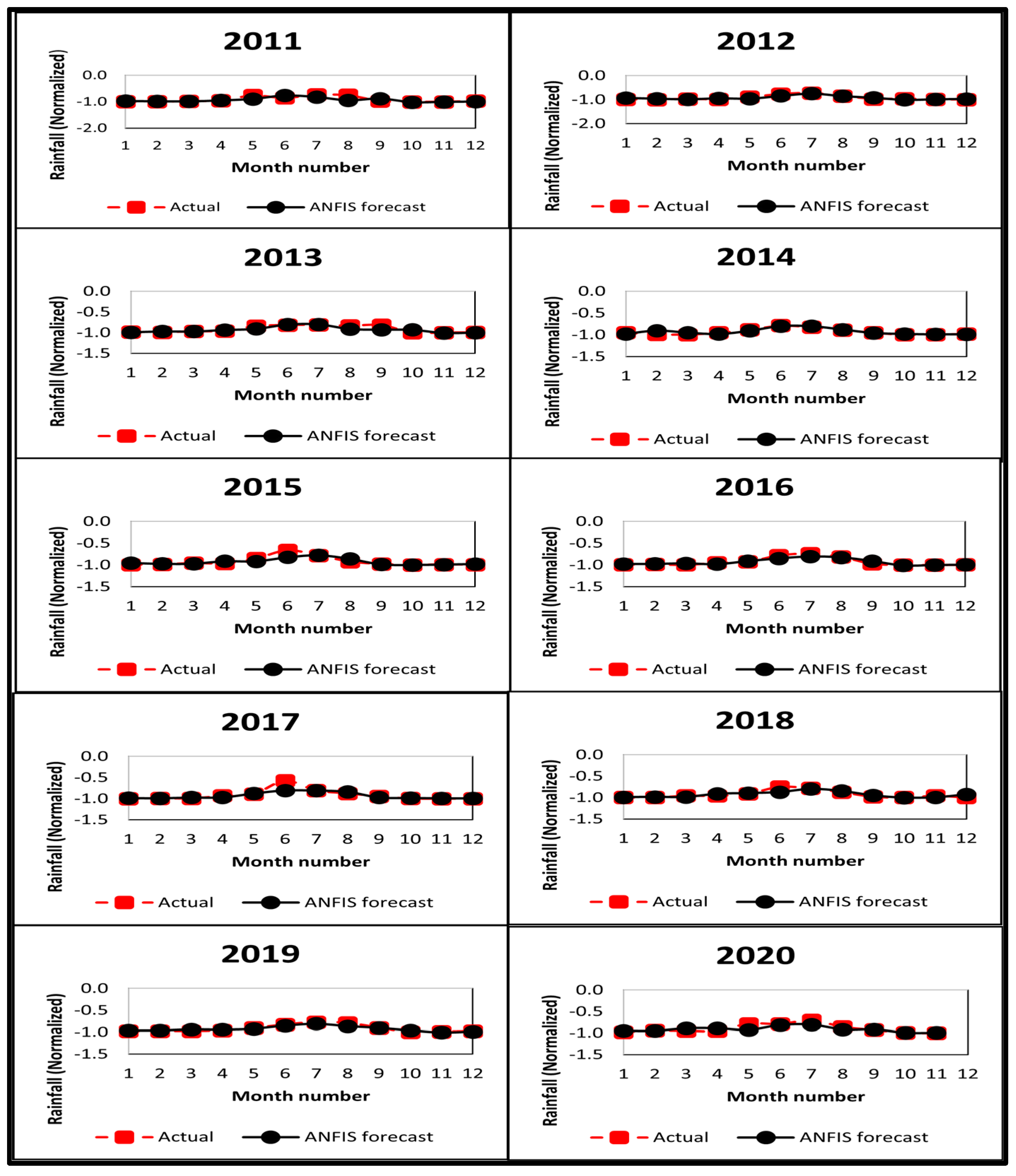
3.1. Setup of the Proposed ANFIS Model and Evaluation of Its Performance
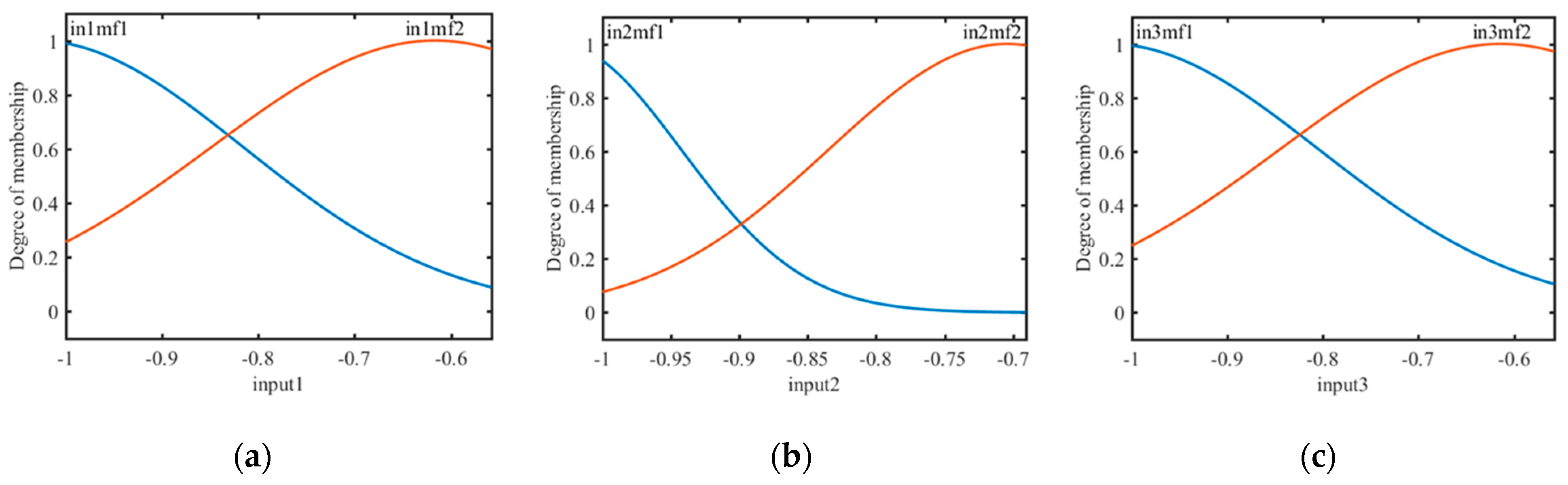
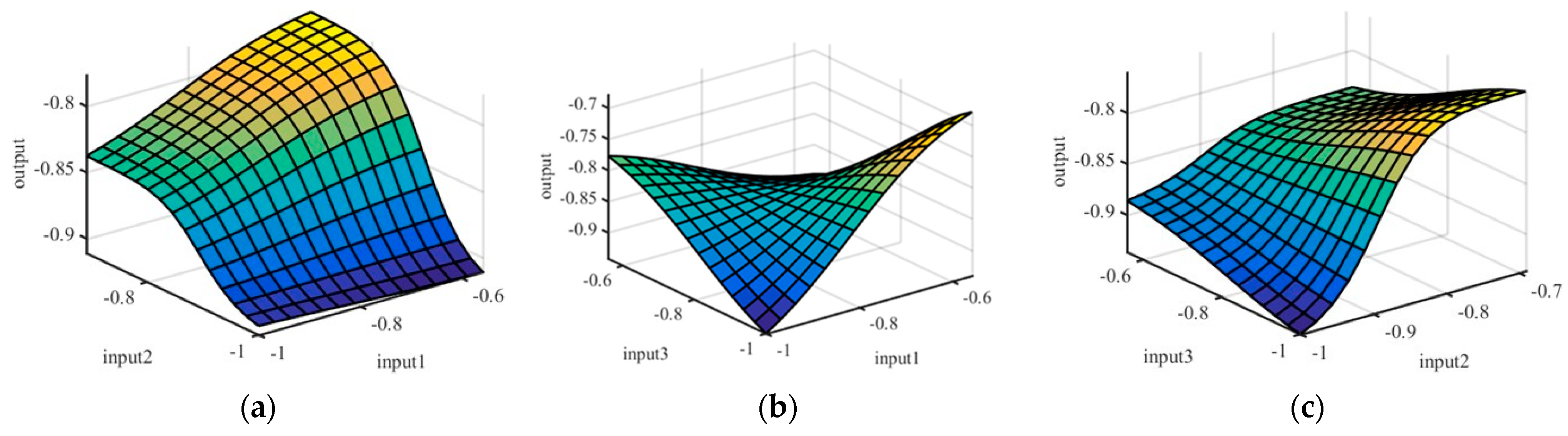
3.2. Parametric Analysis
3.3. Development of an Empirical Expression
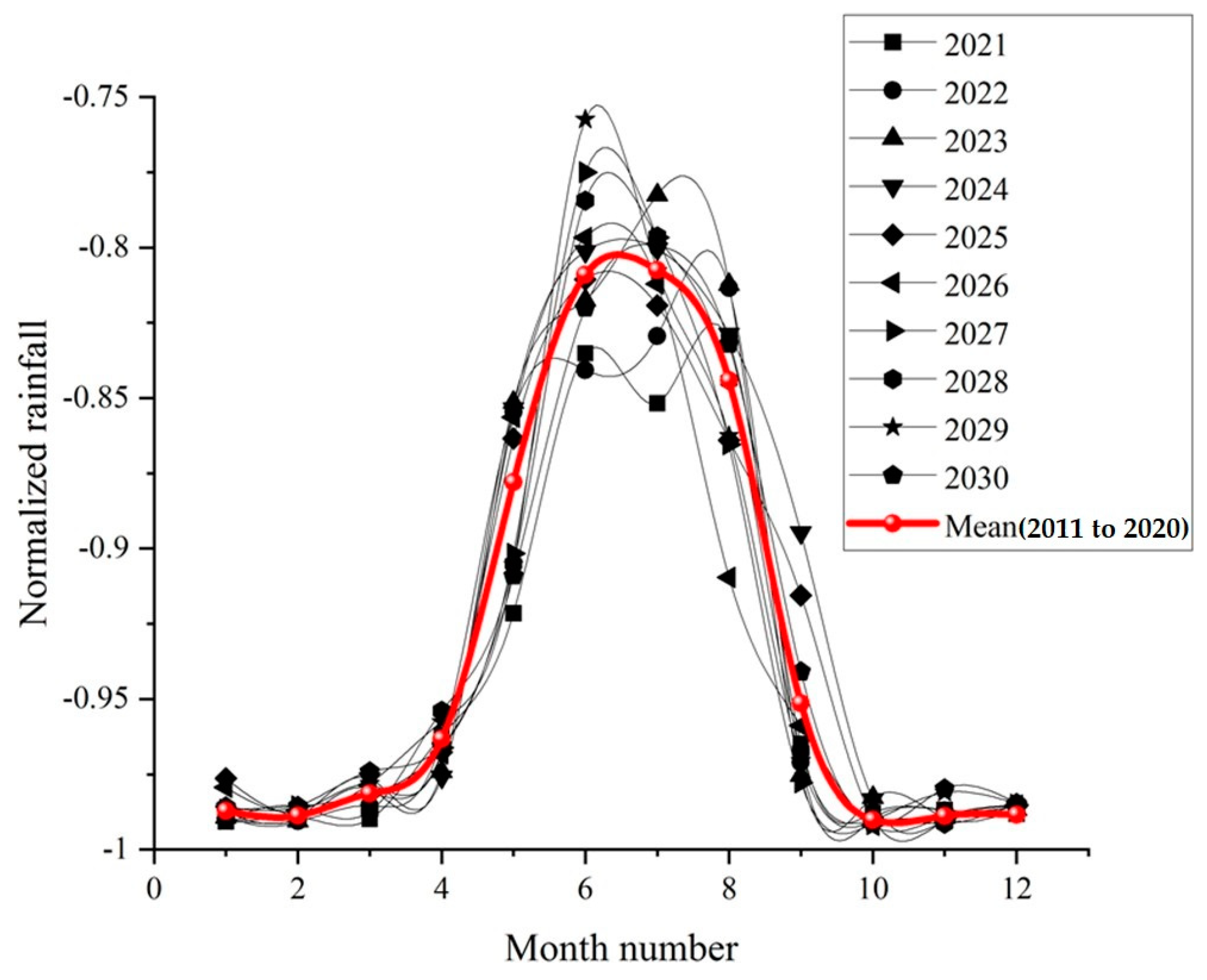
3.4. Forecasting Rainfalls for the Period 2021–2030 by Using the Developed Empirical Equation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rasel, H.M.; Imteaz, M.A. Application of Artificial Neural Network for seasonal rainfall forecasting: A case study for South Australia. In Proceedings of the World Congress on Engineering, London, UK, 29 June–1 July 2016. [Google Scholar]
- del Real, A.J.; Dorado, F.; Durán, J. Energy demand forecasting using deep learning: Applications for the French grid. Energies 2020, 13, 2242. [Google Scholar] [CrossRef]
- Nourani, V.; Komasi, M. A geomorphology-based ANFIS model for multi-station modeling of rainfall-runoff process. J. Hydrol. 2013, 490, 41–55. [Google Scholar] [CrossRef]
- Calp, M.H. A hybrid ANFIS-GA approach for estimation of regional rainfall amount. GU J. Sci. 2019, 32, 145–162. [Google Scholar]
- Emamgholizadeh, S.; Moslemi, K.; Karami, G. Prediction the groundwater level of Bastam Plain (Iran) by Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS). Water Resour. Manage. 2014, 28, 5433–5446. [Google Scholar] [CrossRef]
- Bacanli, U.G.; Firat, M.; Dikbas, F. Adaptive Neuro-Fuzzy Inference System for drought forecasting. Stoch. Environ. Res. Risk Assess. 2009, 23, 1143–1154. [Google Scholar] [CrossRef]
- Aldrian, E.; Djamil, Y.S. Application of multivariate ANFIS for daily rainfall prediction: Influences of training data size. Makara Sains 2008, 12, 7–14. [Google Scholar] [CrossRef]
- Tektas, M. Weather forecasting using ANFIS and ARIMA models. Environ. Res. Eng. Manag. 2010, 51, 5–10. [Google Scholar]
- Zhang, X.-d.; Li, A.; Pan, R. Stock trend prediction based on a new status box method and AdaBoost probabilistic Support Vector Machine. Appl. Soft. Comput. 2016, 49, 385–398. [Google Scholar] [CrossRef]
- Zhang, X.; Mohanty, S.N.; Parida, A.K.; Pani, S.K.; Dong, B.; Cheng, X. Annual and non-monsoon rainfall prediction modelling using SVR-MLP: An empirical study from Odisha. IEEE Access 2020, 8, 30223–30233. [Google Scholar] [CrossRef]
- Kiani, R.S.; Ali, S.; Ashfaq, M.; Khan, F.; Muhammad, S.; Reboita, M.S.; Farooqi, A. Hydrological projections over the Upper Indus Basin at 1.5 °C and 2.0 °C temperature increase. Sci. Total Environ. 2021, 788, 147759. [Google Scholar] [CrossRef]
- Mekanik, F.; Imteaz, M.A.; Talei, A. Seasonal rainfall forecasting by adaptive network-based fuzzy inference system (ANFIS) using large scale climate signals. Clim. Dyn. 2016, 46, 3097–3111. [Google Scholar] [CrossRef]
- Aftab, S.; Ahmad, M.; Hameed, N.; Bashir, M.S.; Ali, I.; Nawaz, Z. Rainfall prediction in Lahore City using data mining techniques. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 254–260. [Google Scholar] [CrossRef]
- Kyada, P.M.; Kumar, P.; Sojitra, M.A. Rainfall forecasting using Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS) models. Int. J. Agric. Sci. 2018, 10, 6153–6159. [Google Scholar]
- Usha, S.; Priya, S.B. An effective approach for promoting agriculture by predicting rainfall in India by using Machine Learning Techniques. J. Chem. Pharm. Sci.-Special Issue 2016, 37–43. [Google Scholar]
- Khajure, S.; Mohod, S.W. Future weather forecasting using soft computing techniques. Procedia Comput. Sci. 2016, 78, 402–407. [Google Scholar] [CrossRef] [Green Version]
- Chantry, M.; Christensen, H.; Dueben, P.; Palmer, T. Opportunities and challenges for machine learning in weather and climate modelling: Hard, medium and soft AI. Philos. Trans. A Math. Phys. Eng. Sci. 2021, 379, 20200083. [Google Scholar] [CrossRef]
- Novitasari, D.C.R.; Rohayani, H.; Suwanto; Arnita; Rico; Junaidi, R.; Setyowati, R.D.; Pramulya, R.; Setiawan, F. Weather parameters forecasting as variables for rainfall prediction using Adaptive Neuro Fuzzy Inference System (ANFIS) and Support Vector Regression (SVR). J. Phys. Conf. Ser. 2020, 1501, 012012. [Google Scholar] [CrossRef]
- Rani, S.I.; Arulalan, T.; George, J.P.; Rajagopal, E.N.; Renshaw, R.; Maycock, A.; Barker, D.M.; Rajeevan, M. IMDAA: High-resolution satellite-era reanalysis for the Indian monsoon region. J. Climate 2021, 34, 5109–5133. [Google Scholar] [CrossRef]
- Jang, J.-S.R.J. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE T. Syst. Man Cyb. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Karaboga, D.; Kaya, E. Adaptive network-based fuzzy inference system (ANFIS) training approaches: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2263–2293. [Google Scholar] [CrossRef]
- Kişi, Ö. Daily pan evaporation modelling using a neuro-fuzzy computing technique. J. Hydrol. 2006, 329, 636–646. [Google Scholar] [CrossRef]
- Rao, K.K.; Kulkarni, A.; Patwardhan, S.; Kumar, B.V.; Kumar, T.V.L. Future changes in precipitation extremes during northeast monsoon over south peninsular India. Theor. Appl. Climatol. 2020, 142, 205–217. [Google Scholar] [CrossRef]
- Ashrafi, M.; Chua, L.H.C.; Quek, C.; Qin, X. A fully-online Neuro-Fuzzy model for flow forecasting in basins with limited data. J. Hydrol. 2017, 545, 424–435. [Google Scholar] [CrossRef]
- Suparta, W.; Samah, A.A. Rainfall prediction by using ANFIS times series technique in South Tangerang, Indonesia. Geod. Geodyn. 2020, 11, 411–417. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-W. Flood prediction using Machine Learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Goyal, M.K. A comparison of three soft computing techniques, Bayesian Regression, Support Vector Regression, and Wavelet Regression, for monthly rainfall forecast. J. Intell. Syst. 2017, 26, 641–655. [Google Scholar] [CrossRef]
- Tarun, G.B.S.; Sriram, J.V.; Sairam, K.; Sreenivas, K.T.; Santhi, M.V.B.T. Rainfall prediction using Machine Learning Techniques. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 957–963. [Google Scholar]






| Parameters | Rainfall | Tmax | Tmin | RH | WS | SR |
|---|---|---|---|---|---|---|
| Unit | mm/day | °C | °C | % | m/s | kw-hr/m2/day |
| Frequency | Daily | |||||
| Time | 1983–2020 | |||||
| Source | Indian Monsoon Data Assimilation and Analysis (IMDAA) | |||||
| Spatial Resolution | 0.25° × 0.25° | |||||
| Inputs | Membership Function | |||
|---|---|---|---|---|
| Unit | MF1 | MF2 | ||
| σ | C | σ | C | |
| I1 | 0.2152 | −1.031 | 0.2323 | −0.6165 |
| I2 | 0.08962 | −1.032 | 0.1304 | −0.7043 |
| I3 | 0.2201 | −1.024 | 0.2318 | −0.6137 |
| Input | Constant |
|---|---|
| 1 | −1.084 |
| 2 | −0.783 |
| 3 | −1.099 |
| 4 | −0.6866 |
| 5 | −0.8932 |
| 6 | −0.9446 |
| 7 | −0.5058 |
| 8 | −0.9508 |
| Year | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | 0.007 | 0.002 | 0.002 | 0.001 | 0.003 | 0.001 | 0.005 | 0.002 | 0.001 | 0.003 |
| MAPE | 7.04 | 4.15 | 3.93 | 2.54 | 4.49 | 3.22 | 4.78 | 3.80 | 2.72 | 5.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, M.U.M.; Patra, K.C.; Sasmal, S.K.; Sharma, A.; Oliveto, G. Forecasting of Rainfall across River Basins Using Soft Computing Techniques: The Case Study of the Upper Brahmani Basin (India). Water 2023, 15, 499. https://doi.org/10.3390/w15030499
Rao MUM, Patra KC, Sasmal SK, Sharma A, Oliveto G. Forecasting of Rainfall across River Basins Using Soft Computing Techniques: The Case Study of the Upper Brahmani Basin (India). Water. 2023; 15(3):499. https://doi.org/10.3390/w15030499
Chicago/Turabian StyleRao, M. Uma Maheswar, Kanhu Charan Patra, Suvendu Kumar Sasmal, Anurag Sharma, and Giuseppe Oliveto. 2023. "Forecasting of Rainfall across River Basins Using Soft Computing Techniques: The Case Study of the Upper Brahmani Basin (India)" Water 15, no. 3: 499. https://doi.org/10.3390/w15030499







