Modeling Potential Evapotranspiration by Improved Machine Learning Methods Using Limited Climatic Data
Abstract
:1. Introduction
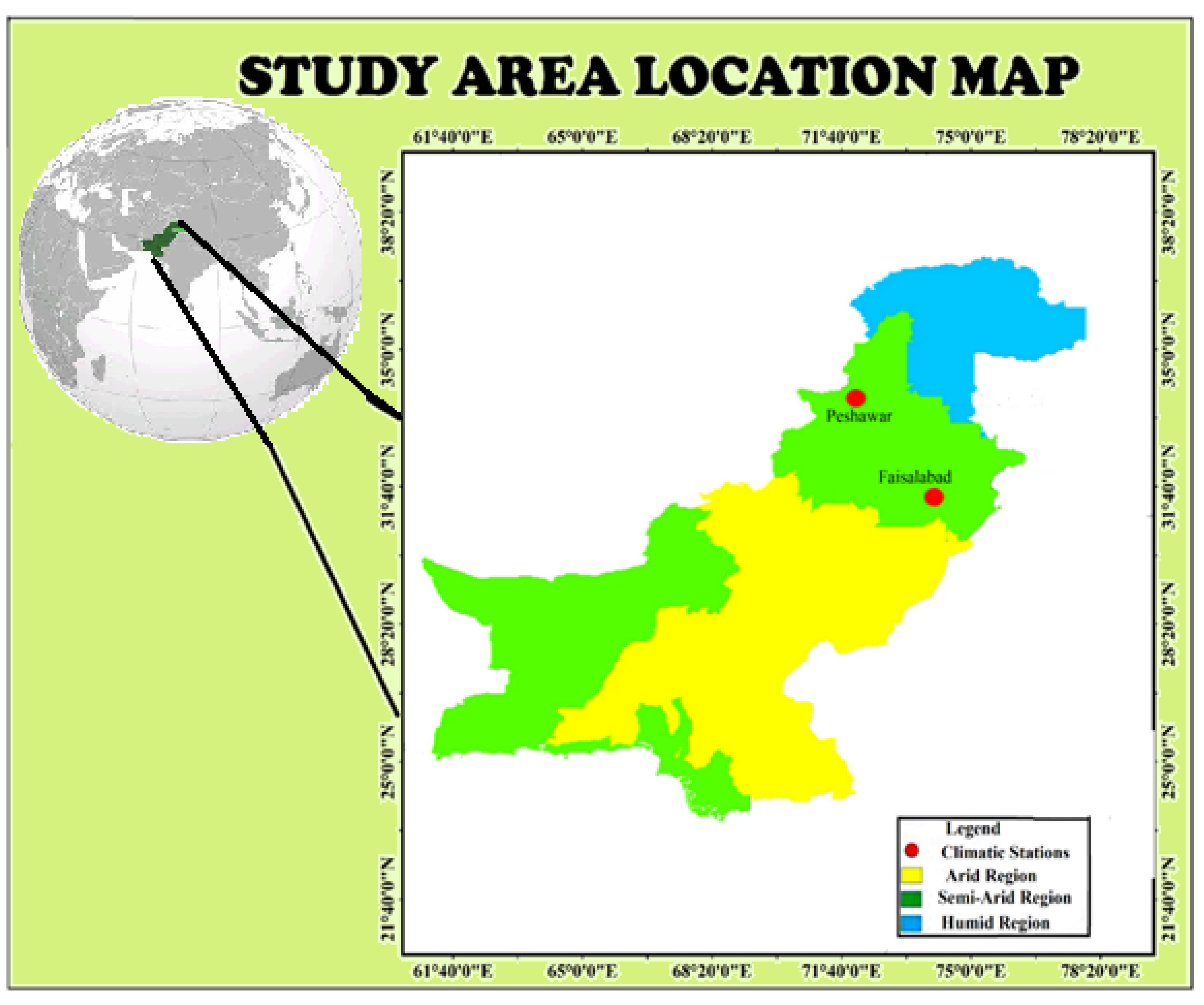
2. Case Study
3. Methods
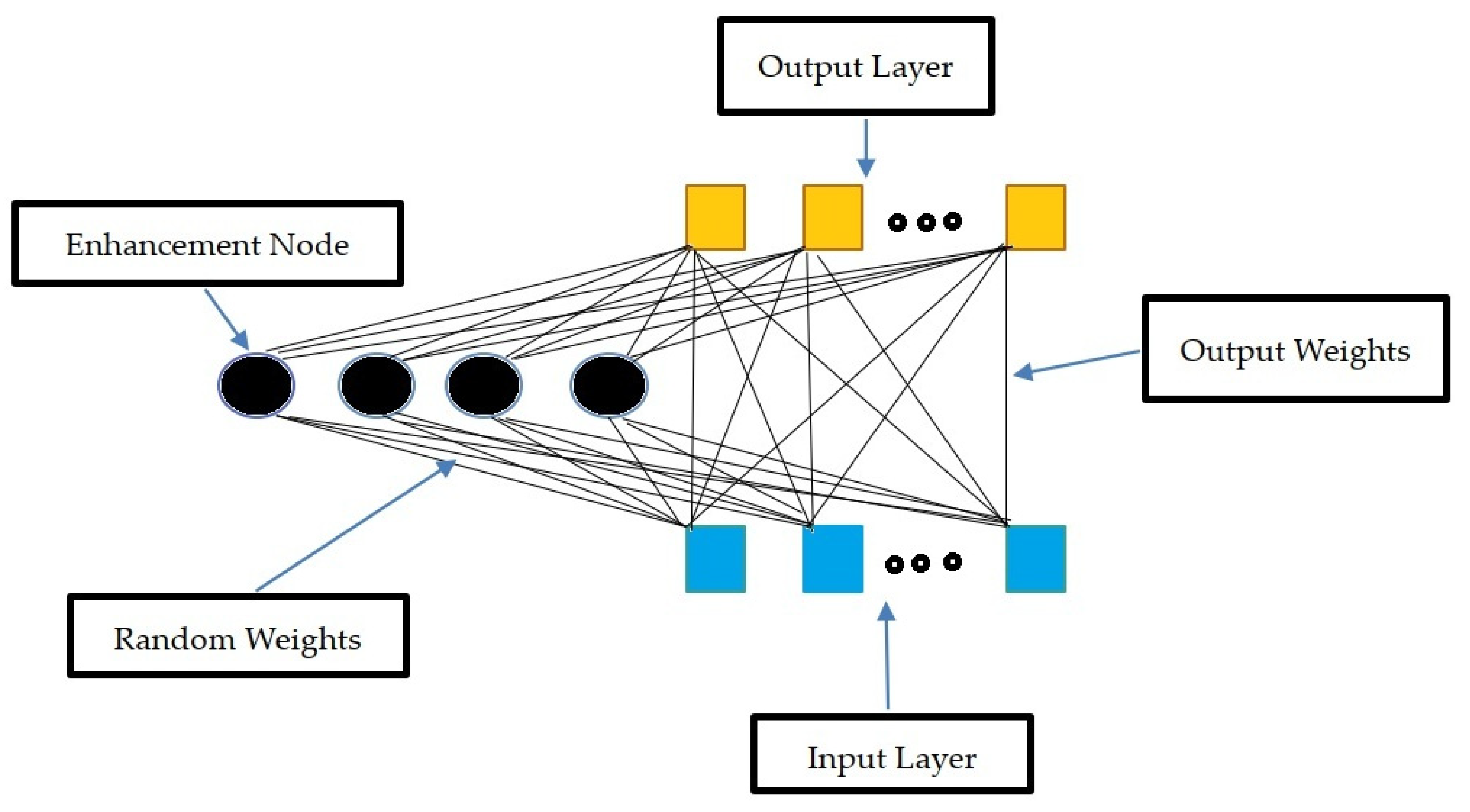
3.1. Random Vector Functional Link Networks (RVFL)
3.2. Relevance Vector Machine (RVM)
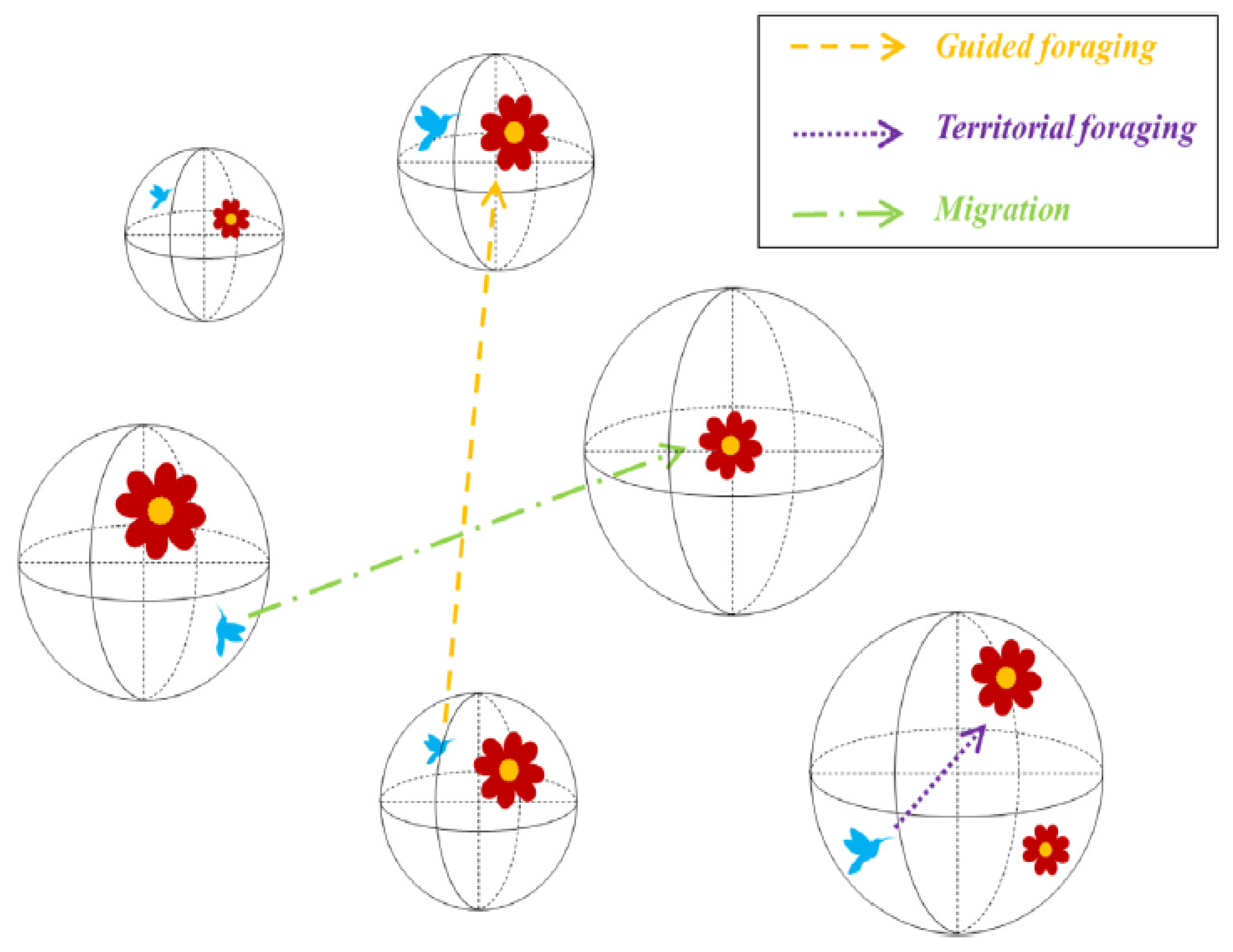
3.3. Artificial Hummingbird Algorithm (AHA)
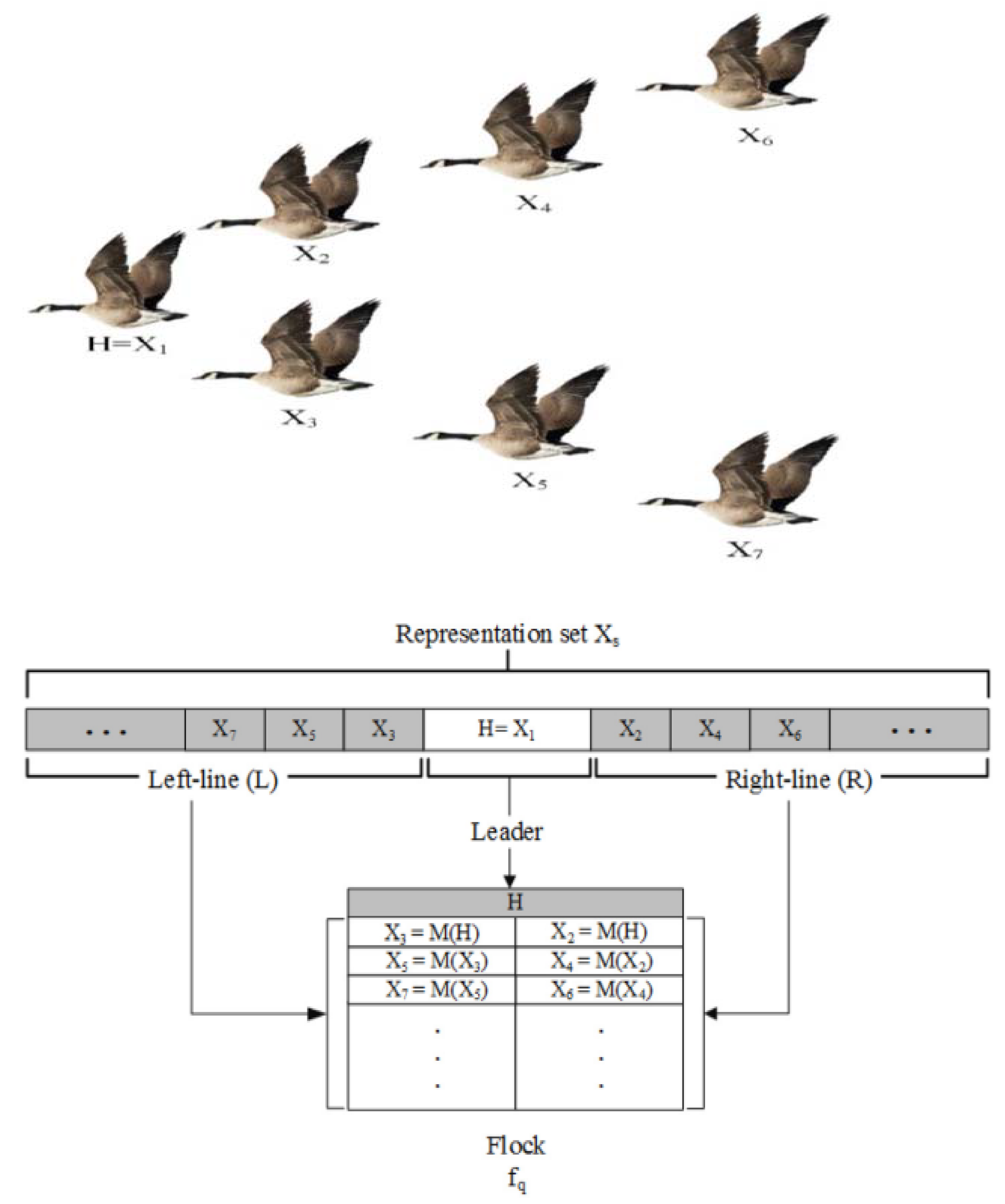
3.4. Quantum-Based Avian Navigation Optimizer Algorithm (QANA)
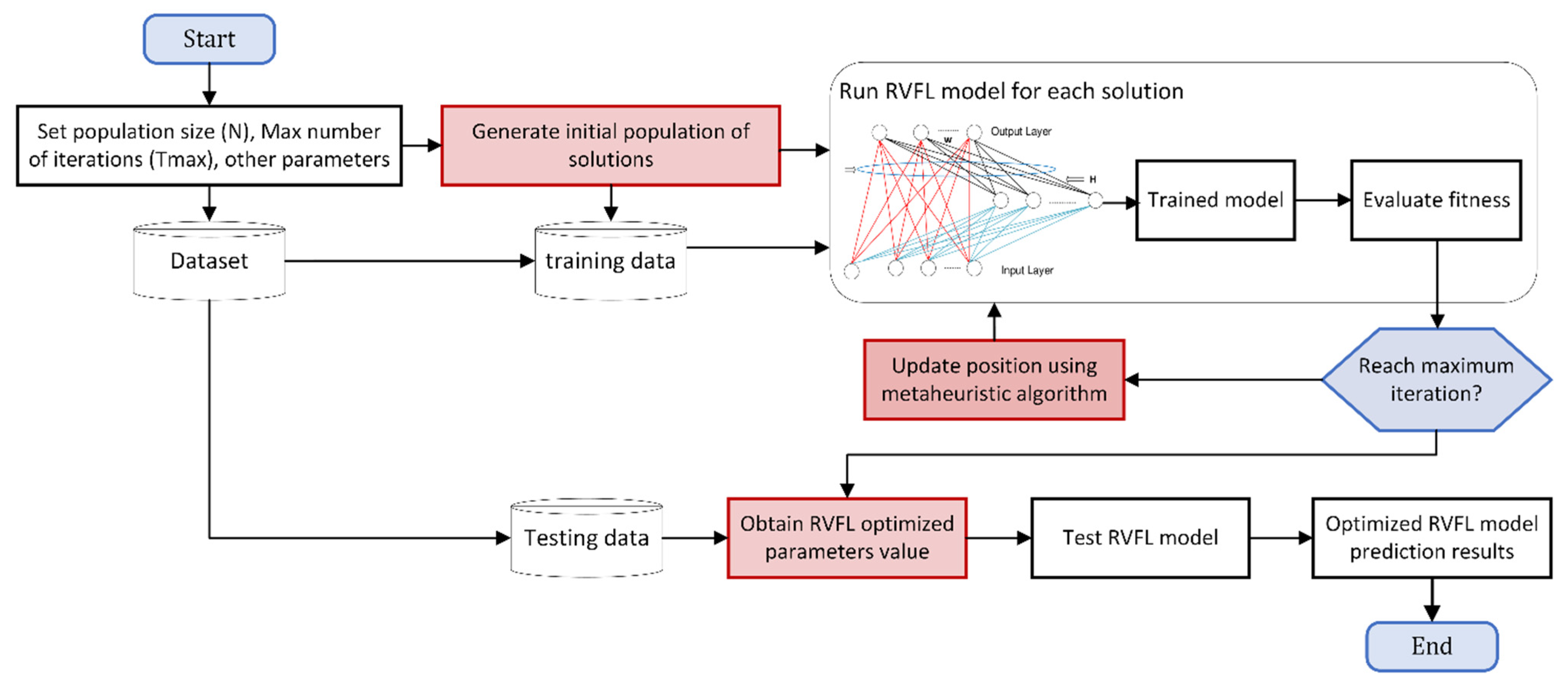
3.5. Proposed Optimized RVM and RVFL Models
3.6. Assessment of the Developed Methods and Parameters
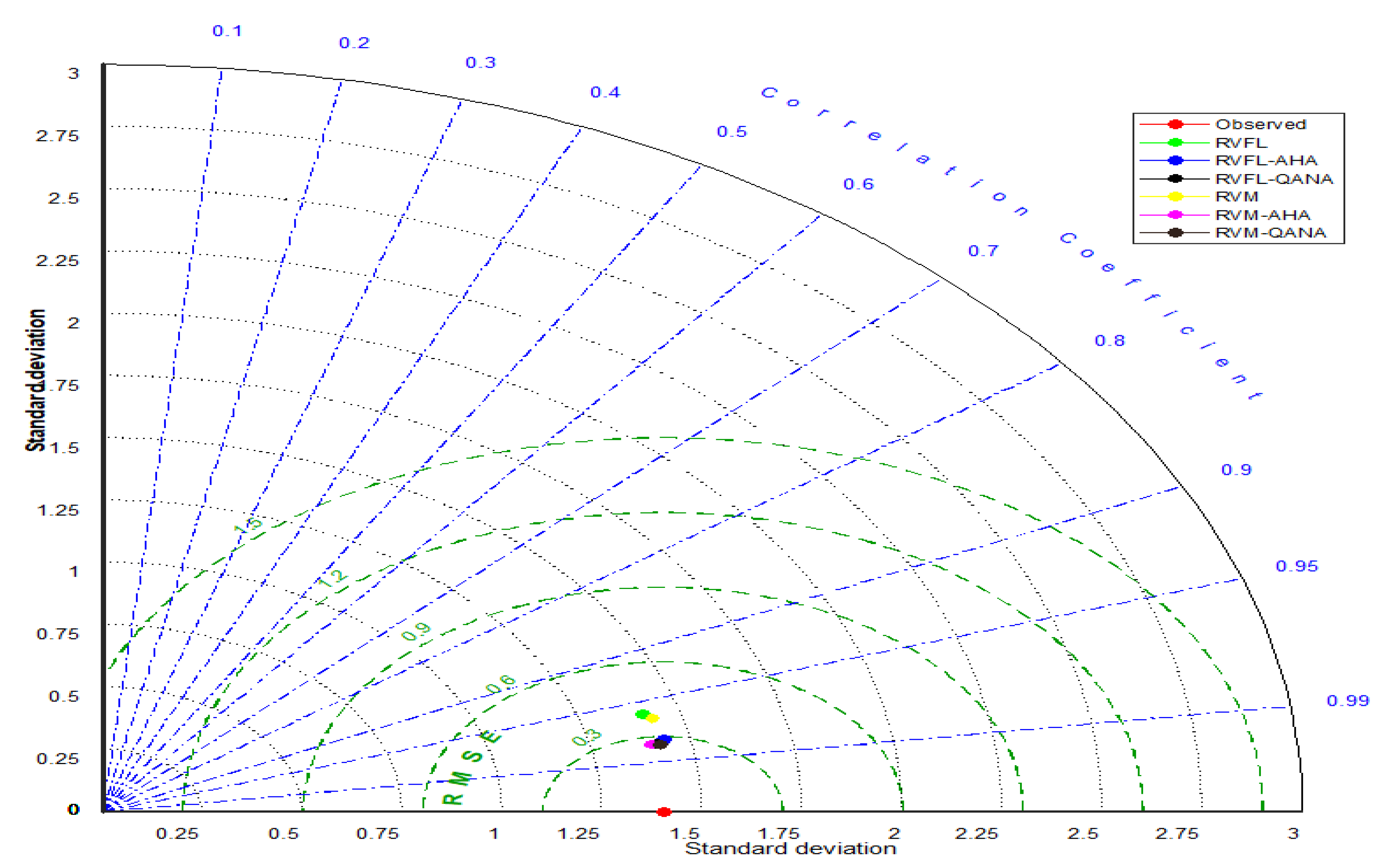
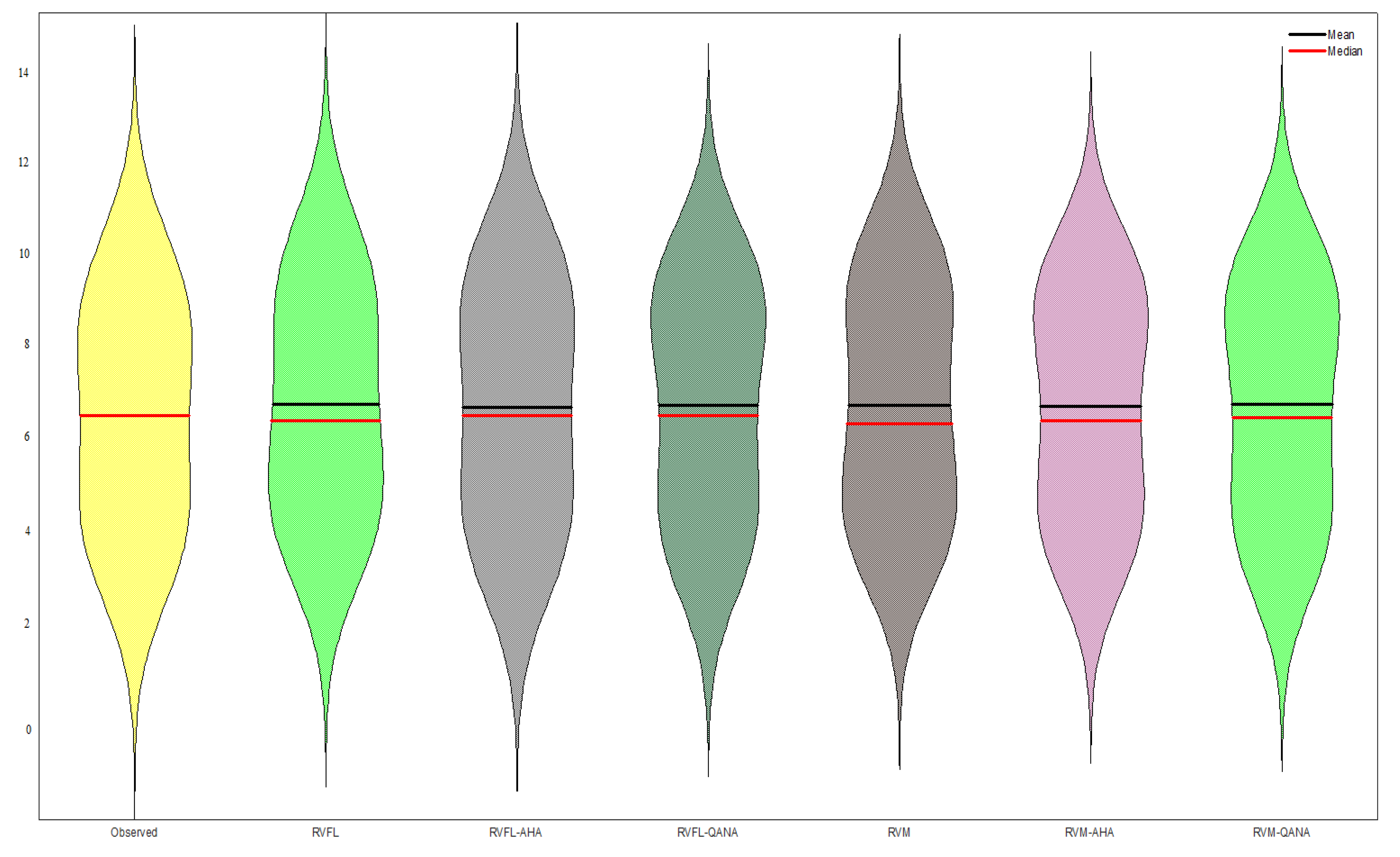
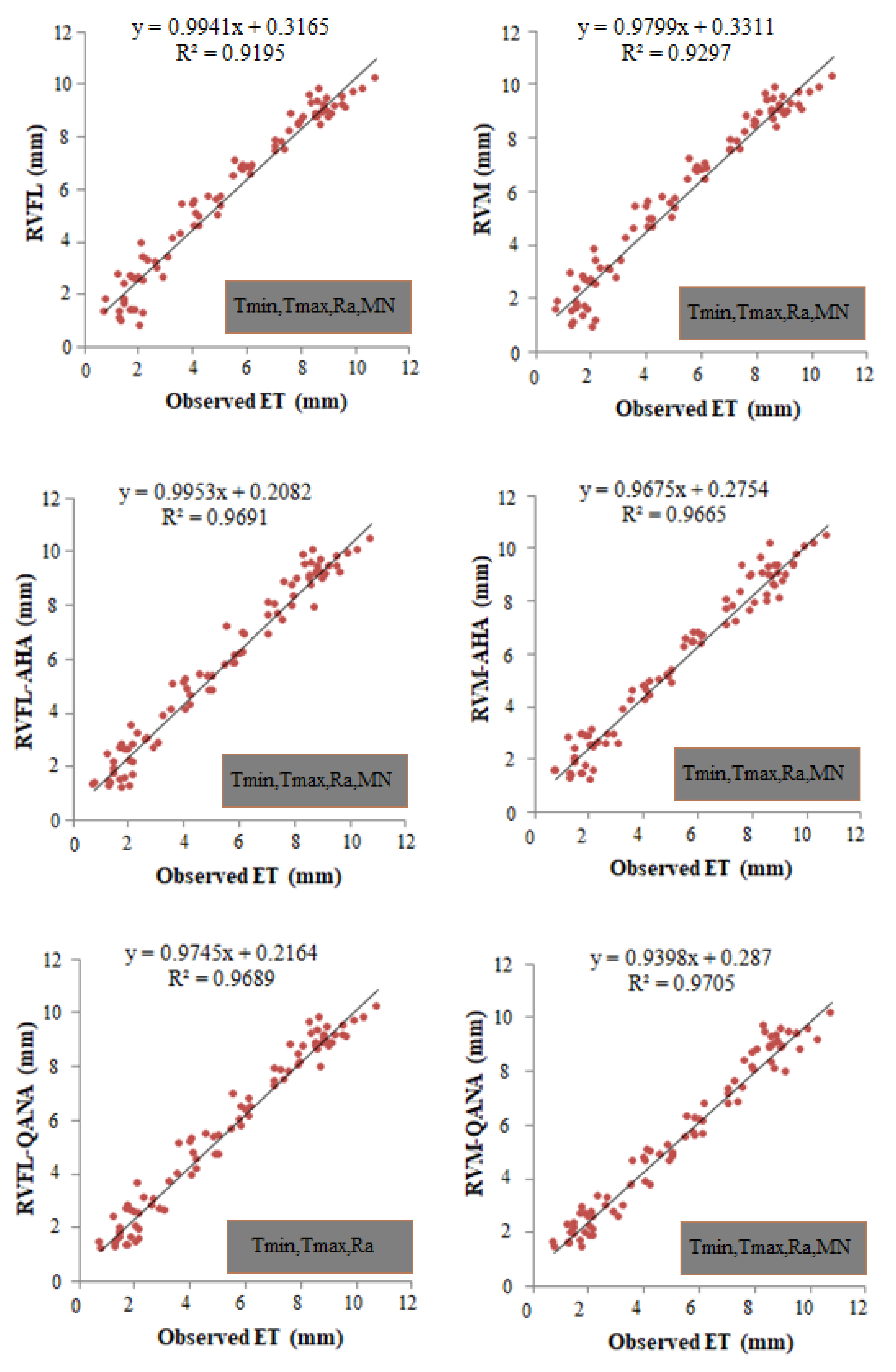
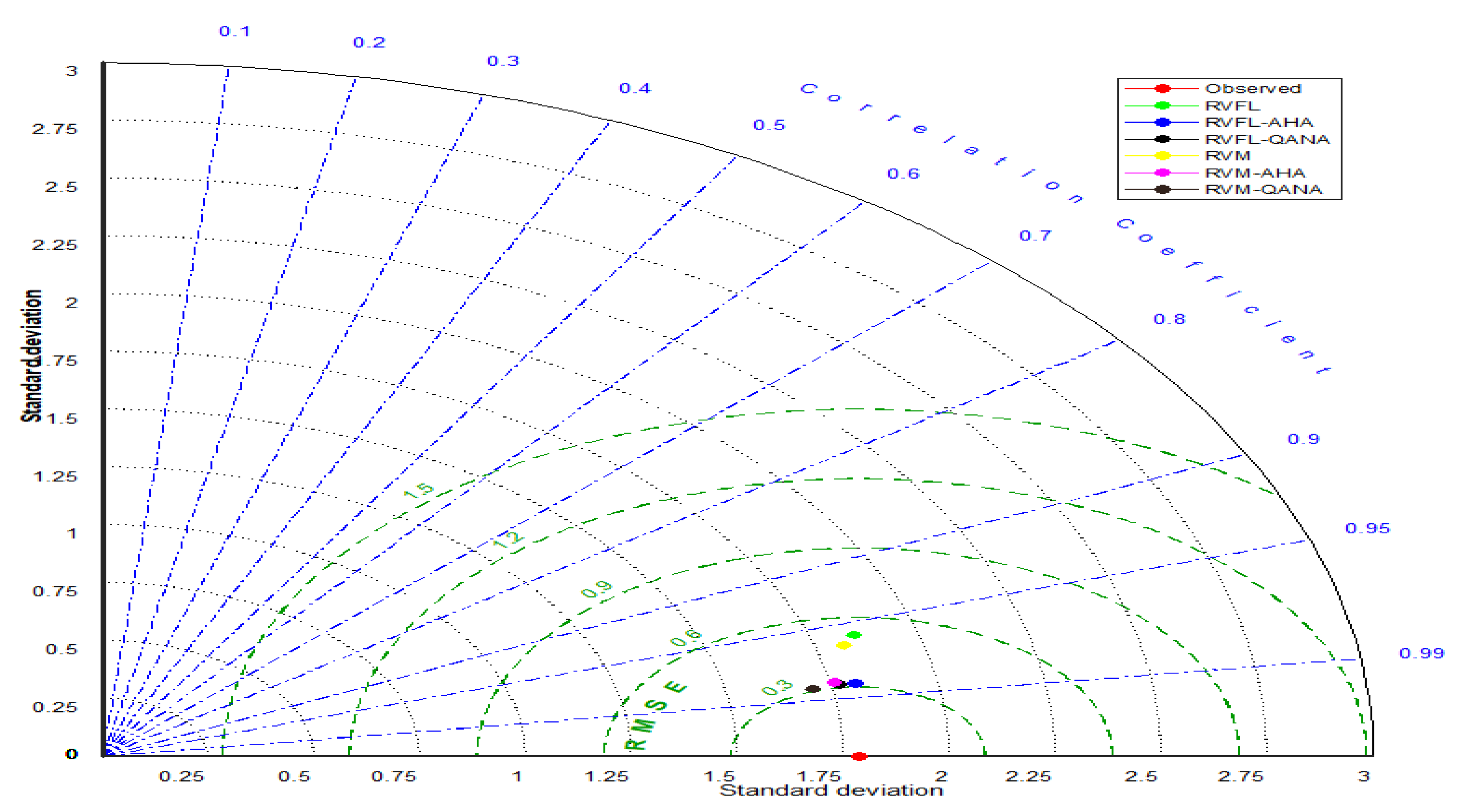
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Bejarano, M.D.; Garrote, L. Ecological impacts of run-of-river hydropower plants—Current status and future prospects on the brink of energy transition. Renew. Sustain. Energy Rev. 2021, 142, 110833. [Google Scholar] [CrossRef]
- Rost, S.; Gerten, D.; Bondeau, A.; Lucht, W.; Rohwer, J.; Schaphoff, S. Agricultural green and blue water consumption and its influence on the global water system. Water Resour. Res. 2008, 44, W09405. [Google Scholar] [CrossRef] [Green Version]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [Green Version]
- Zheng, C.; Jia, L.; Hu, G. Global land surface evapotranspiration monitoring by ETMonitor model driven by multi-source satellite earth observations. J. Hydrol. 2022, 613, 128444. [Google Scholar] [CrossRef]
- DehghaniSanij, H.; Yamamoto, T.; Rasiah, V. Assessment of evapotranspiration estimation models for use in semi-arid environments. Agric. Water Manag. 2004, 64, 91–106. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Adnan, R.M.; Kuriqi, A. Modelling reference evapotranspiration by combining neuro-fuzzy and evolutionary strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- El-Kenawy, E.-S.M.; Zerouali, B.; Bailek, N.; Bouchouich, K.; Hassan, M.A.; Almorox, J.; Kuriqi, A.; Eid, M.; Ibrahim, A. Improved weighted ensemble learning for predicting the daily reference evapotranspiration under the semi-arid climate conditions. Environ. Sci. Pollut. Res. 2022, 29, 81279–81299. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, J.; Xu, C.-Y.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- Malik, A.; Saggi, M.K.; Rehman, S.; Sajjad, H.; Inyurt, S.; Bhatia, A.S.; Farooque, A.A.; Oudah, A.Y.; Yaseen, Z.M. Deep learning versus gradient boosting machine for pan evaporation prediction. Eng. Appl. Comput. Fluid Mech. 2022, 16, 570–587. [Google Scholar] [CrossRef]
- Monteiro, A.F.M.; Martins, F.B.; Torres, R.R.; de Almeida, V.H.M.; Abreu, M.C.; Mattos, E.V. Intercomparison and uncertainty assessment of methods for estimating evapotranspiration using a high-resolution gridded weather dataset over Brazil. Theor. Appl. Clim. 2021, 146, 583–597. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Resolving data-hungry nature of machine learning reference evapotranspiration estimating models using inter-model ensembles with various data management schemes. Agric. Water Manag. 2021, 261, 107343. [Google Scholar] [CrossRef]
- Aryalekshmi, B.; Biradar, R.C.; Chandrasekar, K.; Ahamed, J.M. Analysis of various surface energy balance models for evapotranspiration estimation using satellite data. Egypt. J. Remote Sens. Space Sci. 2021, 24, 1119–1126. [Google Scholar] [CrossRef]
- Gocić, M.; Motamedi, S.; Shamshirband, S.; Petković, D.; Ch, S.; Hashim, R.; Arif, M. Soft computing approaches for forecasting reference evapotranspiration. Comput. Electron. Agric. 2015, 113, 164–173. [Google Scholar] [CrossRef]
- Kaya, Y.Z.; Zelenakova, M.; Üneş, F.; Demirci, M.; Hlavata, H.; Mesaros, P. Estimation of daily evapotranspiration in Košice City (Slovakia) using several soft computing techniques. Theor. Appl. Clim. 2021, 144, 287–298. [Google Scholar] [CrossRef]
- Gavili, S.; Sanikhani, H.; Kisi, O.; Mahmoudi, M.H. Evaluation of several soft computing methods in monthly evapotranspiration modelling. Meteorol. Appl. 2017, 25, 128–138. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Ma, X.; Wu, L.; Zhang, F.; Yu, X.; Zeng, W. Light Gradient Boosting Machine: An efficient soft computing model for estimating daily reference evapotranspiration with local and external meteorological data. Agric. Water Manag. 2019, 225, 105758. [Google Scholar] [CrossRef]
- Shamshirband, S.; Amirmojahedi, M.; Gocić, M.; Akib, S.; Petković, D.; Piri, J.; Trajkovic, S. Estimation of Reference Evapotranspiration Using Neural Networks and Cuckoo Search Algorithm. J. Irrig. Drain. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Aghelpour, P.; Bahrami-Pichaghchi, H.; Karimpour, F. Estimating Daily Rice Crop Evapotranspiration in Limited Climatic Data and Utilizing the Soft Computing Algorithms MLP, RBF, GRNN, and GMDH. Complexity 2022, 2022, 4534822. [Google Scholar] [CrossRef]
- Mokari, E.; DuBois, D.; Samani, Z.; Mohebzadeh, H.; Djaman, K. Estimation of daily reference evapotranspiration with limited climatic data using machine learning approaches across different climate zones in New Mexico. Theor. Appl. Clim. 2021, 147, 575–587. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; Filho, E.I.F. Exploring machine learning and multi-task learning to estimate meteorological data and reference evapotranspiration across Brazil. Agric. Water Manag. 2021, 259, 107281. [Google Scholar] [CrossRef]
- Sharma, G.; Singh, A.; Jain, S. A hybrid deep neural network approach to estimate reference evapotranspiration using limited climate data. Neural Comput. Appl. 2021, 34, 4013–4032. [Google Scholar] [CrossRef]
- Sharma, G.; Singh, A.; Jain, S. DeepEvap: Deep reinforcement learning based ensemble approach for estimating reference evapotranspiration. Appl. Soft Comput. 2022, 125, 109113. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H.; Ng, J.L.; Ahmed, A.N.; El-Shafie, A. Long-term forecasting of monthly mean reference evapotranspiration using deep neural network: A comparison of training strategies and approaches. Appl. Soft Comput. 2022, 126, 109221. [Google Scholar] [CrossRef]
- Thongkao, S.; Ditthakit, P.; Pinthong, S.; Salaeh, N.; Elkhrachy, I.; Linh, N.T.T.; Pham, Q.B. Estimating FAO Blaney-Criddle b-Factor Using Soft Computing Models. Atmosphere 2022, 13, 1536. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, X.; Li, Y.; Shi, Y.; Zhou, H.; Li, X.; Wang, X.; Xing, X. Applicability of hybrid bionic optimization models with kernel-based extreme learning machine algorithm for predicting daily reference evapotranspiration: A case study in arid and semi-arid regions, China. Environ. Sci. Pollut. Res. 2022, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Zounemat-Kermani, M. Advanced Hybrid Metaheuristic Machine Learning Models Application for Reference Crop Evapotranspiration Prediction. Agronomy 2023, 13, 98. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Raza, A.; Hu, Y.; Al-Ansari, N.; Kushwaha, N.L.; Srivastava, A.; Vishwakarma, D.K.; Zubair, M. Data intelligence and hybrid metaheuristic algorithms-based estimation of reference evapotranspiration. Appl. Water Sci. 2022, 12, 1–18. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Gorgij, A.D.; Kuriqi, A.; Kisi, O. Improving Drought Modeling Using Hybrid Random Vector Functional Link Methods. Water 2021, 13, 3379. [Google Scholar] [CrossRef]
- Caesarendra, W.; Widodo, A.; Yang, B.-S. Application of relevance vector machine and logistic regression for machine degradation assessment. Mech. Syst. Signal Process. 2010, 24, 1161–1171. [Google Scholar] [CrossRef]
- Pao, Y.-H.; Park, G.-H.; Sobajic, D.J. Learning and generalization characteristics of the random vector functional-link net. Neurocomputing 1994, 6, 163–180. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT-Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Guo, R.; Wang, J.; Zhang, N.; Dong, J. tate prediction for the actuators of civil aircraft based on a fusion framework of relevance vector machine and autoregressive integrated moving average. Proceedings of the Institution of Mechanical Engineers Part I. J. Syst. Control Eng. 2018, 232, 095965181876297. [Google Scholar]
- Zhang, Z.; Huang, C.; Ding, D.; Tang, S.; Han, B.; Huang, H. Hummingbirds optimization algorithm-based particle filter for maneuvering target tracking. Nonlinear Dyn. 2019, 97, 1227–1243. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2021, 388, 114194. [Google Scholar] [CrossRef]
- Bajec, I.L.; Heppner, F.H. Organized flight in birds. Anim. Behav. 2009, 78, 777–789. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece. Hydrology 2022, 9, 124. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Artificial Neural Networks for the Prediction of the Reference Evapotranspiration of the Peloponnese Peninsula, Greece. Water 2022, 14, 2027. [Google Scholar] [CrossRef]
- Shiri, J.; Zounemat-Kermani, M.; Kisi, O.; Karimi, S.M. Comprehensive assessment of 12 soft computing approaches for modelling reference evapotranspiration in humid locations. Meteorol. Appl. 2019, 27, e1841. [Google Scholar] [CrossRef] [Green Version]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Heddam, S. Estimating reference evapotranspiration using hybrid adaptive fuzzy inferencing coupled with heuristic algorithms. Comput. Electron. Agric. 2021, 191, 106541. [Google Scholar] [CrossRef]
- Niaghi, A.R.; Hassanijalilian, O.; Shiri, J. Estimation of Reference Evapotranspiration Using Spatial and Temporal Machine Learning Approaches. Hydrology 2021, 8, 25. [Google Scholar] [CrossRef]


| Tmin | Tmax | ET0 | Ra | |
|---|---|---|---|---|
| Faisalabad Station | ||||
| Min. | 3.25 | 16.15 | 1.07 | 18.83 |
| Max. | 28.8 | 42.2 | 10.53 | 41.34 |
| Mean | 17.5 | 31.1 | 4.71 | 31.05 |
| Skewness | −0.241 | −0.403 | 0.105 | −0.181 |
| Std. dev. | 8.326 | 7.324 | 2.444 | 8.051 |
| Peshawar Station | ||||
| Min. | −1.45 | 15.95 | 1.41 | 17.23 |
| Max. | 26.7 | 40.5 | 10.04 | 41.58 |
| Mean | 16.5 | 29.6 | 5.36 | 30.25 |
| Skewness | −0.176 | −0.344 | 0.267 | −0.147 |
| Std. dev. | 7.936 | 6.824 | 2.127 | 8.697 |
| Algorithm | Parameter | Value |
|---|---|---|
| AHA | Migration coefficient | 2n |
| r | ∈ [0,1] | |
| QANA | The number of flocks (𝑘) | 10 |
| K’ | 9 | |
| K’ | 50 | |
| Common Settings | Population | 30 |
| Number of iterations | 100 | |
| Number of runs for each Algorithm | 30 |
| Inputs Combinations | Training Period | Test Period | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| RFVL | ||||||||
| (i) Tmin, Tmax | 0.9049 | 0.7135 | 0.8012 | 0.8012 | 0.9181 | 0.7261 | 0.7987 | 0.7940 |
| (ii) Tmin, Ra | 0.7069 | 0.5387 | 0.9156 | 0.9128 | 0.7173 | 0.5458 | 0.9081 | 0.9058 |
| (iii) Tmax, Ra | 0.6849 | 0.5206 | 0.9240 | 0.9210 | 0.6875 | 0.5234 | 0.9180 | 0.9177 |
| (iv) Tmin, Tmax, Ra | 0.6919 | 0.5314 | 0.9216 | 0.9210 | 0.6983 | 0.5361 | 0.9166 | 0.9144 |
| (v) Tmin, Tmax, Ra, MN | 0.6825 | 0.5183 | 0.9228 | 0.9203 | 0.6866 | 0.5222 | 0.9221 | 0.9186 |
| Mean | 0.7342 | 0.5645 | 0.8970 | 0.8953 | 0.7416 | 0.5707 | 0.8927 | 0.8901 |
| RFVL-AHA | ||||||||
| (i) Tmin, Tmax | 0.8893 | 0.6939 | 0.8116 | 0.8114 | 0.9122 | 0.7140 | 0.8056 | 0.8021 |
| (ii) Tmin, Ra | 0.6375 | 0.4868 | 0.9492 | 0.9473 | 0.6447 | 0.4901 | 0.9469 | 0.9456 |
| (iii) Tmax, Ra | 0.6182 | 0.4569 | 0.9583 | 0.9567 | 0.6235 | 0.4625 | 0.9558 | 0.9543 |
| (iv) Tmin, Tmax, Ra | 0.6081 | 0.4524 | 0.9621 | 0.9596 | 0.6164 | 0.4599 | 0.9587 | 0.9572 |
| (v) Tmin, Tmax, Ra, MN | 0.6059 | 0.4507 | 0.9637 | 0.9605 | 0.6158 | 0.4562 | 0.9591 | 0.9580 |
| Mean | 0.6718 | 0.5081 | 0.9290 | 0.9271 | 0.6825 | 0.5165 | 0.9252 | 0.9234 |
| RFVL-QANA | ||||||||
| (i) Tmin, Tmax | 0.8565 | 0.6715 | 0.8340 | 0.8321 | 0.9082 | 0.7051 | 0.8058 | 0.8055 |
| (ii) Tmin, Ra | 0.6329 | 0.4816 | 0.9483 | 0.9462 | 0.6466 | 0.4861 | 0.9451 | 0.9448 |
| (iii) Tmax, Ra | 0.6034 | 0.4517 | 0.9625 | 0.9617 | 0.6082 | 0.4553 | 0.9608 | 0.9604 |
| (iv) Tmin, Tmax, Ra | 0.5958 | 0.4452 | 0.9649 | 0.9632 | 0.6068 | 0.4471 | 0.9625 | 0.9616 |
| (v) Tmin, Tmax, Ra, MN | 0.6028 | 0.4459 | 0.9638 | 0.9617 | 0.6079 | 0.4491 | 0.9616 | 0.9609 |
| Mean | 0.6583 | 0.4992 | 0.9347 | 0.9330 | 0.6755 | 0.5085 | 0.9272 | 0.9266 |
| Inputs Combinations | Training Period | Test Period | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| RVM | ||||||||
| (i) Tmin, Tmax | 0.9042 | 0.7125 | 0.8074 | 0.8043 | 0.9115 | 0.7134 | 0.8061 | 0.8025 |
| (ii) Tmin, Ra | 0.6873 | 0.5397 | 0.9253 | 0.9242 | 0.6960 | 0.5414 | 0.9204 | 0.9200 |
| (iii) Tmax, Ra | 0.6827 | 0.5209 | 0.9279 | 0.9269 | 0.6854 | 0.5220 | 0.9259 | 0.9244 |
| (iv) Tmin, Tmax, Ra | 0.6809 | 0.5204 | 0.9283 | 0.9274 | 0.6826 | 0.5227 | 0.9269 | 0.9260 |
| (v) Tmin, Tmax, Ra, MN | 0.6695 | 0.5106 | 0.9324 | 0.9315 | 0.6734 | 0.5134 | 0.9307 | 0.9294 |
| Mean | 0.7249 | 0.5608 | 0.9043 | 0.9029 | 0.7298 | 0.5626 | 0.9020 | 0.9005 |
| RVM-AHA | ||||||||
| (i) Tmin, Tmax | 0.8615 | 0.6672 | 0.8269 | 0.8257 | 0.9020 | 0.7139 | 0.8125 | 0.8087 |
| (ii) Tmin, Ra | 0.6396 | 0.4835 | 0.9503 | 0.9486 | 0.6437 | 0.4890 | 0.9472 | 0.9460 |
| (iii) Tmax, Ra | 0.5798 | 0.4348 | 0.9681 | 0.9681 | 0.6229 | 0.4594 | 0.9548 | 0.9546 |
| (iv) Tmin, Tmax, Ra | 0.5546 | 0.4149 | 0.9775 | 0.9775 | 0.6068 | 0.4487 | 0.9621 | 0.9610 |
| (v) Tmin, Tmax, Ra, MN | 0.5460 | 0.4062 | 0.9805 | 0.9805 | 0.6047 | 0.4462 | 0.9626 | 0.9617 |
| Mean | 0.6363 | 0.4813 | 0.9407 | 0.9401 | 0.6760 | 0.5114 | 0.9278 | 0.9264 |
| RVM-QANA | ||||||||
| (i) Tmin, Tmax | 0.8067 | 0.6214 | 0.8560 | 0.8560 | 0.8900 | 0.7048 | 0.8164 | 0.8163 |
| (ii) Tmin, Ra | 0.6119 | 0.4492 | 0.9569 | 0.9569 | 0.6413 | 0.4824 | 0.9484 | 0.9470 |
| (iii) Tmax, Ra | 0.6076 | 0.4583 | 0.9612 | 0.9603 | 0.6143 | 0.4547 | 0.9587 | 0.9580 |
| (iv) Tmin, Tmax, Ra | 0.5766 | 0.4262 | 0.9706 | 0.9706 | 0.6070 | 0.4542 | 0.9616 | 0.9609 |
| (v) Tmin, Tmax, Ra, MN | 0.5604 | 0.4141 | 0.9765 | 0.9765 | 0.6062 | 0.4438 | 0.9639 | 0.9622 |
| Mean | 0.6326 | 0.4738 | 0.9442 | 0.9441 | 0.6718 | 0.5080 | 0.9298 | 0.9289 |
| Inputs Combinations | Training Period | Test Period | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| RFVL | ||||||||
| (i) Tmin, Tmax | 0.7186 | 0.5687 | 0.8571 | 0.8571 | 0.8369 | 0.6786 | 0.8525 | 0.8303 |
| (ii) Tmin, Ra | 0.7392 | 0.5541 | 0.9220 | 0.9196 | 0.7554 | 0.6083 | 0.9136 | 0.9038 |
| (iii) Tmax, Ra | 0.6791 | 0.5034 | 0.9333 | 0.9333 | 0.7144 | 0.5371 | 0.9159 | 0.9098 |
| (iv) Tmin, Tmax, Ra | 0.6495 | 0.4879 | 0.9444 | 0.9441 | 0.6961 | 0.5452 | 0.9178 | 0.9128 |
| (v) Tmin, Tmax, Ra, MN | 0.6483 | 0.4861 | 0.9446 | 0.9444 | 0.6943 | 0.5360 | 0.9195 | 0.9141 |
| Mean | 0.6869 | 0.5200 | 0.9203 | 0.9197 | 0.7394 | 0.5810 | 0.9039 | 0.8942 |
| RFVL-AHA | ||||||||
| (i) Tmin, Tmax | 0.6998 | 0.5617 | 0.8649 | 0.8645 | 0.7852 | 0.6376 | 0.8342 | 0.8366 |
| (ii) Tmin, Ra | 0.5047 | 0.4150 | 0.9531 | 0.9352 | 0.5342 | 0.4101 | 0.9524 | 0.9301 |
| (iii) Tmax, Ra | 0.4198 | 0.3594 | 0.9634 | 0.9467 | 0.4905 | 0.3828 | 0.9572 | 0.9447 |
| (iv) Tmin, Tmax, Ra | 0.4268 | 0.3360 | 0.9651 | 0.9543 | 0.4367 | 0.3617 | 0.9623 | 0.9502 |
| (v) Tmin, Tmax, Ra, MN | 0.3841 | 0.2876 | 0.9724 | 0.9635 | 0.3917 | 0.2904 | 0.9691 | 0.9567 |
| Mean | 0.4870 | 0.3919 | 0.9438 | 0.9328 | 0.5277 | 0.4165 | 0.9350 | 0.9237 |
| RFVL-QANA | ||||||||
| (i) Tmin, Tmax | 0.6519 | 0.5101 | 0.8835 | 0.8824 | 0.7756 | 0.6052 | 0.8535 | 0.8413 |
| (ii) Tmin, Ra | 0.4895 | 0.3827 | 0.9564 | 0.9361 | 0.5016 | 0.3921 | 0.9543 | 0.9348 |
| (iii) Tmax, Ra | 0.3935 | 0.3060 | 0.9648 | 0.9526 | 0.4408 | 0.3451 | 0.9637 | 0.9514 |
| (iv) Tmin, Tmax, Ra | 0.3426 | 0.2690 | 0.9693 | 0.9671 | 0.3754 | 0.2935 | 0.9689 | 0.9632 |
| (v) Tmin, Tmax, Ra, MN | 0.3892 | 0.3022 | 0.9704 | 0.9581 | 0.4223 | 0.3435 | 0.9670 | 0.9541 |
| Mean | 0.4533 | 0.3540 | 0.9489 | 0.9393 | 0.5031 | 0.3959 | 0.9415 | 0.9290 |
| Inputs Combinations | Training Period | Test Period | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| RVM | ||||||||
| (i) Tmin, Tmax | 0.7157 | 0.5647 | 0.8584 | 0.8583 | 0.8346 | 0.6260 | 0.8092 | 0.7915 |
| (ii) Tmin, Ra | 0.6678 | 0.5502 | 0.9215 | 0.9136 | 0.6759 | 0.5900 | 0.9199 | 0.8929 |
| (iii) Tmax, Ra | 0.6410 | 0.4934 | 0.9363 | 0.9333 | 0.6578 | 0.5414 | 0.9216 | 0.9201 |
| (iv) Tmin, Tmax, Ra | 0.6100 | 0.4815 | 0.9328 | 0.9256 | 0.6435 | 0.5362 | 0.9289 | 0.9205 |
| (v) Tmin, Tmax, Ra, MN | 0.5951 | 0.4725 | 0.9461 | 0.9452 | 0.6436 | 0.5369 | 0.9297 | 0.9283 |
| Mean | 0.6459 | 0.5125 | 0.9190 | 0.9152 | 0.6911 | 0.5661 | 0.9019 | 0.8907 |
| RVM-AHA | ||||||||
| (i) Tmin, Tmax | 0.7060 | 0.5649 | 0.8629 | 0.8621 | 0.7853 | 0.6096 | 0.8577 | 0.8466 |
| (ii) Tmin, Ra | 0.4567 | 0.3540 | 0.9499 | 0.9198 | 0.5385 | 0.4169 | 0.9474 | 0.9346 |
| (iii) Tmax, Ra | 0.4284 | 0.3501 | 0.9620 | 0.9418 | 0.4338 | 0.3612 | 0.9575 | 0.9410 |
| (iv) Tmin, Tmax, Ra | 0.4110 | 0.3409 | 0.9662 | 0.9560 | 0.4258 | 0.3529 | 0.9650 | 0.9534 |
| (v) Tmin, Tmax, Ra, MN | 0.3618 | 0.2988 | 0.9695 | 0.9594 | 0.3688 | 0.3009 | 0.9665 | 0.9573 |
| Mean | 0.4728 | 0.3817 | 0.9421 | 0.9278 | 0.5104 | 0.4083 | 0.9388 | 0.9266 |
| RVM-QANA | ||||||||
| (i) Tmin, Tmax | 0.5643 | 0.4390 | 0.9119 | 0.9119 | 0.7823 | 0.6087 | 0.8537 | 0.8480 |
| (ii) Tmin, Ra | 0.4104 | 0.3208 | 0.9618 | 0.9534 | 0.4682 | 0.3880 | 0.9548 | 0.9312 |
| (iii) Tmax, Ra | 0.3659 | 0.2810 | 0.9630 | 0.9630 | 0.3999 | 0.3185 | 0.9623 | 0.9498 |
| (iv) Tmin, Tmax, Ra | 0.3088 | 0.2328 | 0.9736 | 0.9736 | 0.4347 | 0.3616 | 0.9685 | 0.9407 |
| (v) Tmin, Tmax, Ra, MN | 0.3132 | 0.2452 | 0.9729 | 0.9729 | 0.3252 | 0.2696 | 0.9705 | 0.9668 |
| Mean | 0.3925 | 0.3038 | 0.9566 | 0.9550 | 0.4821 | 0.3893 | 0.9420 | 0.9273 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mostafa, R.R.; Kisi, O.; Adnan, R.M.; Sadeghifar, T.; Kuriqi, A. Modeling Potential Evapotranspiration by Improved Machine Learning Methods Using Limited Climatic Data. Water 2023, 15, 486. https://doi.org/10.3390/w15030486
Mostafa RR, Kisi O, Adnan RM, Sadeghifar T, Kuriqi A. Modeling Potential Evapotranspiration by Improved Machine Learning Methods Using Limited Climatic Data. Water. 2023; 15(3):486. https://doi.org/10.3390/w15030486
Chicago/Turabian StyleMostafa, Reham R., Ozgur Kisi, Rana Muhammad Adnan, Tayeb Sadeghifar, and Alban Kuriqi. 2023. "Modeling Potential Evapotranspiration by Improved Machine Learning Methods Using Limited Climatic Data" Water 15, no. 3: 486. https://doi.org/10.3390/w15030486











