Assessing 1D Hydrodynamic Modeling of Júcar River Behavior in Mancha Oriental Aquifer Domain (SE Spain)
Abstract
1. Introduction
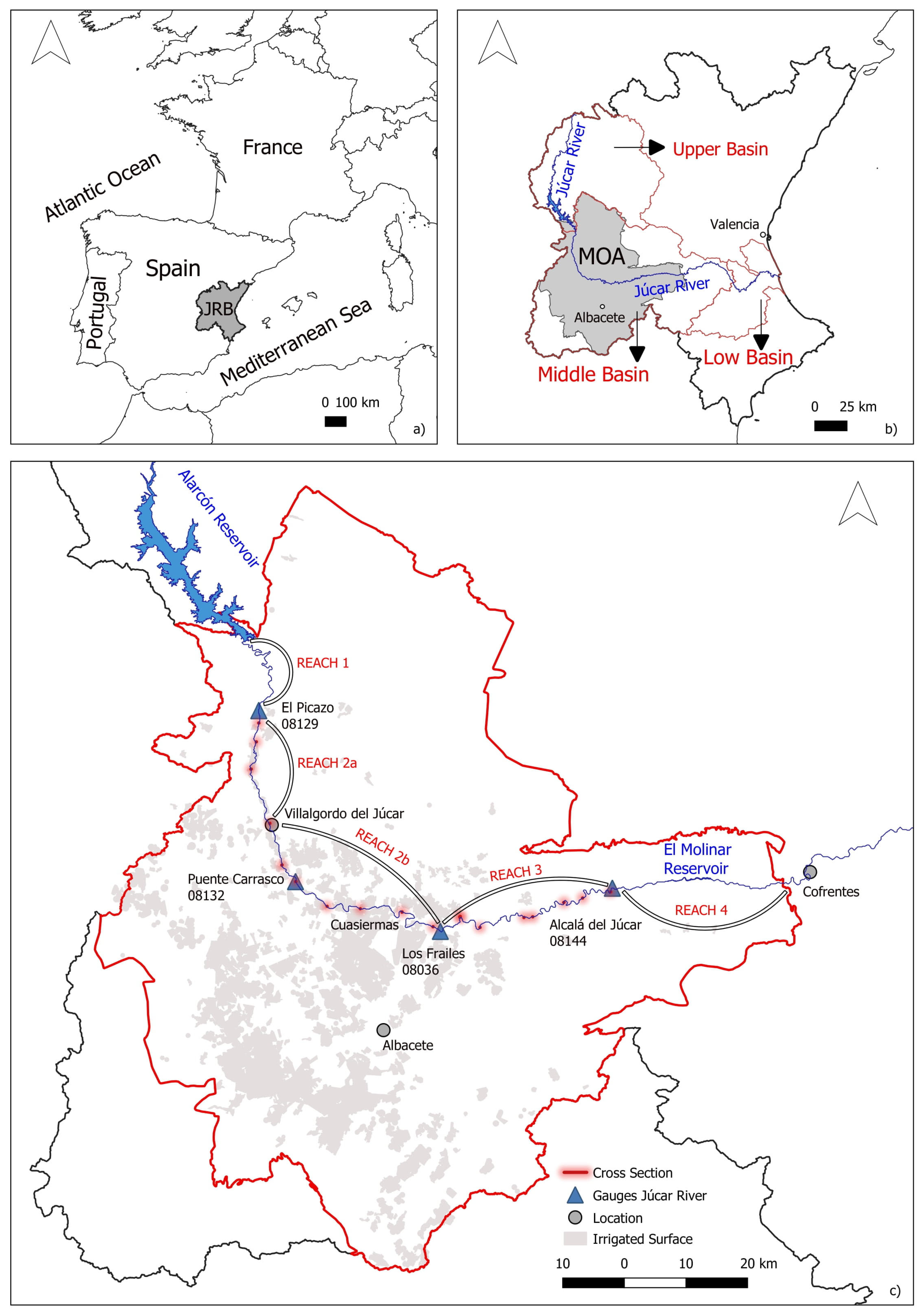
2. Study Area
3. Materials and Methods
3.1. Data Acquisition
| General Description | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| CHJ Code | 08129 | 08132 | 08036 | 08144 | |||||
| Location | El Picazo | Puente Carrasco | Los Frailes | Alcalá del Júcar | |||||
| UTM ETRS89 H30 X | 578628 | 584728 | 608082 | 635980 | |||||
| UTM ETRS89 H30 Y | 4368600 | 4341164 | 43327912 | 4339792 | |||||
| Elevation, (m.a.s.l.) | 694 | 647 | 605 | 514 | |||||
| Studied variables | QPicazo | hPicazo | QCarrasco | hCarrasco | QFrailes | hFrailes | QAlcalá | hAlcalá | |
| (m3s−1) | (m) | (m3s−1) | (m) | (m3s−1) | (m) | (m3s−1) | (m) | ||
| Time periods with data availability * | 01.01.1974– 30.09.2019 | 01.01.1974– 30.09.2019 | 01.01.1974– 30.09.1986 | 01.01.1974– 30.09.1986 | 01.01.1974– 30.09.1988 25.10.1991– 30.09.2019 | 01.01.1974– 30.09.1988 26.10.1991– 30.09.2019 | 01.10.1974– 30.09.1980 12.06.1984– 30.09.2019 | 13.06.1984– 18.04.2011 30.09.2015– 30.09.2019 | |
| Data use in the model | Boundary cond. in | Calibration | Validation | Validation | Calibration | Calibration | Boundary cond. out | Boundary cond. out | |
| Descriptive statistics | |||||||||
| Mean (m3s−1) | 8.055 | 0.568 | 10.120 | 0.907 | 9.416 | 0.480 | 9.915 | 0.400 | |
| Minimum (m3s−1) | 0.044 | 0.080 | 0.000 | 0.000 | 0.344 | 0.010 | 0.001 | 0.130 | |
| Maximum (m3s−1) | 42.440 | 3.440 | 46.600 | 1.990 | 57.102 | 1.220 | 74.000 | 1.170 | |
| Standard deviation (m3s−1) | 8.260 | 0.263 | 8.267 | 0.335 | 9.165 | 0.199 | 8.283 | 0.215 | |
| Coefficient of variation | 1.025 | 0.463 | 0.770 | 0.369 | 0.973 | 0.4715 | 0.835 | 0.508 | |
| Variance | 68.230 | 0.069 | 68.342 | 0.112 | 84.005 | 0.0395 | 68.606 | 0.046 | |
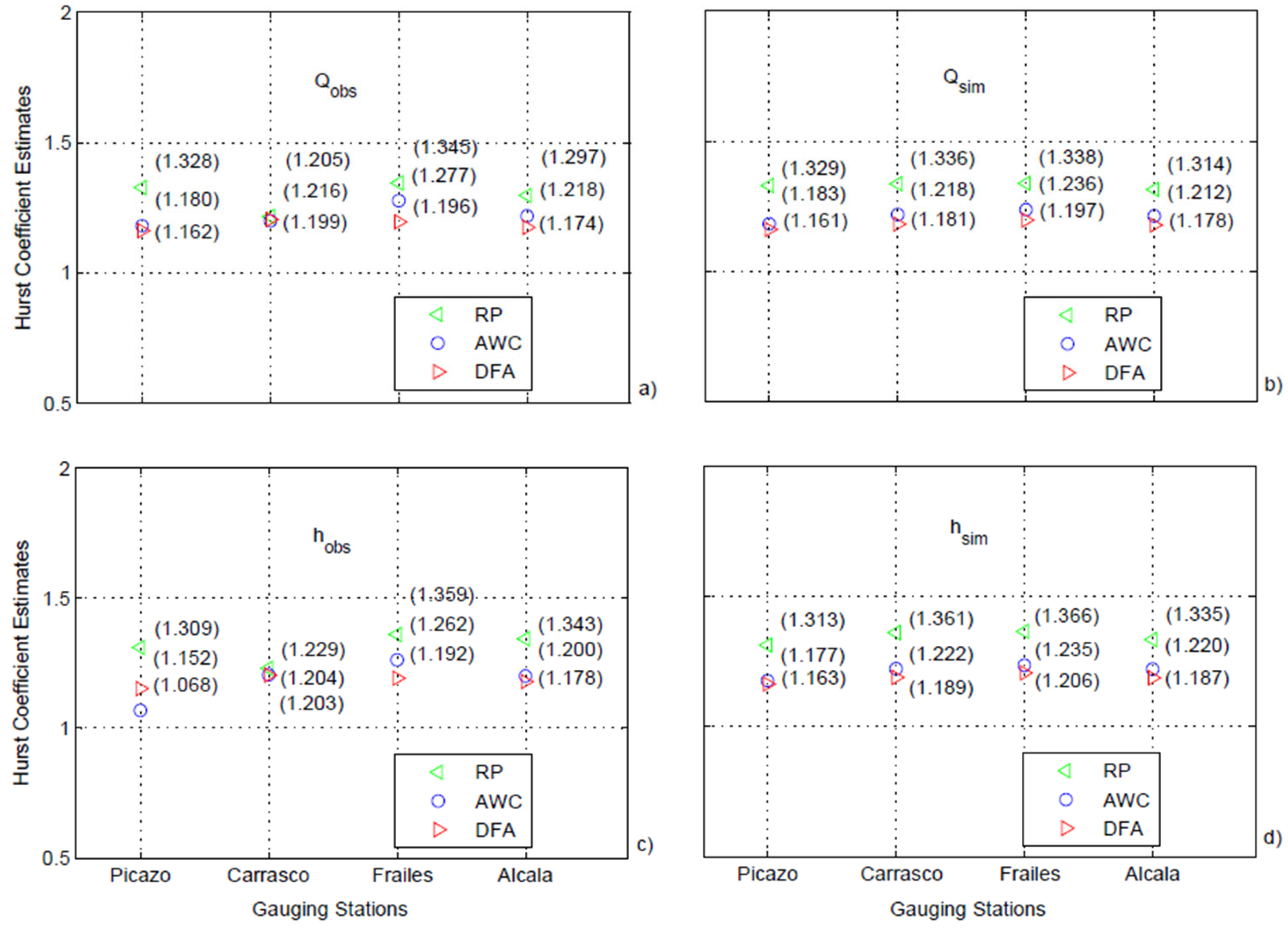
| H—RP | 1.328 | 1.310 | 1.216 | 1.230 | 1.345 | 1.360 | 1.297 | 1.335 | |
| H—AWC | 1.180 | 1.068 | 1.199 | 1.204 | 1.277 | 1.262 | 1.218 | 1.220 | |
| H—DFA | 1.162 | 1.152 | 1.205 | 1.203 | 1.196 | 1.192 | 1.174 | 1.187 | |
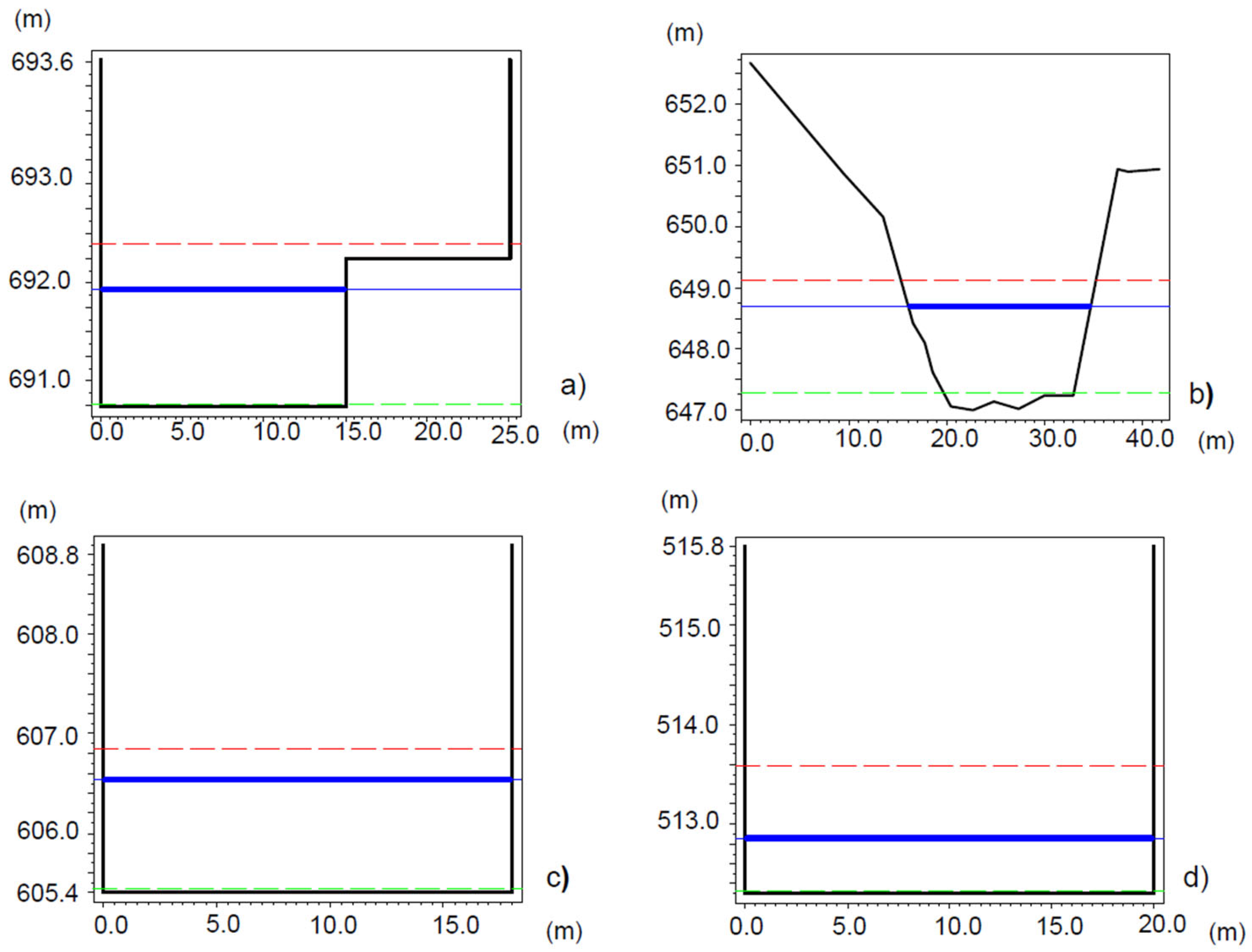
3.2. Model Setup
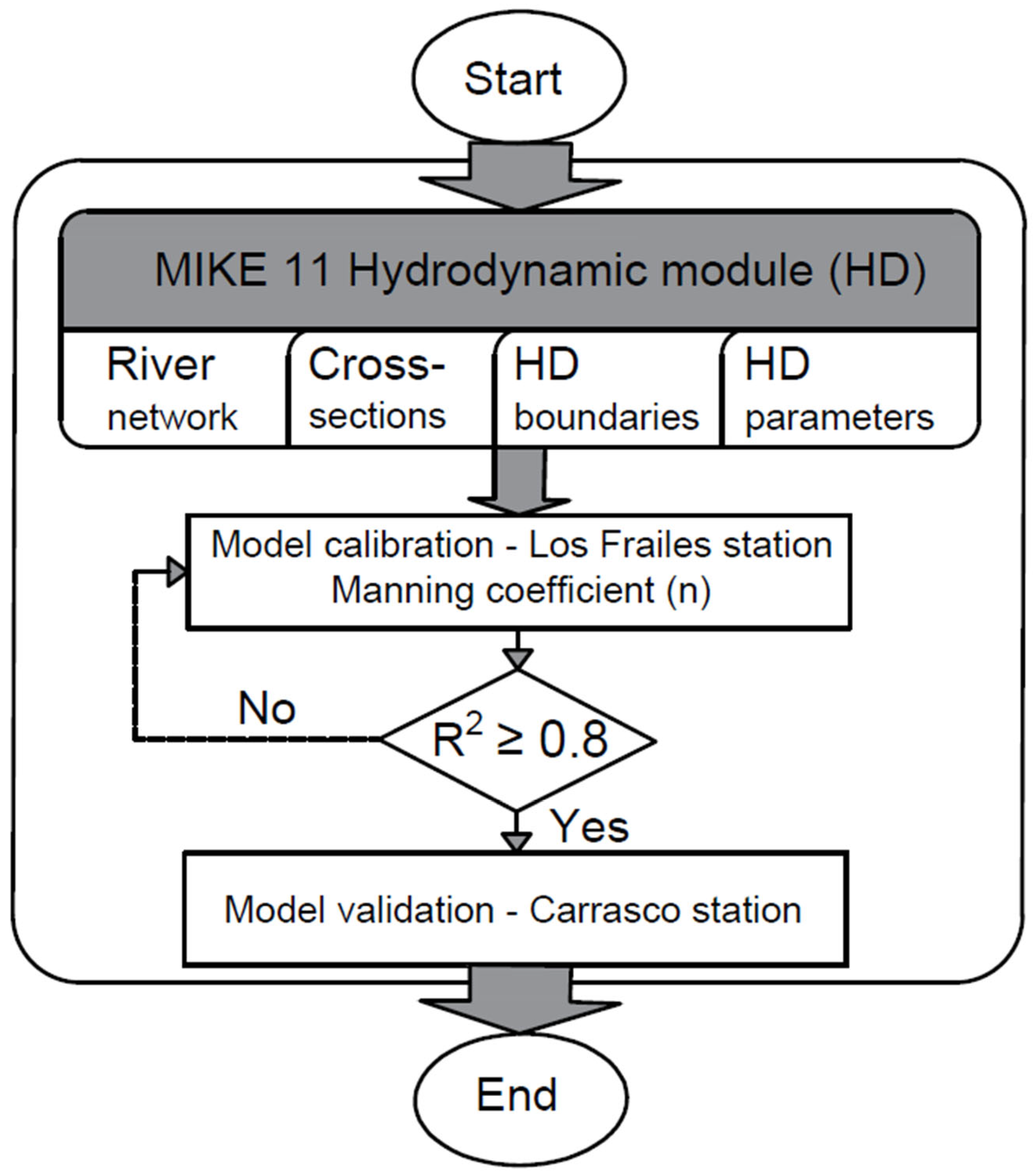
3.2.1. Hydrodynamic Modeling Setting
3.2.2. Conceptual Model, Discretization, and Boundary Conditions
3.2.3. Calibration and Validation Model Evaluation Criteria
4. Results and Discussion
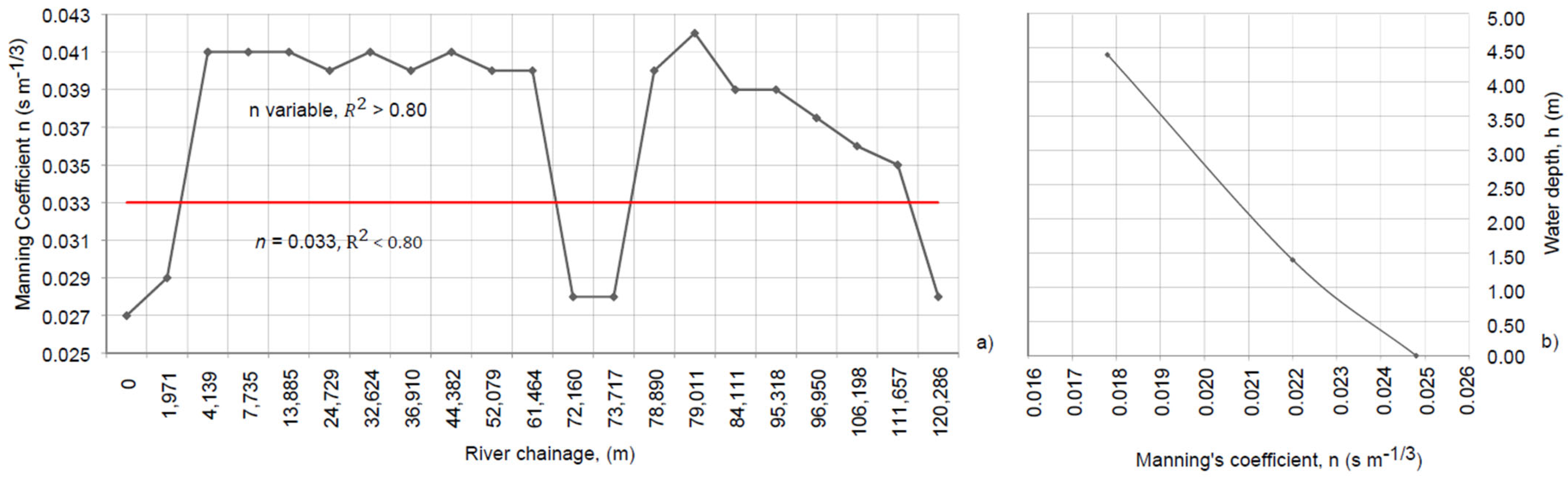
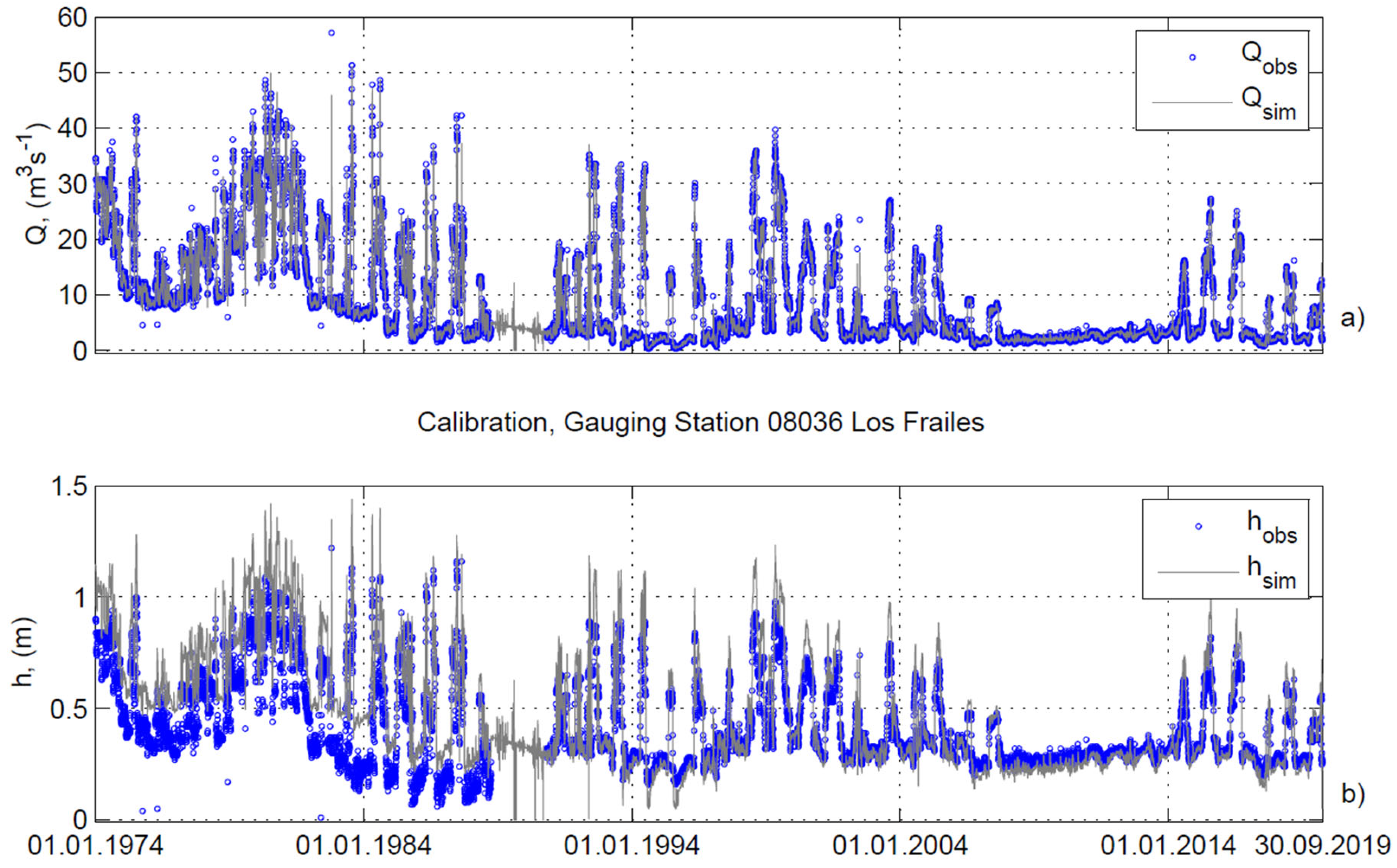
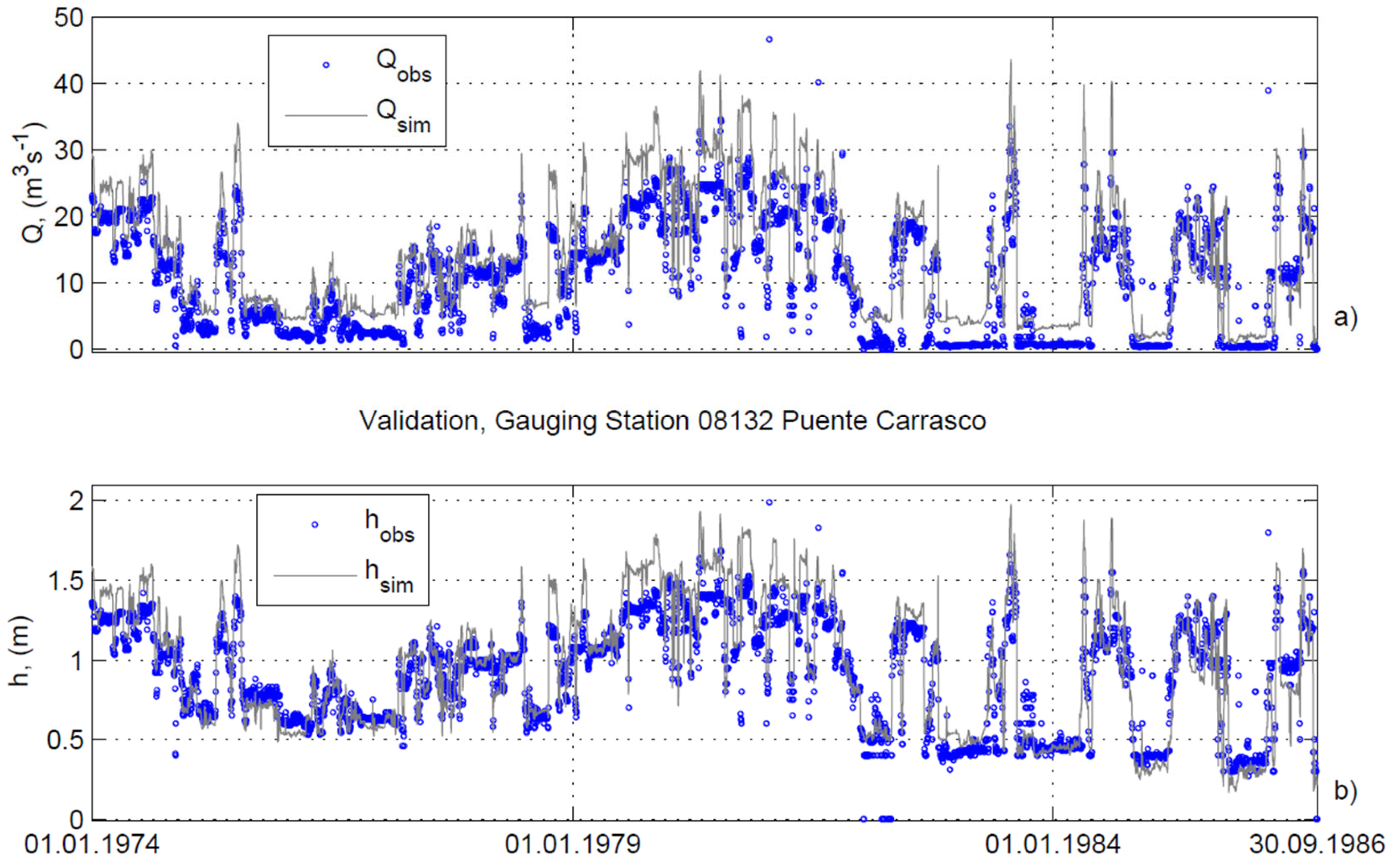
4.1. Calibration and Validation Results of HD Modeling
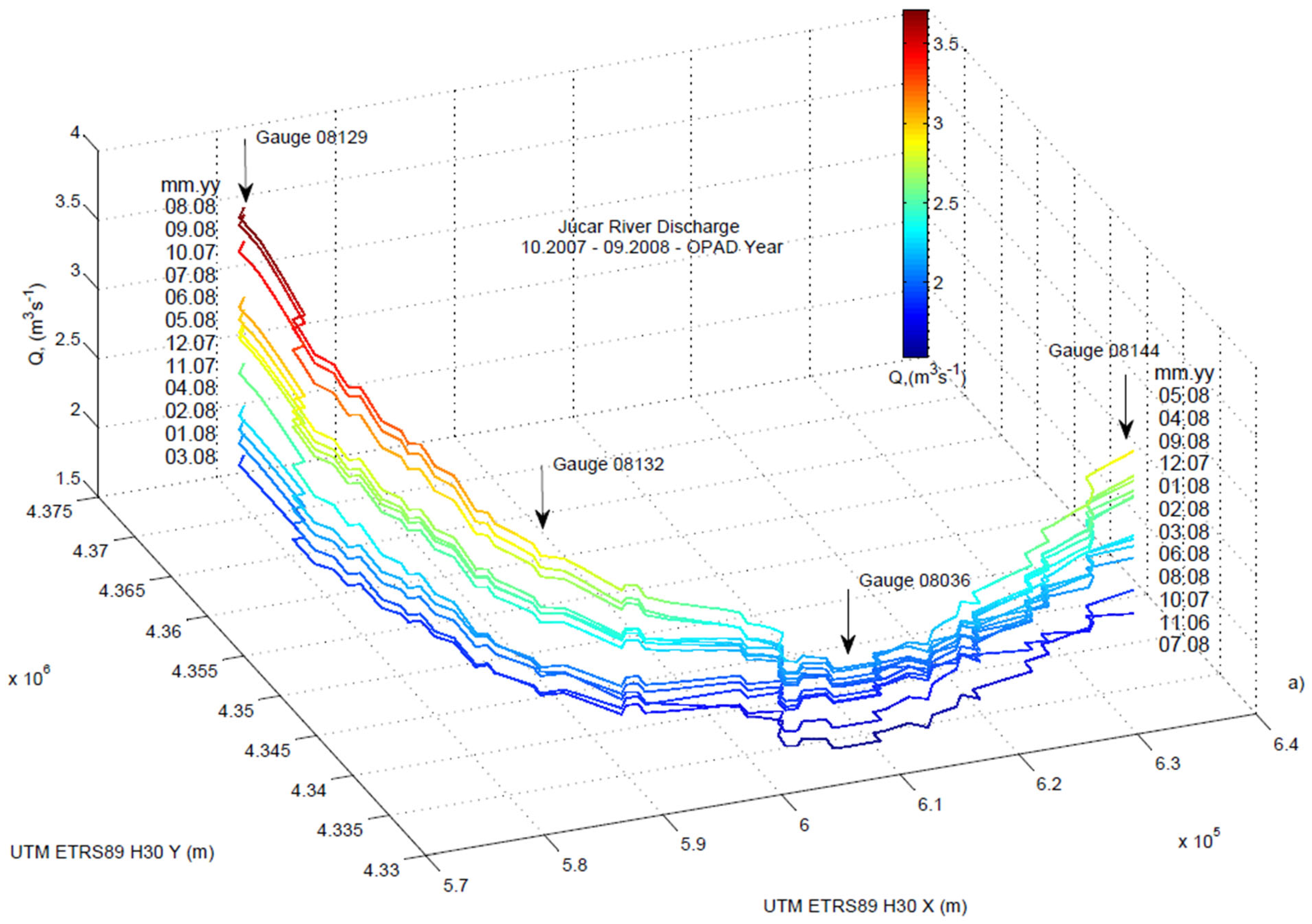
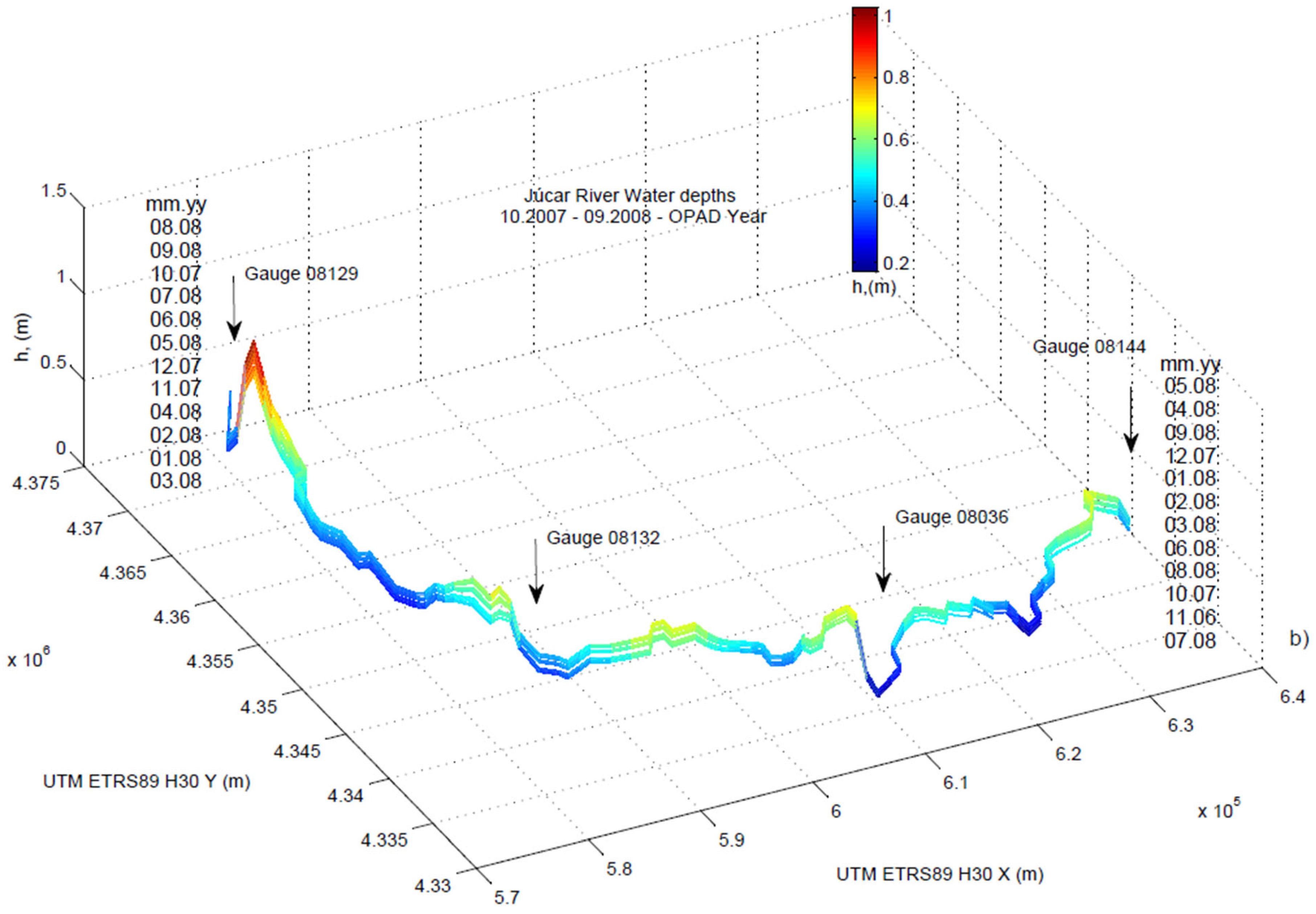
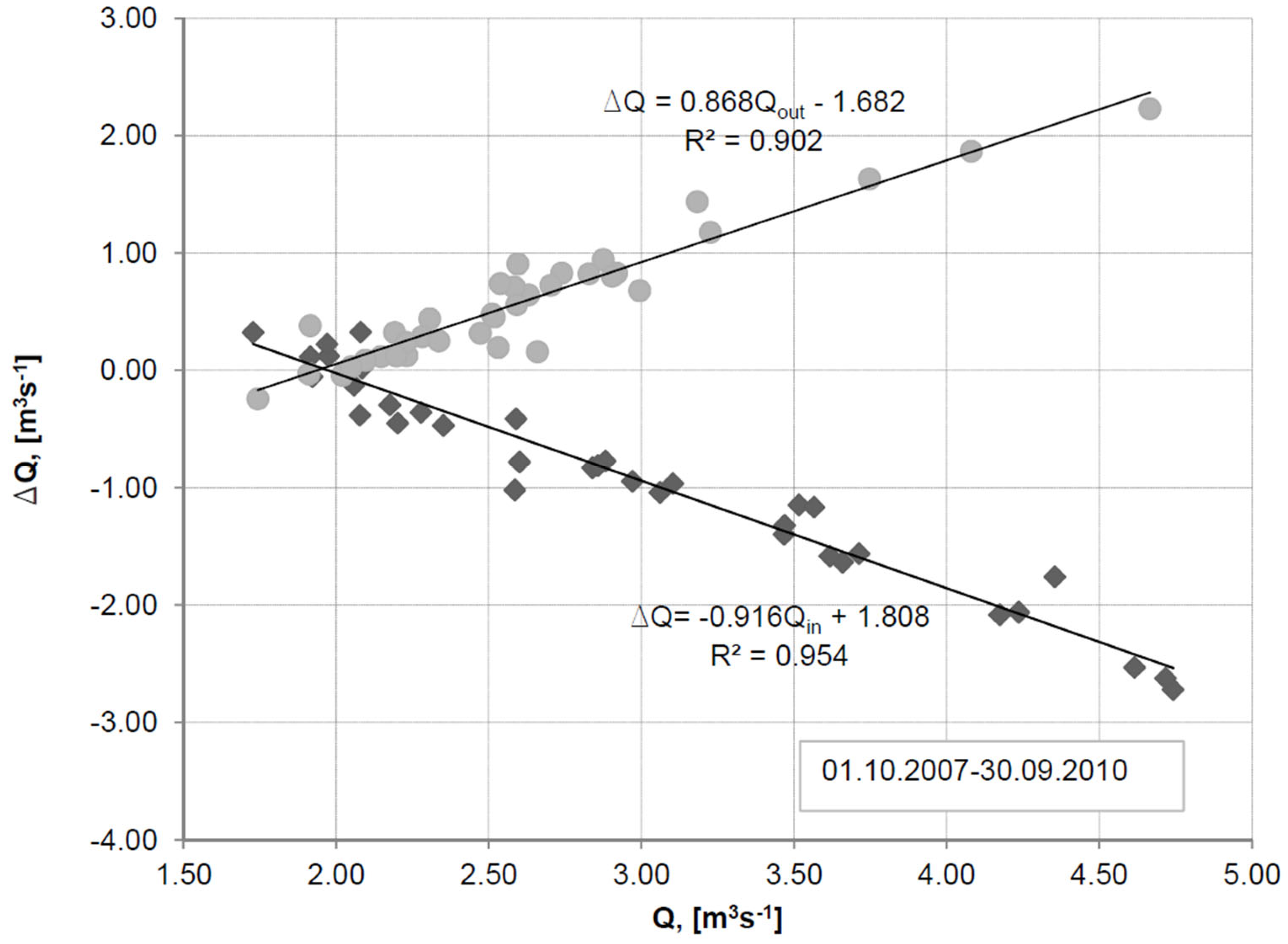
4.2. Discussion (Implications for the Water Resources Management)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gerbens-Leenes, W.; Hoekstra, A.Y.; van der Meer, T.H. The water footprint of Bioenergy. Proc. Natl. Acad. Sci. USA 2009, 106, 10219–10223. [Google Scholar] [CrossRef]
- Raffensperger, J.F. Matching users’ rights to available groundwater. Ecol. Econ. 2011, 70, 1041–1050. [Google Scholar] [CrossRef]
- Lovarelli, D.; Bacenetti, J.; Fiala, M. Water footprint of Crop Productions: A Review. Sci. Total Environ. 2016, 548–549, 236–251. [Google Scholar] [CrossRef] [PubMed]
- Khilchevskyi, V.; Karamushka, V. Global Water Resources: Distribution and demand. In Encyclopedia of the UN Sustainable Development Goals; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–11. [Google Scholar]
- Zhongming, Z.; Linong, L.; Xiaona, Y.; Wangqiang, Z.; Wei, L. Valuing Water. In UN World Water Development Report; United Nations: New York, NY, USA, 2021; Available online: https://www.unwater.org/un-world-water-development-report-2021-valuing-water/ (accessed on 15 March 2022).
- Esteban, E.; Albiac, J. Groundwater and ecosystems damages: Questioning the Gisser–Sánchez effect. Ecol. Econ. 2011, 70, 2062–2069. [Google Scholar] [CrossRef]
- Sanz, D.; Castaño, S.; Cassiraga, E.; Sahuquillo, A.; Gómez-Alday, J.J.; Peña, S.; Calera, A. Modeling Aquifer–River Interactions under the influence of groundwater abstraction in the Mancha Oriental System (SE Spain). Hydrogeol. J. 2011, 19, 475–487. [Google Scholar] [CrossRef]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A review of water scarcity and drought indexes in Water Resources Planning and Management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef]
- Pollak, J.D. Conjunctive Water Management in the San Joaquin Basin: A Case for Groundwater Management Reform. Master’s Thesis, University of California, Berkeley, CA, USA, 2010. [Google Scholar]
- Braaten, R.; Gates, G. Groundwater–surface water interaction in inland New South Wales: A scoping study. Water Sci. Technol. 2003, 48, 215–224. [Google Scholar] [CrossRef]
- Bredehoeft, J.D.; Young, R.A. Conjunctive use of groundwater and surface water for irrigated agriculture: Risk aversion. Water Resour. Res. 1983, 19, 1111–1121. [Google Scholar] [CrossRef]
- Gorelick, S.M.; Zheng, C. Global change and the Groundwater Management Challenge. Water Resour. Res. 2015, 51, 3031–3051. [Google Scholar] [CrossRef]
- Sahuquillo, A.; Cassiraga, E.; Gómez-Hernández, J.J.; Andreu, J.; Pulido-Velazquez, M.; Pulido-Velazquez, D.; Álvarez-Villa, O.D.; Estrela, T. Management Alternatives of Aquifer Storage, Distribution, and Simulation in Conjunctive Use. Water 2022, 14, 2332. [Google Scholar] [CrossRef]
- Sahuquillo, A. Economic aspects of the conjunctive use of ground and surface water. Groundw. Econ. Sel. Pap. A United Nations Symp. Held Barc. 1989, 39, 347–359. [Google Scholar] [CrossRef]
- Naghdi, S.; Bozorg-Haddad, O.; Khorsandi, M.; Chu, X. Multi-objective optimization for allocation of surface water and groundwater resources. Sci. Total Environ. 2021, 776, 146026. [Google Scholar] [CrossRef]
- Foster, S.; van Steenbergen, F. Conjunctive groundwater use: A ‘lost opportunity’ for water management in the developing world? Hydrogeol. J. 2011, 19, 959–962. [Google Scholar] [CrossRef]
- Toran, L. Groundwater–Surface Water Interaction. Encycl. Water Sci. Technol. Soc. 2019, 1–12. [Google Scholar] [CrossRef]
- Gianni, G.; Richon, J.; Perrochet, P.; Vogel, A.; Brunner, P. Rapid identification of transience in streambed conductance by inversion of floodwave responses. Water Resour. Res. 2016, 52, 2647–2658. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Jun, S.-C.; Cheon, J.-Y.; Park, M. A review on clogging mechanisms and managements in aquifer storage and recovery (ASR) applications. Geosci. J. 2018, 22, 667–679. [Google Scholar] [CrossRef]
- Koren, E.; Veselič, M.; Vižintin, G. Assessment of riverbed clogging in reservoirs by analysis of periodic oscillation of reservoir level and groundwater level. Energies 2021, 14, 6226. [Google Scholar] [CrossRef]
- Partington, D.; Therrien, R.; Simmons, C.T.; Brunner, P. Blueprint for a coupled model of sedimentology, hydrology, and hydrogeology in streambeds. Rev. Geophys. 2017, 55, 287–309. [Google Scholar] [CrossRef]
- Ulrich, C.; Hubbard, S.S.; Florsheim, J.; Rosenberry, D.; Borglin, S.; Trotta, M.; Seymour, D. Riverbed clogging associated with a California riverbank filtration system: An assessment of mechanisms and monitoring approaches. J. Hydrol. 2015, 529, 1740–1753. [Google Scholar] [CrossRef]
- Sanz, D.; Vos, J.; Rambags, F.; Hoogesteger, J.; Cassiraga, E.; Gómez-Alday, J.J. The Social Construction and consequences of groundwater modelling: Insight from the Mancha Oriental Aquifer, Spain. Int. J. Water Resour. Dev. 2018, 35, 808–829. [Google Scholar] [CrossRef]
- Dountcheva, I.; Sanz, D.; Cassiraga, E.; Galabov, V.; Gómez-Alday, J.J. Identifying non-stationary and long-term river–aquifer interactions as a response to large climatic patterns and anthropogenic pressures using wavelet analysis (Mancha Oriental Aquifer, Spain). Hydrol. Process. 2020, 34, 5134–5145. [Google Scholar] [CrossRef]
- Directive 2000/60/EC of the European Parliament and of the Council of 23 october 2000 establishing a framework for community action in the field of water policy (oj L 327 22.12.2000 p. 1). In Documents in European Community Environmental Law; Cambridge University Press: Cambridge, UK, 2006. [CrossRef]
- Cassiraga, E.; Sanz, D.; Gómez-Alday, J.J.; Gómez-Hernández, J.J. Groundwater management in Spain: The case of the Eastern Mancha aquifer system. Hydrolink Mag. 2019, 81–83. Available online: https://aplicat.upv.es/senia-app/edicion/listaArticulos.jsf# (accessed on 5 April 2022).
- Sanz, D.; Gómez-Alday, J.J.; Castaño, S.; Moratalla, A.; De las Heras, J.; Martínez-Alfaro, P.E. Hydrostratigraphic framework and hydrogeological behaviour of the Mancha Oriental System (SE Spain). Hydrogeol. J. 2009, 17, 1375–1391. [Google Scholar] [CrossRef]
- Confederación Hidrográfica de Júcar (CHJ). Júcar River Basin Management Plan 2015–2021; Júcar River Basin Authority (Demarcación hidrográfica del Júcar): Valencia, Spain, 2015. (In Spanish) [Google Scholar]
- Confederación Hidrográfica de Júcar (CHJ). Júcar River Basin Management Plan 2022–2027; Júcar River Basin Authority (Demarcación hidrográfica del Júcar): Valencia, Spain, 2022. (In Spanish) [Google Scholar]
- Instituto Geográfico Nacional (IGN), Vértices de las Redes Geodésicas REGENTE y ROI. Available online: https://www.ign.es/web/ign/portal/gds-vertices (accessed on 5 April 2022).
- Ministerio para la Transición Ecológica y el Reto Demográfico (MiTECO). Available online: https://www.miteco.gob.es/es/agua/temas/evaluacion-de-los-recursos-hidricos/sistema-informacion-anuario-aforos/ (accessed on 23 March 2022).
- Geweke, J.; Porter-Hudak, S. The estimation and application of long memory time series models. J. Time Ser. Anal. 1983, 4, 221–238. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 82–87. [Google Scholar] [CrossRef]
- Abry, P.; Veitch, D. Wavelet analysis of long-range-dependent traffic. IEEE Trans. Inf. Theory 1998, 44, 2–15. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of Nonstationary Time Series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Koutsoyannis, D. The Hurst phenomenon and fractional Gaussian Noise made easy. Hydrol. Sci. J. 2002, 47, 573–595. [Google Scholar] [CrossRef]
- Bryce, R.M.; Sprague, K.B. Revisiting detrended fluctuation analysis. Sci. Rep. 2012, 2, 1–6. [Google Scholar] [CrossRef]
- DHI. MIKE 11 A Modelling System for Rivers and Channels User Guide; Danish Hydraulic Institute: Hørsholm, Denmark, 2017; p. 510. [Google Scholar]
- Sanz, D. Contribución a la Caracterización Geométrica de las Unidades Hidrogeológicas que Integran el Sistema de Acuíferos de la Mancha Oriental (Contribution to the Geometric Characterization of the Hydrogeological Units of the La Mancha Oriental Aquifer System). PhD Thesis, Universidad Complutense de Madrid, Facultad de Ciencias Geológicas, Departamento de Geodinámica, Madrid, Colombia, 2005. [Google Scholar]
- Instituto Geológico y Minero de España (IGME), Identificación y Caracterización de la Interrelación que se Presenta Entre Aguas Subterráneas, Cursos Fluviales, Descargas por Manantiales, Zonas húmedas y Otros Ecosistemas Naturales de Especial Interés Hídrico. 2009. Available online: https://www.chj.es/Descargas/ProyectosOPH/Consulta%20publica/PHC-2015-2021/ReferenciasBibliograficas/AguasSubterraneas/IGME-DGA,2009.Act04_RelacSuperf_SubtMEMORIA%20RESUMEN.pdf (accessed on 15 February 2022).
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Boulomytis, V.T.; Zuffo, A.C.; Dalfré Filho, J.G.; Imteaz, M.A. Estimation and calibration of Manning’s roughness coefficients for ungauged watersheds on coastal floodplains. Int. J. River Basin Manag. 2017, 15, 199–206. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; Blackburn Press: Caldwell, NJ, USA, 2009. [Google Scholar]
- Barnes, H.H. Roughness Characteristics of Natural Channels; U.S.G.P.O.: Washington, DC, USA, 1987. [Google Scholar]
- Attari, M.; Hosseini, S.M. A simple innovative method for calibration of Manning’s roughness coefficient in rivers using a similarity concept. J. Hydrol. 2019, 575, 810–823. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H.; Tominaga, A. Secondary currents in a straight channel flow and the relation to its aspect ratio. In Turbulent Shear Flows 4; Springer: Berlin/Heidelberg, Germany, 1985; pp. 246–260. [Google Scholar]
- Box, G.E. Science and statistics. J. Am. Stat. Assoc. 1976, 71, 791–799. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of Hydrology. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Arnold, J.G.; Youssef, M.A.; Yen, H.; White, M.J.; Sheshukov, A.Y.; Sadeghi, A.M.; Moriasi, D.N.; Steiner, J.L.; Amatya, D.M.; Wayne Skaggs, R.; et al. Hydrological processes and model representation: Impact of soft data on calibration. Trans. ASABE 2015, 58, 1637–1660. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Duda, P.B.; Hummel, P.R.; Donigian, A.S., Jr.; Imhoff, J.C. Basins/HSPF: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Skaggs, R.W.; Youssef, M.A.; Chescheir, G.M. DRAINMOD: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1509–1522. [Google Scholar] [CrossRef]
- Chen, W.-B.; Liu, W.-C. Modeling the influence of river cross-section data on a river stage using a two-dimensional/three-dimensional hydrodynamic model. Water 2017, 9, 203. [Google Scholar] [CrossRef]
- Jahandideh-Tehrani, M.; Helfer, F.; Zhang, H.; Jenkins, G.; Yu, Y. Hydrodynamic modelling of a flood-prone tidal river using the 1D model Mike Hydro River: Calibration and Sensitivity Analysis. Environ. Monit. Assess. 2020, 192, 97. [Google Scholar] [CrossRef]
- Thu Minh, H.V.; Tri, V.P.; Ut, V.N.; Avtar, R.; Kumar, P.; Dang, T.T.; Hoa, A.V.; Ty, T.V.; Downes, N.K. A model-based approach for improving surface water quality management in aquaculture using Mike 11: A case of the long xuyen quadangle, Mekong Delta, Vietnam. Water 2022, 14, 412. [Google Scholar] [CrossRef]
- Papadimos, D.; Demertzi, K.; Papamichail, D. Assessing lake response to extreme climate change using the coupled Mike she/mike 11 model: Case study of lake zazari in Greece. Water 2022, 14, 921. [Google Scholar] [CrossRef]
- Castaño, S.; Sanz, D.; Gómez-Alday, J.J. Sensitivity of a groundwater flow model to both climatic variations and management scenarios in a semi-arid region of Se Spain. Water Resour. Manag. 2013, 27, 2089–2101. [Google Scholar] [CrossRef]
- Confederación Hidrográfica de Júcar (CHJ). Post-Drought Report Paragraph 10 PES. 2010. Available online: https://www.chj.es/es-es/medioambiente/gestionsequia/Documents/Informes%20Seguimiento/INFORME_POST_SEQUIA_2010.pdf (accessed on 14 December 2021). (In Spanish).
- Centro de Estudios y Experimentación de Obras Públicas (CEDEX). Hispagua Sistema Español de Información sobre el Agua. Available online: https://hispagua.cedex.es/documentacion/noticia/49087 (accessed on 6 July 2022).
| Statistic | Symbol | Equation | Range | Optimal Value | (Eq) |
|---|---|---|---|---|---|
| Coefficient of correlation | R | −1 to 1 | −1(negative slope) 1(positive slope) | (7) | |
| Coefficient of determination | R2 | 0 to 1 | 1 | (8) | |
| Nash–Sutcliffe Efficiency | NSE | −∞ to1 | 1 | (9) | |
| Root mean square error | RMSE | 0 to ∞ | 0 | (10) |
| Error Statistics | R | R2 | NSE | RMSE |
|---|---|---|---|---|
| Calibration—08036 Los Frailes | ||||
| Q (01.01.1974–30.09.1988) | 0.997 | 0.994 | 0.994 | 0.798 |
| h (01.01.1974–30.09.1988) | 0.983 | 0.967 | 0.446 | 0.181 |
| Q (25.10.1991–30.09.2019) | 0.998 | 0.996 | 0.997 | 0.375 |
| h (25.10.1991–30.09.2019) | 0.998 | 0.995 | 0.812 | 0.064 |
| Validation—08132 Puente Carrasco | ||||
| Q (01.01.1974–30.09.1986) | 0.946 | 0.896 | 0.723 | 4.345 |
| h (01.01.1974–30.09.1986) | 0.946 | 0.895 | 0.791 | 0.153 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dountcheva, I.; Sanz, D.; Penchev, P.; Cassiraga, E.; Galabov, V.; Gómez-Alday, J.J. Assessing 1D Hydrodynamic Modeling of Júcar River Behavior in Mancha Oriental Aquifer Domain (SE Spain). Water 2023, 15, 485. https://doi.org/10.3390/w15030485
Dountcheva I, Sanz D, Penchev P, Cassiraga E, Galabov V, Gómez-Alday JJ. Assessing 1D Hydrodynamic Modeling of Júcar River Behavior in Mancha Oriental Aquifer Domain (SE Spain). Water. 2023; 15(3):485. https://doi.org/10.3390/w15030485
Chicago/Turabian StyleDountcheva, Iordanka, David Sanz, Philip Penchev, Eduardo Cassiraga, Vassil Galabov, and Juan José Gómez-Alday. 2023. "Assessing 1D Hydrodynamic Modeling of Júcar River Behavior in Mancha Oriental Aquifer Domain (SE Spain)" Water 15, no. 3: 485. https://doi.org/10.3390/w15030485
APA StyleDountcheva, I., Sanz, D., Penchev, P., Cassiraga, E., Galabov, V., & Gómez-Alday, J. J. (2023). Assessing 1D Hydrodynamic Modeling of Júcar River Behavior in Mancha Oriental Aquifer Domain (SE Spain). Water, 15(3), 485. https://doi.org/10.3390/w15030485








