3.1. Clustering Results
Since the process of selecting clusters is random at the stage of the initial separation, the result may not be optimal. Therefore, for each k value from 2 to 8 clusterings were carried out, from which the variant with the optimal values of the above indices was selected. Naturally, under such conditions, we are still not guaranteed that the partition will be optimal, but the chance of optimality increases significantly. From the analysis of the resulting partitions, it follows that the process of selecting clusters has about 2–3 limit states, so choosing the most optimal one is not a problem.
Table 2 presents the results of the performed clusterings with the number of clusters identified from
to 5, and
Figure 2 and
Figure 3 show the geographical location of elements of these clusters:
Figure 2 presents the number of elements in whole vertical column for each model grid cell and
Figure 3 shows their depth-latitude distribution by means of blue dots. Only elements with
m
/s are considered. The table shows that in the case of selecting two clusters, their size (the number of elements in them) differs by an order of magnitude. A large cluster is presented, covering 91% of all elements, and a small one, including 9% of the elements. Geographically, the former is distributed throughout the entire Kara Sea basin over the entire range of depths. The second is localized in the coastal part in the places where the waters of Siberian rivers spread, and vertically, it is located in the upper layer within a few tens of meters. The latter, in our opinion, indicates that the elements of this cluster correspond to a set of parameters that describe the specifics of the distribution of the river plume and the development of the salinity front in the upper layer of the sea. Different number of elements in clusters is related to a small number of grid nodes representing the river plume compared to others. Geometrically, it means that these elements are distant from others in a 7D space area, at least in terms of variables representing the vertical components of density gradient.
With an increase in the number of clusters to three, the previously mentioned cluster with river influence remains practically unchanged and makes up the same 9% of the elements. For brevity, we will denote this cluster as B. An even smaller cluster, covering only 3%, is separated from the large cluster. We will mark it with the symbol C. Thus, the number of elements in the largest cluster has decreased to 88%. This cluster will be marked by the symbol A. Cluster C turned out to be geographically localized in a narrow strip of the steepest slope at the boundary between the shelf and the deep ocean and its elements are distant in the 7D space area from others, at least due to the extremely large
s variable. Thus, this cluster contains elements with parameters that describe the specifics of mesoscale movements in the region of a steep shelf slope. This partition has the smallest Davies–Bouldin index among the considered ones and the largest Dunn index, which indicates its optimality according to these criteria (see index descriptions in
Appendix A.1,
Appendix A.2 and
Appendix A.3). Its silhouette coefficient turned out to be somewhat smaller compared to splitting into two clusters (0.74 instead of 0.78), but the silhouette coefficient of the largest cluster slightly increased from 0.95 to 0.96. This partition will be further considered as the main one.
An increase in the number of clusters to four and five leads to the formation of an intermediate cluster associated with the upper layer being no deeper than 100 m, due to a decrease in the proportion of the large cluster A and the proportion of the river cluster B, the latter becomes the smallest as a result and covers the areas immediately adjacent to the river mouths. Our interpretation of the intermediate cluster is to identify areas of convective and wind mixing. In addition, a large cluster also splits into two, while part of the intermediate cluster is captured. As a result, a reduced version is formed from its remaining part. Also, with an increase in the number of clusters the quality of clustering decreases. We also checked 25 clustering, which also proves a further quality decrease.
The introduced designations of clusters for reference are presented in
Table 2.
3.2. Parametrization Dependencies—Cluster A
We restrict our analysis of the resulting partition to the consideration of the largest obtained cluster A, leaving consideration of other clusters and other partitions for future research.
The dependence of the eddy diffusion coefficient K on large-scale parameters was estimated based on dividing the variability ranges of each of the parameters into successive intervals with an equal number of sample elements in them. Dividing by more intervals results in a lot of computations when evaluating sensitivity because the number of boxes in N-dimensional hyperspace is . In the considered case their number is = 78,125.
Cluster A covers 88% of all sample elements. The coefficient of eddy diffusion
K in the representation of eddy mass transport (3) revealed the strongest dependence on the value of the vertical derivative of the density, which is related to the Brunt–Väisälä frequency
by the relation
This value is involved in explaining 69% of the variability in the value in this cluster.
The second most important value is the rate of density change along the direction of the bottom slope, which is responsible for 47% of the variability. The third value, which explains 39% of the variability, is the rate of the bottom slope. It is from these values that the individual dependence of the value
on one-dimensional functions in representation (18) is most pronounced:
– 33.4%,
– 7.6%, and
s – 1.7%. The distributions of the cluster elements against these values are presented in
Figure 4 using histograms in terms of their normalized deviations from the mean. The role of other parameters in explaining the dependence is not negligible and varies from 24 to 33%. Among the two-dimensional functions, the most pronounced dependence on pairs of variables is
– 3% and
– 1.3%. For multivariate functions, it can be noted that any combination of six variables explains from 0.8 to 1.6%, totaling about 8%, and the term with a function of all variables explains 2.8% of the variability. The analysis of such multidimensional dependencies requires extensive theoretical substantiation, and in our analysis, we will restrict ourselves mainly to one-dimensional dependencies.
Having obtained an estimate of the sensitivity of the eddy flux characteristics to the selected set of parameters, we can now refine the dependence on them by increasing the number of intervals in the discretization of variables. The dependence on the vertical component of the density gradient
is shown in
Figure 5 for the case of dividing the range of variability into
intervals.
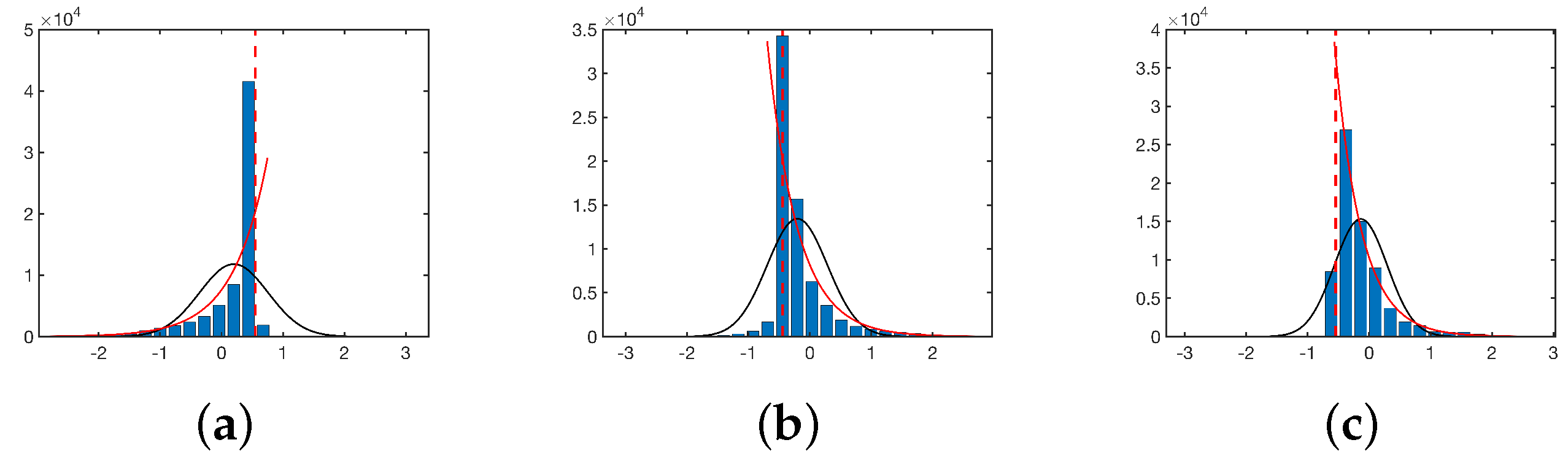
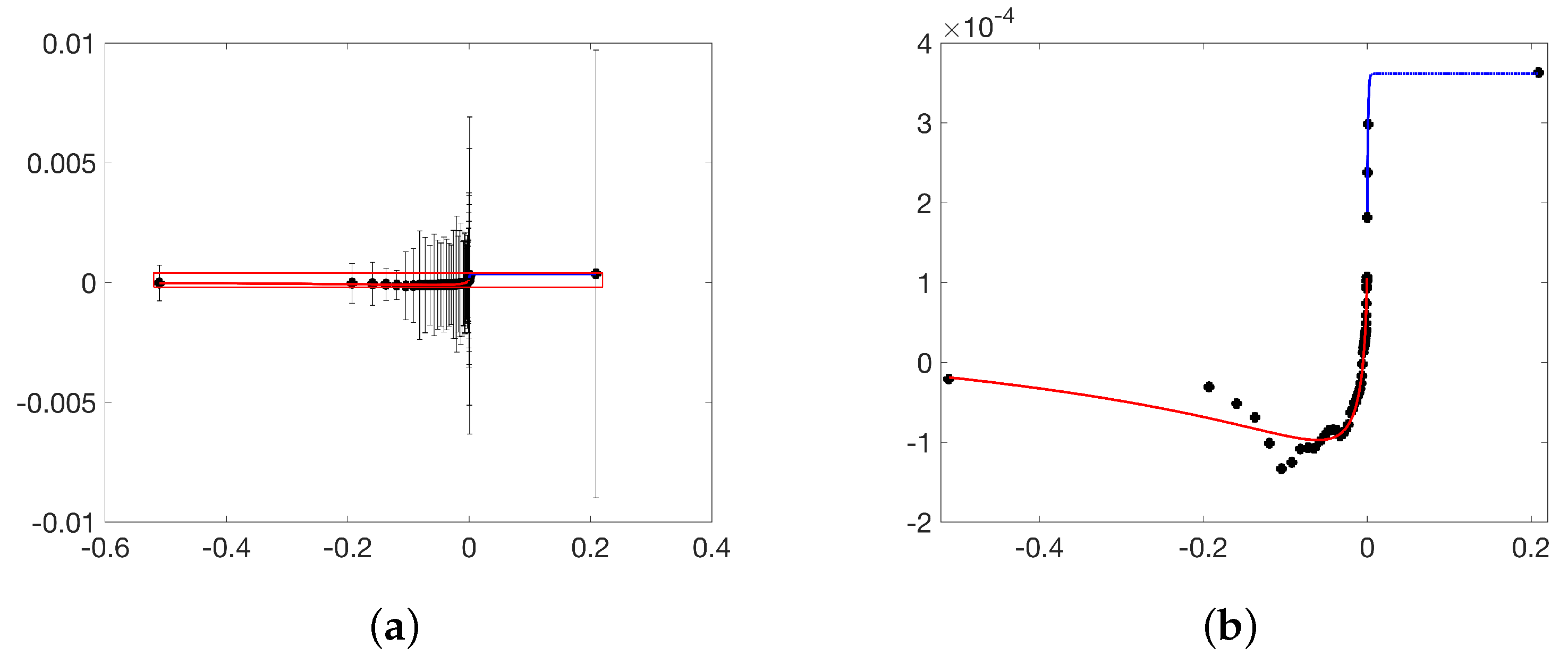
The histogram of the distribution of sample elements depending on
(
Figure 4a) has the form of an exponential distribution with only a small number of elements that go into the region of positive values (unstable stratification), and the highest concentration of elements is observed in the region of zero value. In this case, it makes sense to look for dependence in the form of an exponent for values
less than zero and for values greater than zero. This gives a tendency towards some extreme values in the case of neutral stratification, and a limiting value when
tends to infinity. The value
is defined so that
is equal to the average value of the value
in the given cluster. In the case under consideration,
, which corresponds to
m
/s.
Figure 5 shows the exponential curves with the help of red and blue lines, which most closely describe the
behavior in the region of small absolute values of
and somewhat worse in the case of large values:
where the assumed
dimension is expressed in kg/m
. These dependencies have a standard deviation
for the range of negative values of the argument, and
for positive values. This means that the coefficient
K is determined up to a factor of
in the first case and
in the second. Alternatively, one can also use tabular values corresponding to the depicted points in
Figure 5.
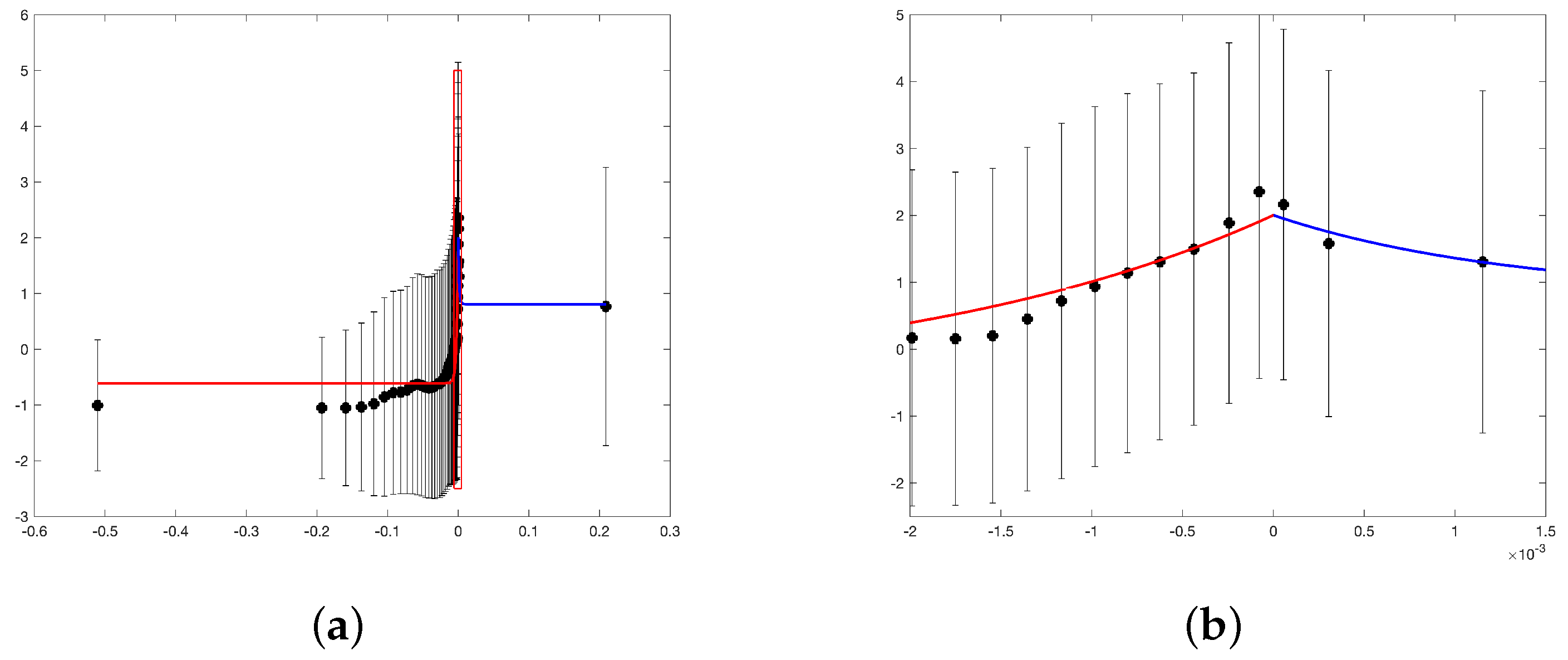
The dependence on the parameter
is shown in
Figure 6. It is interesting that the range of this parameter also includes negative values (see also
Figure 4b); that is, the bottom density decreases along the sloping bottom. This is a characteristic condition for the formation of cascading [
30]. As we have shown earlier in [
29], the movement of dense waters along the sloping bottom is accompanied by the active generation of mesoscale eddies due to the released potential energy.
We searched for the curve closest to the given arrangement of points in
Figure 6 in the form of a hyperbolic tangent by adjusting its slope, the position of the center of symmetry, and reaching a plateau for the parameter values to the right and left of the center. The following curve turned out to be optimal in this class
Here, as before, the dimension of is expressed in kg/m. The value of the standard deviation from the averages over the intervals is , that is, taking into account the logarithmic dependence, the value K is determined with an accuracy of up to a factor or divisor of .
The one-dimensional dependence on the bottom slope
s explains only 1.7% of the variability in
. The dependence on this parameter is shown in
Figure 7. We looked for the closest fitness to the location of the points in the form of a linear combination of two exponentials: the first with a slow decay to provide a general dependence, and the second with a fast decay to ensure growth near small slope values. In this representation, the following curve turned out to be optimal in terms of the smallest standard deviation
The value is dimensionless and represents the increase in depth when moving along the slope per unit length (for example, m/m). The standard error in this formula is , which gives the value a multiplier or divisor of .
The dependence of the characteristic in representation (18) turned out to be not so pronounced. The mean value and standard deviation in cluster A for the counter-gradient flux turned out to be kg/(ms) and kg/(ms). The same parameters as before, but in a different order , s, and turned out to be most useful in explaining the variability of this value at the level of 69%, 65%, and 53%, respectively. However, the one-dimensional dependence on these parameters explains only 7.6%, 3.4%, and 2.2% of the variability. The largest contribution of up to 20%, as it turned out, is given in the aggregate by functions of five variables, while one-dimensional ones give only 16%, and two-dimensional ones only 12%. The total proportion of the explained variability was 98.7%.
To obtain a more detailed picture of the dependence on these three parameters, we reduced the number of variables considered to , while increasing the number of intervals to , so that the total number of boxes became = 125,000. As a result, the total part of the explained variability decreased to 78.9%, but the dependence pattern became clearer. The parameter is involved in explaining 92% of the variability of the value , the parameter explains 78%, and s explains 63%. The one-dimensional dependence on explains 14% of the variability of this value, the contribution is 4%, and the s contribution is less than 1%. Among the two-dimensional dependences, the maximum contribution is made by the dependence on the pair with 19%. The rest consists of , giving 8%, and , giving 3%. The three-dimensional dependence on all three parameters explains 51% of the variability.
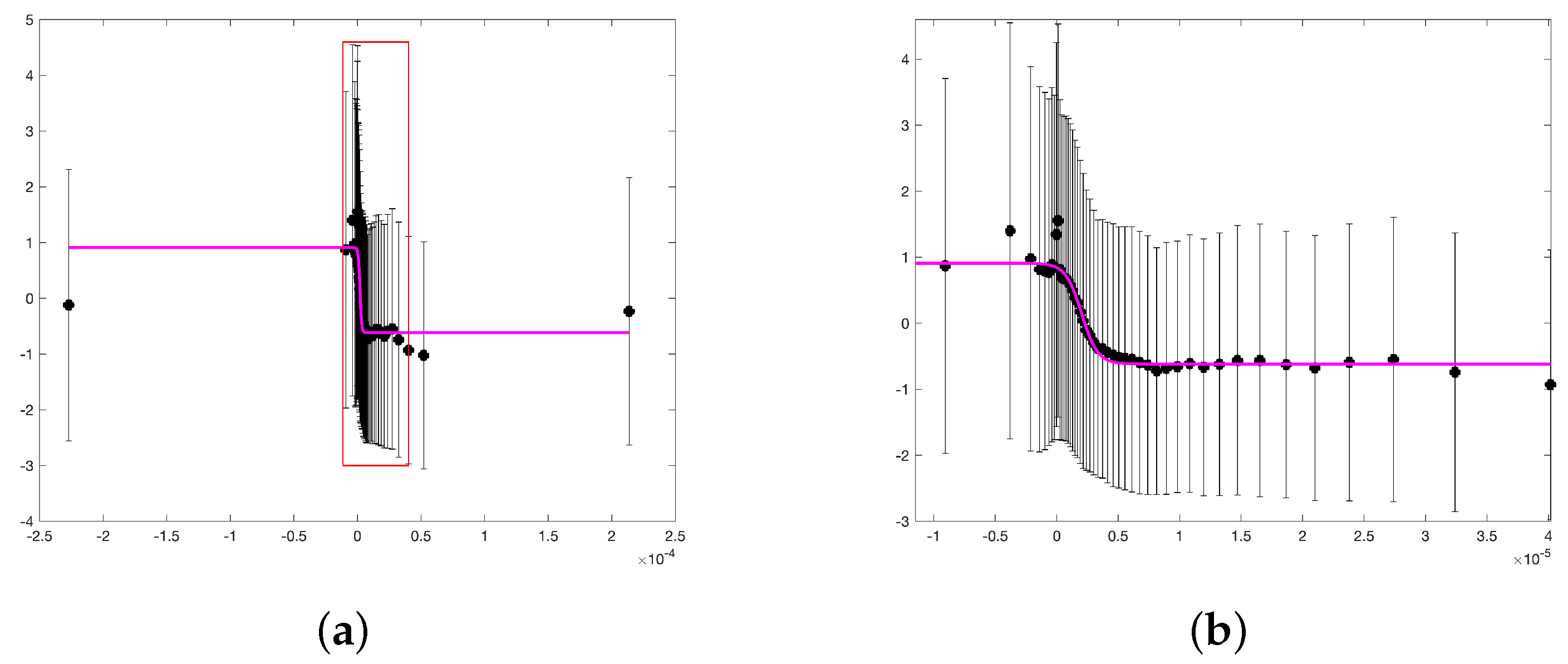
Next, we aimed to consider one-dimensional functions of the parameters
and
and to neglect the dependence on
s.
Figure 8 shows a one-dimensional dependence of
on the parameter
expressed in units (kg/m
). The closest functional dependence was sought in the form of a hyperbolic tangent, which resulted in the expression
where
is equal to the average value of
in cluster A. The standard deviation of graph points from this dependence is
. This leads to an error in determining the value
q of the order of
kg/(m
s), even though the maximum value within this dependence will be 0.34, and the minimum will be −0.03 kg/(m
s). The latter turns out to be at the error level, so the presence of negative values of counter-gradient fluxes remains questionable. A positive mass flux, as can be seen from
Figure 8, takes place in the presence of a negative value of the density derivative in the direction of the slope, that is, under conditions of cascading. Based on the distribution of the value
presented in
Figure 4b, this does not happen often.
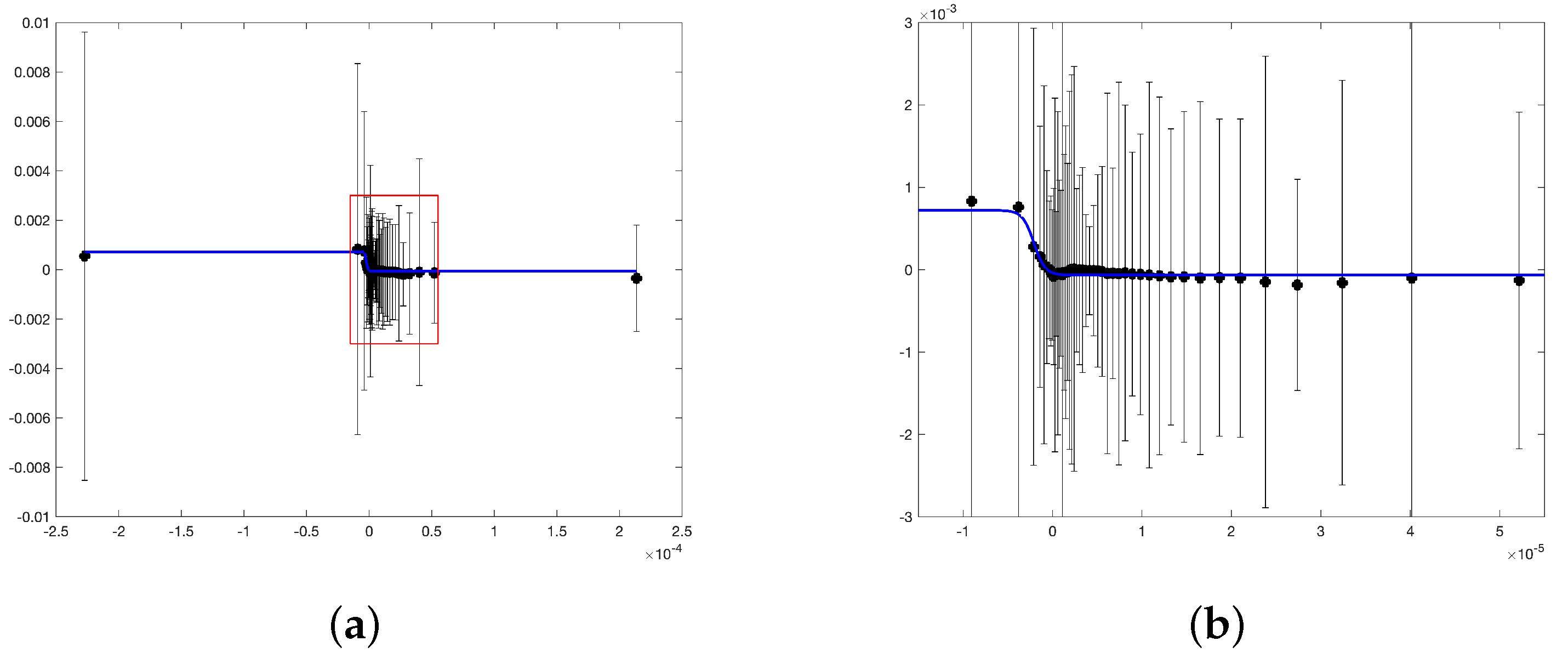
The one-dimensional dependence of the value
on the parameter
(kg/m
) in cluster A in the region of negative values of the parameter resembles a log-normal distribution and an exponential one in the region of its positive values (
Figure 9). The best dependence in this class of functions is given by the following expression:
Standard deviation in first case is , in the second .
3.3. Practical Use
The system of equations of numerical models usually proceeds from the Boussinesq approximation, which reduces the mass conservation equation to a continuity equation, and therefore the mass flux is not explicitly taken into account. However, it can be calculated if we assume that the heat and salt fluxes can be represented in the equations for temperature
T and salinity
S in a form, similar to (3), i.e.,
If the equation of state is presented in a linearized form, then the density change can be written as
, where
and
. Then, multiplying the first row in (
26) by
, and the second by
and after adding them and comparing with (3), we get
To ensure that the first term on the left is equal to the expression in the first bracket on the right, we set
. For counter-gradient fluxes, then we get
We assume that
and
, where
and
are some constants. Then, after substitution, we obtain for them the following expression
First, we assume that
. It means that the more sensitive the density is to changes in a variable, the greater the eddy flux of that variable is. In this case, we get
Assuming the opposite, that
, that is, the more sensitive the density is to changes in the variable the less eddy flux of this variable will be needed for mass transfer, we get
In general
where
p is a parameter which could be equal to any value from
but giving (
30) in case
and (
31) in case
. When
p is outside
interval then the terms in (
32) will have opposite signs. Since the expressions (
26) give the values of the eddy flux modulus in the direction of the bottom slope
, then finally for the heat fluxes in the direction of the model coordinates we obtain a two-component vector
The same is for salinity flux. The first term in (
33) could be written as
where
The diagonal elements of R are always positive (not negative) but off-diagonal elements could be both positive or negative depending on the vector direction.
The next series of numerical experiments is to apply the obtained parametrizations and the proposed way of including them in a large-scale model. As such a model, we used the coupled ocean–ice model SibCIOM, the computational domain of which includes the Atlantic Ocean north of the 20
S and the Arctic Ocean, whose boundary with the Pacific Ocean in the Bering Strait is considered to be the boundary of the domain. The model is described in more detail in [
41]. The horizontal resolution of the model is 0.5
in the Atlantic Ocean and is variable from 10 to 25 km in the Arctic. The application of the obtained parametrizations in numerical experiments was extended beyond the Arctic to the entire domain, including not only middle latitudes but also the subtropics and tropics of the Atlantic Ocean. However, only the results of numerical experiments related to the Arctic region are presented below. Numerical experiments cover the period from 2000 to 2022.
3.4. Diffusion Coefficient Test
In the first experiment B, we set the eddy diffusion coefficient equal to the sum of the coefficients obtained using expressions (
21)–(
23) along with the assumption
and (
33). The experiment is a restart from the fields of 1 January 2000, obtained during the experiment from 1948 to 2020 using the state of the lower atmosphere and radiation fluxes from the NCEP/NCAR reanalysis data as forcing data (see details in [
41]).
Since the proposed parametrization is designed to take into account additional eddy mass fluxes, and associated fluxes of heat and salts, we consider the integral difference of these values at latitudes above 65 N latitude for two numerical experiments: A—without the inclusion of the proposed parametrization; and B—with the inclusion of this parametrization in the variant proposed above, that is, without taking into account the counter-gradient.
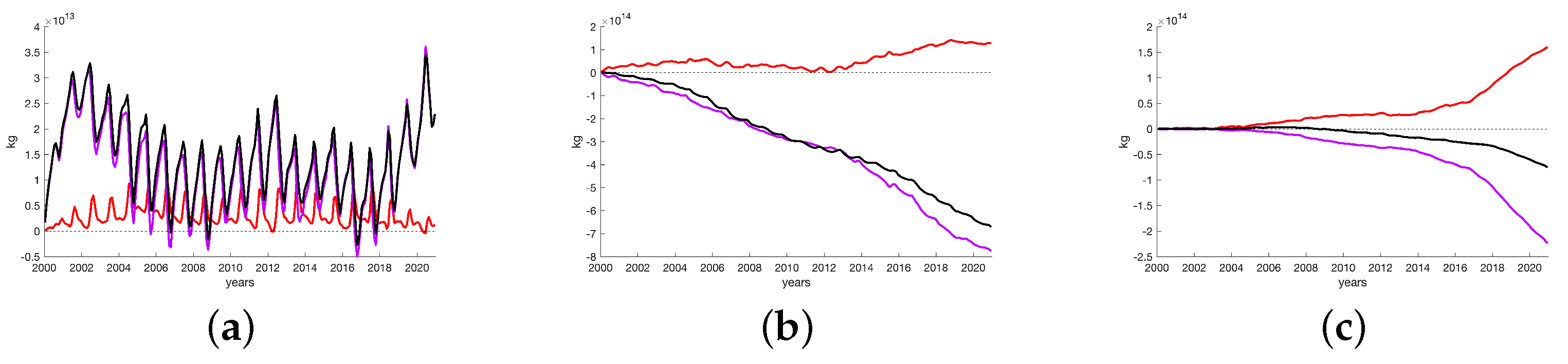
Figure 10a shows the timeseries of the difference in mass, heat content, and salinity in terms of the increment in the mass of water in the Arctic. More precisely, we consider the change in time and the difference in the mass of water between two experiments located north of latitude 65 N. For reference, the total mass of water in this region according to the model grid is 1.77 × 10
kg.
The heat content of water decreases until about 2007, which in terms of mass means an increase (red curve in the graph), after which it reaches a certain quasi-constant level. However, after 2013 it continues growing. On average, the change in the heat content of one cubic meter of water decreased by 0.25 J by the end of the period, which is equivalent to a decrease in temperature by 6 × 10°C.
The salinity has been decreasing (magenta curve) during all this time, and since 2004 the rate of decrease has been approximately constant, but in 2013 the rate of decrease grew significantly. This lead to a decrease in the integral mass (black curve). As a result, the fluxes of heat and salts act in different directions, but the change in salinity is dominant and therefore we see a general reduction in the mass of water in the Arctic. The maximum difference between the two numerical experiments was 7.23 × 10 kg, which is approximately 0.00004 of the total mass, or in terms of water density, about 42 g per cubic meter.
Figure 10b shows the vertical distribution of mass change due to heat and salt fluxes. In the upper 30 m layer, the salt content (magenta curve) is on average higher in experiment B than in experiment A, while the situation is reversed in the layer from 30 to 600 m. As for the heat content (red curve), it decreases in both cases, but the changes are several times smaller in terms of mass change. As a result, the average change in the mass of the layers (black curve) is only slightly greater than a result of the action of salt fluxes. Thus, the general trend of water mass reduction in the Arctic during experiment B is achieved by increasing the difference between the mass inflow in the 30 m layer and its decrease in the 30–600 m layer.
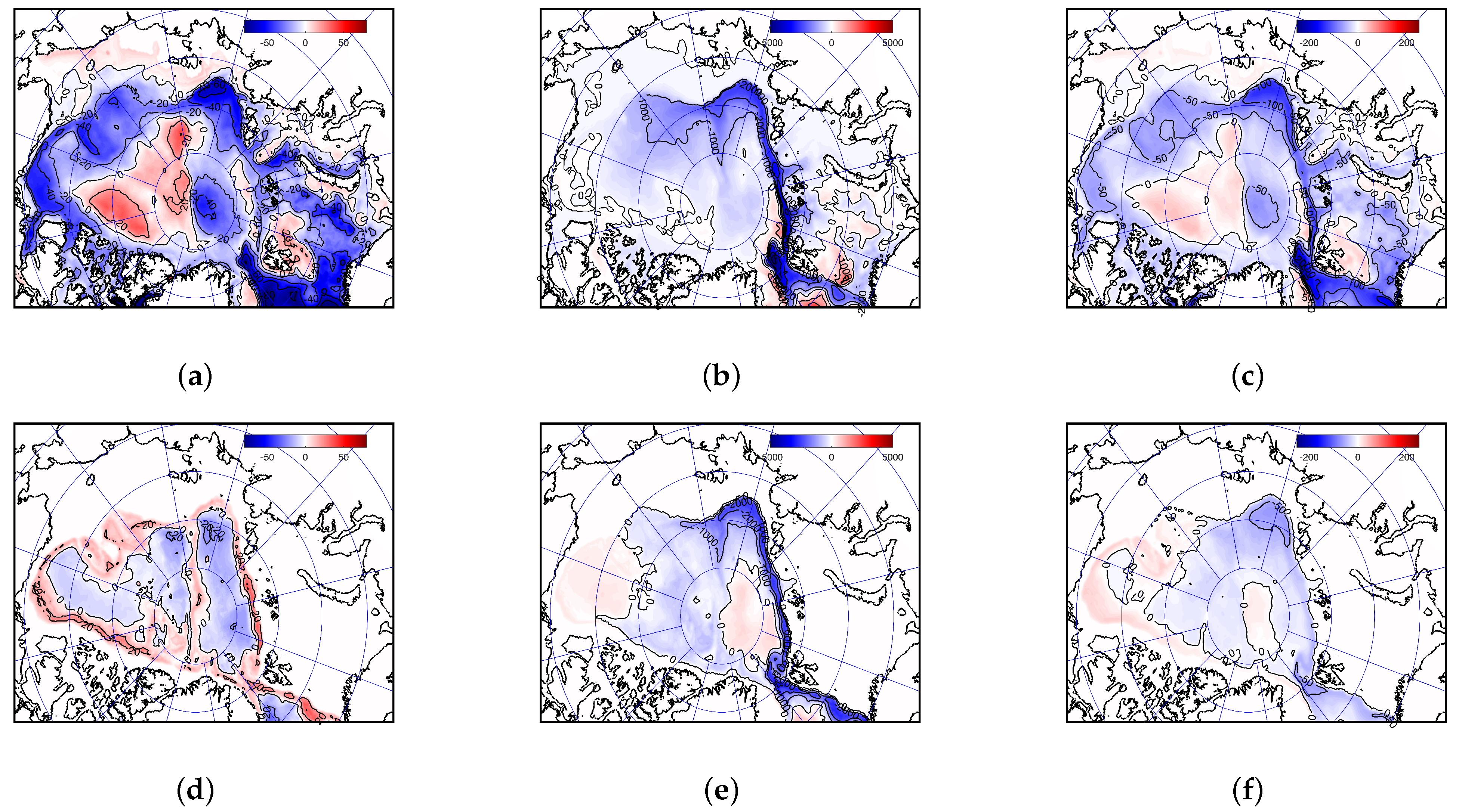
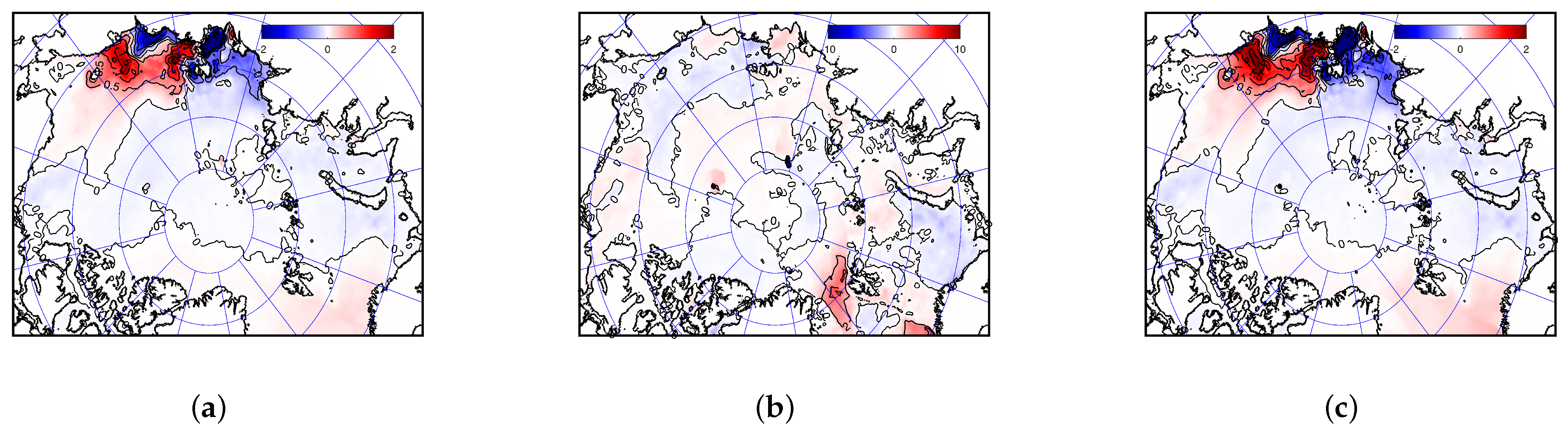
Figure 11 shows the deviations in the mass of water, its heat content, and the mass of salt per square meter of the basin area obtained as a result of vertical integration from the surface to the ocean floor. The growth of salinity in the area of the East Siberian and Chukchi Seas, off the shelf break in the Barents and Kara Seas, and also in the eastern part of the Beaufort Sea leads to a subsequent growth in the mass per unit area in these regions. Heat content changes play a minor role but its reduction at the very shelf break makes the whole region in the vicinity of the Barents and Kara Seas shelf break be of positive mass change. Salinity content reduces substantially in the northern part of the Laptev Sea and farther off to the east, making mass tendency similar to it despite heat content acting in the opposite way.
Seasonal changes are strongest in the upper 30 m layer (
Figure 12), but even here it can be noted that the seasonal differences between all values in the period of their positive values from April to June, compared to the period of their negative values in the period from September to November, are not so large (
Figure 13). In general, it can be noted that the changes associated with the introduction of parametrization in experiment B do not exceed 2–5% of the total seasonal variability and enhance it, that is, they work towards increasing the seasonal variability of the mass, heat, and salt content of water in the Arctic.
In the upper 30 m layer, as a whole, one can note (regardless of the season) an increase in the salt content in the shelf areas of the East Siberian and Chukchi Seas in the southeastern part of the Laptev Sea and in the shallow waters of the Kara Sea, where the influence of the river runoff of the Lena, Ob, and Yenisei rivers is strongest. In our analysis, we did not consider the role of cluster B associated with river plumes. Therefore, we can assume that the selection of the last two areas as the areas with the most important change in salinity is not entirely fair.
The strongest manifestation of positive trends in salinity, as can be seen in
Figure 12a, is observed in the first 5–6 years of integration after the introduction of the proposed parametrization. Further, in years 7–9, the role of salinity decreases to almost zero, after which it rises again. The greatest positive deviation of salinity is in the winter–spring period (the period of ice growth), and the negative one is at the end of summer (the period of thawing). Thus, we again note an increase in seasonal changes in salinity. The role of temperature changes, as can be seen in
Figure 13b,e, is not so significant and more important in the seas of the North Atlantic and partly in the Barents Sea, but has almost no effect on changes in water mass.
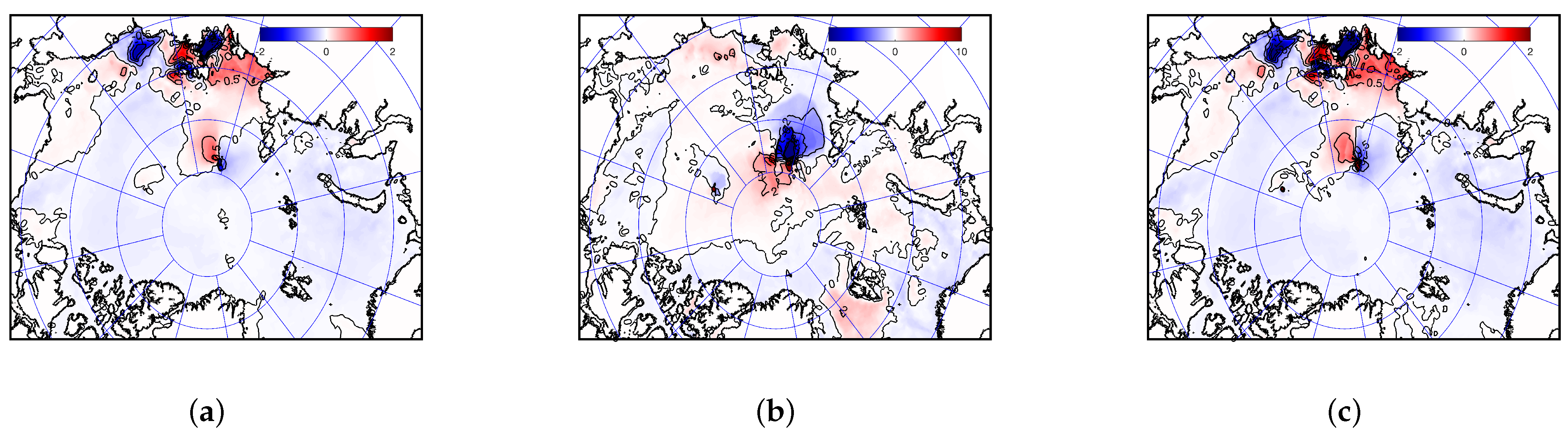
Deeper layers show less seasonal variability and significant trends in heat and salt content (
Figure 12b,c). The salt content in the 30–600 m layer falls almost linearly, which provides a corresponding trend in the mass of this layer. At the same time, the temperature drop of this layer works in the opposite direction to increase the mass, but the changes themselves are insufficient to withstand changes in salinity. The largest decrease in mass is observed in the area of the Barents Sea, the Amundsen Basin, in the north of the Laptev, East Siberian, and Chukchi Seas off the shelf slope, as well as along the coast of the Beaufort Sea (
Figure 14a). In all of the above areas, there is also a drop in the salt content in the layer (
Figure 14c). An increase in mass can be seen only near the islands of the Canadian Archipelago, along the Lomonosov Ridge, and off the shelf slope of the Barents and Kara Seas. In the latter case, an increase in mass occurs not only due to an increase in salinity but also due to a decrease in the temperature of the layer (
Figure 14b).
In the deepest layer from 600 m to the bottom, changes become noticeable only after 5 years (
Figure 12c), and in the next 5 years, changes in the content of heat and salt affect the water mass in different directions and almost completely compensate each other. Only after 10 years, the influence of salinity becomes dominant and its fall causes a decrease in the mass of water in the layer. At the same time, the decrease in mass, according to
Figure 14d, occurs in the central part of all basins, where the bottom depth is maximum, and the increase occurs in shallower areas of the ridges and shelf slopes bordering these basins.
3.5. Counter-Gradient Tests
The next two numerical experiments are related to the introduction of the counter-gradient parametrization based on the derived expressions for the counter-gradient mass flux, as well as using Equations (
28), (
29), and (
32) under the assumption that the counter-gradient fluxes of heat and salts are expressed as
and
with
and
dependent on two linearization coefficients derived from the equation of state
and
.
In the first C1 experiment, we assumed the
p parameter in Equation (
32) to be equal to zero, which corresponds to the situation when the heat and salt fluxes are taken in proportion to the contribution of temperature and salinity variations to density variations following the equation of state. In this case, the counter-gradient salt flux turns out to be co-directed with the counter-gradient mass flux, and the heat flux is opposite to them. The coefficient
in Equation (
29) is approximately 16 times greater than the value of the coefficient
and is approximately equal to 0.94, while the coefficient
is approximately 0.06.
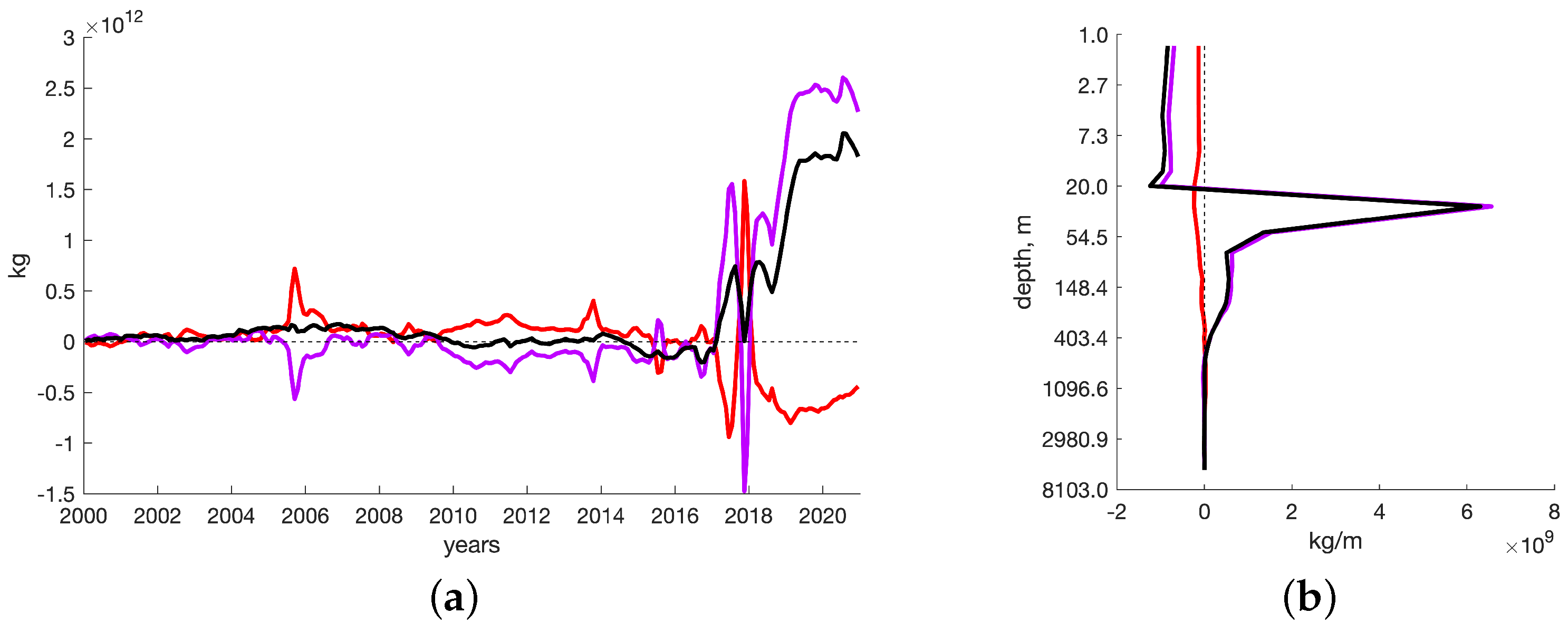
Figure 15a shows the time series of mass increments due to changes in water temperature and salinity. It can be seen that, compared with numerical experiment B, the mass increment is more than two orders of magnitude smaller and mostly becomes noticeable about 17 years after the start of the experiment. As expected, the contribution of salinity changes has a more significant effect on mass changes and is mostly negative within the first 17 years and becomes positive after. A decrease in density due to an increase in temperature counteracts this increment in mass but is not dominating.
Figure 15b shows that the average over the basin density drop is most pronounced in the upper 20 m layer but substantial growth happens in the deeper 20–50 m layer and is less distinct but more extended in the 50–400 m layer. In both cases, the salinity contribution is dominating.
According to
Figure 16, the greatest changes in salinity occur on the shelf and its vicinity in the Laptev Sea and the East Siberian Sea. Moreover, salinity increases in the East Siberian Sea extending a positive trend toward the Chukchi Sea and decreases in the Laptev Sea and less significantly in the rest of the Arctic. The reason for this is the accelerated eddy counter-gradient fluxes of fresh waters of the Lena, Olenek, and Khataga rivers towards the open ocean and the subsequent deficit of these waters in the East Siberian Sea. As a result, a similar picture develops in the field of changes in the water mass. The rise in temperature in the Laptev Sea and its fall in the East Siberian Sea act in concert and also contribute to mass trends in these areas. However, in general, the opposite positive effect of temperature is manifested in the vicinity of the Fram Strait, where Atlantic waters intrude into the polar Arctic. According to the vertical distribution of temperature changes, the strongest temperature growth occurs precisely in the Atlantic water layer (
Figure 15b does not show it clearly because of its small contribution to the mass distribution). Since the difference between two numerical experiments C1 and B lies in taking into account counter-gradient fluxes, it is the ordered eddy motions in the area of the shelf-slope that affect the noticed changes in the heat content of the Atlantic water layer in this area.
In the second numerical experiment C2, we set the parameter
p in Equation (
32) to be equal to one, which corresponds to the situation when the heat and salt fluxes are taken inversely proportional to the contribution of temperature and salinity variations to density variations following the equation of state. As in experiment C1, the counter-gradient salt flux turns out to be co-directed with the counter-gradient mass flux, and the heat flux is opposite to it. The coefficient
in Equation (
29) is equal to the coefficient
and, accordingly, both are equal to 0.5. Thus, the contribution of the counter-gradient heat flux becomes more significant relative to the counter-gradient salinity flux than in the C1 experiment. Nevertheless, the resulting mass increment is lower than in the C1 experiment, and even three orders of magnitude smaller than in the B experiment.
Figure 17a shows that in first ten years, both the salinity and temperature contribution to water mass were growing negative. Right after this period, the density change rate due to salinity started growing, so that in 2019–2020 it became positive. At the same time, temperature contribution became positive, but after 2017 was mostly negative. Vertical salinity tendencies decreased water density in the upper 400 m layer, but temperature tendencies worked in the opposite way in the upper 150 m but supported them in the 150–1000 m layer.
The area most influenced by counter-gradient fluxes is still in the Laptev and East Siberian seas, but the anomaly distribution is more complicated than in the C1 experiment (
Figure 18). We still have a heat content growth in the vicinity of the Fram Strait in the upper layer but also there is a noticeable area of counter-gradient fluxes in the vicinity of the Lomonosov ridge in the central Arctic where the Atlantic water current following the Laptev Sea shelf break turns northward along the ridge.