Electrohydrodynamic (In)Stability of Microfluidic Channel Flows: Analytical Expressions in the Limit of Small Reynolds Number

Abstract

We study electrohydrodynamic (EHD) linear (in)stability of microfluidic channel flows, i.e., the stability of interface between two shearing viscous (perfect) dielectrics exposed to an electric field in large aspect ratio microchannels. We then apply our results to particular microfluidic systems known as two-liquid electroosmotic (EO) pumps. Our novel results are detailed analytical expressions for the growth rate of two-dimensional EHD modes in Couette–Poiseuille flows in the limit of small Reynolds number (R); the expansions to both zeroth and first order in R are considered. The growth rates are complicated functions of viscosity-, height-, density-, and dielectric-constant ratio, as well as of wavenumbers and voltages. To make the results useful to experimentalists, e.g., for voltage-control EO pump operations, we also derive equations for the impending voltages of the neutral stability curves that divide stable from unstable regions in voltage–wavenumber stability diagrams. The voltage equations and the stability diagrams are given for all wavenumbers. We finally outline the flow regimes in which our first-order-R voltage corrections could potentially be experimentally measured. Our work gives insight into the coupling mechanism between electric field and shear flow in parallel-planes channel flows, correcting an analogous EHD expansion to small R from the literature. We also revisit the case of pure shear instability, when the first-order-R voltage correction equals zero, and replace the renowned instability mechanism due to viscosity stratification at small R with the mechanism due to discontinuity in the slope of the unperturbed velocity profile.

1. Introduction

When exposed to an electric (E) field, an interface between two stationary superposed (positioned on top of each other) dielectric fluids can become unstable, forming periodic undulations that can further grow and deform [1,2,3,4,5]. The well-studied phenomenon, known as electrohydrodynamic (EHD) instability, depends on the nature of dielectrics (perfect dielectrics without free surface charge [6], or leaky dielectrics [7]), the direction of E-fields (normal [2] vs. tangential [8]) and is generally a function of (the ratios of) the fluids’ conductivities, dielectric constants, densities, and heights, as well as applied voltages. The seminal work on EHD stability, both experimental and theoretical, was carried out on a macroscopic scale (≳ 10 cm) [1].

When two superposed fluids are in motion, such as, e.g., in parallel-plane channel flows, things are more complicated since instabilities arise even in the absence of the E-fields [9,10,11,12,13], and, in fact, for arbitrary small Reynolds numbers [14]. When E-fields are present, the stability of the growth modes is changed as the fields in general couple to flow; see, e.g., [15]. The EHD instability of two shearing (perfect) dielectrics in channel flow was studied in Ref. [16], but, as we show, not correctly analyzed. A correct (theoretical) approach of EHD instability of two shearing (leaky) dielectrics in channel flows was carried out in Ref. [17], where the unstable modes with largest growth rate were solved numerically and then explored systematically over a selected range of parameters; however, the analysis was applied to microfluidic channels and these are typically much longer than wider and higher, so two flowing immiscible dielectrics will generally arrange themselves interspersed between, rather than on top of, each other, as they try to minimize the free interface energy and, thus, the contact [18,19]. As we discuss below, special conditions are needed to enable the parallel flow of two superposed liquids in microfluidic channels.

Our article is four-pronged. First, we explore the fundamental coupling mechanism between the electric fields and the viscous shear in parallel microchannel flows with two immiscible viscous (perfect) dielectric liquids at small Reynolds number. To achieve that, we employ an analytical (closed-form) approach and are able to derive the correct EHD expansions to zeroth and first order in R. Our methodology resolves the inconsistencies in Ref. [16], which attempted the same task. Our analytical methods give us a deeper theoretical insight into the parameter dependencies, in contrast to numerical studies such as Ref. [17].

Second, we apply the results to realistic microfluidic systems that operate at small Reynolds numbers in the hope that the EHD coupling could eventually be measured. We recognize that not every microchannel flow will make possible the superposition of two immiscible liquids on top of each other: only specially made systems known as two-liquid electroosmotic (EO) pumps, featuring large aspect ratio channels (Figure 1a) and a driving velocity at the wall, are able to do that [20,21]. The EO pumps have a more complicated flow profile: Couette–Poiseuille, i.e., combined EO/pressure-driven flow, rather than a pure pressure-driven one. Typical velocities are around 1 mm/s.

Third, we find it useful to study the onset of instability, i.e., the impending voltages that define neutral stability curves (dividing stability diagrams into stable and unstable regions) under various pump operations, rather than to parametrically explore the largest growth mode(s). We aim to obtain the corrections to the impending voltages when the shear stress becomes relevant at the first order R expansion—this will be the most informative phenomenon to measure to elucidate the fundamental EHD coupling. These type of corrections do not currently exist in the literature. As for the modes, they will definitely be constrained by finite size of microfluidic channels (typical length scales of 1–100 $\mathsf{\mu }$m) and may even be excluded altogether from the systems.

Lastly, we are able to revisit the phenomenon known as the instability due to viscosity stratification, postulated by Yih in the seminal study [14]. This appears as a special case in the expansion to first order in R when E-field is zero. We demonstrate that the instability is, in fact, due to the discontinuity of the zero-order velocity profile.

It is now useful to summarize the differences between our work and similar work in the literature due to some overlap.

Our study vs. Ref. [14]: EHD analytical vs. viscous shear analytical study, perfect viscous dielectrics vs. viscous fluids, special case for $E=0$ vs. $E=0$, small R arbitrary k vs. small k arbitrary R, instability due to discontinuity in the slope vs. instability due to viscosity stratification, experimental proposal vs. no experimental proposal.

Our study vs. Ref. [16]: EHD analytical vs. EHD analytical study, perfect viscous vs. perfect viscous dielectrics, consistent zero- and first-order expansion in small R vs. inconsistent expansions in small R, application to microfluidics (EO pumps) vs. no applications, impending voltages to both orders in R vs. no impending voltages, Yih’s special case vs. no special cases.

Our study vs. Ref. [17]: EHD analytical vs. EHD numerical study, general parametric dependency of growth rates vs. parametric plots of growth rates, perfect viscous vs. leaky viscous dielectrics, combined EO/pressure driven flows vs. pressure driven flows, impending voltages to zero- and first-order R vs. no impending voltages.

Structure of the Article

In this comprehensive article, we systematically explore the mechanism of EHD (in)stability of two shearing perfect dielectric fluids in a parallel-plane microfluidic Couette–Poiseuille flow, and apply it to EO pumps. The governing equations and the boundary conditions for velocity/pressure and E-fields (E-potentials) are those of two-dimensional flow (the flow between two-infinite planes—an approximation), and are nondimensionalized suitable to microfluidic regime (Section 2). We linearize them first with respect to small interface displacement, $\zeta$, considering two-dimensional disturbances (these suffice for the stability analysis), obtaining the zeroth- and the first-order approximations in $\zeta$ (Section 3).

The perturbed flow to first order in $\zeta$ is still two-dimensional, allowing us to make use of the stream functions. These identically satisfy the continuity equations and enable transformation of the Navier–Stokes second-degree partial-differential equations for velocity and pressure into the corresponding Orr–Sommerfeld fourth-degree ordinary-differential equations solely for the stream functions (Section 3.3). In the nonlinear boundary conditions, Section 3.5, the balance of normal stresses contains the coupling of electric fields with the flow.

We then make another linearization, i.e., expand the stream functions, E-potentials and the phase velocity of the disturbances in small Reynolds number. This is used then to expand and solve the governing Orr–Sommerfeld equations for each fluid and the accompanying boundary conditions to zeroth (Section 4) and first order in R (Section 5). Our analysis leads to sets of complicated eigenvalue problems to each order in R for the phase velocity of (un)stable modes. The imaginary part of the phase velocity—a complicated function of all flow/E-field nondimensional parameters as well as wavenumbers—determines the growth rate of the disturbances for all wavenumbers. The analytical expressions for the phase velocity to zeroth and first order in R are our main results.

The EHD instability occurs for normal E-fields and already in the zeroth-R expansion (independent of viscosity or zeroth-$\zeta$ velocity). The equation for impending voltages for all wavenumbers, plotted in the corresponding stability diagram, is another of our results (Section 4.3). Unlike the zeroth-R voltages, the impending voltages to first-order R depend on the viscosity and zeroth-$\zeta$ velocity due to the coupling between the E-fields and shearing flows (Section 5.2). The stability diagram, thus, is modified for each flow regime, but the first-order-R voltages are very small and would likely be hard to measure. Our zeroth- and first-order-R expansions correct the erroneous expansions attempted in [16]. We also revisit and refine the instability due to viscosity stratification at small R [14], which is a special case obtained to first order in R when no E-fields are present (pure shear; Section 5.1).

The analytical expressions for the phase velocity and the voltage to first order in R are extremely cumbersome and could not be made possible without a symbolic manipulation of computer-algebra software such as Mathematica [22] (similarly observed in [23]). The compressed closed form for the phase velocity, separated into smaller pieces, is in Appendix C.

The article is long, but it is necessary to showcase the formalism to enable validation of (partial) results.

2. Problem Formulation

2.1. General Equations of Motion

Our problem is sketched in Figure 1: the large aspect ratio configuration of a microfluidic EO pump is approximated by the flow of two viscous dielectrics placed between two parallel infinite planes and exposed to a normal or tangential E-field. The velocity profile is the superposition of the Couette and the (adverse) Poiseuille flow profiles; see Figure 2a.

The equation of motion for a single, isotropic, incompressible Newtonian fluid placed in an electric field, is given by

$$\rho D_t^{}\mathbf{U}=-\nabla P+\mu {\nabla }^2\mathbf{U}+{\mathbf{F}}_e^{},$$

(1)

where $\rho$ is the density, P the pressure, $\mu$ the dynamical viscosity, $\mathbf{U}$ the velocity field, and ${\mathbf{F}}_e^{}$ the electric body force. $D_t^{}$ is the convective derivative:

$$D_t^{}={\partial }_t^{}+\mathbf{U}·\nabla .$$

(2)

The complete electric body force ${\mathbf{F}}_e^{}$ on an isothermal fluid at temperature T can be expressed as [24]

$${\mathbf{F}}_e^{}=\frac{1}{2}\nabla \left[E^2\rho {\left({\partial }_{\rho }^{}ϵ\right)}_T\right]-\frac{1}{2}{E}^2\nabla ϵ+{\rho }_e^{}\mathbf{E},$$

(3)

where $ϵ$ is the dielectric constant and ${\rho }_e^{}$ is the charge density. The three contributions on the right-hand side in Equation (3) are due to isotropic deformations (electrostriction), variations of the (relative) dielectric constant, and free charges within the fluid, respectively. In the case of a homogeneous, perfect dielectric, ($ϵ=$ const.,${\rho }_e^{}=0$), we see from Equation (3) that there is no electric body force in the bulk of the fluid. However, a net electric stress will appear on the boundary between two dissimilar dielectrics. This stress can conveniently be expressed as the divergence

$${\mathbf{F}}_e^{}=\nabla ·T^M$$

(4)

of the Maxwell stress tensor $T^M$ given by

$$T_{ik}^M=-\frac{1}{2}ϵ\left[1-\frac{\rho }{ϵ}{\left({\partial }_{\rho }^{}ϵ\right)}_T\right]E^2{\delta }_{ik}^{}+ϵE_i^{}{E}_k^{}.$$

(5)

This describes the coupling of the electric field at the interface of the two dielectrics. In the case of incompressible fluids, the deformation term in Equations (3) and (5) can be absorbed into a redefined pressure.

Additional equations include the continuity equation for incompressible liquids,

$$\nabla ·\mathbf{U}=0,$$

(6)

and the Maxwell equations for electric fields, which in the absence of free charges and radiation effects reduce to the quasistatic approximation [25]:

$$\begin{array}{cc}\hfill \nabla ·\left(ϵ\mathbf{E}\right)& =0,\hfill \end{array}$$

(7a)

$$\begin{array}{cc}\hfill \mathbf{\nabla }\times \mathbf{E}& =0.\hfill \end{array}$$

(7b)

From Equation (7b), we can introduce an electrical potential $\Phi$:

$$\mathbf{E}=-\nabla \Phi ,$$

(8)

which, together with Equation (7a) and a constant $ϵ$, yields the Laplace equation:

$${\nabla }^2\Phi =0.$$

(9)

2.2. General Boundary Conditions

To ease later referencing, we discuss here the general boundary conditions of our problem. While the perturbation analysis will be introduced in Section 3, we keep in mind that the velocity field $\mathbf{U}(x,y,z,t)=(U,V,W)$ and the electric field $\mathbf{E}$ are sums of a zeroth-order field, superscript (0), and a small perturbation, superscript (1), e.g., $\mathbf{U}={\mathbf{U}}^{\left(0\right)}+{\mathbf{U}}^{\left(1\right)}$.

Let us first consider a deformable interface between two dielectrics; Figure 1b. When unperturbed, the interface is described by the equation $z=0$. Upon a two-dimensional disturbance, the surface is described by

$$z=\zeta (x,t),$$

(10)

where $\zeta$ is the vertical displacement from the equilibrium position $z=0$. We consider only small values of $\zeta$. Any deformed surface is characterized by a unit normal vector $\mathbf{n}$, which, for small deformations, becomes

$$\mathbf{n}=(-{\partial }_x^{}\zeta ,1).$$

(11)

We denote the change in any function $f(x,z,t)$ across the interface by $\left[\right[f\left]\right]$,

$$\begin{array}{cc}\hfill \left[\right[f\left]\right]& \equiv f(x,{\zeta }^{-},t)-f(x,{\zeta }^{+},t)\hfill \\ \hfill & ={\left(f_2^{}-f_1^{}\right)}_{z=\zeta }.\hfill \end{array}$$

(12)

The interface conditions include the continuity of velocities and tangential stresses, as well as the continuity of tangential electric fields and normal dielectric displacements [26,27]; they also include the discontinuity of normal stresses at the interface caused by the surface tension. At the interface $z=\zeta$, we write

$$\begin{array}{cc}\hfill & \left[\right[U\left]\right]=\left[\right[V\left]\right]=\left[\right[W\left]\right]=0,\hfill \end{array}$$

(13a)

$$\begin{array}{cc}\hfill & W_1^{}=W_2^{}=({\partial }_t^{}+U{\partial }_x^{})\zeta ,\hfill \end{array}$$

(13b)

$$\begin{array}{cc}\hfill & \mathbf{n}\times \left[\right[\mathbf{E}\left]\right]=0\Rightarrow \left[\right[\Phi \left]\right]=0,\hfill \end{array}$$

(13c)

$$\begin{array}{cc}\hfill & \mathbf{n}·\left[\right[ϵ\mathbf{E}\left]\right]=\mathbf{n}·\left[\right[ϵ\nabla \Phi \left]\right]=0,\hfill \end{array}$$

(13d)

$$\begin{array}{cc}\hfill & \left[[-P]\right]n_i^{}+\left[\left[{\tau }_{ik}^{}+T_{ik}^M\right]\right]n_k^{}=\gamma {\partial }_x^2\zeta n_i^{},\hfill \end{array}$$

(13e)

where ${\tau }_{ik}^{}$ is the viscous stress, $\gamma$ the surface tension, and ${\partial }_x^2\zeta$ describes the surface curvature for small deformations in Equation (13e). Equation (13b) expresses the kinematic boundary condition which conserves the motion of the interface points. Equation (13c) is expressed in the simplest form, applicable also to unperturbed normal fields.

For the unperturbed velocity field ${\mathbf{U}}^{\left(0\right)}$, the boundary conditions at the microchannel walls are

$$\begin{array}{cccc}\hfill {\mathbf{U}}_1^{\left(0\right)}& =U_0^{}{\mathbf{e}}_x^{},\hfill & \hfill z& =+h_1^{}\hfill \end{array}$$

(14a)

$$\begin{array}{cccc}\hfill {\mathbf{U}}_2^{\left(0\right)}& =0,\hfill & \hfill z& =-h_2^{},\hfill \end{array}$$

(14b)

while for the perturbation ${\mathbf{U}}^{\left(1\right)}$ no-slip applies,

$$\begin{array}{cccc}\hfill {\mathbf{U}}_1^{\left(1\right)}& =0,\hfill & \hfill z& =+h_1^{}\hfill \end{array}$$

(15a)

$$\begin{array}{cccc}\hfill {\mathbf{U}}_2^{\left(1\right)}& =0,\hfill & \hfill z& =-h_2^{}.\hfill \end{array}$$

(15b)

In the case of a normal electric field, it is assumed that the rigid walls are perfectly conducting electrodes kept at a potential difference $V_0^{}$ and in direct contact with the liquids. The two electrodes are large enough that the fringing fields close to the edges are not important. The unperturbed potential ${\Phi }^{\left(0\right)}$ thus satisfies the boundary conditions

$$\begin{array}{cccc}\hfill {\Phi }_1^{\left(0\right)}& =V_0^{},\hfill & \hfill z& =+h_1^{}\hfill \end{array}$$

(16a)

$$\begin{array}{cccc}\hfill {\Phi }_2^{\left(0\right)}& =0,\hfill & \hfill z& =-h_2^{},\hfill \end{array}$$

(16b)

while the small perturbation ${\Phi }^{\left(1\right)}$ obeys

$$\begin{array}{cccc}\hfill {\Phi }_1^{\left(1\right)}& =0,\hfill & \hfill z& =+h_1^{}\hfill \end{array}$$

(17a)

$$\begin{array}{cccc}\hfill {\Phi }_2^{\left(1\right)}& =0,\hfill & \hfill z& =-h_2^{},\hfill \end{array}$$

(17b)

In the case of an imposed tangential electric field, we assume that the liquids are placed between two insulating walls in a uniform horizontal field produced by two large electrodes spaced far apart at $x=\pm \infty$. The uniform-field assumption is particularly valid in the microfluidic case, where the distance between the confining planes is very small. At the insulating rigid wall boundaries, the Neumann conditions apply for the E-potentials:

$$\begin{array}{cccc}\hfill {\partial }_z^{}{\Phi }_1^{\left(1\right)}& =0,\hfill & \hfill z& =+h_1^{},\hfill \end{array}$$

(18a)

$$\begin{array}{cccc}\hfill {\partial }_z^{}{\Phi }_2^{\left(1\right)}& =0,\hfill & \hfill z& =-h_2^{}.\hfill \end{array}$$

(18b)

2.3. Two-Dimensional Flow and Nondimensional Equations

The symmetry of our problem with an interfacial wave (see Figure 1b) implies a y-independent two-dimensional flow, $\widehat{\mathbf{U}}(x,z,t)=\widehat{U}(x,z,t){\mathbf{e}}_x^{}+\widehat{W}(x,z,t){\mathbf{e}}_z^{}$, where the direction of the traveling interfacial wave coincides with ${\mathbf{e}}_x^{}$. By virtue of Squire’s theorem in uniform and stratified fluids, it suffices to consider the stability of two-dimensional disturbances [28,29]. Note that physical variables in this section are marked by hats. For each fluid $i=1,2$ we have

$$\begin{array}{cc}\hfill {\widehat{\rho }}_i^{}{\widehat{D}}_t^{}{\widehat{U}}_i^{}& =-{\widehat{\partial }}_x^{}{\widehat{P}}_i^{}+{\widehat{\mu }}_i^{}{\widehat{\nabla }}_s^2{\widehat{U}}_i^{},\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill {\widehat{\rho }}_i^{}{\widehat{D}}_t^{}{\widehat{W}}_i^{}& =-{\widehat{\partial }}_z^{}{\widehat{P}}_i^{}+{\widehat{\mu }}_i^{}{\widehat{\nabla }}_s^2{\widehat{W}}_i^{},\hfill \end{array}$$

(19b)

where ${\widehat{D}}_t^{}={\widehat{\partial }}_t^{}+\widehat{U}{\widehat{\partial }}_x^{}+\widehat{W}{\widehat{\partial }}_z^{}$ and ${\widehat{\nabla }}_s^2={\widehat{\partial }}_x^2+{\widehat{\partial }}_z^2$. As mentioned earlier, the electric terms do not enter the bulk equations, but only the interface conditions. The continuity equation becomes

$${\widehat{\partial }}_x^{}{\widehat{U}}_i^{}+{\widehat{\partial }}_z^{}{\widehat{W}}_i^{}=0,$$

(19c)

and the Maxwell equations reduce to

$${\widehat{\nabla }}_s^2{\widehat{\Phi }}_i=0.$$

(19d)

We now introduce the nondimensional variables (no hats):

$$\begin{array}{cccccccccc}\hfill (U_i^{},W_i^{})& =\hfill & & \frac{1}{{\widehat{U}}_0^{}}({\widehat{U}}_i^{},{\widehat{W}}_i^{}),\hfill & \hfill (x,z)& =\hfill & & & & \frac{1}{{\widehat{h}}_1^{}}(\widehat{x},\widehat{z}),\hfill \end{array}$$

(20a)

$$\begin{array}{cccccccccc}\hfill P_i^{}& =\hfill & & \frac{{\widehat{h}}_1^{}}{{\widehat{\mu }}_i^{}{\widehat{U}}_0^{}}{\widehat{P}}_i^{},\hfill & \hfill t& =\hfill & & & & \frac{{\widehat{U}}_0^{}}{{\widehat{h}}_1^{}}\widehat{t},\hfill \end{array}$$

(20b)

$$\begin{array}{cccccccccc}\hfill {ϵ}_i^{}{E}_i^2& =\hfill & & \frac{{\widehat{h}}_1^{}}{{\widehat{\mu }}_1^{}{\widehat{U}}_0^{}}{\widehat{ϵ}}_i^{}{\widehat{E}}_i^2,\hfill & \hfill {\Phi }_i^{}& =\hfill & & & & \frac{1}{{\widehat{V}}_0^{}}{\widehat{\Phi }}_i^{}.\hfill \end{array}$$

(20c)

We chose the length scale as in [14] but adapted a pressure scale relating to microfluidics due to the small Reynolds numbers. Note that the pressure scales in the two layers differ from each other in Equation (20b), so that the governing Equations (24a)–(24d) appear symmetric for both layers. We also introduce the four other relevant parameters, also listed in Figure 2b:

$$h=\frac{{\widehat{h}}_2^{}}{{\widehat{h}}_1^{}},\mu =\frac{{\widehat{\mu }}_2^{}}{{\widehat{\mu }}_1^{}},\rho =\frac{{\widehat{\rho }}_2^{}}{{\widehat{\rho }}_1^{}},\epsilon =\frac{{\widehat{ϵ}}_2^{}}{{\widehat{ϵ}}_1^{}},$$

(21)

and the Reynolds numbers corresponding to the two fluid regions:

$$\begin{array}{cc}\hfill R{e}_1^{}& \equiv R=\frac{{\widehat{\rho }}_1^{}{\widehat{U}}_0^{}{\widehat{h}}_1^{}}{{\widehat{\mu }}_1^{}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill R{e}_2^{}& =\frac{{\widehat{\rho }}_2^{}{\widehat{U}}_0^{}{\widehat{h}}_1^{}}{{\widehat{\mu }}_2^{}}=\frac{\rho }{\mu }R.\hfill \end{array}$$

(23)

In the nondimensional form, Equations (19a)–(19d) are

$$\begin{array}{cc}\hfill R{e}_i^{}{D}_t{U}_i& =-{\partial }_x{P}_i+{\nabla }_s^2{U}_i,\hfill \end{array}$$

(24a)

$$\begin{array}{cc}\hfill R{e}_i^{}{D}_t{W}_i& =-{\partial }_z{P}_i+{\nabla }_s^2{W}_i,\hfill \end{array}$$

(24b)

$$\begin{array}{cc}\hfill {\partial }_x^{}{U}_i^{}+{\partial }_z^{}{W}_i^{}& =0,\hfill \end{array}$$

(24c)

$$\begin{array}{cc}\hfill {\nabla }_s^2{\Phi }_i^{}& =0.\hfill \end{array}$$

(24d)

3. Linearization in the Interface Displacement $\zeta$

We now apply standard linearization theory to Equations (24a)–(24d), as in [30]. In a two-dimensional flow, we consider a harmonic displacement $\zeta$ given by

$$\zeta (x,t)={\zeta }_0^{}exp\left[ik(x-ct)\right],$$

(25)

where ${\zeta }_0^{}$ is the amplitude, $k=2\pi /\lambda$ the wavenumber, and c the complex phase velocity of the disturbance. Any field f (the velocity $\mathbf{U}$, the pressure P, the electric field $\mathbf{E}$, the potential $\Phi$, and the normal vector $\mathbf{n}$) is then written as

$$f=f^{\left(0\right)}+f^{\left(1\right)}$$

(26)

where $f^{\left(0\right)}$ represents the unperturbed steady-state solution, while $f^{\left(1\right)}$ is a small perturbation. Placing the perturbed fields f into the governing equations and invoking boundary and interface conditions, the steady-state solutions cancel out, and by only maintaining terms up to linear order in $f^{\left(1\right)}$, we arrive at linearized equations that govern the perturbations. In compliance with the linearization, the fields at the interface $z=\zeta$ are also expanded up to first order in $\zeta$ as follows:

$$f\left(\zeta \right)=f^{\left(0\right)}\left(0\right)+\zeta {\partial }_z{f}^{\left(0\right)}\left(0\right)+f^{\left(1\right)}\left(0\right).$$

(27)

The first-order solutions are further expressed in terms of normal modes, Equation (25):

$$f^{\left(1\right)}(x,z,t)=f^{\left(1\right)}\left(z\right)exp\left[ik(x-ct)\right].$$

(28)

When the normal modes are inserted back into the linearized equations, the problem is transformed into an eigenvalue problem for the complex phase velocity $c=c_r^{}+i{c}_i^{}$. It is seen from Equation (28) that

$$f^{\left(1\right)}(x,z,t)\propto exp[-ik{c}_r^{}t]exp\left[k{c}_i^{}t\right],$$

(29)

which means that instability (the exponential growth in time) happens for $c_i^{}>0$. The neutral stability condition $c_i^{}=0$ divides the stable from the unstable regions.

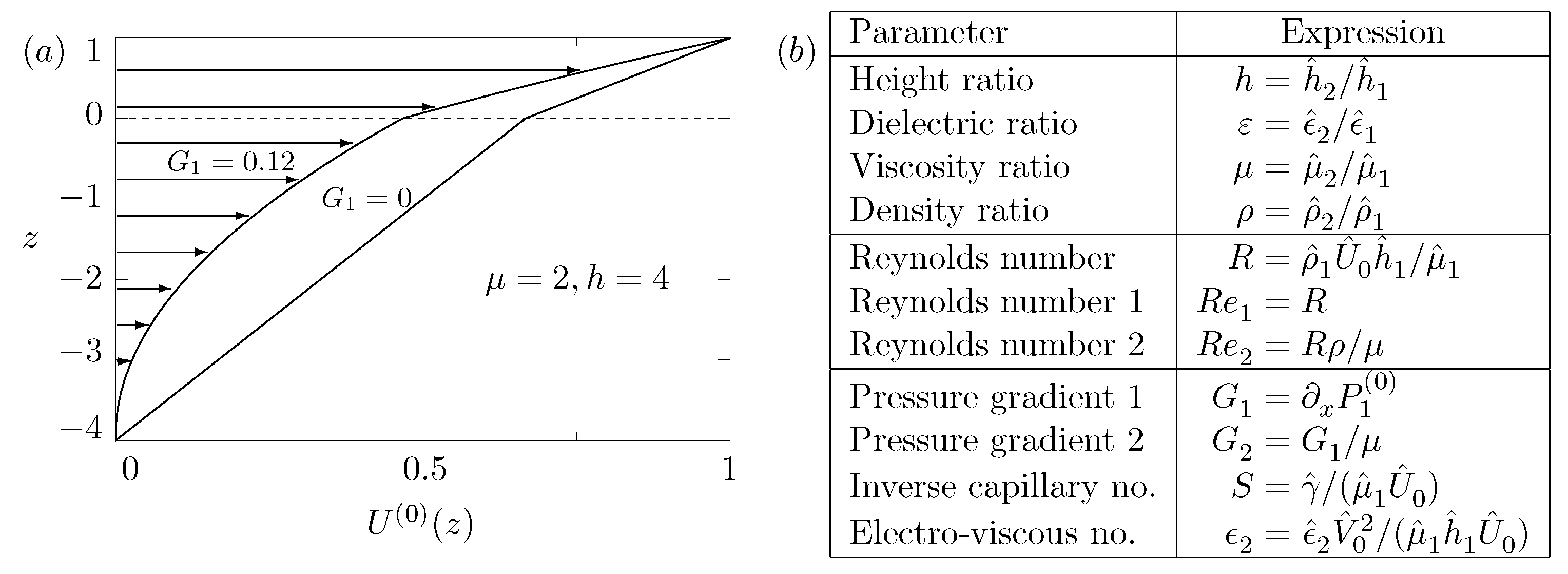
3.1. Velocity Field to Zeroth Order in $\zeta$ (The Unperturbed Flow)

The zeroth-order-$\zeta$ flow is a steady-state, parallel flow $\mathbf{U}=U^{\left(0\right)}{\mathbf{e}}_z$, with the velocity $U_0^{}=1$ at the upper boundary; Figure 1b. The left-hand sides in Equations (24a) and (24b)) drop out and we solve

$${\partial }_z^2{U}_i^{\left(0\right)}={\partial }_x^{}{P}_i^{\left(0\right)}\equiv G_i^{},$$

(30)

where the pressure gradient $G_i^{}$ is constant due to the translation invariance.

The boundary and interface conditions obtained from Equations (13c)–(14) with ${\mathbf{n}}^{\left(0\right)}={\mathbf{e}}_z$ are

$$\begin{array}{cc}\hfill & U_1^{\left(0\right)}\left(1\right)=1,\hfill \end{array}$$

(31a)

$$\begin{array}{cc}\hfill & U_2^{\left(0\right)}(-h)=0,\hfill \end{array}$$

(31b)

$$\begin{array}{cc}\hfill & \left[\left[U^{\left(0\right)}\left(0\right)\right]\right]=0,\hfill \end{array}$$

(31c)

$$\begin{array}{cc}\hfill & \left[\left[\mu {\partial }_z^{}{U}^{\left(0\right)}\left(0\right)\right]\right]=0,\hfill \end{array}$$

(31d)

$$\begin{array}{cc}\hfill -& \left[\left[P^{\left(0\right)}\right]\right]+\left[\left[\frac{ϵ}{2}\left({E_{\mathrm{N}}^{\left(0\right)}}^2-{E_{\mathrm{T}}^{\left(0\right)}}^2\right)\right]\right]=0.\hfill \end{array}$$

(31e)

Note that the electric term in Equation (31d) vanishes since the continuity of the electric tangential stresses is trivially satisfied. Furthermore, the zeroth-order electric fields set up a constant equilibrium pressure; Equation (31e). The well-known solution of the above zeroth-order system is

$$U_i^{\left(0\right)}=\frac{1}{2}{G}_i^{}{z}^2+a_i^{}z+b,$$

(32)

with

$$\begin{array}{ccccccc}\hfill G_1^{}& =\hfill & & {\partial }_x^{}{P}_1^{\left(0\right)}=\frac{{\widehat{h}}_1^2}{{\widehat{\mu }}_1^{}{\widehat{U}}_0^{}}\widehat{G},\hfill & \hfill G_2^{}& =\hfill & \hfill \frac{G_1^{}}{\mu },\end{array}$$

(33a)

$$\begin{array}{ccccccc}\hfill a_1^{}& =\hfill & & \frac{\mu -\frac{1}{2}{G}_1^{}(\mu -h^2)}{\mu +h},\hfill & \hfill a_2^{}& =\hfill & \hfill \frac{a_1^{}}{\mu },\end{array}$$

(33b)

$$\begin{array}{cccc}\hfill b& =\hfill & & \frac{h}{\mu +h}\left[1-\frac{1}{2}{G}_1^{}(1+h)\right],\hfill \end{array}$$

(33c)

where $\widehat{G}={\widehat{\partial }}_x^{}{\widehat{P}}^{\left(0\right)}$ is a constant physical pressure gradient. Two zeroth-order (unperturbed) flow profiles are shown in Figure 2a.

3.2. Electric Potentials to Zeroth Order in $\zeta$ (The Unperturbed Electric Potentials)

Now, turning to externally applied electric fields, we first consider the normal electric field between two metallic electrodes kept at a constant potential difference. The condition of a constant normal E-field in the region i

$${\mathbf{E}}_i^{\left(0\right)}=E_{i,\mathrm{N}}^{\left(0\right)}{\mathbf{e}}_z,$$

(34)

which, together with Equation (24d), yields

$${\Phi }_{i,\mathrm{N}}^{\left(0\right)}=-E_{i,\mathrm{N}}^{\left(0\right)}z+C_i^{}.$$

(35)

The constants $C_i^{}$ are determined from the boundary conditions

$$\begin{array}{cc}\hfill & {\Phi }_{1,\mathrm{N}}^{\left(0\right)}\left(1\right)=1,\hfill \end{array}$$

(36a)

$$\begin{array}{cc}\hfill & {\Phi }_{1,\mathrm{N}}^{\left(0\right)}(-h)=0,\hfill \end{array}$$

(36b)

$$\begin{array}{cc}\hfill & \left[\left[{\Phi }_{\mathrm{N}}^{\left(0\right)}\left(0\right)\right]\right]=0,\hfill \end{array}$$

(36c)

$$\begin{array}{cc}\hfill & \left[\left[ϵ{\partial }_z^{}{\Phi }_{\mathrm{N}}^{\left(0\right)}\left(0\right)\right]\right]=0.\hfill \end{array}$$

(36d)

We find

$$\begin{array}{cc}\hfill {\Phi }_{1,\mathrm{N}}^{\left(0\right)}& =\frac{\epsilon z+h}{\epsilon +h},\hfill \end{array}$$

(37a)

$$\begin{array}{cc}\hfill {\Phi }_{2,\mathrm{N}}^{\left(0\right)}& =\frac{z+h}{\epsilon +h},\hfill \end{array}$$

(37b)

and

$$\begin{array}{cc}\hfill E_{1,\mathrm{N}}^{\left(0\right)}& =-\frac{\epsilon }{\epsilon +h},\hfill \end{array}$$

(37c)

$$\begin{array}{cc}\hfill E_{2,\mathrm{N}}^{\left(0\right)}& =-\frac{1}{\epsilon +h},\hfill \end{array}$$

(37d)

where h and $\epsilon$ are given by Equation (21) and Figure 2b.

In the case of a constant tangential E-field in the x-direction, Equation (13c) yields

$$\begin{array}{cc}\hfill {\mathbf{E}}_{1,\mathrm{T}}^{\left(0\right)}& ={\mathbf{E}}_{2,\mathrm{T}}^{\left(0\right)}=E_0^{}{\mathbf{e}}_x,\hfill \end{array}$$

(38a)

$$\begin{array}{cc}\hfill {\Phi }_{1,\mathrm{T}}^{\left(0\right)}& ={\Phi }_{2,\mathrm{T}}^{\left(0\right)}=-E_0^{}x.\hfill \end{array}$$

(38b)

In order to simplify the notation, we skip the N and T subscripts and introduce the curly brackets:

$$\begin{array}{cc}\hfill {\Phi }_1^{\left(0\right)}& =\left\{\begin{array}{c}\frac{\epsilon z+h}{\epsilon +h}\\ -E_0^{}x\end{array}\right\},\hfill \end{array}$$

(39a)

$$\begin{array}{cc}\hfill {\Phi }_2^{\left(0\right)}& =\left\{\begin{array}{c}\frac{z+h}{\epsilon +h}\\ -E_0^{}x\end{array}\right\},\hfill \end{array}$$

(39b)

where the upper and lower parts within the brackets pertain to the case of the normal and tangential E-field, respectively.

3.3. Velocity Field to First Order in $\zeta$

Introducing the interface deformation $\zeta$, the velocity and pressure fields up to the linear order become

$$\begin{array}{cc}\hfill \mathbf{U}& =\left[U^{\left(0\right)}\left(z\right)+U^{\left(1\right)}(x,z,t)\right]{\mathbf{e}}_x+W^{\left(1\right)}(x,z,t){\mathbf{e}}_z,\hfill \end{array}$$

(40a)

$$\begin{array}{cc}\hfill P& =P^{\left(0\right)}+P^{\left(1\right)}(x,z,t).\hfill \end{array}$$

(40b)

For the upper liquid, Equations (24a)–(24c) yield

$$\begin{array}{cc}\hfill R\left({\partial }_t^{}{U}_1^{\left(1\right)}+U_1^{\left(0\right)}{\partial }_x^{}{U}_1^{\left(1\right)}+W_1^{\left(1\right)}{\partial }_z^{}{U}_1^{\left(0\right)}\right)& =-{\partial }_x^{}{P}_1^{\left(1\right)}+{\nabla }_s^2{U}_1^{\left(1\right)},\hfill \end{array}$$

(41a)

$$\begin{array}{cc}\hfill R\left({\partial }_t^{}{W}_1^{\left(1\right)}+U_1^{\left(0\right)}{\partial }_x^{}{W}_1^{\left(1\right)}\right)& =-{\partial }_z^{}{P}_1^{\left(1\right)}+{\nabla }_s^2{W}_1^{\left(1\right)},\hfill \end{array}$$

(41b)

$$\begin{array}{cc}\hfill {\partial }_x^{}{U}_1^{\left(1\right)}+{\partial }_z^{}{W}_1^{\left(1\right)}& =0.\hfill \end{array}$$

(41c)

Equation (41c) allows the use of a stream function $\Psi$:

$$\left(U_1^{\left(1\right)},W_1^{\left(1\right)}\right)=\left({\partial }_z^{}{\Psi }_1^{},-{\partial }_x^{}{\Psi }_1^{}\right).$$

(42)

Expanding ${\Psi }_1^{}$ and $P_1^{\left(1\right)}$ into the normal modes

$$\left({\Psi }_1^{},P_1^{\left(1\right)}\right)=\left({\psi }_1^{}\left(z\right),p_1^{\left(1\right)}\left(z\right)\right)exp\left[ik(x-ct)\right],$$

(43)

and using Equation (42), Equations (41a) and (41b) become

$$\begin{array}{cc}\hfill ikR\left[\left(U_1^{\left(0\right)}-c\right){\partial }_z^{}{\psi }_1^{}-{\partial }_z^{}{U}_1^{\left(0\right)}{\psi }_1^{}\right]& =-ik{p}_1^{\left(1\right)}+\left({\partial }_z^3{\psi }_1^{}-k^2{\partial }_z^{}{\psi }_1^{}\right),\hfill \end{array}$$

(44a)

$$\begin{array}{cc}\hfill k^{2}R\left(c-U_1^{\left(0\right)}\right){\psi }_1^{}& ={\partial }_z^{}{p}_1^{\left(1\right)}+ik\left({\partial }_z^2{\psi }_1^{}-k^2{\psi }_1^{}\right).\hfill \end{array}$$

(44b)

After eliminating $p_1^{\left(1\right)}$, Equations (44a) and (44b) yield the known Orr–Sommerfeld equation for the upper liquid:

$$\begin{array}{cc}\hfill {\psi }_1^{″″}-2k^2{\psi }_1^{″}+k^4{\psi }_1^{}& =ikR\left[\left(U_1^{\left(0\right)}-c\right)\left({\psi }_1^{″}-k^2{\psi }_1\right)-{U_1^{\left(0\right)}}^{″}{\psi }_1^{}\right],\hfill \end{array}$$

(45)

where we introduced primes for $\mathrm{d}/\mathrm{d}z$ since both $U_1^{\left(0\right)}$ and ${\psi }_1^{}$ are functions of z only. In the same manner, using the stream function ${\Psi }_2^{}$, we obtain for the lower liquid

$$\begin{array}{cc}\hfill {\psi }_2^{″″}-2k^2{\psi }_2^{″}+k^4{\psi }_2^{}& =i\frac{\rho }{\mu }kR\left[\left(U_2^{\left(0\right)}-c\right)\left({\psi }_2^{″}-k^2{\psi }_2\right)-{U_2^{\left(0\right)}}^{″}{\psi }_2^{}\right].\hfill \end{array}$$

(46)

3.4. Electric Potentials to First Order in $\zeta$

To first order, the total potential is

$$\Phi ={\Phi }^{\left(0\right)}+{\Phi }^{\left(1\right)}(x,z,t).$$

(47)

Since both $\Phi$ and ${\Phi }^{\left(0\right)}$ satisfy the Laplace Equation (24d), it follows

$${\nabla }_s^2{\Phi }^{\left(1\right)}=0,$$

(48)

for which the general solution in terms of the normal modes are

$$\begin{array}{cc}\hfill {\Phi }_1^{\left(1\right)},{\Phi }_2^{\left(1\right)}& \propto \left\{\begin{array}{c}exp[\pm kz]exp\left[ik\right(x-ct\left)\right]\\ exp[\pm kz]exp\left[ik\right(x-ct\left)\right]\end{array}\right\}.\hfill \end{array}$$

(49)

The boundary and interface conditions for the normal E-field include Equations (13c) and (13d) on the interface and Equation (17) on the rigid electrodes. The linearized conditions are

$$\begin{array}{cc}\hfill & {\Phi }_1^{\left(1\right)}\left(1\right)=0,\hfill \end{array}$$

(50a)

$$\begin{array}{cc}\hfill & {\Phi }_2^{\left(1\right)}(-h)=0,\hfill \end{array}$$

(50b)

$$\begin{array}{cc}\hfill & \left[\left[\zeta {\partial }_z^{}{\Phi }^{\left(0\right)}\left(0\right)+{\Phi }^{\left(1\right)}\left(0\right)\right]\right]=0,\hfill \end{array}$$

(50c)

$$\begin{array}{cc}\hfill & \left[\left[ϵ{\partial }_z^{}{\Phi }^{\left(1\right)}\left(0\right)\right]\right]=0.\hfill \end{array}$$

(50d)

In a similar manner, we have Equation (18) together with the linearized Equations (13c) and (13d) for a tangential field

$$\begin{array}{cc}\hfill & {\partial }_z^{}{\Phi }_1^{\left(1\right)}\left(1\right)=0,\hfill \end{array}$$

(51a)

$$\begin{array}{cc}\hfill & {\partial }_z^{}{\Phi }_2^{\left(1\right)}(-h)=0,\hfill \end{array}$$

(51b)

$$\begin{array}{cc}\hfill & \left[\left[{\Phi }^{\left(1\right)}\left(0\right)\right]\right]=0,\hfill \end{array}$$

(51c)

$$\begin{array}{cc}\hfill & \left[\left[ϵ{\partial }_z^{}{\Phi }^{\left(1\right)}\left(0\right)+ik\zeta ϵE_0^{}\right]\right]=0.\hfill \end{array}$$

(51d)

Solving the above system, we arrive at the first-order potentials in the regions 1 and 2:

$$\begin{array}{cc}\hfill {\Phi }_1^{\left(1\right)}& =\left\{\begin{array}{c}-\zeta \frac{\epsilon (1-\epsilon )}{\epsilon +h}\frac{sinh\left[k\right(z-1\left)\right]}{cosh\left[k\right]\left(\epsilon tanh\left[k\right]+tanh\left[kh\right]\right)}\\ -i\zeta E_0^{}(1-\epsilon )\frac{cosh\left[k\right(z-1\left)\right]}{cosh\left[k\right]\left(\epsilon tanh\left[kh\right]+tanh\left[k\right]\right)}\end{array}\right\},\hfill \end{array}$$

(52a)

$$\begin{array}{cc}\hfill {\Phi }_2^{\left(1\right)}& =\left\{\begin{array}{c}-\zeta \frac{1-\epsilon }{\epsilon +h}\frac{sinh\left[k\right(z+h\left)\right]}{cosh\left[kh\right]\left(\epsilon tanh\left[k\right]+tanh\left[kh\right]\right)}\\ -i\zeta E_0^{}(1-\epsilon )\frac{cosh\left[k\right(z+h\left)\right]}{cosh\left[kh\right]\left(\epsilon tanh\left[kh\right]+tanh\left[k\right]\right)}\end{array}\right\},\hfill \end{array}$$

(52b)

from which the first-order electric fields and stresses are calculated. Note how the voltages’ phases differ, as normal and tangential E-fields affect the interface differently.

3.5. Boundary Conditions

The flow equations Equations (45) and (46) are subject to the following eight linearized boundary and interface conditions, BC1–BC8, expressed in terms of the stream function $\Psi$, Equation (42).

• BC1–BC4: no-slip conditions at the rigid boundaries:

  $$\begin{array}{cccc}\hfill {\psi }_1^{}\left(1\right)& =0,\hfill & \hfill {\psi }_1^{\prime }\left(1\right)& =0,\hfill \end{array}$$

  (53)

  $$\begin{array}{cccc}\hfill {\psi }_2^{}(-h)& =0,\hfill & \hfill {\psi }_2^{\prime }(-h)& =0,\hfill \end{array}$$

  (54)

  where, as before, primes denote $\mathrm{d}/\mathrm{d}z$.
• BC5: continuity of W at the interface

  $${\psi }_1^{}\left(0\right)={\psi }_2^{}\left(0\right),$$

  (55)
• BC6: continuity of U at the interface

  $${\psi }_1^{\prime }\left(0\right)-{\psi }_2^{\prime }\left(0\right)=\frac{{\psi }_1^{}\left(0\right)}{\tilde{c}}(1-\mu )a_2^{},$$

  (56)

  where $\mu$ and $a_2^{}$ are given in Equations (21) and (33b), respectively, and $\tilde{c}=c-U^{\left(0\right)}\left(0\right)=c-b$. This result is obtained as follows: the linearized kinematic condition

  $$W^{\left(1\right)}\left(0\right)=\left({\partial }_t^{}+U^{\left(0\right)}\left(0\right){\partial }_x^{}\right)\zeta$$

  (57a)

  yields

  $$\zeta =\frac{{\psi }_1^{}\left(0\right)}{\tilde{c}}exp\left[ik(x-ct)\right].$$

  (57b)
  We note that if $\tilde{c}=0$, a second-order expansion of the kinematic condition is required to avoid problems involving division by $\tilde{c}$. Now, Equation (57b) together with the linearized Equation (13a) for U

  $$\left[\left[{\partial }_z^{}{U}^{\left(0\right)}\left(0\right)\zeta +U^{\left(1\right)}\left(0\right)\right]\right]=0,$$

  (57c)

  results in Equation (56).
• BC7: continuity of tangential stresses at the interface

  $${\psi }_1^{″}\left(0\right)+k^2{\psi }_1^{}\left(0\right)=\mu \left({\psi }_2^{″}\left(0\right)+k^2{\psi }_2^{}\left(0\right)\right),$$

  (58)

  where use is made of the fact that at the interface of two perfect dielectrics, tangential electric stresses are always continuous:

  $$\left[\left[T_{\mathrm{T}\mathrm{k}}^{M_{}}\right]\right]n_k^{}=\left[\left[ϵE_{\mathrm{T}}^{}{E}_{\mathrm{N}}^{}\right]\right]=E_{\mathrm{T}}^{}\left[\left[ϵE_{\mathrm{N}}^{}\right]\right]=0,$$

  (59a)

  due to Equations (13c) and (13d). The remaining tangential viscous stresses of Equation (13e) give

  $$\left[\left[\mu \left({\partial }_z^2{U}^{\left(0\right)}\zeta +{\partial }_z^{}{U}^{\left(1\right)}\left(0\right)+{\partial }_x^{}{W}^{\left(1\right)}\left(0\right)\right)\right]\right]=0,$$

  (59b)

  which becomes Equation (58).
• BC8: balance of normal stresses

  $$\begin{array}{cc}\hfill ik\left(k^{2}S+T_{\mathrm{el}}^{}\right)\frac{{\psi }_1^{}\left(0\right)}{\tilde{c}}& =\mu \left({\psi }_2^{‴}\left(0\right)-3k^2{\psi }_2^{\prime }\left(0\right)\right)+i\rho kR\left(\tilde{c}{\psi }_2^{\prime }\left(0\right)+a_2^{}{\psi }_2\left(0\right)\right)\hfill \\ \hfill & -\left({\psi }_1^{‴}\left(0\right)-3k^2{\psi }_1^{\prime }\left(0\right)\right)-ikR\left(\tilde{c}{\psi }_1^{\prime }\left(0\right)+a_1^{}{\psi }_1\left(0\right)\right),\hfill \end{array}$$

  (60)

  which is found by linearizing Equation (13e) and making use of Equation (44a). In Equation (60), $\rho$ is the density ratio of Equation (21), and the nondimensional number S

  $$S=\frac{\widehat{\gamma }}{{\widehat{\mu }}_1^{}{\widehat{U}}_0^{}},$$

  (61)

  is the inverse of the capillary number and gives the normal-stress contribution due to the surface tension $\widehat{\gamma }$. $T_{\mathrm{el}}$ is given by

  $$T_{\mathrm{el}}=\left\{\begin{array}{c}-k\frac{{\widehat{ϵ}}_2^{}{\widehat{V}}_0^2}{{\widehat{\mu }}_1^{}{\widehat{h}}_1^{}{\widehat{U}}_0^{}}\frac{{(1-\epsilon )}^2}{{(h+\epsilon )}^2}\frac{1}{\epsilon tanh\left[k\right]+tanh\left[kh\right]}\\ +k\frac{{\widehat{ϵ}}_1^{}{\widehat{E}}_0^2{\widehat{h}}_1^{}}{{\widehat{\mu }}_1^{}{\widehat{U}}_0^{}}{(1-\epsilon )}^2\frac{1}{\epsilon tanh\left[kh\right]+tanh\left[k\right]},\end{array}\right\},$$

  (62)

  and gives the normal-stress contributions of the applied electric fields, which are found using Equations (5), (39a), (39b), (52a), and (52b),

  $$\begin{array}{cc}\hfill \left[\left[T_{\mathrm{N}\mathrm{k}}^{M_{}}\right]\right]n_k^{}& =\left\{\begin{array}{c}\left[\left[ϵ{\partial }_z^{}{\Phi }^{\left(0\right)}\left(0\right){\partial }_z^{}{\Phi }^{\left(1\right)}\left(0\right)\right]\right]\\ E_0^{}\left[\left[-ϵ{\partial }_x^{}{\Phi }^{\left(1\right)}\left(0\right)\right]\right]\end{array}\right\}\hfill \end{array}$$

  (63a)

  $$\begin{array}{cc}\hfill & =\left\{\begin{array}{c}-k{ϵ}_2^{}\frac{{(1-\epsilon )}^2}{{(h+\epsilon )}^2}\frac{1}{\epsilon tanh\left[k\right]+tanh\left[kh\right]}\zeta \\ +k{ϵ}_1^{}{E}_0^2{(1-\epsilon )}^2\frac{1}{\epsilon tanh\left[kh\right]+tanh\left[k\right]}\zeta \end{array}\right\}.\hfill \end{array}$$

  (63b)
  Note that the effective nondimensional values of ${ϵ}_2^{}$ in the case of the normal E-field, and of ${ϵ}_1^{}{E}_0^2$ in the case of the tangential E-field, in dimensional units correspond to ${\widehat{ϵ}}_2^{}{\widehat{V}}_0^2/\left({\widehat{\mu }}_1^{}{\widehat{h}}_1^{}{\widehat{U}}_0^{}\right)$ and ${\widehat{ϵ}}_1^{}{\widehat{E}}_0^2{\widehat{h}}_1^{}/\left({\widehat{\mu }}_1^{}{\widehat{U}}_0^{}\right)$, respectively. Equations (62) and (63b) were derived here for our bounded system, but recover known results when (one of the) boundaries effectively go to infinity ($kh\gg 1,k\gg 1$).

It is seen from Equations (62) and (63b) that a normal E-field gives a negative first-order stress contribution, whereas a tangential E-field gives a positive first-order stress contribution (the known result). The interface will, thus, be affected differently by the two types of electric fields. We will further investigate only effects of the destabilizing, normal E-field.

4. Perturbation Expansion in the Reynolds Number $\mathit{R}$ to Zeroth Order

Equations (45) and (46) together with the eight boundary and interface conditions from the previous section present the system of differential equations, which we solve in the limit of small Reynolds number R and arbitrary wavenumber k. We apply the following perturbation expansion in R of the stream function $\psi$, the phase velocity c, and the potential (voltage) V,

$$\begin{array}{cc}\hfill \psi & ={\psi }^{\left[0\right]}+R{\psi }^{\left[1\right]}+R^2{\psi }^{\left[2\right]}+\cdots ,\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill c& =c^{\left[0\right]}+R{c}^{\left[1\right]}+R^2{c}^{\left[2\right]}+\cdots ,\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill V& =V^{\left[0\right]}+R{V}^{\left[1\right]}+R^2{V}^{\left[2\right]}+\cdots ,\hfill \end{array}$$

(66)

where square brackets distinguish it from the previous linearization in $\zeta$ marked by round parentheses. With these expansions, the zeroth-order equations in R become

$$\begin{array}{cc}\hfill {{\psi }_1^{{\left[0\right]}_{}}}^{″″}-2k^2{{\psi }_1^{{\left[0\right]}_{}}}^{″}+k^4{\psi }_1^{\left[0\right]}& =0\hfill \end{array}$$

(67a)

$$\begin{array}{cc}\hfill {{\psi }_2^{{\left[0\right]}_{}}}^{″″}-2k^2{{\psi }_2^{{\left[0\right]}_{}}}^{″}+k^4{\psi }_2^{\left[0\right]}& =0,\hfill \end{array}$$

(67b)

with the boundary and interface conditions

$$\begin{array}{cc}\hfill & {\psi }_1^{\left[0\right]}\left(1\right)=0;{{\psi }_1^{\left[0\right]}}^{\prime }\left(1\right)=0,\hfill \end{array}$$

(68a)

$$\begin{array}{cc}\hfill & {\psi }_2^{\left[0\right]}(-h)=0;{{\psi }_2^{\left[0\right]}}^{\prime }(-h)=0,\hfill \end{array}$$

(68b)

$$\begin{array}{cc}\hfill & {\psi }_1^{\left[0\right]}\left(0\right)-{\psi }_2^{\left[0\right]}\left(0\right)=0,\hfill \end{array}$$

(68c)

$$\begin{array}{cc}\hfill & {{\psi }_1^{\left[0\right]}}^{\prime }\left(0\right)-{{\psi }_2^{\left[0\right]}}^{\prime }\left(0\right)=\frac{{\psi }_1^{\left[0\right]}\left(0\right)}{{\tilde{c}}^{\left[0\right]}}(1-\mu )a_2^{},\hfill \end{array}$$

(68d)

$$\begin{array}{cc}\hfill & {{\psi }_1^{\left[0\right]}}^{″}\left(0\right)+k^2{\psi }_1^{\left[0\right]}\left(0\right)=\mu \left({{\psi }_2^{\left[0\right]}}^{″}\left(0\right)+k^2{\psi }_2^{\left[0\right]}\left(0\right)\right),\hfill \end{array}$$

(68e)

$$\begin{array}{cc}\hfill & ik{S}_k^{*}\frac{{\psi }_1^{\left[0\right]}\left(0\right)}{{\tilde{c}}^{\left[0\right]}}=\mu \left[{{\psi }_2^{\left[0\right]}}^{‴}\left(0\right)-3k^2{{\psi }_2^{\left[0\right]}}^{\prime }\left(0\right)\right]-\left[{{\psi }_1^{\left[0\right]}}^{‴}\left(0\right)-3k^2{{\psi }_1^{\left[0\right]}}^{\prime }\left(0\right)\right],\hfill \end{array}$$

(68f)

where

$$\begin{array}{cc}\hfill {\tilde{c}}^{\left[0\right]}& =c^{\left[0\right]}-b,\hfill \end{array}$$

(68g)

$$\begin{array}{cc}\hfill S_k^{*}& \equiv k^{2}S+T_{\mathrm{el}}^{}.\hfill \end{array}$$

(68h)

Strictly speaking, the above zeroth-order approximation is valid for R arbitrary close to, but not equal to, zero. The reason for this is the rescaling involving division by ${\widehat{\mu }}_1^{}{\widehat{U}}_0^{}$, see Equations (61) and (62). General solutions of Equations (67a) and (67b) can be written as

$$\begin{array}{cc}\hfill {\psi }_1^{\left[0\right]}=& sinh\left[k(z-1)\right]+B_1^{}cosh\left[k(z-1)\right]\hfill \\ \hfill & +C_1^{}zsinh\left[k(z-1)\right]+D_1^{}zcosh\left[k(z-1)\right],\hfill \end{array}$$

(69a)

$$\begin{array}{cc}\hfill {\psi }_2^{\left[0\right]}=& A_2^{}sinh\left[k(z+h)\right]+B_2^{}cosh\left[k(z+h)\right]\hfill \\ \hfill & +C_2^{}zsinh\left[k(z+h)\right]+D_2^{}zcosh\left[k(z+h)\right].\hfill \end{array}$$

(69b)

Note that $A_2^{}$ generally differs from unity in order to satisfy the boundary conditions, Equations (68d) and (68f). By inputting the above solutions into Equations (68a)–(68f), we arrive at fairly complicated expressions for the coefficients $A_2^{},B_{1,2}^{},C_{1,2}^{},D_{1,2}^{}$ (given in the Appendix A for the special case $S_k^{*}=0$, for later use). The important result is the expression of the phase velocity ${\tilde{c}}^{\left[0\right]}$ that determines the stability; Equation (29). We obtain

$${\tilde{c}}^{\left[0\right]}={\tilde{c}}_r^{\left[0\right]}+i{\tilde{c}}_i^{\left[0\right]},$$

(70a)

where

$$\begin{array}{cc}\hfill {\tilde{c}}_r^{\left[0\right]}& =8a_2^{}{k}^3\mu (\mu -1)\left[-2kh(1+h)+h^{2}sinh\left[2k\right]+sinh\left[2kh\right]\right]{\mathcal{D}}^{-1},\hfill \end{array}$$

(70b)

$$\begin{array}{cc}\hfill {\tilde{c}}_i^{\left[0\right]}& =S_k^{*}(4k\mu hcosh\left[2k\right]+4kcosh\left[2kh\right]+(2+4k^2{h}^2)sinh\left[2k\right]\hfill \\ \hfill & -4k\left[1+h(\mu +2k^2\mu +2k^{2}h)\right]+(2\mu +4k^2\mu )sinh\left[2kh\right]\hfill \\ \hfill & -(\mu +1)sinh\left[2k(h+1)\right]+(\mu -1)sinh\left[2k(1-h)\right]){\mathcal{D}}^{-1},\hfill \end{array}$$

(70c)

$$\begin{array}{cc}\hfill \mathcal{D}& =2k^2(2({\mu }^2-1)(2k^2{h}^2+1)cosh\left[2k\right]+{(\mu -1)}^{2}cosh\left[2k(h-1)\right]\hfill \\ \hfill & -2(2k^2+1)({\mu }^2-1)cosh\left[2kh\right]+{(\mu +1)}^{2}cosh\left[2k(h+1)\right]\hfill \\ \hfill & -2\left[1+{\mu }^2+2k^2\left(1+{\mu }^2+4\mu h+h^2\left[1+{\mu }^2+2k^2{(\mu -1)}^2\right]\right)\right]).\hfill \end{array}$$

(70d)

In Equation (70c), ${\tilde{c}}_i^{\left[0\right]}$ that governs the growth rate of the waves is independent of $\rho$ and $G_1^{}$ (nondimensional pressure gradient), but depends on k, $\mu$, h, and, importantly, on the electric fields through $S_k^{*}$.

Our analytical results could be compared to a degree with the numerical studies of Ref. [17], which deals with more complicated leaky dielectrics. In Figure 3, graphs of ${\tilde{c}}_i^{\left[0\right]}$ are shown for single values of h, S, and ${ϵ}_2^{}$, and three values of $\mu$, over a broad range of wavenumbers (note that in microfluidics, ${ϵ}_2^{}\sim$ 1–100, and that we used a much larger ${ϵ}_2^{}$ value to emphasize the main features in a single graph). The trend of the curves in Figure 3 is identical to the trend observed in Figure 4 in Ref. [17].

However, in our case of perfect dielectrics, the k-regions of instability, for which ${\tilde{c}}_i^{\left[0\right]}>0$, are independent of the viscosity ratio, whereas in Ref. [17], they do depend on it. In other words, our curves intersect at the same point, $k_c^{\left[0\right]}$, and theirs do not (Figure 5 in Ref. [17]). Evidently, the viscous tangential stresses that arise to balance the nonzero electric tangential interfacial stresses in leaky dielectrics affect the EHD stability regions to zero order in R. It is surprising, though, that in the case of two perfect viscous dielectrics, viscosity does not play a similar role.

We now explore this and other electrohydrodynamic aspects of Equations (70b) and (70c) in terms of k, $\mu$, h, and $T_{\mathrm{el}}$, with the emphasis on microfluidics.

Figure 3. For a normal E-field, the imaginary phase velocity ${\tilde{c}}_i^{\left[0\right]}$ to zeroth order in R is plotted as function of the wavenumber k, for the viscosity ratio $\mu =0,0.2,1$ and a fixed set of S, ${ϵ}_2^{}$, h, and $\epsilon$. The instability region $0<k<k_c^{\left[0\right]}$, for which ${\tilde{c}}_i^{\left[0\right]}>0$ is independent of $\mu$, which can be deduced from the impending voltage Equation (78). The increase in $\mu$ decreases the growth rates of unstable waves for small k, but also decreases the damping rates for large k, i.e., makes the short waves relatively less stable, although it does not cause the actual instability. In the limit $k\to \infty$, ${\tilde{c}}_i^{\left[0\right]}$ reaches the value $-S/\left[2\right(\mu +1\left)\right]$. Note that in microfluidic systems ${ϵ}_2^{}\sim 1$, which makes the positive ${\tilde{c}}_i^{\left[0\right]}\sim 1$, i.e., ${10}^3$ times smaller than depicted; we used a large ${ϵ}_2^{}$ to better emphasize the trends.

Figure 3. For a normal E-field, the imaginary phase velocity ${\tilde{c}}_i^{\left[0\right]}$ to zeroth order in R is plotted as function of the wavenumber k, for the viscosity ratio $\mu =0,0.2,1$ and a fixed set of S, ${ϵ}_2^{}$, h, and $\epsilon$. The instability region $0<k<k_c^{\left[0\right]}$, for which ${\tilde{c}}_i^{\left[0\right]}>0$ is independent of $\mu$, which can be deduced from the impending voltage Equation (78). The increase in $\mu$ decreases the growth rates of unstable waves for small k, but also decreases the damping rates for large k, i.e., makes the short waves relatively less stable, although it does not cause the actual instability. In the limit $k\to \infty$, ${\tilde{c}}_i^{\left[0\right]}$ reaches the value $-S/\left[2\right(\mu +1\left)\right]$. Note that in microfluidic systems ${ϵ}_2^{}\sim 1$, which makes the positive ${\tilde{c}}_i^{\left[0\right]}\sim 1$, i.e., ${10}^3$ times smaller than depicted; we used a large ${ϵ}_2^{}$ to better emphasize the trends.

4.1. Validation of Results: Limit of Vanishingly Small Wavenumbers

To validate our general analytical results, we directly compare them with the analytical limits published in Refs. [14,16]. In the limit of small wavenumbers $k\to 0$, ${\tilde{c}}_r^{{\left[0\right]}_{}}$ and ${\tilde{c}}_i^{\left[0\right]}$ from Equations (70b) and (70c) become

$$\begin{array}{cc}\hfill \underset{k\to 0}{lim}{\tilde{c}}_r^{\left[0\right]}& =\frac{2a_2^{}\mu h^2(\mu -1)(h+1)}{{\mu }^2+h^4+2\mu h(2+3h+2h^2)}\hfill \\ \hfill & =\frac{h^2(\mu -1)(h+1)\left[G_1^{}{h}^2+(2-G_1^{})\mu \right]}{(\mu +h)\left[{\mu }^2+h^4+2\mu h(2+3h+2h^2)\right]},\hfill \end{array}$$

(71a)

$$\begin{array}{cc}\hfill \underset{k\to 0}{lim}{\tilde{c}}_i^{\left[0\right]}& =0.\hfill \end{array}$$

(71b)

The above two limits mean that our ${\tilde{c}}^{\left[0\right]}(={\tilde{c}}_r^{\left[0\right]}+i{\tilde{c}}_i^{\left[0\right]})$ = ${\tilde{c}}_r^{\left[0\right]}$ for $k\to 0$; this is identical to the ${\tilde{c}}^{\left[0\right]}$ obtained for $k\to 0$ in the seminal study [14], so it follows that we correctly recover the small-k limit from the literature. On the other hand, our result differs from the ${\tilde{c}}^{\left[0\right]}$ given in [16] (page 75) also obtained in the approximation to zeroth order in R. There, ${\tilde{c}}^{\left[0\right]}=0$ for $k\to 0$, thus not recovering results from [14], making the further calculations and conclusions invalid.

We also note that in [14] (page 344) it is stated that Equation (71a) must change the sign but not the magnitude upon the simultaneous exchanges $\mu \to 1/\mu$ and $h\to 1/h$. This, however, is true only in two special cases: (i) $G_1^{}=0$ (pure Couette flow, considered in [14]), arbitrary $\mu$ and h; (ii) $h=\sqrt{\mu }$, arbitrary $G_1^{}$.

4.2. Validation of Results: Limit of Large Wavenumbers

Next, we consider the limit of very large wavenumbers, i.e., very short wavelengths. For a given $h>0$ (and a fixed electric field), the leading terms give

$$\begin{array}{cc}\hfill {\tilde{c}}_r^{\left[0\right]}& \propto \frac{ksinh\left[2kh\right]}{cosh\left[2k\right(h+1\left)\right]}=kexp(-2k),\mathrm{for}k\to \infty \hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill {\tilde{c}}_i^{\left[0\right]}& =\frac{-S_k^{*}(\mu +1)sinh\left[2k(h+1)\right]}{2k^2{(\mu +1)}^{2}cosh\left[2k(h+1)\right]}\hfill \\ \hfill & =-\frac{S}{2(\mu +1)},\mathrm{for}k\to \infty \hfill \end{array}$$

(73)

where, as expected, only the stabilizing contribution of the surface tension remains for very large k. Note that Equation (73) is independent of E-fields or electric stresses, thus yielding the same limiting result, whether the perfect or the leaky dielectrics are considered. This is the reason why the trends for large k of our Figure 3 depicting perfect dielectrics are identical to those seen in Figure 4 of [17], where surface tension dependency is explored for the leaky dielectrics. Equation (73), in fact, derives (quantifies) the trends for large wavenumbers.

Reverting to the phase velocity c, we obtain in this limit

$$c^{\left[0\right]}=b+i{\tilde{c}}^{\left[0\right]}=b-\frac{iS}{2(\mu +1)},$$

(74)

where b is given in Equation (33c).

Equation (73) shows that in the limit $k\to \infty$ the short waves are damped within the expansion to zeroth order in R. From Equations (29), (61) and (73), the physical rate of damping for very large wavenumbers is

$$\frac{k}{{\widehat{h}}_1^{}}{c}_i^{\left[0\right]}{\widehat{U}}_0^{}=-\frac{\widehat{k}\widehat{\gamma }}{2\left({\widehat{\mu }}_1^{}+{\widehat{\mu }}_2^{}\right)},$$

(75)

which decreases with the increase in viscosities; Figure 3. Shorter waves thus become relatively less stable (less damped) if either of the layers becomes more viscous—an example of destabilizing role of viscosity, as similarly observed by [31].

4.3. Onset of EHD Instability to Zeroth Order in R

The two terms in $S_k^{*}$ from Equation (68h) are each proportional to the square of the phase velocity of the corresponding surface waves—the capillary and the EHD waves—whose interplay can destabilize the system. $S_k^{*}$ explicitly enters the expression for ${\tilde{c}}_i^{\left[0\right]}$ in Equation (70c) and, in fact, determines its sign; the condition

$$S_k^{*}=0,$$

(76)

is a neutral stability condition in the expansion to zeroth order in R.

With no electric field applied, $c_i^{\left[0\right]}\le 0$ for all k and the system is never unstable. In order to induce the instability, $S_k^{*}$ must become negative. From Equations (62), (68h) and (76), it is seen that only a normal electric field, with a negative stress contribution, can destabilize a system of two perfect dielectric liquids. Using the nondimensional units, the condition for onset of the EHD instability caused by a normal electric field is given by

$${ϵ}_2^{}=\frac{kS{(\epsilon +h)}^2}{{(\epsilon -1)}^2}\left(\epsilon tanh\left[k\right]+tanh\left[kh\right]\right),$$

(77)

where ${ϵ}_2^{}/S$ is the electric Weber number proportional to the square of the applied electric field. Equation (77) is identical to inviscid results from the literature, and more precisely combines in a single equation the findings separately obtained in different limits [1]: ${ϵ}_2^{}\propto k^2$ for $k,kh\ll 1$ and ${ϵ}_2^{}\propto k$ for $k,kh\gg 1$. Note that the EHD instability is not possible in the case that $\epsilon =1$ since no interfacial electric stresses exist for a single dielectric.

Reverting Equation (77) to the physical (dimensional) variables, we obtain for the impending voltage

$${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}=\frac{\epsilon {\widehat{h}}_1^{}+{\widehat{h}}_2^{}}{\mid \epsilon -1\mid }{\left[\frac{\widehat{\gamma }\widehat{k}}{{\widehat{ϵ}}_2^{}}\left(\epsilon tanh\left[\widehat{k}{\widehat{h}}_1^{}\right]+tanh\left[\widehat{k}{\widehat{h}}_2^{}\right]\right)\right]}^{\frac{1}{2}}.$$

(78)

The significance of Equation (78) is that ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$ is independent of both ${\widehat{U}}_0^{}$ and $\mu$. In other words, in the limit $R\to 0$, the onset of the EHD instability for two moving, viscous, dielectric fluids coincides with the result for two static, inviscid dielectrics [1].

After its hyperbolic tangents are expanded in the limits of small and large wavenumbers, Equation (78) gives, respectively,

$$\begin{array}{cc}\hfill {\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}(\widehat{k}{\widehat{h}}_1^{},\widehat{k}{\widehat{h}}_2^{}\ll 1)& =\frac{{\left(\epsilon {\widehat{h}}_1^{}+{\widehat{h}}_2^{}\right)}^{\frac{3}{2}}}{\mid \epsilon -1\mid }{\left(\frac{\widehat{\gamma }}{{\widehat{ϵ}}_2^{}}\right)}^{\frac{1}{2}}\widehat{k},\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill {\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}(\widehat{k}{\widehat{h}}_1^{},\widehat{k}{\widehat{h}}_2^{}\gg 1)& =\frac{\left(\epsilon {\widehat{h}}_1^{}+{\widehat{h}}_2^{}\right)}{\mid \epsilon -1\mid }{\left[\frac{(\epsilon +1)\widehat{\gamma }}{{\widehat{ϵ}}_2^{}}\right]}^{\frac{1}{2}}{\widehat{k}}^{\frac{1}{2}}.\hfill \end{array}$$

(80)

The voltages in Equations (79) and (80) increase with $\widehat{k}$; thus, for a given ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$, a critical wavenumber $k_c^{\left[0\right]}$, independent of $\mu$, $\rho$, and $G_1^{}$, is determined so that all $k<k_c^{\left[0\right]}$ are unstable; see Figure 3. A system can be operated (or designed) to exclude those unstable wavenumbers. For a given size, the maximal operating voltage then needs to make the smallest allowed wavenumber in the system—largest allowed wavelength—to coincide with $k_c^{\left[0\right]}$, i.e., neutrally stable.

We now make an estimate of finite-size constraints. For a large finite 2D surface ($\widehat{L}>\widehat{W}$), the smallest allowed wavenumber is ${\widehat{k}}_c^{}={\widehat{k}}_x^{}=\pi /\widehat{L}$, where $\widehat{L}$ is the longer dimension. When $\widehat{L}\gg {\widehat{h}}_1^{},{\widehat{h}}_2^{}$, we can apply Equation (79). Using the two-liquid EO pump parameters from [20], $\widehat{L}=280\mu$m, ${\widehat{h}}_1^{}=2\mu$m, ${\widehat{h}}_2^{}=8\mu$m, $\epsilon \simeq 0.04$, ${\widehat{ϵ}}_{2\mathrm{r}}^{}=3.1$, $\widehat{\gamma }=18\times {10}^{-3}{\mathrm{Nm}}^{-1}$, we obtain for the impending voltage ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}=6.85$ V.

In the limits $\epsilon \ll \min \{1,h\}$ and $\epsilon \gg \max \{1,h\}$, the instability voltages of Equations (79) and (80) depend only on the parameters of the dielectric with smaller permitivity. If $\widehat{h}$ is the layer thickness of the “weaker” dielectric, the voltages scale in both cases with ${\widehat{h}}^{3/2}$ and ${\widehat{h}}^{}$ in the limits of small and large wavenumbers, respectively. Incidentally, the same results appear in the case of a perfect conductor and a perfect dielectric, where, also, no electric shear stresses exist at the interface [8]. This allows us to use our results in the corresponding limits to asses a system with a highly conducting and a nonconducting fluid such as water and oil.

In the limit $\epsilon \ll 1$, ${\widehat{h}}_2^{}\to 0^{+}$, the electric field in the dielectric no. 2 with the smaller permittivity becomes enormous; Equation (37d). For the wavenumber $\pi /\widehat{L}$ from the pump example, we apply Equation (79) to obtain the impending voltage ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}=6.4$ mV.

All of the above points are summarized in the stability diagram for the water–oil system, Figure 4, where plots are shown of the neutral stability line separating stable ($\mathrm{s}$) and unstable ($\mathrm{u}$) regions in the ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$– $k(=\widehat{k}{\widehat{h}}_1^{})$ plane. Four different height ratios h are featured and a fixed set of ${\widehat{h}}_1^{}$, $\widehat{\gamma }$, ${\widehat{ϵ}}_1^{}$, and ${\widehat{ϵ}}_2^{}$. Note how the impending voltage ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$ in accordance with Equations (79) and (80) is seen to scale as k and $k^{1/2}$ in the limit of small and large wavenumbers, respectively. Note also that the lines in the stability diagram are, in fact, the loci of the critical wavenumbers $k_c^{\left[0\right]}$ of Figure 3.

Figure 4. Plots of the neutral stability line separating stable ($\mathrm{s}$) and unstable ($\mathrm{u}$) regions in the ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$–$\widehat{k}{\widehat{h}}_1^{}$ plane (with log–log axes) for $h=0,1,4,20$. The increase in h causes lower electric fields and, thus, increases the stable regions and the impending voltages.

Figure 4. Plots of the neutral stability line separating stable ($\mathrm{s}$) and unstable ($\mathrm{u}$) regions in the ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$–$\widehat{k}{\widehat{h}}_1^{}$ plane (with log–log axes) for $h=0,1,4,20$. The increase in h causes lower electric fields and, thus, increases the stable regions and the impending voltages.

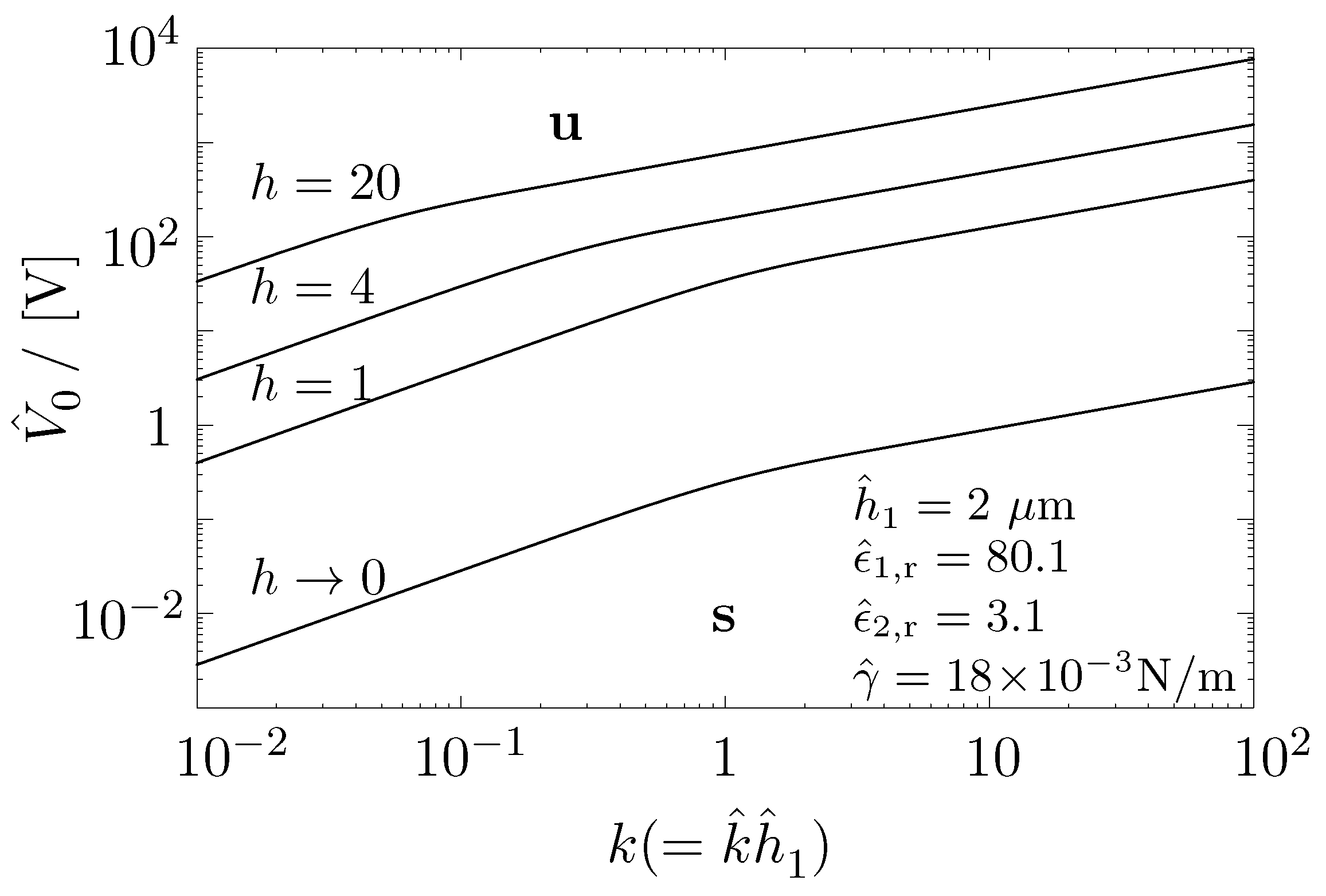
5. Perturbation Expansion in the Reynolds Number $\mathit{R}$ to First Order

We now proceed with the expansion to first order in R using Equations (64)–(66). It suffices to consider a system brought to the neutral stability within the zeroth order in R, Equation (76). This is achieved when the applied voltage is equal to the critical impending voltage ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$, determining the $k_c^{\left[0\right]}$. In other words, we are at the neutral stability lines of Figure 4 (the case $S=T_{\mathrm{el}}^{}=0$, valid for all k, is of purely theoretical significance and can be analyzed as a special case).

A slight increase in the Reynolds number then induces a change in the velocities, also at the interface, Equation (56), giving rise to a small change in the phase velocity of the neutrally-stable perturbations, $c^{\left[1\right]}$; a small change in voltage, $V^{\left[1\right]}$, is needed to counteract the change and bring the system to neutral stability to first order in R. Note that only the normal stress condition, Equation (60), is affected by (the change in) voltage.

One thus solves the eigenvalue problem for $c^{\left[1\right]}$ from the newly expanded equations and boundary conditions. The first-order corrections for the impending voltages, $V^{\left[1\right]}$, are found from the first-order-R neutral stability condition $c_i^{\left[1\right]}\left(V^{\left[1\right]}\right)=0$.

The first-order-R equations are

$$\begin{array}{cc}\hfill & {{\psi }_1^{\left[1\right]}}^{″″}-2k^2{{\psi }_1^{\left[1\right]}}^{″}+k^4{\psi }_1^{\left[1\right]}\hfill \\ \hfill & =ik\left[\left(U_1^{\left(0\right)}-c^{\left[0\right]}\right)\left({{\psi }_1^{\left[0\right]}}^{″}-k^2{\psi }_1^{\left[0\right]}\right)-{U_1^{\left(0\right)}}^{″}{\psi }_1^{\left[0\right]}\right],\hfill \end{array}$$

(81)

$$\begin{array}{cc}\hfill & {{\psi }_2^{\left[1\right]}}^{″″}-2k^2{{\psi }_2^{\left[1\right]}}^{″}+k^4{\psi }_2^{\left[1\right]}\hfill \\ \hfill & =i\frac{\rho }{\mu }k\left[\left(U_2^{\left(0\right)}-c^{\left[0\right]}\right)\left({{\psi }_2^{\left[0\right]}}^{″}-k^2{\psi }_2^{\left[0\right]}\right)-{U_2^{\left(0\right)}}^{″}{\psi }_1^{\left[0\right]}\right],\hfill \end{array}$$

(82)

where we expanded the zeroth-order-R Equations (67a) and (67b) with the RHS of the full Equations (45) and (46) (note that the RHS are, in fact, the first-order-R contributions). $U_1^{\left(0\right)}$ and $U_2^{\left(0\right)}$ are unperturbed (zeroth-order-$\zeta$) velocities, given in Equation (32).

The first-order-R boundary and interface conditions are

$$\begin{array}{cc}\hfill & {\psi }_1^{\left[1\right]}\left(1\right)=0,{{\psi }_1^{\left[1\right]}}^{\prime }\left(1\right)=0,\hfill \end{array}$$

(83)

$$\begin{array}{cc}\hfill & {\psi }_2^{\left[1\right]}(-h)=0,{{\psi }_2^{\left[1\right]}}^{\prime }(-h)=0,\hfill \end{array}$$

(84)

$$\begin{array}{cc}\hfill & {\psi }_1^{\left[1\right]}\left(0\right)-{\psi }_2^{\left[1\right]}\left(0\right)=0,\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill & {{\psi }_1^{\left[1\right]}}^{\prime }\left(0\right)-{{\psi }_2^{\left[1\right]}}^{\prime }\left(0\right)=\left(\frac{{\psi }_1^{\left[1\right]}\left(0\right)}{{\tilde{c}}^{\left[0\right]}}-\frac{{\psi }_1^{\left[0\right]}\left(0\right){\tilde{c}}^{\left[1\right]}}{{\left({\tilde{c}}^{\left[0\right]}\right)}^2}\right)(1-\mu )a_2^{},\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill & {{\psi }_1^{\left[1\right]}}^{″}\left(0\right)+k^2{\psi }_1^{\left[1\right]}\left(0\right)=\mu \left({{\psi }_2^{\left[1\right]}}^{″}\left(0\right)+k^2{\psi }_2^{\left[1\right]}\left(0\right)\right),\hfill \\ \hfill & ik2T_{\mathrm{el},\mathrm{N}}^{\left[0\right]}{V}^{\left[1\right]}\frac{{\psi }_1^{\left[0\right]}\left(0\right)}{{\tilde{c}}^{\left[0\right]}}=\mu \left({{\psi }_2^{\left[1\right]}}^{‴}\left(0\right)-3k^2{{\psi }_2^{\left[1\right]}}^{\prime }\left(0\right)\right)+i\rho k\left({\tilde{c}}^{\left[0\right]}{{\psi }_2^{\left[0\right]}}^{\prime }\left(0\right)+a_2^{}{\psi }_2^{\left[0\right]}\left(0\right)\right)\hfill \end{array}$$

(87)

$$\begin{array}{cc}\hfill & -\left({{\psi }_1^{\left[1\right]}}^{‴}\left(0\right)-3k^2{{\psi }_1^{\left[1\right]}}^{\prime }\left(0\right)\right)-ik\left({\tilde{c}}^{\left[0\right]}{{\psi }_1^{\left[0\right]}}^{\prime }\left(0\right)+a_1^{}{\psi }_1^{\left[0\right]}\left(0\right)\right).\hfill \end{array}$$

(88)

In Equation (86), both $\psi$ and c were expanded. Since $\tilde{c}$ differs from c by a constant factor, Equation (68g), we see from Equation (65) that ${\tilde{c}}^{\left[1\right]}=c^{\left[1\right]}(={(\partial c/\partial R)}_{\mathrm{R}=0})$. Furthermore, ${\tilde{c}}^{\left[0\right]}={\tilde{c}}_r^{\left[0\right]}$ in Equations (86) and (88), since ${\tilde{c}}_i^{\left[0\right]}=0$ at the neutral stability to zeroth-R, Equation (70a).

The LHS of Equation (88), where the voltage change $V^{\left[1\right]}$ enters, is obtained by calculating ${(\partial S_k^{*}/\partial R)}_{R=0}={(\partial T_{\mathrm{el}}/\partial R)}_{R=0}={(\partial T_{\mathrm{el}}/\partial V·\partial V/\partial R)}_{R=0}$, where $T_{\mathrm{el}}=T_{\mathrm{el},\mathrm{N}}^{\left[0\right]}$ is the zeroth-order-R Maxwell’s stress tensor for a normal E-field, the upper part of Equation (62). Note that in dimensional units, $V^{\left[1\right]}={\widehat{V}}^{\left[1\right]}/{\widehat{V}}_0^{\left[0\right]}$.

The overall solution of Equation (81) or Equation (82) has the form

$${\psi }^{\left[1\right]}={\psi }_H^{\left[1\right]}+{\psi }_P^{\left[1\right]},$$

(89)

where ${\psi }_H^{\left[1\right]}$ is a general solution of the homogeneous equation, and ${\psi }_P^{\left[1\right]}$ is a particular solution of the inhomogeneous equation. We write the solutions of the two homogeneous equations

$$\begin{array}{cc}\hfill {\psi }_{1,\mathrm{H}}^{\left[1\right]}& =\Delta B_1^{}cosh\left[k(z-1)\right]\hfill \\ \hfill & +\Delta C_1^{}zsinh\left[k(z-1)\right]+\Delta D_1^{}zcosh\left[k(z-1)\right],\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill {\psi }_{2,\mathrm{H}}^{\left[1\right]}& =\Delta A_2^{}sinh\left[k(z+h)\right]+\Delta B_2^{}cosh\left[k(z+h)\right]\hfill \\ \hfill & +\Delta C_2^{}zsinh\left[k(z+h)\right]+\Delta D_2^{}zcosh\left[k(z+h)\right],\hfill \end{array}$$

(91)

where coefficients $\Delta A_2^{},\Delta B_{1,2}^{},\Delta C_{1,2}^{}$ and $\Delta D_{1,2}^{}$ give the small changes to the corresponding zeroth-order coefficients in Equations (69a) and (69b). Note that $\Delta A_1^{}=0$, since we chose to normalize the entire solution ${\psi }_1^{}$ with respect to $A_1^{}$, as was performed with ${\psi }_1^{\left[0\right]}$, Equation (69a). However, $\Delta A_2^{}\ne 0$, since $A_2^{}\ne 0$ in Equation (69b), in order to satisfy the boundary and interface conditions of Equations (83)–(88).

The particular solutions of Equations (81) and (82) have the form [14]

$$\begin{array}{cc}\hfill {\psi }_{1,\mathrm{P}}^{\left[1\right]}& =ik{z}^2\left[sinh\left[k(z-1)\right]P_1^{}\left(z\right)+cosh\left[k(z-1)\right]Q_1^{}\left(z\right)\right],\hfill \end{array}$$

(92)

$$\begin{array}{cc}\hfill {\psi }_{2,\mathrm{P}}^{\left[1\right]}& =ik{z}^2\left[sinh\left[k(z+h)\right]P_2^{}\left(z\right)+cosh\left[k(z+h)\right]Q_2^{}\left(z\right)\right],\hfill \end{array}$$

(93)

where $P_{1,2}^{}\left(z\right)$ and $Q_{1,2}^{}\left(z\right)$ are the second-degree polynomials fully written in the Appendix B.

Inserting the complete solution ${\psi }^{\left[1\right]}$ into Equations (83)–(88), we obtain the system

$$\begin{array}{cc}\hfill & \Delta B_1^{}+\Delta D_1^{}+ik{L}_1^{}=0,\hfill \end{array}$$

(94)

$$\begin{array}{cc}\hfill & k\Delta C_1^{}+\Delta D_1^{}+ik{L}_2^{}=0,\hfill \end{array}$$

(95)

$$\begin{array}{cc}\hfill & \Delta B_2^{}-h\Delta D_2^{}+ik\frac{\rho }{\mu }{L}_3^{}=0,\hfill \end{array}$$

(96)

$$\begin{array}{cc}\hfill & k\Delta A_2^{}-kh\Delta c_2^{}+\Delta D_2^{}+ik\frac{\rho }{\mu }{L}_4^{}=0,\hfill \end{array}$$

(97)

$$\begin{array}{cc}\hfill & cosh\left[k\right]\Delta B_1^{}-cosh\left[kh\right]\Delta B_2^{}-sinh\left[kh\right]\Delta A_2^{}=0,\hfill \end{array}$$

(98)

$$\begin{array}{cc}\hfill & ksinh\left[k\right]\Delta B_1^{}+sinh\left[k\right]\Delta C_1^{}-cosh\left[k\right]\Delta D_1^{}\hfill \\ \hfill & +kcosh\left[kh\right]\Delta A_2^{}+ksinh\left[kh\right]\Delta B_2^{}+sinh\left[kh\right]\Delta C_2^{}\hfill \\ \hfill & +cosh\left[kh\right]\Delta D_2^{}+a_2^{}(1-\mu )\frac{{\tilde{c}}_r^{\left[0\right]}cosh\left[k\right]\Delta B_1^{}-c^{\left[1\right]}{L}_6^{}}{{\left({\tilde{c}}_r^{\left[0\right]}\right)}^2}=0,\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill & kcosh\left[k\right]\Delta B_1^{}+cosh\left[k\right]\Delta C_1^{}-sinh\left[k\right]\Delta D_1^{}\hfill \\ \hfill & -k\mu sinh\left[kh\right]\Delta A_2^{}-k\mu cosh\left[kh\right]\Delta B_2^{}-\mu cosh\left[kh\right]\Delta C_2^{}\hfill \\ \hfill & -\mu sinh\left[kh\right]\Delta D_2^{}+i{L}_7^{}=0,\hfill \end{array}$$

(100)

$$\begin{array}{cc}\hfill & 2k^{3}sinh\left[k\right]\Delta B_1^{}+2k^3\mu cosh\left[kh\right]\Delta A_2^{}\hfill \\ \hfill & +2k^3\mu sinh\left[kh\right]\Delta B_2^{}-ik{L}_8^{}=0,\hfill \end{array}$$

(101)

where $L_1^{}$–$L_8^{}$ are short labels. The system of Equations (94)–(101) can finally be solved for the nontrivial eigenvalue $c^{\left[1\right]}(k,\mu ,h,\rho ,G_1^{},V^{\left[1\right]})$. The analytical expression for $c^{\left[1\right]}$ and the expanded $L_1^{}$–$L_8^{}$ ($L_8^{}$ contains $V^{\left[1\right]}$) are given in the Appendix C.

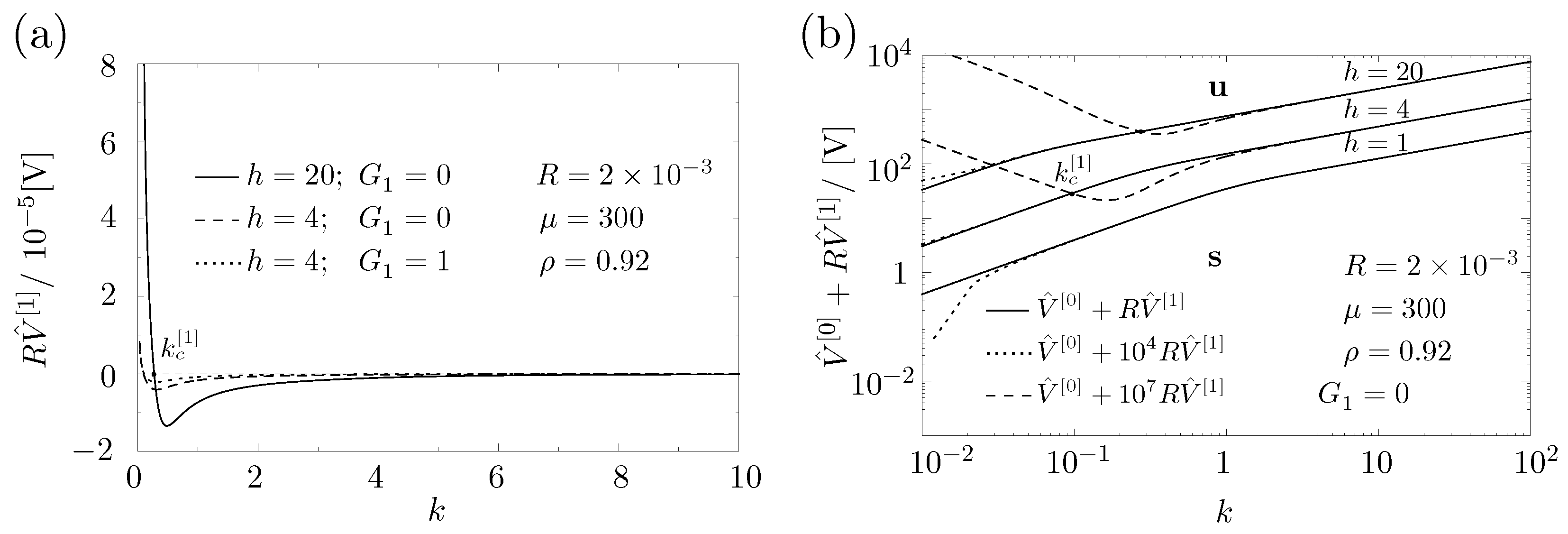
5.1. Pure Shear Stress Instability to First Order in R

It follows from Equation (A13)

$$c^{\left[1\right]}=i{c}_i^{\left[1\right]}=i\mathcal{C}(k,\mu ,h,\rho ,G_1^{},V^{\left[1\right]}),$$

(102)

where $\mathcal{C}$ is a very complicated real function of the flow parameters k, $\mu$, h, $\rho$, $G_1^{}$, and of voltage $V^{\left[1\right]}$. The phase velocity $c^{\left[1\right]}$ is, thus, a purely imaginary number and the first-order-R instability happens for $c_i^{\left[1\right]}=\mathcal{C}>0$.

One can investigate the vast parameter space of Equation (102), but we focus here on a handful of features. We first consider pure shear instability, i.e., the case without a voltage correction, $V^{\left[1\right]}=0$.

Shown in Figure 5a is $R{c}_i^{\left[1\right]}\left(k\right)$, the total change in the phase velocity c per Equation (65), for two sets of parameters $(R,\mu ,h,\rho ,G_1^{},V^{\left[1\right]})$, differing in h: $(2\times {10}^{-3},2,4,1,0,0)$ and $(2\times {10}^{-3},2,1/4,1,0,0)$. For $h=4$, there is a critical wavenumber $k_c^{\left[1\right]}$ for which the system is at the neutral stability to first order in R, analogous to $k_c^{\left[0\right]}$ of Figure 3, but the trends in the two figures are opposite: in Figure 5a, the small wavenumbers, $k<k_c^{\left[1\right]}$, are stable, and the large ones, $k>k_c^{\left[1\right]}$, are unstable. For $h=1/4$, a configuration with a thinner bottom liquid, the system is unstable for all k.

Figure 5. (a) The first-order-R correction $R{c}_i^{\left[1\right]}$ vs. k for the pure shear flow, i.e., without the first-order electric field (voltage). Two sets of flow parameters are featured: for $h=4$, instability happens for $k>k_c^{\left[1\right]}$, and for $h=1/4$ for all k. The instability is caused by the discontinuity of the slope of the zero-order-$\zeta$ velocity, which happens here due to viscosity stratification $\mu =2\ne 1$ (see text for details). Note the small magnitudes. Compare with Figure 3. (b) The physical voltage correction $R{\widehat{V}}^{\left[1\right]}$ vs. k, corresponding to the cases in (a). The voltages counteract the stability trends due to shear to bring the system to neutral stability to first order in R; for $h=4$, positive values of ${\widehat{V}}^{\left[1\right]}$ are needed to destabilize the stable wavenumbers $k<k_c^{\left[1\right]}$ of $c_i^{\left[1\right]}$ and vice versa; for $h=1/4$, the voltages are always negative to dampen the modes unstable for all k. The EHD system is coupled; Equations (94)–(101), and, in general, the extrema of the functions $c_i^{\left[1\right]}$ and ${\widehat{V}}^{\left[1\right]}$ do not coincide. However, the value $k_c^{\left[1\right]}(=1.836)$ is the same in the two panels as it should be. Note the very small magnitudes.

Figure 5. (a) The first-order-R correction $R{c}_i^{\left[1\right]}$ vs. k for the pure shear flow, i.e., without the first-order electric field (voltage). Two sets of flow parameters are featured: for $h=4$, instability happens for $k>k_c^{\left[1\right]}$, and for $h=1/4$ for all k. The instability is caused by the discontinuity of the slope of the zero-order-$\zeta$ velocity, which happens here due to viscosity stratification $\mu =2\ne 1$ (see text for details). Note the small magnitudes. Compare with Figure 3. (b) The physical voltage correction $R{\widehat{V}}^{\left[1\right]}$ vs. k, corresponding to the cases in (a). The voltages counteract the stability trends due to shear to bring the system to neutral stability to first order in R; for $h=4$, positive values of ${\widehat{V}}^{\left[1\right]}$ are needed to destabilize the stable wavenumbers $k<k_c^{\left[1\right]}$ of $c_i^{\left[1\right]}$ and vice versa; for $h=1/4$, the voltages are always negative to dampen the modes unstable for all k. The EHD system is coupled; Equations (94)–(101), and, in general, the extrema of the functions $c_i^{\left[1\right]}$ and ${\widehat{V}}^{\left[1\right]}$ do not coincide. However, the value $k_c^{\left[1\right]}(=1.836)$ is the same in the two panels as it should be. Note the very small magnitudes.

We further notice the orders-of-magnitude smaller values of the first-order corrections. We remember that typical values of $c_i^{\left[0\right]}$ in microfluidics are on the order of 1 ($\sim {10}^3$ times smaller than those in Figure 3, used to showcase the trends). Hence, $R{c}_i^{\left[1\right]}/c_i^{\left[0\right]}\sim {10}^{-7}$. It is perhaps surprising that the shear instability occurs at all. This is the famed Yih’s instability due to viscosity stratification first studied in the limit of small k [14]. We performed here the analysis for small R, confirming Yih’s findings as a special case (revisit Section 4.1): by inspecting Equation (A13) and the comment below Equation (A21), we find the proportionality on the account of the common factor ${\tilde{c}}_r^{\left[0\right]}$:

$$c_i^{\left[1\right]}\sim a_2^{}(\mu -1),$$

(103)

where $a_2^{}$ is the pressure-gradient-dependent factor in the zero-order-$\zeta$ flow, Equation (33b), and $\mu$ is the viscosity ratio. It immediately follows from Equation (103) that the condition $\mu =1$ (two equal viscosities) is the neutral stability condition to first order in R, i.e., $c_i^{\left[1\right]}(\mu =1)=0$ for all k, and there is no instability; since Yih considered pure Couette flow ($G_1^{}=0$) for which $a_2^{}\ne 0$, the instability $c_i^{\left[1\right]}>0$ is, indeed, induced for a viscous stratification $\mu \ne 1$.

However, in our more general Couette–Poiseuille flow, the neutral stability for all k happens also when $a_2^{}=0$, which occurs for a nonzero forward pressure gradient $G_1^{}<0$ and the value $\mu =-G_1^{}/(2-G_1^{})h^2$ (e.g., for $G_1^{}=-1$ and $h=4$, $\mu =5.\dot{3}$ yields the neutral stability for all k). This is the case when the compounded zero-order-$\zeta$ velocity becomes the smooth (unbroken) parabola; Equation (32). Hence, the viscosity stratification is not the sufficient condition—the generalized mechanism of the instability is the discontinuity in the slope (kink) of the zero-order-$\zeta$ velocity. The criterion does not pertain, though, to the single $k_c^{\left[1\right]}$ that is independently neutrally stable to first order in R, as determined by the complicated bracketed term in Equation (A13).

We make a final remark. We just saw that $c_i^{\left[1\right]}$ is identically zero for all wavenumbers for $\mu =1$ or $a_2^{}=0$, on the account of ${\tilde{c}}_r^{\left[0\right]}$ being, then, zero. At the same time, we are already at the zeroth-order-R neutral stability for which ${\tilde{c}}_i^{\left[0\right]}=0$. Hence, ${\tilde{c}}_0^{}=0$, Equation (70a), and the denominator of Equation (57b) becomes zero, making the disturbance infinite. In such cases, we must employ second-order expansion of the kinematic condition, as already noted. Nevertheless, a minute change from $\mu =1$ and $a_2^{}=0$ brings forth the instability, as discussed.

5.2. Onset of EHD Instability to First Order in R

As earlier mentioned, our main interest is the voltage correction $V^{\left[1\right]}$ that brings the system to neutral stability to first order in R, i.e., how much the voltage $V^{\left[0\right]}$ needs to change to compensate for the unstable growth of $c^{\left[1\right]}$ due to the shear flow at small R. The first-order change is found by solving

$$c^{\left[1\right]}(k,\mu ,h,\rho ,G_1^{},V^{\left[1\right]})=0,$$

(104)

for $V^{\left[1\right]}$. The analytical solution for $V^{\left[1\right]}$ is too complicated for display; we use the closed form of $c^{\left[1\right]}$, Equation (A13), and work from there to obtain $V^{\left[1\right]}$.

To bring the system to first-order-R neutral EHD stability, we expect the stable regions of $c_i^{\left[1\right]}$, i.e., those wavenumbers for which $k<k_c^{\left[1\right]}$, to be destabilized by an increasing voltage $V^{\left[1\right]}$ (of normal E-field), whereas the unstable regions $k>k_c^{\left[1\right]}$ are to be stabilized by a decreasing voltage.

This is indeed the case. Figure 5b shows the first-order-R voltage corrections $R{\widehat{V}}^{\left[1\right]}$ vs. k, corresponding to the two cases of Figure 5a. For $h=4$, the voltage increases sharply for very stable small wavenumbers, $k<k_c^{\left[1\right]}$, to destabilize them, but decreases for $k>k_c^{\left[1\right]}$ (the correction is negative), to dampen the growth of unstable ones. Note that $k_c^{\left[1\right]}(=1.836)$ is the same in the two panels as it should be, since $c_i^{\left[1\right]}\left(k_c^{\left[1\right]}\right)={\widehat{V}}^{\left[1\right]}\left(k_c^{\left[1\right]}\right)=0$. For $h=1/4$, the voltage correction is negative for all k, in accordance with the all-positive growth rates of the $c_i^{\left[1\right]}\left(k\right)$ in panel (a).

Note that we depicted the overall change in the physical voltage, $R{\widehat{V}}^{\left[1\right]}$, in volts, in order to obtain the feel for the actual experimental change to first order in R. Technically, ${ϵ}_2^{}$ in the term $T_{\mathrm{el},\mathrm{N}}^{\left[0\right]}{V}^{\left[1\right]}$ of Equation (88) is expressed as ${\widehat{ϵ}}_2^{}{\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}{\widehat{V}}^{\left[1\right]}/({\widehat{\mu }}_1^{}{\widehat{h}}_1^{}{\widehat{U}}_0^{}$), where ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$ is the impending voltage of Equation (78). Like with $c^{\left[1\right]}$, the first-order-R voltage corrections are six to seven orders of magnitude smaller compared to zeroth-order-R values, making them challenging, if not impossible, to measure.

We emphasize that the first-order-R corrections are found from the coupled EHD system of Equations (94)–(101). The overall coupling of the first-order E-field and the shear flow means that the phase velocities $c_i^{\left[1\right]}$ of the pure shear relative to those of the coupled EHD cases will have different extremal points in general. The maximal voltage corrections ${\widehat{V}}^{\left[1\right]}$ in the panel (b), thus, do not coincide with the maximal $c_i^{\left[1\right]}$ of (a).

Unlike the impending ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$ voltages, the $R{\widehat{V}}^{\left[1\right]}$ corrections depend on the flow parameters $\mu ,\rho ,G_1^{}$ and R. This is shown in Figure 6a, where three graphs are featured for different parameters of the EO pump of Section 4.3. The pump drags a viscous oil by a thin layer of water: $\mu =300,\rho =0.92$; h = 4, 20.

Comparing Figure 6a with Figure 5b, we first notice that the magnitudes of $R{\widehat{V}}^{\left[1\right]}$ are 100 times larger in Figure 6a due to larger damping/growth rates around $k_c^{\left[1\right]}$, with more pronounced local minima. Second, $k_c^{\left[1\right]}$ is shifted to the left enlarging the range of unstable wavenumbers (i.e., the area of negative voltage corrections). Stability, thus, nontrivially depends on parameters: the increase in $\mu$ relatively destabilizes the system for $h>1$ by shifting $k_c^{\left[1\right]}$ to the left, and by making the negative voltage corrections for $k>k_c^{\left[1\right]}$ larger; but at the same time, it makes the positive voltage corrections for $k<k_c^{\left[1\right]}$ also larger, the indication that already stable wavenumbers for $\mu =2$ became even more stable for $\mu =300$.

Figure 6. (a) First-order-R physical voltages $R{\widehat{V}}^{\left[1\right]}$ vs. k for three different flow cases for an EO pump. Magnitudes are small, but larger than in Figure 5b. The increase in h and adverse pressure $G_1^{}$ increase the stability by shifting $k_c^{\left[1\right]}$ to the right (stable k regions enlarged), but the increase in h enhances the voltage corrections around $k_c^{\left[1\right]}$, whereas the increase in $G_1^{}$ dampens them. (b) Neutral stability diagram of the overall impending voltage ${\widehat{V}}_{\mathrm{tot}}^{}={\widehat{V}}^{\left[0\right]}+R{\widehat{V}}^{\left[1\right]}$ vs. k to both orders, for a set of parameters for the EO pump (updated Figure 4). The small first-order magnitudes show up only when enhanced. EHD stability increases with h, as the impending voltages increase with h. For $h=4$ and $h=20$, stable regions protrude into unstable ones for $k<k_c^{\left[1\right]}$, and withdraw for $k>k_c^{\left[1\right]}$; compare with Figure 5b. For $h=1$, the first-order-R voltages are negative for all k, i.e., the system is unstable to first-order-R shear, like $h=1/4$ in Figure 5a. The stability diagrams differ for different flow parameters.

Figure 6. (a) First-order-R physical voltages $R{\widehat{V}}^{\left[1\right]}$ vs. k for three different flow cases for an EO pump. Magnitudes are small, but larger than in Figure 5b. The increase in h and adverse pressure $G_1^{}$ increase the stability by shifting $k_c^{\left[1\right]}$ to the right (stable k regions enlarged), but the increase in h enhances the voltage corrections around $k_c^{\left[1\right]}$, whereas the increase in $G_1^{}$ dampens them. (b) Neutral stability diagram of the overall impending voltage ${\widehat{V}}_{\mathrm{tot}}^{}={\widehat{V}}^{\left[0\right]}+R{\widehat{V}}^{\left[1\right]}$ vs. k to both orders, for a set of parameters for the EO pump (updated Figure 4). The small first-order magnitudes show up only when enhanced. EHD stability increases with h, as the impending voltages increase with h. For $h=4$ and $h=20$, stable regions protrude into unstable ones for $k<k_c^{\left[1\right]}$, and withdraw for $k>k_c^{\left[1\right]}$; compare with Figure 5b. For $h=1$, the first-order-R voltages are negative for all k, i.e., the system is unstable to first-order-R shear, like $h=1/4$ in Figure 5a. The stability diagrams differ for different flow parameters.

From Figure 6a alone, an increase in h stabilizes the system by shifting $k_c^{\left[1\right]}$ to the right, but, like the increase in $\mu$, enhances the magnitudes of the voltage corrections from both sides of $k_c^{\left[1\right]}$. Increase in adverse pressure ($G_1^{}>0$) shifts $k_c^{\left[1\right]}$ to the right, but dampens the magnitude of the voltage corrections on the two sides.

The voltage corrections $R{\widehat{V}}^{\left[1\right]}$ for the largest wavenumber $\widehat{k}=\pi /\widehat{L}$ allowed in the pump ($\widehat{L}=280\mathsf{\mu }$m, Section 4.3) are $69\times {10}^{-5}$ V, $1.2\times {10}^{-5}$ V, and $1.1\times {10}^{-5}$ V for the three cases $(h=20,G_1^{}=0),(h=4,G_1^{}=0)$, and $(h=4,G_1^{}=1)$, respectively. Interestingly, if the driving velocity could be increased by a factor 10 to $U_0^{}=1$ cm/s (and correspondingly $R=0.02$), the voltage corrections $R{\widehat{V}}^{\left[1\right]}$ grow by another factor 100 and come into the experimentally feasible mV range: 69 mV, 1.2 mV, and 1.1 mV, respectively.

Finally, the overall trends are best seen in the updated neutral stability diagram: in Figure 6b, the overall voltage ${\widehat{V}}_{\mathrm{tot}}^{}={\widehat{V}}^{\left[0\right]}+R{\widehat{V}}^{\left[1\right]}$ vs. k is shown on a log–log scale for a set of parameters for the EO pump. The actual small changes relative to those of Figure 4 are too small to be seen (full line), and the magnification of $R{\widehat{V}}^{\left[1\right]}$ by a factor ${10}^4$ (dotted line) and ${10}^7$ (dashed line) is imposed to resolve the trends. The lines thus express the (magnified) neutral stability curves up to first order in R, i.e., the curves for which $c_i^{\left[0\right]}=c_i^{\left[1\right]}=0$.

For $h=4$ and $h=20$, we see how stable regions, i.e., positive voltage corrections, increase with height, protruding into unstable domains for $k<k_c^{\left[1\right]}$. For $k>k_c^{\left[1\right]}$, the voltage corrections are negative, and so the unstable domain bulges into the stable one.

For $h=1$, the stable regions are overall diminished (the voltage correction is always negative), as the system is unstable for all k, like $h=1/4$ of Figure 5. We finally remind the reader that the neutral stability diagrams differ for different flow regimes.

This ends our comprehensive EHD stability analysis to first order in R.

6. Conclusions

We analyzed in depth the EHD stability of two superposed viscous dielectric immiscible liquids in a parallel flow in a microfluidic channel in the limit of small Reynolds number R, under a general Couette–Poiseuille flow. We applied our findings to microfluidic systems (EO pumps), paving the way to experimental validation.

Our study involves three basic approximations. First, gravity is negligible in microfluidic flows and is thus excluded from the analysis. Second, we treat two infinite parallel planes and accompanying 2D disturbances, which are reasonable surrogates for large 2D surfaces of the microfluidic systems considered. Finite-size effects beyond our given estimates and the 3D disturbances are left for future work. Third, we treat perfect dielectrics. More realistic leaky dielectrics can be easily incorporated in our methodology which has already given novel EHD insights.

There are two prominent and novel findings. First, we obtained the closed-form solutions for the EHD growth rates (the complex-numbered phase velocities) of 2D disturbances, to both zero order in R, Equations (70b) and (70c), and the first order in R, Equation (A13). The solutions are (very) complicated functions of parameters providing, thus, a rich parameter space for numerical explorations.

Second, based on the neutral stability condition for the growth rates (the stagnant growth, $c{}_i=0$), we derived the impending voltages ${\widehat{V}}_{\mathrm{inst}}$ for the onset of EHD instability to both zero order in R, Equation (78), and first order in R. They are depicted in the informative voltage vs. wavenumbers stability diagrams, Figure 4 and Figure 6b.

The zero-order-R impending voltage ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$ for two viscous streaming perfect dielectrics is independent of viscosity and velocity. The first-order-R impending voltage ${\widehat{V}}_{\mathrm{inst}}^{\left[1\right]}$ depends on the flow parameters, but is smaller than ${\widehat{V}}_{\mathrm{inst}}^{\left[0\right]}$ by several orders of magnitude. The significance of ${\widehat{V}}_{\mathrm{inst}}^{\left[1\right]}$ is that it elucidates, in detail, the fundamental coupling between the electric fields and viscous shear at small Reynolds numbers. By adjusting the flow parameters, ${\widehat{V}}_{\mathrm{inst}}^{\left[1\right]}$ could be brought within measurable millivolt range.

Importantly, our analysis provides new insight with respect to the existing literature. We correct inconsistencies in the EHD stability study of [16] by providing the correct analytical expressions to both order in small R. And we refine and further expand on the seminal study of Yih and his instability due to viscosity stratification [14]. We find that the pure shear instability (the case $E=0$) arises, in fact, due to discontinuity in the slope (kink) of the unperturbed (zeroth-order-$\zeta$) velocity, which becomes transparent in a Couette–Poiseuille flow. Instability due to viscosity stratification becomes, thus, just a necessary condition and our ${\widehat{V}}_{\mathrm{inst}}^{\left[1\right]}$ correction is a viable proof of the elusive phenomenon proposed by Yih more than 50 years ago.