A Simple Method to Assess Key Soil Hydraulic Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calibration
2.2. Field Validation
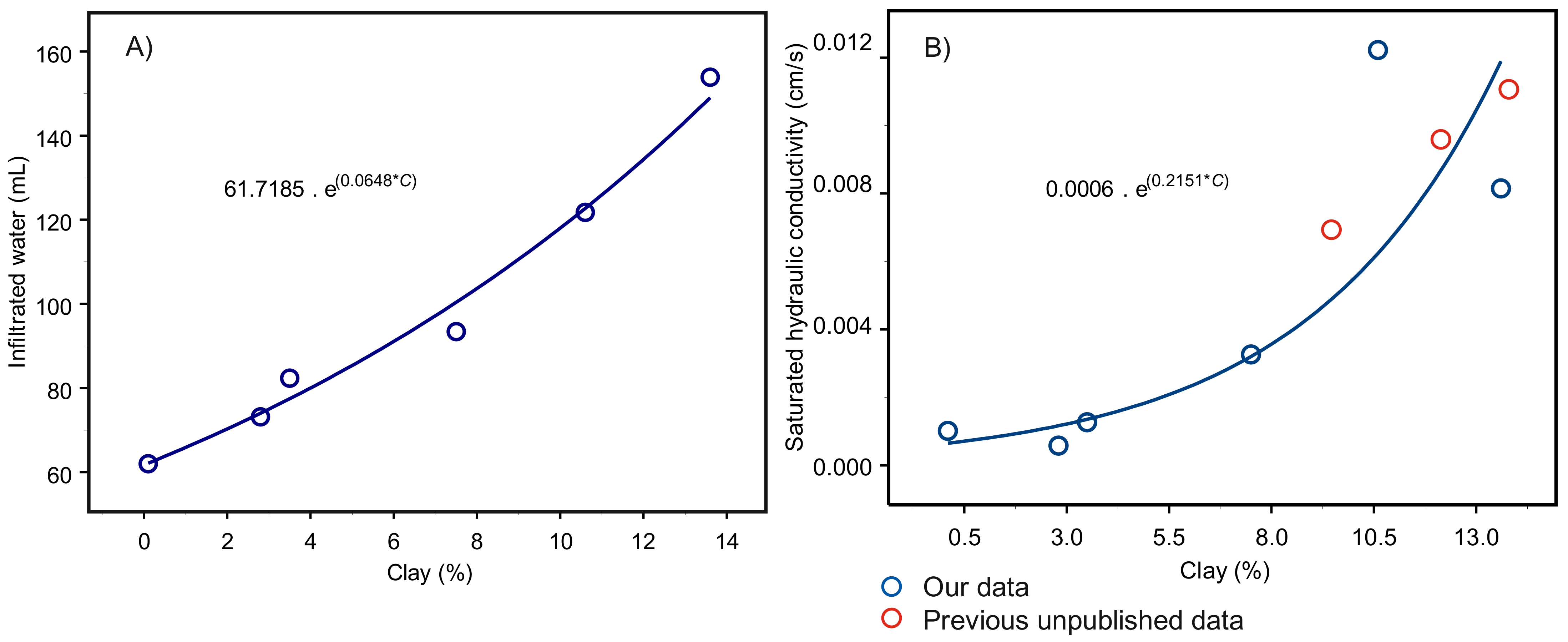
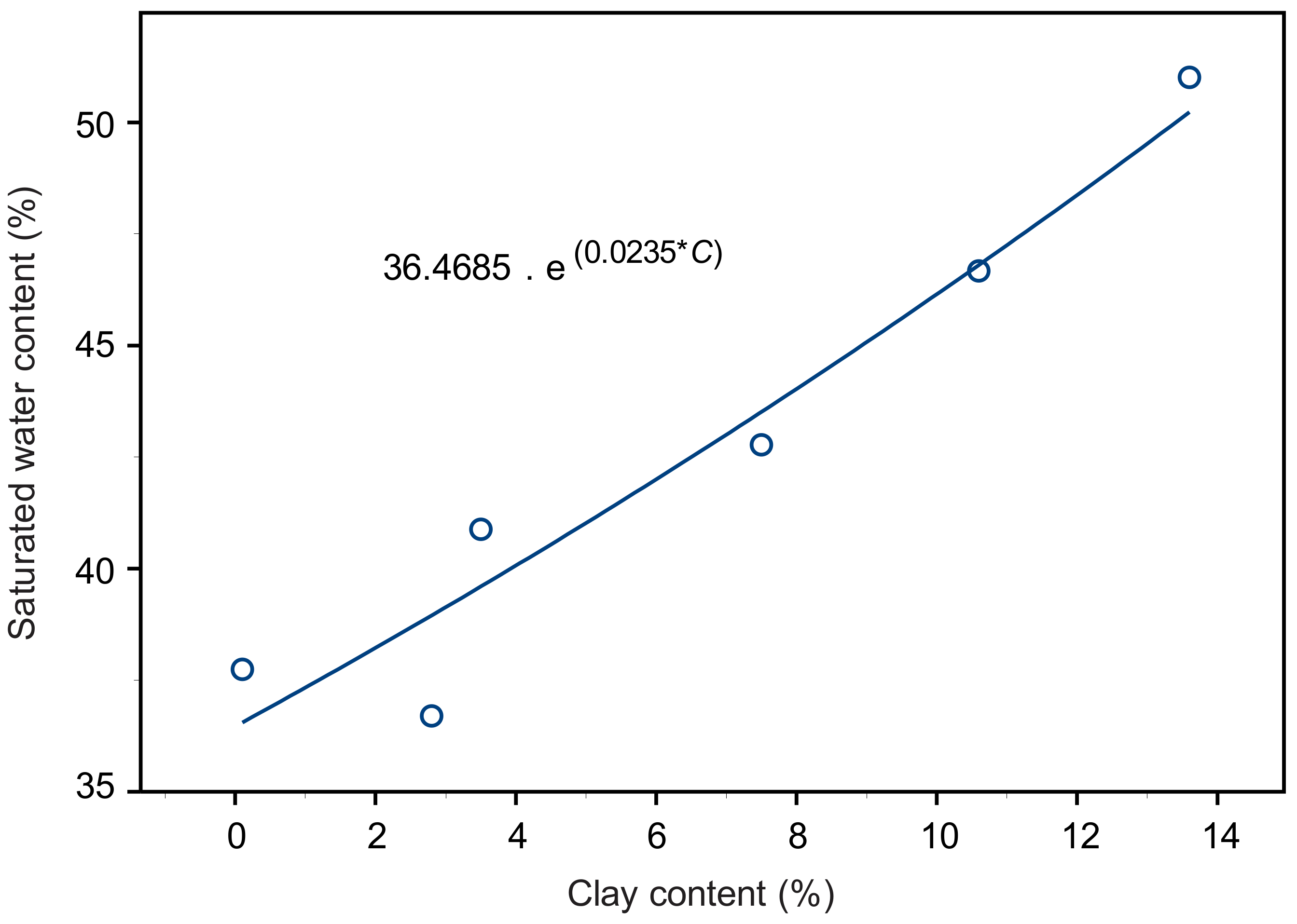
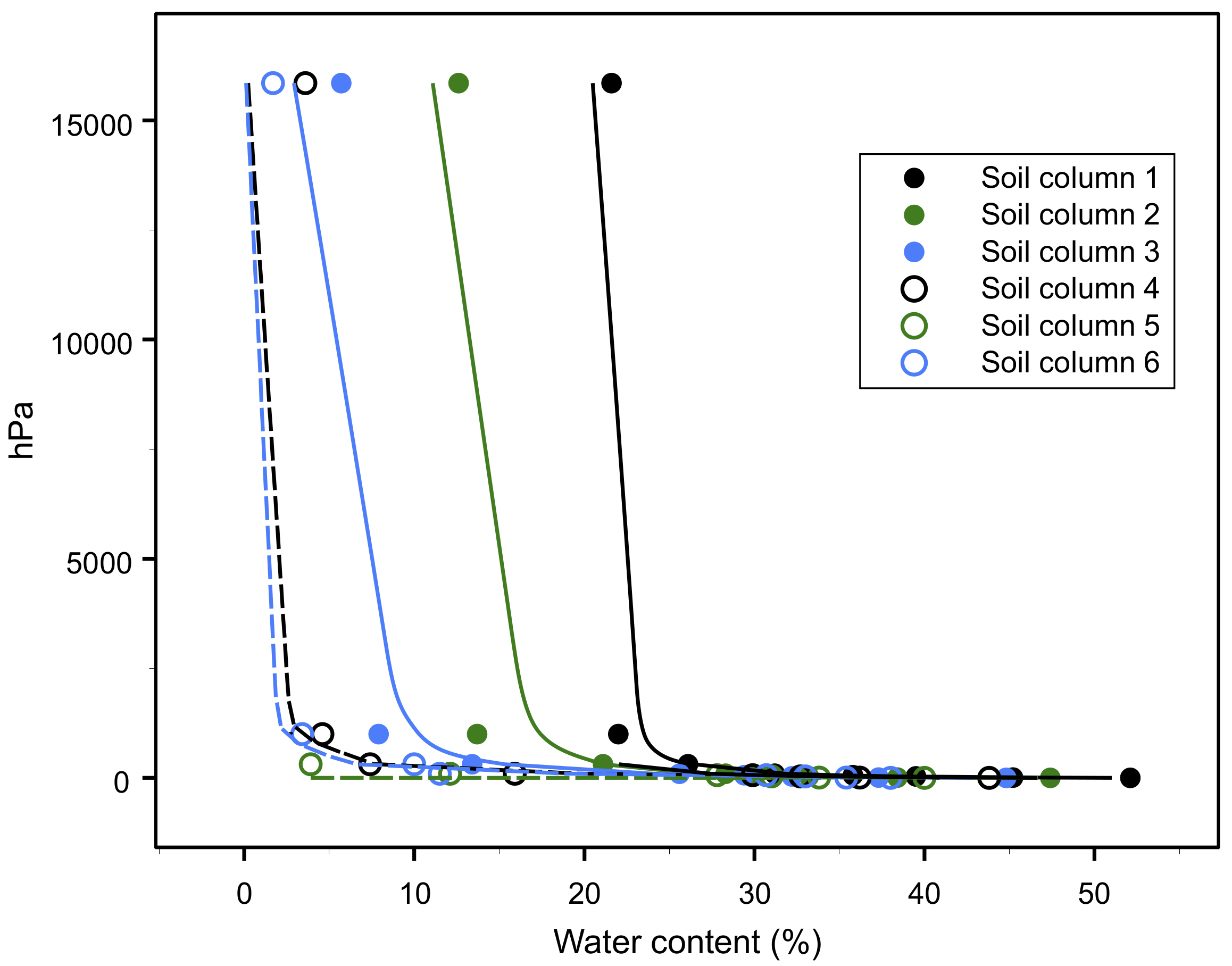
3. Results
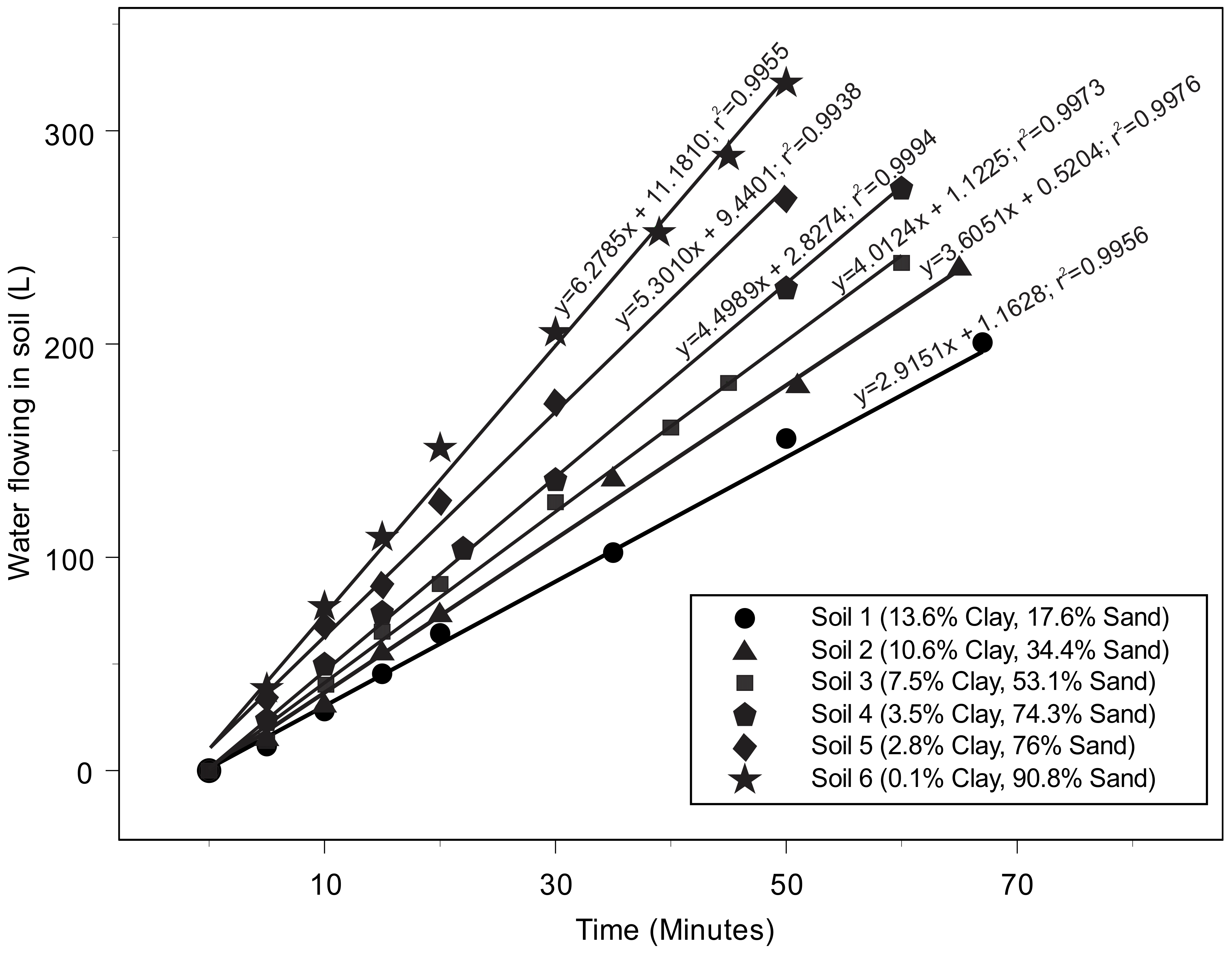
Validation
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alaoui, A.; Rogger, M.; Peth, S.; Blöschl, G. Does soil compaction increase floods? A review. J. Hydrol. 2018, 557, 631–642. [Google Scholar] [CrossRef]
- Allen, D.E.; Singh, B.P.; Dalal, R.C. Soil Health Indicators Under Climate Change: A Review of Current Knowledge. In Soil Health and Climate Change, Soil Biology; Singh, B., Cowie, A., Chan, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 29. [Google Scholar] [CrossRef]
- Schwilch, G.; Bestelmeyer, B.; Bunning, S.; Critchley, W.; Herrick, J.; Kellner, K.; Liniger, H.; Nachtergaele, F.; Ritsema, C.; Schuster, B.; et al. Experiences in Monitoring and Assessment of Sustainable Land Management. Land Degrad. Develop. 2011, 22, 214–225. [Google Scholar] [CrossRef]
- Doran, J.W.; Parkin, T.B. Defining and assessing soil quality. In Defining Soil Quality for a Sustainable Environment; Soil Science Society America Special Publication No. 35; Doran, J.W., Coleman, D.C., Bezedick, D.F., Steward, B.A., Eds.; American Society of Agronomy: Madison, WI, USA, 1994; pp. 3–21. [Google Scholar]
- Karlen, D.L.; Mausbach, M.J.; Doran, J.W.; Cline, R.G.; Harris, R.F.; Schuman, G.E. Soil quality: A concept, definition and framework for evaluation. Soil Sci. Soc. Am. J. 1997, 61, 4–10. [Google Scholar] [CrossRef] [Green Version]
- Topp, G.C.; Reynolds, W.D.; Cook, F.J.; Kirby, J.M.; Carter, M.R. Physical attributes of soil quality. In Soil Quality for Crop Production and Ecosystem Health; Gregorich, E.G., Carter, M.R., Eds.; Elsevier: Ottawa, ON, Canada, 1997; Volume 25, pp. 21–58. [Google Scholar]
- Alaoui, A.; Hallama, M.; Bär, R.; Panagea, I.; Bachmann, F.; Pekrun, C.; Fleskens, L.; Kandeler, E.; Hessel, R. A New Framework to Assess Sustainability of Soil Improving Cropping Systems in Europe. Land 2022, 11, 729. [Google Scholar] [CrossRef]
- Andrews, S.S.; Karlen, D.L.; Cambardella, C.A. The soil management assessment framework. Soil Sci. Soc. Am. J. 2004, 68, 1945–1962. [Google Scholar] [CrossRef]
- Velasquez, E.; Lavelle, P.; Andrade, M. GISQ, a multifunctional indicator of soil quality. Soil Biol. Biochem. 2007, 39, 3066–3080. [Google Scholar] [CrossRef]
- Morvan, X.; Saby, N.P.A.; Arrouays, D.; Le Bas, C.; Jones, R.J.A.; Verheijen, F.G.A.; Bellamy, P.H.; Stephens, M.; Kibblewhite, M.G. Soil monitoring in Europe: A review of existing systems and requirements for harmonization. Sci. Total Environ. 2008, 391, 1–12. [Google Scholar] [CrossRef]
- Cécillon, L.; Barthès, B.G.; Gomez, C.; Ertlen, D.; Genot, V.; Hedde, M.; Stevens, A.; Brun, J.J. Assessment and monitoring of soil quality using near-infrared reflectance spectroscopy (NIRS). Eur. J. Soil Sci. 2009, 60, 770–784. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, W.D.; Drury, C.F.; Yang, X.M.; Fox, C.A.; Tan, C.S.; Zhang, T.Q. Land management effects on the near-surface physical quality of a clay loam soil. Soil Till. Res. 2007, 96, 316–330. [Google Scholar] [CrossRef]
- Alaoui, A.; Lipiec, J.; Gerke, H.H. A review of the changes in the soil pore system due to soil deformation: A hydrodynamic perspective. Soil Till. Res. 2011, 115–116, 1–15. [Google Scholar] [CrossRef]
- Lal, R.; Shukla, M.K. Principles of Soil Physics; Marcel Dekker: New York, NY, USA, 2004; p. 716. ISBN 0-8247-5324-0. [Google Scholar]
- Reynolds, W.D.; Drury, C.F.; Tan, C.S.; Fox, C.A.; Yang, X.M. Use of indicators and pore volume-function characteristics to quantify soil physical quality. Geoderma 2009, 152, 252–263. [Google Scholar] [CrossRef]
- Alaoui, A.; Helbling, A. Evaluation of soil compaction using hydrodynamic water content variation: Comparison between compacted and non-compacted soil. Geoderma 2006, 134, 97–108. [Google Scholar] [CrossRef]
- Ward, R.C.; Robinson, M. Principles of Hydrology; McGraw-Hill: London, UK, 1990; 365p. [Google Scholar]
- Angulo-Jaramillo, R.; Vandervaere, J.; Roulier, S.; Thony, J.; Gaudet, J.; Vaucklin, M. Field measurement of soil surface hydraulic properties by disc and ring infiltrometers. A review and recent developments. Soil Till. Res. 2000, 55, 1–29. [Google Scholar] [CrossRef]
- Lassabatère, L.; Angulo-Jaramillo, R.; Soria Ugalde, J.M.; Cuenca, R.; Braud, I.; Haverkamp, R. Beerkan estimation of soil transfer parameters through infiltration experiments—BEST. Soil Sci. Soc. Am. J. 2006, 70, 521–532. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Stefano, C.; Iovino, M.; Sgroi, A. Using a transient infiltrometric technique for intensively sampling field-saturated hydraulic conductivity of a clay soil in two runoff plots. Hydrol. Process. 2012, 27, 3415–3423. [Google Scholar] [CrossRef]
- Gonzalez-Sosa, E.; Braud, I.; Dehotin, J.; Lassabatere, L.; Angulo-Jaramillo, R.; Lagouy, M.; Branger, F.; Jacqueminet, C.; Kermadi, S.; Michel, K. Impact of land use on the hydraulic properties of the topsoil in a small French catchment. Hydrol. Process. 2010, 24, 2382–2399. [Google Scholar] [CrossRef] [Green Version]
- Mubarak, I.; Angulo-Jaramillo, R.; Mailhol, J.C.; Ruelle, P.; Khaledian, M.; Vauclin, M. Spatial analysis of soil surface hydraulic properties: Is infiltration method dependent? Agric. Water Manag. 2010, 97, 1517–1526. [Google Scholar] [CrossRef]
- Yilmaz, D.; Lassabatere, L.; Angulo-Jaramillo, R.; Deneele, D.; Legret, M. Hydrodynamic characterization of basic oxygen furnace slag through an adapted best method. Vadose Zone J. 2010, 9, 107–116. [Google Scholar] [CrossRef]
- Bagarello, V.; Iovino, M. Testing the BEST procedure to estimate the soil water retention curve. Geoderma 2012, 187–188, 67–76. [Google Scholar] [CrossRef]
- Nasta, P.; Lassabatere, L.; Kandelous, M.M.; Šimunek, J.; Angulo-Jaramillo, R. Analysis of the role of tortuosity and infiltration constants in the Beerkan method. Soil Sci. Soc. Am. J. 2012, 76, 1999–2005. [Google Scholar] [CrossRef]
- Ghavidelfar, S.; Shamseldin, A.Y.; Melville, B.W. Estimation of soil hydraulic properties and their uncertainty through the Beerkan infiltration experiment. Hydrol. Process. 2015, 29, 3699–3713. [Google Scholar] [CrossRef]
- Xu, X.; Kiely, G.; Lewis, C. Estimation and analysis of soil hydraulic properties through infiltration experiments: Comparison of BEST and DL fitting methods. Soil Use Manag. 2009, 25, 354–361. [Google Scholar] [CrossRef]
- Lassabatere, L.; Angulo-Jaramillo, R.; Goutaland, D.; Letellier Gaudet, J.P.L.; Winiarski, T.; Delolme, C. Effect of the settlement of sediments on water infiltration in two urban infiltration basins. Geoderma 2010, 156, 316–325. [Google Scholar] [CrossRef]
- Xu, X.; Lewis, C.; Liu, W.; Albertson, J.D.; Kiely, G. Analysis of singlering infiltrometer data for soil hydraulic properties estimation: Comparison of BEST and Wu methods. Agric. Water Manag. 2012, 107, 34–41. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E. A method for simultaneous in situ measurement in the vadose zone of field-saturated hydraulic conductivity, sorptivity and the conductivity- pressure head relationship. Ground Water Monit. Rev. 1986, 6, 84–95. [Google Scholar] [CrossRef]
- Elrick, D.E.; Reynolds, W.D. Methods for analyzing constant-head well permeameter data. Soil Sci. Soc. Am. J. 1992, 56, 320–323. [Google Scholar] [CrossRef]
- Constantz, J.; Herkelrath, W.N.; Murphy, F. Air encapsulation during infiltration. Soil Sci. Soc. Am. J. 1988, 52, 10–16. [Google Scholar] [CrossRef]
- Rodger, H.A. Tracking Changes in Hydraulic Conductivity of Soil Reclamation Covers with The Use of Air Permeability Measurements. Ph.D. Thesis, Department of Civil Engineering, University of Saskatechewan, Saskatoon, SK, Canada, 2008; p. 116. [Google Scholar]
- Bouwer, H. Intake rate: Cylinder infiltrometer. In Methods of Soil Analysis; ASA Monograph 9; Klute, A., Ed.; ASA: Madison, WI, USA, 1986; pp. 825–843. [Google Scholar]
- ASTM D3385-18; Standard Test Method for Infiltration Rate of Soils in Field Using Double-Ring Infiltrometer. ASTM International: West Conshohocken, PA, USA, 2003.
- Gregory, J.H.; Dukes, M.D.; Miller, G.L.; Jones, P.H. Analysis of double-ring infiltration techniques and development of a simple automatic water delivery system. Appl. Turfgrass Sci. 2005, 2, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Konen, M.E.; Jacobs, P.M.; Lee Burras, C.; Talaga, B.J.; Mason, J.A. Equations for predicting soil organic carbon using loss-on-ignition for north central U.S. Soils. Soil Sci. Soc. Am. J. 2002, 66, 1878–1881. [Google Scholar] [CrossRef]
- Klute, A.; Dirksen, C. Hydraulic conductivity and diffusivity: Laboratory methods. In Methods of Soil Analysis: Part 1. Physical and Mineralogical Methods, 2nd ed.; Monograph, Klute, A., Eds.; American Society of Agronomy: Madisson, WI, USA, 1986; Volume 9, pp. 687–734. [Google Scholar]
- van Genuchten, M.T.; Lesch, S.M.; Yates, S.R. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; Version 1.0; U.S. Salinity Laboratory, USDA: Riverside, CA, USA, 1991.
- FAO; UNESCO. Soil Map of the World, Vol 60, Revised Legend. Soil Map of the World; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1988. [Google Scholar]
- Lange, B.; Germann, P.F.; Lüscher, P. Greater abundance of Fagus sylvatica in coniferous flood protection forests due to climate change: Impact of modified root densities on infiltration. Eur. J. Forest Res. 2013, 132, 151. [Google Scholar] [CrossRef] [Green Version]
- Richard, F.; Lüscher, P. Physikalische Eigenschaften von Böden der Schweiz; Eidg. Anstalt für das Forstliche Versuchswesen: Birmensdorf, Switzerland, 1987; Volume 4. [Google Scholar]
- Oades, J.M. The role of biology in the formation, stabilization and degradation of soil structure. Geoderma 1993, 56, 377–400. [Google Scholar] [CrossRef]
- Hamblin, A.P. The influence of soil structure on water movement, crop root growth, and water uptake. Adv. Agron. 1985, 38, 95–158. [Google Scholar]
- Cass, A.; Hansen, D.; Dowley, A. Grape performance and soil conditions. In Sustainable Viticultural Production: Optimising Soil Resources; GWRDC Final Report: CRS 95/1; Cass, A., Ed.; Alfred Cass & Associates: Calistoga, CA, USA, 2002; pp. 5–15. [Google Scholar]
- Vogeler, I.; Horn, R.; Wetzel, H.; Kruemmelbein, J. Tillage effects on soil strength and solute transport. Soil Till. Res. 2006, 88, 193–204. [Google Scholar] [CrossRef]
- Alaoui, A. Modelling susceptibility of grassland soil to macropore flow. J. Hydrol. 2015, 525, 536–546. [Google Scholar] [CrossRef]
- Meiers, G.P. The Use of Field Measurements of Hydraulic Conductivity to Characterize the Performance of Reclamation Soil Covers with Time; M. Eng. Report; University of Saskatchewan: Saskatoon, SK, Canada, 2002. [Google Scholar]


| Soil Column Number | Particle Size Distribution (%) | Texture * | Ks | BD | OC | ||
|---|---|---|---|---|---|---|---|
| Clay (<2 μm) | Silt (2–50 μm) | Sand (>50 μm) | (cm s−1) | (g cm−3) | (%) | ||
| Undisturbed forest soil | 11.6 | 53.3 | 35.1 | Silt loam | 3.11 × 10−2 | 0.87 | 10.6 |
| Undisturbed grassland soil | 10.6 | 43.8 | 45.6 | Loam | 1.60 × 10−3 | 1.44 | 3.5 |
| Reconstructed soil columns | |||||||
| 1 | 13.6 | 68.8 | 17.6 | Silt loam | 1.0178 × 10−3 | (*) | 0 |
| 2 | 10.6 | 55.0 | 34.4 | Silt loam | 5.84 × 10−3 | (*) | 0 |
| 3 | 7.5 | 39.4 | 53.1 | Sandy loam | 1.268 × 10−3 | (*) | 0 |
| 4 | 3.5 | 22.2 | 74.3 | Loamy sand | 3.2624 × 10−3 | (*) | 0 |
| 5 | 2.8 | 21.2 | 76.0 | Loamy sand | 1.222 × 10−2 | (*) | 0 |
| 6 | 0.1 | 9.1 | 90.8 | Sand | 8.152 × 10−3 | (*) | 0 |
| Land Cover | Param. to Determine | Observation V1 vs. V2 | Equations for the Calculation | Eq. | Factor F | Eq. |
|---|---|---|---|---|---|---|
| Loose soil | Ks | V2 > V1 Ks1 < Ks2 | (3) | (4) | ||
| Compact soil | Ks | V1 > V′2 Ks1 > K′s2 | (5) | (6) | ||
| Loose soil | θs | V2 > V1 θs1 < θs2 | (7) | (8) | ||
| Compact soil | θs | V1 > V′2 θs1 > θ′s2 | (9) | (10) | ||
| Loose soil | α, van Genuchten | V2 > V1 α1 > α2 | (11) | (12) | ||
| Compact soil | α, van Genuchten | V1 > V′2 α1 < α′2 | (13) | (14) | ||
| Loose soil | n, van Genuchten | V2 > V1 n1 > n2 | (15) | (16) | ||
| Compact soil | n, van Genuchten | V1 > V′2 n1 > n′2 | (17) | (18) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaoui, A. A Simple Method to Assess Key Soil Hydraulic Properties. Water 2023, 15, 467. https://doi.org/10.3390/w15030467
Alaoui A. A Simple Method to Assess Key Soil Hydraulic Properties. Water. 2023; 15(3):467. https://doi.org/10.3390/w15030467
Chicago/Turabian StyleAlaoui, Abdallah. 2023. "A Simple Method to Assess Key Soil Hydraulic Properties" Water 15, no. 3: 467. https://doi.org/10.3390/w15030467





