Abstract
The flood discharge atomization of high dams involves a complex coupled flow of water and air. Small-scale model tests are typically used to predict the atomization of flood discharge. However, the accuracy of the prediction results often suffers because of the scale effect between the model and the prototype. Considering that the numerical simulation method has the advantage of not being restricted by similarity scales, this paper studies the influence of the scale effect on the atomization of flood discharge based on the principle of water-air two-phase flow. Taking the Shuibuya Hydropower Station as the research object, the distribution of the flood discharge atomized rainfall and the atomized wind speed are studied when the boundary conditions, ambient atmospheric pressure, and geometric dimensions meet similar requirements. The research results show that under the same boundary conditions, the geometric scale is the most important factor affecting flood discharge atomization. The smaller the geometric scale, the smaller the atomization wind speed and rainfall intensity obtained by the model, which means that smaller monitoring errors lead to larger prediction deviations. When the calculation model satisfies similar atmospheric pressure conditions, the atomization wind speed and rainfall obtained by the models with different geometric scales satisfy the standard exponential function relationship. By comparing with the atomized rainfall and wind speed data observed by the Shuibuya prototype, it is found that the prediction accuracy of the prototype can be greatly improved when the model satisfies a similar atmospheric pressure.
1. Introduction
Flood discharge atomization (FDA) is a phenomenon of water-air dispersion that occurs during flood discharge at water conservancy projects. The strong wind and heavy rainfall accompanying FDA can cause harm to the safe and stable operation of power stations, the stability of river valley slopes, and the productivity and lives of residents [1,2]. At present, prototype observations [3,4,5], model tests [6,7,8], and numerical simulations [9,10,11,12] are mainly used to predict the atomization of flood discharge. Among them, model testing is one of the essential steps in the feasibility study design stage of most large- and medium-sized hydropower projects [13,14]. A model test mainly measures the atomization of a scaled-down physical model similar to the prototype, establishes a connection between the model and the prototype, and realizes the prediction of the temporal–spatial distribution of the prototype’s atomization wind field and rain field [15,16]. However, because FDA involves complicated water-air two-phase flow, physical model tests have significant scaling effects, resulting in the transformation relationship between the prototype and model not meeting the gravitational similarity criterion [17]. Taking the prediction of atomized rainfall intensity as an example, under the premise of satisfying the similarity of gravity, the results monitored by the model are usually considered to be an exponential relationship between the atomized rain intensity scale (Sr) and the geometric scale (Lr), namely, . The value of n is related to factors such as flood discharge capacity, energy dissipater body shape, and Weber number, and its value has a great influence on the accuracy of the prediction results [17]. Yu Kaiwen (2020) et al. [17] concluded that when the geometric scale is smaller, a small change in the value of n causes the predicted rainfall intensity to exhibit a change that is greater by tens or even hundreds of times, and the error is unacceptable.
Numerous scholars have studied the effects of similar scales on the atomization of flood discharge through model tests. Based on the original view data of the FDA of the Wujiangdu Hydropower Station, the Nanjing Hydraulic Research Institute (NHRI) carried out a series of model test studies (the similar model scales were 1:35, 1:60, 1:80, and 1:100). A comparative analysis of the experimental results and the prototype observation data showed that when the water surface Weber number in the model exceeded 500 and the water flow velocity was not less than 6.0 m/s, the relationship between the rain intensity scale and geometric scale was . Wu Shiqiang et al. [18] recommended this relation as the outer envelope control of the atomized rainfall intensity. For small-scale model tests, the similarity of surface tension is one of the factors to be considered [19,20]. The atomized rainfall intensity and atomized wind speed between the prototype and the model can be converted by similar scales, but the conversion relationship is difficult to determine. The similarity scale of atomized rainfall intensity of different geometric scale models has great dispersion, which can reach 10~100 times [1]. In addition, the model test results can be affected by a combination of factors. There are many factors that affect the atomization of flood discharge: not only the flood discharge capacity, the shape of the energy dissipater, the Weber number of water flow, etc. [2], but also the geometric size of the model test, the atmospheric pressure of the environment where the test is located, boundary conditions, and other factors. Therefore, it is difficult to quantitatively analyze the influence of a single factor, so it is impossible to find the main factor that affects the model test results, resulting in lower accuracy of the prediction results of a small-scale model test.
China’s national standard “Hydraulic (Conventional) Model Test Regulations (SL155-2012)” [21] notes that the hydraulic model should be corrected for the similarity of surface tension and viscosity under the premise of satisfying the gravity similarity criterion. However, in terms of current test conditions and test technology, it is still relatively difficult to accurately realize the correction of these influencing factors. Considering that the numerical simulation method is not limited by the similarity scale of the model, it can reflect the real FDA process to a certain extent. Therefore, based on the theory of water-air two-phase flow, this paper uses a numerical simulation method to study the conversion relationship between the model and a prototype of atomizing rainfall and atomizing wind speed and explores the influence of boundary conditions, geometric dimensions, environmental pressure, and other factors on the conversion relationship. Furthermore, the method to improve the prediction accuracy of the flood discharge atomization model is analyzed.
2. Mathematical Model of FDA and Its Solution
2.1. Mathematical Model of FDA
FDA is essentially a process in which the potential energy of water is transformed into water, air kinetic energy, and heat energy. This process follows the laws of conservation of mass, momentum, and energy [22]. Considering that the temperature change during flood discharge is minimal, the law of conservation of energy is not considered. The law of conservation of mass and the law of conservation of momentum are used to describe the movement of water and air in the process of FDA. The law of conservation of mass followed by the movement of water and air can be expressed as [23]:
In the formula, is the density of water, is the speed of water in the i direction, is the density of air, and is the speed of air in the i direction.
The law of conservation of momentum followed by the movement of water and air in the process of flood discharge can be expressed as:
In the formula, is the viscosity coefficient of water, is the pressure, is the component of gravitational acceleration in the i direction, is the viscosity coefficient of air, and is the interphase force between water and air in the i direction, which can be expressed as a function of the volume fraction of water, density of water, and relative acceleration:
where is the coefficient of additional mass.
To realize the prediction of FDA is to predict the distribution of the atomized wind field and the atomized rain field generated during the flood discharge process. When the mass and momentum conservation laws are used to describe the FDA, the movement speed of air, namely, the wind field generated by the atomization of flood discharge, can be obtained. The formation of the atomized rain field mainly comes from the water mist dispersed in the air. When the concentration of water mist in the air reaches a certain level, the water mist is converted into rain. Therefore, the formula for solving the concentration of water mist and the conversion formula for fog and rain are introduced into the mathematical model of FDA.
The water mist concentration transmission equation can be derived from the deformation of the mass conservation equation of water:
In the formula, represents the concentration of water, and the other variables are the same as defined above.
The intensity of fog and rain in the flood discharge process cannot be obtained by solving Equations (1)–(4) as a basic unknown quantity. Research has shown that the intensity of fog and rain in the flood discharge process is related to the water mist concentration. As the water mist concentration increases, the probability of collision between fog drops increases, and the greater the formation of heavy raindrops, the greater the rainfall intensity [24]. In this study, the fog and rain conversion formula proposed in the literature [25] is used to calculate the fog and rain intensity:
In the formula, is the rainfall intensity and is the concentration of water; the following concentrations all refer to the concentration of water: is the wind speed along the vertical direction, and x represents the direction downstream along the river channel.
2.2. Model Solution Strategy
The solution of the FDA mathematical model is achieved with computational fluid dynamics (CFD), which is needed to determine the motion of water and gas. Since the forces between the water and gas phases are opposite to each other, their magnitude has a greater impact on the stability and convergence of the numerical solution. In this study, to increase the stability and convergence in the numerical solution, the mass conservation equation and momentum conservation equation of two phases were added separately to obtain the total mass and momentum conservation equations of water and gas to reduce the solution shock caused by the inaccurate estimation of the force between the water and the gas phase. After adding the mass and momentum conservation equations of the two phases of water and gas, the total mass and momentum conservation equations of the water–gas mixed fluid are obtained:
where is the density of the water–gas mixed fluid, is the speed of the mixed fluid in the i (x, y, z) direction, is the dynamic viscosity coefficient of the water–gas mixed fluid, and is the component of the gravitational acceleration of the mixed fluid in the i direction.
When solving the mixed fluid mass conservation Equation (8), the main unknown quantity in the equation is the density and velocity of mixed water and air. To facilitate the solution, the relationship between the density and pressure of the mixed fluid is introduced here to establish the relationship between fluid pressure and flow velocity [26]. The relationship between the pressure and density of the mixed fluid can be expressed as:
In the formula, is the density of the mixed fluid under standard atmospheric pressure, is the pressure, is the elastic modulus of the mixed fluid, and is the standard atmospheric pressure, taking 101 kPa. Substituting this into Equation (8), we can obtain:
Considering that the elastic modulus of the mixed fluid is usually much larger than the pressure increment , the increment part in the denominator can be ignored, and then Equation (11) can be expressed as:
Therefore, the solution strategy of the mathematical model of FDA can be expressed as follows: first, solve the mass and momentum conservation Equations (8) and (9) of the water–gas mixed fluid to obtain the pressure and the velocity of the mixed fluid at this time step; then, use the pressure value to solve the gas-phase momentum conservation Equation (4) to obtain the gas-phase velocity; and then, use momentum conservation characteristics to explicitly derive the movement speed of the water phase, solve the water concentration according to the concentration transmission equation of the water phase (6), and finally obtain the atomized rainfall intensity and wind speed according to the fog–rain conversion Equation (7). The Newton-Raphson method is used for nonlinear iteration, and the biconjugate gradient stabilized method (BCGSTAB) is used to solve the linear equations. The large eddy simulation (LES) method is used to address turbulence.
2.3. Calculation Example Verification
To solve the movement of water and air in the FDA process, a finite element calculation code is written. Figure 1 shows the convergence process of pressure and velocity solutions when solving the mass and momentum conservation equation of mixed water and air. The iterative convergence standard of velocity and pressure is 10−5. Figure 1 shows that the iterative convergence process of pressure is relatively slow, while the iterative solution process of velocity is faster.
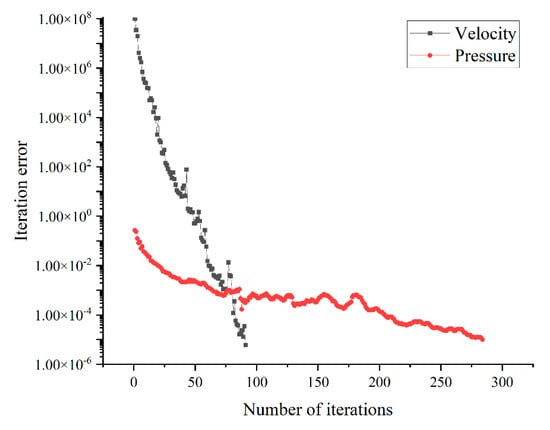
Figure 1.
Iterative convergence processes of velocity and pressure.
Flood discharge atomization is essentially a process of water-air two-phase flow, so the key to its numerical simulation is to solve the water-air two-phase movement. To further verify the correctness of the solution code, a water faucet example is used to verify the solution code. The water faucet calculation example describes the free fall process of water in a vertical pipe [27,28]. As the flow rate of water at the outlet is greater than that at the inlet, the water keeps narrowing in the falling process, and the gap between the water body and the tube wall is filled with air. Through simulation, the process of water falling in the vertical pipe can be obtained, as shown in Figure 2. Figure 2 shows the volume fraction of water in the pipe at different times. The grey picture is from the reference (a–c), and the color picture is obtained from the numerical simulation in this paper (a’–c’).
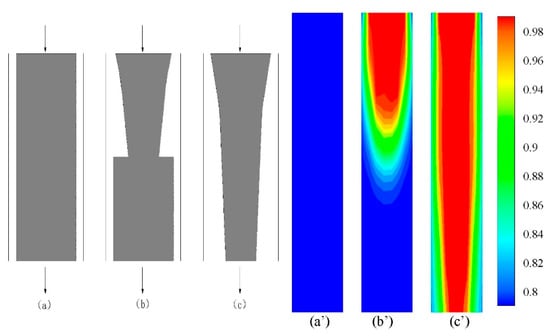
Figure 2.
Distribution of liquid phase volume fraction at different moments: (a,a’) Initial; (b,b’) Transient state; (c,c’) Stable.
A comparison of Figure 2 with the reference [28] indicates that the liquid-phase concentration distribution diagram at different times obtained by the program simulation is consistent with those in the literature. The initial state is that the liquid phase with a volume fraction of 0.8 fills the entire pipeline (Figure 2a,a’). When the liquid phase starts to flow in from the inlet, the concentration at the lower part of the pipeline remains unchanged, while the concentration at the inlet gradually increases. When the flow is stable, the volume fraction of the liquid phase is distributed in an inverted cone shape along the pipeline. From the perspective of the dynamic process of water flow, the calculation program can simulate the two-phase flow of water and air. Figure 3 shows the comparison between the theoretical value and calculated average velocity of water at different distances from the pipeline inlet.
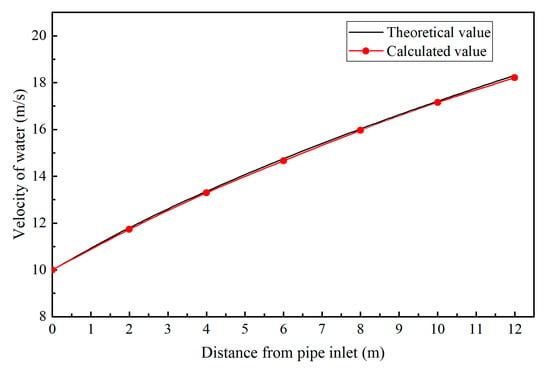
Figure 3.
Comparison between theoretical value and calculated value of water velocity at different distances from pipeline inlet.
According to the comparative analysis of the average velocity of water at different sections, the calculated value of the numerical model is close to the theoretical value, which further verifies the simulation ability of the numerical program for water–gas two-phase flow.
3. Influence of the Geometric Scale on FDA
3.1. Calculation Model
In this study, the FDA process of the Shuibuya Power Station was used as the research object, and a three-dimensional finite element calculation grid was established. The simulated similarity scales are 1:1, 1:2, 1:5, 1:10, 1:20, 1:50, and 1:100 for the FDA process of the Shuibuya Power Station. The calculation grid is shown in Figure 4. The grid dependency is verified on a 1:1 computing grid, and hexahedral meshes are used. Considering the calculation efficiency and calculation accuracy, the number of calculation grid nodes used is 59,939, and the number of grid elements is 53,244. The calculation grids of other scales are all reduced proportionally on the basis of the 1:1 scale calculation grid. The number of meshes used in numerical simulation with different geometric scales is the same, so the mesh size is different and the Reynolds number is not preserved in small-scale models. The mesh size used in the model with a small geometric scale is smaller. Considering that the size of models with different geometric scales is different and the mesh size adopted by models with different geometric scales cannot be consistent, a consistent mesh number strategy is adopted. It should be noted that the change in mesh size affects the calculation results but does not affect the trend of the calculation results.

Figure 4.
Calculation grids of different geometric scales.
The initial boundary conditions are important factors affecting the calculation results. To study the influence of the geometric scale, different models adopt similar boundary conditions, that is, the types of boundary conditions are the same, but the values are different. Taking the 1:1 scale calculation model as an example, the boundary conditions are mainly divided into velocity boundary conditions, pressure boundary conditions, and concentration boundary conditions. The velocity boundary conditions are as follows: at the entrance of the spillway, the velocity in the x-direction below the water surface is known, which equals the discharge divided by the corresponding mesh area, and the velocity of the air above the water surface in the x-, y-, and z-directions is 0; the velocities of water and air at the spillway and the river channel are both 0; the velocities in the y- and z-directions at the downstream exit are 0, and the velocities in the downstream direction are calculated through calculations; and the velocities in the x-, y-, and z-directions at the top of the model are all 0. The discharge of the geometric scale of 1:1 is 3848 m3/s. The pressure boundary conditions are as follows: the model outlet is a known pressure boundary, the pressure below the water surface is calculated by water depth, and the pressure above the water surface is calculated by elevation coordinates; the top of the model is a known pressure boundary; and the pressure of the remaining parts is obtained by calculation. The concentration boundary conditions are as follows: the concentration boundary below the spillway inlet water surface is known, and the concentration in the rest of the area is obtained by calculation. For models with other geometric scales, the speed at the boundary is reduced according to the geometric dimensions, which meets the criterion of equal Froude number, while the pressure boundary conditions and concentration boundary conditions are consistent with the 1:1 model.
The initial conditions of the model calculation for different scales are all kept the same, and the initial velocity in the model calculation domain is 0; the initial concentration of water below the surface of the downstream river is 1, and the concentration of water above the surface is 0.
3.2. Evolution Process of Atomization Wind Speed and Rainfall
By numerically simulating the flood discharge process under different similar scale conditions, the velocity of water vapor movement and the concentration of water mist at a certain place in space at any time can be obtained. We select the node at the 230 m platform (#22 in Figure 10) on the left bank and analyze the changes in wind speed in the x-direction (along the river) component, z-direction (vertical direction) component, and wind speed at this part under different similarity scales. Generally, according to Figure 5, the x-direction component of atomization wind speed at the 230 m platform on the left bank first increases and then gradually tends to stabilize with the flood discharge process, and the final stable speed is also different under different similarity scales. When the similarity scale is 1, the x-direction component of the atomization wind speed is the largest. As the similarity scale decreases from 1:1 to 1:50, the x-direction component of atomization wind speed gradually changes from positive to negative. When the similarity scale decreases to 1:100, the x-direction component of atomization wind speed changes to positive again. This shows that the position of the air flow gyration formed by the atomized wind on the 230 m platform on the left bank is greatly affected by the geometric scale. At the same position, under different geometric scales, it may be located on the left side of the counterclockwise cyclone center (the x-direction component is positive) or on the right side of the cyclone center (the x-direction component is negative).
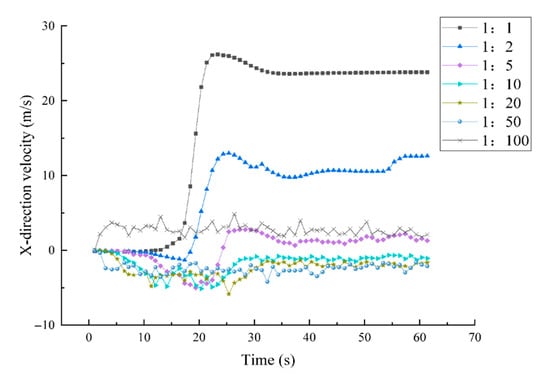
Figure 5.
The x-direction component of wind speed under different similarity scales.
Figure 6 shows the components of the atomization wind speed in the z-direction under different similar scale conditions. With the progress of flood discharge, the component of atomization wind speed in the z-direction increases first, then decreases gradually, and tends to be stable. Since the water flows mainly downward, the z-direction component of the atomized wind speed produced mainly moves vertically downward on the 230 m platform on the left bank. The larger the similarity scale, the greater the stable value of the atomizing wind speed component in the z-direction, and the earlier this value starts to change. This shows that under the same initial conditions, the larger the similar scale, the shorter the time for the water to flow down to the 230 m platform on the left bank.
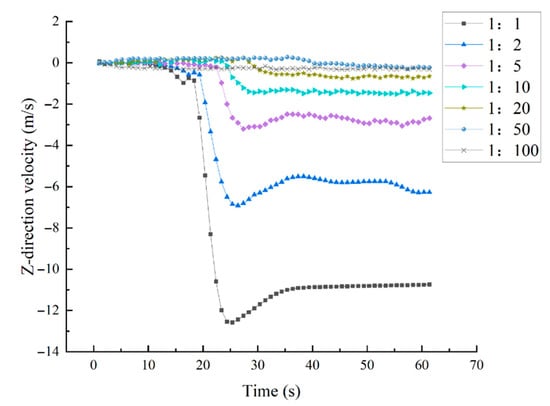
Figure 6.
Wind speed component in the z-direction under different similar scale conditions.
Through the components of the atomization wind speed in the x-, y-, and z-directions, the change process of the atomization wind speed with time during the flood discharge process can be obtained, as shown in Figure 7. The change process of atomization wind speed with time is similar to the component of atomization wind speed in the x-direction, and both increase first and then gradually stabilize with the progress of flood discharge. On the whole, the smaller the similarity scale, the smaller the atomization wind speed when the flood discharge is stable, and the more severe the fluctuations. When the similarity scale reaches 1:100, the atomization wind speed fluctuates the most. Figure 6 shows that the geometric similarity scale of the model has a greater impact on the atomization wind speed. From the perspective of energy conversion, the potential energy of the water body is transformed into the kinetic energy of water and air during the flood discharge process. When the potential energy of the water body is greater, the corresponding atomization wind speed is also greater. The atomization wind speed during the flood discharge process is affected by many factors, including the drop between the upstream and downstream, the atmospheric pressure, and the boundary conditions [29,30]. When a smaller similar scale is used, the influence of each influencing factor on the atomization wind speed is not negligible.
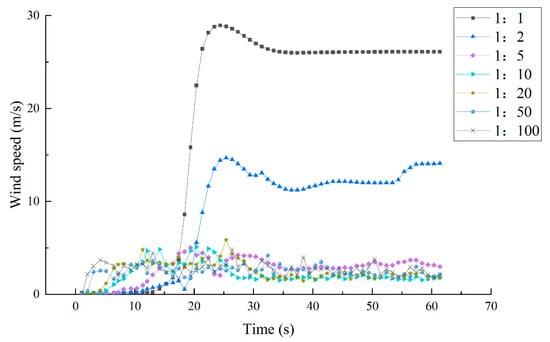
Figure 7.
Change process of atomization wind speed with time under different similarity scales.
Figure 8 shows the change process of the water concentration above the 230 m platform on the left bank under different similar scale conditions with time. The water concentration at this location first increases rapidly and then gradually decreases to a stable trend as the flood discharge progresses. When the similarity scale is less than 1:50, the concentration of water at the 230 m platform on the left bank does not have a decreasing stage. The larger the similarity scale, the greater the maximum value that can be reached by the water concentration above the 230 m platform on the left bank, and the greater the concentration that can be reached in a steady state, the earlier the water concentration at the 230 m platform on the left bank changes.
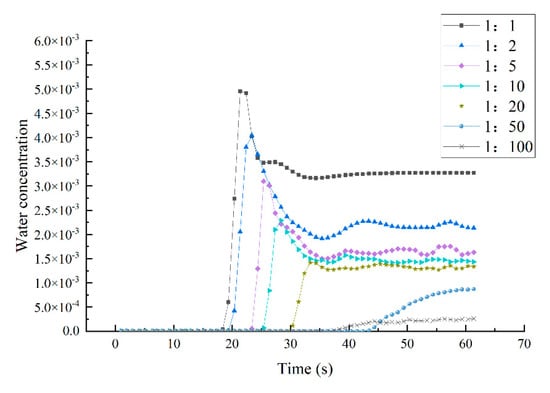
Figure 8.
Water concentration changes with time under different similarity scales.
The atomized rainfall intensity is mainly affected by wind speed and water mist concentration (Figure 9). The variation law of atomized rainfall is similar to that of water mist concentration, which first increases rapidly and then decreases gradually to become stable. The higher the wind speed, the higher the water mist concentration, and the greater the atomization rainfall intensity in this part. When the model scale is less than 1:10, the atomized rainfall intensity measured in the model test is approximately 0. At this time, the rainfall intensity is greatly affected by the surrounding environment, and the accuracy of the results is poor. When the geometric similarity scale of the model is large, the deviation of the predicted prototype rainfall intensity is also large.
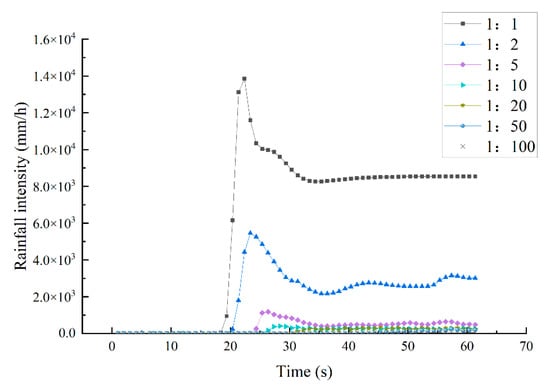
Figure 9.
Change process of atomized rain intensity over time under different similarity scales.
3.3. Influence of Geometric Scale on the FDA Wind Field and Rain Field
In 2016, the Shuibuya Hydropower Station carried out a prototype observation test of FDA [31] in which the discharge flow was 3848 m3/s. The atomization wind speed at 7 measuring points and the atomization rain intensity at 21 effective measuring points were monitored (Figure 10) [22]. Generally, we pay more attention to the maximum value and the influence range of atomized rainfall. Therefore, measuring point #22 with the largest rainfall intensity among all monitoring points (left bank  230 m platform) is selected, and the stable atomization wind speed and rainfall intensity obtained under different geometric scale conditions are plotted in Figure 11 and Figure 12.
230 m platform) is selected, and the stable atomization wind speed and rainfall intensity obtained under different geometric scale conditions are plotted in Figure 11 and Figure 12.

Figure 10.
FDA scene and atomization rain intensity monitoring points of Shuibuya Hydropower Station.
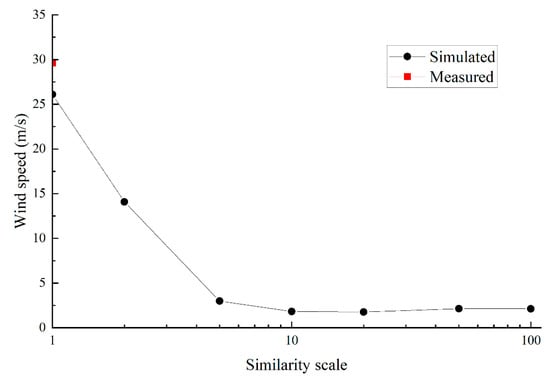
Figure 11.
Stable atomization wind speed under different geometric scale conditions.
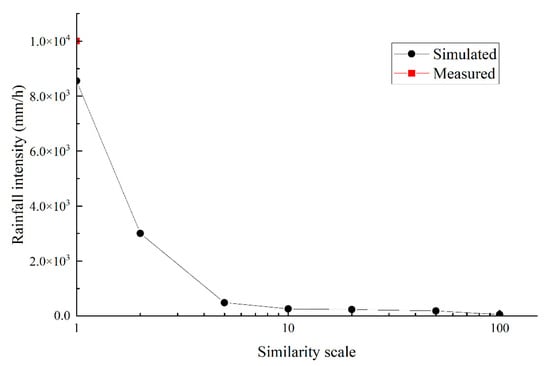
Figure 12.
Intensity of atomized rain at the stable moment under different geometric scale conditions.
Figure 11 shows that the smaller the geometric scale, the smaller the stable atomization wind speed obtained. When the similarity scale is less than 1:10, the stable atomization wind speed calculated by the model tends to be basically stable, which means that the monitoring data at a small scale are very indistinguishable. From another point of view, the smaller the similar scale, the greater the error caused by the test.
The atomized rainfall is affected by the concentration of water mist and the atomization wind speed. The atomized rain intensity at the 230 m platform on the left bank under different geometric scale conditions obtained through the numerical model is shown in Figure 12. Similar to the variation law of atomization wind speed, the larger the geometric scale, the greater the atomization rain intensity calculated by the model. In the prototype test, the maximum rainfall intensity of this part can reach 10,000 mm/h. By comparing with the calculation results of the model with a geometric scale of 1:1, it can be seen that the deviation of the model prediction results is −14.5%. When the 1:1 scale is used to predict the FDA of the Shuibuya Hydropower Station, the maximum deviation between the numerical model calculation results and the prototype observation results can reach 14.5%. There are many reasons for this deviation, including computational boundary conditions, model parameters, and numerical solution methods. Generally, the numerical model can be modified through prototype observation data to improve prediction accuracy. However, it is necessary to carry out indoor model tests under the condition of no construction project and a lack of prototype observation data, which can provide a corresponding basis for the modification of numerical calculation models.
When the reduced scale model is used to predict the FDA wind speed and rainfall, it is necessary to establish the conversion relationship between the model and the prototype. Generally, this relationship can be expressed by an exponential function with a geometric scale as the base. For example, the atomized rain intensity scale can be expressed as a function of the geometric scale , where the value of n is affected by flood discharge hydraulic conditions, flow Weber number, geometric scale, energy dissipation shape, and other factors. Using the atomization wind speed and rainfall intensity at the 230 m platform on the left bank, the relationship between the rain intensity scale , the wind speed scale , and the geometric scale can be obtained, as shown in Table 1.

Table 1.
Conversion coefficient n between the atomized rain intensity and wind speed.
As shown in Table 1, under similar boundary conditions and calculation parameters, by changing only the size of the geometric grid, the index n of the atomization rain intensity scale obtained by simulation is between 1.019 and 1.734, the conversion coefficient of fog–rain intensity is between 3.33 and 179.47, and the smaller the geometric scale, the greater the conversion value of fog–rain intensity. Wu Shiqiang et al. [18] recommended that the atomized rain intensity scale be converted to the 1.53 power of the geometric scale, which can be used as the outer envelope control line of the atomized rain intensity. This value is within the range of the conversion coefficient of the atomized rain intensity scale in Table 1. The index n of the atomization wind speed scale is between 0.572 and 1.43, and there is no detectable monotonic relationship between different geometric scales. The conversion value of atomization wind speed also fluctuates greatly, ranging from 2.1 to 16.81. When the physical model test is used to predict the FDA wind speed and rainfall, the smaller the geometric scale, the larger the rain intensity scale and the wind speed scale, but a larger rain intensity scale causes a larger prediction deviation. Under different combined scale conditions, the prediction deviation of the atomization wind speed and rain intensity at each measurement point is shown in Figure 13.
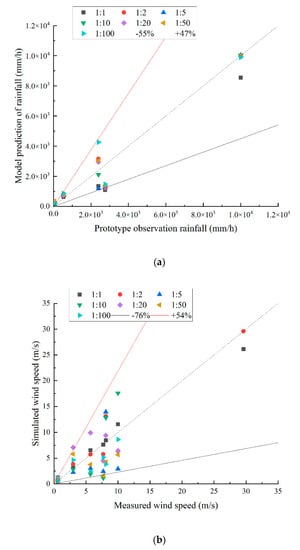
Figure 13.
Comparison of simulated rainfall intensity (a) and wind speed (b) with prototype observations under different geometric scale conditions.
According to Figure 13, when models with different geometric scales are used to predict atomization wind speed and rainfall intensity at different measuring points, the prediction deviations of models with different geometric scales are different for each measuring point of the prototype. Generally, the prediction deviation of the atomization fraction of models with different geometric scales is −76~+54%, while the prediction deviation of atomization rainfall is −55~+47%. When determining the conversion relationship between the model and the prototype, the coefficient n is calculated from the values of the maximum measuring points of wind speed and rainfall. When the conversion relationship is applied to other measuring points, the deviation of the predicted value is large. It should be noted that the monitoring data compared here are the prototype observation data of the Shuibuya Hydropower Station, not the data from the reduced geometric scale model experiment.
3.4. Influence of Atmospheric Pressure on the Model Test
Through the research in Section 3.3, it is found that when the geometric similarity is satisfied, the coefficient n in the conversion relationship between the prototype and the model is solved through the prototype observation data, and then the coefficient is used to predict the atomization wind speed and rainfall intensity of other measurement points. The calculation model with a small geometric scale still causes a large deviation. In fact, the occurrence of atomization during flood discharge depends not only on the turbulence of the water flow itself but also on its ability to eliminate surface tension. The surface tension of water is essentially caused by the imbalance of pressure on the interface, so the atmospheric pressure where the flood discharge is located also has a greater impact on atomization. Liu Haitao (2019) et al. [30] studied the influence of altitude on FDA and reported that as the altitude increases, the area of atomization downstream of the flood discharge tunnel tends to increase. Considering that most physical model tests are carried out under normal temperature and pressure, the atmospheric pressure between the prototype and model does not meet similar conditions. In this section, on the premise that the calculation model meets the gravity similarity, the atmospheric pressure of the model is changed to make the environmental pressure of flood discharge meet similar conditions to explore the impact of atmospheric pressure on FDA. The atmospheric pressure of the calculation model with a geometric scale of 1:1 is standard atmospheric pressure, and the pressure of the other calculation models is reduced on the basis of standard atmospheric pressure according to the geometric scale. The other calculation conditions are the same as those in Section 3.3.
Figure 14 shows the relationship curve between the atomization wind speed and the atomization rain intensity at the 230 m platform on the left bank with different geometric scales and geometric scales under the condition of similar pressure. It can be seen that the smaller the similarity scale, the smaller the atomization wind speed and atomization rainfall calculated by the model. As the geometric scale decreases, the atomization wind speed and rainfall decrease in a power function relationship with the geometric scale as the base. The atomization wind speed calculated by the models of different geometric scales shows a power function relationship with an exponent of 0.529, and the correlation reaches 0.99, while the atomized rainfall obtained by calculation models of different geometric scales presents a power function relationship with an exponent of 0.554, and the correlation can reach approximately 0.97. From the perspective of numerical simulation, when the calculation model meets geometric similarity and atmospheric pressure similarity, the conversion relationship between different geometric scale models is relatively fixed, and the power function index is approximately 0.5, which approximately meets the gravity similarity criterion.
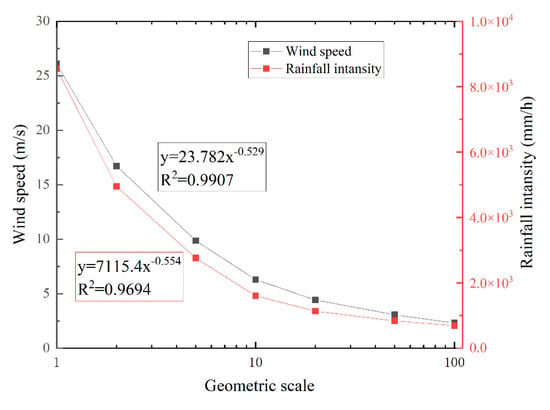
Figure 14.
Model atomization rainfall and atomization wind speed under different geometric scale conditions.
The conversion relationship coefficient n between the model and prototype with different geometric scale values is solved by using the prototype observation values of the maximum atomization wind speed and rainfall measurement points, as shown in Table 2.

Table 2.
Atomization wind speed and rainfall conversion coefficient n under different geometric scale conditions.
According to Table 2, when the models with different geometric scales meet similar pressure conditions, the variation range of the conversion relationship coefficient n between the atomization wind speed and rainfall intensity and the prototype observation results is significantly reduced. The conversion coefficient n obtained in Table 2 is used to predict the atomization wind speed and rainfall intensity at other observation points. The deviation of the prediction results is shown in Figure 15.
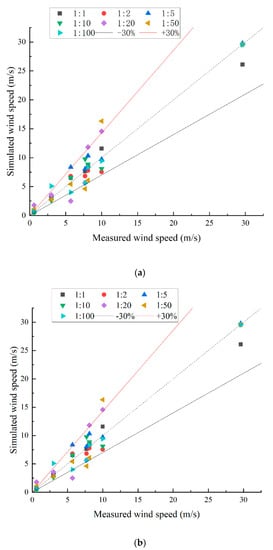
Figure 15.
Comparison of simulated wind speed (a) and rainfall intensity (b) with prototype observations under the condition of similar atmospheric pressure.
Figure 15 shows the comparison between the predicted value of the calculation model of different geometric scales and the observed value of the prototype. Under the condition of similar atmospheric pressure, the deviation between the atomization wind speed obtained by the geometric models with different scales and the measured wind speed is smaller than that of the models that did not meet similar atmospheric pressure, and the deviation between the predicted value of the model and the measured value is ±30%. After considering similar atmospheric pressure conditions, the prediction accuracy of the prototype’s atomization wind speed and rainfall intensity is greatly improved by the calculation model.
4. Discussion and Conclusions
It is important to use a similar model to predict the atomization of flood discharge, but due to the influence of the scale effect between the prototype and the model, the prediction accuracy of this method is limited. Considering that there are many factors affecting FDA, such as model initial conditions, boundary conditions, and atmospheric pressure, the influence of various factors cannot be accurately defined when using physical model tests. In this study, numerical simulation is used to study the effects of geometric scale and atmospheric pressure on FDA wind speed and rainfall under similar boundary conditions. Then, the results calculated by the 1:1 model are verified with the data obtained from the prototype observation. On this basis, the effects of geometric scale, boundary conditions, and atmospheric pressure on FDA are analyzed. Theoretically, a series of small-scale model tests should be used to verify the numerical results, but it is very challenging to ensure that the boundary conditions of the model tests are consistent with the numerical simulation. Moreover, small-scale model tests also have shortcomings, which means that they cannot completely simulate the real FDA process, and are affected by parameter values.
Although there are some shortcomings in the verification of numerical calculation results, they do not affect our ability to find the influence of the scale effect on flood discharge atomization through numerical simulation. The research shows that the geometric scale is the main factor affecting FDA in FDA model tests. The smaller the geometric scale, the smaller the stable atomization wind speed and rainfall intensity simulated by the model. When models with different geometric scales are used to predict the FDA wind speed and rain intensity, the prediction deviation is between −76% and +54%. The transformation relationship between the predicted value and the calculated value of the model is usually an exponential function relationship with the geometric scale at the bottom. The smaller the geometric scale, the larger the corresponding rain intensity scale and wind speed scale. Therefore, a smaller model calculation error also causes a greater prediction deviation. When the atmospheric pressure similarity is considered in the numerical calculation model, the deviation of atomization wind speed and rain intensity predicted by different geometric scales can be controlled within ±30%. Under the condition of pressure similarity, the prediction accuracy of the model can be greatly improved.
Author Contributions
Conceptualization, G.L.; methodology, G.L.; validation, J.L.; formal analysis, J.L.; writing—original draft, G.L.; supervision, F.T. and B.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Hubei Key Laboratory of Construction and Management in Hydropower Engineering (2020KSD11) and the National Natural Science Foundation of China (Grant No. 51939004).
Data Availability Statement
The data associated in this publication is totally presented in this paper. No data is present in any other repository anywhere.
Conflicts of Interest
The authors declare that there are no conflict of interest.
References
- Lian, J.; Liu, D.; Liu, F. Research progress and frontiers on flood discharge atomization of Chinese high dam projects. J. Hydraul. Eng. 2019, 50, 283–293. [Google Scholar]
- Wang, S.; Wang, C.; Chen, D. Advances in Research on Flood Discharge Atomization. J. Yangtze River Sci. Res. Inst. 2013, 30, 53–58, 63. [Google Scholar]
- Yang, C.; Wu, S.; Liu, S. Prototype observation of discharge atomization at Baozhusi Hydropower Station. Water Resour. Hydropower Eng. 2007, 38, 69–73. [Google Scholar]
- Wu, X.; Wu, S.; Zhou, H. Atomization measurement for Wantang Hydroplant. Hydro-Sci. Eng. 2001, 4, 71–74. [Google Scholar]
- Liu, J.; Han, S.; Kong, D. Prototype observation and model test study on flood discharging atomization. Water Resour. Hydropower Northeast China 2002, 2, 41–45+56. [Google Scholar]
- Chen, D.; Jin, F.; Zhang, H. Physical model test for flood discharge atomization of Goupitan Hydropower Project. Hubei Water Power 2007, 3, 48–51. [Google Scholar]
- Huang, G.; Wu, S.; Chen, H. Model test studies of atomized flow for high dams. Hydro-Sci. Eng. 2008, 4, 91–94. [Google Scholar]
- Kehua, Y.; Bo, X.; Jingxue, Q. Experimental study on flood discharge atomization model. Sichuan Water Resour. 2007, 3, 19–22. [Google Scholar]
- He, G. Research of Flood Discharge Atomization Numerical Simulation Based on the WRF Model and SPH. Master’s Thesis, North China Electric Power University, Beijing, China, 2017. [Google Scholar]
- Shen, W.; Shi, M.; Xu, S. Research on flood discharge atomization rain prediction based on genetic neural network. China Water Transp. Second. Half Mon. 2015, 15, 155–157. [Google Scholar]
- Zhang, H.; Lian, J. Prediction of rain intensity distribution of flood discharge atomization by using water droplet random splash mathematical model. J. China Three Gorges Univ. Nat. Sci. Ed. 2004, 3, 210–213. [Google Scholar]
- Liu, G.; Tong, F.; Tian, B. Finite element analysis on the flood discharge atomization of Shuibuya hydropower station based on water-air two-phase flow. J. Chongqing Univ. 2020, 43, 90–102. [Google Scholar]
- Zhou, H.; Wu, S.; Chen, H. Discussion on the scale effect of discharge atomization-rainfall model. Adv. Water Sci. 2009, 20, 58–62. [Google Scholar]
- Xu, W. Mesoscale Analysis of Flood Discharge Atomization. In Mesoscale Analysis of Hydraulics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 179–217. [Google Scholar] [CrossRef]
- Lian, J.; Zhang, S.; He, J. An improved numerical model of ski-jump flood discharge atomization. J. Mt. Sci. 2022, 19, 1263–1273. [Google Scholar] [CrossRef]
- Lian, J.; Li, C.; Liu, F.; Wu, S. A prediction method of flood discharge atomization for high dams. J. Hydraul. Res. 2014, 52, 274–282. [Google Scholar] [CrossRef]
- Yu, K.; Han, C.; Han, K. A study of similarity scale classification for flood discharge-induced atomized rainfall model. Hydro-Sci. Eng. 2020, 2, 58–65. [Google Scholar]
- Wu, S.; Wu, X.; Zhou, H.; Chen, H.; Sha, H.; Zhou, J. Analysis and application of the scale effect of flood discharge atomization model. Sci. China 2011, 54, 64–71. [Google Scholar] [CrossRef]
- Han, C.; Wang, X.; Shi, S. Principles of similarity in the hydraulic models. China Water Transp. (Acad. Ed.) 2006, 10, 67–70. [Google Scholar]
- Zhou, H.; Wu, S.; Chen, H. Similarity criterion of flood discharge atomization. Water Sci. Eng. 2008, 1, 59–65. [Google Scholar]
- Ministry of Water Resources. SL155-2012 Hydraulic (Conventional) Model Test Specification; Ministry of Water Resources: Beijing, China, 2012.
- Liu, G.; Tong, F.; Tian, B.; Gong, J. Finite element analysis of flood discharge atomization based on water-air two-phase flow. Appl. Math. Model. 2020, 81, 473–486. [Google Scholar] [CrossRef]
- Chahed, J.; Roig, V.; Masbernat, L. Eulerian—Eulerian two-fluid model for turbulent gas-liquid bubbly flows. Int. J. Multiph. Flow. 2003, 29, 23–49. [Google Scholar] [CrossRef]
- Liu, H.; Sun, S.; Liu, Z. Mathematical model for rain-fog transportation during flood discharge and its verification. Adv. Sci. Technol. Water Resour. 2011, 31, 45–48. [Google Scholar]
- Li, J.; Ran, C.; He, L. Treatment design of accumulation body in atomization area of Flood discharge of Zhuangyan Hydropower Station. Yangtze River 2014, 45, 51–54. [Google Scholar]
- Liu, G. Research on Numerical Calculation of Flood Discharge Atomization of High Dam Based on Water-Air Two Phase Flow. Ph.D. Thesis, China Three Gorges University, Yichang, China, 2020. [Google Scholar]
- Ransom, V.H. Faucet flow. Numer. Benchmark Tests 1987, 3, 465–467. [Google Scholar]
- Wang, Z.; Zou, G.; Gong, J.; Bai, J.; Zhai, B. A pressure-based algorithm for numerical simulation of one-dimensional two-phase flow. Chin. J. Comput. Phys. 2019, 36, 413–420. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, H.; Wu, S. Effects of flaring gate pier on energy dissipation and atomization caused by flow through the flood discharge facility. J. Hydroelectr. Eng. 2008, 27, 58–63. [Google Scholar]
- Liu, H.; Xu, J.; Sun, S.; Peng, Y. Sensitive analysis of the effect of elevation on flood discharge atomization. J. Hydraul. Eng. 2019, 50, 1365–1373. [Google Scholar] [CrossRef]
- CRSRI. Hydraulic Prototype Observation Report of the Spillway of Shuibuya Hydropower Station in 2016; CRSRI: Yichang, China, 2016. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).