A Combined Noise Reduction Method for Floodgate Vibration Signals Based on Adaptive Singular Value Decomposition and Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise
Abstract
:1. Introduction
2. Basic Principles
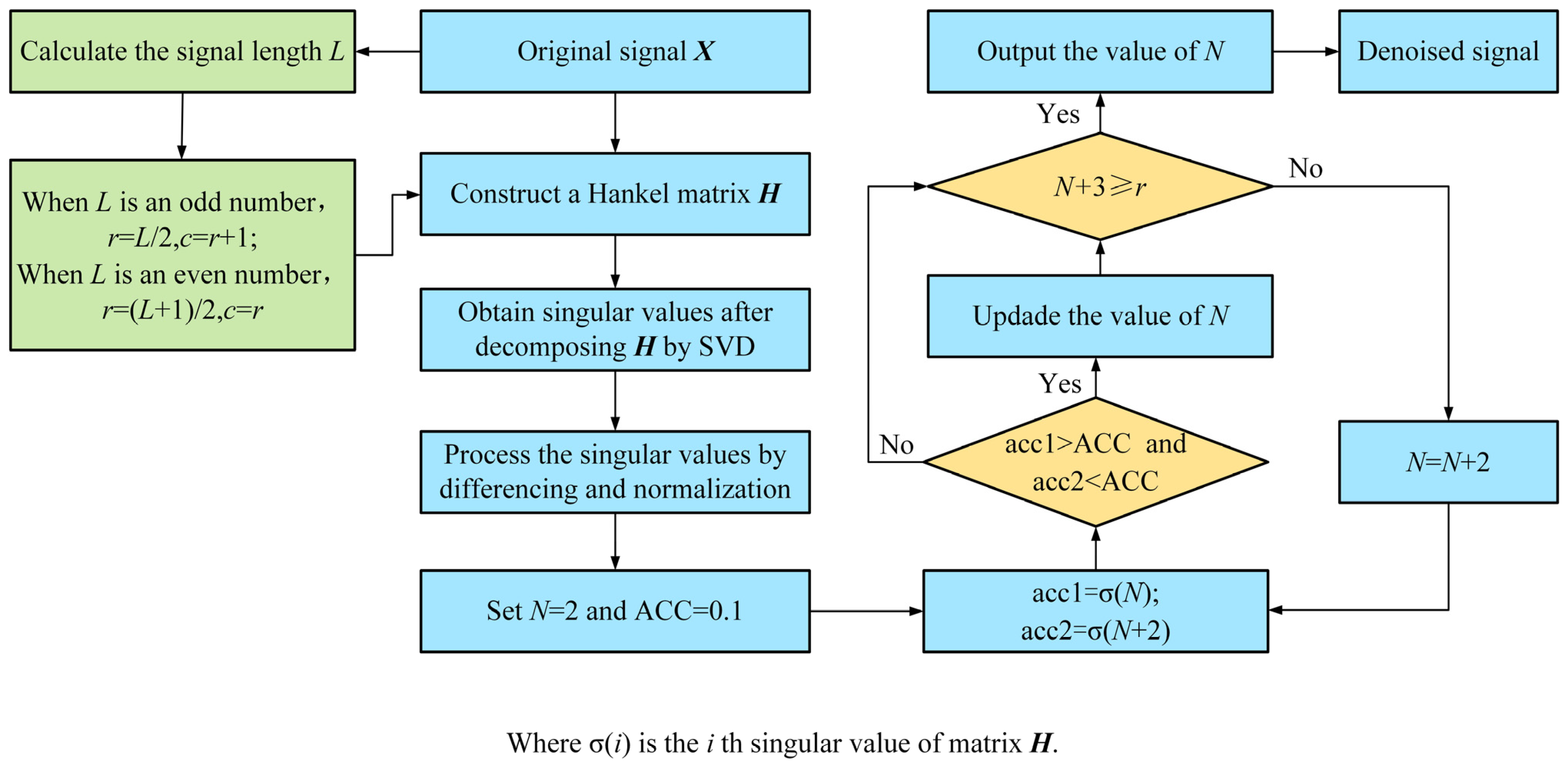
2.1. ASVD Noise Reduction
- (1)
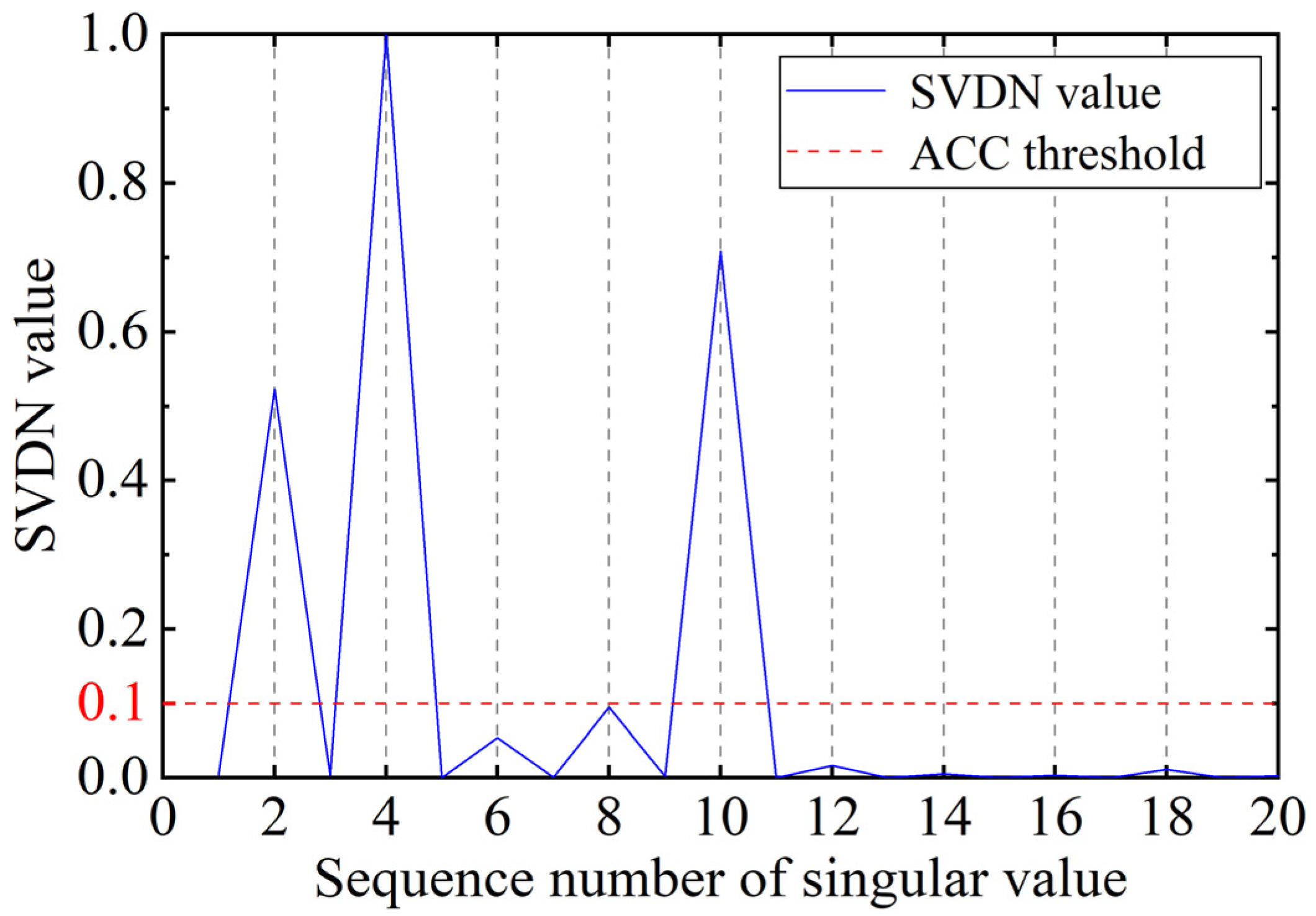
- Each frequency component of the signal relates to a singular value group consisting of two adjacent singular values that have small differences between them.
- (2)
- Due to significant energy differences between different frequency components of the signal, a jump phenomenon is observed between adjacent groups of ESVs.
- (3)
- The energy of white noise is uniformly distributed in the broadband frequency domain, which makes the jump phenomenon of singular value inconspicuous.
2.2. ICEEMDAN Method
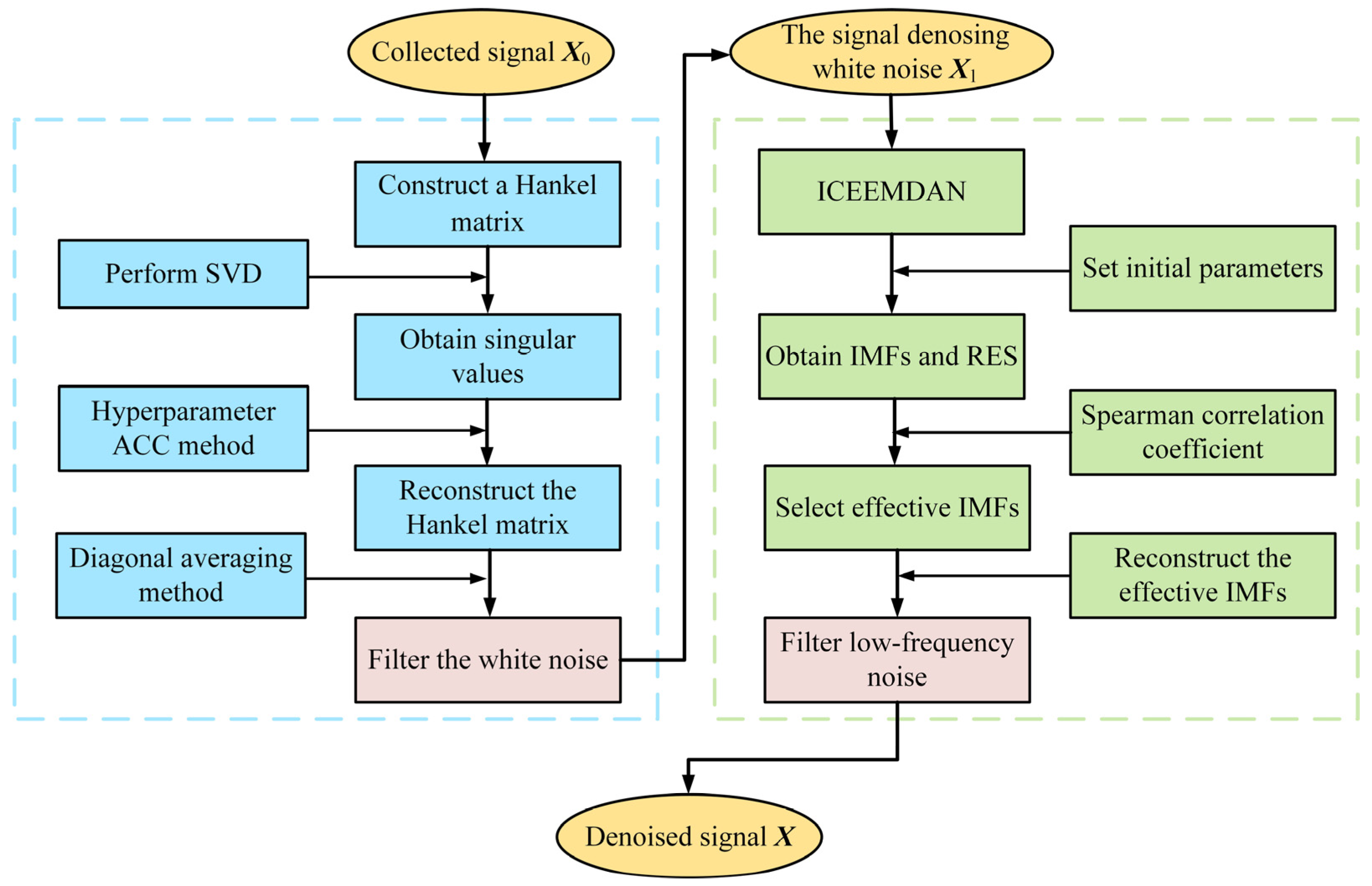
2.3. Combined ASVD–ICEEMDAN Noise Reduction
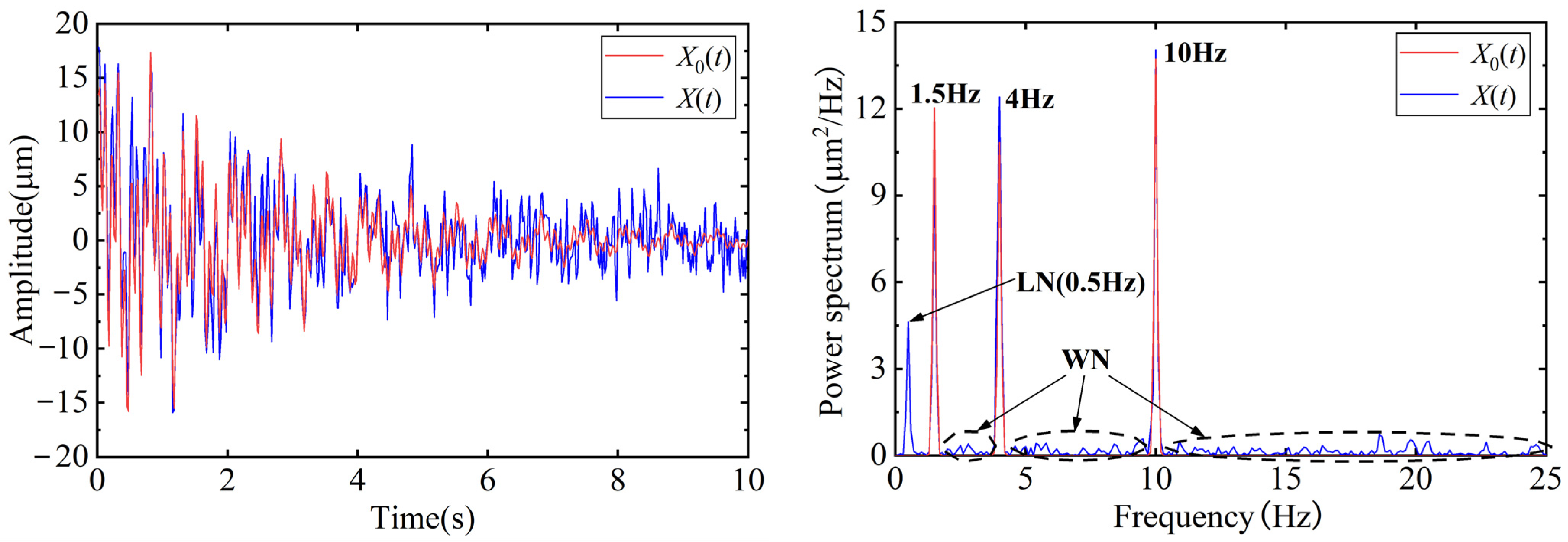
3. Numerical Simulation
4. Engineering Example
5. Conclusions
- (1)
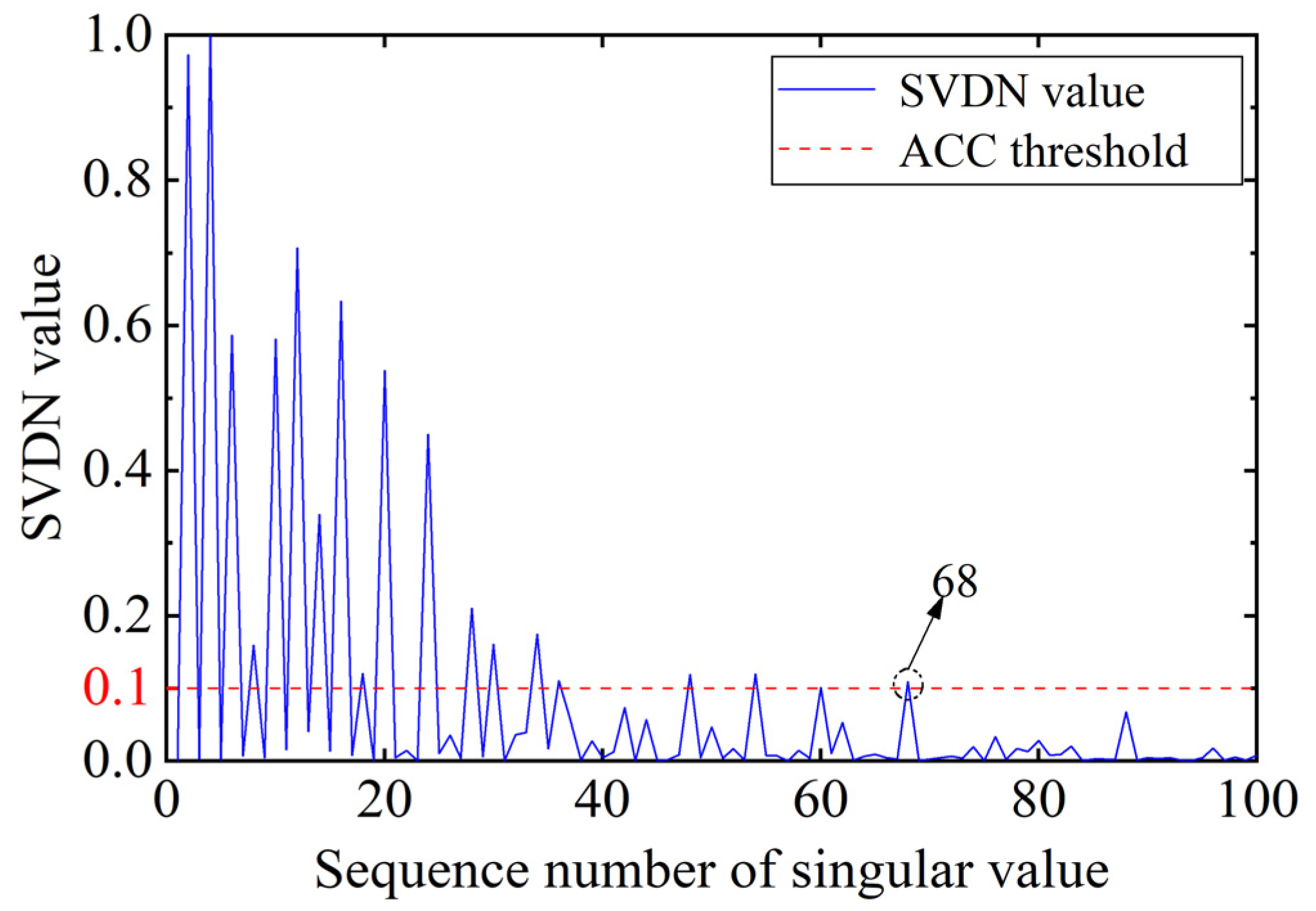
- An ASVD method is proposed to select effective singular values automatically based on the relationship between singular values and signal components. It avoids the uncertainty of manual selection and improves the efficiency of noise reduction.
- (2)
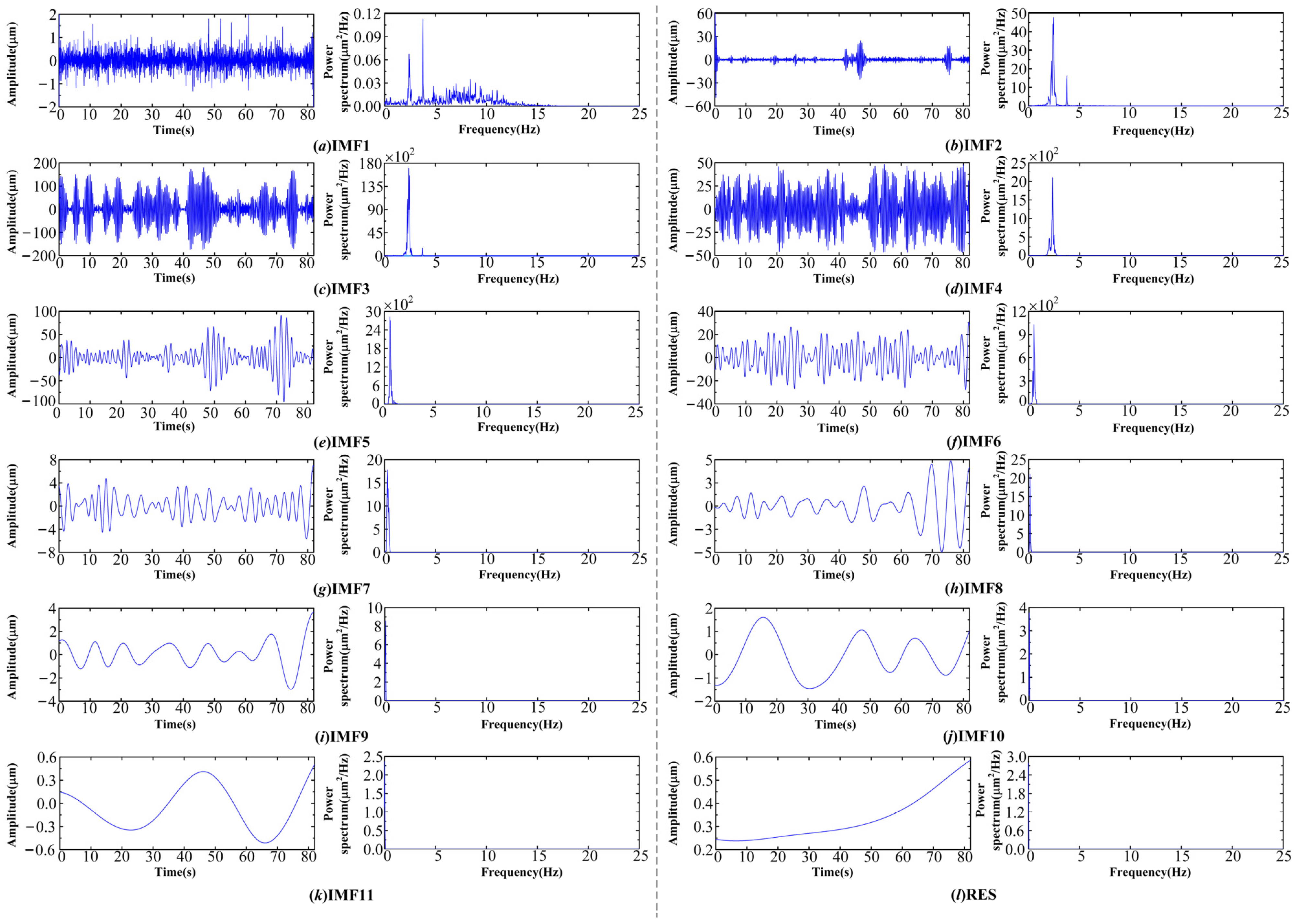
- The ICEEMDAN algorithm can automatically decompose the signal into several IMF components whose center frequencies are arranged from high to low. Compared to the CEEMDAN algorithm, ICEEMDAN algorithm performs better in terms of suppressing mode mixing and reducing residual noise.
- (3)
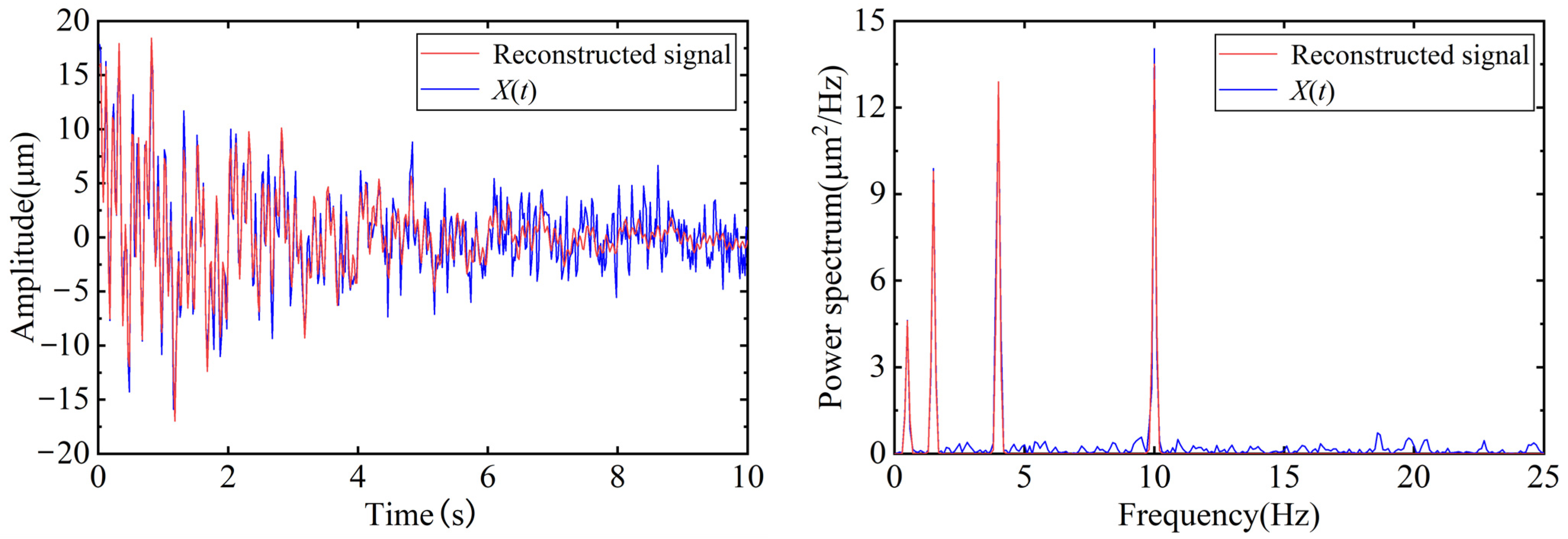
- The ASVD–ICEEMDAN method successfully filters out white noise and low-frequency noise in simulated signals, which increases the SNR of the signal (50% noise level) from 4.417 to 16.237 and reduces the RMSE from 2.286 to 0.586. In the engineering case study, the ASVD–ICEEMDAN method effectively filters out the noise and accurately extracts the structural characteristic vibration information, proving it can provide support in operational modal analyses and damage identification in actual structures.
- (4)
- Vibration signals of discharge structures are mainly affected by white noise and low-frequency noise; thus, this method has the potential to be extended to other hydraulic structures under discharge excitation, such as arch dams, gravity dams, and guide walls.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, H.K.; Zhong, Y.W.; Wei, B.W.; Du, L.; Wang, G. Beat vibration mechanism of a sluice pier under high-speed flood discharge excitation. J. Low Freq. Noise. Vib. Act. Control 2020, 39, 28–43. [Google Scholar] [CrossRef]
- Li, H.K.; Liu, B.; Huang, W.; Liu, H.Y.; Wang, G. Vibration load identification in the time-domain of high arch dam under discharge excitation based on hybrid LSQR algorithm. Mech. Syst. Signal Process. 2022, 177, 109193. [Google Scholar] [CrossRef]
- Liu, B.; Li, H.K.; Wang, G.; Wu, P.Z.; Li, Y.K. Dynamic material parameter inversion of high arch dam under discharge excitation based on the modal parameters and Bayesian optimised deep learning. Adv. Eng. Inform. 2023, 56, 102016. [Google Scholar] [CrossRef]
- Li, H.K.; Wang, G.; Wei, B.W.; Liu, H.Y.; Huang, W. Improved variational mode decomposition method for vibration signal processing of flood discharge structure. J. Vib. Control 2022, 28, 2556–2569. [Google Scholar] [CrossRef]
- Zhang, Y.; Lian, J.J.; Liu, F. An improved filtering method based on EEMD and wavelet-threshold for modal parameter identification of hydraulic structure. Mech. Syst. Signal Process. 2016, 68, 316–329. [Google Scholar] [CrossRef]
- Zhang, J.W.; Jiang, Q.; Zhao, Y.; Zhu, L.H.; Guo, J. De-noising method for vibration signal of flood discharge structure. J. Vib. Shock 2015, 34, 179–184. [Google Scholar]
- Yang, X.; Wang, W. Chaotic signal denoising based on energy selection TQWT and adaptive SVD. Sci. Rep. 2023, 13, 18873. [Google Scholar] [CrossRef]
- Bi, L.; Yu, X.; Jiang, D.R.; Peng, H.L.; Hu, F.; Shi, K.K.; Liang, K.; Ye, X. Denoising Method of Hydro-turbine Vibration Signal Based on Joint WOA-VMD and Improved Wavelet Threshold. In Journal of Physics: Conference Series; IOP Publishing Ltd.: Bristol, UK, 2023; Volume 2607, p. 012005. [Google Scholar]
- Fattorini, M.; Brandini, C. Observation strategies based on singular value decomposition for ocean analysis and forecast. Water 2020, 12, 3445. [Google Scholar] [CrossRef]
- Zhao, S.X.; Ma, L.S.; Xu, L.Y.; Liu, M.N.; Chen, X.L. A Study of Fault Signal Noise Reduction Based on Improved CEEMDAN-SVD. Appl. Sci. 2023, 13, 10713. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Nie, Z.G.; Ye, B.Y.; Chen, T.J. Number law of effective singular values of signal and its application to feature extraction. J. Vib. Eng. 2016, 29, 532–541. [Google Scholar]
- Koppolu, P.K.; Chemmangat, K. Automatic Selection of IMFs to Denoise the sEMG Signals using EMD. J. Electromyogr. Kinesiol. 2023, 73, 102834. [Google Scholar] [CrossRef]
- Wang, C.G.; Cui, Y.C.; Liu, Y.; Li, K.; Shen, C. High-G MEMS Accelerometer Calibration Denoising Method Based on EMD and Time-Frequency Peak Filtering. Micromachines 2023, 14, 970. [Google Scholar] [CrossRef] [PubMed]
- Chu, T.Y.; Huang, W.C. Application of empirical mode decomposition method to synthesize flow data: A case study of Hushan Reservoir in Taiwan. Water 2020, 12, 927. [Google Scholar] [CrossRef]
- Singh, J.; Darpe, A.K.; Singh, S.P. Bearing damage assessment using Jensen-Rényi Divergence based on EEMD. Mech. Syst. Signal Process. 2017, 87, 307–339. [Google Scholar] [CrossRef]
- Ameri, R.; Hsu, C.C.; Band, S.S.; Zamani, M.; Shu, C.M.; Khorsandroo, S. Forecasting PM 2.5 concentration based on integrating of CEEMDAN decomposition method with SVM and LSTM. Ecotoxicol. Environ. Saf. 2023, 266, 115572. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, X.M.; Huang, Q.; Wu, L. Study on suppression of EMD endpoint effect of blasting seismic wave signal. Eng. Blasting 2023, 29, 138–143. [Google Scholar]
- Zhang, S.H.; Gao, W.X.; Liu, J.C.; Li, X.S.; Hu, Y.; Zhang, X.J. Extraction and analysis of principal components of blasting vibration signal based on EMD decomposition. Eng. Blasting 2022, 28, 8–14. [Google Scholar]
- Zheng, J.D.; Cheng, J.S.; Yang, Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing. Signal Process. 2014, 96, 362–374. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Li, X.J.; Wang, K.; Wang, G.B.; Li, Q. Denoising of the Base Vibration Signal based on EEMD. Appl. Mech. Mater. 2012, 143, 689–693. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Peng, Y.X.; Liu, Y.S.; Zhang, C.; Wu, L. A novel denoising model of underwater drilling and blasting vibration signal based on CEEMDAN. Arab. J. Sci. Eng. 2021, 46, 4857–4865. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Yuan, C.Q.; Hu, Z.W.; Liu, Y.; He, S.Y.; Du, J.S. Application of ICEEMDAN to noise reduction of near-seafloor geomagnetic field survey data. J. Appl. Geophys. 2023, 209, 104933. [Google Scholar] [CrossRef]
- Zhang, J.W.; Hou, G.; Bao, Z.L.; Zhang, Y.N.; Ma, Y. A signal de-noising method for vibration signals from flood discharge structures based on CEEMDAN and SVD. J. Vib. Shock 2017, 36, 138–143. [Google Scholar]
- Zhang, J.W.; Jiang, Q.; Ma, B.; Zhao, Y.; Zhu, L.H. Signal de-noising method for vibration signal of flood discharge structure based on combined wavelet and EMD. J. Vib. Control 2017, 23, 2401–2417. [Google Scholar] [CrossRef]
- Li, H.K.; Wu, P.Z.; Huang, W.; Liu, H.Y. Joint noise reduction method of hydraulic structure vibration signals based on CEEMDAN and improvedwavelet threshold. J. Nanchang Univ. (Eng. Technol.) 2022, 44, 1–8. [Google Scholar]
- Lv, Y.L.; Lang, R.L.; Liang, J.C. Decision of threshold for singular value decomposition filter based on SNR’s empirical value. Appl. Res. Comput. 2009, 26, 3253–3255. [Google Scholar]
- Zhang, Y.; Xing, P.F.; Wang, M.J.; Zhou, Y.N.; Zhou, X.D.; Wei, Y.W. Pipeline Signal Complementary Denoising Method Based on GAHE-VMD and SVD-SCEC. Noise Vib. Control 2023, 43, 122–129. [Google Scholar]
- Wang, Q.H.; Wang, L.J.; Yu, H.T.; Wang, D.; Nandi, A.K. Utilizing SVD and VMD for denoising non-stationary signals of roller bearings. Sensors 2021, 22, 195. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Li, S. Selection of the number of effective singular values for noise reduction. Mech. Syst. Signal Process. 2023, 191, 110175. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, K.W.; Zhao, H.; Shi, W.W. Snow depth retrieval using GPS signal-to-noise ratio data based on improved complete ensemble empirical mode decomposition. GPS Solut. 2023, 27, 201. [Google Scholar] [CrossRef]
- Gao, Y.; Hang, Y.; Yang, M. A cooling load prediction method using improved CEEMDAN and Markov Chains correction. J. Build. Eng. 2021, 42, 103041. [Google Scholar] [CrossRef]
- Luo, C.L.; Liu, Q.H.; Li, W.G. EWT-SSA joint denoising and its application in the analysis of hob vibration signal. China Meas. Test 2022, 48, 109–116. [Google Scholar]
- Lian, J.J.; Li, H.K.; Zhang, J.W. ERA modal identification method for hydraulic structures based on order determination and noise reduction of singular entropy. Sci. China Ser. E Technol. Sci. 2009, 52, 400–412. [Google Scholar] [CrossRef]
- Guo, Y.J.; You, Z.Z.; Wei, B.W. Working Mode Identification Method for High Arch Dam Discharge Structure Based on Improved Wavelet Threshold–EMD and RDT Algorithm. Water 2022, 14, 3735. [Google Scholar] [CrossRef]


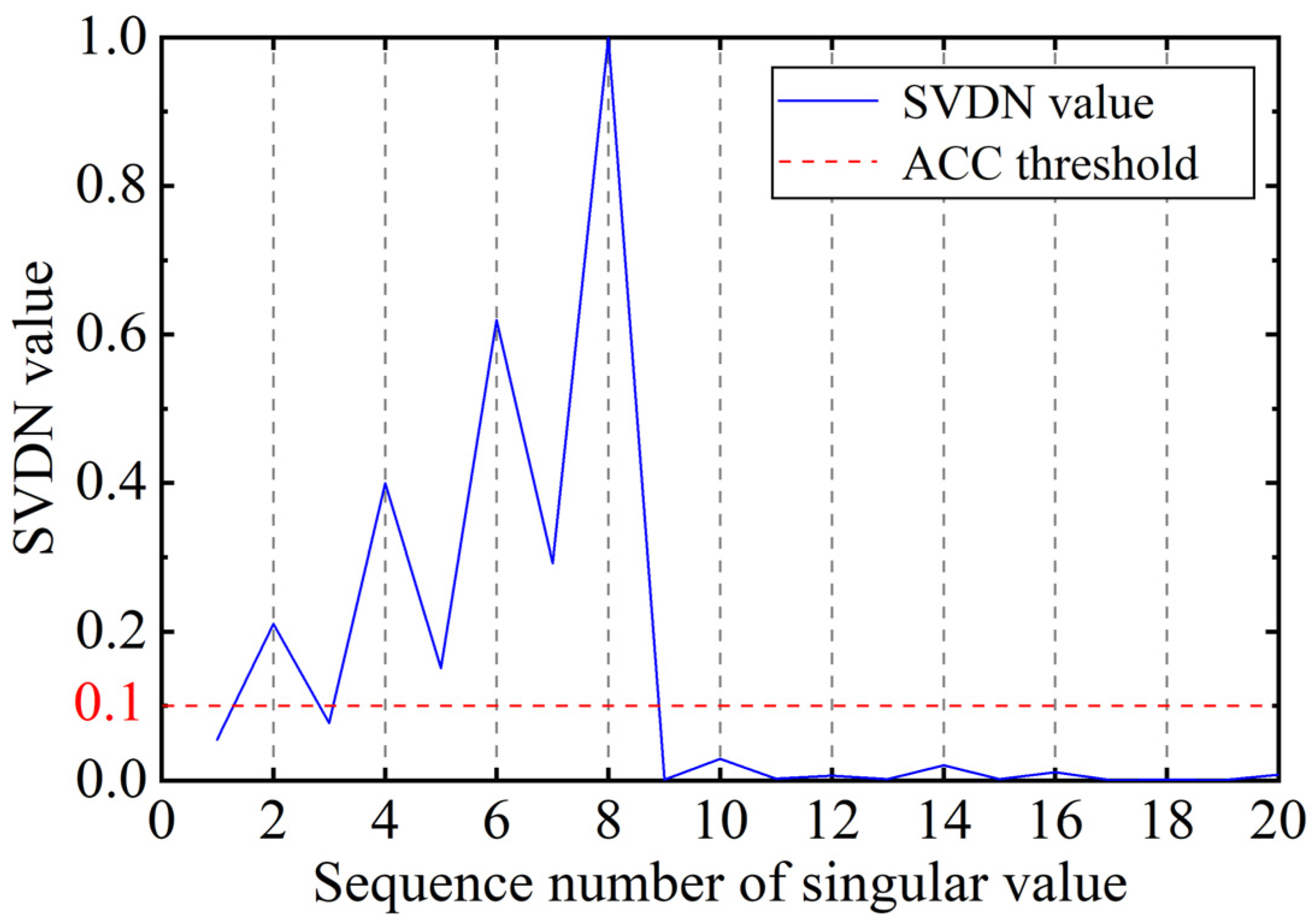





| Sequence Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Singular value | 332.520 | 327.151 | 306.594 | 299.108 | 260.133 | 245.444 | 185.043 | 156.517 | 58.924 | 58.764 |
| SVDN value | 0.055 | 0.211 | 0.077 | 0.399 | 0.151 | 0.619 | 0.292 | 1.000 | 0.002 | 0.029 |
| Sequence number | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Singular value | 55.940 | 55.672 | 55.038 | 54.870 | 52.886 | 52.711 | 51.616 | 51.524 | 51.410 | 51.344 |
| SVDN value | 0.003 | 0.006 | 0.002 | 0.020 | 0.002 | 0.011 | 0.001 | 0.001 | 0.001 | 0.008 |
| IMF Component | IMF Component | ||
|---|---|---|---|
| IMF1 | 0.536 | IMF5 | 0.397 |
| IMF2 | 0.578 | IMF6 | 0.303 |
| IMF3 | 0.498 | IMF7 | 0.094 |
| IMF4 | 0.458 | RES | 0.076 |
| Noise Reduction Method | Index | |
|---|---|---|
| SNR/dB | RMSE | |
| Original signal | 4.417 | 2.286 |
| Moving average | 5.414 | 2.038 |
| IIR digital filters | 5.544 | 2.008 |
| ASVD | 9.387 | 1.290 |
| ICEEMDAN | 5.711 | 1.969 |
| ASVD-CEEMDAN | 16.104 | 0.595 |
| ASVD–ICEEMDAN | 16.237 | 0.586 |
| Sensor Number | Model | Range of Frequency Response | Sensitivity |
|---|---|---|---|
| 1~10 | DPS-0.5-15-H | 0.5~200 Hz | 5 mv/μm |
| Working Condition | Order | Suggested Method/Hz | ERA/Hz | Relative Error */% |
|---|---|---|---|---|
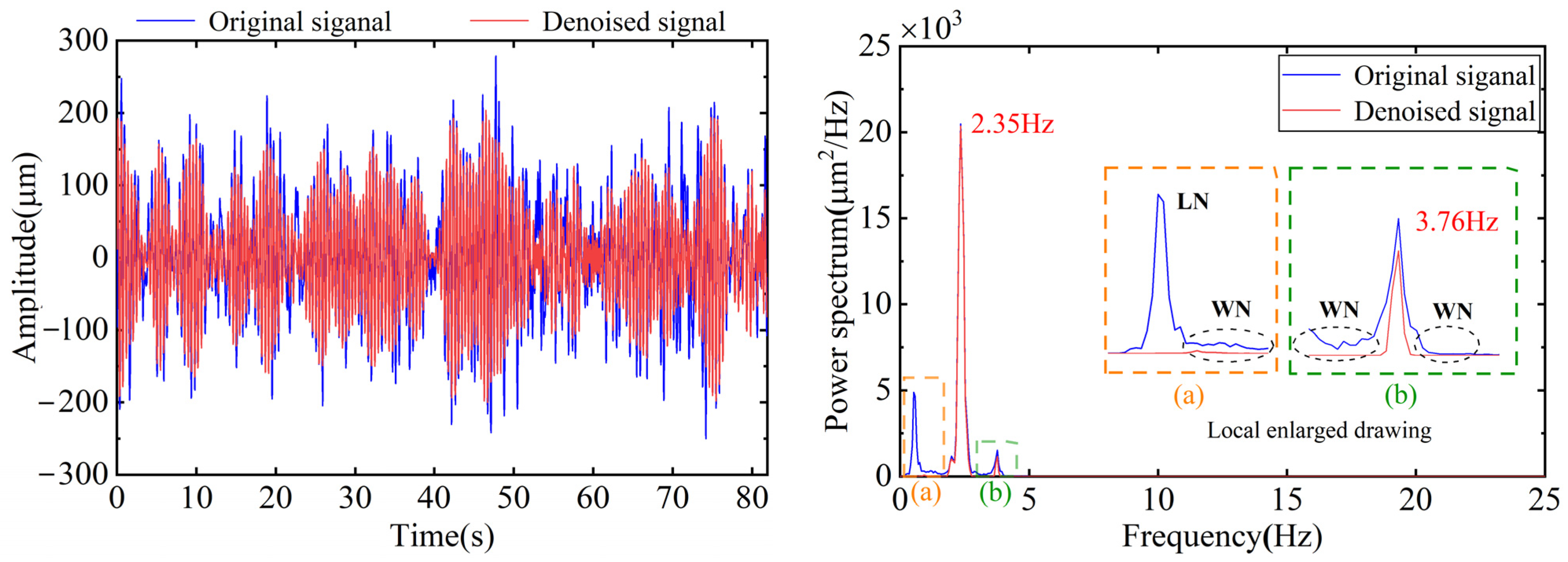
| Condition 1 | 1 | 2.35 | 2.39 | 1.67 |
| 2 | 3.76 | 3.77 | 0.27 | |
| Condition 2 | 1 | 2.47 | 2.43 | 1.65 |
| 2 | 3.82 | 3.82 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Zhu, H.; Cheng, Y.; Tang, Y.; Liu, B.; Li, H.; Yang, F.; Zhang, W.; Huang, W.; Zheng, F. A Combined Noise Reduction Method for Floodgate Vibration Signals Based on Adaptive Singular Value Decomposition and Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. Water 2023, 15, 4287. https://doi.org/10.3390/w15244287
Wang W, Zhu H, Cheng Y, Tang Y, Liu B, Li H, Yang F, Zhang W, Huang W, Zheng F. A Combined Noise Reduction Method for Floodgate Vibration Signals Based on Adaptive Singular Value Decomposition and Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. Water. 2023; 15(24):4287. https://doi.org/10.3390/w15244287
Chicago/Turabian StyleWang, Wentao, Huiqi Zhu, Yingxin Cheng, Yiyuan Tang, Bo Liu, Huokun Li, Fan Yang, Wenyuan Zhang, Wei Huang, and Fang Zheng. 2023. "A Combined Noise Reduction Method for Floodgate Vibration Signals Based on Adaptive Singular Value Decomposition and Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise" Water 15, no. 24: 4287. https://doi.org/10.3390/w15244287





