Parametric Mathematical Model of the Electrochemical Degradation of 2-Chlorophenol in a Flow-by Reactor under Batch Recirculation Mode
Abstract
:1. Introduction
| Process | Reactor Configuration | Environmental Conditions | Solution Via | Ref. |
|---|---|---|---|---|
| Electrooxidation of 2-CP | 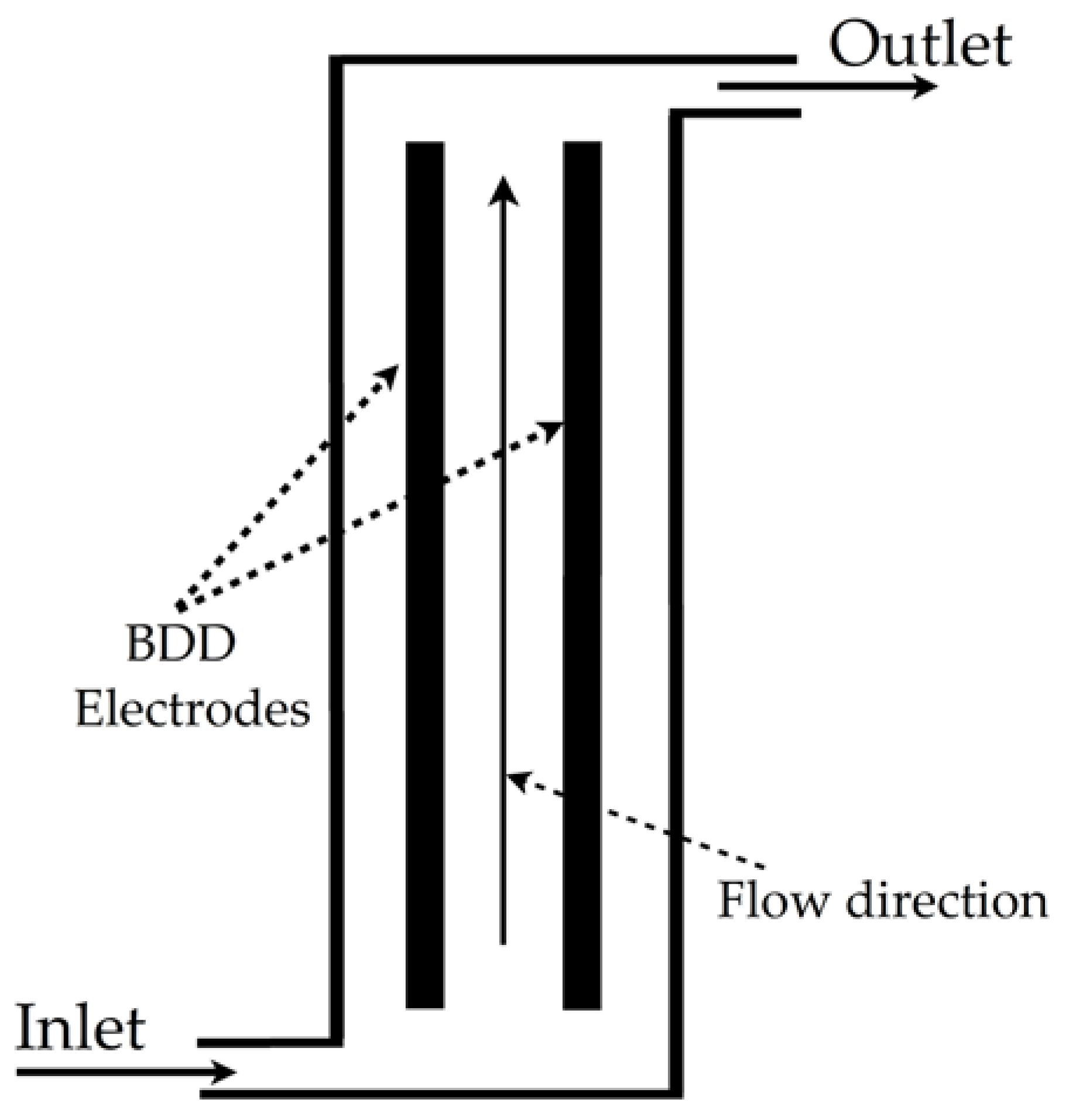 | Hydroxyl radicals, volumetric flow rate of 1.0 L/min, pH of 3, volume treated of 2.5 L, current density of 140 mA/cm2, 0.1 mol/L of Na2SO4, Dax of 0.0005 m2/s, temperature of 25 °C | Software COMSOL Multiphysics® 5.3/Win64 interacting with the software MATLAB® 2017a | [18] |
| Electrochemical oxidation of crystal violet dye | 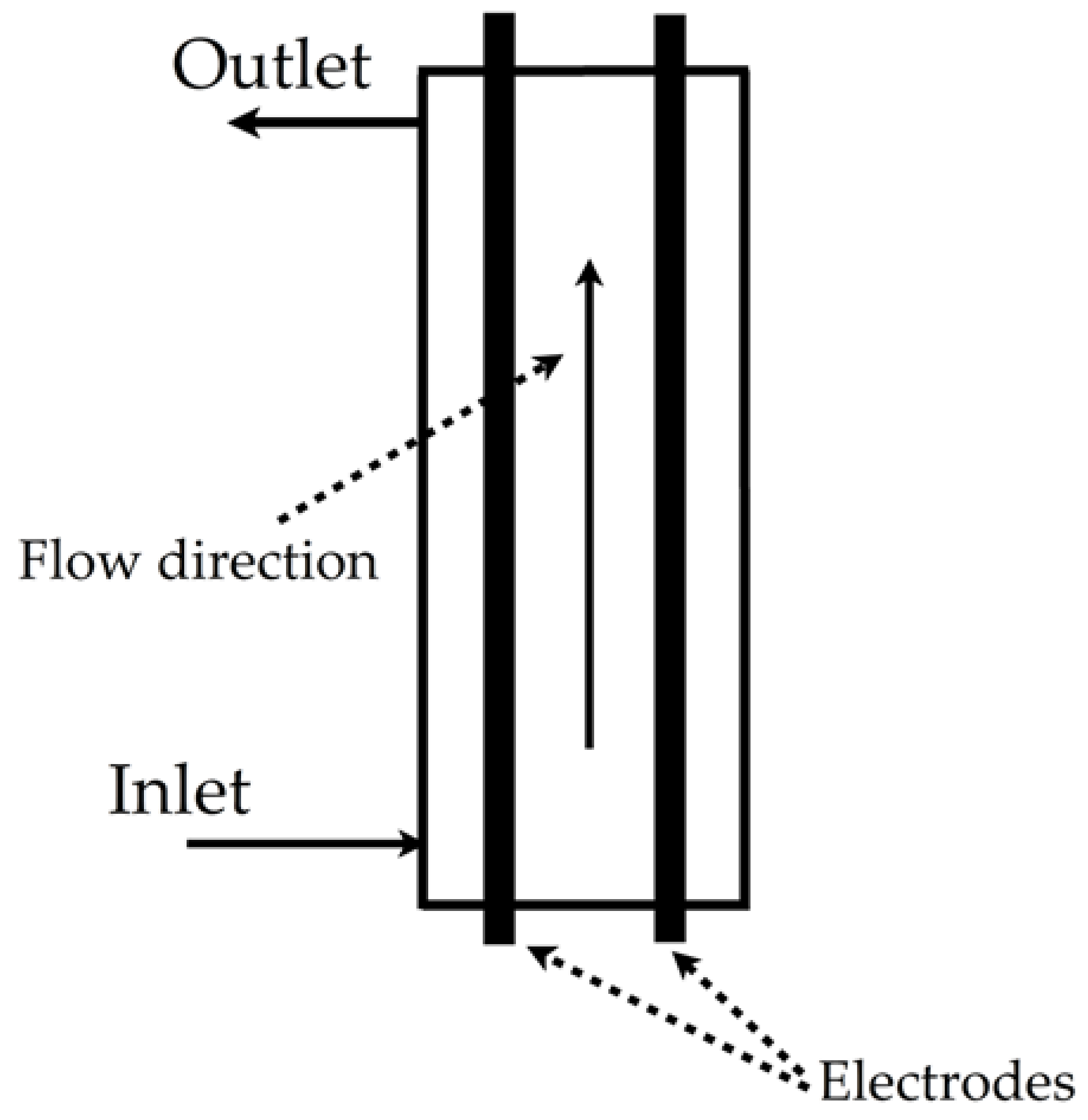 | Hydroxyl radical, pH of 6.4, currents density of 10 mA/cm2, 0.25 mol/L of Na2SO4, Dax of 0.00042 m2/s, volumetric flow rate of 3 L/min, temperature of 25 °C | Software FlexPDE academic version 6.36/W32 | [22] |
| Electro-peroxone degradation of orange reactive 16-dye | 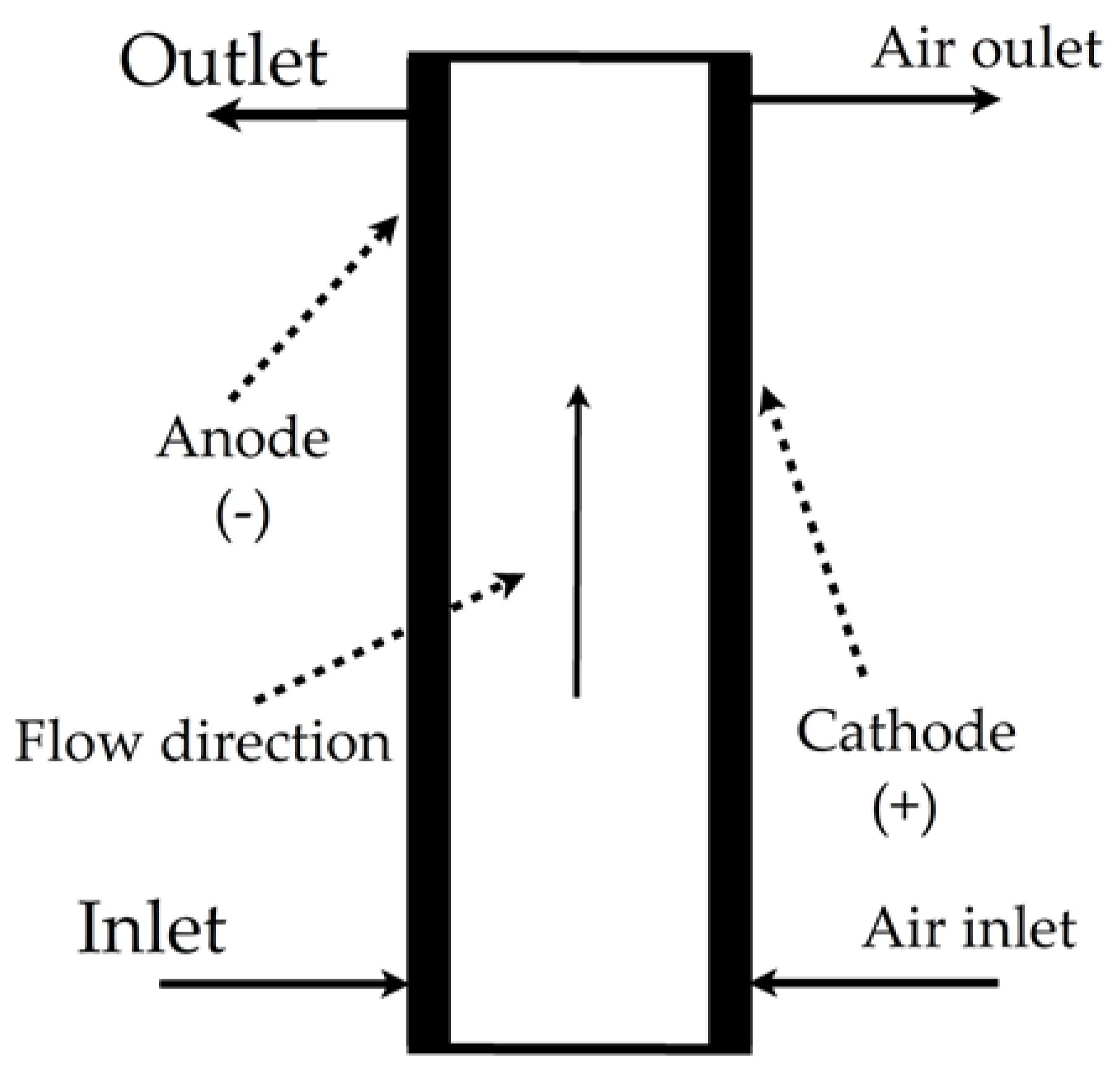 | Hydrogen peroxide, pH of 3, volumetric flow rate of 1.135 L/min, Dax of 0.00153 m2/s, volume treated of 2 L, current density of 10 mA/cm2, 0.05 mol/L of Na2SO4, and 0.5 L/min of O3, temperature of 25 °C | Software COMSOL Multiphysics® 5.3/Win64 | [20] |
| Sulfamethoxazole degradation | 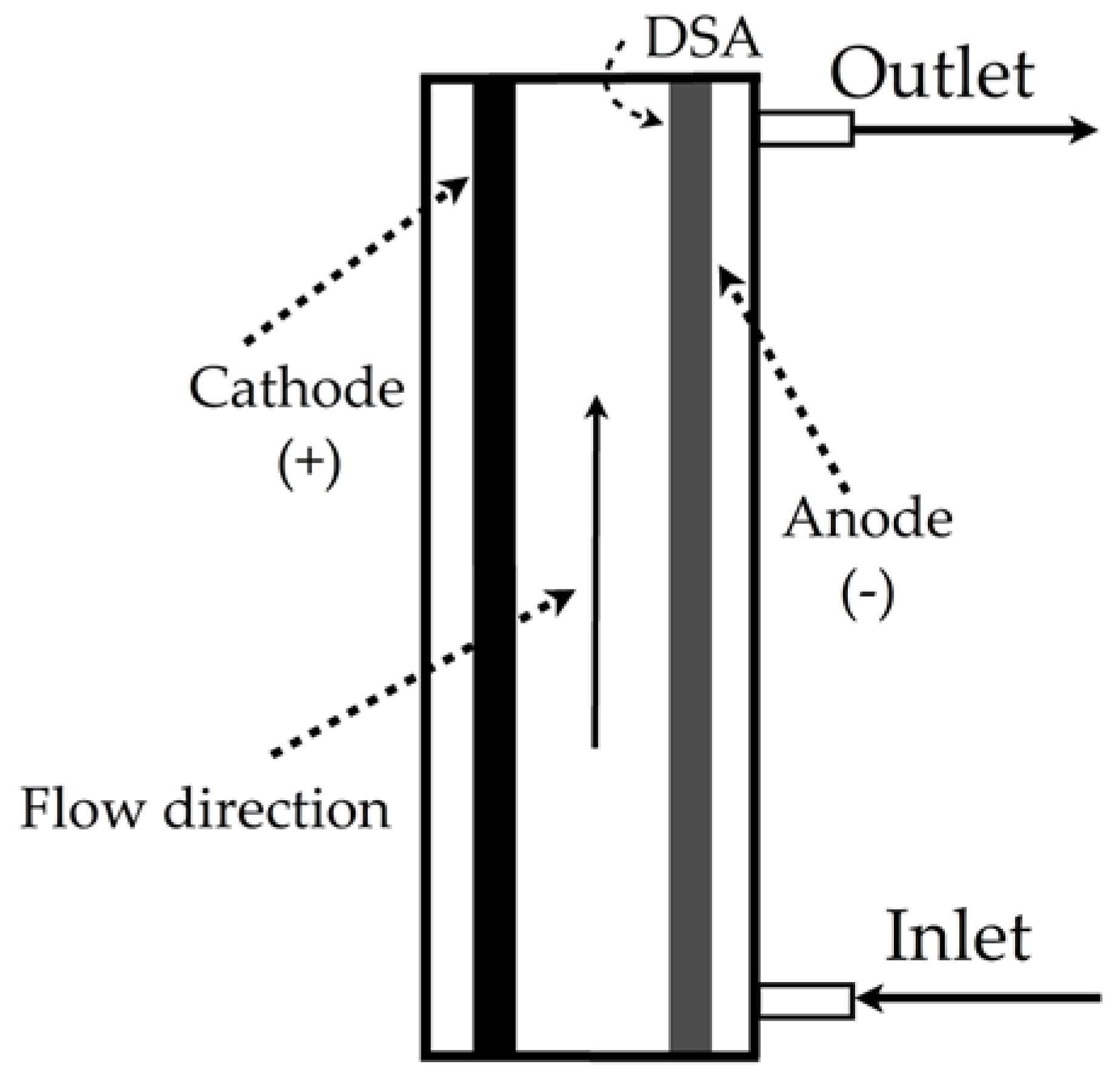 | Active chlorine (HOCl), current density of 10 mA/cm2, 0.02 mol/L of NaCl, volumetric flow rate of 5 L/min, temperature of 25 °C | Software COMSOL Multiphysics® 5.2a commercial | [19] |
| Indigo carmine dye | 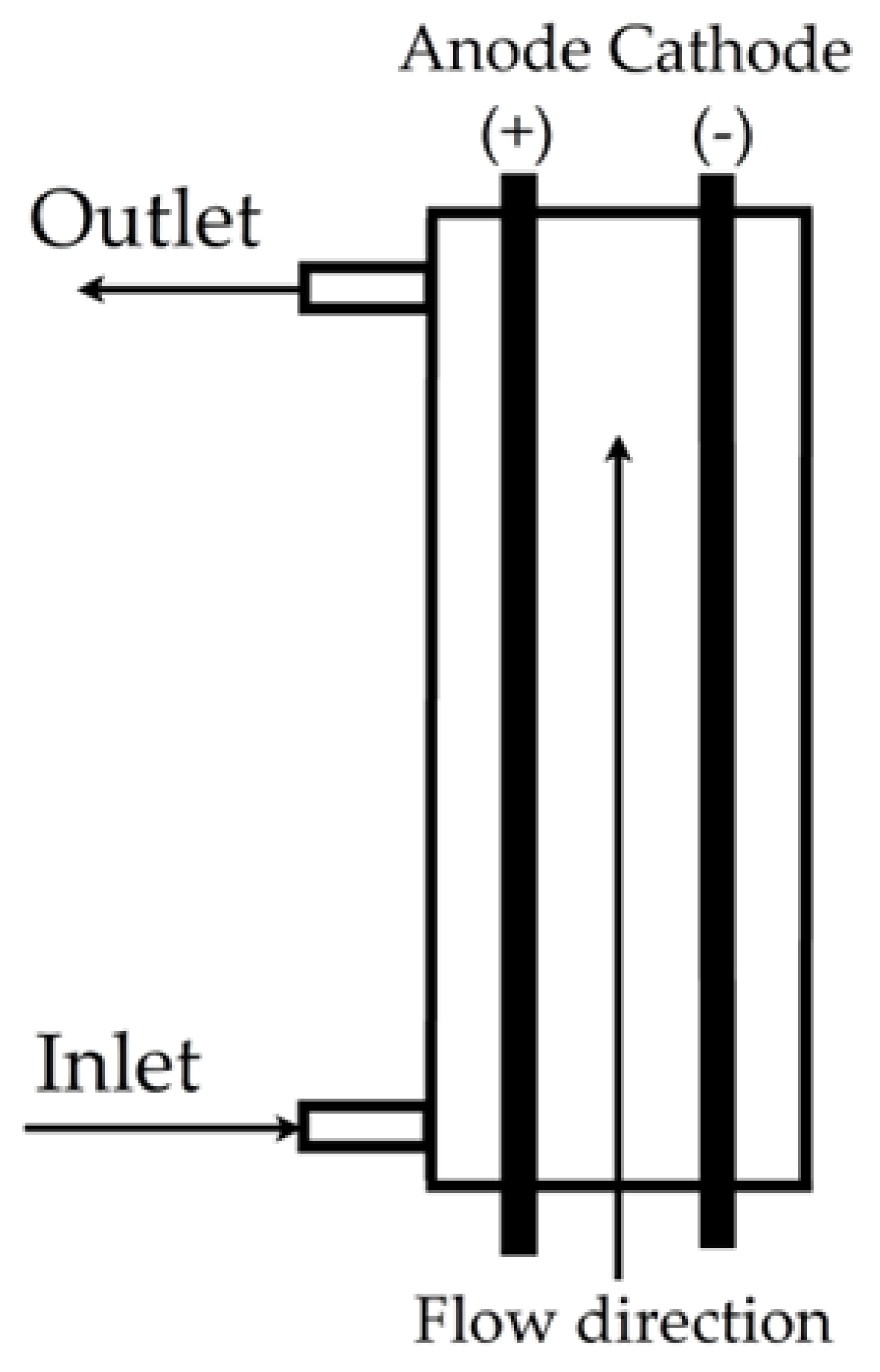 | Active chlorine (HOCl), 0.05 mol/L of NaCl, volumetric flow rate of 0.9 L/min, current density of 200 mA/cm2, temperature of 25 °C | Software FlexPDE professional version 6.5/W64 3D | [23] |
| Reactive Black 5 | 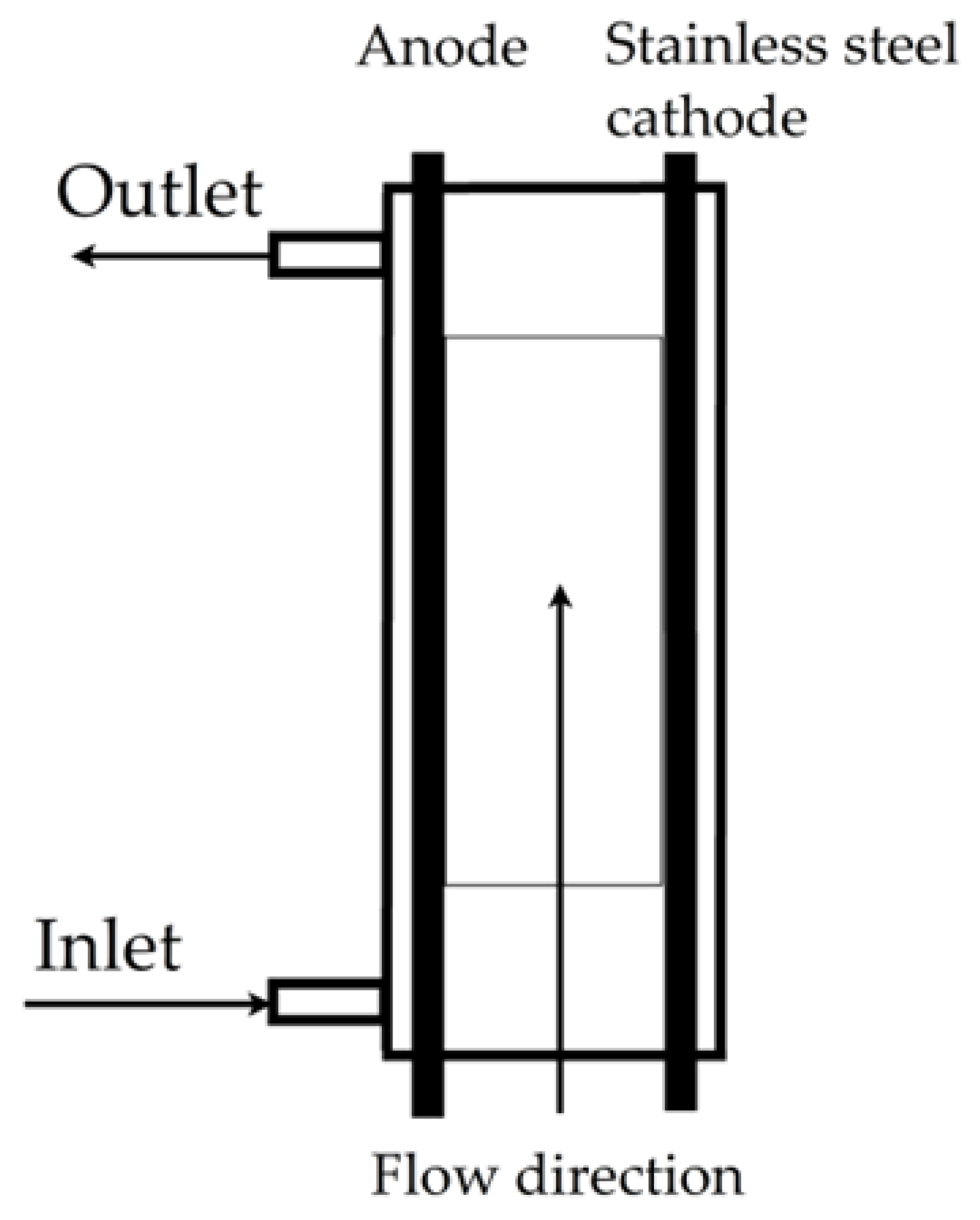 | Active chlorine (HOCl), 0.05 mol/L of NaCl, volumetric flow rate of 0.8 L/min, current density of 200 mA/cm2, temperature of 25 °C | Software COMSOL Mul-tiphysics® | [14] |
2. Materials and Methods
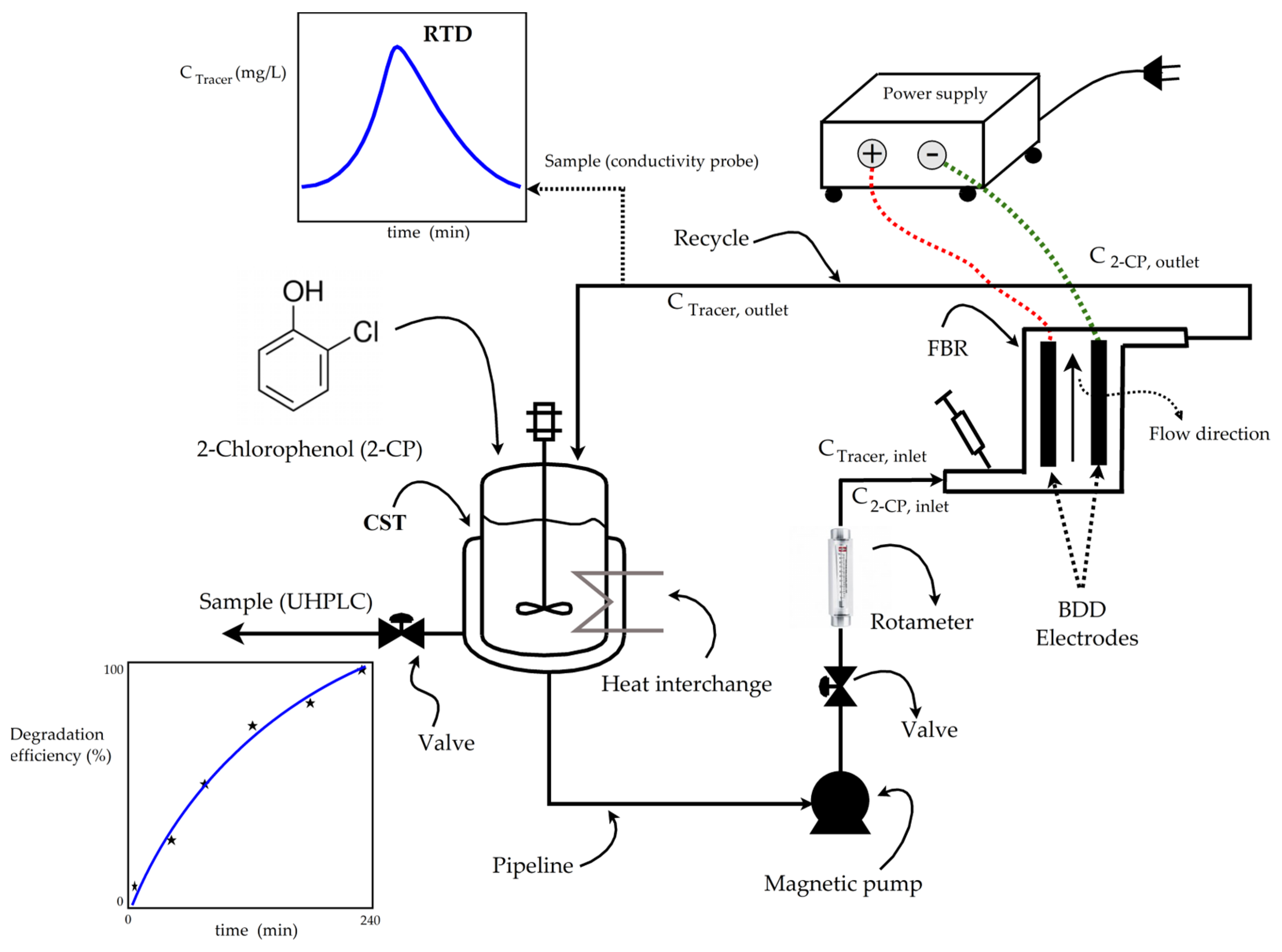
2.1. System Description
2.2. RTD Analysis
2.3. Electrolysis of 2-CP
2.4. Parametric Mathematical Model and Solution Method
- The reservoir tank was simulated using a CST.
- The boundaries of the FBR inlet and outlet were both of the closed–closed vessel type [17].
- The electrooxidation of 2-CP took place on the electrode surface at a constant current.
- The hydroxyl radicals were uniformly formed on the surface of the electrode [26]. Hence, the reaction rate of 2-CP was modeled using a pseudo-first order.
- The FBR was isothermally operated.
- The electrooxidation of 2-CP was limited by the mass transfer of 2-CP from the bulk to the electrode surface [18].
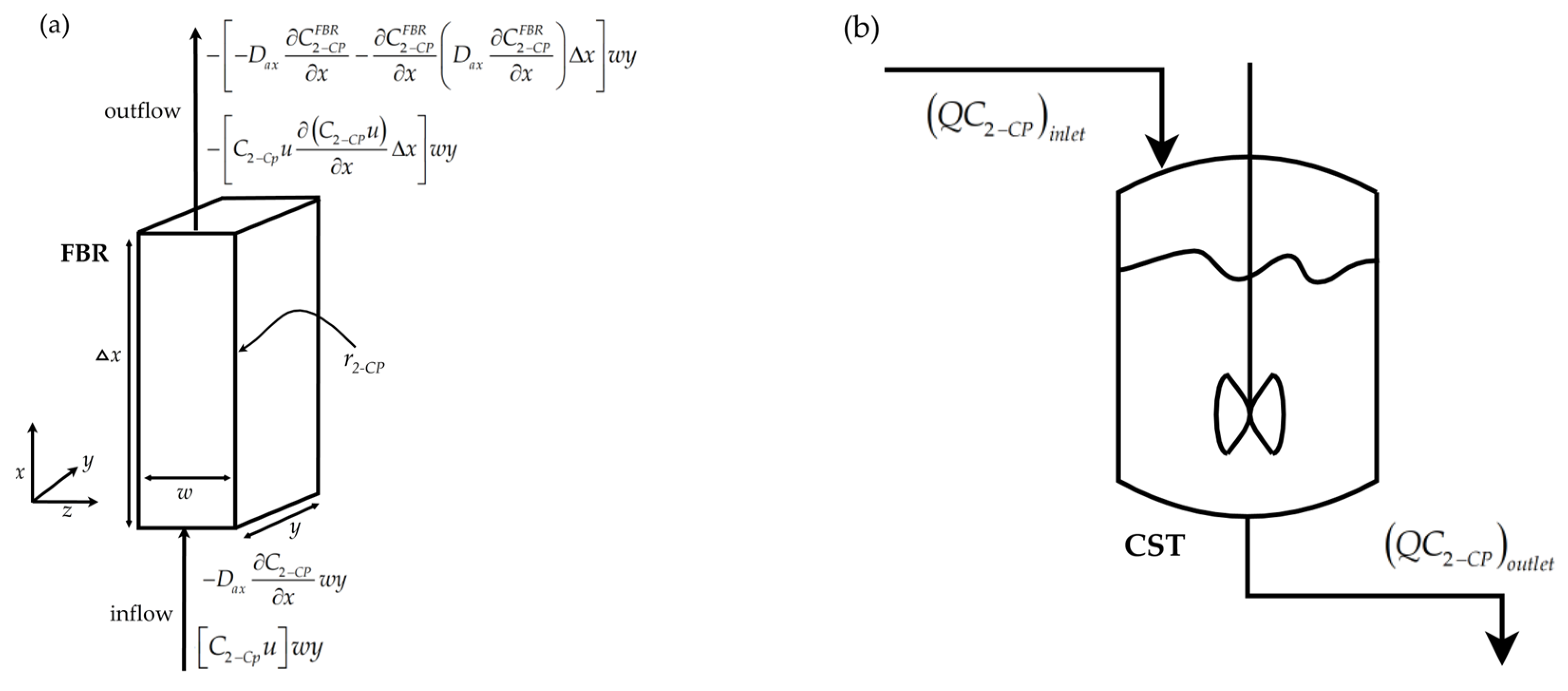
2.4.1. Axial Dispersion Mathematical Model for the Flow-By Reactor
2.4.2. Continuous Stirred Tank (CST) Model for the Reservoir Tank
2.4.3. Numerical Solution Approach
2.4.4. Performance of the Model
2.4.5. Energy Balance and Total Operating Cost
3. Results and Discussions
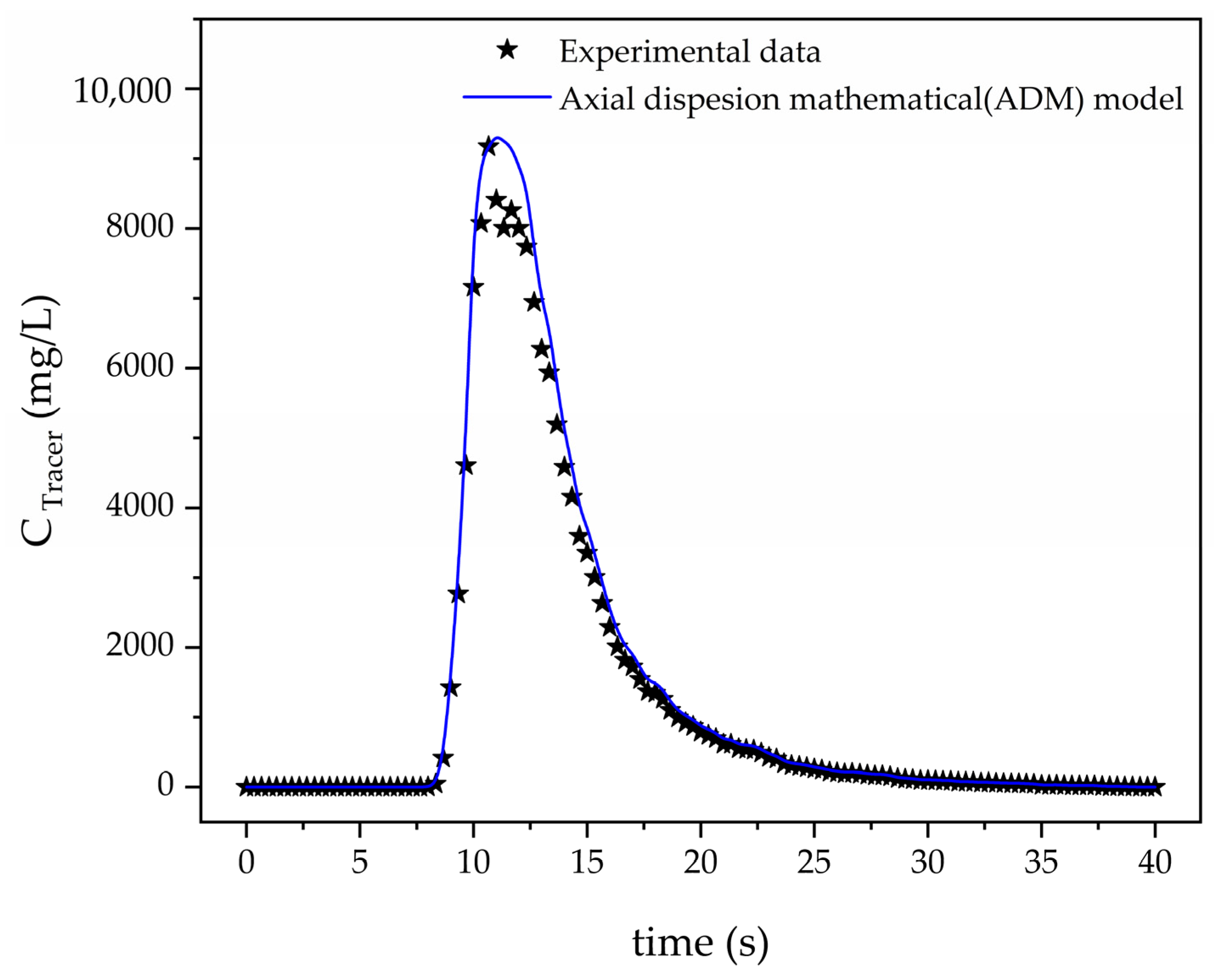
3.1. ADM Validation
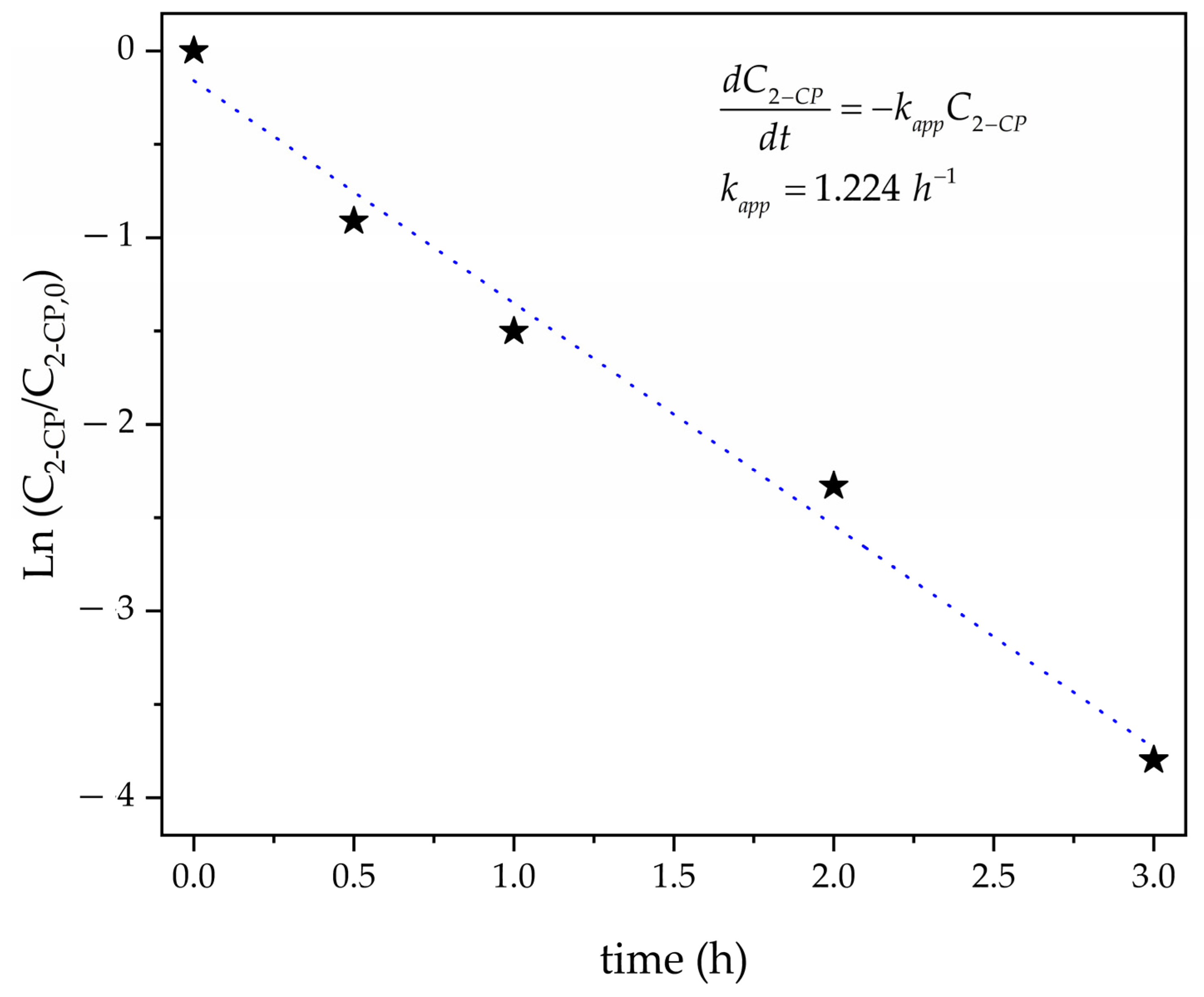
3.2. Kinetic Reaction of 2-CP
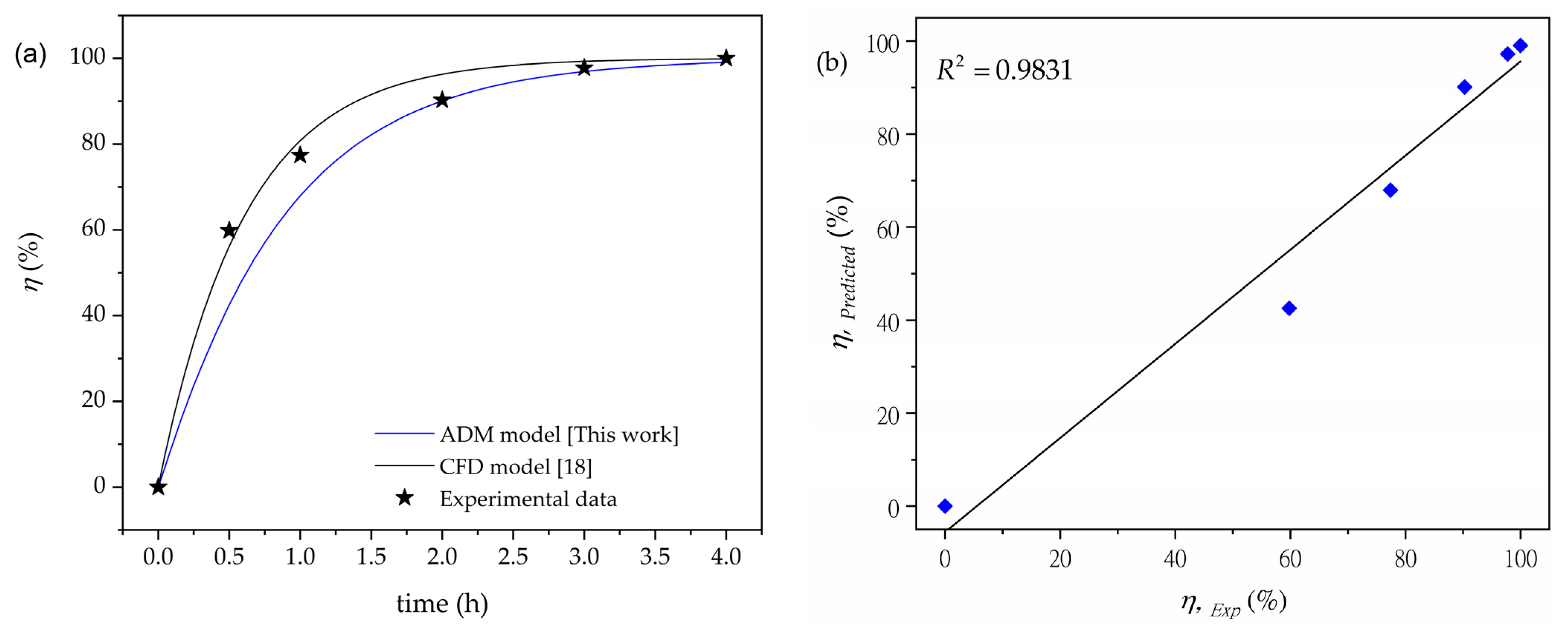
3.3. Modeling of the Complete Degradation Efficiency of 2-CP
3.4. Total Operating Cost
3.5. Future Works
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Axial Dispersion Mathematical Model for the Flow-By Reactor
Appendix A.2. Continuous Stirred Tank (CST) Model for the Reservoir Tank
References
- Valadez-Renteria, E.; Barrera-Rendon, E.; Oliva, J.; Rodriguez-Gonzalez, V. Flexible CuS/TiO2 Based Composites Made with Recycled Bags and Polystyrene for the Efficient Removal of the 4-CP Pesticide from Drinking Water. Sep. Purif. Technol. 2021, 270, 118821. [Google Scholar] [CrossRef]
- Xu, J.; Lv, X.; Li, J.; Li, Y.; Shen, L.; Zhou, H.; Xu, X. Simultaneous Adsorption and Dechlorination of 2,4-Dichlorophenol by Pd/Fe Nanoparticles with Multi-Walled Carbon Nanotube Support. J. Hazard. Mater. 2012, 225–226, 36–45. [Google Scholar] [CrossRef]
- Ahmaruzzaman, M. Adsorption of Phenolic Compounds on Low-Cost Adsorbents: A Review. Adv. Colloid Interface Sci. 2008, 143, 48–67. [Google Scholar] [CrossRef]
- Janda, V.; Ävecov¡, M. By-Products in Drinking Water Disinfection. Chemické Listy 2000, 94. Available online: http://www.chemicke-listy.cz/ojs3/index.php/chemicke-listy/article/view/2477 (accessed on 29 October 2023).
- Machado, L.M.M.; Lütke, S.F.; Perondi, D.; Godinho, M.; Oliveira, M.L.S.; Collazzo, G.C.; Dotto, G.L. Treatment of Effluents Containing 2-Chlorophenol by Adsorption onto Chemically and Physically Activated Biochars. J. Environ. Chem. Eng. 2020, 8, 104473. [Google Scholar] [CrossRef]
- Barbeni, M.; Minero, C.; Pelizzetti, E.; Borgarello, E.; Serpone, N. Chemical Degradation of Chlorophenols with Fenton’s Reagent (Fe2+ + H2O2). Chemosphere 1987, 16, 2225–2237. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Wu, C.-H. Kinetics of the Biodegradation of Phenol and 2-Chlorophenol in a Fixed Biofilm Reactor Using a Dewatered Sludge-Fly Ash Composite Ceramic Particle as a Supporting Medium. Desalination Water Treat. 2019, 157, 39–52. [Google Scholar] [CrossRef]
- Rao, N.N.; Dubey, A.K.; Mohanty, S.; Khare, P.; Jain, R.; Kaul, S.N. Photocatalytic Degradation of 2-Chlorophenol: A Study of Kinetics, Intermediates and Biodegradability. J. Hazard. Mater. 2003, 101, 301–314. [Google Scholar] [CrossRef]
- Muddemann, T.; Haupt, D.; Sievers, M.; Kunz, U. Electrochemical Reactors for Wastewater Treatment. ChemBioEng Rev. 2019, 6, 142–156. [Google Scholar] [CrossRef]
- Silva, B.S.; Ribeiro, M.C.B.; Ramos, B.; de Castro Peixoto, A.L. Removal of Amoxicillin from Processing Wastewater by Ozonation and UV-Aided Ozonation: Kinetic and Economic Comparative Study. Water 2022, 14, 3198. [Google Scholar] [CrossRef]
- Bany Abdelnabi, A.A.; Al Theeb, N.; Almomani, M.A.; Ghanem, H.; Rosiwal, S.M. Effect of Electrode Parameters in the Electro-Production of Reactive Oxidizing Species via Boron-Doped Diamond under Batch Mode. Water Environ. Res. 2022, 94, e10830. [Google Scholar] [CrossRef]
- Legrini, O.; Oliveros, E.; Braun, A.M. Photochemical Processes for Water Treatment. Chem. Rev. 1993, 93, 671–698. [Google Scholar] [CrossRef]
- Yu, S.; Liu, S.; Jiang, X.; Yang, N. Recent Advances on Electrochemistry of Diamond Related Materials. Carbon 2022, 200, 517–542. [Google Scholar] [CrossRef]
- Rivero, E.P.; Rodríguez, F.A.; Cruz-Díaz, M.R.; González, I. Reactive Diffusion Migration Layer and Mass Transfer Wall Function to Model Active Chlorine Generation in a Filter Press Type Electrochemical Reactor for Organic Pollutant Degradation. Chem. Eng. Res. Des. 2018, 138, 533–545. [Google Scholar] [CrossRef]
- Rivera, F.F.; Castañeda, L.; Hidalgo, P.E.; Orozco, G. Study of Hydrodynamics at AsahiTM Prototype Electrochemical Flow Reactor, Using Computational Fluid Dynamics and Experimental Characterization Techniques. Electrochim. Acta 2017, 245, 107–117. [Google Scholar] [CrossRef]
- Rivera, F.F.; Pérez, T.; Castañeda, L.F.; Nava, J.L. Mathematical Modeling and Simulation of Electrochemical Reactors: A Critical Review. Chem. Eng. Sci. 2021, 239, 116622. [Google Scholar] [CrossRef]
- Levenspiel, O. The Dispersion Model. In Tracer Technology: Modeling the Flow of Fluids; Levenspiel, O., Ed.; Springer: New York, NY, USA, 2012; pp. 47–70. ISBN 978-1-4419-8074-8. [Google Scholar]
- Regalado-Méndez, A.; Cruz-López, A.; Mentado-Morales, J.; Cordero, M.E.; Zárate, L.G.; Cruz-Díaz, M.R.; Fontana, G.; Peralta-Reyes, E. Mathematical Modeling of the Electrochemical Degradation of 2-Chlorophenol Using an Electrochemical Flow Reactor Equipped with BDD Electrodes. J. Flow Chem. 2019, 9, 59–71. [Google Scholar] [CrossRef]
- Palma-Goyes, R.E.; Sosa-Rodríguez, F.S.; Rivera, F.F.; Vazquez-Arenas, J. Modeling the Sulfamethoxazole Degradation by Active Chlorine in a Flow Electrochemical Reactor. Environ. Sci. Pollut. Res. 2021, 29, 42201–42214. [Google Scholar] [CrossRef] [PubMed]
- Castañeda Ulloa, L.F.; Cornejo, O.M.; Nava, J.L. Modeling of the Electro-Peroxone Process for the Degradation of Orange Reactive 16 Dye. ECS Trans. 2018, 86, 129–138. [Google Scholar] [CrossRef]
- Zier, T.; Bouafia, S.; Rechidi, Y.; Chabani, M. Hydrodynamics Modeling and Electrochemical Performance of a Lab-Scale Single-Channel Cell through Residence Time Distribution and Kinetic Studies. Desalination Water Treat. 2022, 279, 187–194. [Google Scholar] [CrossRef]
- Rivera, F.F.; Rodríguez, F.A.; Rivero, E.P.; Cruz-Díaz, M.R. Parametric Mathematical Modelling of Cristal Violet Dye Electrochemical Oxidation Using a Flow Electrochemical Reactor with BDD and DSA Anodes in Sulfate Media. Int. J. Chem. React. Eng. 2018, 16, 20170116. [Google Scholar] [CrossRef]
- Cruz-Díaz, M.R.; Rivero, E.P.; Rodríguez, F.A.; Domínguez-Bautista, R. Experimental Study and Mathematical Modeling of the Electrochemical Degradation of Dyeing Wastewaters in Presence of Chloride Ion with Dimensional Stable Anodes (DSA) of Expanded Meshes in a FM01-LC Reactor. Electrochim. Acta 2018, 260, 726–737. [Google Scholar] [CrossRef]
- Regalado-Méndez, A.; Mentado-Morales, J.; Vázquez, C.E.; Martínez-Villa, G.; Cordero, M.E.; Zárate, L.G.; Skogestad, S.; Peralta-Reyes, E. Modeling and Hydraulic Characterization of a Filter-Press-Type Electrochemical Reactor by Using Residence Time Distribution Analysis and Hydraulic Indices. Int. J. Chem. React. Eng. 2018, 16, 20170210. [Google Scholar] [CrossRef]
- Peralta-Reyes, E.; Natividad, R.; Castellanos, M.; Mentado-Morales, J.; Cordero, M.E.; Amado-Piña, D.; Regalado-Méndez, A. Electro-Oxidation of 2-Chlorophenol with BDD Electrodes in a Continuous Flow Electrochemical Reactor. J. Flow Chem. 2020, 10, 437–447. [Google Scholar] [CrossRef]
- Pérez, T.; León, M.I.; Nava, J.L. Numerical Simulation of Current Distribution along the Boron-Doped Diamond Anode of a Filter-Press-Type FM01-LC Reactor during the Oxidation of Water. J. Electroanal. Chem. 2013, 707, 1–6. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Continuous Flow Systems: Distribution of Residence Times. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.K. Apparent Desorption Kinetics of Phenol in Organic Solvents from Spent Activated Carbon Saturated with Phenol. Chem. Eng. J. 2004, 98, 237–243. [Google Scholar] [CrossRef]
- Karunasingha, D.S.K. Root Mean Square Error or Mean Absolute Error? Use Their Ratio as Well. Inf. Sci. 2022, 585, 609–629. [Google Scholar] [CrossRef]
- Guisan, A.; Thuiller, W.; Zimmermann, N.E. Measuring Model Accuracy: Which Metrics to Use? In Habitat Suitability and Distribution Models; Cambridge University Press: Cambridge, UK, 2017; pp. 241–269. [Google Scholar]
- Levenspiel, O. The Tracer Method. Fluid Mech. Its Appl. 2012, 96, 1–3. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 6th ed.; Pearson Education Limited: London, UK, 2022; ISBN 1-292-41666-1. [Google Scholar]
- Fitch, A.; Balderas-Hernandez, P.; Ibanez, J.G. Electrochemical Technologies Combined with Physical, Biological, and Chemical Processes for the Treatment of Pollutants and Wastes: A Review. J. Environ. Chem. Eng. 2022, 10, 107810. [Google Scholar] [CrossRef]
- Abbasi, P.; Bahrami Moghadam, E. Electrochemical Degradation of Ciprofloxacin from Water: Modeling and Prediction Using ANN and LSSVM. Phys. Chem. Earth Parts A/B/C 2023, 132, 103509. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 2nd ed.; Wiley: New York, NY, USA, 1984. [Google Scholar]
- Mequanient, M.B.; Kebede, H.H. Simulation of Sediment Yield and Evaluation of Best Management Practices in Azuari Watershed, Upper Blue Nile Basin. H2Open J. 2023, 6, 493–506. [Google Scholar] [CrossRef]
- Tyagi, K.; Rane, C.; Harshvardhan; Manry, M. Regression Analysis. In Artificial Intelligence and Machine Learning for EDGE Computing; Academic Press: Cambridge, MA, USA, 2022; pp. 53–63. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Wang, F.; Xu, N.; Li, P.; Wang, A. Numerical Modeling of the Dispersion Characteristics of Pollutants in the Confluence Area of an Asymmetrical River. Water 2023, 15, 3766. [Google Scholar] [CrossRef]
- Vallejo, M.; San Román, M.F.; Ortiz, I. Quantitative Assessment of the Formation of Polychlorinated Derivatives, PCDD/Fs, in the Electrochemical Oxidation of 2-Chlorophenol as Function of the Electrolyte Type. Environ. Sci. Technol. 2013, 47, 12400–12408. [Google Scholar] [CrossRef]
- Yoon, J.H.; Jeong, E.D.; Shim, Y.B.; Won, M.S. Anodic Degradation of Toxic Aromatic Compound in the Flow Through Cell with Carbon Fiber Electrode. Key Eng. Mater. 2005, 277–279, 445–449. [Google Scholar] [CrossRef]
- Yoon, J.-H.; Shim, Y.-B.; Lee, B.-S.; Choi, S.-Y.; Won, M.-S. Electrochemical Degradation of Phenol and 2-Chlorophenol Using Pt/Ti and Boron-Doped Diamond Electrodes. Bull. Korean Chem. Soc. 2012, 33, 2274–2278. [Google Scholar] [CrossRef]
- Polcaro, A.M.; Palmas, S.; Renoldi, F.; Mascia, M. On the Performance of Ti/SnO2 and Ti/PbO2 Anodes in Electrochemical Degradation of 2-Chlorophenol for Wastewater Treatment. J. Appl. Electrochem. 1999, 29, 147–151. [Google Scholar] [CrossRef]
- Yang, K.; Zhao, Y.; Zhou, X.; Wang, Q.; Pedersen, T.H.; Jia, Z.; Cabrera, J.; Ji, M. “Self-Degradation” of 2-Chlorophenol in a Sequential Cathode-Anode Cascade Mode Bioelectrochemical System. Water Res. 2021, 206, 117740. [Google Scholar] [CrossRef]
| Index Performance | Value | Remark |
|---|---|---|
| R2 | 0.9831 | Excellent model fit |
| MSE | 0.0307 | Very good model fit |
| RMSE | 0.1754 | Very good model fit |
| Current Density (mA/cm2) | Vtreated (L) | A (cm2) | C (mol/m3) | Electrodes | η (%) | Reference | ||
|---|---|---|---|---|---|---|---|---|
| Anode | Cathode | Exp. | Pred. | |||||
| 140.0 | 2.50 | 32 | 1.00 | BDD | BDD | 99.99 | 99.06 | [This work] |
| 100.0 | 0.025 | 2 | 5.00 | Carbon fiber | - | 98.00 | - | [40] |
| 32.7 | 0.030 | 14 | 10.00 | BDD | - | 83.60 | - | [41] |
| 90.0 | 1.00 | 70 | 15.56 | BDD | Stainless steel | 100.00 | - | [39] |
| 16.0 | 0.30 | - | 4.70 | Ti/SnO2 | - | 50.00 | - | [42] |
| 33.0 | 0.07 | 9 | 1.56 | Graphite felts | Pt | 58.91 | - | [43] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Regalado-Méndez, A.; Ramos-Hernández, G.; Natividad, R.; Cordero, M.E.; Zárate, L.; Robles-Gómez, E.E.; Pérez-Pastenes, H.; Peralta-Reyes, E. Parametric Mathematical Model of the Electrochemical Degradation of 2-Chlorophenol in a Flow-by Reactor under Batch Recirculation Mode. Water 2023, 15, 4276. https://doi.org/10.3390/w15244276
Regalado-Méndez A, Ramos-Hernández G, Natividad R, Cordero ME, Zárate L, Robles-Gómez EE, Pérez-Pastenes H, Peralta-Reyes E. Parametric Mathematical Model of the Electrochemical Degradation of 2-Chlorophenol in a Flow-by Reactor under Batch Recirculation Mode. Water. 2023; 15(24):4276. https://doi.org/10.3390/w15244276
Chicago/Turabian StyleRegalado-Méndez, Alejandro, Guadalupe Ramos-Hernández, Reyna Natividad, Mario E. Cordero, Luis Zárate, Edson E. Robles-Gómez, Hugo Pérez-Pastenes, and Ever Peralta-Reyes. 2023. "Parametric Mathematical Model of the Electrochemical Degradation of 2-Chlorophenol in a Flow-by Reactor under Batch Recirculation Mode" Water 15, no. 24: 4276. https://doi.org/10.3390/w15244276







