Fractional Linear Reservoir Model as Elementary Hydrologic Response Function
Abstract
:1. Introduction
2. Theoretical Background
2.1. Linear Reservoir Model
2.2. Fractional Calculus
2.3. Mittag–Leffler Function
3. Fractional Linear Reservoir Model
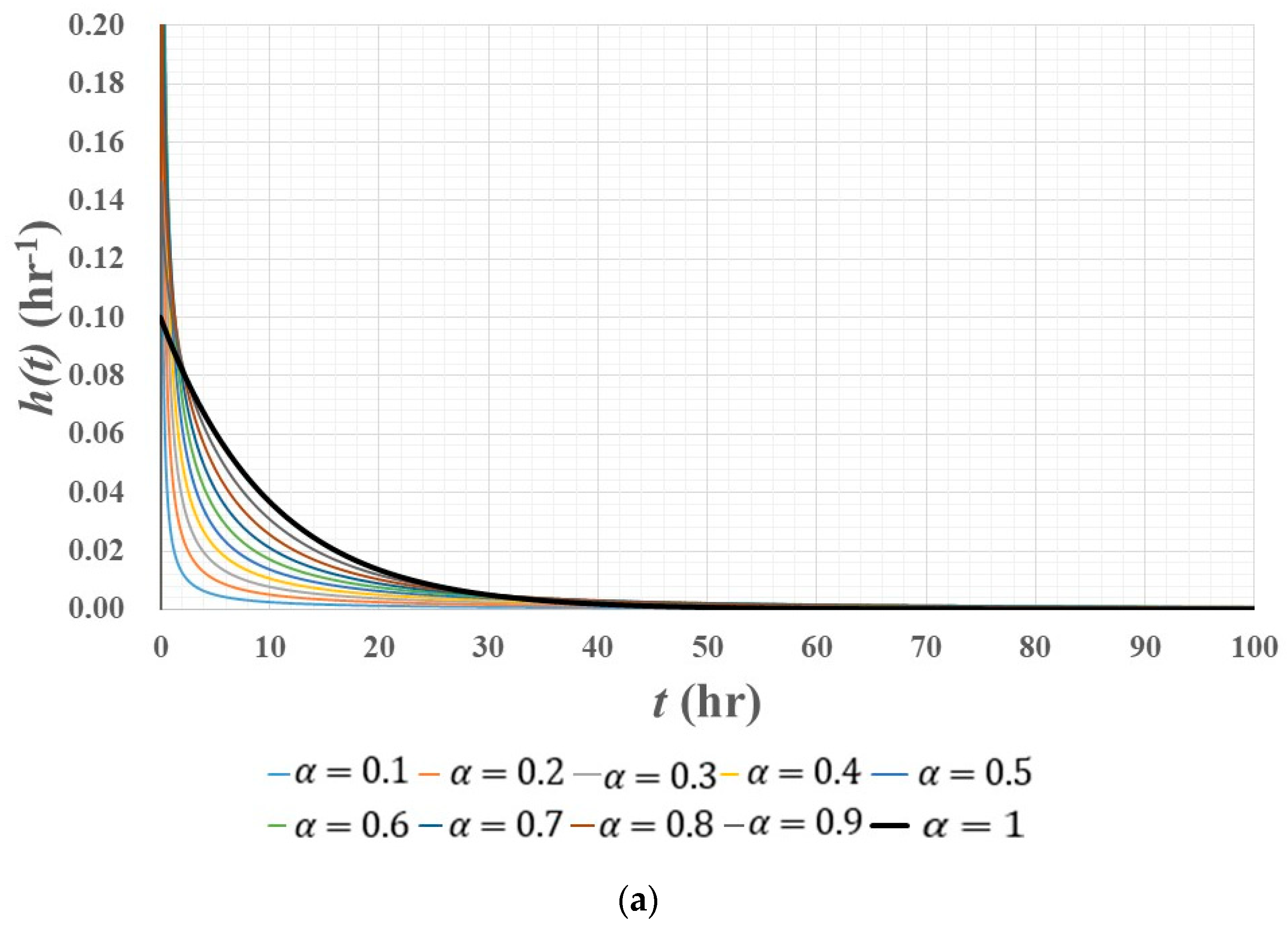
3.1. Impulse Response Function
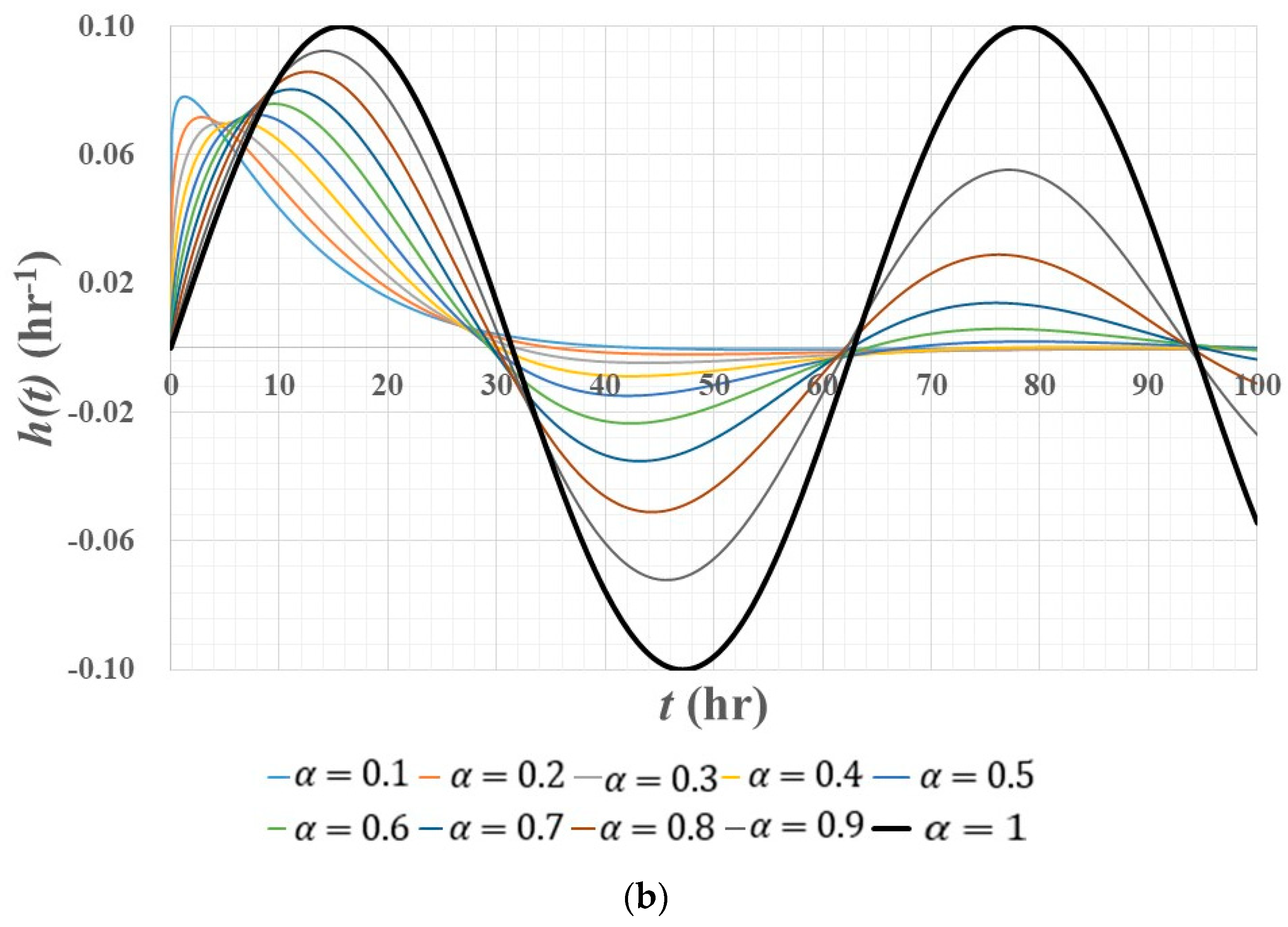
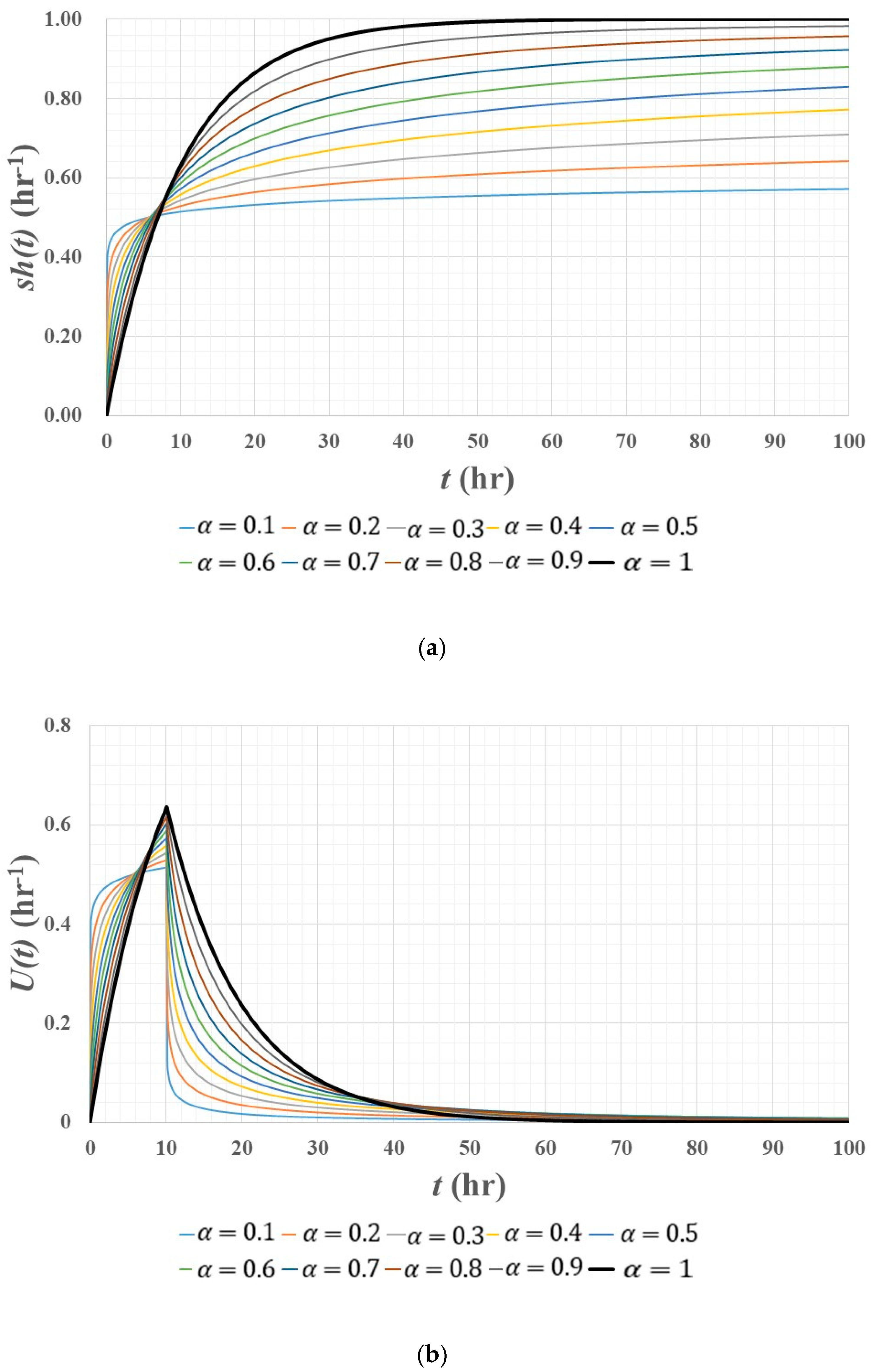
3.2. Unit Pulse Response Function
4. Results and Discussions
4.1. Methodology
4.2. Results
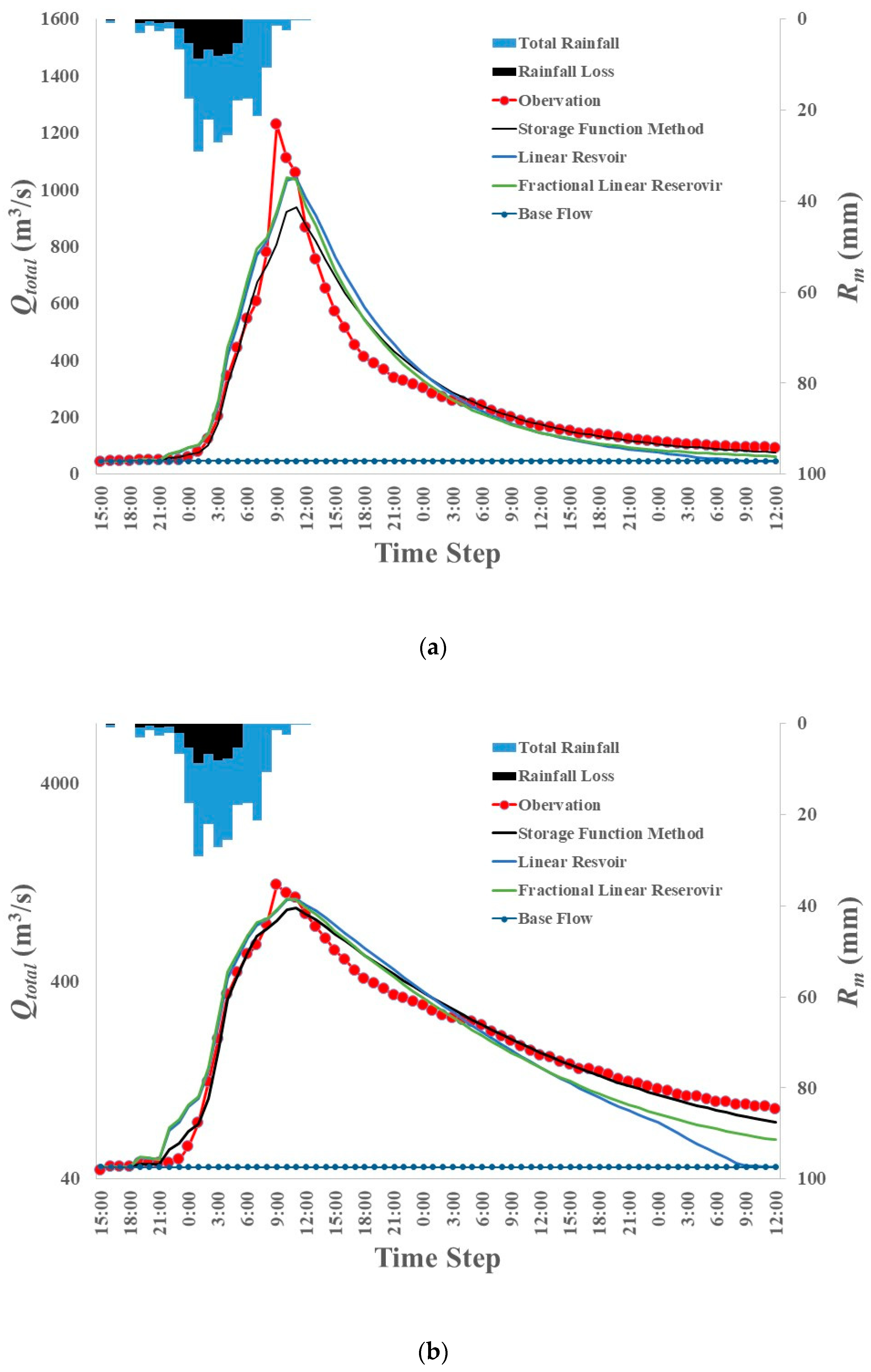
4.3. Discussions
5. Conclusions
- (1)
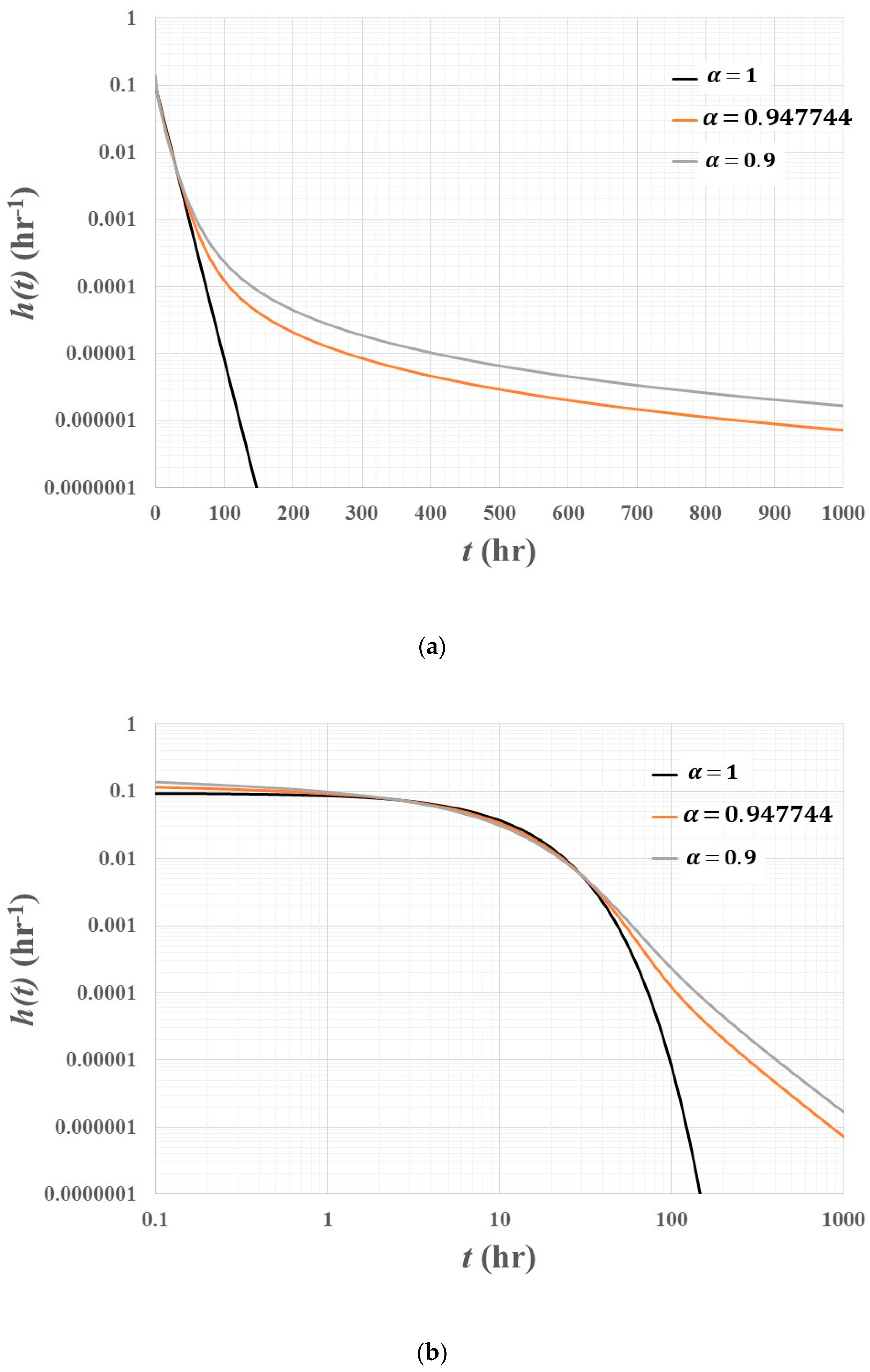
- The impulse response function of a fractional linear reservoir model has a nonlinear nature, which can be characterized by different rates of variation in terms of time.
- (2)
- The lag and route versions of fractional linear reservoir models produce the fast-rising and slow-recession of runoff hydrographs, that is, the mixed response of linear and nonlinear reservoir models to rainfall. So, a fractional linear reservoir model could be considered to be an effective tool in terms of reflecting the nonlinearity of rainfall–runoff phenomena within the framework of linear hydrologic system theory.
- (3)
- The fractional order, specifying a fractional linear reservoir model, can be viewed as a kind of parameter to quantify the heterogeneity of runoff generation within a river basin.
- (4)
- It could be possible for the span of base time to be much longer than that commonly acknowledged in hydrological practice, so a much wider time window would be required to separate the rainfall–runoff event from the continuous observation records in the context of a fractional linear reservoir model.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amorocho, J. The nonlinear prediction problem in the study of the runoff cycle. Water Resour. Res. 1967, 3, 861–880. [Google Scholar] [CrossRef]
- Sherman, L.K. Streamflow from rainfall by the unit-graph method. Eng. News Record 1932, 108, 501–505. [Google Scholar]
- Zoch, R.T. On the relation between rainfall and stream flow. Mon. Weather Rev. 1934, 62, 315–322. [Google Scholar] [CrossRef]
- Kimura, T. The Flood Runoff Analysis Method by the Storage Function Model; The Public Works Research Institute, Ministry of Construction: Tsukuba, Japan, 1961.
- La Barbera, P.; Rosso, R. On the Fractal dimension of stream networks. Water Resour. Res. 1989, 25, 735–741. [Google Scholar] [CrossRef]
- Rosso, R.; Bacchi, B.; La Barbera, P. Fractal relation of mainstream length to catchment area in river networks. Water Resour. Res. 1991, 27, 381–387. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. The Fractal nature of river networks. Water Resour. Res. 1988, 24, 1317–1322. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kulish, V.V.; Lage, J.L. Application of fractional calculus to fluid mechanics. J. Fluids Eng. 2002, 124, 803–806. [Google Scholar] [CrossRef]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- Benson, D.A.; Meerschaert, M.M.; Revielle, J. Fractional calculus in hydrologic modeling: A numerical perspective. Adv. Water Resour. 2013, 51, 479–497. [Google Scholar] [CrossRef]
- Guinot, V.; Savéan, M.; Jourde, H.; Neppel, L. Conceptual rainfall–runoff model with a two-parameter, infinite characteristic time transfer function. Hydrol. Process. 2015, 29, 4756–4778. [Google Scholar] [CrossRef]
- Kavvas, M.L.; Ercan, A. Fractional governing equations of diffusion wave and kinematic wave open-channel flow in fractional time-space. I. Development of the equations. J. Hydrol. Eng. 2015, 20, 04014096. [Google Scholar] [CrossRef]
- Su, N.; Zhang, F. Anomalous overland flow on hillslopes: A fractional kinematic wave model, its solutions and verification with data from laboratory observations. J. Hydrol. 2022, 604, 127202. [Google Scholar] [CrossRef]
- Unami, K.; Fadhil, R.M.; Mohawesh, O. Bounding linear rainfall-runoff models with fractional derivatives applied to a barren catchment of the Jordan Rift Valley. J. Hydrol. 2021, 593, 125879. [Google Scholar] [CrossRef]
- Wheatcraft, S.W.; Meerschaert, M.M. Fractional conservation of mass. Adv. Water Resour. 2008, 31, 1377–1381. [Google Scholar] [CrossRef]
- Xiang, X.; Ao, T.; Li, X. Application of a Fractional Instantaneous Unit Hydrograph in the TOPMODEL: A Case Study in Chengcun Basin, China. Appl. Sci. 2023, 13, 2245. [Google Scholar] [CrossRef]
- Borthwick, M.F. Application of Fractional Calculus to Rainfall Streamflow Modelling. Ph.D. Dissertation, University of Plymouth, Plymouth, UK, 2010. [Google Scholar]
- Chow, V.T.; Kulandaiswamy, V.C. General hydrologic system model. J. Hydraul. Div. 1971, 97, 791–804. [Google Scholar] [CrossRef]
- Dooge, J.C.I. A general theory of the unit hydrograph. J. Geophys. Res. 1959, 64, 241–256. [Google Scholar] [CrossRef]
- Nash, J.E. The form of the instantaneous unit hydrograph. Comptes Rendus Rapp. Assem. Gen. Tor. 1957, 3, 114–121. [Google Scholar]
- Singh, K.P. Nonlinear instantaneous unit hydrograph theory. J. Hydraul. Div. 1964, 90, 313–347. [Google Scholar] [CrossRef]
- Kisela, T. Fractional Differential Equations and Their Applications. Ph.D. Thesis, BRNO University of Technology, Brno, Czech Republic, 2008. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler functions and their applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef]
- Mainardi, F. Why the Mittag-Leffler function can be considered the Queen function of the Fractional Calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef] [PubMed]
- Dooge, J.C.I. Linear Theory of Hydrologic Systems; Agricultural Research Service, US Department of Agriculture: Washington, DC, USA, 1973.
- Singh, V.P. Hydrologic Systems: Rainfall-Runoff Modeling; Prentice Hall: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Garrappa, R. The Mittag-Leffler Function. Available online: https://www.mathworks.com/matlabcentral/fileexchange/48154-the-mittag-leffler-functionMATLABFileExchange (accessed on 2 January 2023).
- Diskin, M.H.; Boneh, A. Determination of an optimal IUH for linear, time invariant systems from multi-storm records. J. Hydrol. 1975, 24, 57–76. [Google Scholar] [CrossRef]
- Kwon, O.H.; Ryu, T.S.; Yoo, J.H. A derivation of the representative unit hydrograph from multiperiod complex storm by linear programming. KSCE J. Civ. Environ. Eng. Res. 1993, 13, 173–182. (In Korean) [Google Scholar]
- Pillai, R.N. On Mittag-Leffler functions and related distributions. Ann. Inst. Stat. Math. 1990, 42, 157–161. [Google Scholar] [CrossRef]
- Cahoy, D.O. Estimation of Mittag-Leffler parameters. Commun. Stat-Simul. C 2013, 42, 303–315. [Google Scholar] [CrossRef]
- Cahoy, D.O.; Polito, F. Renewal processes based on generalized Mittag–Leffler waiting times. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 639–650. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Valdés, J.B. The geomorphologic structure of hydrologic response. Water Resour. Res. 1979, 15, 1409–1420. [Google Scholar] [CrossRef]
- Chow, V.T. Applied Hydrology; McGraw Hill: New York, NY, USA, 1988. [Google Scholar]
- Botter, G.; Bertuzzo, E.; Rinaldo, A. Transport in the hydrologic response: Travel time distributions, soil moisture dynamics, and the old water paradox. Water Resour. Res. 2010, 46, W03514. [Google Scholar] [CrossRef]
- Yoon, Y.N. Hydrology: Basics and Applications; Cheongmungak: Seoul, Republic of Korea, 2007. (In Korean) [Google Scholar]
- Wang, G.T.; Wu, K. The unit-step function response for several hydrological conceptual models. J. Hydrol. 1983, 62, 119–128. [Google Scholar] [CrossRef]
- Rani, G.S.; Jayan, S.; Nagaraja, K.V. An extension of golden section algorithm for n-variable functions with MATLAB code. IOP Conf. Ser. Mater. Sci. Eng. 2019, 577, 012175. [Google Scholar] [CrossRef]
- Mainardi, F. A note on the equivalence of fractional relaxation equations to differential equations with varying coefficients. Mathematics 2018, 6, 8. [Google Scholar] [CrossRef]
- Cheng, B.L.M. A Study of Geomorphologic Instantaneous Unit Hydrograph. Ph.D. Thesis, University of Illinois, Champaign, IL, USA, 1982. [Google Scholar]
- Dunne, T.; Black, R.D. Partial area contributions to storm runoff in a small New England watershed. Water Resour. Res. 1970, 6, 1296–1311. [Google Scholar] [CrossRef]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
| Linear Reservoir | Fractional Linear Reservoir | |
|---|---|---|
| Linear Reservoir | Fractional Linear Reservoir | |
|---|---|---|
| 10.669011 | 10.669011 (10.901208) | |
| 0.947744 (0.945768) |
| Storage Function Method | Linear Reservoir | Fractional Linear Reservoir | |
|---|---|---|---|
| MBE () | 6 | 15 | 12 |
| RMSE () | 72.9 | 83.4 | 71.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, Y.-J.; Kim, J.-C. Fractional Linear Reservoir Model as Elementary Hydrologic Response Function. Water 2023, 15, 4254. https://doi.org/10.3390/w15244254
Yoon Y-J, Kim J-C. Fractional Linear Reservoir Model as Elementary Hydrologic Response Function. Water. 2023; 15(24):4254. https://doi.org/10.3390/w15244254
Chicago/Turabian StyleYoon, Yeo-Jin, and Joo-Cheol Kim. 2023. "Fractional Linear Reservoir Model as Elementary Hydrologic Response Function" Water 15, no. 24: 4254. https://doi.org/10.3390/w15244254




