A Multiple Model Approach for Flood Forecasting, Simulation, and Evaluation Coupling in Zhouqu County
Abstract
:1. Introduction
2. Flood Control Simulation and Dispatching System
3. Flood Forecasting Method Based on MOCSCDE
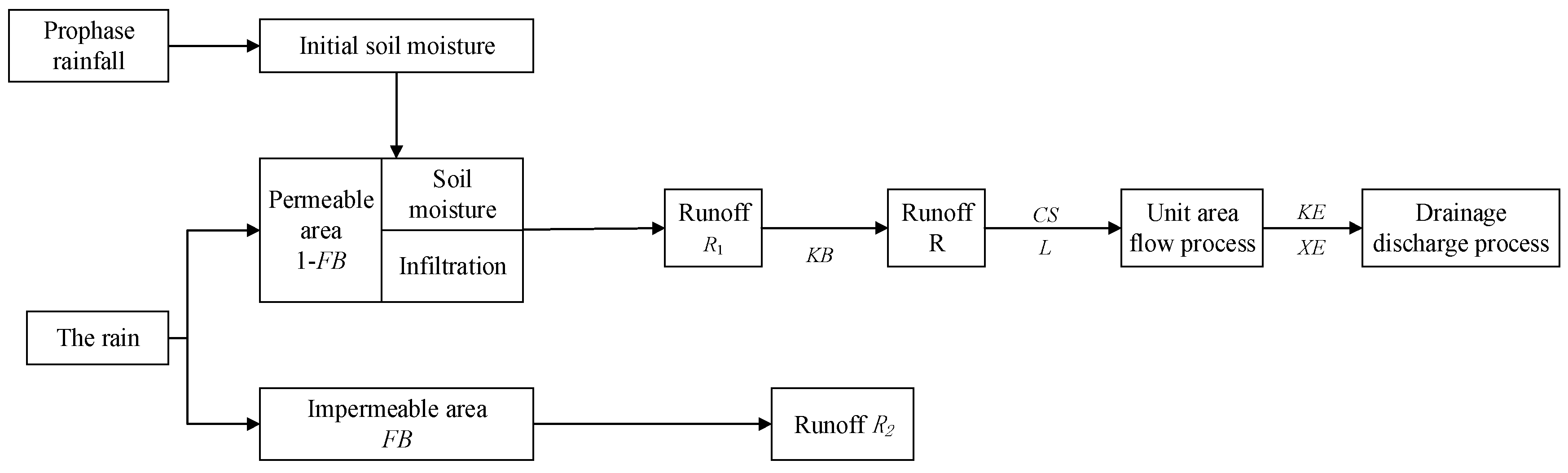
3.1. Model Theory
3.2. Model Parameters and Calibration Method
4. Flood Risk and Disaster Estimation
4.1. Flood Risk Estimation
4.2. Flood Disaster Estimation
5. Experiment
5.1. Study Area
5.2. Experimental Settings
5.2.1. Datasets
5.2.2. Evaluation Metrics
5.2.3. Implementation Details
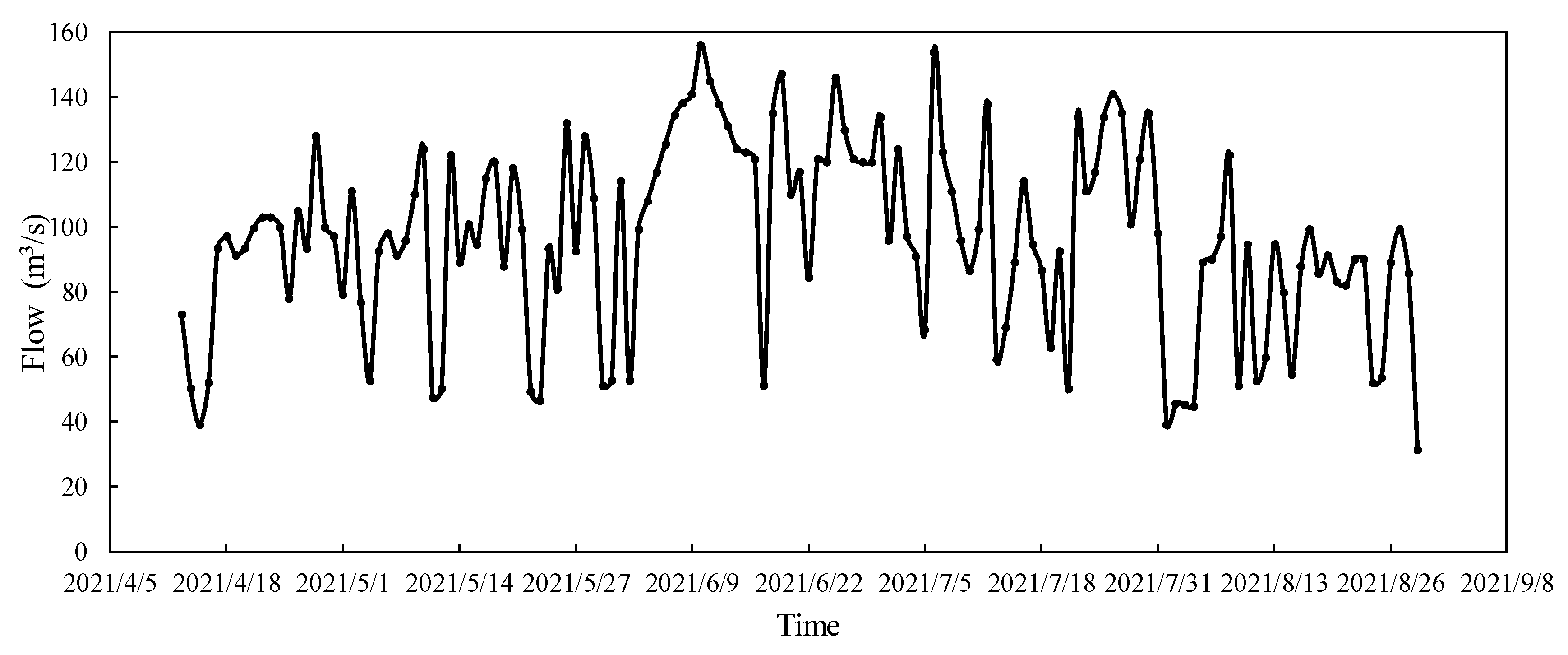
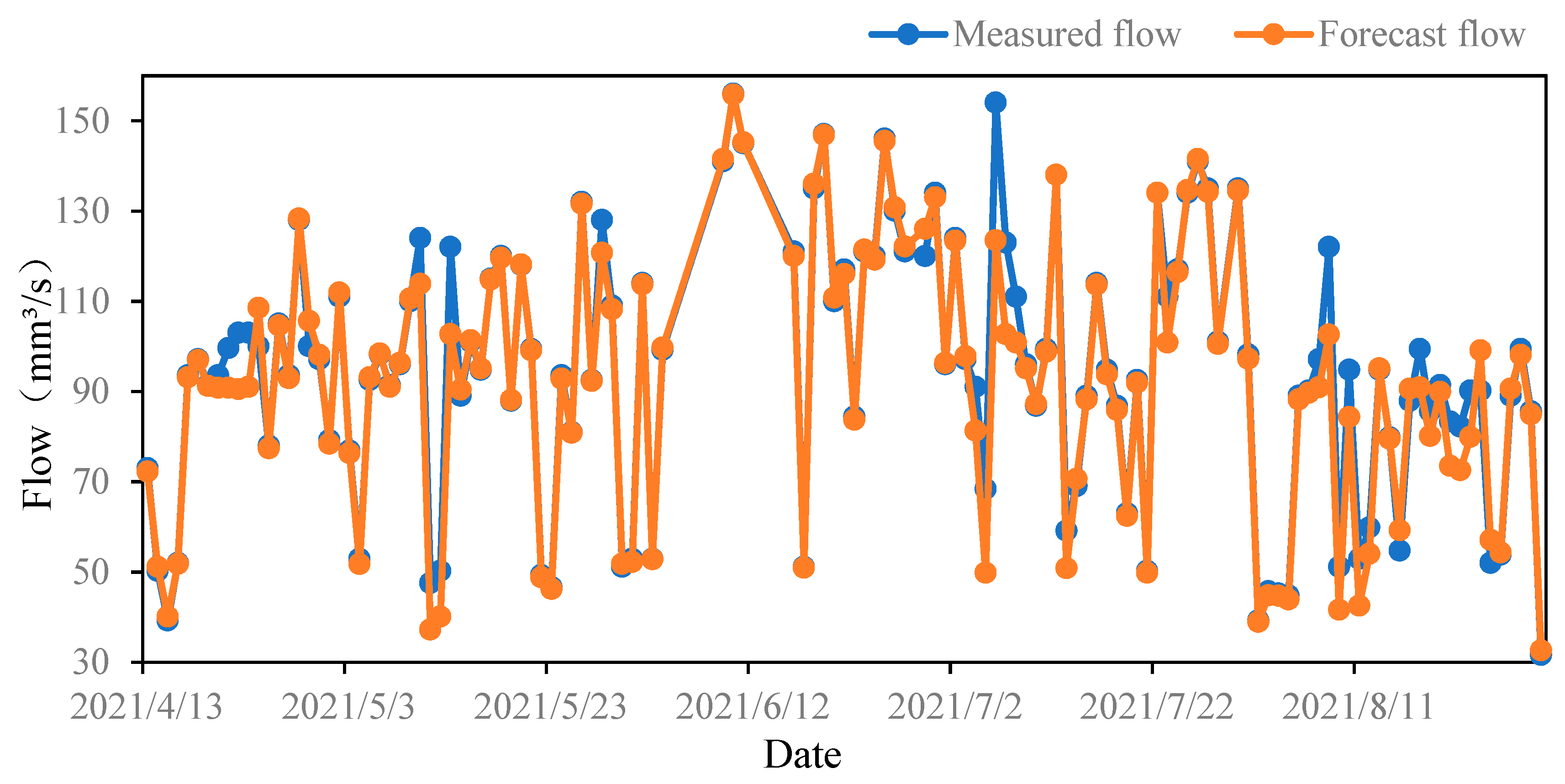
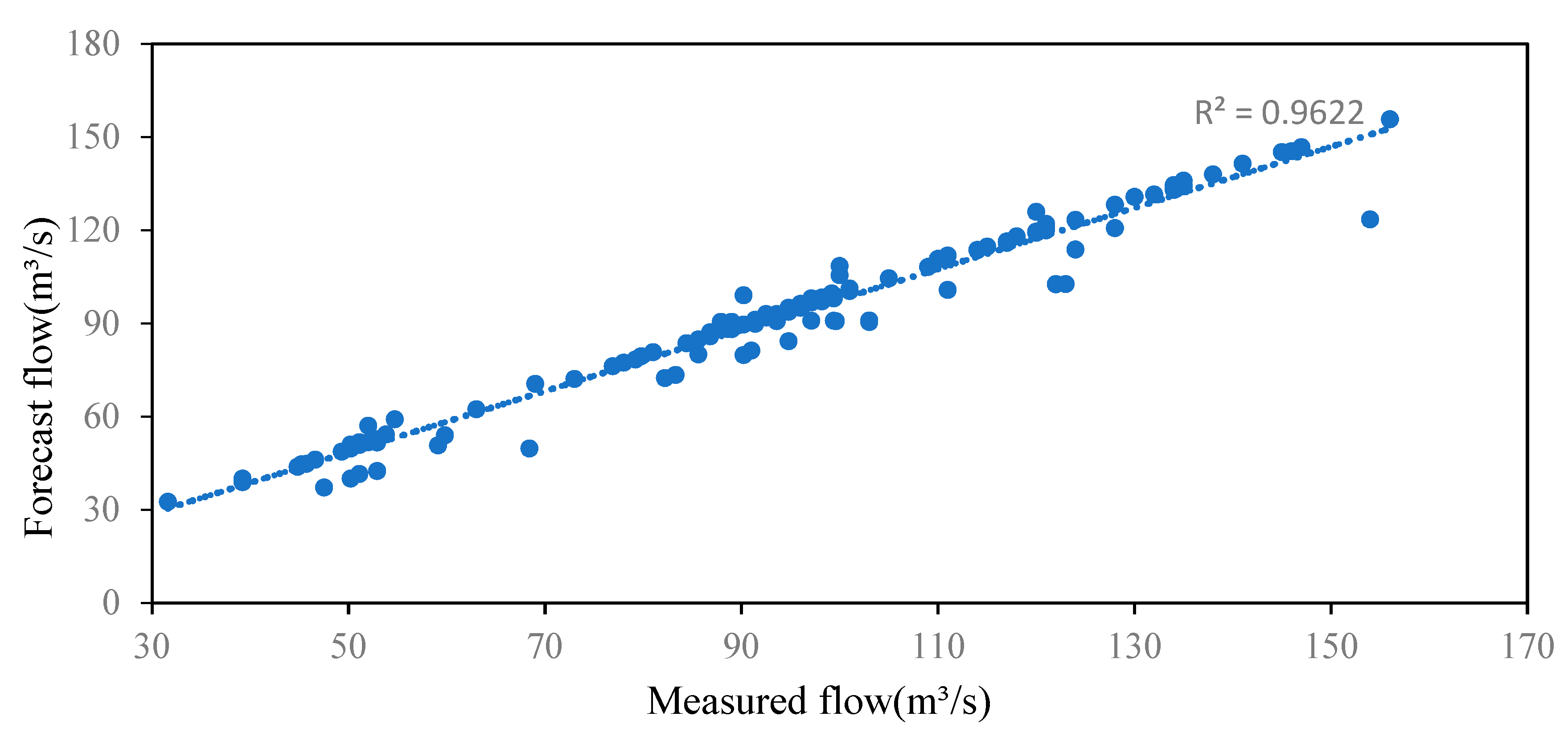
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Che, H.; Wang, J. Sparse Nonnegative Matrix Factorization Based on Collaborative Neurodynamic Optimization. In Proceedings of the 2019 9th International Conference on Information Science and Technology (ICIST), Hulunbuir, China, 2–5 August 2019; pp. 114–121. [Google Scholar]
- Xu, Y.; Wang, X.; Jiang, Z.; Liu, Y.; Zhang, L.; Li, Y. An Improved Fineness Flood Risk Analysis Method Based on Digital Terrain Acquisition. Water Resour. Manag. 2023, 37, 3973–3998. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, Z.; Liu, Y.; Zhang, L.; Yang, J.; Shu, H. An Adaptive Ensemble Framework for Flood Forecasting and Its Application in a Small Watershed Using Distinct Rainfall Interpolation Methods. Water Resour. Manag. 2023, 37, 2195–2219. [Google Scholar] [CrossRef]
- Burstein, O.; Grodek, T.; Enzel, Y.; Helman, D. SatVITS-Flood: Satellite Vegetation Index Time Series Flood Detection Model for Hyperarid Regions. Water Resour. Res. 2023, 59, e2023WR035164. [Google Scholar] [CrossRef]
- Guo-wei, L. Definition and classification of non-structure measures for flood prevention. Adv. Water Sci. 2003, 14, 98. [Google Scholar]
- Ye, J.; Wu, Y.; Li, Z.; Chang, L. Research and application of small and medium-sized flash flood forecasting methods in humid regions. Hehai Univ. Sci. (Ed.) 2012, 40, 615–621. [Google Scholar]
- Zhang, J.; Na, L.; Zhang, B. Applicability of the distributed hydrological model of HEC-HMS in a small watershed of the Loess Plateau area. J. Beijing For. Univ. 2009, 31, 52–57. [Google Scholar]
- Liu, Z.; Li, L.; Zhu, C.; Wu, J.; Dai, R. Comparative study of distributed hydrological models in flood forecasting. Hydropower Energy Sci. 2006, 2, 70–73. [Google Scholar]
- Li, Z.; Hu, W.; Ding, J.; Hu, Y.; Wu, Y.; Li, J. Research on distributed hydrological model based on physical foundation and grid. J. Hydroelectr. Power 2012, 2, 5–13. [Google Scholar]
- Javier, J.R.N.; Smith, J.A.; Meierdiercks, K.L.; Baeck, M.L.; Miller, A. Flash flood forecasting for small urban watersheds in the Baltimore metropolitan region. Weather. Forecast. 2007, 22, 1331–1344. [Google Scholar] [CrossRef]
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine Learning for the Geosciences: Challenges and Opportunities. IEEE Trans. Knowl. Data Eng. 2019, 31, 1544–1554. [Google Scholar] [CrossRef]
- Sainju, A.M.; He, W.; Jiang, Z. A Hidden Markov Contour Tree Model for Spatial Structured Prediction. IEEE Trans. Knowl. Data Eng. 2022, 34, 1530–1543. [Google Scholar] [CrossRef]
- Singh Vijay, P.; Woolhiser David, A. Mathematical Modeling of Watershed Hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
- Sahoo, R.; Zhao, S.; Chen, A.; Ermon, S. Reliable decisions with threshold calibration. Adv. Neural Inf. Process. Syst. 2021, 34, 1831–1844. [Google Scholar]
- Shen, Y.; Wang, S.; Zhang, B.; Zhu, J. Development of a stochastic hydrological modeling system for improving ensemble streamflow prediction. J. Hydrol. 2022, 608, 127683. [Google Scholar] [CrossRef]
- Chilkoti, V.; Bolisetti, T.; Balachandar, R. Investigating the role of hydrological model parameter uncertainties in future streamflow projections. J. Hydrol. Eng. 2020, 25, 05020035. [Google Scholar] [CrossRef]
- Eidsvik, J.; Mukerji, T.; Bhattacharjya, D. Value of Information in the Earth Sciences: Integrating Spatial Modeling and Decision Analysis; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Zhang, X.; Srinivasan, R.; Zhao, K.; Liew, M. Evaluation of global optimization algorithms for parameter calibration of a computationally intensive hydrologic model. Hydrol. Process. 2009, 23, 430–441. [Google Scholar] [CrossRef]
- Arsenault, R.; Poulin, A.; Côté, P.; Brissette, F. Comparison of stochastic optimization algorithms in hydrological model calibration. J. Hydrol. Eng. 2014, 19, 1374–1384. [Google Scholar] [CrossRef]
- Huo, J.; Liu, L.; Zhang, Y. Comparative research of optimization algorithms for parameters calibration of watershed hydrological model. J. Comput. Methods Sci. Eng. 2016, 16, 653–669. [Google Scholar] [CrossRef]
- Chu, W.; Gao, X.; Sorooshian, S. A solution to the crucial problem of population degeneration in high-dimensional evolutionary optimization. IEEE Syst. J. 2011, 5, 362–373. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Xu, H. Improving flood forecasting capability of physically based distributed hydrological models by parameter optimization. Hydrol. Earth Syst. Sci. 2016, 20, 375–392. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Parallel Problem Solving from Nature-PPSN VI, Proceedings of the 6th International Conference, Paris, France, 18-20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Guo, J.; Zhou, J.; Zou, Q.; Liu, Y.; Song, L. A novel multi-objective shuffled complex differential evolution algorithm with application to hydrological model parameter optimization. Water Resour. Manag. 2013, 27, 2923–2946. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; ETH Zurich, Computer Engineering and Networks Laboratory: Zurich, Switzerland, 2001; Volume 103. [Google Scholar]
- Li, C.; Han, Z.; Li, Y.; Li, M.; Wang, W.; Dou, J.; Xu, L.; Chen, G. Physical information-fused deep learning model ensembled with a subregion-specific sampling method for predicting flood dynamics. J. Hydrol. 2023, 620, 129465. [Google Scholar] [CrossRef]
- Zhang, M.; Ding, D.; Pan, X.; Yang, M. Enhancing Time Series Predictors With Generalized Extreme Value Loss. IEEE Trans. Knowl. Data Eng. 2023, 35, 1473–1487. [Google Scholar] [CrossRef]
- Binkowski, M.; Marti, G.; Donnat, P. Autoregressive convolutional neural networks for asynchronous time series. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 580–589. [Google Scholar]
- Fu, S.; Zhong, S.; Lin, L.; Zhao, M. A Novel Time-Series Memory Auto-Encoder With Sequentially Updated Reconstructions for Remaining Useful Life Prediction. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7114–7125. [Google Scholar] [CrossRef]
- Kang, S.; Yin, J.; Gu, L.; Yang, Y.; Liu, D.; Slater, L. Observation-Constrained Projection of Flood Risks and Socioeconomic Exposure in China. Earth’s Future 2023, 11, e2022EF003308. [Google Scholar] [CrossRef]
- Awasthi, C.; Archfield, S.A.; Reich, B.J.; Sankarasubramanian, A. Beyond Simple Trend Tests: Detecting Significant Changes in Design-Flood Quantiles. Geophys. Res. Lett. 2023, 50, e2023GL103438. [Google Scholar] [CrossRef]
- Shi, P.; Du Juan, J.M.; Liu, J.; Wang, J. Urban risk assessment research of major natural disasters in China. Adv. Earth Sci. 2006, 21, 170. [Google Scholar]
- Altan, A.; Karasu, S.; Zio, E. A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl. Soft Comput. 2021, 100, 106996. [Google Scholar] [CrossRef]
- Mohamed, T.; Sayed, S.; Salah, A.; Houssein, E.H. Long Short-Term Memory Neural Networks for RNA Viruses Mutations Prediction. Math. Probl. Eng. 2021, 2021, 9980347. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Wang, J.; Bao, W.; Gao, Q.; Si, W.; Sun, Y. Coupling the Xinanjiang model and wavelet-based random forests method for improved daily streamflow simulation. J. Hydroinformatics 2021, 23, 589–604. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, W.; Yu, Q.; Feng, J.; Lu, T. Hierarchical Bayesian Network Based Incremental Model for Flood Prediction. In MultiMedia Modeling, Proceedings of the 25th International Conference, MMM 2019, Thessaloniki, Greece, 8–11 January 2019; Springer: Cham, Switzerland, 2019; pp. 556–566. [Google Scholar]
- Zhou, Y.; Wu, Z.; Xu, H.; Wang, H.; Ma, B.; Lv, H. Integrated dynamic framework for predicting urban flooding and providing early warning. J. Hydrol. 2023, 618, 129205. [Google Scholar] [CrossRef]





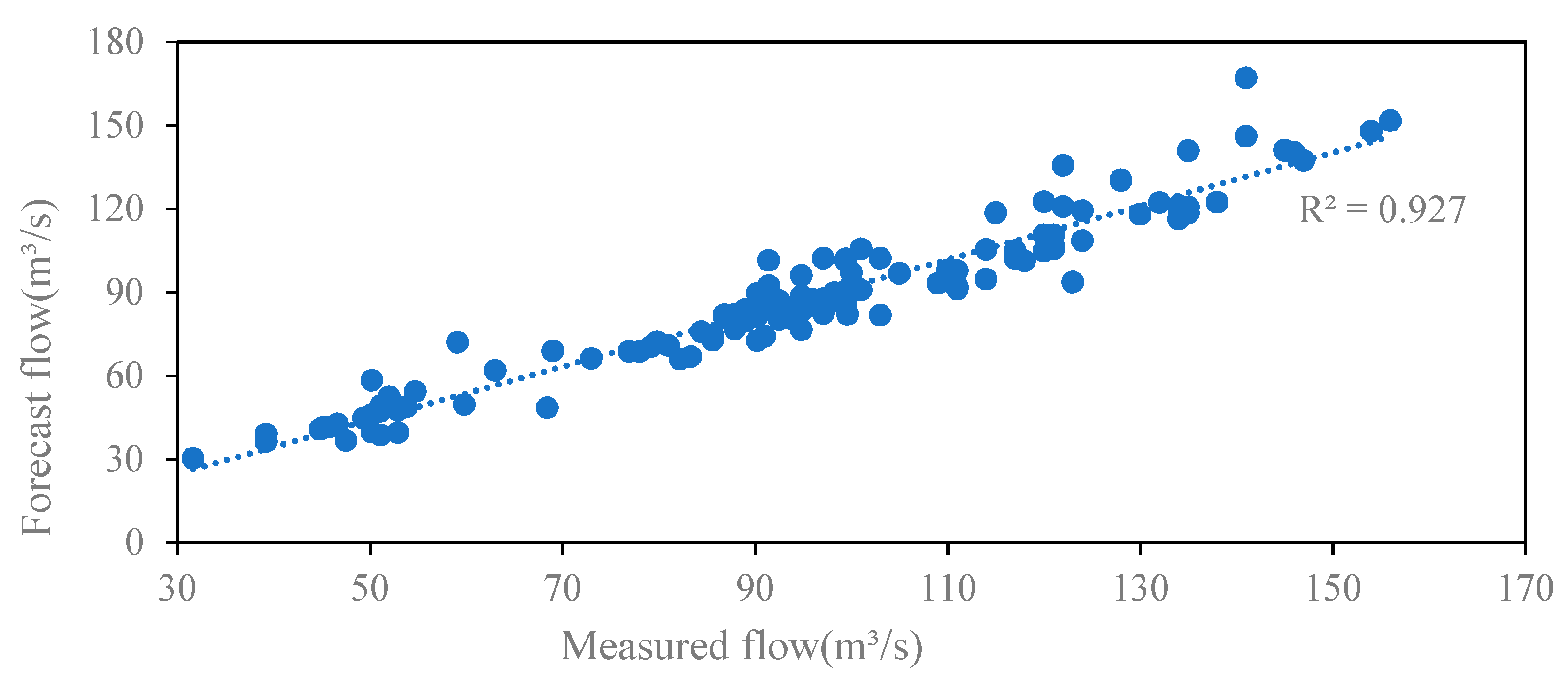


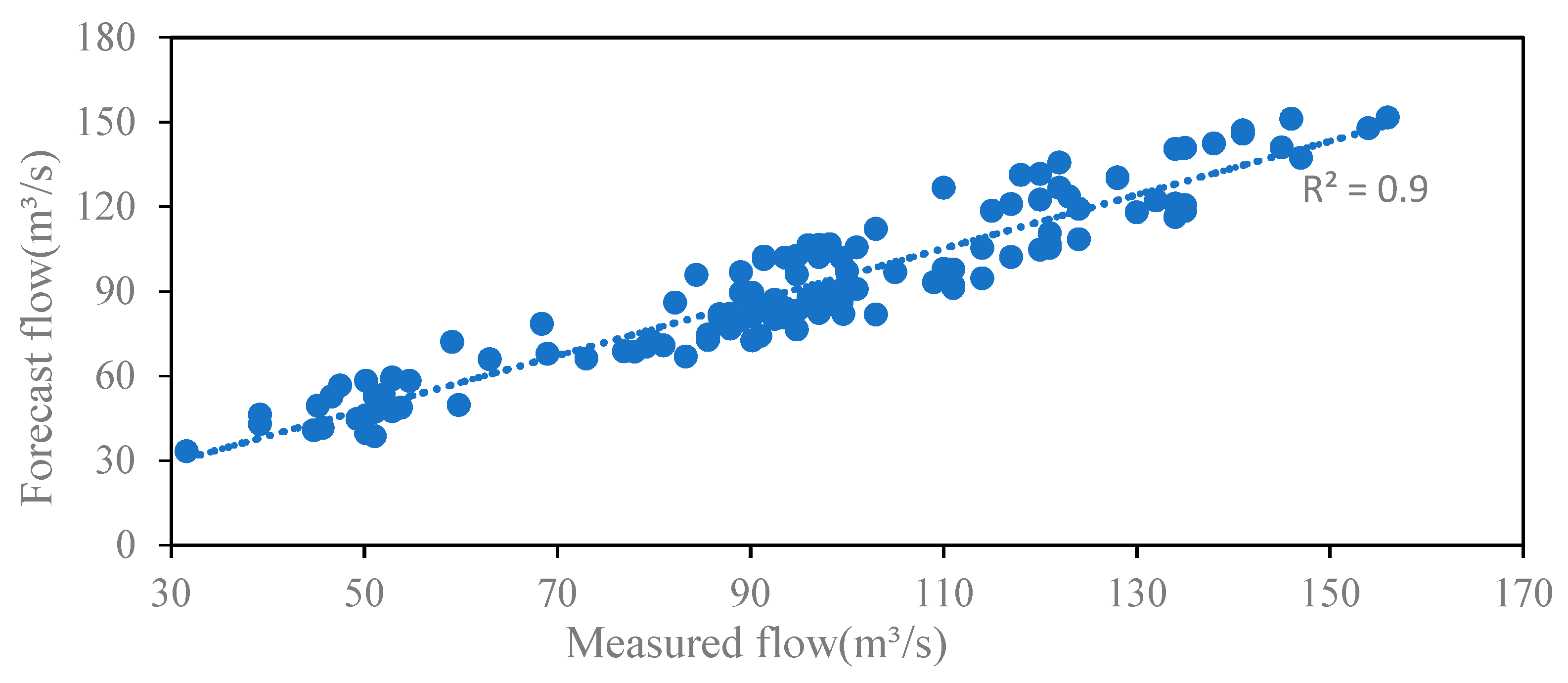
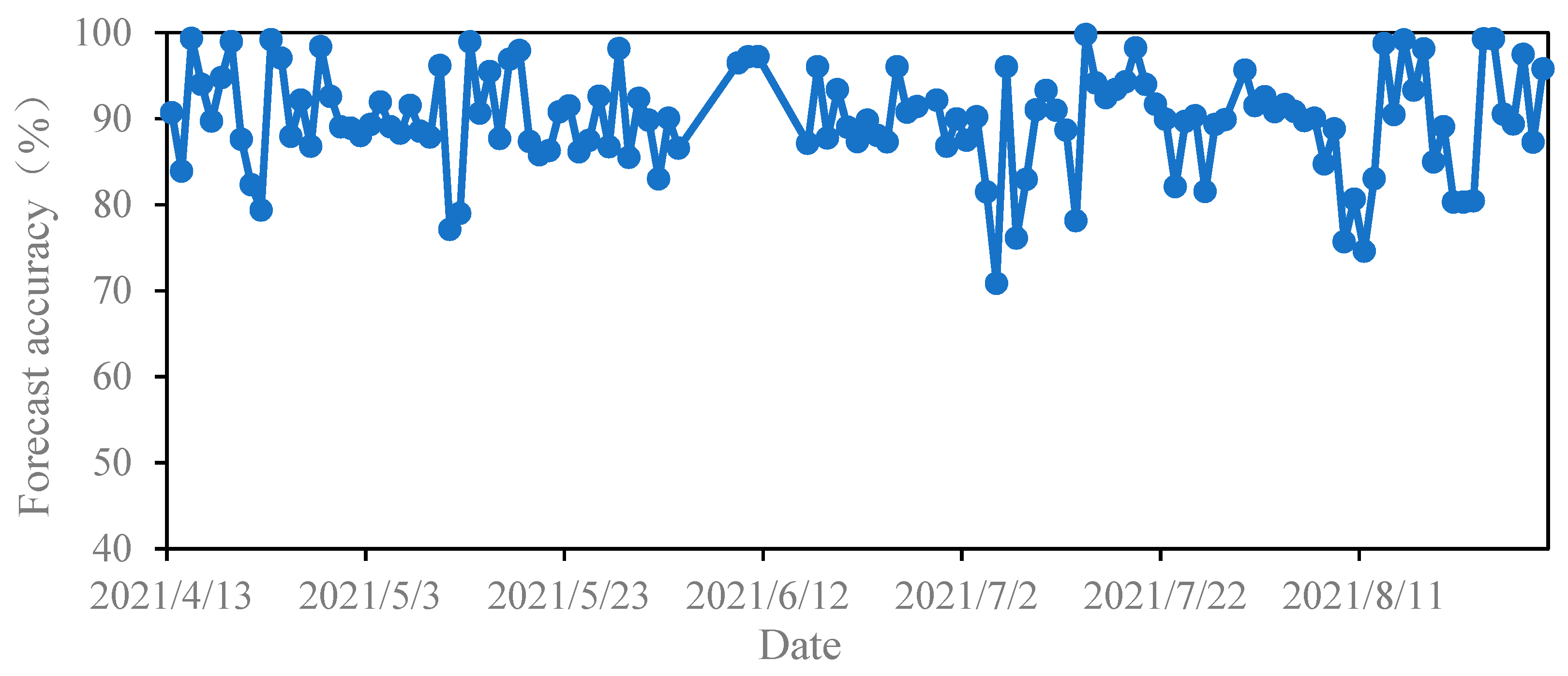
| Situation | Serial Number | Parameter | Reference Parameter Value | Lower Limit | Upper Limit |
|---|---|---|---|---|---|
| Before parameter optimization | 1 | KC | 0.6 | 0.5 | 1.0 |
| 2 | θm | 80 | 60 mm | 80 mm | |
| 3 | FB | 0.5 | 0 | 1 | |
| 4 | f0 | 1.8 | 1 mm/min | 2 mm/min | |
| 5 | fc | 0.4 | 0.3 mm/min | 0.5 mm/min | |
| 6 | K | 0.05 | 0.04/min | 0.05/min | |
| 7 | B | 4 | 0 | 5 | |
| 8 | CS | 0.5 | 0.1 | 1.0 | |
| 9 | L | 2 | 1 | 5 | |
| After parameter optimization | 1 | KC | 0.55 | 0.5 | 1.0 |
| 2 | θm | 70 | 60 mm | 80 mm | |
| 3 | FB | 0.5 | 0 | 1 | |
| 4 | f0 | 1.8 | 1 mm/min | 2 mm/min | |
| 5 | fc | 0.4 | 0.3 mm/min | 0.5 mm/min | |
| 6 | K | 0.04 | 0.04/min | 0.05/min | |
| 7 | B | 4 | 0 | 5 | |
| 8 | CS | 0.7 | 0.1 | 1.0 | |
| 9 | L | 2 | 1 | 5 |
| Accuracy Indicators | MAE | MRE | R2 | |
|---|---|---|---|---|
| Conditions | ||||
| Before parameter optimization | 6.16 | 8.62% | 0.90 | |
| After parameter optimization | 5.16 | 7.60% | 0.96 | |
| Accuracy Indicators | MAE | MRE | R2 | |
|---|---|---|---|---|
| Model Category | ||||
| XAJ | 6.03 | 8.60% | 0.90 | |
| LSTM | 10.26 | 9.50% | 0.89 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, Y.; Liu, X.; Shen, C. A Multiple Model Approach for Flood Forecasting, Simulation, and Evaluation Coupling in Zhouqu County. Water 2023, 15, 4246. https://doi.org/10.3390/w15244246
Li Y, Liu Y, Liu X, Shen C. A Multiple Model Approach for Flood Forecasting, Simulation, and Evaluation Coupling in Zhouqu County. Water. 2023; 15(24):4246. https://doi.org/10.3390/w15244246
Chicago/Turabian StyleLi, Yongfeng, Yi Liu, Xiaoming Liu, and Chao Shen. 2023. "A Multiple Model Approach for Flood Forecasting, Simulation, and Evaluation Coupling in Zhouqu County" Water 15, no. 24: 4246. https://doi.org/10.3390/w15244246
APA StyleLi, Y., Liu, Y., Liu, X., & Shen, C. (2023). A Multiple Model Approach for Flood Forecasting, Simulation, and Evaluation Coupling in Zhouqu County. Water, 15(24), 4246. https://doi.org/10.3390/w15244246







