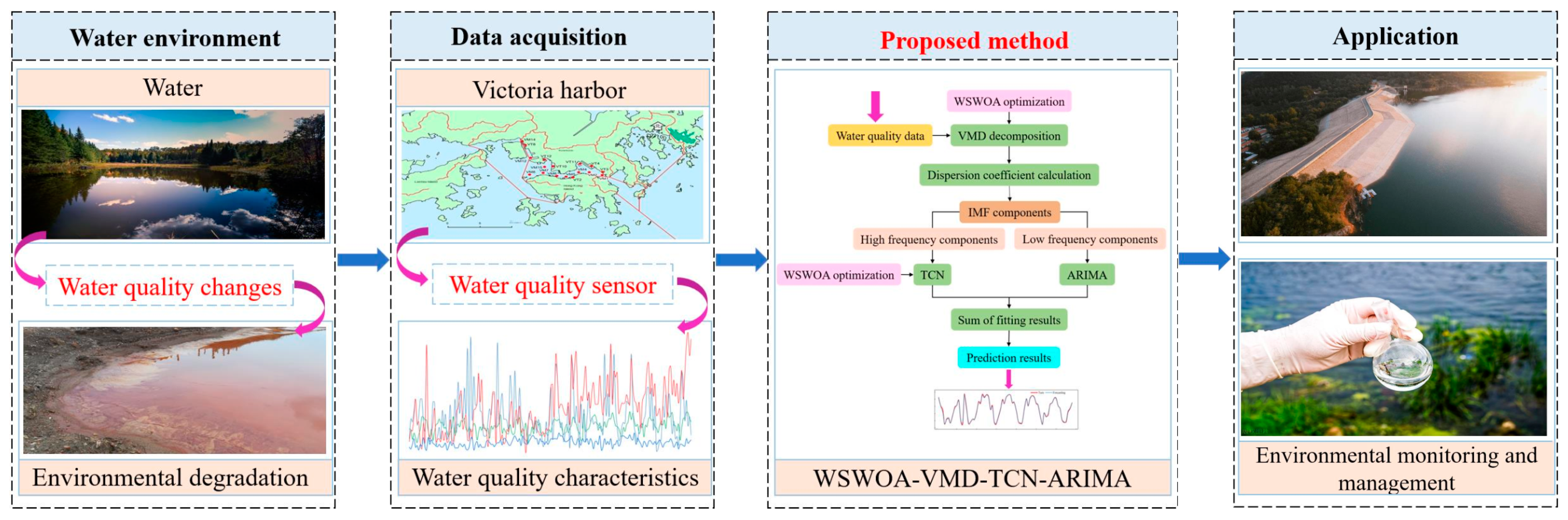
A Combined Model for Water Quality Prediction Based on VMD-TCN-ARIMA Optimized by WSWOA
Abstract
:1. Introduction
- A new optimization algorithm WSWOA is proposed based on the WOA algorithm. It introduces the perturbation strategy of dual weight factors and the particle swarm search method, which enhances the update ability of the later population and improves the convergence speed of the algorithm.
- The adaptive algorithm WSWOA-VMD is used to process water quality data. The number of modes and penalty parameters of VMD decomposition are optimized through WSWOA to improve the input quality of the prediction model.
- A TCN-ARIMA combination model is proposed to achieve water quality prediction. The different types of modal components obtained via decomposition are input into the corresponding prediction algorithms, which improves the accuracy and efficiency of the model.
2. Methodology
2.1. Parameter Optimization Model
2.1.1. WOA
- Step 1: Encircling prey
- Step 2: Bubble net fishing
- Step 3: Random search
2.1.2. WSWOA
- Encircling prey:
- Bubble net fishing:
- Random search:
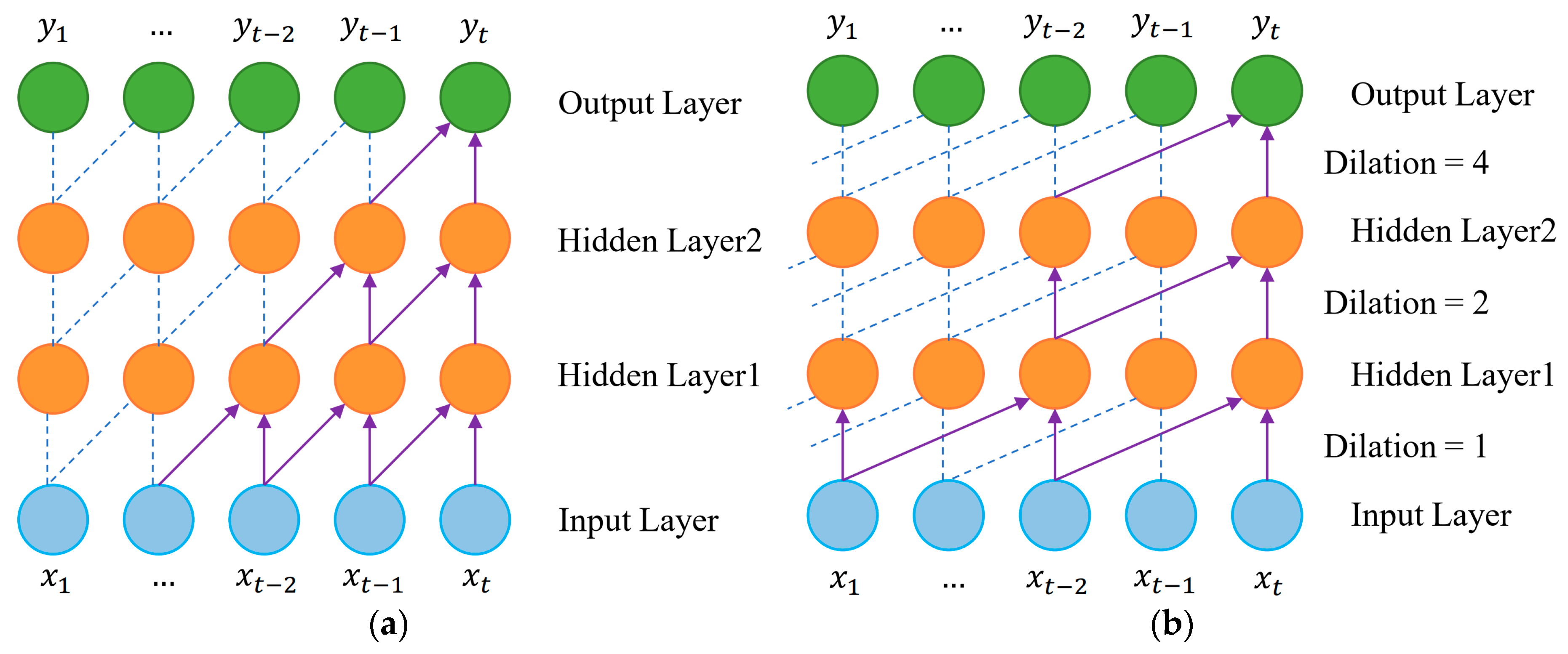
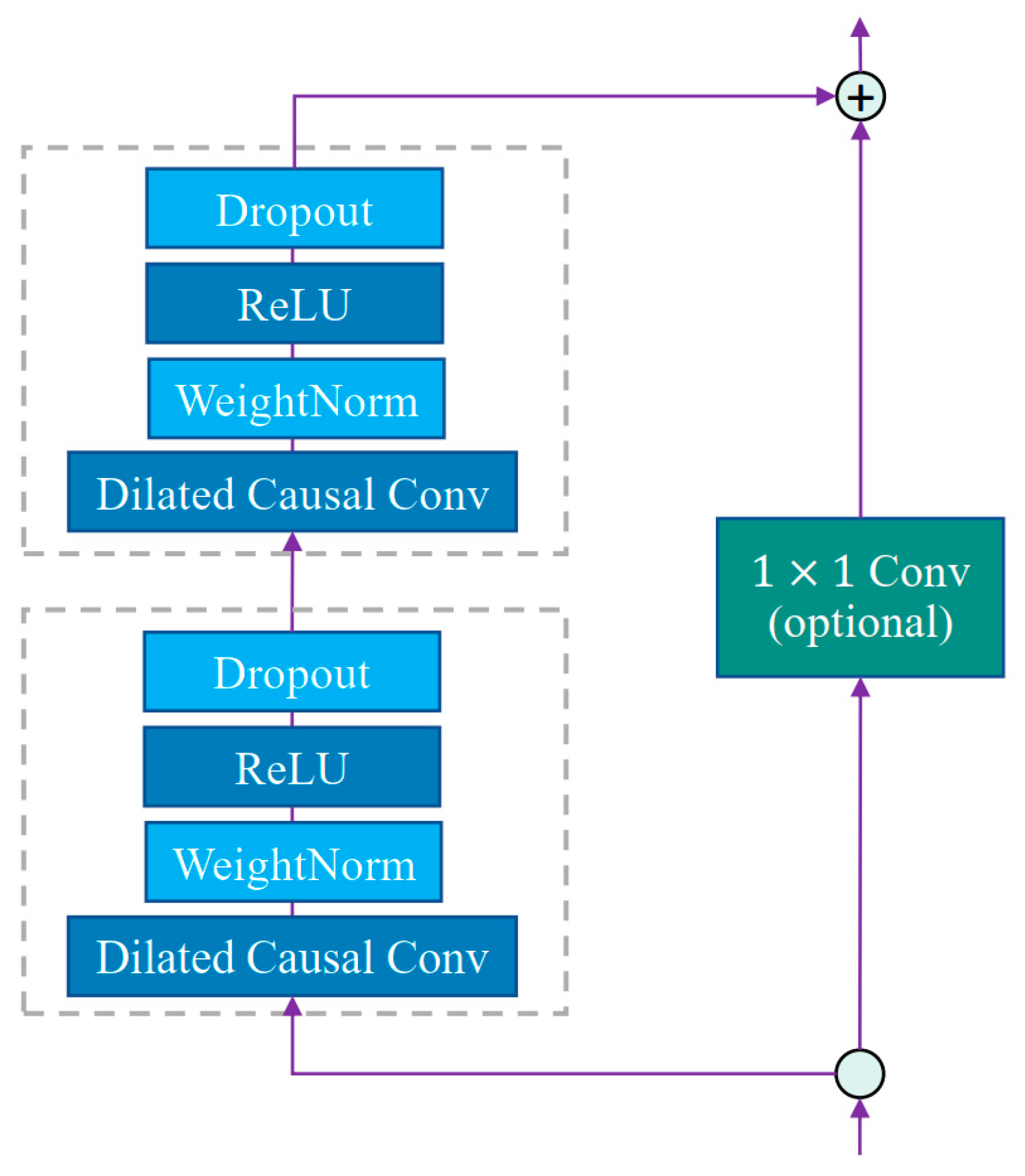
2.2. Feature Extraction Model
2.2.1. VMD
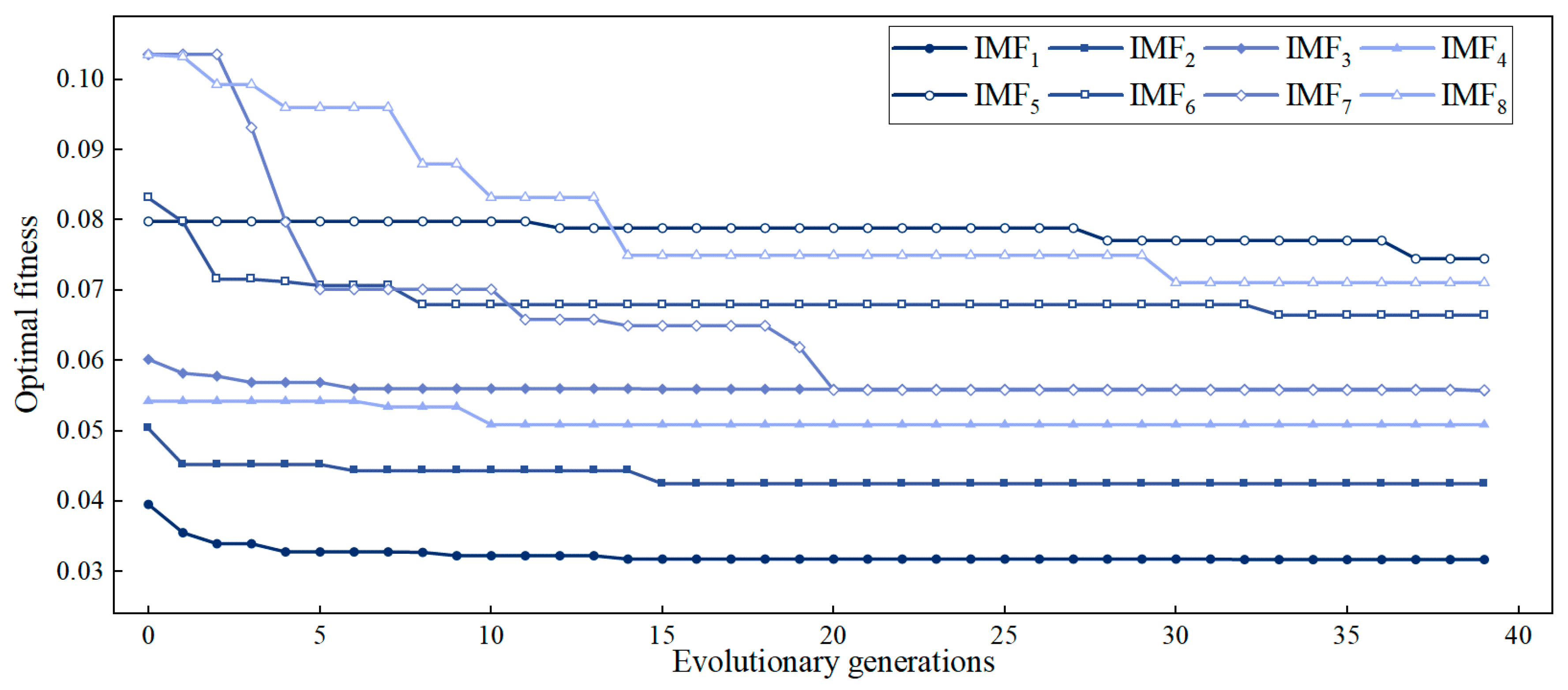
2.2.2. VMD Parameters Optimized Based on WSWOA
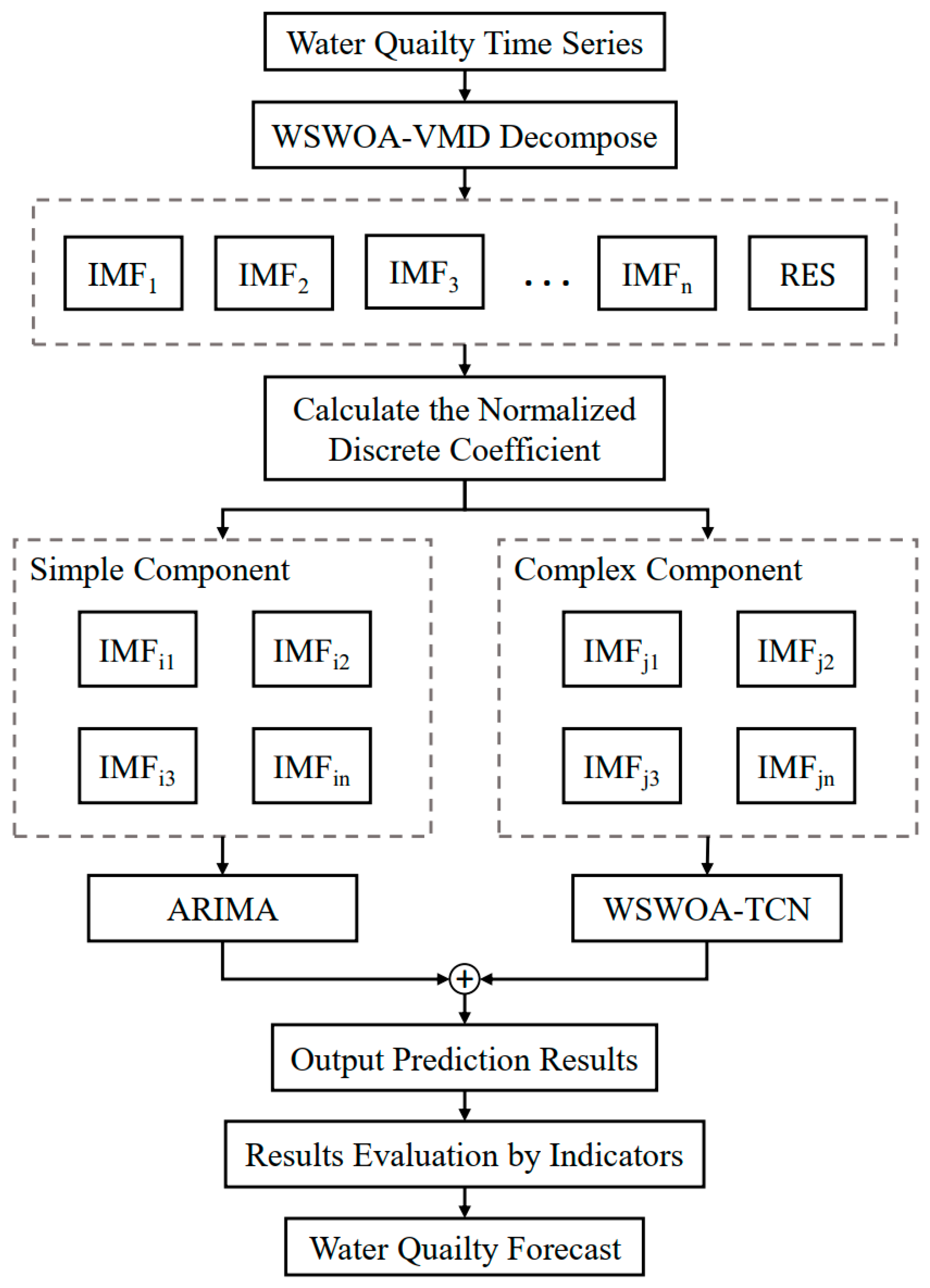
2.3. Combined Forecasting Model
2.3.1. Feature Classification
2.3.2. Model Selection
2.4. VMD-TCN-ARIMA Model Optimized by WSWOA
3. The Result of the Proposed Model
3.1. Dataset Settings
3.2. Evaluation Metrics
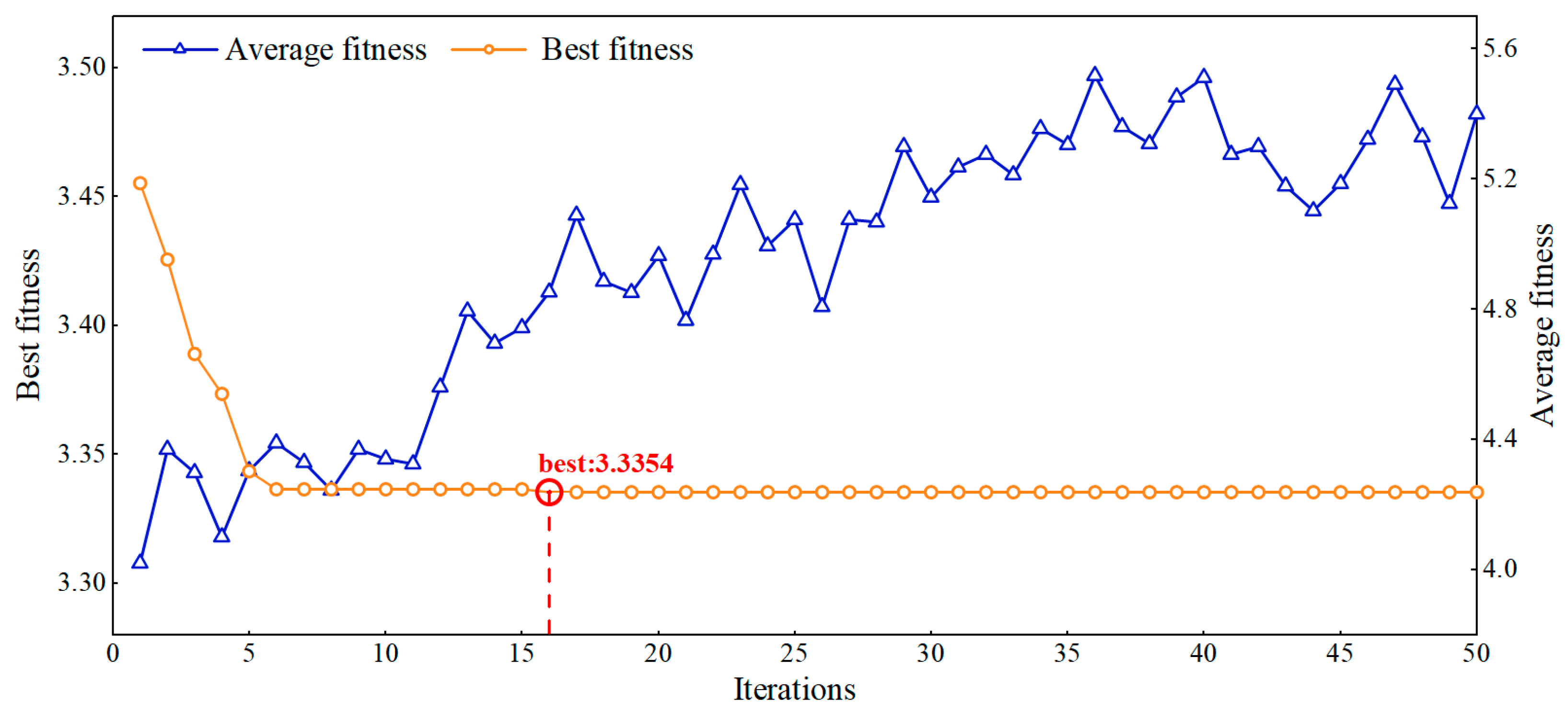
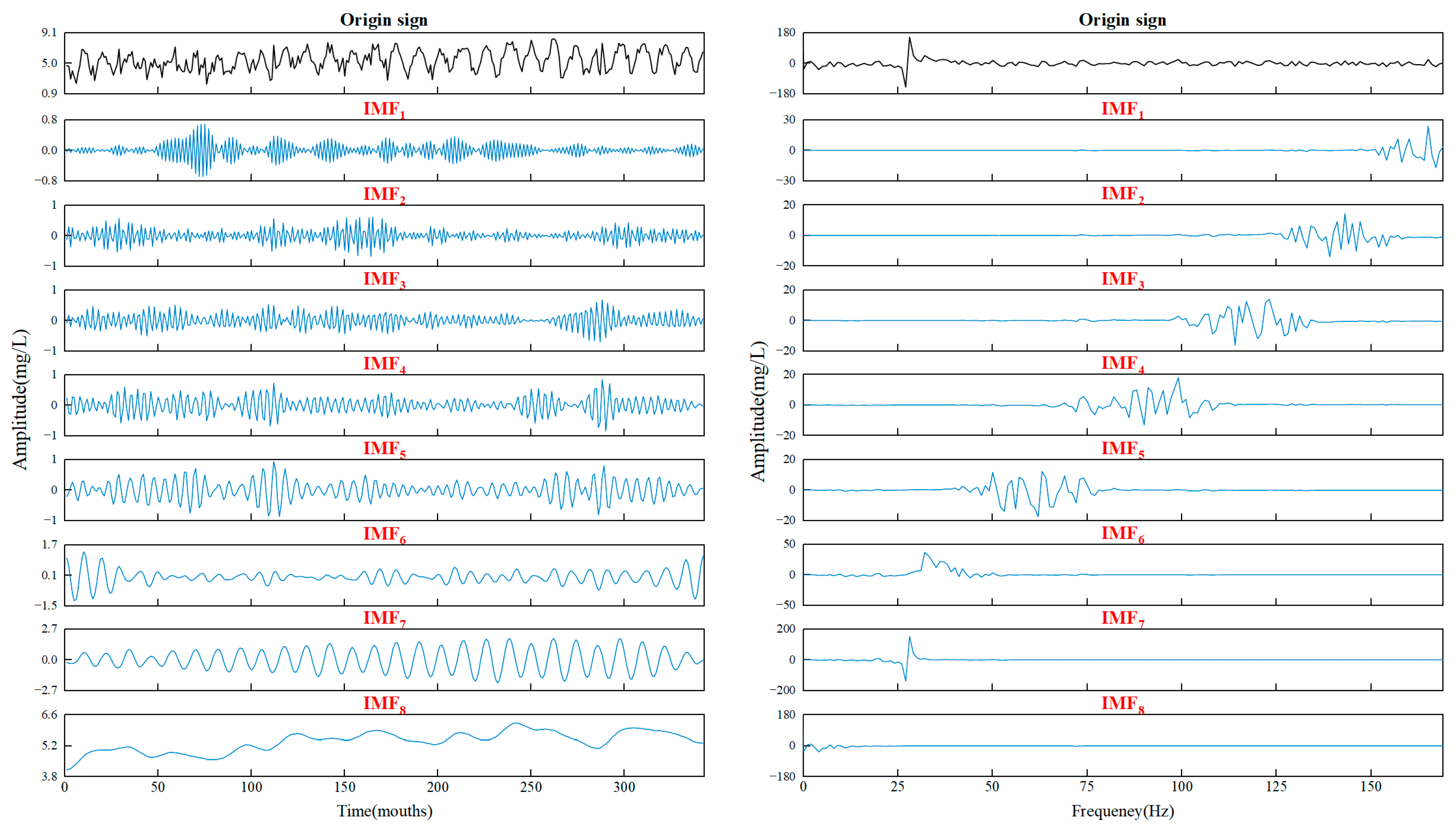
3.3. Model Decomposition Results Based on WSWOA-VMD
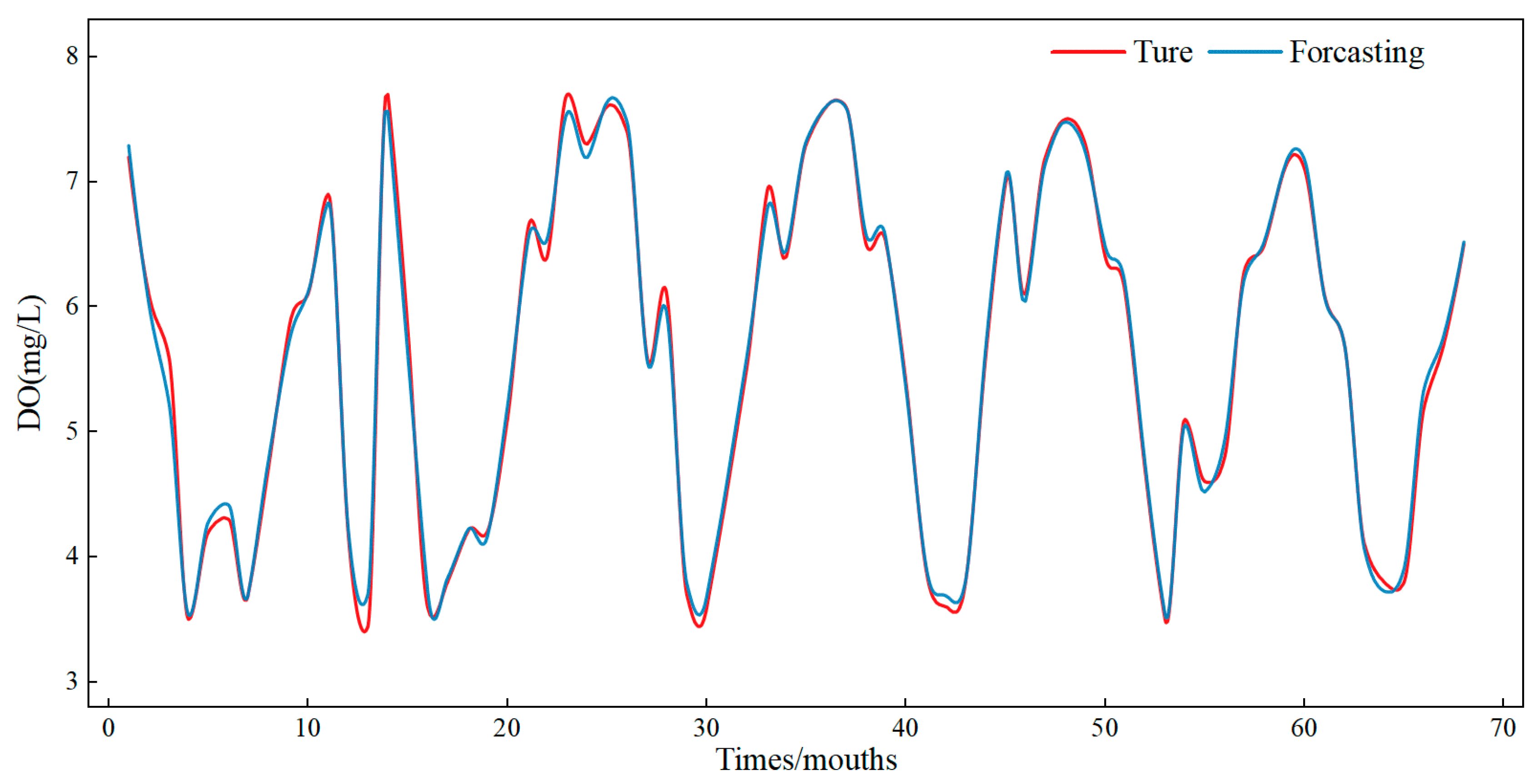
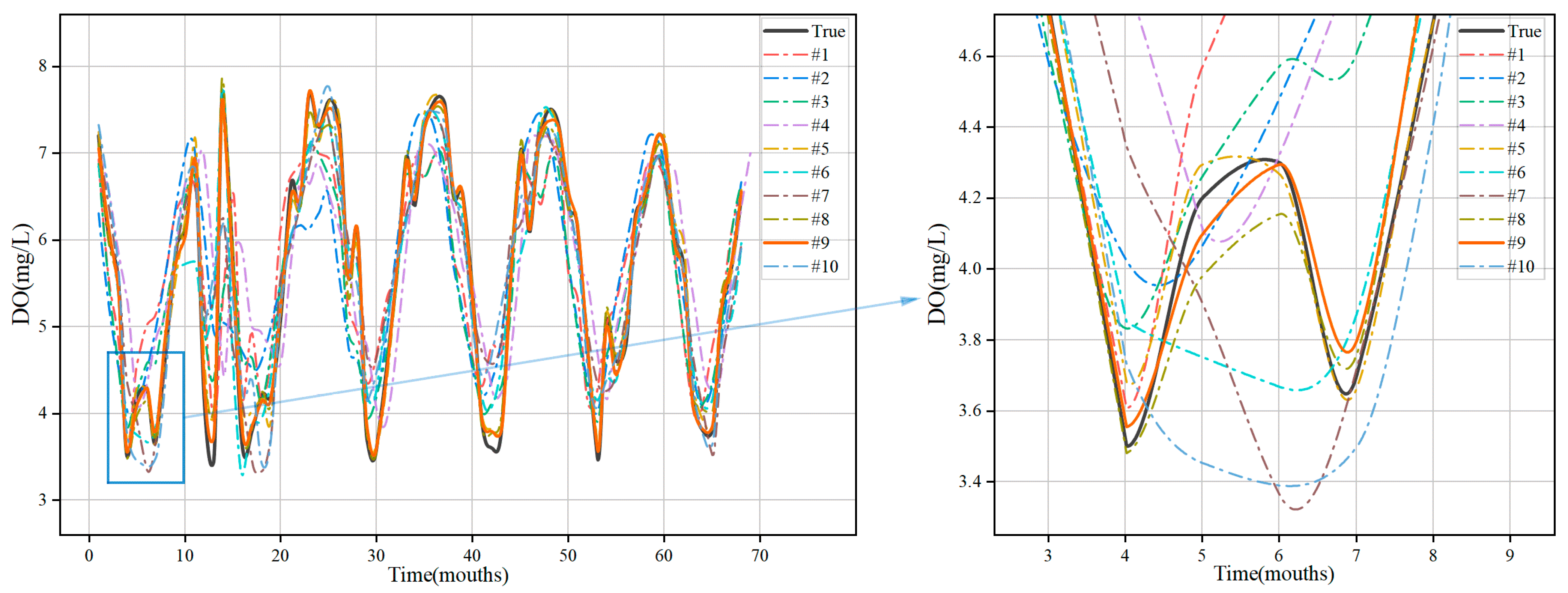
3.4. Water Quality Prediction Results Based on WSWOA-VMD-TCN-ARIMA
4. Analysis of Experimental Results
4.1. Multi-Model Comparison
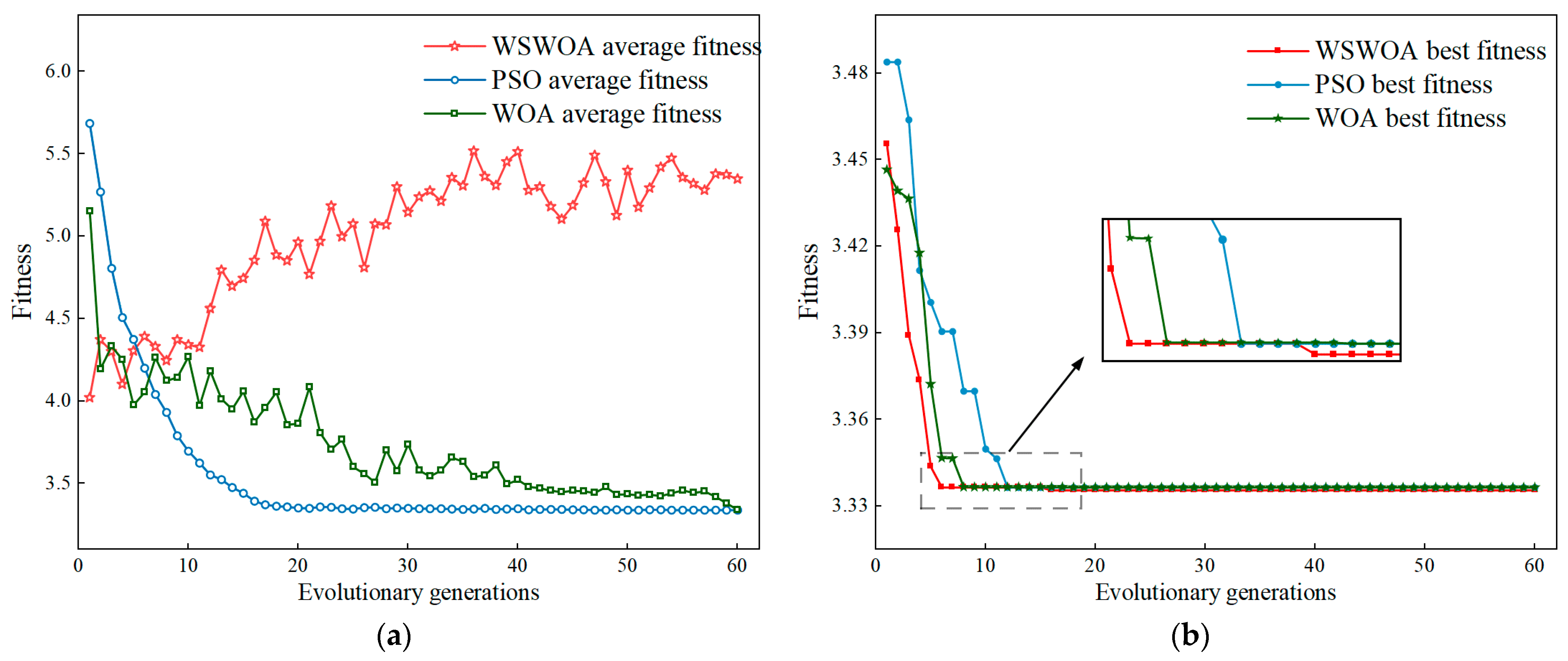
4.1.1. The Influence of Using Optimization Algorithm WSWOA
4.1.2. The Influence of Using Combined Model
- The influence of adding WSWOA-VMD
- 2.
- The influence of using TCN-ARIMA
4.2. Further Research
5. Discussion
6. Conclusions
- The results of decomposing the time series demonstrate that the VMD optimized by WSWOA can effectively suppress the mixing of modal components, extract various features from the original sequence, and enhance the accuracy of the subsequent prediction steps. Compared with other existing parameter optimization algorithms, this method has stronger global search capabilities and faster convergence speed, providing an effective new method for existing model parameter optimization technology.
- Comparisons with different forecasting models show that the combined model is more accurate and efficient in forecasting than a single model. It is demonstrated that the TCN-ARIMA combined model can effectively suit the modal components following VMD decomposition of the original data and achieve more precise and faster prediction results.
- The results of predicting multiple water quality characteristics demonstrate that the model in this study is distinct from the majority of models at this stage, which must be restricted to a fixed range of water quality areas and characteristics. The model proposed in this study can adaptively find the optimal model parameters for different types of time series data by utilizing the WSWOA, which removes the need for manual adjustments and greatly improves the generalizability and intelligence of the model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, Z.X.; Zhang, Q.; Singh, V.P.; Pokhrel, Y.; Li, J.P.; Xu, C.Y.; Wu, W.H. Drying in the low-latitude Atlantic Ocean contributed to terrestrial water storage depletion across Eurasia. Nat. Commun. 2022, 13, 10. [Google Scholar] [CrossRef]
- Yan, T.; Shen, S.-L.; Zhou, A. Indices and models of surface water quality assessment: Review and perspectives. Environ. Pollut. 2022, 308, 119611. [Google Scholar] [CrossRef] [PubMed]
- Li, H.M.; Wang, F.Q.; Zhang, C.Y.; Wang, L.Y.; An, X.W.; Dong, G.H. Sustainable supplier selection for water environment treatment public-private partnership projects. J. Clean. Prod. 2021, 324, 18. [Google Scholar] [CrossRef]
- Han, M.; Su, Z.Y.; Na, X.D. Predict water quality using an improved deep learning method based on spatiotemporal feature correlated: A case study of the Tanghe Reservoir in China. Stoch. Environ. Res. Risk Assess. 2023, 37, 2563–2575. [Google Scholar] [CrossRef]
- Li, H.M.; Xia, Q.; Wen, S.P.; Wang, L.Y.; Lv, L.L. Identifying Factors Affecting the Sustainability of Water Environment Treatment Public-Private Partnership Projects. Adv. Civ. Eng. 2019, 2019, 15. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Rahman, A.; Olbert, A.I. A comprehensive method for improvement of water quality index (WQI) models for coastal water quality assessment. Water Res. 2022, 219, 20. [Google Scholar] [CrossRef]
- Dong, Y.A.; Ren, Z.; Li, L.H. Forecast of Water Structure Based on GM (1,1) of the Gray System. Sci. Program. 2022, 2022, 7. [Google Scholar] [CrossRef]
- Zhang, J.P.; Wang, Y.H.; Zhao, Y.; Fang, H.Y. Multi-scale flood prediction based on GM (1,2)-fuzzy weighted Markov and wavelet analysis. J. Water Clim. Chang. 2021, 12, 2217–2231. [Google Scholar] [CrossRef]
- Ghaemi, E.; Tabesh, M.; Nazif, S. Improving the ARIMA Model Prediction for Water Quality Parameters of Urban Water Distribution Networks (Case Study: CANARY Dataset). Int. J. Environ. Res. 2022, 16, 10. [Google Scholar] [CrossRef]
- Doorn, N. Artificial intelligence in the water domain: Opportunities for responsible use. Sci. Total Environ. 2021, 755, 10. [Google Scholar] [CrossRef]
- Noori, R.; Karbassi, A.R.; Ashrafi, K.; Ardestani, M.; Mehrdadi, N. Development and application of reduced-order neural network model based on proper orthogonal decomposition for BOD5 monitoring: Active and online prediction. Environ. Prog. Sustain. Energy 2013, 32, 120–127. [Google Scholar] [CrossRef]
- Chen, L.H.; Li, L. Evaluation of dissolved oxygen in water by artificial neural network and sample optimization. J. Cent. South Univ. Technol. 2008, 15, 416–420. [Google Scholar] [CrossRef]
- AlDahoul, N.; Essam, Y.; Kumar, P.; Ahmed, A.N.; Sherif, M.; Sefelnasr, A.; Elshafie, A. Suspended sediment load prediction using long short-term memory neural network. Sci. Rep. 2021, 11, 22. [Google Scholar] [CrossRef]
- Fu, Y.X.; Hu, Z.H.; Zhao, Y.C.; Huang, M.X. A Long-Term Water Quality Prediction Method Based on the Temporal Convolutional Network in Smart Mariculture. Water 2021, 13, 2907. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Kavianpour, M.R. Development of wavelet-ANN models to predict water quality parameters in Hilo Bay, Pacific Ocean. Mar. Pollut. Bull. 2015, 98, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Noori, R.; Karbassi, A.; Ashrafi, K.; Ardestani, M.; Mehrdadi, N.; Nabi Bidhendi, G.-R. Active and online prediction of BOD5 in river systems using reduced-order support vector machine. Environ. Earth Sci. 2012, 67, 141–149. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.J.; Wang, K.; Zhang, D. Simulation of Pollution Load at Basin Scale Based on LSTM-BP Spatiotemporal Combination Model. Water 2021, 13, 516. [Google Scholar] [CrossRef]
- Baek, S.S.; Pyo, J.; Chun, J.A. Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Li, S.X.; Xie, J.C.; Yang, X.; Jing, X. Comparison of hybrid machine learning models to predict short-term meteorological drought in Guanzhong region, China. Water Sci. Technol. 2023, 87, 2756–2775. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Li, C.L.; Jiang, Y.Q.; Sun, L.; Zhao, R.B.; Yan, K.F.; Wang, W.H. Accurate prediction of water quality in urban drainage network with integrated EMD-LSTM model. J. Clean. Prod. 2022, 354, 12. [Google Scholar] [CrossRef]
- Wang, F.H.; Zhang, D.M.; Min, G.Y.; Li, J.X. Reservoir Production Prediction Based on Variational Mode Decomposition and Gated Recurrent Unit Networks. IEEE Access 2021, 9, 53317–53325. [Google Scholar] [CrossRef]
- Geng, G.C.; He, Y.; Zhang, J.; Qin, T.X.; Yang, B. Short-Term Power Load Forecasting Based on PSO-Optimized VMD-TCN-Attention Mechanism. Energies 2023, 16, 4616. [Google Scholar] [CrossRef]
- Liu, F.P.; Liu, Y.; Yang, C.; Lai, R.X. A New Precipitation Prediction Method Based on CEEMDAN-IWOA-BP Coupling. Water Resour. Manag. 2022, 36, 4785–4797. [Google Scholar] [CrossRef]
- Yan, T.; Zhou, A.N.; Shen, S.L. Prediction of long-term water quality using machine learning enhanced by Bayesian optimisation. Environ. Pollut. 2023, 318, 10. [Google Scholar] [CrossRef] [PubMed]
- Flores, V.; Bravo, I.; Saavedra, M. Water Quality Classification and Machine Learning Model for Predicting Water Quality Status-A Study on Loa River Located in an Extremely Arid Environment: Atacama Desert. Water 2023, 15, 2868. [Google Scholar] [CrossRef]
- Kumar, Y.; Kaur, A. Variants of bat algorithm for solving partitional clustering problems. Eng. Comput. 2022, 38, 1973–1999. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Lu, K.Z.; Ma, Z.M. A modified whale optimization algorithm for parameter estimation of software reliability growth models. J. Algorithms Comput. Technol. 2021, 15, 14. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Pan, G.F.; Chen, B.; Han, J.Y.; Zhao, Y.; Zhang, C.H. Short-term wind speed prediction model based on GA-ANN improved by VMD. Renew. Energy 2020, 156, 1373–1388. [Google Scholar] [CrossRef]
- Noori, R.; Safavi, S.; Nateghi Shahrokni, S.A. A reduced-order adaptive neuro-fuzzy inference system model as a software sensor for rapid estimation of five-day biochemical oxygen demand. J. Hydrol. 2013, 495, 175–185. [Google Scholar] [CrossRef]
- Wang, L.S.; Liu, Y.H.; Li, T.S.; Xie, X.Z.; Chang, C.M. Short-Term PV Power Prediction Based on Optimized VMD and LSTM. IEEE Access 2020, 8, 165849–165862. [Google Scholar] [CrossRef]
- Rajabi, S.; Azari, M.S.; Santini, S.; Flammini, F. Fault diagnosis in industrial rotating equipment based on permutation entropy, signal processing and multi-output neuro-fuzzy classifier. Expert Syst. Appl. 2022, 206, 16. [Google Scholar] [CrossRef]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. IEEE. Temporal Convolutional Networks for Action Segmentation and Detection. In Proceedings of the 30th IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1003–1012. [Google Scholar] [CrossRef]
- Liu, X.L.; Zhao, J.J.; Lin, S.F.; Li, J.Q.; Wang, S.H.; Zhang, Y.M.; Gao, Y.Y.; Chai, J.C. Fine-Grained Individual Air Quality Index (IAQI) Prediction Based on Spatial-Temporal Causal Convolution Network: A Case Study of Shanghai. Atmosphere 2022, 13, 959. [Google Scholar] [CrossRef]
- Song, T.Z.; Song, Y.; Wang, Y.X.; Huang, X.G. Residual network with dense block. J. Electron. Imaging 2018, 27, 9. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J.; Nazarko, L.; Rabayah, H.S.; Abendeh, R.M.; Alawneh, R. ARIMA Models in Solar Radiation Forecasting in Different Geographic Locations. Energies 2023, 16, 5029. [Google Scholar] [CrossRef]
- Han, Z.Y.; Zhao, J.; Leung, H.; Ma, A.; Wang, W. A Review of Deep Learning Models for Time Series Prediction. IEEE Sens. J. 2021, 21, 7833–7848. [Google Scholar] [CrossRef]
| Metrics | Formula | Explanation |
|---|---|---|
| RMSE (Root Mean Square Error) | RMSE denotes the mean error, which is more sensitive to extreme values, and it can be used as the benchmark for the robustness test of the model. | |
| MAE (Mean Absolute Error) | MAE is a linear score in which all individual differences are equally weighted on the mean. | |
| SMAPE (Symmetric Mean Absolute Percentage Error) | SMAPE uses a percentage 0–100% to represent the error size of the model. | |
| NSE (Nash–Sutcliffeefficiency Coefficient) | NSE is widely utilized model performance indices in the water-related research domain, and the closer the value is to 1, the better the predictive ability of the model. | |
| R2 (Coefficient of Determination) | R2 represents the goodness of model fitting. The closer the value is to 1, the better the fit between the fitted value and the actual value, and the better the model performance. |
| Time Step T | Learning Rate LR | Classification | ||
|---|---|---|---|---|
| IMF1 | 7 | 0.105 | 1.000 | complex |
| IMF2 | 7 | 0.099 | 0.857 | complex |
| IMF3 | 7 | 0.052 | 0.594 | complex |
| IMF4 | 8 | 0.073 | 0.401 | complex |
| IMF5 | 5 | 0.114 | 0.225 | complex |
| IMF6 | 4 | 0.325 | 0.158 | simple |
| IMF7 | 4 | 0.097 | 0.076 | simple |
| IMF8 | 4 | 0.032 | 0.000 | simple |
| Model | Abbreviation | RMSE/mg | MAE/mg | SMAPE | NSE | R2 | TIME |
|---|---|---|---|---|---|---|---|
| BP | #1 | 0.936 | 0.684 | 12.86% | 0.518 | 0.723 | 1.89 |
| LSTM | #2 | 0.890 | 0.675 | 12.61% | 0.564 | 0.756 | 7.65 |
| ARIMA | #3 | 1.139 | 0.843 | 15.32% | 0.487 | 0.691 | 0.82 |
| TCN | #4 | 0.872 | 0.629 | 11.98% | 0.582 | 0.763 | 6.82 |
| VMD-TCN | #5 | 0.163 | 0.121 | 2.39% | 0.985 | 0.994 | 42.44 |
| EMD-TCN | #6 | 0.495 | 0.372 | 7.31% | 0.866 | 0.935 | 32.39 |
| CEEMDAN-TCN | #7 | 0.572 | 0.426 | 8.47% | 0.822 | 0.901 | 34.58 |
| VMD-LSTM-ARIMA | #8 | 0.158 | 0.123 | 2.38% | 0.986 | 0.994 | 44.42 |
| VMD-TCN-ARIMA | #9 | 0.096 | 0.075 | 1.48% | 0.995 | 0.996 | 31.38 |
| CEEMDAN-IWOA-BP | #10 | 0.632 | 0.414 | 8.26% | 0.828 | 0.911 | 11.96 |
| VMD Optimal Solutions | RMSE | MAE | SMAPE | NSE | R2 | ||
|---|---|---|---|---|---|---|---|
| K | σ | ||||||
| DOsat | 9 | 1190 | 1.467 | 1.146 | 1.40% | 0.985 | 0.994 |
| SS | 8 | 1277 | 0.436 | 0.349 | 8.17% | 0.987 | 0.994 |
| turbidity | 8 | 1013 | 0.293 | 0.239 | 9.55% | 0.988 | 0.995 |
| Salinity | 9 | 2082 | 0.185 | 0.146 | 0.48% | 0.989 | 0.996 |
| Pheophytin | 7 | 1761 | 0.113 | 0.092 | 13.09% | 0.986 | 0.995 |
| SD | 9 | 1311 | 0.098 | 0.072 | 3.02% | 0.980 | 0.994 |
| SiO2 | 9 | 1769 | 0.041 | 0.032 | 6.09% | 0.985 | 0.995 |
| BOD | 9 | 1569 | 0.033 | 0.027 | 7.66% | 0.985 | 0.993 |
| TN | 9 | 1149 | 0.023 | 0.019 | 5.51% | 0.983 | 0.993 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, H.; Gou, X.; Wang, X.; Zhang, M. A Combined Model for Water Quality Prediction Based on VMD-TCN-ARIMA Optimized by WSWOA. Water 2023, 15, 4227. https://doi.org/10.3390/w15244227
Zuo H, Gou X, Wang X, Zhang M. A Combined Model for Water Quality Prediction Based on VMD-TCN-ARIMA Optimized by WSWOA. Water. 2023; 15(24):4227. https://doi.org/10.3390/w15244227
Chicago/Turabian StyleZuo, Hongyu, Xiantai Gou, Xin Wang, and Mengyin Zhang. 2023. "A Combined Model for Water Quality Prediction Based on VMD-TCN-ARIMA Optimized by WSWOA" Water 15, no. 24: 4227. https://doi.org/10.3390/w15244227





