Addressing Nitrate Contamination in Groundwater: The Importance of Spatial and Temporal Understandings and Interpolation Methods
Abstract
:1. Introduction
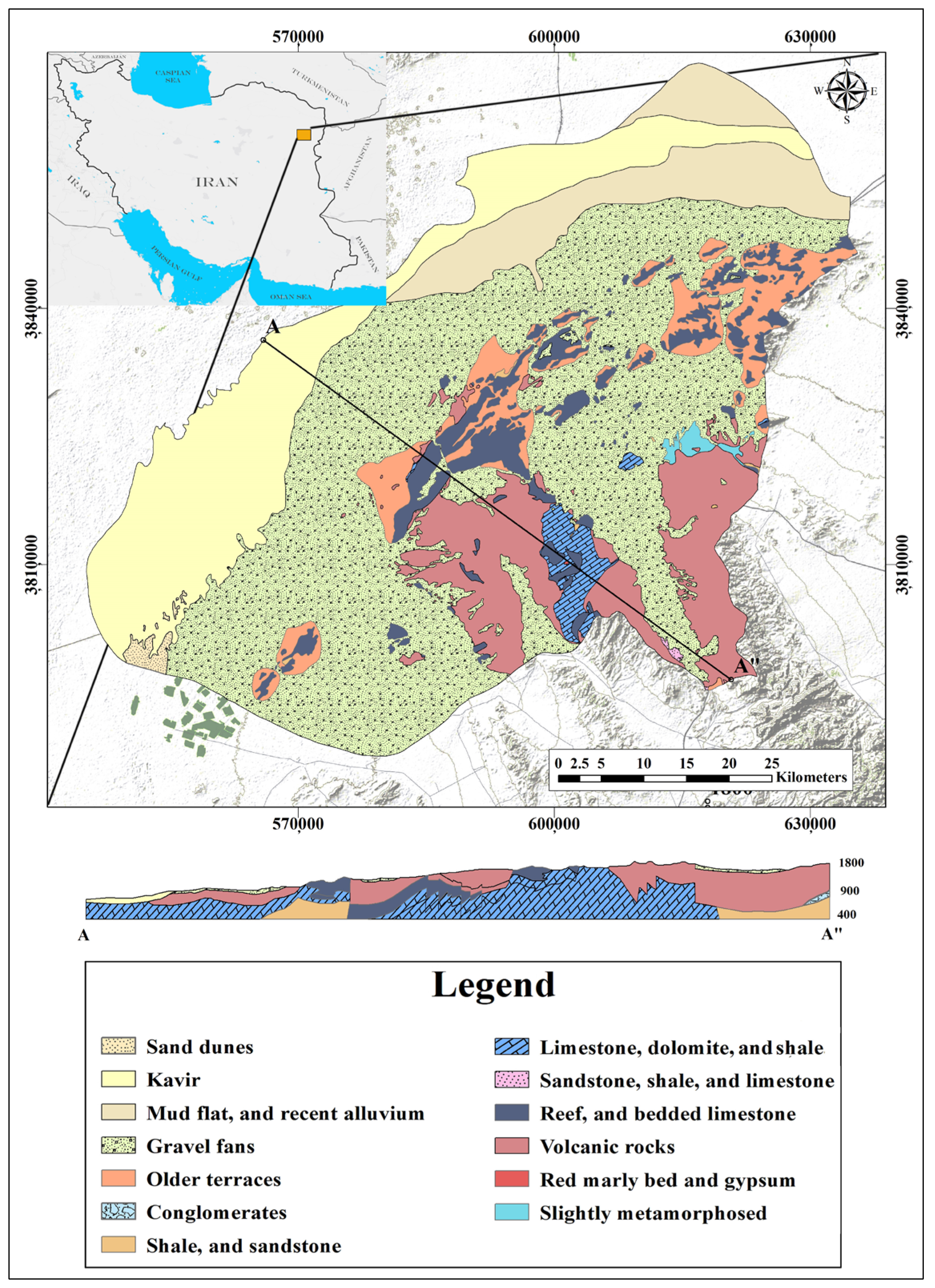
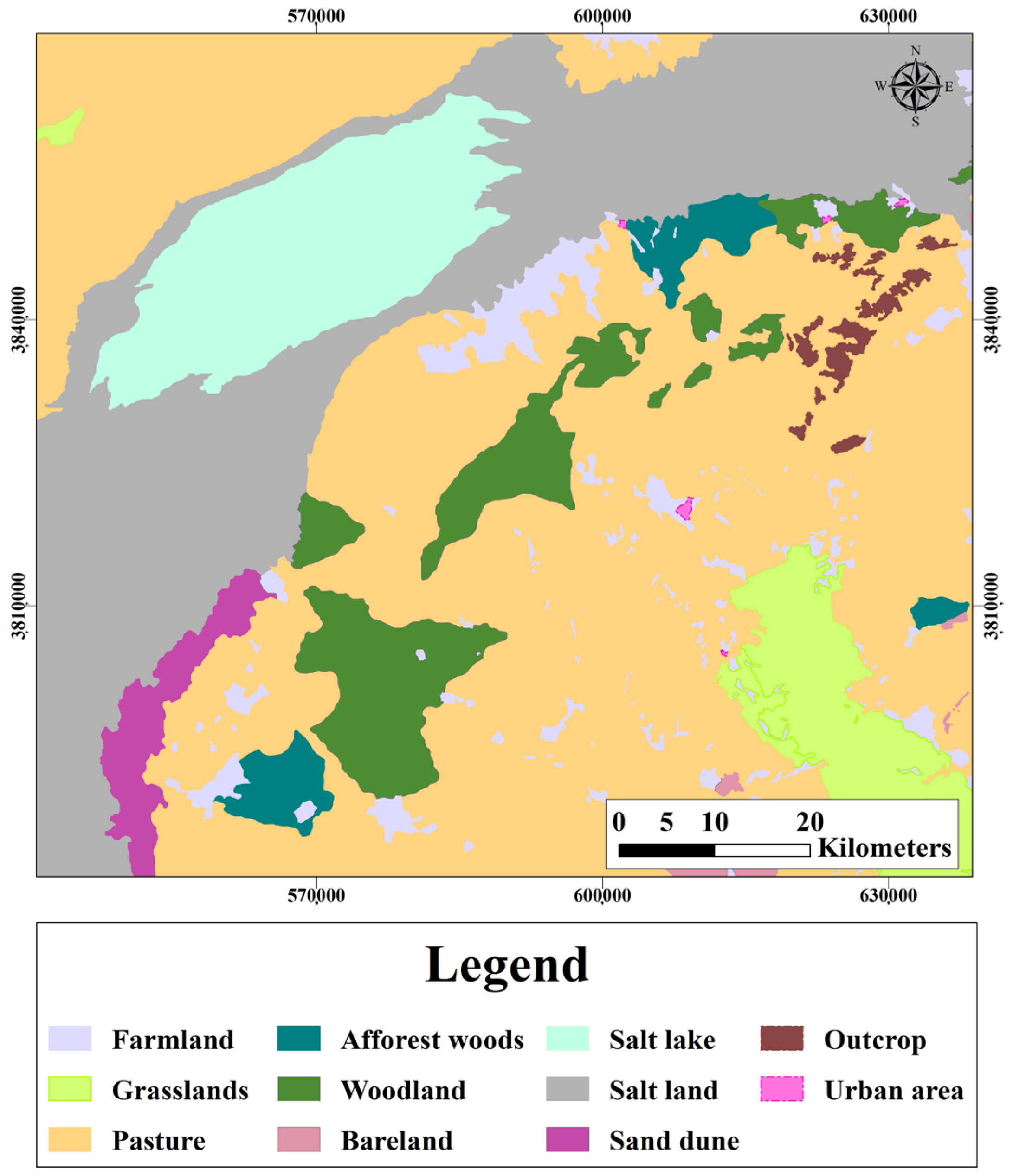
2. Study Area, Hydrology and Hydrogeology Setting
3. Materials and Methods
3.1. Interpolation and Spatial Analysis
3.2. Interpolation Methods
3.2.1. LPI Method
3.2.2. IDW
3.2.3. Classical Kriging Methods
- OK
- SK
- UK
3.2.4. EBK
3.3. Interpolation and Validation
4. Results and Discussion
4.1. Measured NO3 Concentrations
4.2. Visualisation of Prediction
4.3. Cross-Validation Analyses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zaresefat, M.; Derakhshani, R. Revolutionizing Groundwater Management with Hybrid AI Models: A Practical Review. Water 2023, 15, 1750. [Google Scholar] [CrossRef]
- Rezaei, A.; Hassani, H.; Hassani, S.; Jabbari, N.; Fard Mousavi, S.B.; Rezaei, S. Evaluation of Groundwater Quality and Heavy Metal Pollution Indices in Bazman Basin, Southeastern Iran. Groundw. Sustain. Dev. 2019, 9, 100245. [Google Scholar] [CrossRef]
- Rezaei, A.; Hassani, H.; Jabbari, N. Evaluation of Groundwater Quality and Assessment of Pollution Indices for Heavy Metals in North of Isfahan Province, Iran. Sustain. Water Resour. Manag. 2019, 5, 491–512. [Google Scholar] [CrossRef]
- Mammeri, A.; Tiri, A.; Belkhiri, L.; Salhi, H.; Brella, D.; Lakouas, E.; Tahraoui, H.; Amrane, A.; Mouni, L. Assessment of Surface Water Quality Using Water Quality Index and Discriminant Analysis Method. Water 2023, 15, 680. [Google Scholar] [CrossRef]
- Tiri, A.; Lahbari, N.; Boudoukha, A. Hydrochemical Characterization of Surface Water in the Timgad Watershed, East Algeria. Desalination Water Treat. 2016, 57, 562–571. [Google Scholar] [CrossRef]
- Zaresefat, M.; Derakhshani, R.; Nikpeyman, V.; GhasemiNejad, A.; Raoof, A. Using Artificial Intelligence to Identify Suitable Artificial Groundwater Recharge Areas for the Iranshahr Basin. Water 2023, 15, 1182. [Google Scholar] [CrossRef]
- Galloway, J.N.; Townsend, A.R.; Erisman, J.W.; Bekunda, M.; Cai, Z.; Freney, J.R.; Martinelli, L.A.; Seitzinger, S.P.; Sutton, M.A. Transformation of the Nitrogen Cycle: Recent Trends, Questions, and Potential Solutions. Science 2008, 320, 889–892. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Z. Evaluation of Shallow Groundwater Contamination and Associated Human Health Risk in an Alluvial Plain Impacted by Agricultural and Industrial Activities, Mid-West China. Expo Health 2016, 8, 311–329. [Google Scholar] [CrossRef]
- He, S.; Wu, J. Hydrogeochemical Characteristics, Groundwater Quality, and Health Risks from Hexavalent Chromium and Nitrate in Groundwater of Huanhe Formation in Wuqi County, Northwest China. Expo. Health 2019, 11, 311–329. [Google Scholar] [CrossRef]
- Childs, D.B. Water Source and Thyroid Disease Mortality in Georgia. ABNF J. 2020, 31, 127–131. [Google Scholar]
- Ward, M.H.; Jones, R.R.; Brender, J.D.; de Kok, T.M.; Weyer, P.J.; Nolan, B.T.; Villanueva, C.M.; van Breda, S.G. Drinking Water Nitrate and Human Health: An Updated Review. Int. J. Environ. Res. Public Health 2018, 15, 1557. [Google Scholar] [CrossRef]
- World Health Organization. WHO Guidelines for Drinking-Water Quality; World Health Organization: Geneva, Switzerland, 2011; Volume 216, pp. 303–304.
- Xi, Y.; Xu, P. Global Colorectal Cancer Burden in 2020 and Projections to 2040. Transl. Oncol. 2021, 14, 101174. [Google Scholar] [CrossRef]
- Ahmed, N.; Bodrud-Doza, M.; Towfiqul Islam, A.R.M.; Hossain, S.; Moniruzzaman, M.; Deb, N.; Bhuiyan, M.A.Q. Appraising Spatial Variations of As, Fe, Mn and NO3 Contaminations Associated Health Risks of Drinking Water from Surma Basin, Bangladesh. Chemosphere 2019, 218, 726–740. [Google Scholar] [CrossRef]
- Busico, G.; Kazakis, N.; Colombani, N.; Mastrocicco, M.; Voudouris, K.; Tedesco, D. A Modified SINTACS Method for Groundwater Vulnerability and Pollution Risk Assessment in Highly Anthropised Regions Based on NO3− and SO42− Concentrations. Sci. Total Environ. 2017, 609, 1512–1523. [Google Scholar] [CrossRef] [PubMed]
- Nejatijahromi, Z.; Nassery, H.R.; Hosono, T.; Nakhaei, M.; Alijani, F.; Okumura, A. Groundwater Nitrate Contamination in an Area Using Urban Wastewaters for Agricultural Irrigation under Arid Climate Condition, Southeast of Tehran, Iran. Agric. Water Manag. 2019, 221, 397–414. [Google Scholar] [CrossRef]
- Griffioen, J.; Vermooten, S.; Janssen, G. Geochemical and Palaeohydrological Controls on the Composition of Shallow Groundwater in the Netherlands. Appl. Geochem. 2013, 39, 129–149. [Google Scholar] [CrossRef]
- Severini, E.; Bartoli, M.; Pinardi, M.; Celico, F. Reactive Silica Traces Manure Spreading in Alluvial Aquifers Affected by Nitrate Contamination: A Case Study in a High Plain of Northern Italy. Water 2020, 12, 2511. [Google Scholar] [CrossRef]
- Brella, D.; Belkhiri, L.; Tiri, A.; Salhi, H.; Lakouas, F.E.; Nouibet, R.; Amrane, A.; Merdoud, R.; Mouni, L. Identification of the Groundwater Quality and Potential Noncarcinogenic Health Risk Assessment of Nitrate in the Groundwater of El Milia Plain, Kebir Rhumel Basin, Algeria. Hydrology 2023, 10, 171. [Google Scholar] [CrossRef]
- He, X.; Wu, J.; He, S. Hydrochemical Characteristics and Quality Evaluation of Groundwater in Terms of Health Risks in Luohe Aquifer in Wuqi County of the Chinese Loess Plateau, Northwest. Hum. Ecol. Risk Assess. Int. J. 2018, 25, 32–51. [Google Scholar] [CrossRef]
- Yu, L.; Zheng, T.; Zheng, X.; Hao, Y.; Yuan, R. Nitrate Source Apportionment in Groundwater Using Bayesian Isotope Mixing Model Based on Nitrogen Isotope Fractionation. Sci. Total Environ. 2020, 718, 137242. [Google Scholar] [CrossRef]
- Kazakis, N.; Matiatos, I.; Ntona, M.M.; Bannenberg, M.; Kalaitzidou, K.; Kaprara, E.; Mitrakas, M.; Ioannidou, A.; Vargemezis, G.; Voudouris, K. Origin, Implications and Management Strategies for Nitrate Pollution in Surface and Ground Waters of Anthemountas Basin Based on a δ15N -NO3− and δ18O- -NO3− Isotope Approach. Sci. Total Environ. 2020, 724, 138211. [Google Scholar] [CrossRef] [PubMed]
- Ahada, C.P.S.; Suthar, S. Groundwater Nitrate Contamination and Associated Human Health Risk Assessment in Southern Districts of Punjab, India. Environ. Sci. Pollut. Res. 2018, 25, 25336–25347. [Google Scholar] [CrossRef] [PubMed]
- Jalali, M. Nitrates Leaching from Agricultural Land in Hamadan, Western Iran. Agric. Ecosyst. Environ. 2005, 110, 210–218. [Google Scholar] [CrossRef]
- Solgi, E.; Jalili, M. Zoning and Human Health Risk Assessment of Arsenic and Nitrate Contamination in Groundwater of Agricultural Areas of the Twenty Two Village with Geostatistics (Case Study: Chahardoli Plain of Qorveh, Kurdistan Province, Iran). Agric. Water Manag. 2021, 255, 107023. [Google Scholar] [CrossRef]
- Bahrami, M.; Zarei, A.R.; Rostami, F. Temporal and Spatial Assessment of Groundwater Contamination with Nitrate by Nitrate Pollution Index (NPI) and GIS (Case Study: Fasarud Plain, Southern Iran). Environ. Geochem. Health 2020, 42, 3119–3130. [Google Scholar] [CrossRef] [PubMed]
- Ghahremanzadeh, H.; Noori, R.; Baghvand, A.; Nasrabadi, T. Evaluating the Main Sources of Groundwater Pollution in the Southern Tehran Aquifer Using Principal Component Factor Analysis. Environ. Geochem. Health 2017, 40, 1317–1328. [Google Scholar] [CrossRef]
- Badrzadeh, N.; Samani, J.M.V.; Mazaheri, M.; Kuriqi, A. Evaluation of Management Practices on Agricultural Nonpoint Source Pollution Discharges into the Rivers under Climate Change Effects. Sci. Total Environ. 2022, 838, 156643. [Google Scholar] [CrossRef]
- Karavidas, I.; Ntatsi, G.; Vougeleka, V.; Karkanis, A.; Ntanasi, T.; Saitanis, C.; Agathokleous, E.; Ropokis, A.; Sabatino, L.; Tran, F.; et al. Agronomic Practices to Increase the Yield and Quality of Common Bean (Phaseolus vulgaris L.): A Systematic Review. Agronomy 2022, 12, 271. [Google Scholar] [CrossRef]
- Foroushani, T.S.; Balali, H.; Movahedi, R.; Kurban, A.; Värnik, R.; Stamenkovska, I.J.; Azadi, H. Importance of Good Groundwater Governance in Economic Development: The Case of Western Iran. Groundw. Sustain. Dev. 2023, 21, 100892. [Google Scholar] [CrossRef]
- Ehteshami, M.; Salari, M.; Zaresefat, M. Sustainable Development Analyses to Evaluate Groundwater Quality and Quantity Management. Model. Earth Syst. Environ. 2016, 2, 133. [Google Scholar] [CrossRef]
- Zaresefat, M.; Kalantari, N.; Aram, E.; Rouhi, H. Potential for Natural Feeding of Groundwater Using FAHP Method and GIS Software. In Proceedings of the Thirtieth Meeting of Earth Sciences, Tehran, Iran, 16 May 2011; pp. 1–5. [Google Scholar]
- Zaresefat, M.; Ahrari, M.; Reza Shoaei, G.; Etemadifar, M.; Aghamolaie, I.; Derakhshani, R. Identification of Suitable Site-Specific Recharge Areas Using Fuzzy Analytic Hierarchy Process (FAHP) Technique: A Case Study of Iranshahr Basin (Iran). Air Soil Water Res. 2022, 15, 1–12. [Google Scholar] [CrossRef]
- Liu, C.W.; Jang, C.S.; Liao, C.M. Evaluation of Arsenic Contamination Potential Using Indicator Kriging in the Yun-Lin Aquifer (Taiwan). Sci. Total Environ. 2004, 321, 173–188. [Google Scholar] [CrossRef]
- Freitag, P.; Martac, E.; Reichenauer, T. On the Effectiveness of Site Investigation in Regard to Project Costs—A Case Study. Ce/papers 2018, 2, 439–444. [Google Scholar] [CrossRef]
- Bhunia, G.S.; Shit, P.K.; Maiti, R. Comparison of GIS-Based Interpolation Methods for Spatial Distribution of Soil Organic Carbon (SOC). J. Saudi Soc. Agric. Sci. 2018, 17, 114–126. [Google Scholar] [CrossRef]
- Murphy, R.R.; Curriero, F.C.; Ball, W.P. Comparison of Spatial Interpolation Methods for Water Quality Evaluation in the Chesapeake Bay. J. Environ. Eng. 2010, 136, 160–171. [Google Scholar] [CrossRef]
- Saha, A.; Gupta, B.S.; Patidar, S.; Martínez-Villegas, N. Spatial Distribution Based on Optimal Interpolation Techniques and Assessment of Contamination Risk for Toxic Metals in the Surface Soil. J. S. Am. Earth Sci. 2022, 115, 103763. [Google Scholar] [CrossRef]
- Amah, V.E.; Agu, F.A. Geostatistical Modelling of Groundwater Quality at Rumuola Community, Port Harcourt, Nigeria. Asian J. Environ. Ecol. 2020, 12, 37–47. [Google Scholar] [CrossRef]
- Koussa, M.; Berhail, S. Evaluation of Spatial Interpolation Techniques for Mapping Groundwater Nitrates Concentrations—Case Study of Ain Elbel-Sidi Makhlouf Syncline in The Djelfa Region (Algeria). LARHYSS 2021, 45, 119–140. [Google Scholar]
- Mukherjee, I.; Singh, U.K. Characterization of Groundwater Nitrate Exposure Using Monte Carlo and Sobol Sensitivity Approaches in the Diverse Aquifer Systems of an Agricultural Semiarid Region of Lower Ganga Basin, India. Sci. Total Environ. 2021, 787, 147657. [Google Scholar] [CrossRef]
- Güler, M.; Kara, T. Comparison of Different Interpolation Techniques for Modelling Temperatures in Middle Black Sea Region. J. Agric. Fac. Gaziosmanpasa Univ. 2014, 31, 61–71. [Google Scholar] [CrossRef]
- Hengl, T. A Practical Guide to Geostatistical Mapping, 2nd ed.; EUR 22904 EN Scientific and Technical Research Series; Office for Official Publications of the European Communities: Luxembourg, 2009. [Google Scholar]
- Stahl, K.; Moore, R.D.; Floyer, J.A.; Asplin, M.G.; McKendry, I.G. Comparison of Approaches for Spatial Interpolation of Daily Air Temperature in a Large Region with Complex Topography and Highly Variable Station Density. Agric. For. Meteorol. 2006, 139, 224–236. [Google Scholar] [CrossRef]
- Wu, W.; Tang, X.-P.; Ma, X.-Q.; Liu, H.-B. A Comparison of Spatial Interpolation Methods for Soil Temperature over a Complex Topographical Region. Theor. Appl. Climatol. 2016, 125, 657–667. [Google Scholar] [CrossRef]
- Majid Padashi, S.; Büdel, C.; Ullmann, T.; Tintrup, A.; Baumhauer, R.; Majid Padashi, S.; Büdel, C.; Ullmann, T.; Tintrup, A.; Baumhauer, R. Preliminary Results on Quaternary Studies from Bajestan Basin (Kavir-e Namak), Iran. EGUGA 2017, 19, 16532. [Google Scholar]
- Nematollahi, M.J.; Ebrahimi, P.; Ebrahimi, M. Evaluating Hydrogeochemical Processes Regulating Groundwater Quality in an Unconfined Aquifer. Environ. Process. 2016, 3, 1021–1043. [Google Scholar] [CrossRef]
- Dehghani, M.H.; Zarei, A.; Yousefi, M.; Asgharia, F.B.; Haghighat, G.A. Fluoride Contamination in Groundwater Resources in the Southern Iran and Its Related Human Health Risks. Desalination Water Treat. 2019, 153, 95–104. [Google Scholar] [CrossRef]
- Mohammadzadeh, F.; Ekhtesasi, M.R.; Hosseini, S.Z.; Negaresh, A.; Hashemi, H.; Allaee, M. Investigating the Effect of Drinking and Sanitary Water Separation on the Quality of Drinking Water and Preparing a Groundwater Quality Map (Case Study: Bajestan Watershed). J. Watershed Manag. Res. 2022, 13, 215–229. [Google Scholar] [CrossRef]
- Qasemi, M.; Afsharnia, M.; Farhang, M.; Bakhshizadeh, A.; Allahdadi, M.; Zarei, A. Health Risk Assessment of Nitrate Exposure in Groundwater of Rural Areas of Gonabad and Bajestan, Iran. Environ. Earth Sci. 2018, 77, 551. [Google Scholar] [CrossRef]
- Mohammadzadeh, F.; Ekhtesasi, M.R.; Hosseini, S.Z. The Effects of Geological Formations on Groundwater Quality with the Application of Boolean Logic, Case Study: Bajestan Watershed Plain. Watershed Eng. Manag. 2017, 9, 11–21. [Google Scholar]
- WHO. Nitrate and Nitrite in Drinking-Water Background Document for Development of WHO Guidelines for Drinking-Water Quality; WHO/FWC/WSH/16.52; World Health Organization: Geneva, Switzerland, 2016.
- de Smith, M.J.; Goodchild, M.F.; Longley, P. Geospatial Analysis: A Comprehensive Guide to Principles, Techniques and Software Tools, 6th ed.; Troubador Publishing Ltd.: Market Harborough, UK, 2021; ISBN 9781912556038. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 0470517263. [Google Scholar]
- Smith, J.E.; von Winterfeldt, D. Decision Analysis in Management Science. Manag. Sci. 2004, 50, 561–574. [Google Scholar] [CrossRef]
- Hani, A.; Abari, S.A.H. Determination of Cd, Zn, K, PH, TNV, Organic Material and Electrical Conductivity (EC) Distribution in Agricultural Soils Using Geostatistics and GIS (Case Study: South–Western of Natanz–Iran). Int. J. Biol. Life Agric. Sci. 2011, 12, 852–855. [Google Scholar] [CrossRef]
- Gribov, A.; Krivoruchko, K. Local Polynomials for Data Detrending and Interpolation in the Presence of Barriers. Stoch. Environ. Res. Risk Assess. 2011, 25, 1057–1063. [Google Scholar] [CrossRef]
- Esri. ArcGIS Geostatistical Analyst—Model Spatial Data & Uncertainty. Available online: https://www.esri.com/en-us/arcgis/products/geostatistical-analyst/overview (accessed on 9 November 2021).
- Paramasivam, C.R.; Venkatramanan, S. An Introduction to Various Spatial Analysis Techniques. In GIS and Geostatistical Techniques for Groundwater Science; Elsevier: Amsterdam, The Netherlands, 2019; pp. 23–30. ISBN 9780128154137. [Google Scholar]
- Lange, J.; Krause, E. Spatial Interpolation with ArcGIS Pro—Esri Training Seminar. 2019. Available online: https://www.esri.com/training/catalog/5c92b940fa73df28264fb8ed/spatial-interpolation-with-arcgis-pro (accessed on 22 June 2022).
- Esri. ArcMap—Documentation. Available online: https://desktop.arcgis.com/en/arcmap/latest/tools/spatial-analyst-toolbox/conditional-evaluation-with-con.htm (accessed on 27 November 2021).
- Viswanathan, R.; Jagan, J.; Samui, P.; Porchelvan, P. Spatial Variability of Rock Depth Using Simple Kriging, Ordinary Kriging, RVM and MPMR. Geotech. Geol. Eng. 2015, 33, 69–78. [Google Scholar] [CrossRef]
- Abdulmanov, R.; Miftakhov, I.; Ishbulatov, M.; Galeev, E.; Shafeeva, E. Comparison of the Effectiveness of GIS-Based Interpolation Methods for Estimating the Spatial Distribution of Agrochemical Soil Properties. Environ. Technol. Innov. 2021, 24, 101970. [Google Scholar] [CrossRef]
- Krivoruchko, K. Spatial Statistical Data Analysis for GIS Users, 1st ed.; Esri Press: Redlands, CA, USA, 2011; ISBN 978-1-58948-161-9. [Google Scholar]
- Li, J.; Heap, A.D. Spatial Interpolation Methods Applied in the Environmental Sciences: A Review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Krivoruchko, K. Empirical Bayesian Kriging. ArcUser Fall 2012, 6, 1145. [Google Scholar]
- Gribov, A.; Krivoruchko, K. Empirical Bayesian Kriging Implementation and Usage. Sci. Total Environ. 2020, 722, 137290. [Google Scholar] [CrossRef] [PubMed]
- Knotters, M.; Heuvelink, G.B.M. A Disposition of Interpolation Techniques; Wettelijke Onderzoekstaken Natuur & Milieu: Wageningen, The Netherlands, 2010. [Google Scholar]
- Krivoruchko, K.; Butler, K. Unequal Probability-Based Spatial Mapping; Esri: Redlands, CA, USA, 2013. [Google Scholar]
- Krivoruchko, K.; Gribov, A. Distance Metrics for Data Interpolation over Large Areas on Earth’s Surface. Spat. Stat. 2020, 35, 100396. [Google Scholar] [CrossRef]
- de Gans, W.; Wong, T.E.; Batjes, D.A.J.; de Jager, J. Geology of the Netherlands; Royal Netherlands Academy of Arts and Sciences: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Jarmołowski, W.; Wielgosz, P.; Ren, X.; Krypiak-Gregorczyk, A. On the Drawback of Local Detrending in Universal Kriging in Conditions of Heterogeneously Spaced Regional TEC Data, Low-Order Trends and Outlier Occurrences. J. Geod. 2021, 95, 2. [Google Scholar] [CrossRef]
- Gong, G.; Mattevada, S.; O’Bryant, S.E. Comparison of the Accuracy of Kriging and IDW Interpolations in Estimating Groundwater Arsenic Concentrations in Texas; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Singh, P.; Verma, P. A Comparative Study of Spatial Interpolation Technique (IDW and Kriging) for Determining Groundwater Quality. GIS Geostat. Tech. Groundw. Sci. 2019, 43–56. [Google Scholar] [CrossRef]
- Tomlinson, K.M. A Spatial Evaluation of Groundwater Quality Salinity and Underground Injection Controlled Wells Activity in Texas. Ph.D. Thesis, The University of Texas at Dallas, Richardson, TX, USA, 2019. [Google Scholar]
- Xie, Y.; Chen, T.; Lei, M.; Yang, J.; Guo, Q.; Song, B.; Zhou, X. Spatial Distribution of Soil Heavy Metal Pollution Estimated by Different Interpolation Methods: Accuracy and Uncertainty Analysis. Chemosphere 2011, 82, 468–476. [Google Scholar] [CrossRef]
- Ahmad, A.Y.; Saleh, I.A.; Balakrishnan, P.; Al-Ghouti, M.A. Comparison GIS-Based Interpolation Methods for Mapping Groundwater Quality in the State of Qatar. Groundw. Sustain. Dev. 2021, 13, 100573. [Google Scholar] [CrossRef]
- Mirzaei, R.; Sakizadeh, M. Comparison of Interpolation Methods for the Estimation of Groundwater Contamination in Andimeshk-Shush Plain, Southwest of Iran. Environ. Sci. Pollut. Res. 2016, 23, 2758–2769. [Google Scholar] [CrossRef]
- Krause, E. Model Water Quality Using Interpolation. Available online: https://learn.arcgis.com/en/projects/model-water-quality-using-interpolation (accessed on 15 February 2023).
- Wagner, P.D.; Fiener, P.; Wilken, F.; Kumar, S.; Schneider, K. Comparison and Evaluation of Spatial Interpolation Schemes for Daily Rainfall in Data Scarce Regions. J. Hydrol. 2012, 464–465, 388–400. [Google Scholar] [CrossRef]
- EPA. Drinking Water Requirements for States and Public Water Systems. Available online: https://www.epa.gov/dwreginfo/drinking-water-regulations (accessed on 4 April 2023).
- EU Guidance Common Implementation Strategy for the Water Framework Directive (2000/60/EC); European Environment Agency: Copenhagen, Denmark, 2003; Volume 7.
- Institute of Standards and Industrial Research of Iran. Drinking Water—Physical and Chemical Specifications; Institute of Standards and Industrial Research of Iran: Tehran, Iran, 2010. [Google Scholar]
- Spalding, R.F.; Exner, M.E. Occurrence of Nitrate in Groundwater—A Review. J. Environ. Qual. 1993, 22, 392–402. [Google Scholar] [CrossRef]
- Boesch, D.F.; Brinsfield, R.B.; Magnien, R.E. Chesapeake Bay Eutrophication: Scientific Understanding, Ecosystem Restoration, and Challenges for Agriculture. J. Environ. Qual. 2001, 30, 303–320. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, C.D.; Genereux, D.P.; Corbett, D.R.; Mitasova, H. Spatial and Temporal Dynamics of Coupled Groundwater and Nitrogen Fluxes through a Streambed in an Agricultural Watershed. Water Resour. Res. 2009, 45, W09401. [Google Scholar] [CrossRef]
- Ki, M.-G.; Koh, D.-C.; Yoon, H.; Kim, H. Temporal Variability of Nitrate Concentration in Groundwater Affected by Intensive Agricultural Activities in a Rural Area of Hongseong, South Korea. Environ. Earth Sci. 2015, 74, 6147–6161. [Google Scholar] [CrossRef]
- Wells, M.J.; Gilmore, T.E.; Nelson, N.; Mittelstet, A.; Böhlke, J.K. Determination of Vadose Zone and Saturated Zone Nitrate Lag Times Using Long-Term Groundwater Monitoring Data and Statistical Machine Learning. Hydrol. Earth Syst. Sci. 2021, 25, 811–829. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Kurtzman, D.; Dahan, O. Real-Time Monitoring of Nitrate Transport in the Deep Vadose Zone under a Crop Field—Implications for Groundwater Protection. Hydrol. Earth Syst. Sci. 2016, 20, 3099–3108. [Google Scholar] [CrossRef]
- Hong, N.; White, J.G.; Weisz, R.; Gumpertz, M.L.; Duffera, M.G.; Cassel, D.K. Groundwater Nitrate Spatial and Temporal Patterns and Correlations: Influence of Natural Controls and Nitrogen Management. Vadose Zone J. 2007, 6, 53–66. [Google Scholar] [CrossRef]
- Bernard-Jannin, L.; Sun, X.; Teissier, S.; Sauvage, S.; Sánchez-Pérez, J.M. Spatio-Temporal Analysis of Factors Controlling Nitrate Dynamics and Potential Denitrification Hot Spots and Hot Moments in Groundwater of an Alluvial Floodplain. Ecol. Eng. 2017, 103, 372–384. [Google Scholar] [CrossRef]
- Kazemi, E.; Karyab, H.; Emamjome, M.-M. Optimisation of Interpolation Method for Nitrate Pollution in Groundwater and Assessing Vulnerability with IPNOA and IPNOC Method in Qazvin Plain. J. Environ. Health Sci. Eng. 2017, 15, 23. [Google Scholar] [CrossRef] [PubMed]
- Bronowicka-Mielniczuk, U.; Mielniczuk, J.; Obroślak, R.; Przystupa, W. A Comparison of Some Interpolation Techniques for Determining Spatial Distribution of Nitrogen Compounds in Groundwater. Int. J. Environ. Res. 2019, 13, 679–687. [Google Scholar] [CrossRef]



| Minimum | Maximum | Mean | Standard Deviation | Variance | |
|---|---|---|---|---|---|
| EC | 602 | 17,450 | 5919 | 4634 | 21,469,697 |
| pH | 7 | 8.66 | 7.69 | 0.28 | 0.08 |
| HCO3 | 0.2 | 8 | 3 | 1 | 1 |
| Cl | 1.1 | 148 | 40 | 39 | 1496 |
| SO4 | 1.1 | 47 | 14 | 10 | 91 |
| Mg | 0.5 | 49 | 5 | 6 | 41 |
| Na | 0.4 | 145 | 48 | 38 | 1416 |
| NO3 | 4.6 | 153 | 49 | 39 | 1504 |
| Purpose | Proper (mg/L) | Good (mg/L) | Fair (mg/L) | Poor |
|---|---|---|---|---|
| Drinking Water Quality | <10 | 10–20 | 20–50 | >50 |
| Sampling Periods | WHO Classification | Count | NO3 Concentration (mg/L) | ||
|---|---|---|---|---|---|
| Minimum | Mean ± SD | Maximum | |||
| Spring | Good | 1 | 15 | 15.3 | 15 |
| Fair | 7 | 23 | 25.6 ± 2.6 | 31 | |
| Poor | 7 | 80 | 111 ± 26 | 153 | |
| Summer | Fair | 11 | 24 | 34 ± 9 | 49 |
| Poor | 8 | 75 | 105.2 ± 24.9 | 148 | |
| Autumn | Excellent | 1 | 5 | 4.6 | 5 |
| Good | 4 | 12 | 15.7 ± 2.9 | 19 | |
| Fair | 15 | 22 | 27.8 ± 6.5 | 47 | |
| Poor | 7 | 55 | 101.9 ± 27.5 | 140 | |
| Winter | Good | 2 | 15 | 16 ± 1.1 | 17 |
| Fair | 12 | 21 | 29.9 ± 7.1 | 41 | |
| Poor | 6 | 57 | 107.8 ± 28.5 | 142 | |
| Interpolation Method | Statistical Indices | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|
| LPI | RMSE | 47.3 | 31.6 | 30.5 | 38.8 |
| Mean CV | 5.1 | 3 | 0.68 | 0.94 | |
| NSE | 0.017 | 0.098 | 0.282 | 0.076 | |
| IDW | RMSE | 37.6 | 36.9 | 28.2 | 35.4 |
| Mean CV | −1.9 | 3.43 | −2.54 | −2.41 | |
| NSE | 0.117 | 0.093 | 0.081 | 0.028 | |
| OK | RMSE | 37.6 | 34.3 | 28.05 | 33.05 |
| Mean CV | 1.19 | −1.03 | −0.44 | 1.89 | |
| NSE | 0.015 | 0.043 | 0.032 | 0.148 | |
| SK | RMSE | 43.1 | 39.7 | 35.5 | 40.1 |
| Mean CV | −0.93 | 0.55 | 2.1 | 0.137 | |
| NSE | 0.186 | 0.173 | 0.193 | 0.185 | |
| UK | RMSE | −0.93 | 44.3 | 37.8 | 42.9 |
| Mean CV | 2.15 | −1.03 | −0.66 | 1.68 | |
| NSE | 0.085 | 0.093 | 0.091 | 0.014 | |
| EBK | RMSE | 28.6 | 26.5 | 28.1 | 30.63 |
| Mean CV | 1.4 | −0.76 | −0.72 | 0.1 | |
| NSE | 0.223 | 0.166 | 0.189 | 0.192 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaresefat, M.; Hosseini, S.; Ahrari Roudi, M. Addressing Nitrate Contamination in Groundwater: The Importance of Spatial and Temporal Understandings and Interpolation Methods. Water 2023, 15, 4220. https://doi.org/10.3390/w15244220
Zaresefat M, Hosseini S, Ahrari Roudi M. Addressing Nitrate Contamination in Groundwater: The Importance of Spatial and Temporal Understandings and Interpolation Methods. Water. 2023; 15(24):4220. https://doi.org/10.3390/w15244220
Chicago/Turabian StyleZaresefat, Mojtaba, Saeedeh Hosseini, and Mohyeddin Ahrari Roudi. 2023. "Addressing Nitrate Contamination in Groundwater: The Importance of Spatial and Temporal Understandings and Interpolation Methods" Water 15, no. 24: 4220. https://doi.org/10.3390/w15244220





