Slope Stability Evaluation Due to Reservoir Draw-Down Using LEM and Stress-Based FEM along with Mohr–Coulomb Criteria
Abstract
:1. Introduction
- -
- To evaluate the approach of LEM and stress-based FEM for defining safe allowable draw-down rates.
- -
- To study the influence of change in permeability of upstream dam shell in the FOS.
- -
- To examine the effect of horizontal upstream filter material in the FOS.
- -
- To evaluate the plastic behaviors on the upstream slope during RDD.
2. Materials and Methods
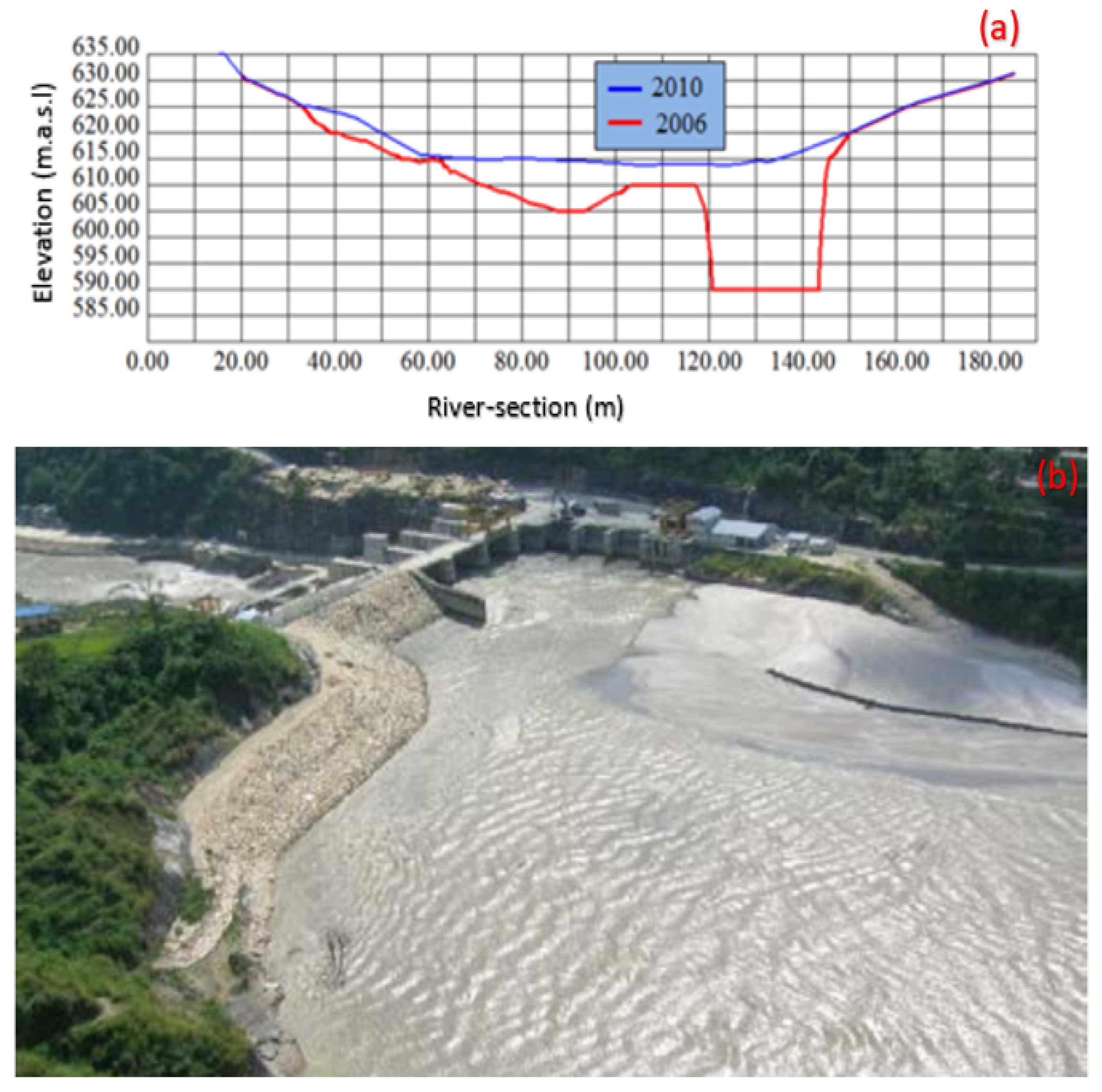
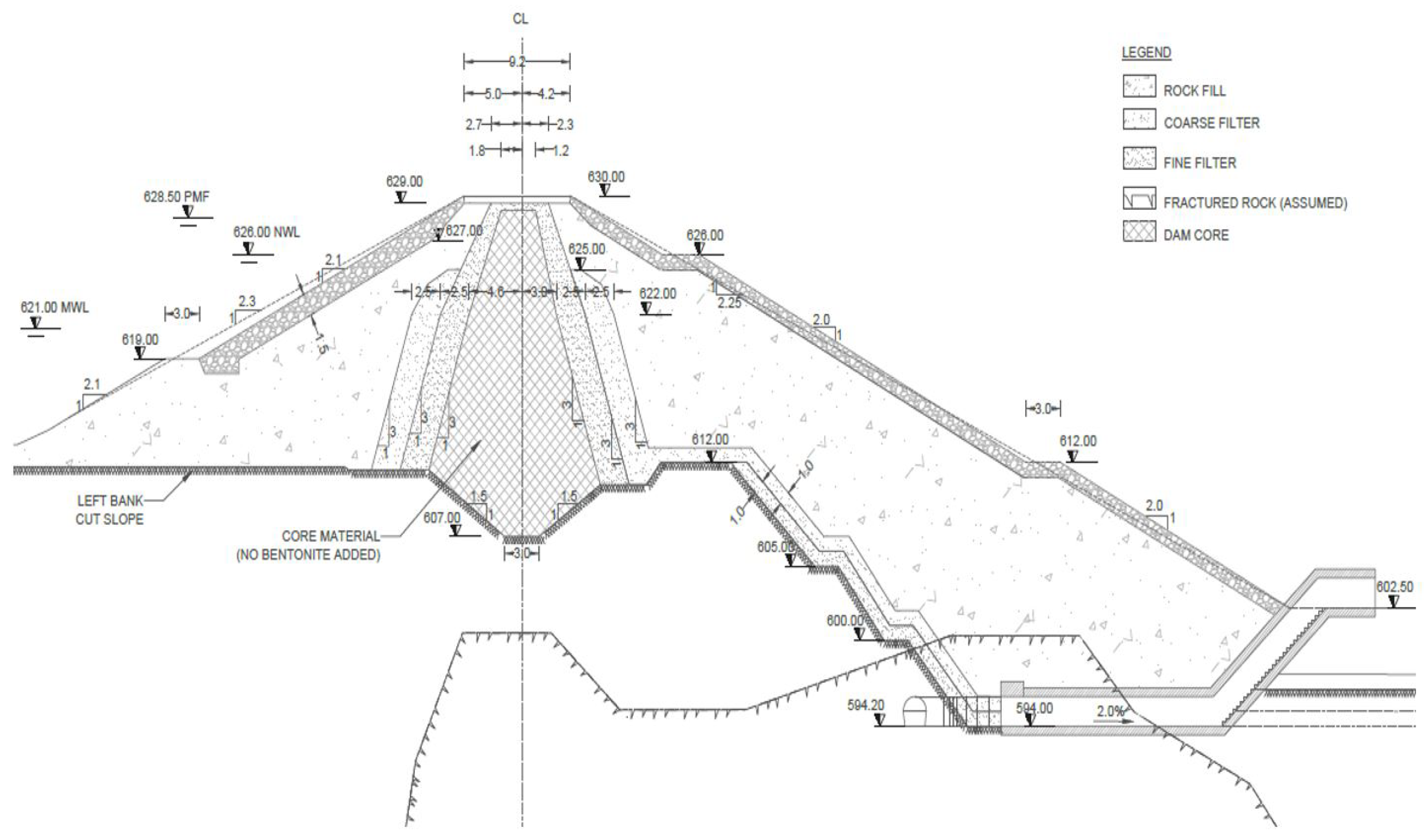
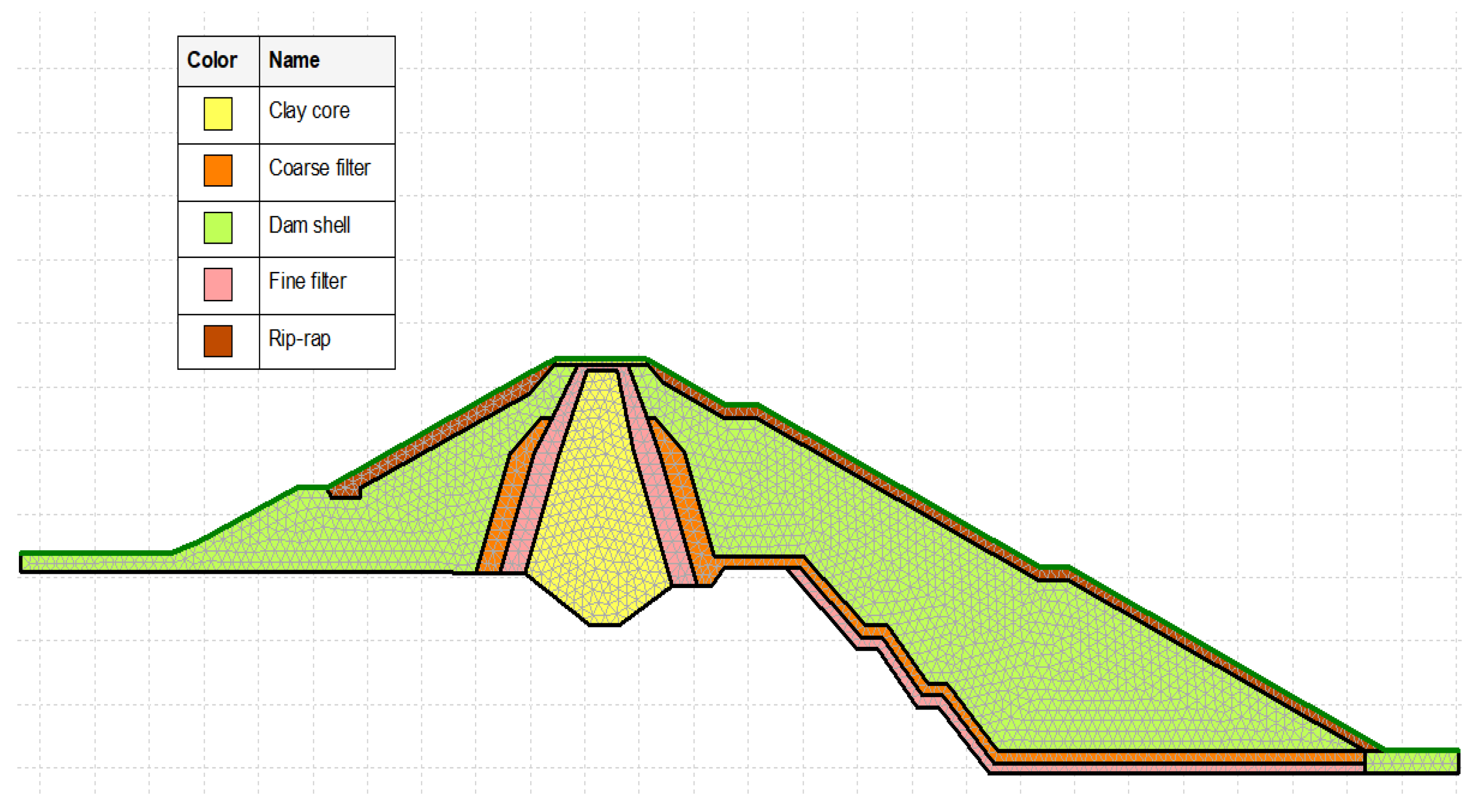
2.1. Case Study
2.2. Material Properties
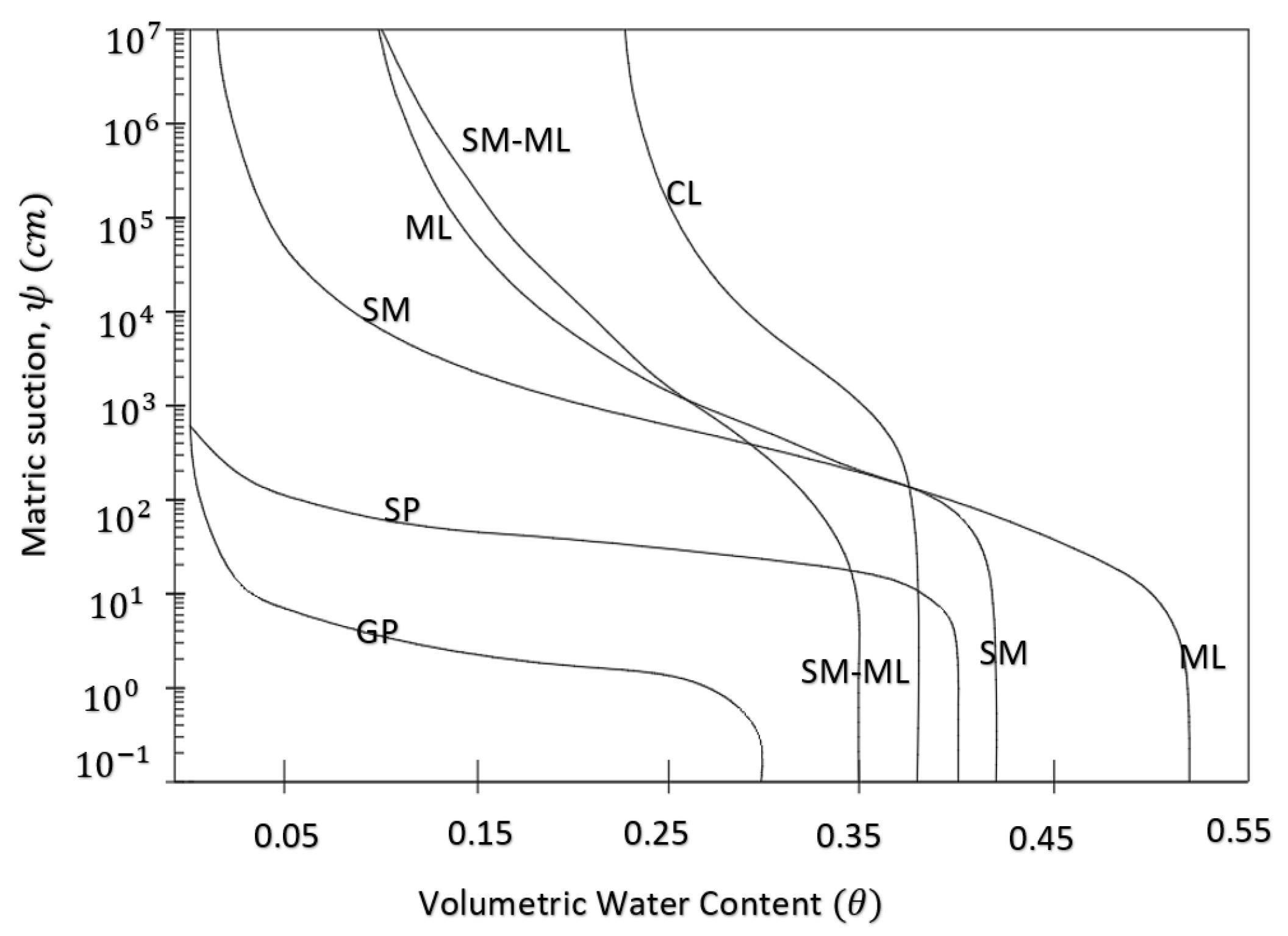
2.2.1. Soil Water Characteristic Curve (SWCC)
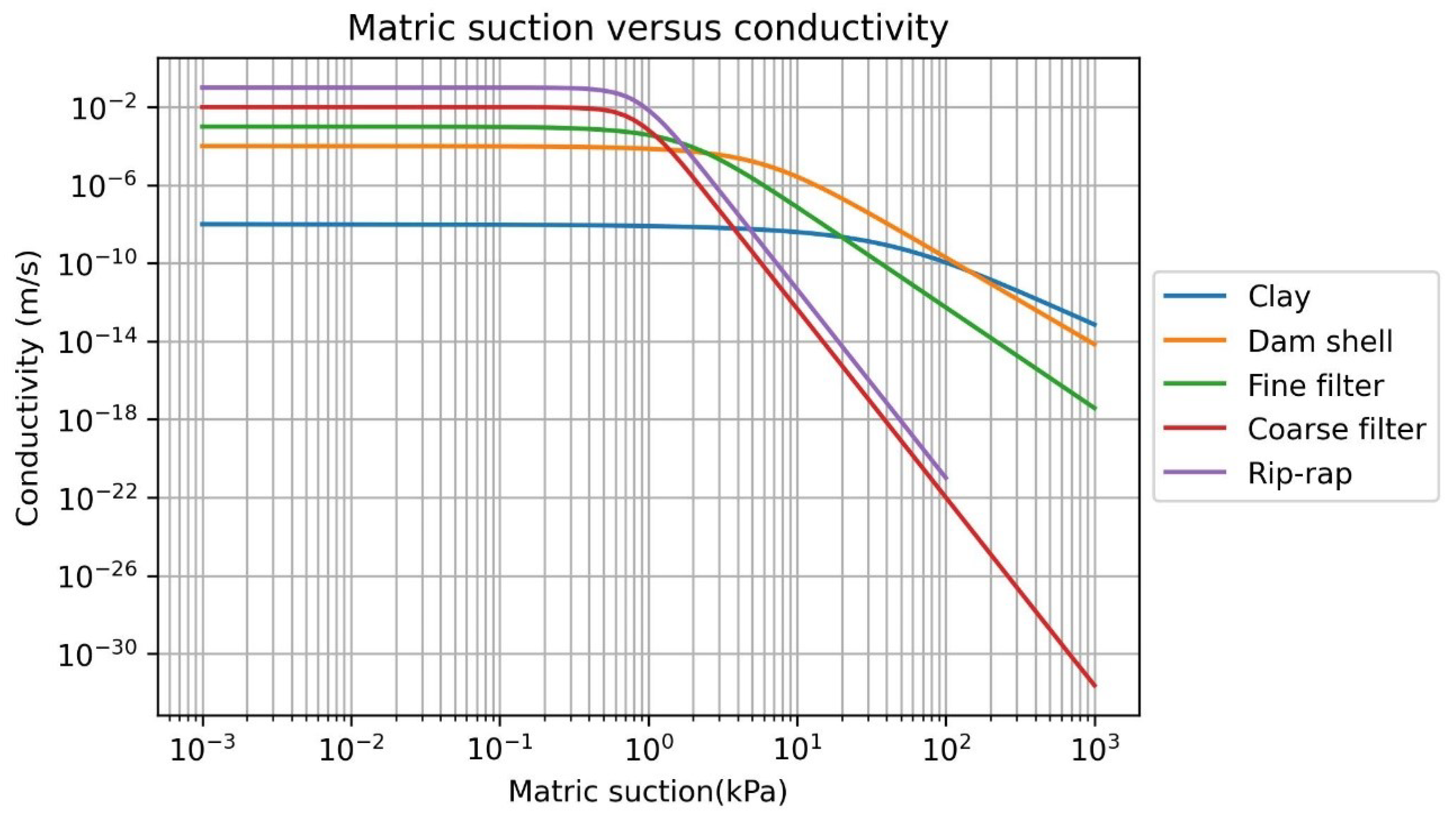
2.2.2. Hydraulic Conductivity/Permeability ()
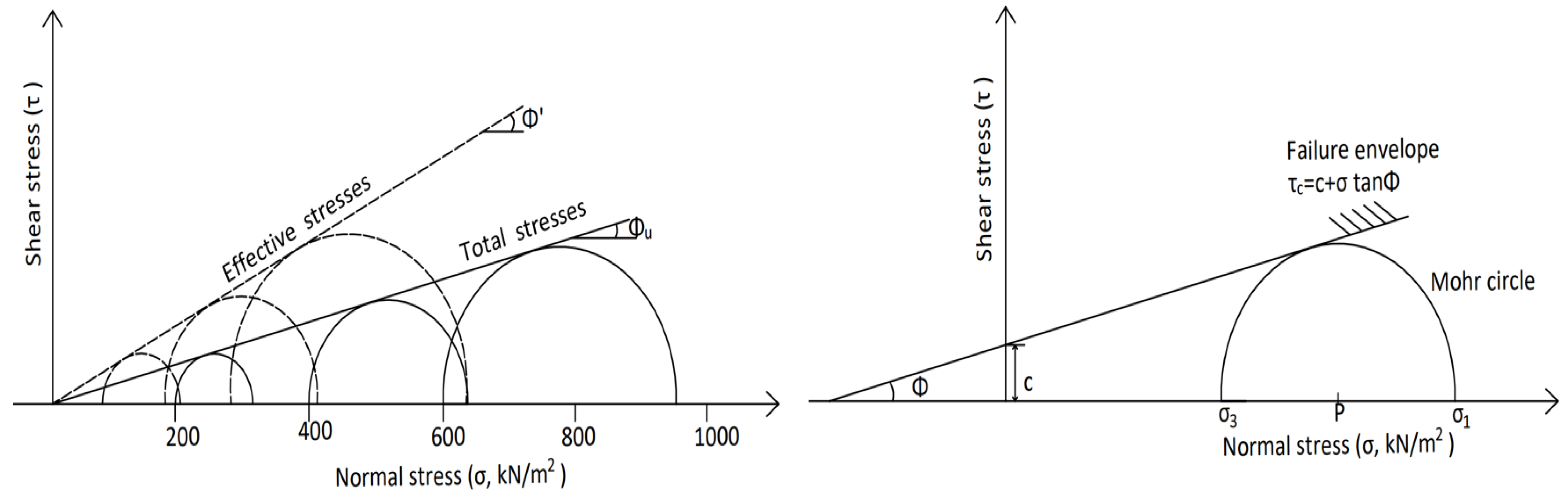
2.2.3. Angle of Friction () and Cohesion ()
2.2.4. Modules of Elasticity (E) and Poisson’s Ratio (v)
2.3. Governing Equations
2.3.1. Darcy’s Law
2.3.2. 2D Partial Differential Flow Water Equation
2.3.3. Hydraulic Conductivity/Permeability ()
2.3.4. Coefficient of Volume Compressibility ()
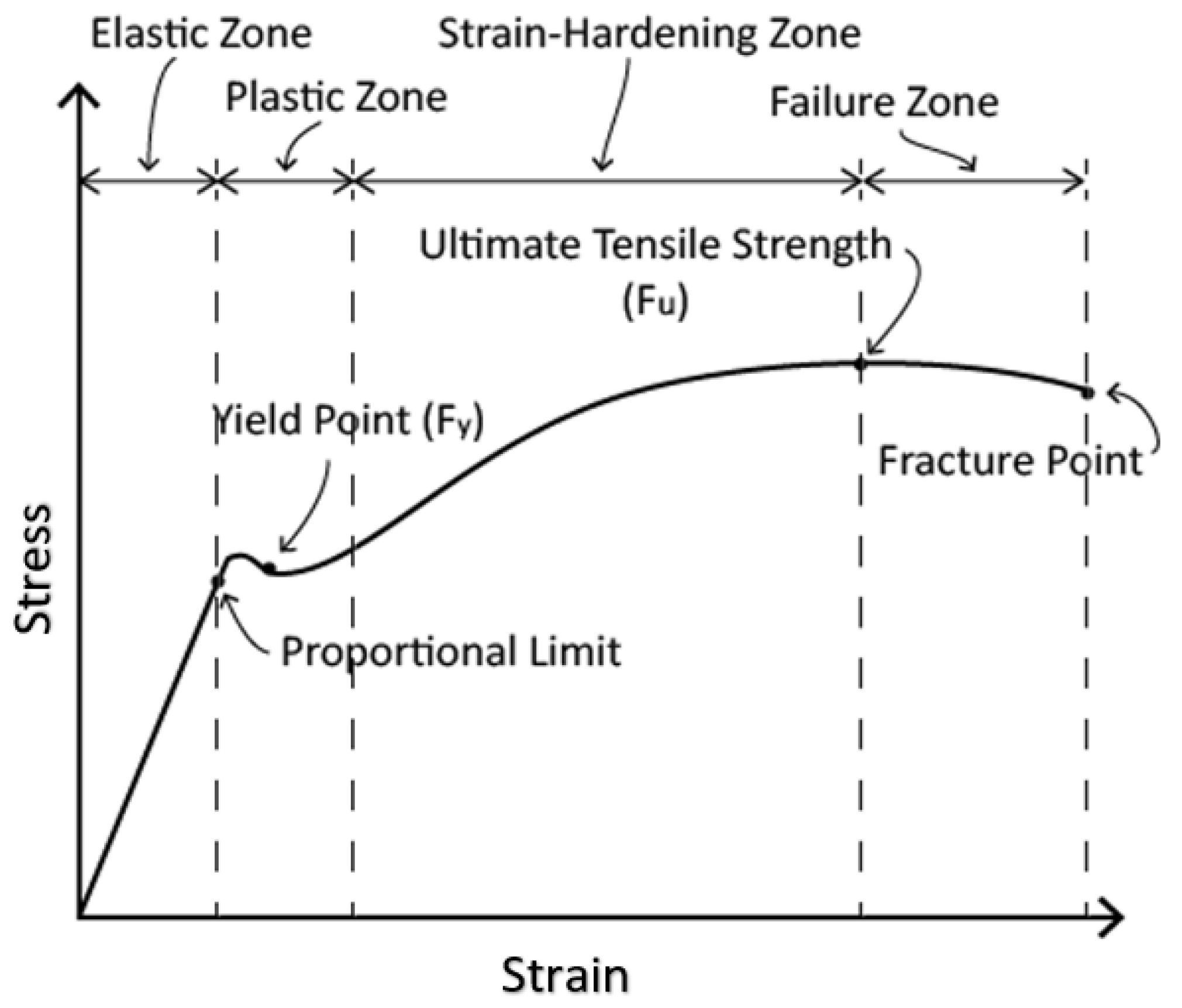
2.3.5. Mohr–Coulomb Theory
2.3.6. Methods for Factor of Safety (FOS)
2.3.7. Limit Equilibrium Method
2.3.8. Stress-Based FEM Method
2.4. Model Parameters
2.5. Correlation Matrix
3. Results
3.1. Steady-State
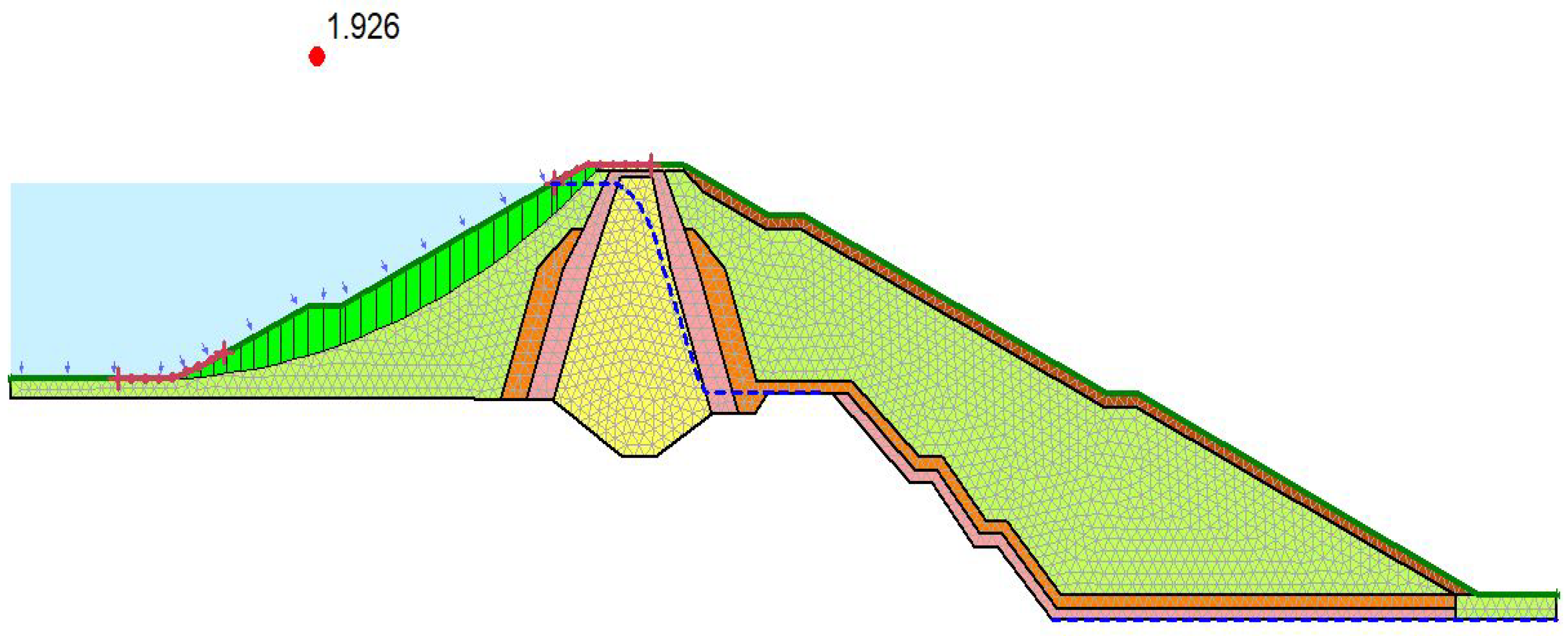
3.1.1. Stress Distribution
3.1.2. Factor of Safety (FOS)
3.2. Transient State
3.2.1. Nonlinear Behavior Analysis
3.2.2. Pressure and Seepage Discharge Variation
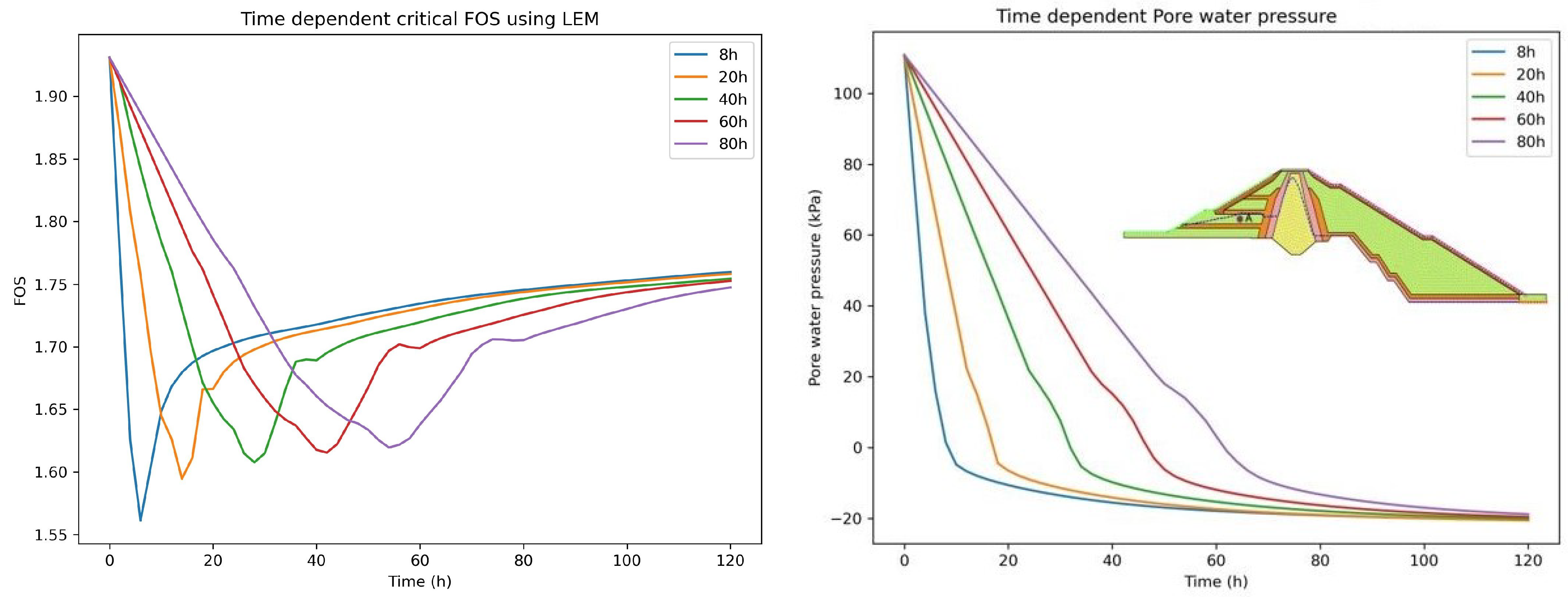
3.2.3. Time-Dependent FOS and Pore Water Pressure Using LEM
4. Discussion
4.1. Steady-State Conditions
4.2. Transient State
5. Conclusions
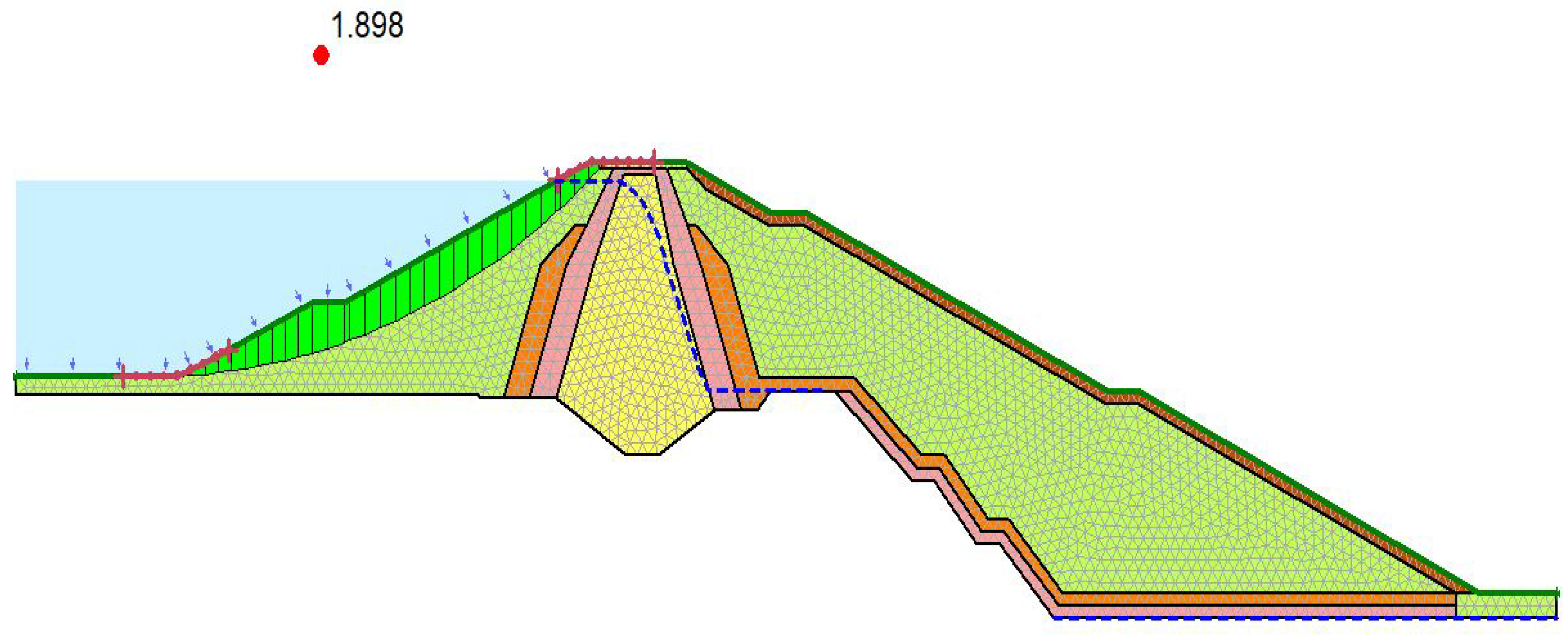
- The long-term steady-state analysis has resulted in a similar FOS of 1.92 with LEM and 1.89 with stress-based FEM. The identical slip circles resulted in similar base stress distribution, using both models. As a result, similar FOS values were obtained.
- Considering the as-built design dam with 8 h of RDD, a critical FOS of less than 1.3 was obtained. It was classified as unsafe according to the guidelines. A safe allowable draw-down rate of 0.76 m/h for 20 h was identified to reach the minimum critical FOS criteria.
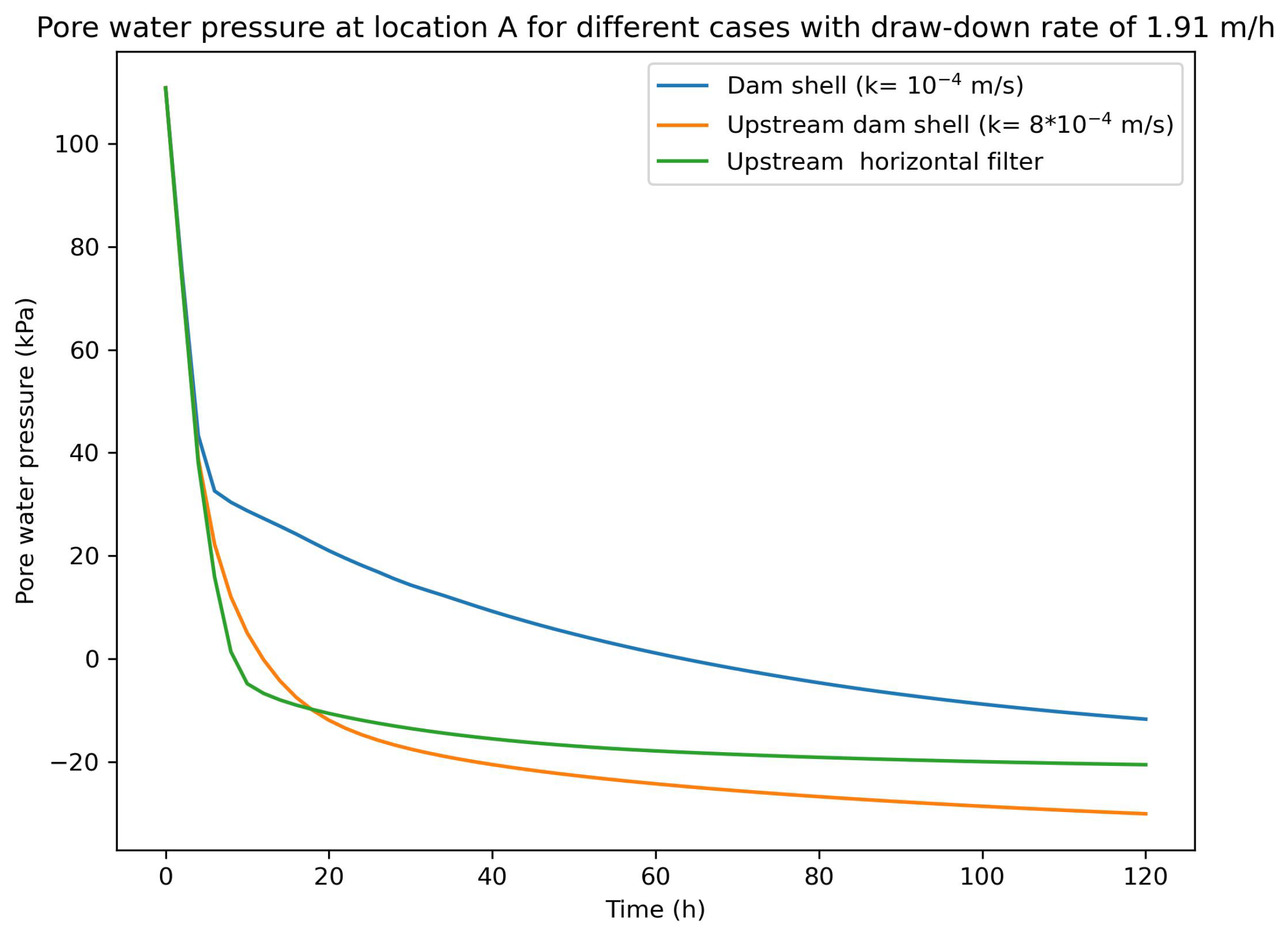
- The sensitivity analyses’ test results have shown that the FOS values are significantly dominated by upstream dam shell permeability and draw-down rates. The slow draw-down rates and quick release of excess pore water pressure are important to ensure safe sliding stability. The additional test case with a horizontal filter provided adequate FOS for all draw-down rates.
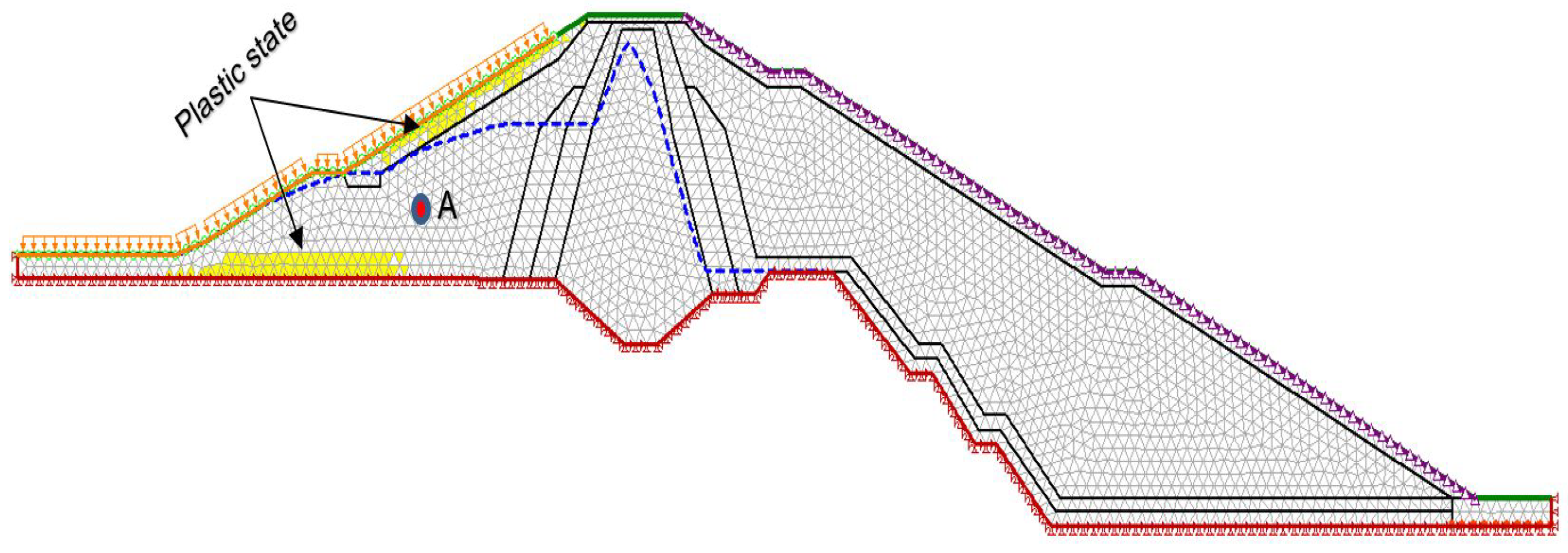
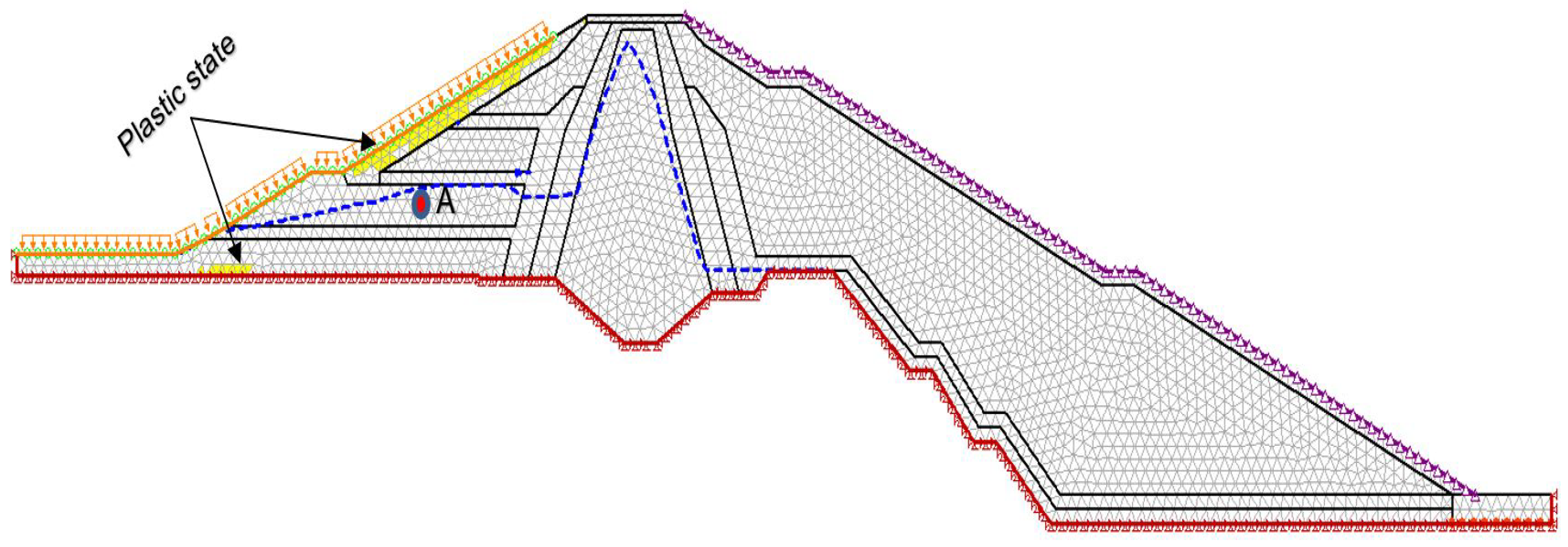
- The coupled stress-based FEM for the nonlinear behavior analysis was carried out in the case of 8 h of RDD. The local plastic deformation in the upstream slope and at the toe of the dam has been observed, which was not seen in the equilibrium method.
- To ensure dam safety during RDD, the allowable draw-down rate should be evaluated. The appropriate permeability of the dam shell and horizontal filters must be considered during the design and construction phase.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sjödahl, P.; Dahlin, T.; Johansson, S. Using resistivity measurements for dam safety evaluation at Enemossen tailings dam in southern Sweden. Environ. Geol. 2005, 49, 267–273. [Google Scholar] [CrossRef]
- Andersen, G.R.; Chouinard, L.E.; Bouvier, C.; Back, W.E. Ranking procedure on maintenance tasks for monitoring of embankment dams. J. Geotech. Geoenviron. Eng. 1999, 125, 247–259. [Google Scholar] [CrossRef]
- Al-Janabi, A.M.S.; Ghazali, A.H.; Ghazaw, Y.M.; Afan, H.A.; Al-Ansari, N.; Yaseen, Z.M. Experimental and numerical analysis for earth-fill dam seepage. Sustainability 2020, 12, 2490. [Google Scholar] [CrossRef]
- Sun, G.; Yang, Y.; Jiang, W.; Zheng, H. Effects of an increase in reservoir drawdown rate on bank slope stability: A case study at the Three Gorges Reservoir, China. Eng. Geol. 2017, 221, 61–69. [Google Scholar] [CrossRef]
- Alonso, E.E.; Pinyol, N.M. Numerical analysis of rapid drawdown: Applications in real cases. Water Sci. Eng. 2016, 9, 175–182. [Google Scholar] [CrossRef]
- Utepov, Y.; Lechowicz, Z.; Zhussupbekov, A.; Skutnik, Z.; Aldungarova, A.; Mkilima, T. The influence of material characteristics on dam stability under rapid drawdown conditions. Arch. Civ. Eng. 2022, 38, 539–553. [Google Scholar]
- Pinyol, N.M.; Alonso, E.E.; Olivella, S. Rapid drawdown in slopes and embankments. Water Resour. Res. 2008, 44, W00D03. [Google Scholar] [CrossRef]
- Duncan, J.M. State of the art: Limit equilibrium and finite-element analysis of slopes. J. Geotech. Eng. 1996, 122, 577–596. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Yip, C. Three-dimensional asymmetrical slope stability analysis extension of Bishop’s, Janbu’s, and Morgenstern—Price’s techniques. J. Geotech. Geoenviron. Eng. 2007, 133, 1544–1555. [Google Scholar] [CrossRef]
- Lane, P.; Griffiths, D. Assessment of stability of slopes under drawdown conditions. J. Geotech. Geoenviron. Eng. 2000, 126, 443–450. [Google Scholar] [CrossRef]
- Oo, H.Z.; Ai, L.Z.; Qiu, Z. Numerical analysis of river bank slope stability during rapid drawdown of water level. Study Civ. Eng. Arch. 2013, 2, 98–103. [Google Scholar]
- Hammouri, N.A.; Malkawi, A.I.H.; Yamin, M.M. Stability analysis of slopes using the finite element method and limiting equilibrium approach. Bull. Eng. Geol. Environ. 2008, 67, 471–478. [Google Scholar] [CrossRef]
- Azadi, A.; Esmatkhah Irani, A.; Azarafza, M.; Hajialilue Bonab, M.; Sarand, F.B.; Derakhshani, R. Coupled numerical and analytical stability analysis charts for an earth-fill dam under rapid drawdown conditions. Appl. Sci. 2022, 12, 4550. [Google Scholar] [CrossRef]
- Utepov, Y.B.; Aldungarova, A.K.; Mkilima, T.; Pidal, I.M.; Tulebekova, A.S.; Zharassov, S.Z.; Abisheva, A.K. Dynamics of Embankment Slope Stability under Combination of Operating Water Levels and Drawdown Conditions. Infrastructures 2022, 7, 65. [Google Scholar] [CrossRef]
- Srivastava, A.; Babu, G.S.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Gottardi, G.; Gragnano, C.G.; Rocchi, I.; Bittelli, M. Assessing river embankment stability under transient seepage conditions. Procedia Eng. 2016, 158, 350–355. [Google Scholar] [CrossRef]
- Bhaskar, P.; Puppala, A.J.; Boluk, B. Influence of unsaturated hydraulic properties on transient seepage and stability analysis of an earthen dam. Int. J. Geomech. 2022, 22, 04022105. [Google Scholar] [CrossRef]
- Li, Z.; Ye, W.; Marence, M.; Bricker, J.D. Unsteady seepage behavior of an earthfill dam during drought-flood cycles. Geosciences 2018, 9, 17. [Google Scholar] [CrossRef]
- Alonso Pérez de Agreda, E.; Pinyol Puigmartí, N.M. Slope stability under rapid drawdown conditions. In Proceedings of the First Italian Workshop on Landslides, Landslides, Napoli, 8–10 June 2009; pp. 11–27. Available online: https://upcommons.upc.edu/bitstream/handle/2117/11200/01_IWL2009_Alonso-Pinyol.pdf?sequence=1 (accessed on 30 October 2023).
- Nepal-Electricity-Authority (NEA). 9th Issue, Generation Operation and Maintenance Business. Technical Report. 2013. Available online: https://www.nea.org.np/admin/assets/uploads/supportive_docs/GenerationOM9thIssue.pdf (accessed on 30 October 2023).
- Giri, S.; Omer, A.; Mool, P.; Kitamura, Y. Morphological modelling of sediment-induced problems at a cascade system of hydropower projects in hilly region of Nepal. In Sustainable and Safe Dams around the World/Un Monde de Barrages Durables et Sécuritaires; CRC Press: Boca Raton, FL, USA, 2019; pp. 1306–1317. Available online: https://www.taylorfrancis.com/chapters/edit/10.1201/9780429319778-113/morphological-modelling-sediment-induced-problems-cascade-system-hydropower-projects-hilly-region-nepal-giri-omer-mool-kitamura (accessed on 30 October 2023).
- Army Engineer Waterways Experiment Station Vicksburg MS. The Unified Soil Classification System. Appendix A. Characteristics of Soil Groups Pertaining to Embankments and Foundations. Appendix B. Characteristics of Soil Groups Pertaining to Roads and Airfields. 1967. Available online: https://apps.dtic.mil/sti/pdfs/ADA026473.pdf (accessed on 30 October 2023).
- Zhai, Q.; Rahardjo, H. Quantification of uncertainties in soil–water characteristic curve associated with fitting parameters. Eng. Geol. 2013, 163, 144–152. [Google Scholar] [CrossRef]
- Leong, E.C.; Rahardjo, H. Review of soil-water characteristic curve equations. J. Geotech. Geoenviron. Eng. 1997, 123, 1106–1117. [Google Scholar] [CrossRef]
- Khire, M.V.; Benson, C.H.; Bosscher, P.J. Capillary barriers: Design variables and water balance. J. Geotech. Geoenviron. Eng. 2000, 126, 695–708. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Ameratunga, J.; Sivakugan, N.; Das, B.M. Correlations of Soil and Rock Properties in Geotechnical Engineering; Springer: New Delhi, India, 2016. [Google Scholar] [CrossRef]
- Bowles, J.E. Physical and Geotechnical Properties of Soils. 1979. Available online: https://trid.trb.org/view/82144 (accessed on 30 October 2023).
- AASTHO. LRFD Bridge Design Specifications (SI); American Association of State Highway and Transportation Officials: Washington, DC, USA, 2007; p. 1037. Available online: https://s36d44bae16611495.jimcontent.com/download/version/1650043778/module/11581789993/name/AASHTO_LRFD_Bridge_Design_Specifications.pdf (accessed on 30 October 2023).
- Verruijt, A. Soil Mechanics/Arnold Verruijt; Delft University of Technology: Delft, The Netherlands, 2001; Available online: https://ocw.tudelft.nl/wp-content/uploads/SoilMechBook.pdf (accessed on 30 October 2023).
- Smith, I. Smith’s Elements of Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2021; Available online: https://ds.amu.edu.et/xmlui/bitstream/handle/123456789/9472/%5BG._N._Smith_G.N._Smith%5D_Elements_of_Soil_Mechanic%28BookFi.org%29.pdf?sequence=1&isAllowed=y (accessed on 30 October 2023).
- Geostudio. Stability Modeling with GeoStudio. 2023. Available online: https://www.geoslope.com/learning/support-resources#dnn_BooksHeaderPane (accessed on 30 October 2023).
- U.S. Army Corps of Engineers. Slope Stability, Engineering Manual. 2023. Available online: https://www.publications.usace.army.mil/Portals/76/Publications/EngineerManuals/EM_1110-2-1902.pdf (accessed on 30 October 2023).












| Material | () | |
|---|---|---|
| Soils | Soft and firm clay of medium to high plasticity, silty clays, loose variable clayey fills, loose sandy silts (use ) | 17–25 |
| Stiff sandy clays, gravelly clays, compacted clayey sands and sandy silts, compacted clay fill (use ) | 26–32 | |
| Gravelly sands, compacted sands, controlled crushed sandstone, and gravel fill, dense well-graded sands (use ) | 32–37 | |
| Weak weathered rock, controlled fills of roadbase, gravelly and recycled concrete (use ) | 36–43 | |
| Rocks | Chalk () | 35 |
| Weathered granite () | 33 | |
| Fresh basalt () | 37 | |
| Weak sandstone () | 32 | |
| Weak siltstone () | 28 | |
| Weak mudstone () | 32 |
| Soil Type | Typical Range of Young’s Modulus (MN/m2) | Poisson’s Ratio |
|---|---|---|
| Clay: Soft sensitive | 2.4–15 | 0.4–0.5 undrained |
| Medium stiff to stiff | 15–50 | |
| Very stiff | 50–100 | |
| Loess Silt | 15–60 | 0.1–0.3 |
| 2–20 | 0.3–0.35 | |
| Fine Sand: Loose | 7.5–10 | 0.25 |
| Medium Dense | 10–20 | |
| Dense | 20–25 | |
| Sand: Loose | 10–25 | 0.25–0.35 |
| Medium Dense | 25–50 | 0.3–0.4 |
| Dense | 50–75 | |
| Gravel: Loose | 25–75 | 0.2–0.35 |
| Medium Dense | 75–100 | 0.3–0.4 |
| Dense | 100–200 |
| Method | Inter-Slice Normal (E) | Inter-Slice Shear (X) | Inclination of X/E Resultant, and X-E Relationship |
|---|---|---|---|
| Ordinary or Fellenius | No | No | No inter-slice forces |
| Bishop’s Simplified | Yes | No | Horizontal |
| Janbu’s Simplified | Yes | No | Horizontal |
| Spencer | Yes | Yes | Constant |
| Morgenstern–Price | Yes | Yes | Variable; user function |
| Corps of Engineers-1 | Yes | Yes | Inclination of a line from crest to |
| Corps of Engineers-2 | Yes | Yes | Inclination of ground surface at top of slice |
| Lowe-Karafiath | Yes | Yes | Average of ground surface and slice base inclination |
| Janbu Generalized | Yes | Yes | Applied line of thrust and moment equilibrium of slice |
| Sarma-vertical slices | Yes | Yes |
| Method | Moment Equilibrium | Force Equilibrium |
|---|---|---|
| Ordinary or Fellenius | Yes | No |
| Bishop’s Simplified | Yes | No |
| Janbu’s Simplified | No | Yes |
| Spencer | Yes | Yes |
| Morgenstern–Price | Yes | Yes |
| Corps of Engineers-1 | No | Yes |
| Corps of Engineers-2 | No | Yes |
| Lowe-Karafiath | No | Yes |
| Janbu Generalized | Yes (by slice) | Yes |
| Sarma-vertical slices | Yes | Yes |
| Materials | (m/s) | Vol. WC | Residual = 10% WC | (kPa) | Unit Wt (kN/m) | Friction Angle () | c (kPa) | Modulus of Elasticity (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|---|
| Clay core | 0.50 | 0.05 | 16 | 25 | 10 | 30 | 0.45 | ||
| Dam shell | 0.40 | 0.040 | 20 | 30 | 8 | 50 | 0.3 | ||
| Fine filter | 0.30 | 0.030 | 18 | 32 | 2 | 25 | 0.25 | ||
| Coarse filter | 0.25 | 0.025 | 22 | 35 | 1 | 60 | 0.3 | ||
| Rip-rap | 0.20 | 0.020 | 27 | 37 | 0.5 | 95 | 0.35 |
| Upstream side of the dam at location A with a draw-down rate after | |
| Hydraulic conductivity m/s | Seepage discharge |
| Three-layers horizontal filter conductivity at location A is | |
| Analysis Condition | Required Minimum Factor of Safety | Slope |
|---|---|---|
| End-of-Construction (including staged construction) | 1.3 | Upstream and Downstream |
| Long-term (Steady seepage, maximum storage pool, spillway crest or top of gates) | 1.5 | Upstream and Downstream |
| Maximum surcharge pool | 1.4 | Downstream |
| Rapid Draw Down | 1.1–1.3 | Upstream |
| Overall Minimum FOS | |||||||
|---|---|---|---|---|---|---|---|
| Draw-Down | Draw-Down Rate | Dam Shell | Dam Shell | Upstream Horizontal Filter | |||
| Using LEM | Using FEM | Using LEM | Using FEM | Using LEM | Using FEM | ||
| 8 h | 1.28 | 1.27 | 1.43 | 1.41 | 1.56 | 1.54 | |
| 20 h | 1.35 | 1.33 | 1.49 | 1.47 | 1.59 | 1.57 | |
| 40 h | 1.42 | 1.38 | 1.53 | 1.51 | 1.60 | 1.58 | |
| 60 h | 1.46 | 1.42 | 1.54 | 1.52 | 1.61 | 1.59 | |
| 80 h | 1.49 | 1.44 | 1.55 | 1.53 | 1.62 | 1.60 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pandey, B.R.; Knoblauch, H.; Zenz, G. Slope Stability Evaluation Due to Reservoir Draw-Down Using LEM and Stress-Based FEM along with Mohr–Coulomb Criteria. Water 2023, 15, 4022. https://doi.org/10.3390/w15224022
Pandey BR, Knoblauch H, Zenz G. Slope Stability Evaluation Due to Reservoir Draw-Down Using LEM and Stress-Based FEM along with Mohr–Coulomb Criteria. Water. 2023; 15(22):4022. https://doi.org/10.3390/w15224022
Chicago/Turabian StylePandey, Binaya Raj, Helmut Knoblauch, and Gerald Zenz. 2023. "Slope Stability Evaluation Due to Reservoir Draw-Down Using LEM and Stress-Based FEM along with Mohr–Coulomb Criteria" Water 15, no. 22: 4022. https://doi.org/10.3390/w15224022