Optimisation of Small Hydropower Units in Water Distribution Systems by Demand Forecasting
Abstract
:1. Introduction
2. Materials and Methods
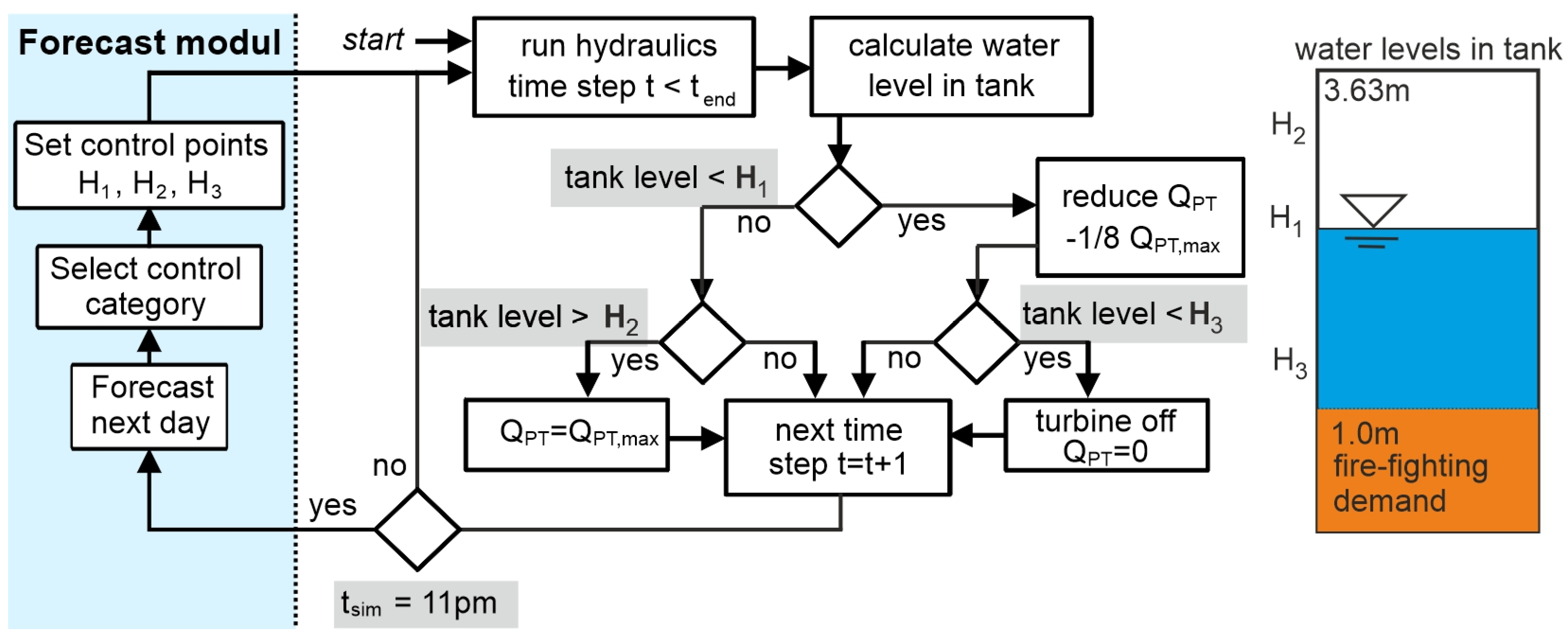
- Maximum flow operation: When the storage tank is approximately full and the water level is above H2, the SHPU operates at maximum flow.
- Normal flow operation: When the water level is between H1 and H2, the turbine operates with the current settings.
- Flow reduction: If the water level falls between H1 and H3, the control strategy involves gradually reducing the turbine’s flow rate by 1/8 of the maximum flow rate. This reduction in flow rate aims to restore the water level in the subsequent simulation time step. However, if the water level in the storage tank continues to decrease despite the flow rate reduction, the turbine’s flow rate is further reduced.
- SHPU shutdown: If the water level falls below H3, the control strategy involves completely shutting off the turbine to ensure an adequate water supply is reserved for firefighting.
- Resuming maximum flow operation: Once the water level rises above H2 again, the control strategy sets the turbine back to maximum flow.
2.1. Optimisation of the Control Strategy
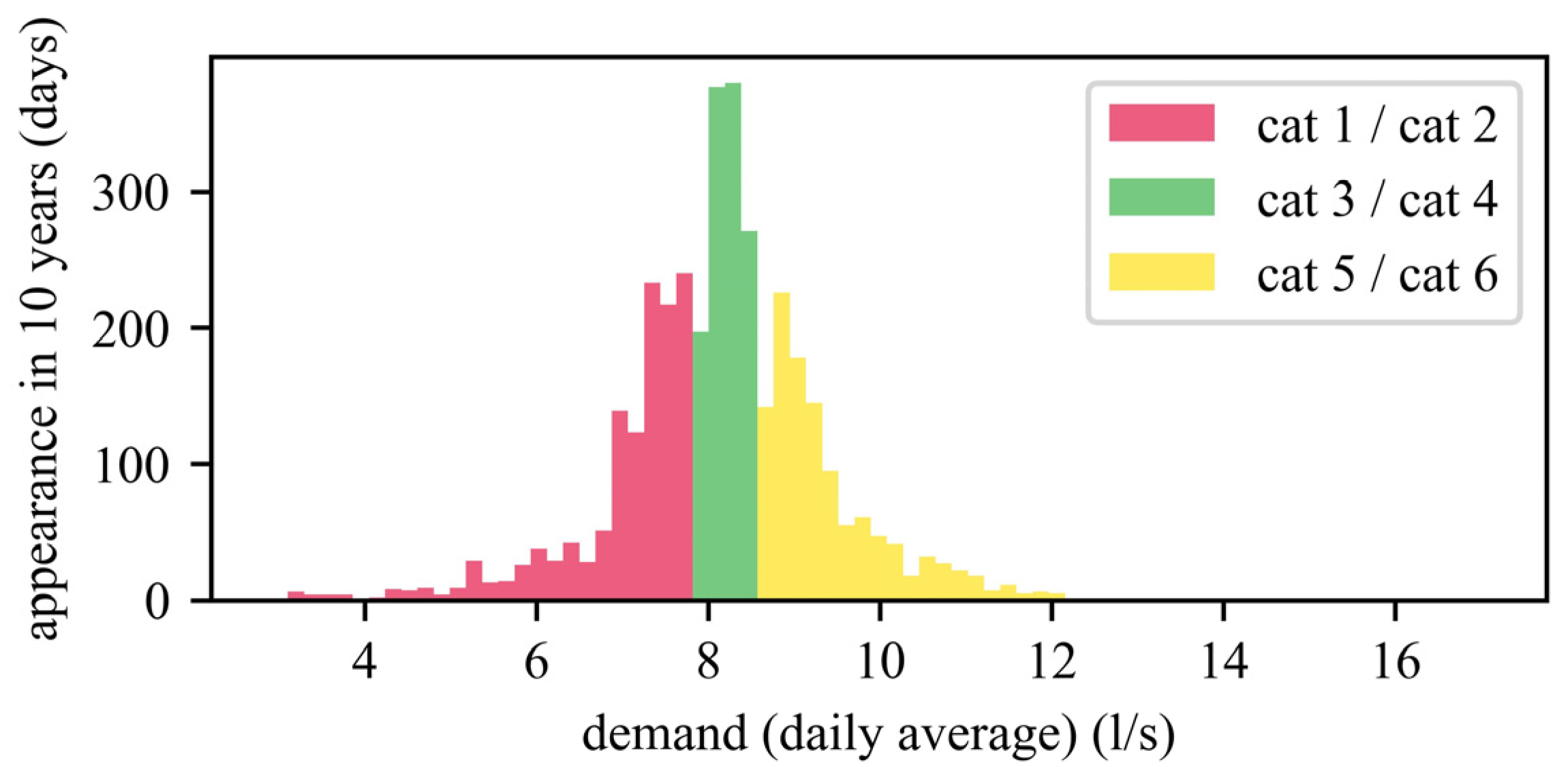
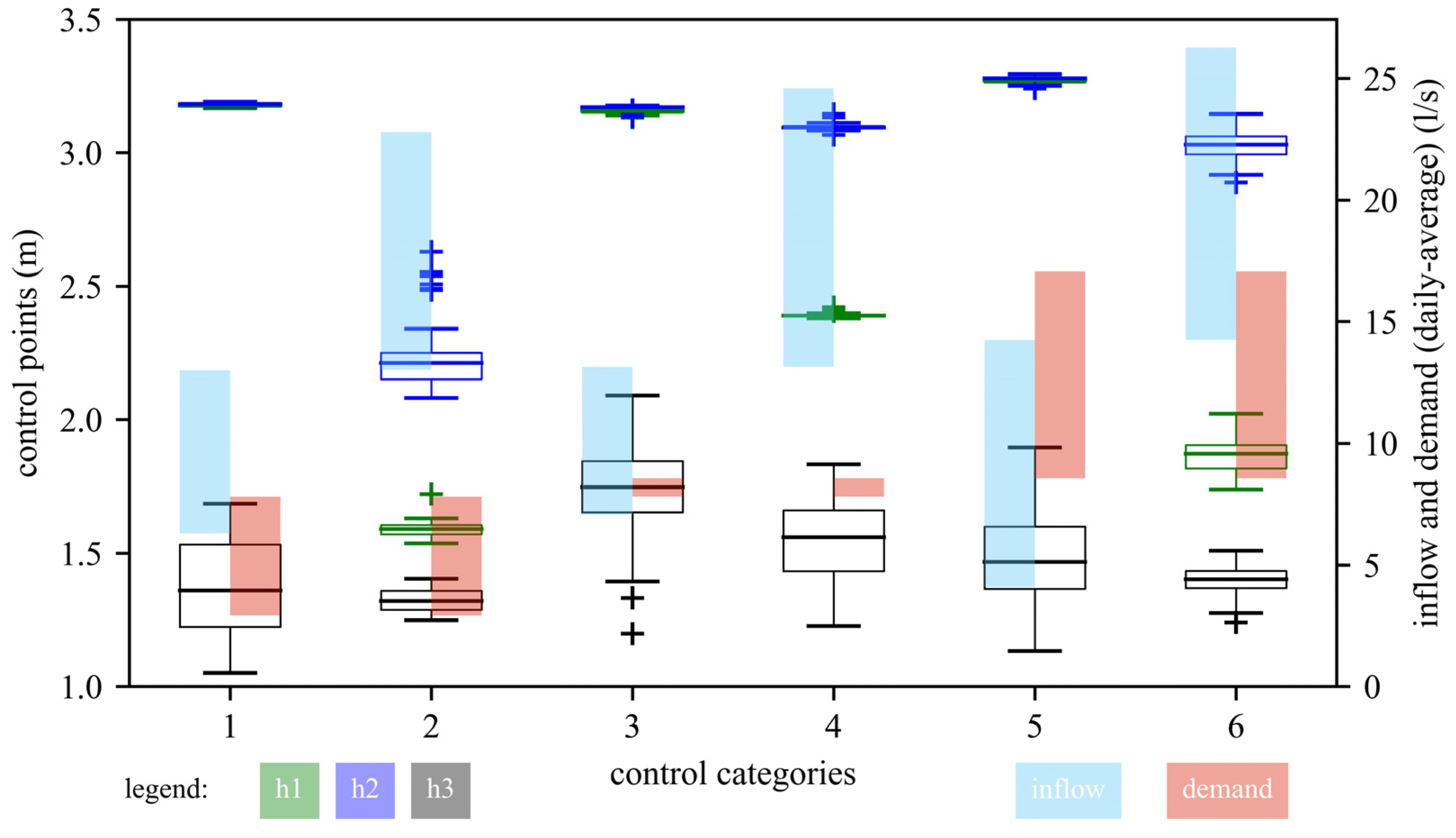
2.1.1. Control Categories
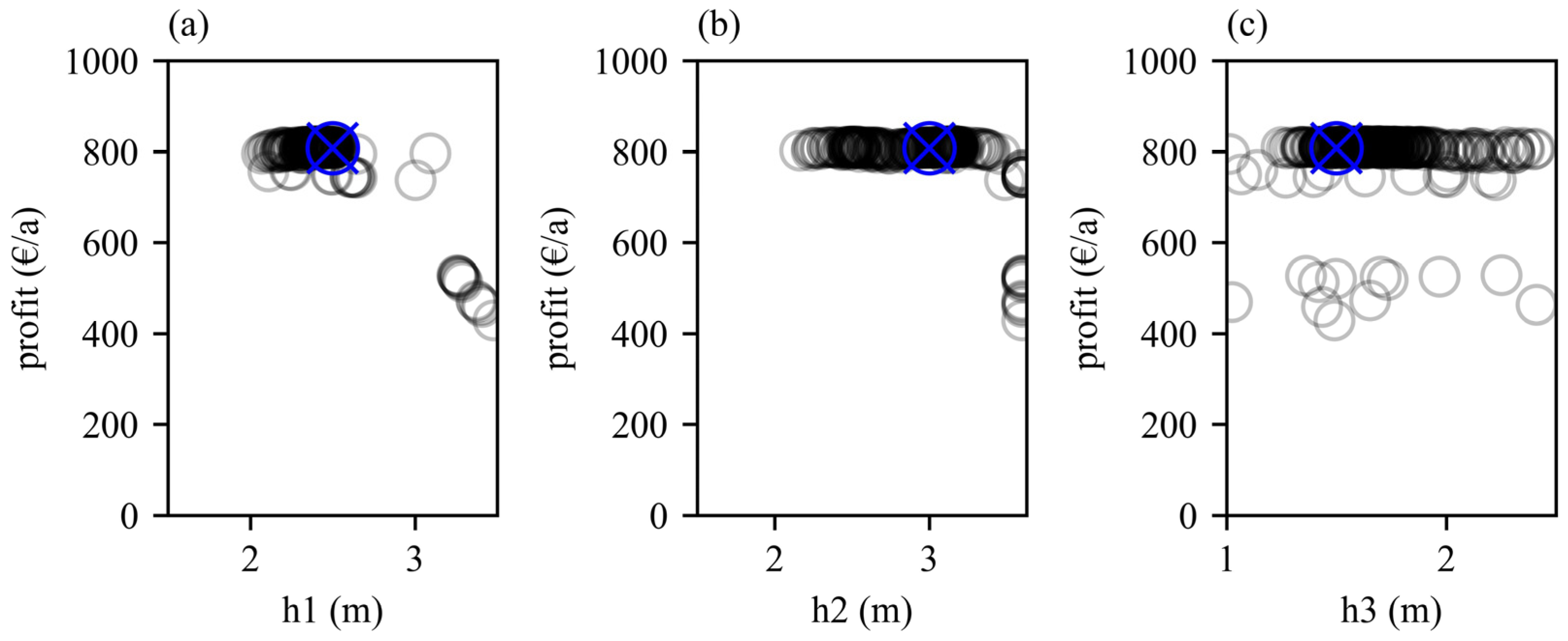
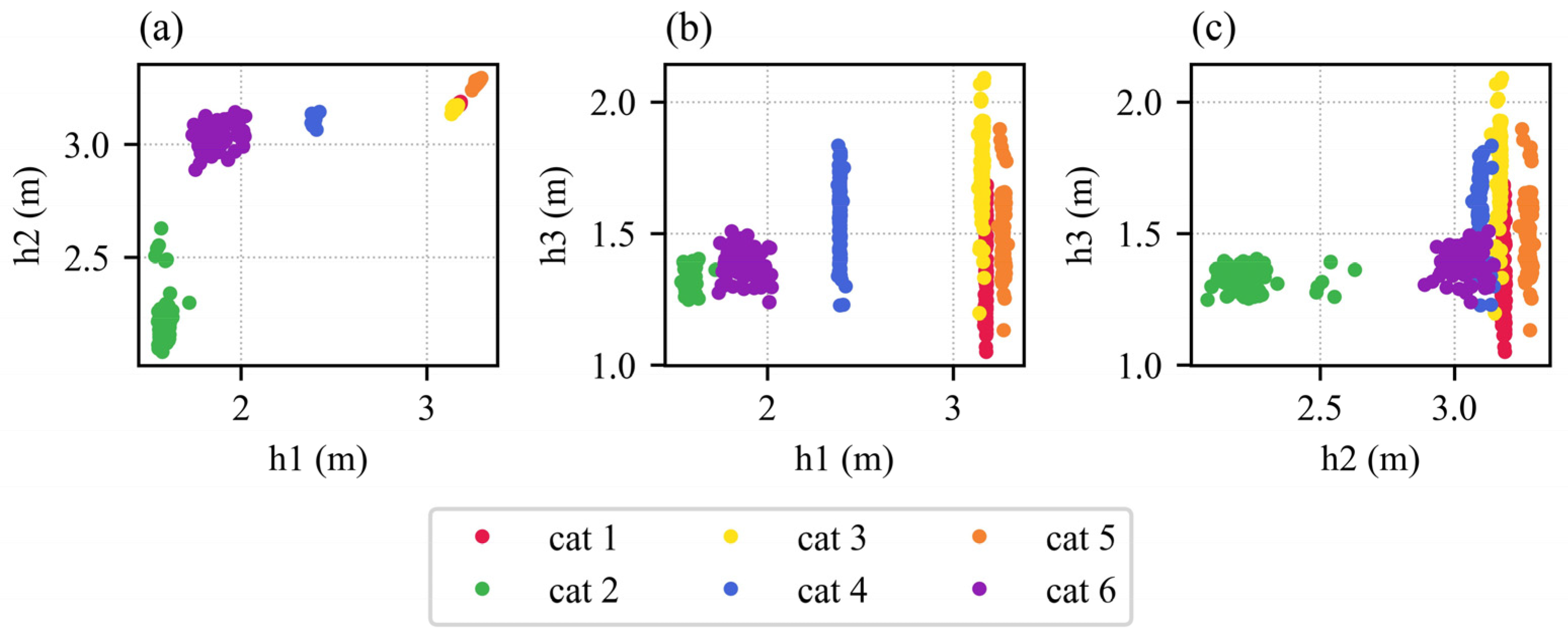
2.1.2. Optimisation of Operating Levels
2.1.3. Forecasting of Control Categories
- Perfect forecast: Assumes a perfect forecast where the predicted control categories match the actual conditions with 100% accuracy, representing the maximum potential of the forecast.
- Tomorrow like today: Assumes that the spring discharge and total water demand will be the same as the current day.
- Tomorrow like last week: Assumes that the spring discharge and total water demand will be the same as the corresponding weekday last week.
- False forecast: Examines the effect of an incorrect forecast as the worst-case performance scenario. The correct control category is disregarded, and the control category for the next day is randomly selected from the remaining categories.
2.2. Profitability Analysis
2.3. Case Study
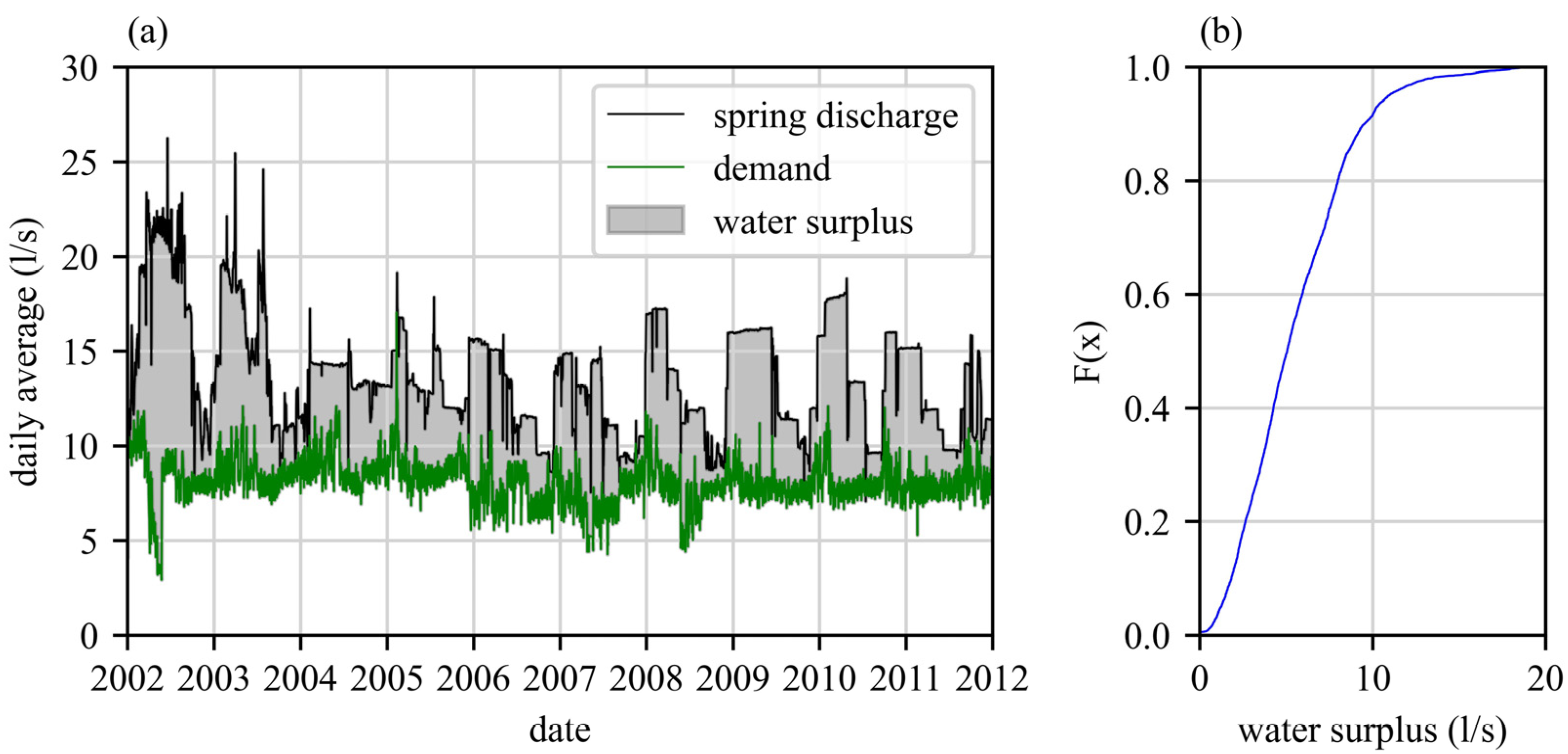
2.3.1. Water Surplus
2.3.2. Numerical Model
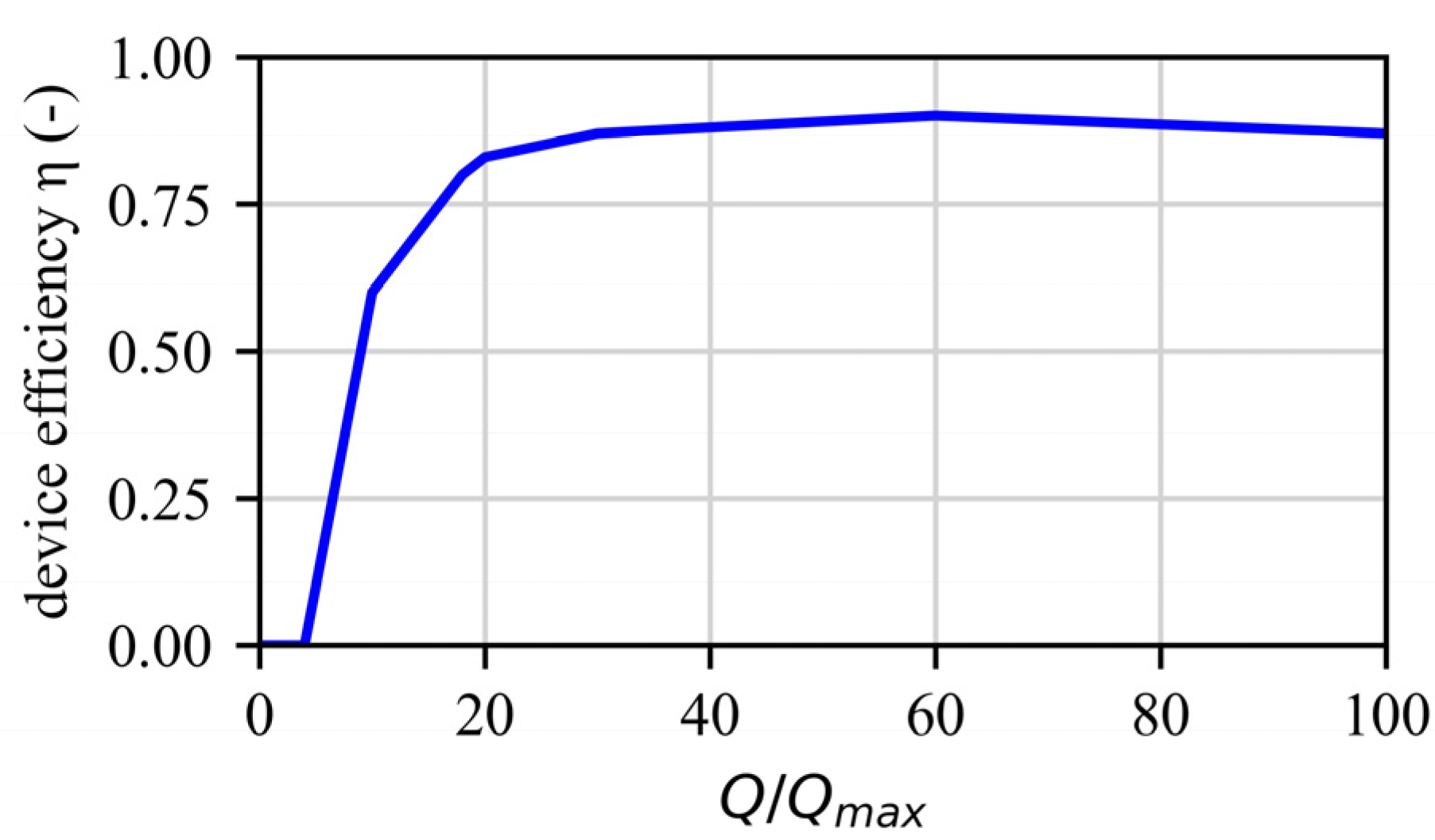
2.3.3. Small Hydropower Unit
3. Results and Discussion
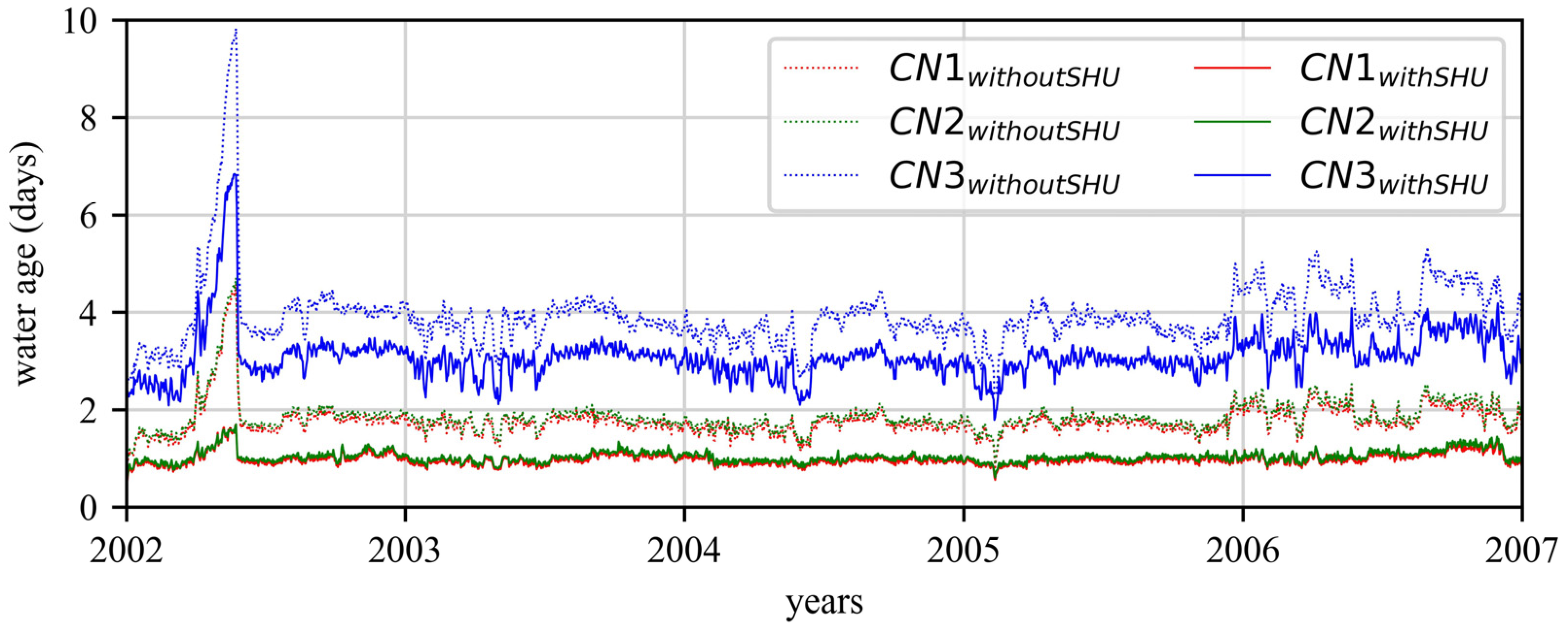
3.1. Optimisation with One Control Category
3.2. Optimisation with Six Control Categories
- Category 1: Low water demand with low spring discharge;
- Category 2: Low water demand with high spring discharge;
- Category 3: Medium water demand with low spring discharge;
- Category 4: Medium water demand with high spring discharge;
- Category 5: High water demand with low spring discharge;
- Category 6: High water demand with high spring discharge.
3.3. Economic Evaluation
3.4. Limitations and Future Research Directions
3.5. Further Discussion
4. Conclusions
- Incorporating demand forecasts and adjusting controls for different flow conditions can improve the electrical energy potential of an SHPU;
- However, it is worth noting that the controls in the reference state were already based on well-reasoned expert knowledge, making improvements marginal compared to the effort required for more complex control strategies in this specific case study;
- The prediction approach shows potential when dealing with devices that have a steep and narrow device efficiency curve, such as pump as turbines, or when considering fluctuating electricity prices;
- Additionally, an SHPU can significantly improve the quality of drinking water due to higher abstraction volumes, and if the generated electrical energy is directly used to operate the network, it also increases the resilience of the water supply system against outages of the power grid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, M.; Keller, A.A.; Chiang, P.-C.; Den, W.; Wang, H.; Hou, C.-H.; Wu, J.; Wang, X.; Yan, J. Water-energy nexus for urban water systems: A comparative review on energy intensity and environmental impacts in relation to global water risks. Appl. Energy 2017, 205, 589–601. [Google Scholar] [CrossRef]
- Vakilifard, N.; Anda, M.; Bahri, A.P.; Ho, G. The role of water-energy nexus in optimising water supply systems—Review of techniques and approaches. Renew. Sust. Energ. Rev. 2018, 82, 1424–1432. [Google Scholar] [CrossRef]
- Wu, W.; Maier, H.R.; Dandy, G.C.; Arora, M.; Castelletti, A. The changing nature of the water–energy nexus in urban water supply systems: A critical review of changes and responses. J. Water Clim. Chang. 2020, 11, 1095–1122. [Google Scholar] [CrossRef]
- Rothausen, S.G.S.A.; Conway, D. Greenhouse-gas emissions from energy use in the water sector. Nat. Clim. Chang. 2011, 1, 210–219. [Google Scholar] [CrossRef]
- Sari, M.A.; Badruzzaman, M.; Cherchi, C.; Swindle, M.; Ajami, N.; Jacangelo, J.G. Recent innovations and trends in in-conduit hydropower technologies and their applications in water distribution systems. J. Environ. Manag. 2018, 228, 416–428. [Google Scholar] [CrossRef]
- Giudicianni, C.; Mitrovic, D.; Wu, W.; Ferrarese, G.; Pugliese, F.; Fernández-García, I.; Campisano, A.; De Paola, F.; Malavasi, S.; Maier, H.R.; et al. Energy recovery strategies in water distribution networks: Literature review and future directions in the net-zero transition. Urban Water J. 2023, 1–16. [Google Scholar] [CrossRef]
- Creaco, E.; Campisano, A.; Fontana, N.; Marini, G.; Page, P.R.; Walski, T. Real time control of water distribution networks: A state-of-the-art review. Water Res. 2019, 161, 517–530. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.; Ramos, H.; López-Jiménez, P. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Möderl, M.; Sitzenfrei, R.; Mair, M.; Jarosch, H.; Rauch, W. Identifying Hydropower Potential in Water Distribution Systems of Alpine Regions. In Proceedings of the World Environmental and Water Resources Congress 2012, Albuquerque, NM, USA, 20–24 May 2012; pp. 3137–3146. [Google Scholar] [CrossRef]
- Meirelles Lima, G.; Brentan, B.M.; Luvizotto, E. Optimal design of water supply networks using an energy recovery approach. Renew. Energy 2018, 117, 404–413. [Google Scholar] [CrossRef]
- Pugliese, F.; Paola, F.D.; Fontana, N.; Marini, G.; Giugni, M. Small-Scale Hydropower Generation in Water Distribution Networks by Using Pumps as Turbines. Proceedings 2018, 2, 1486. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Sinagra, M.; Tucciarelli, T. Cost-Benefit Analysis for Hydropower Production in Water Distribution Networks by a Pump as Turbine. J. Water Resour. Plan. Manag. 2014, 140, 04014002. [Google Scholar] [CrossRef]
- Hamlehdar, M.; Yousefi, H.; Noorollahi, Y.; Mohammadi, M. Energy recovery from water distribution networks using micro hydropower: A case study in Iran. Energy 2022, 252, 124024. [Google Scholar] [CrossRef]
- Latifi, M.; Kerachian, R.; Beig Zali, R. Evaluating energy harvesting from water distribution networks using combined stakeholder and social network analysis. Energy Strateg. Rev. 2023, 49, 101158. [Google Scholar] [CrossRef]
- Amiri-Ardakani, Y.; Najafzadeh, M. Pipe Break Rate Assessment While Considering Physical and Operational Factors: A Methodology based on Global Positioning System and Data-Driven Techniques. Water Resour. Manag. 2021, 35, 3703–3720. [Google Scholar] [CrossRef]
- Zeidan, M.; Ostfeld, A. Hydraulic Ram Pump Integration into Water Distribution Systems for Energy Recovery Application. Water 2021, 14, 21. [Google Scholar] [CrossRef]
- Ramos, H.M.; Morani, M.C.; Pugliese, F.; Fecarotta, O. Integrated Smart Management in WDN: Methodology and Application. Water 2023, 15, 1217. [Google Scholar] [CrossRef]
- Monteiro, L.; Delgado, J.; Covas, D. Improved Assessment of Energy Recovery Potential in Water Supply Systems with High Demand Variation. Water 2018, 10, 773. [Google Scholar] [CrossRef]
- Loots, I.; van Dijk, M.; van Vuuren, S.J.; Bhagwan, J.N.; Kurtz, A. Conduit-hydropower potential in the City of Tshwane water distribution system: A discussion of potential applications, financial and other benefits. J. S. Afr. Inst. Civ. Eng. 2014, 56, 2–13. [Google Scholar]
- Samora, I.; Manso, P.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Opportunity and Economic Feasibility of Inline Microhydropower Units in Water Supply Networks. J. Water Resour. Plan. Manag. 2016, 142, 04016052. [Google Scholar] [CrossRef]
- de Marinis, G.; Granata, F.; Santopietro, S.; Savić, D.; Kapelan, Z.; Gargano, R.; Morley, M.S.; Tricarico, C. Optimal energy recovery by means of pumps as turbines (PATs) for improved WDS management. Water Supply 2018, 18, 1365–1374. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Optimal energy management of water-energy networks via optimal placement of pumps-as-turbines and demand response through water storage tanks. Appl. Energy 2021, 283, 116335. [Google Scholar] [CrossRef]
- Sambito, M.; Piazza, S.; Freni, G. Stochastic Approach for Optimal Positioning of Pumps As Turbines (PATs). Sustainability 2021, 13, 12318. [Google Scholar] [CrossRef]
- Brady, J.; Gallagher, J.; Corcoran, L.; Coughlan, P.; McNabola, A. Effects of Long-Term Flow Variation on Microhydropower Energy Production in Pressure Reducing Valves in Water Distribution Networks. J. Water Resour. Plan. Manag. 2017, 143, 04016076. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G.; Zollo, R. Operation of a Prototype for Real Time Control of Pressure and Hydropower Generation in Water Distribution Networks. Water Resour. Manag. 2018, 33, 697–712. [Google Scholar] [CrossRef]
- Creaco, E.; Galuppini, G.; Campisano, A. Unsteady flow modelling of hydraulic and electrical RTC of PATs for hydropower generation and service pressure regulation in WDN. Urban Water J. 2021, 19, 233–243. [Google Scholar] [CrossRef]
- Fontana, N.; Marini, G.; Creaco, E. Comparison of PAT Installation Layouts for Energy Recovery from Water Distribution Networks. J. Water Resour. Plan. Manag. 2021, 147, 04021083. [Google Scholar] [CrossRef]
- Le Marre, M.; Mandin, P.; Lanoisellé, J.-L.; Zilliox, E.; Rammal, F.; Kim, M.; Inguanta, R. Pumps as turbines regulation study through a decision-support algorithm. Renew. Energy 2022, 194, 561–570. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; von Leon, J. Long-time simulation of water distribution systems for the design of small hydropower systems. Renew. Energy 2014, 72, 182–187. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; von Leon, J.; Rauch, W. Design and Optimization of Small Hydropower Systems in Water Distribution Networks Based on 10-Years Simulation with Epanet2. Procedia Eng. 2014, 89, 533–539. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; Rauch, W. Optimizing Small Hydropower Systems in Water Distribution Systems Based on Long-Time-Series Simulation and Future Scenarios. J. Water Resour. Plan. Manag. 2015, 141, 04015021. [Google Scholar] [CrossRef]
- Hagberg, A.; Swart, P.; Chult, S.D. Exploring Network Structure, Dynamics, and Function Using NetworkX; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2008. [Google Scholar]
- Rossman, L.A.; Woo, H.; Tryby, M.; Shang, F.; Janke, R.; Haxton, T. EPANET 2.2 User Manual; Water Infrastructure Division, Center for Environmental Solutions and Emergency Response; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2020.


| Scenario | Profit (€/a) | Change (%) |
|---|---|---|
| Reference state 1 | 807.64 | - |
| One category—Without forecast | 812.42 | +0.6 |
| Six categories—Perfect forecast | 816.78 | +1.1 |
| Six categories—Tomorrow as today | 816.19 | +0.9 |
| Six categories—Tomorrow as last week | 811.31 | +0.5 |
| Six categories—False forecast | 782.65 | −3.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oberascher, M.; Schartner, L.; Sitzenfrei, R. Optimisation of Small Hydropower Units in Water Distribution Systems by Demand Forecasting. Water 2023, 15, 3998. https://doi.org/10.3390/w15223998
Oberascher M, Schartner L, Sitzenfrei R. Optimisation of Small Hydropower Units in Water Distribution Systems by Demand Forecasting. Water. 2023; 15(22):3998. https://doi.org/10.3390/w15223998
Chicago/Turabian StyleOberascher, Martin, Lukas Schartner, and Robert Sitzenfrei. 2023. "Optimisation of Small Hydropower Units in Water Distribution Systems by Demand Forecasting" Water 15, no. 22: 3998. https://doi.org/10.3390/w15223998






