Impact Evaluation Using Nonstationary Parameters for Historical and Projected Extreme Precipitation
Abstract
:1. Introduction
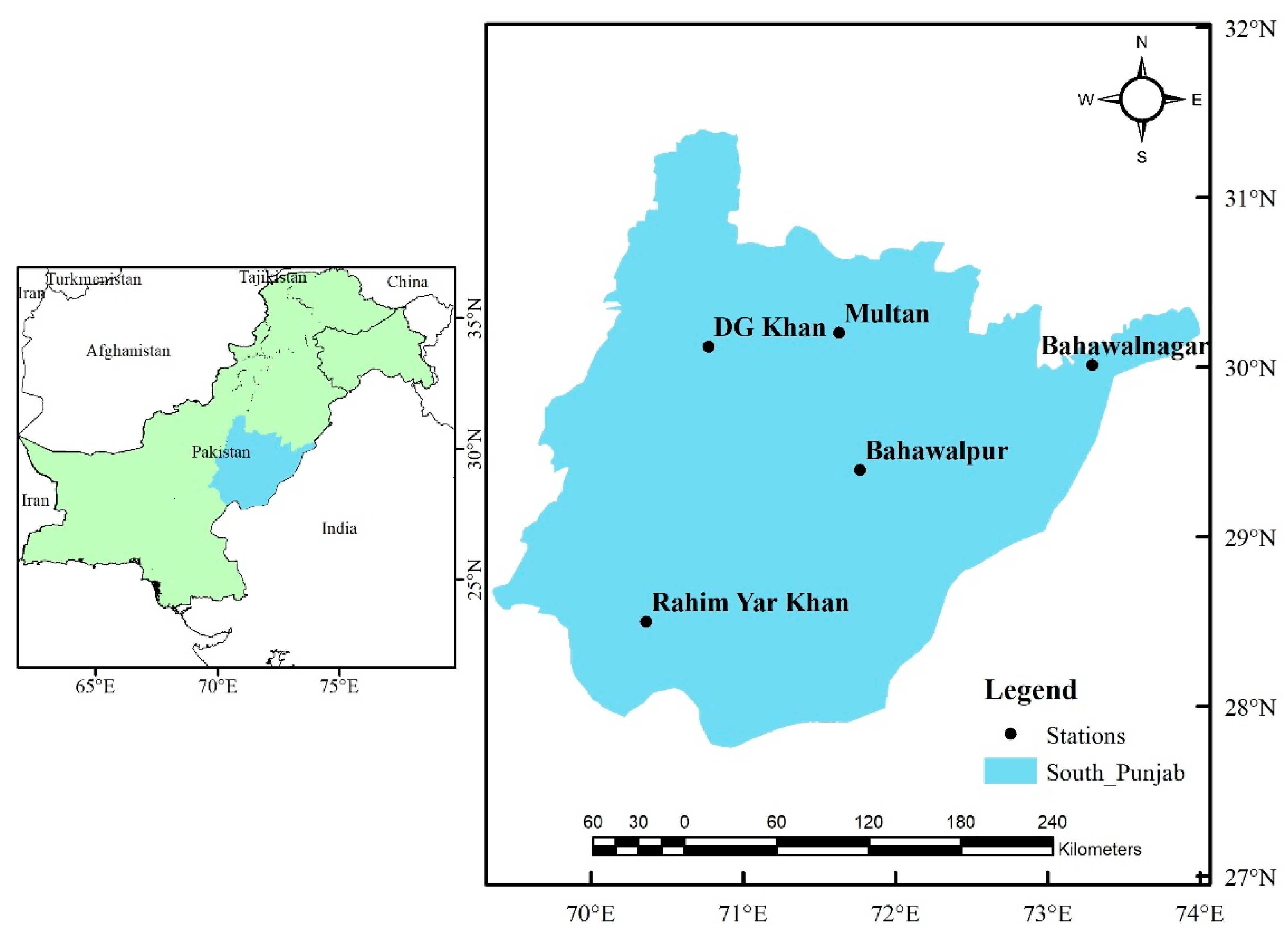
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
3. Methodology
3.1. Statistical Analysis
3.2. Stationarity in Data Series
3.3. Stationary and Nonstationary Frequency Analysis
4. Results
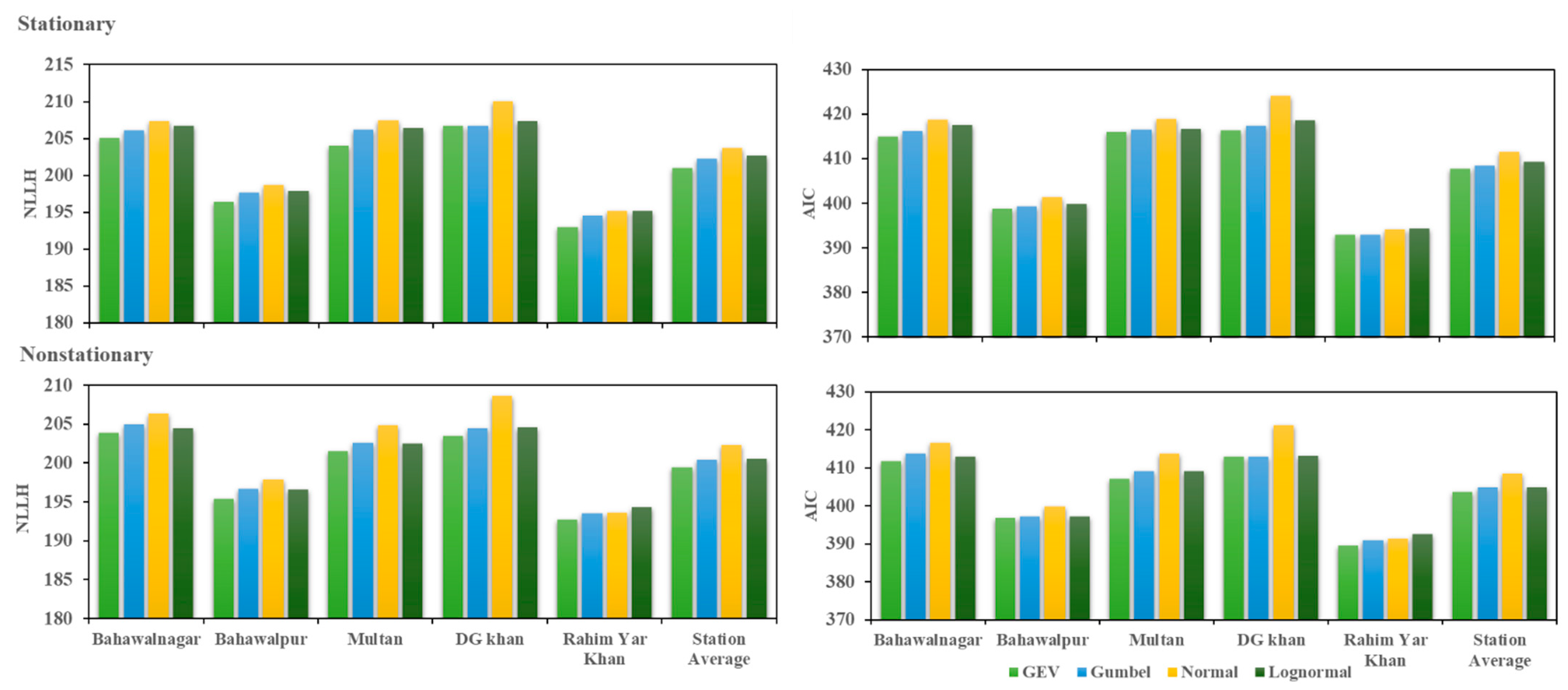
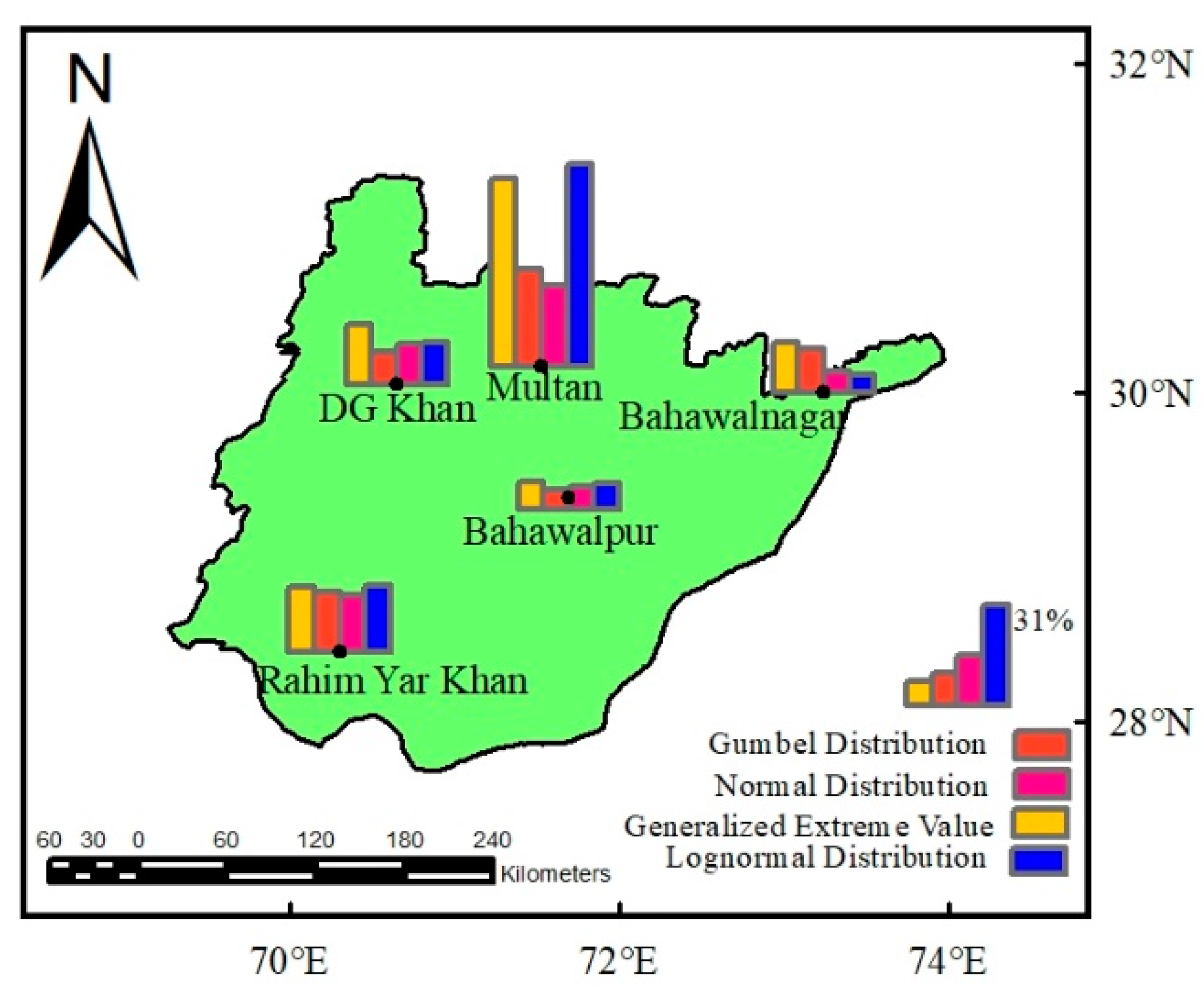
4.1. Selection of Best Probability Distribution Function
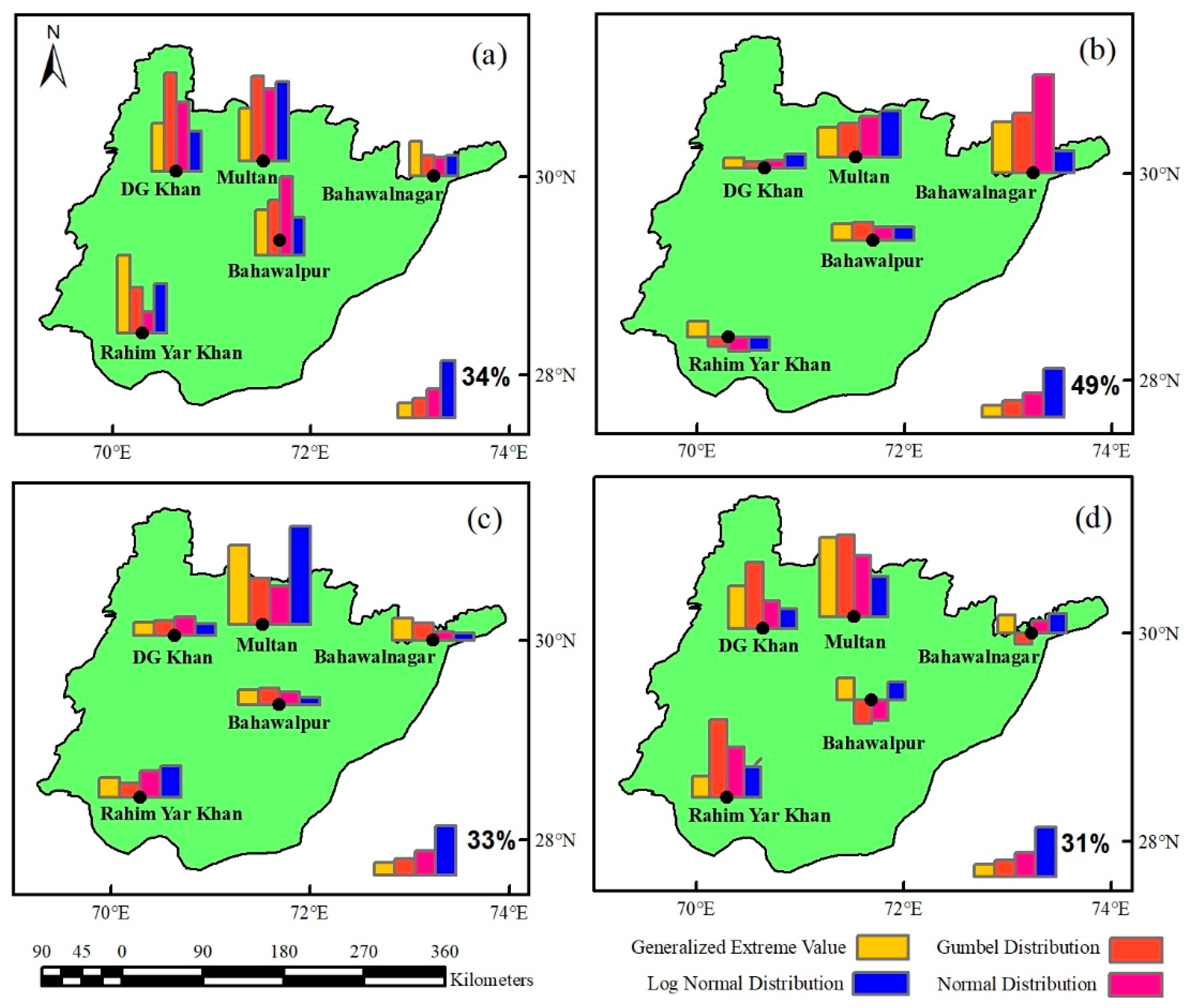
4.2. Impacts of Nonstationarity for the Historic Period (1970–2015)
4.2.1. Yearly Maximum Precipitation (MP)
4.2.2. Seasonal MP
4.3. Impacts of Nonstationarity for Annual Projected Period (2020–2100)
4.4. Projected Seasonally MP
5. Discussion
6. Conclusions
- -
- Although GEV (initially having three components) is a widely used probability distribution. The findings of this study reveal that alternative distributions are also capable of comparing nonstationary impacts. The less complicated distributions (having two parameters) might prove advantageous at a particular station.
- -
- The increase in the return level (magnitude) of extreme precipitation in winter and spring showed causes of flood events, and the reduction in return level of extreme precipitation in summer and autumn may cause less water availability.
- -
- The projected increase in nonstationarity impacts (up to 50%) distinguished the climate change in the region and emphasized the nonstationarity in the design of hydraulic structures (Reservoirs, Barrages, and others).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Mishra, A.K.; Singh, V.P. Changes in extreme precipitation in Texas. J. Geophys. Res. 2010, 15, D14106. [Google Scholar] [CrossRef]
- López, J.; Francés, F. Nonstationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Vogel, R.; Foufoula-Georgiou, E. Frequency analysis of extreme events. Handb. Hydrol. 1993, 18, 68. [Google Scholar]
- Salas, J. Analysis and Modeling of Hydrologic Time Series in Hand Book of Hydrology; Maidment, D.R., Ed.; McGraw Hill Book Co.: New York, NY, USA, 1993. [Google Scholar]
- Council, N.R. Decade-to-Century-Scale Climate Variability and Change: A Science Strategy; National Academies Press: Washington, DC, USA, 1998. [Google Scholar]
- Norrant, C.; Douguédroit, A. Monthly and daily precipitation trends in the Mediterranean (1950–2000). Theor. Appl. Climatol. 2006, 83, 89–106. [Google Scholar] [CrossRef]
- Mudelsee, M.; Börngen, M.; Tetzlaff, G.; Grünewald, U. No upward trends in the occurrence of extreme floods in central Europe. Nature 2003, 425, 166–169. [Google Scholar] [CrossRef]
- Douglas, E.; Vogel, R.; Kroll, C. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Franks, S.W. Identification of a change in climate state using regional flood data. Hydrol. Earth Syst. Sci. 2002, 6, 11–16. [Google Scholar] [CrossRef]
- Milly, P.C.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Villarini, G.; Serinaldi, F.; Smith, J.A.; Krajewski, W.F. On the stationarity of annual flood peaks in the continental united states during the 20th century. Water Resour. Res. 2009, 45, W08417. [Google Scholar] [CrossRef]
- Wilson, D.; Hisdal, H.; Lawrence, D. Has streamflow changed in the nordic countries?—Recent trends and comparisons to hydrological projections. J. Hydrol. 2010, 394, 334–346. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Bales, J.; Bates, P.D.; Krajewski, W.F. Flood frequency analysis for nonstationary annual peak records in an urban drainage basin. Adv. Water Resour. 2009, 32, 1255–1266. [Google Scholar] [CrossRef]
- Vogel, R.M.; Yaindl, C.; Walter, M. Nonstationarity: Flood magnification and recurrence reduction factors in the United States. J. Am. Water Resour. Assoc. 2011, 47, 464–474. [Google Scholar] [CrossRef]
- Hejazi, M.I.; Markus, M. Impacts of urbanization and climate variability on floods in northeastern Illinois. J. Hydrol. Eng. 2009, 14, 606–616. [Google Scholar] [CrossRef]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Nawaz, Z.; Li, X.; Chen, Y.; Guo, Y.; Wang, X.; Nawaz, N. Temporal and spatial characteristics of precipitation and temperature in Punjab, Pakistan. Water 2019, 11, 1916. [Google Scholar] [CrossRef]
- Jain, S.K.; Kumar, V.; Saharia, M. Analysis of rainfall and temperature trends in northeast India. Int. J. Climatol. 2013, 33, 968–978. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; van Dijk, A.I.J.M.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef]
- Hamdi, M.R.; Abu-Allaban, M.; Elshaieb, A.; Jaber, M.; Momani, N.M. Climate change in Jordan: A comprehensive examination approach. Am. J. Environ. Sci. 2009, 5, 740–750. [Google Scholar] [CrossRef]
- Matti, C.; Pauling, A.; Küttel, M.; Wanner, H. Winter precipitation trends for two selected European regions over the last 500 years and their possible dynamical background. Theor. Appl. Climatol. 2009, 95, 9–26. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, V.; Thomas, T.; Arora, M. Basin-wide assessment of temperature trends in northwest and central India/Estimation par bassin versant de tendances de température au nord-ouest et au centre de l’Inde. Hydrol. Sci. J. 2008, 53, 421–433. [Google Scholar] [CrossRef]
- De la Casa, A.; Nasello, O. Breakpoints in annual rainfall trends in Córdoba, Argentina. Atmos. Res. 2010, 95, 419–427. [Google Scholar] [CrossRef]
- Gleick, P.H. Climate change, hydrology, and water resources. Rev. Geophys. 1989, 27, 329–344. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q.; Qian, W. Quality control of daily meteorological data in China, 1951–2000: A new dataset. Int. J. Climatol. A J. R. Meteorol. Soc. 2004, 24, 853–870. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Hong, Y.; Yong, B.; Yang, X.; Yuan, F.; Ma, M. Comprehensive evaluation of multi-satellite precipitation products with a dense rain gauge network and optimally merging their simulated hydrological flows using the Bayesian model averaging method. J. Hydrol. 2012, 452, 213–225. [Google Scholar] [CrossRef]
- Liu, X.; Yang, T.; Hsu, K.; Liu, C.; Sorooshian, S. Evaluating the streamflow simulation capability of PERSIANN-CDR daily rainfall products in two river basins on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2017, 21, 169–181. [Google Scholar] [CrossRef]
- Fischer, E.; Knutti, R. Anthropogenic contribution to global occurrence of heavy-precipitation and high-temperature extremes. Nat. Clim. Chang. 2015, 5, 560–564. [Google Scholar] [CrossRef]
- Donat, M.; Lowry, A.; Alexander, L.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; A Special Report of Working Groups I and II of the Intergovernmental Panel on Climate, Change; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; 582p. [Google Scholar]
- Schellnhuber, H.J.; Hare, B.; Serdeczny, O. Turn Down the Heat: Climate Extremes, Regional Impacts, and the Case for Resilience; A Report for the World Bank by the Potsdam Institute for Climate Impact Research and Climate Analytics; World Bank: Washington, DC, USA, 2013. [Google Scholar]
- Eckstein, D.; Hutfils, M.-L.; Winges, M. Global Climate Risk Index; Germanwatch: Berlin, Germany, 2019. [Google Scholar]
- Khan, F.; Ali, S.; Ullah, H.; Muhammad, S. Twenty-first century climate extremes’ projections and their spatio-temporal trend analysis over Pakistan. J. Hydrol. Reg. Stud. 2023, 45, 101295. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation Trends over Time Using Mann-Kendall and Spearman’s rho Tests in Swat River Basin, Pakistan. Adv. Meteorol. 2015, 2015, 431860. [Google Scholar] [CrossRef]
- Khattak, M.S.; Reman, N.U.; Sharif, M.; Khan, M.A. Analysis of streamflow data for trend detection on major rivers of the Indus Basin. J. Himal. Earth Sci. 2015, 48, 87. [Google Scholar]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Vogel, R.M.; Read, L.K. Reliability, return periods and risk under nonstationarity. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar] [CrossRef]
- Aziz, R.; Yucel, I.; Yozgatligil, C. Nonstationarity impacts on frequency analysis of yearly and seasonal extreme precipitation in Turkey. Theor. Appl. Climatol. 2021, 143, 1213–1226. [Google Scholar] [CrossRef]
- Sertac, O. Nonstationary Investigation of Extreme Rainfall. Civ. Eng. J. 2021, 7, 1620–1633. [Google Scholar]
- Nashwan, M.S.; Tarmizi, I.; Kamal, A. Nonstationary Analysis of extreme Rainfall in Peninsular Malaysia. J. Sust. Sci. Mgmt. 2019, 14, 17–34. [Google Scholar]
- Mirza, M.M.Q. Climate change and extreme weather events: Can developing countries adapt? Clim. Policy 2003, 3, 233–248. [Google Scholar] [CrossRef]
- Linnenluecke, M.K.; Stathakis, A.; Griffiths, A. Firm relocation as adaptive response to climate change and weather extremes. Glob. Environ. Chang. 2011, 21, 123–133. [Google Scholar] [CrossRef]
- Chen, X.C.; Xu, Y.; Xu, C.H.; Yao, Y. Assessment of precipitation simulations in China by CMIP5 multi-models. Clim. Chang. Res. 2014, 10, 217–225. [Google Scholar]
- Ta, Z.; Yu, Y.; Sun, L.; Chen, X.; Mu, G.; Yu, R. Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models. Water 2018, 10, 1516. [Google Scholar] [CrossRef]
- Huang, X.H.; Yue, Q.; Zhang, M. Future precipitation change in the Belt and Road Region under Representative Concentration Pathway Scenarios. J. Yangtze River Sci. Res. Inst. 2020, 37, 53–60. [Google Scholar]
- Salman, S.A.; Nashwan, M.S.; Ismail, T.; Shahid, S. Selection of CMIP5 general circulation model outputs of precipitation for peninsular Malaysia. Hydrol. Res. 2020, 51, 781–798. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Wang, R.; Jiang, T.; Chen, S.S. Projection of extreme precipitation in the Hanjiang River basin under different RCP scenarios. Clim. Chang. Res. 2020, 16, 276–286. [Google Scholar]
- Huang, J.L.; Wang, Y.J.; Su, B.D.; Zhai, J.Q. Future climate change and its impact on runoff in the upper reaches of the Yangtze River under RCP4.5 scenario. Meteor Mon. 2016, 42, 614–620. [Google Scholar]
- Montroull, N.B.; Saurral, R.I.; Camilloni, I.A. Hydrological impacts in La Plata basin under 1.5, 2 and 3 °C global warming above the pre-industrial level. Int. J. Climatol. 2018, 38, 3355–3368. [Google Scholar] [CrossRef]
- Ashiq, M.W.; Zhao, C.; Ni, J.; Akhtar, M. GIS-based high-resolution spatial interpolation of precipitation in mountain–plain areas of Upper Pakistan for regional climate change impact studies. Theor. Appl. Climatol. 2010, 99, 239. [Google Scholar] [CrossRef]
- Ali, A.F.; Xiao, C.-D.; Zhang, X.-P.; Adnan, M.; Iqbal, M.; Khan, G. Projection of future streamflow of the Hunza River Basin, Karakoram Range (Pakistan) using HBV hydrological model. J. Mt. Sci. 2018, 15, 2218–2235. [Google Scholar] [CrossRef]
- Syed, Z.; Ahmad, S.; Dahri, Z.H.; Azmat, M.; Shoaib, M.; Inam, A.; Qamar, M.U.; Hussain, S.Z.; Ahmad, S. Hydroclimatology of the Chitral River in the Indus Basin under Changing Climate. Atmosphere 2022, 13, 295. [Google Scholar] [CrossRef]
- Waseem, M.; Ajmal, M.; Ahmad, I.; Khan, N.M.; Azam, M.; Sarwar, M.K. Projected drought pattern under climate change scenario using multivariate analysis. Arab. J. Geosci. 2021, 14, 544. [Google Scholar] [CrossRef]
- Masood, M.U.; Khan, N.M.; Haider, S.; Anjum, M.N.; Chen, X.; Gulakhmadov, A.; Iqbal, M.; Ali, Z.; Liu, T. Appraisal of Land Cover and Climate Change Impacts on Water Resources: A Case Study of Mohmand Dam Catchment, Pakistan. Water 2023, 15, 1313. [Google Scholar] [CrossRef]
- Diaz-Nieto, J.; Wilby, R.L. A comparison of statistical downscaling and climate change factor methods: Impacts on low flows in the River Thames, United Kingdom. Clim. Chang. 2005, 69, 245–268. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50.e60. [Google Scholar] [CrossRef]
- Fawad, M.; Yan, T.; Chen, L.; Huang, K.; Singh, V.P. Multiparameter probability distributions for at-site frequency analysis of annual maximum wind speed with L-Moments for parameter estimation. Energy 2019, 181, 724–737. [Google Scholar] [CrossRef]
- Iqbal, M.; Wen, J.; Wang, X.; Lan, Y.; Tian, H.; Anjum, M.N.; Adnan, M. Assessment of Air Temperature Trends in the Source Region of Yellow River and Its Sub-Basins, China. Asia-Pac. J. Atmos. Sci. 2017, 54, 111–123. [Google Scholar] [CrossRef]
- Aziz, R.; Yücel, I.; Yozgatlıgil, C. Nonstationarity impacts on frequency analysis of yearly and seasonal extreme temperature in Turkey. Atmos. Res. 2020, 238, 104875. [Google Scholar] [CrossRef]
- Seo, J.; Sangdan, K. Uncertainty of Rate of change in Korean Future Rainfall Extremes Using Non-Stationary GEV Model. Atmos. J. 2021, 12, 227. [Google Scholar] [CrossRef]
- Gellens, D. Combining regional approach and data extension procedure for assessing GEV distribution of extreme precipitation in Belgium. J. Hydrol. 2002, 268, 113–126. [Google Scholar] [CrossRef]
- Gründemann, G. Extreme precipitation return levels for multiple durations on a global scale. J. Hydrol. 2022, 621, 129558. [Google Scholar] [CrossRef]
- Kang, D. Determination of extreme wind values using the Gumbel distribution. Energy 2015, 86, 51–58. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Katz, R.W. Chapter 2, Extremes in a changing climate: Detection, analysis and uncertainty. In Statistical Methods for Nonstationary Extremes; Kouchak, A., Easterling, D., Hsu, K., Eds.; Springer: New York, NY, USA, 2013; Volume 65. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: London, UK, 2021. [Google Scholar]
- Cannon, A.J. GEVcdn: An R package for nonstationary extreme value analysis by generalized extreme value conditional density estimation network. Comput. Geosci. 2011, 37, 1532L–1533L. [Google Scholar] [CrossRef]
- Heffernan, J.; Stephenson, A. Ismev: An Introduction to Statistical Modeling of Extreme Values. R Package Version 1.39, Original S Functions Written by Janet E. Heffernan with R port and R Documentation Provided by Alec G. Stephenson. 2012. Available online: https://CRAN.R-project.org/package=ismev (accessed on 3 March 2023).
- Gilleland, E.; Katz, R. New software to analyze how extremes change over time. EOS Trans. Am. Geophys. Union 2011, 92, 13–14. [Google Scholar] [CrossRef]
- Gilleland, E. extRemes: Extreme Value Analysis. R Package Version 2.0-8. 2016. Available online: https://CRAN.R-project.org/package=extRemes (accessed on 3 March 2023).
- Trenberth, K.E.; Jones, P.D.; Ambenje, P.; Bojariu, R.; Easterling, D.; Klein, T.A.; Parker, D.; Rahimzadeh, F.; Renwick, J.A.; Rusticucci, M.; et al. Observations: Surface and atmospheric climate change. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Marquis, M., Averyt, K., Tignor, M.M.B., Miller, H.L., Jr., Chen, Z., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 235–336. [Google Scholar]
- IPCC. Climate Change 2007: Impacts, Adaptation, and Vulnerability; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Xiao, M.; Zhang, Q.; Singh, V.P. Spatiotemporal variations of extreme precipitation regimes during 1961–2010 and possible teleconnections with climate indices across China. Int. J. Climatol. 2017, 37, 468–479. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Montanari, A. Global and regional increase of precipitation extremes under global warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Huang, H.F.; Cui, H.J.; Ge, Q.S. Assessment of potential risks induced by increasing extreme precipitation under climate change. Nat. Hazards 2021, 108, 2059–2079. [Google Scholar] [CrossRef]
- Valdez, B.; Schorr, M.; Quintero, M.; García, R.; Rosas, N. Effect of climate change on durability of engineering materials in hydraulic infrastructure: An overview. Corros. Eng. Sci. Technol. 2010, 45, 34–41. [Google Scholar] [CrossRef]
- Mailhot, A.; Duchesne, S. Design criteria of urban drainage infrastructures under climate change. J. Water Resour. Plann. Manag. 2010, 136, 201–208. [Google Scholar] [CrossRef]
- Al-Ghadi, M.S.; Mohtar, W.H.M.W.; Razali, S.F.M.; El-Shafie, A. The practical influence of climate change on the performance of road stormwater drainage infrastructure. J. Eng. 2020, 2020, 8582659. [Google Scholar] [CrossRef]
- Akhtar, A.A.; Esquivel, A.; Sharma, M.; Tandon, V. Understanding Climate Change Impact on Highway Hydraulic Design Procedures; Southern Plains Transportation Center: Norman, OK, USA, 2018. [Google Scholar]
- Akhter, A.A. Assessment of Climate Change Impact on Hydraulic Design Procedures of Bridges. Master’s Thesis, The University of Texas at El Paso, El Paso, TX, USA, 2018. [Google Scholar]
- Pan, H.; Jin, Y.; Zhu, X. Comparison of Projections of Precipitation over Yangtze River Basin of China by Different Climate Models. Water 2022, 14, 1888. [Google Scholar] [CrossRef]
- Wang, H.-M.; Chen, J.; Xu, C.-Y.; Zhang, J.; Chen, H. A framework to quantify the uncertainty contribution of GCMs over multiple sources in hydrological impacts of climate change. Earth′s Future 2020, 8, e2020EF001602. [Google Scholar] [CrossRef]


| Institution ID | Model Name | Resolution (Long, Lat) |
|---|---|---|
| NOAA-GFDL | GFDL | 1.3° × 1.0° |
| MIROC | MIROC6 | 1.4° × 1.4° |
| MPIESM1-2HR | MPI-ESM1-2HR | 0.9° × 0.9° |
| MPI-M | MPIESM1-2LR | 1.9° × 1.9° |
| MRIESM2-0 | MRIESM2-0 | 1.12° × 1.12° |
| Stations | Latitude | Longitude | Elevation | Mean | STD | Cv | Cs | Ck |
|---|---|---|---|---|---|---|---|---|
| Bahawalnagar | 29°20′ | 73°51′ | 161.05 | 254.34 | 126.55 | 0.50 | 0.42 | −0.59 |
| Bahawalpur | 29°20′ | 71°47′ | 110 | 177.58 | 119.34 | 0.67 | 1.67 | 4.08 |
| Multan | 30°12′ | 71°26′ | 121.95 | 197.48 | 104.59 | 0.53 | 0.46 | 0.90 |
| Rahim Yar Khan | 28°26′ | 70°19′ | 82.93 | 112.35 | 78.70 | 0.70 | 0.86 | 0.39 |
| DG Khan | 30°03′ | 70°38′ | 148.1 | 170.12 | 109.83 | 0.65 | 0.85 | 0.56 |
| Station | Annual | Winter | Spring | Summer |
|---|---|---|---|---|
| Bahawalnagar | 0.09 | 0.15 | 0.65 | 0.15 |
| Bahawalpur | 0.88 | 0.03 | 0.58 | 1.00 |
| DG Khan | 0.79 | 0.71 | 0.84 | 0.58 |
| Multan | 0.38 | 0.17 | 0.49 | 0.38 |
| Rahim Yar Khan | 0.30 | 0.2 | 0.76 | 0.31 |
| Station | GCM Model | GFDL | MIROC6 | MPI-ESM1-2HR | MPI-ESM1-2LR | MRISEM1-0 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Season | SSP2 | SSP5 | SSP2 | SSP5 | SSP2 | SSP5 | SSP2 | SSP5 | SSP2 | SSP5 | |
| Bahawalnagar | Winter | 25.8 | −5.3 | 23.4 | −3.5 | 22.7 | 1.9 | 21.5 | 1.8 | 24.1 | −4.4 |
| Spring | 33.0 | 2.4 | 30.3 | −2.9 | 30.2 | −2.6 | 29.4 | −3.8 | 31.3 | 2.0 | |
| Summer | 33.3 | 9.5 | 31.1 | 2.5 | 32.7 | 3.0 | 32.3 | 2.6 | 32.4 | 2.8 | |
| Autumn | 13.9 | 3.4 | 14.0 | 11.3 | 16.1 | 5.2 | 13.7 | 12.9 | 14.5 | 6.9 | |
| Bahawalpur | Winter | −4.0 | 12.6 | −9.9 | 13.5 | 2.6 | 13.2 | 2.1 | 12.6 | −3.3 | 13.8 |
| Spring | 23.5 | 7.8 | 20.8 | 5.2 | 20.7 | 3.0 | 19.9 | 5.0 | 21.8 | 5.4 | |
| Summer | 3.7 | 3.2 | 4.1 | 2.7 | 2.7 | 2.1 | 3.7 | 3.6 | 2.9 | 3.4 | |
| Autumn | 5.6 | 9.9 | 7.5 | −5.2 | 10.4 | −3.1 | 8.3 | −7.1 | 4.4 | −3.7 | |
| DG Khan | Winter | 5.6 | 16.0 | 5.2 | 15.9 | 5.0 | −5.4 | 4.7 | −4.5 | 5.2 | −6.4 |
| Spring | −11.3 | 3.3 | −15.3 | −11.0 | 3.5 | 2.9 | 2.5 | −10.6 | 3.9 | −11.3 | |
| Summer | 3.9 | 1.5 | 3.8 | 5.6 | 3.3 | 7.3 | 3.7 | 6.5 | 2.6 | 8.2 | |
| Autumn | 8.7 | 17.1 | 8.3 | 13.2 | 8.0 | 11.1 | 12.5 | 12.8 | 8.3 | 13.8 | |
| Multan | Winter | −2.5 | 12.6 | −1.9 | 11.8 | 2.4 | 11.5 | −6.5 | 10.8 | 3.2 | 12.2 |
| Spring | 19.2 | 5.3 | 17.6 | 15.3 | 17.5 | 14.9 | 12.4 | 14.5 | 18.2 | 15.4 | |
| Summer | 2.2 | −6.4 | 2.5 | 2.4 | 3.9 | 2.5 | 5.4 | −5.5 | 2.0 | 3.4 | |
| Autumn | 12.8 | 8.4 | 14.6 | 12.9 | 16.8 | 12.4 | 11.5 | 11.7 | 19.4 | 4.3 | |
| Rahim Yar khan | Winter | 11.1 | 2.5 | 9.8 | 4.3 | 9.4 | −4.2 | 8.8 | −5.9 | 10.1 | −4.5 |
| Spring | −10.5 | 3.7 | −4.2 | 2.5 | −6.3 | −9.9 | 3.9 | −9.2 | 4.1 | −11.2 | |
| Summer | 12.9 | 15.5 | 13.2 | 5.8 | 13.5 | 8.4 | 12.4 | 9.5 | 11.2 | 10.3 | |
| Autumn | 6.9 | 6.4 | 6.5 | 8.8 | 8.5 | 5.5 | 10.2 | 9.0 | 6.6 | 9.8 | |
| Station | GCM Model | GFDL | MIROC6 | MPI-ESM1-2HR | MPI ESM1-2LR | MRISEM1-0 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Season | SSP2 | SSP5 | SSP2 | SSP5 | SSP2 | SSP5 | SSP2 | SSP5 | SSP2 | SSP5 | |
| Bahawalnagar | Winter | 3.8 | 7.0 | −2.9 | −9.7 | −3.5 | −10.6 | 7.8 | 8.3 | −4.5 | −10.3 |
| Spring | 12.6 | 2.3 | 12.2 | 7.9 | 12.1 | 6.1 | 8.9 | 6.9 | 10.1 | 8.4 | |
| Summer | 2.1 | 8.0 | −11.2 | −11.7 | −9.5 | −13.3 | −9.4 | −11.0 | −10.5 | −12.6 | |
| Autumn | 2.8 | 3.9 | −7.5 | 3.1 | −5.2 | 3.3 | −7.5 | 3.2 | 2.3 | 3.5 | |
| Bahawalpur | Winter | 4.6 | 7.1 | −4.8 | 4.1 | −4.6 | 6.8 | 2.7 | 4.8 | −4.6 | 6.9 |
| Spring | 2.2 | 3.1 | −1.8 | 4.0 | −2.8 | 5.2 | 3.8 | 4.8 | 4.5 | 5.8 | |
| Summer | 4.1 | 4.7 | 3.3 | −12.9 | 4.2 | −14.3 | 4.3 | −11.2 | 3.9 | −9.3 | |
| Autumn | 3.7 | 2.6 | −5.5 | −6.5 | −12.5 | −2.5 | −7.5 | 2.2 | −10.8 | −1.5 | |
| DG Khan | Winter | 25.4 | 11.6 | 27.2 | 8.5 | 26.5 | 9.8 | 27.1 | 8.6 | 26.7 | 9.1 |
| Spring | 3.5 | 5.0 | −13.4 | −14.9 | −12.2 | −15.1 | 5.3 | 7.5 | −12.2 | −14.6 | |
| Summer | 30.1 | 17.5 | 28.4 | 22.4 | 27.5 | 16.8 | 25.5 | 12.6 | 22.5 | 24.1 | |
| Autumn | 12.6 | 2.0 | 6.4 | −1.6 | 7.9 | −1.3 | 9.2 | 1.7 | 13.9 | −1.9 | |
| Multan | Winter | 18.9 | 7.7 | 19.5 | 5.9 | 18.3 | 6.2 | 18.9 | 6.1 | 18.3 | 6.5 |
| Spring | 5.5 | 18.8 | 12.2 | 12.7 | 9.4 | 13.1 | 15.2 | 12.8 | 7.4 | 12.7 | |
| Summer | 4.2 | 9.4 | 3.2 | 14.5 | 4.5 | 14.9 | 4.9 | 13.9 | 5.9 | 17.4 | |
| Autumn | 11.2 | 5.1 | 7.5 | −3.3 | 9.9 | −7.2 | 13.5 | 3.2 | 8.3 | −8.5 | |
| Rahim Yar khan | Winter | 1.5 | 1.4 | 12.6 | 2.6 | 15.5 | 3.2 | 11.7 | 3.6 | 9.5 | 4.6 |
| Spring | 5.0 | 5.6 | 4.9 | 8.8 | −4.7 | 8.8 | −4.9 | 8.7 | −7.7 | 9.0 | |
| Summer | 3.5 | 6.0 | −10.5 | −11.1 | −10.4 | −13.7 | 8.4 | −9.4 | −2.8 | −10.3 | |
| Autumn | 2.7 | 6.3 | 5.1 | 5.1 | 8.8 | 3.3 | 11.6 | 4.7 | 4.8 | 5.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.U.; Ijaz, M.W.; Iqbal, M.; Aziz, R.; Masood, M.; Tariq, M.A.U.R. Impact Evaluation Using Nonstationary Parameters for Historical and Projected Extreme Precipitation. Water 2023, 15, 3958. https://doi.org/10.3390/w15223958
Khan MU, Ijaz MW, Iqbal M, Aziz R, Masood M, Tariq MAUR. Impact Evaluation Using Nonstationary Parameters for Historical and Projected Extreme Precipitation. Water. 2023; 15(22):3958. https://doi.org/10.3390/w15223958
Chicago/Turabian StyleKhan, Muhammad Usman, Muhammad Wajid Ijaz, Mudassar Iqbal, Rizwan Aziz, Muhammad Masood, and Muhammad Atiq Ur Rehman Tariq. 2023. "Impact Evaluation Using Nonstationary Parameters for Historical and Projected Extreme Precipitation" Water 15, no. 22: 3958. https://doi.org/10.3390/w15223958







