A Novel Daily Runoff Probability Density Prediction Model Based on Simplified Minimal Gated Memory–Non-Crossing Quantile Regression and Kernel Density Estimation
Abstract
:1. Introduction
- (1)
- This article proposes NCQR, which can avoid quantile crossing in predicted quantiles.
- (2)
- In order to reduce training time and improve model accuracy, this article simplifies the model structure of MGM and proposes SMGM.
- (3)
- The combination model based on SMGM and NCQR can efficiently generate reliable quantiles, which KDE converts into continuous PDFs.
- (4)
- All models in this article are compared from multiple perspectives using multiple evaluation metrics in three daily runoff datasets. The experimental results show that the model can efficiently obtain reliable and accurate probability density prediction results.
2. Methods
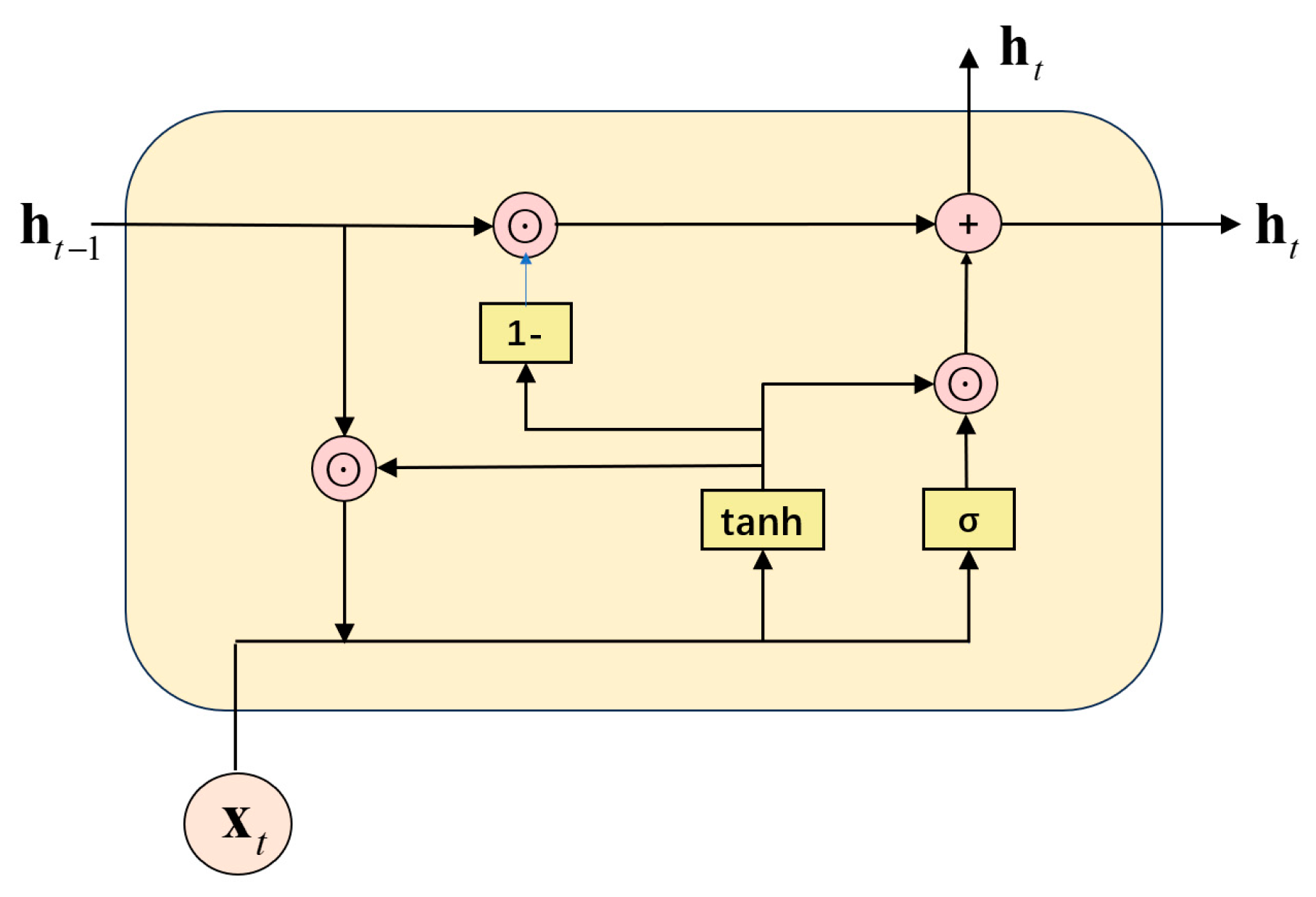
2.1. Simplified Minimal Gated Memory Network
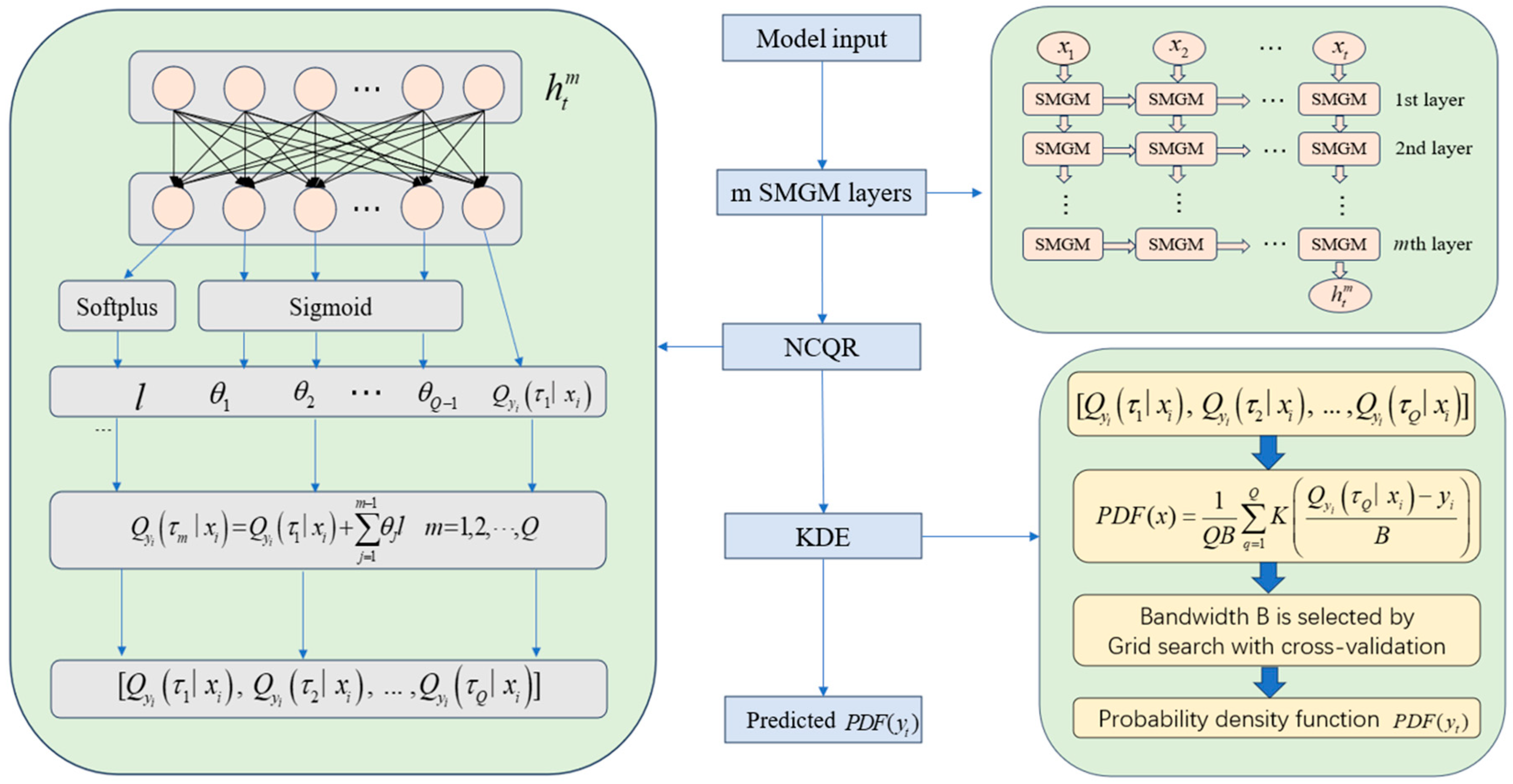
2.2. Novel Non-Crossing Quantile Regression
2.3. Kernel Density Estimation
2.4. Maximal Information Coefficient
2.5. Framework of the Proposed Combined Model
3. Model Evaluation Metrics
3.1. Evaluation Metric of Point Prediction
3.2. Evaluation Metric of Interval Prediction
3.3. Quantifying Indicators of Quantile Crossing Degree
3.4. Evaluation Metric of Probability Density Prediction
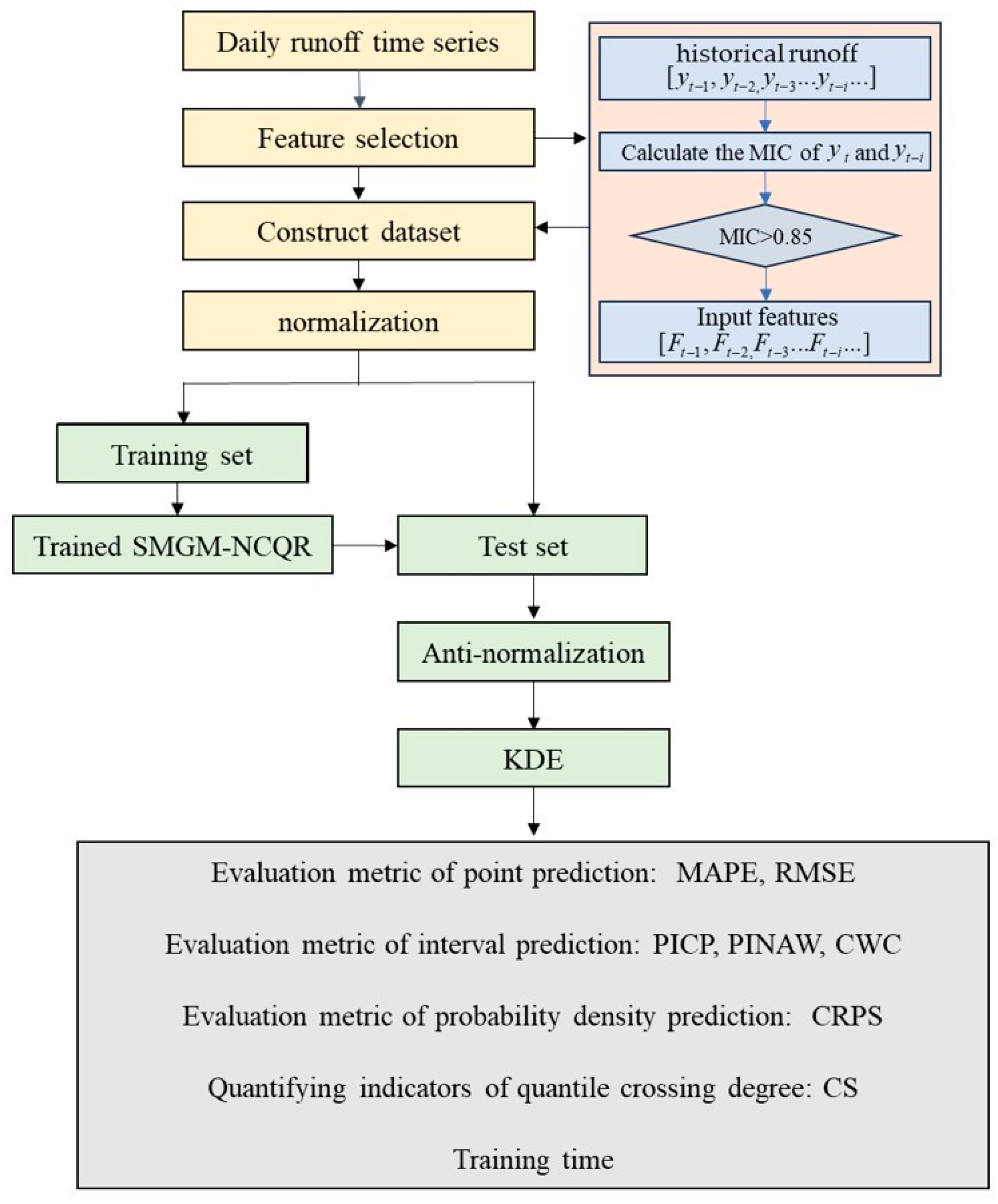
4. Case Study
4.1. Study Area and Data
4.2. Experimental Design and Parameter Settings
4.3. Experimental Results and Comparative Analysis
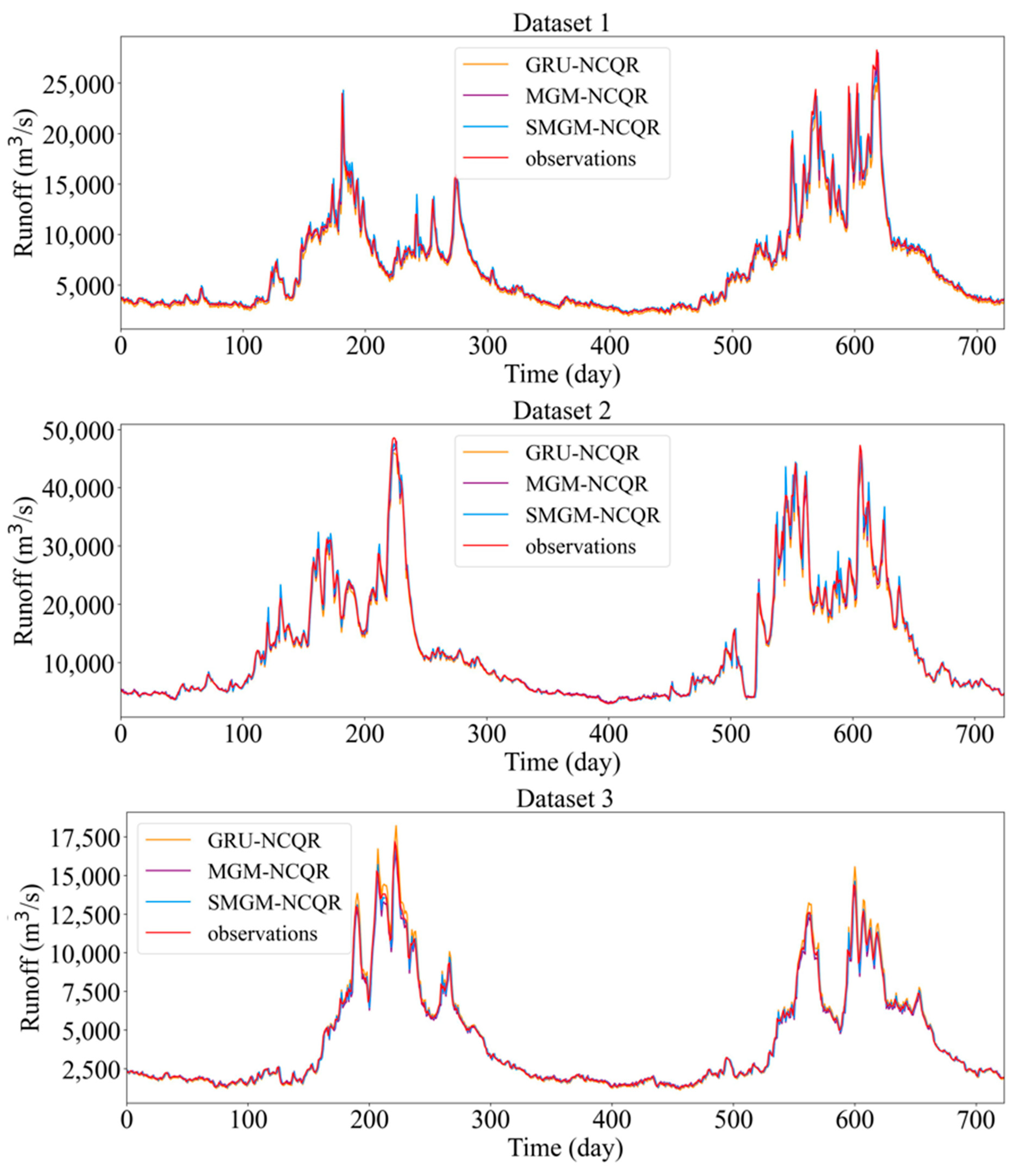
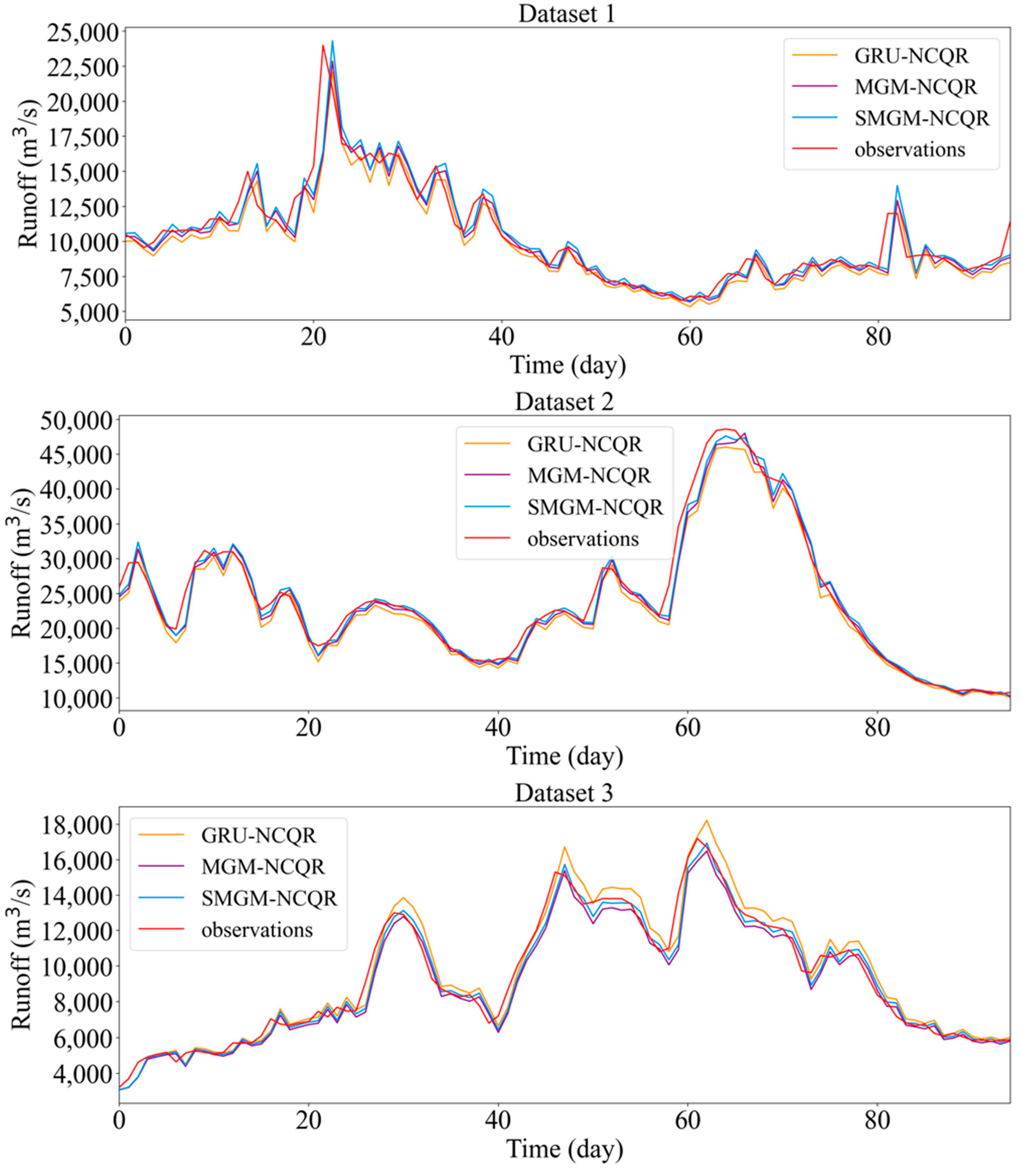
4.3.1. Task I: Evaluation of Probability Models in the Combined Model
4.3.2. Task II: Evaluation of RNN Models with NCQR-Based Models
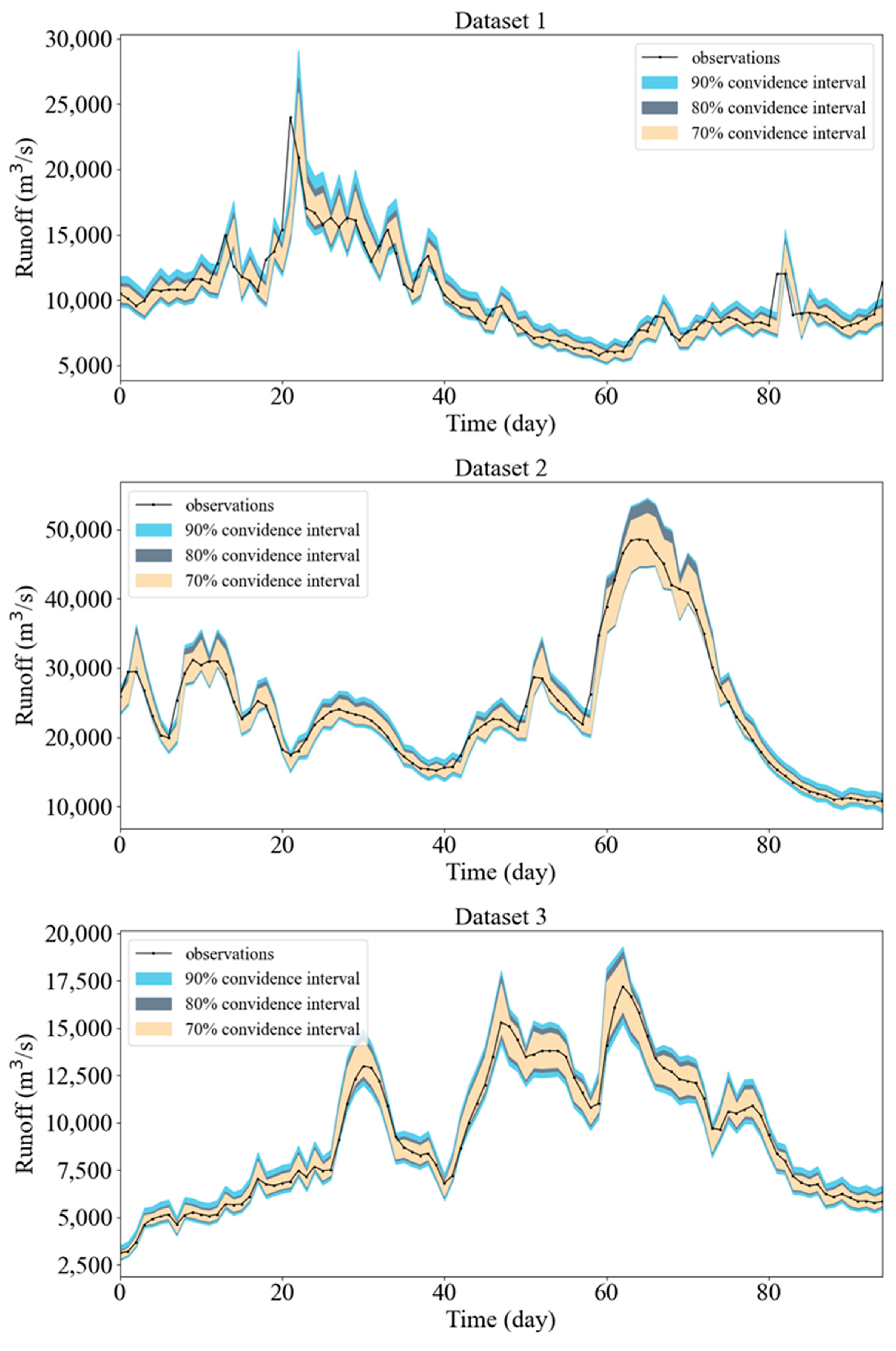
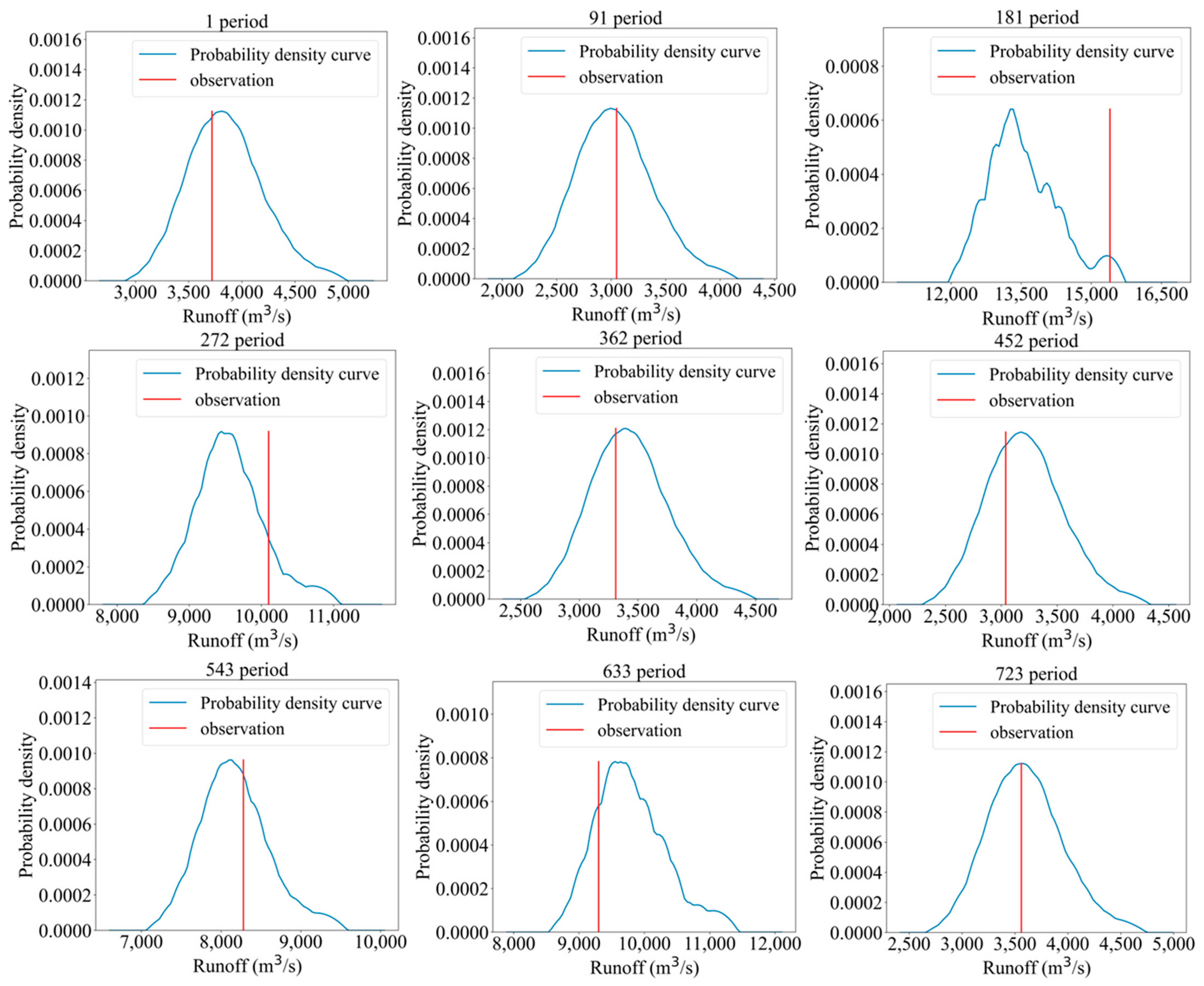
4.3.3. Task III: Displaying the Probability Density Curve
5. Conclusions and Discussion
- (1)
- The NCQR proposed in this article avoids the common quantile crossing observed in QR-based models. At the same time, the prediction performance of the model based on NCQR is superior to that of models based on other probabilistic models.
- (2)
- Among RNN models combined with NCQR, SMGM achieves the best predictive performance with the least training time compared to MGM and GRU. This indicates that SMGM not only has a simpler model structure but also has a better ability to extract effective information from model inputs compared with MGM and GRU.
- (3)
- The new model based on SMGM-NCQR and KDE proposed in this article can efficiently obtain reliable and accurate probability density predictions of future daily runoff. While providing high-precision point predictions, it comprehensively quantifies the uncertainty of predictions, which can provide rich information for decision-makers in water conservancy systems.
- (1)
- The input of the proposed SMGM-NCQR only includes historical runoff and does not consider other factors such as precipitation, daily maximum and minimum temperature. The probability density prediction model for daily runoff considering meteorological data is one of our future research directions.
- (2)
- The parameters of SMGM-NCQR are calibrated based on the relationship between historical runoff and target runoff, ignoring the formation process of runoff. Although SMGM-NCQR has good probability density prediction performance, it is physically unknown and lacks interpretability. Improving the interpretability of SMGM-NCQR while maintaining high prediction accuracy is also one of our future research directions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Chen, X.; Khan, A.; Zhang, Y.-K.; Kuang, X.; Liang, X.; Taccari, M.L.; Nuttall, J. Daily runoff forecasting by deep recursive neural network. J. Hydrol. 2021, 596. [Google Scholar] [CrossRef]
- Amiri, E. Forecasting daily river flows using nonlinear time series models. J. Hydrol. 2015, 527, 1054–1072. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, H. A long short-term components neural network model with data augmentation for daily runoff forecasting. J. Hydrol. 2023, 617, 128853. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Cheng, C.-T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Liu, G.; Tang, Z.; Qin, H.; Liu, S.; Shen, Q.; Qu, Y.; Zhou, J. Short-term runoff prediction using deep learning multi-dimensional ensemble method. J. Hydrol. 2022, 609, 127762. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Z.; Hu, Y.; Tao, S.; Dong, J. Runoff forecasting using convolutional neural networks and optimized bi-directional long short-term memory. Water Resour. Manag. 2023, 37, 937–953. [Google Scholar] [CrossRef]
- Lu, M.; Hou, Q.; Qin, S.; Zhou, L.; Hua, D.; Wang, X.; Cheng, L. A Stacking Ensemble Model of Various Machine Learning Models for Daily Runoff Forecasting. Water 2023, 15, 1265. [Google Scholar] [CrossRef]
- Singh, R.; Subramanian, K.; Refsgaard, J.C. Hydrological modelling of a small watershed using MIKE SHE for irrigation planning. Agric. Water Manag. 1999, 41, 149–166. [Google Scholar] [CrossRef]
- Baker, T.J.; Miller, S.N. Using the Soil and Water Assessment Tool (SWAT) to assess land use impact on water re-sources in an East African watershed. J. Hydrol. 2013, 486, 100–111. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, B.D.; He, B.; Peng, Y.; Ren, M.L. Singular spectrum analysis and ARIMA hybrid model for annual runoff forecasting. Water Resour. Manag. 2011, 25, 2683–2703. [Google Scholar] [CrossRef]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Gizaw, M.S.; Gan, T.Y. Regional flood frequency analysis using support vector regression under historical and future climate. J. Hydrol. 2016, 538, 387–398. [Google Scholar] [CrossRef]
- Ehteram, M.; Afan, H.A.; Dianatikhah, M.; Ahmed, A.N.; Ming Fai, C.; Hossain, M.S.; Elshafie, A. Assessing the predictability of an improved ANFIS model for monthly streamflow using lagged climate indices as predic-tors. Water 2019, 11, 1130. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, J.; Mo, L.; Jia, B.; Yang, Y.; Fang, W.; Qin, Z. A Novel Runoff Forecasting Model Based on the Decomposition-Integration-Prediction Framework. Water 2021, 13, 3390. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, C.; Wu, Q.; Jian, S.; Li, Z.; Chen, Y.; Wang, S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J. Hydrol. 2022, 608, 127553. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Rahimzad, M.; Moghaddam Nia, A.; Zolfonoon, H.; Soltani, J.; Danandeh Mehr, A.; Kwon, H.H. Performance comparison of an LSTM-based deep learning model versus conventional machine learning algorithms for streamflow fore-casting. Water Resour. Manag. 2021, 35, 4167–4187. [Google Scholar] [CrossRef]
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Liu, Y.; Yao, L.; Yu, X.; Lu, J.; Jiang, Z.; Feng, Z. Wind speed forecasting based on quantile regression minimal gated memory network and kernel density estimation. Energy Convers. Manag. 2019, 196, 1395–1409. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, H.; Qin, H.; Luo, B.; Zhou, C.; Zhou, H. Multi-step ahead probabilistic forecasting of multiple hydrological variables for multiple stations. J. Hydrol. 2023, 617, 129094. [Google Scholar] [CrossRef]
- Faucher, D.; Rasmussen, P.F.; Bobée, B. A distribution function based bandwidth selection method for kernel quan-tile estimation. J. Hydrol. 2001, 250, 1–11. [Google Scholar] [CrossRef]
- Sun, A.Y.; Wang, D.; Xu, X. Monthly streamflow forecasting using gaussian process regression. J. Hydrol. 2014, 511, 72–81. [Google Scholar] [CrossRef]
- Bai, H.; Li, G.; Liu, C.; Li, B.; Zhang, Z.; Qin, H. Hydrological probabilistic forecasting based on deep learning and Bayesian optimization algorithm. Hydrol. Res. 2021, 52, 927–943. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, J.; Lei, P.; Li, Y. A novel multi-step ahead forecasting model for flood based on time residual LSTM. J. Hydrol. 2023, 620, 129521. [Google Scholar] [CrossRef]
- Tareghian, R.; Rasmussen, P.F. Statistical downscaling of precipitation using quantile regression. J. Hydrol. 2013, 487, 122–135. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Langousis, A. Probabilistic water demand forecasting using quantile regression algorithms. Water Resour. Res. 2022, 58, e2021WR030216. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, G.H.; Li, Y.P.; Wang, X.Q.; Li, Z. Probabilistic prediction for monthly streamflow through coupling stepwise cluster analysis and quantile regression methods. Water Resour. Res. Manag. 2016, 30, 5313–5331. [Google Scholar] [CrossRef]
- Regression, Q. Handbook of Quantile Regression; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Jahangir, M.S.; You, J.; Quilty, J. A quantile-based encoder-decoder framework for multi-step ahead runoff fore-casting. J. Hydrol. 2023, 619, 129269. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic individual load forecasting using pinball loss guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar] [CrossRef]
- Benson, D.A.; Bolster, D.; Pankavich, S.; Schmidt, M.J. Nonparametric, data-based kernel interpolation for particle-tracking simulations and kernel density estimation. Adv. Water Resour. 2021, 152, 103889. [Google Scholar] [CrossRef]
- He, Y.; Li, H. Probability density forecasting of wind power using quantile regression neural network and kernel density estimation. Energy Convers. Manag. 2018, 164, 374–384. [Google Scholar] [CrossRef]
- Epanechnikov, V.A. Non-parametric estimation of a multivariate probability density. Theory Probab. Its Appl. 1969, 14, 153–158. [Google Scholar] [CrossRef]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Tang, Z.; Gao, J.; Zhang, G. Short-term ship motion attitude prediction based on LSTM and GPR. Appl. Ocean Res. 2022, 118, 102927. [Google Scholar] [CrossRef]
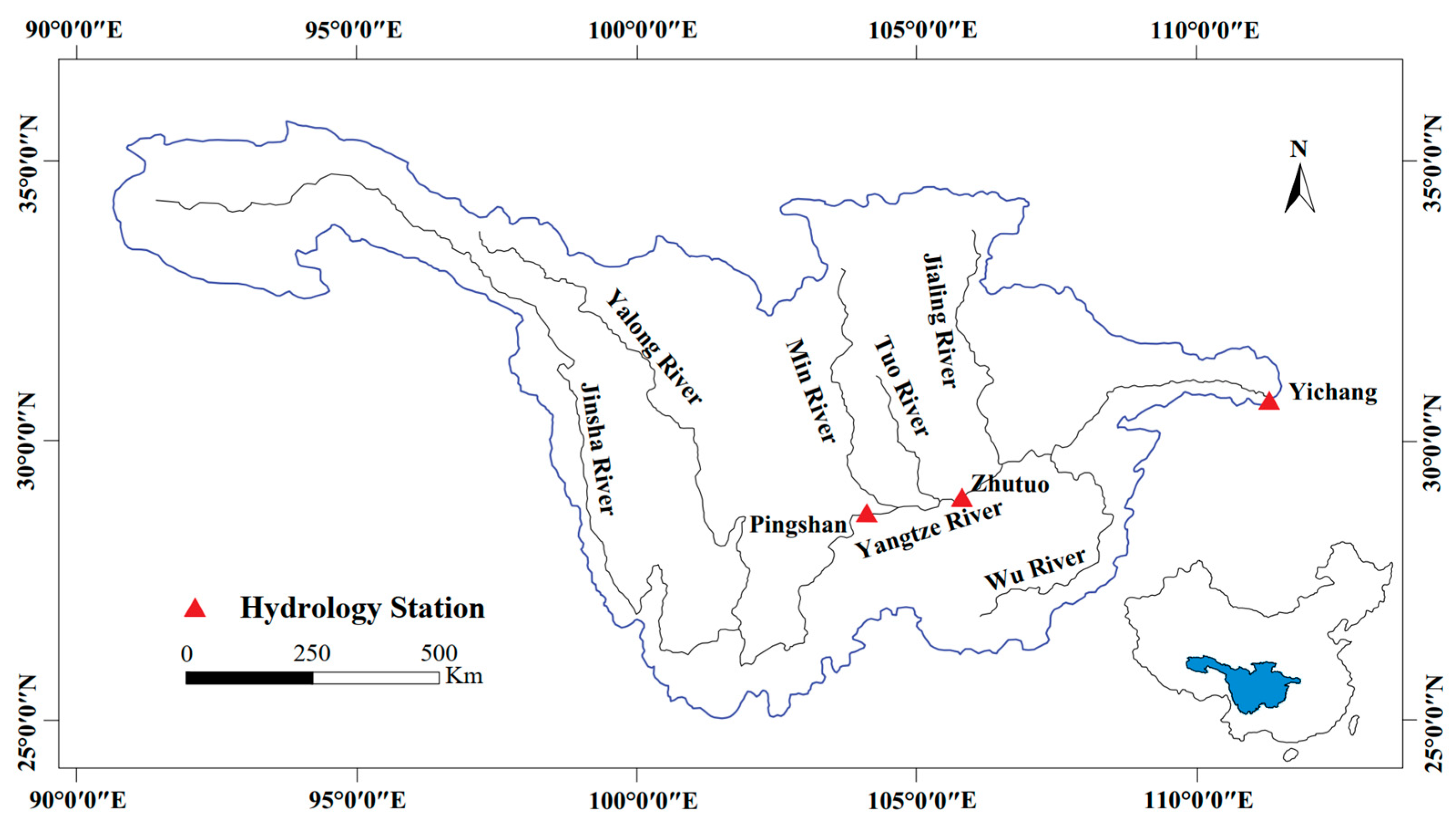

| Dataset | Station | Time | Mean | Maximum | Minimum | Standard Deviation |
|---|---|---|---|---|---|---|
| Dataset 1 | Zhutuo | 1 January 2000–31 December 2007 | 8283.83 | 37,400 | 2180 | 6325.06 |
| Dataset 2 | Yichang | 1 January 1996–31 December 2003 | 13,781.37 | 61,700 | 2950 | 11,377.50 |
| Dataset 3 | Pingshan | 1 January 2003–31 December 2010 | 4516.427 | 20,800 | 1180 | 3612.90 |
| Dataset | yt−1 | yt−2 | yt−3 | yt−4 | yt−5 | yt−6 | yt−7 | yt−8 | yt−9 | yt−10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Dataset 1 | 0.969 | 0.940 | 0.909 | 0.887 | 0.874 | 0.861 | 0.852 | 0.841 | 0.827 | 0.815 |
| Dataset 2 | 0.977 | 0.937 | 0.909 | 0.881 | 0.866 | 0.842 | 0.818 | 0.799 | 0.777 | 0.752 |
| Dataset 3 | 0.960 | 0.931 | 0.905 | 0.884 | 0.870 | 0.855 | 0.841 | 0.829 | 0.822 | 0.819 |
| Model | Parameter | Value |
|---|---|---|
| GRU-GPR | number of GRU layer nodes | 32 |
| number of GRU layers | 4 | |
| GPR kernel function | Rational quadratic kernel | |
| number of output layer nodes | 2 | |
| GRU-DeepAR | number of GRU layer nodes | 32 |
| number of GRU layers | 4 | |
| number of output layer nodes | 2 | |
| GRU-QR | number of GRU layer nodes | 32 |
| number of GRU layers | 4 | |
| number of output layer nodes | 19 | |
| GRU-NCQR | number of GRU layer nodes | 32 |
| number of GRU layers | 4 | |
| number of output layer nodes | 20 | |
| MGM-NCQR | number of MGM layer nodes | 32 |
| number of MGM layers | 4 | |
| number of output layer nodes | 20 | |
| SMGM-NCQR | number of SMGM layer nodes | 32 |
| number of SMGM layers | 4 | |
| number of output layer nodes | 20 | |
| KDE | K-fold cross-validation in grid search for KDE bandwidth | 5 |
| bandwidth range for KDE in grid search | (400, 450, 1) |
| Models | Dataset 1 | Dataset 2 | Dataset 3 | |||
|---|---|---|---|---|---|---|
| RMSE (m3/s) | MAPE (%) | RMSE (m3/s) | MAPE (%) | RMSE (m3/s) | MAPE (%) | |
| GRU-GPR | 1023.14 | 6.35 | 1460.83 | 5.68 | 381.39 | 5.41 |
| GRU-DeepAR | 1132.67 | 7.29 | 1536.66 | 6.88 | 412.01 | 5.93 |
| GRU-QR | 955.81 | 6.06 | 1411.95 | 5.20 | 357.34 | 5.24 |
| GRU-NCQR | 949.98 | 5.86 | 1363.40 | 4.96 | 352.01 | 5.07 |
| Models | Metrics | Dataset 1 | Dataset 2 | Dataset 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 90% | 80% | 70% | 90% | 80% | 70% | 90% | 80% | 70% | ||
| GRU-GPR | PICP | 0.9406 | 0.9199 | 0.8978 | 0.9504 | 0.0872 | 0.8829 | 0.9655 | 0.9241 | 0.8966 |
| PINAW | 0.1387 | 0.1081 | 0.0874 | 0.1119 | 0.0872 | 0.0705 | 0.1074 | 0.0780 | 0.0631 | |
| CWC | 0.1387 | 0.1081 | 0.0874 | 0.1119 | 0.0872 | 0.0705 | 0.1074 | 0.0780 | 0.0631 | |
| GRU-DeepAR | PICP | 0.9461 | 0.8894 | 0.7776 | 0.9380 | 0.8815 | 0.8182 | 0.9448 | 0.8993 | 0.7917 |
| PINAW | 0.1000 | 0.0670 | 0.0631 | 0.0842 | 0.0656 | 0.0530 | 0.0749 | 0.0583 | 0.0472 | |
| CWC | 0.1000 | 0.0670 | 0.0631 | 0.0842 | 0.0656 | 0.0530 | 0.0749 | 0.0583 | 0.0472 | |
| GRU-QR | PICP | 0.9409 | 0.8523 | 0.7693 | 0.9159 | 0.8333 | 0.7479 | 0.9434 | 0.8428 | 0.7697 |
| PINAW | 0.0826 | 0.0497 | 0.0375 | 0.0658 | 0.0432 | 0.0350 | 0.0723 | 0.0480 | 0.0374 | |
| CWC | 0.0826 | 0.0497 | 0.0375 | 0.0658 | 0.0432 | 0.0350 | 0.0723 | 0.0480 | 0.0374 | |
| GRU-NCQR | PICP | 0.9448 | 0.8204 | 0.7127 | 0.9187 | 0.8292 | 0.7507 | 0.9641 | 0.8510 | 0.7379 |
| PINAW | 0.0801 | 0.0379 | 0.0369 | 0.0677 | 0.0417 | 0.0322 | 0.0714 | 0.0457 | 0.0355 | |
| CWC | 0.0801 | 0.0379 | 0.0369 | 0.0677 | 0.0417 | 0.0322 | 0.0714 | 0.0457 | 0.0355 | |
| Model | CS | ||
|---|---|---|---|
| Dataset 1 | Dataset 2 | Dataset 3 | |
| GRU-GPR | 0 | 0 | 0 |
| GRU-DeepAR | 0 | 0 | 0 |
| GRU-QR | 267.71 | 425.36 | 124.15 |
| GRU-NCQR | 0 | 0 | 0 |
| Models | CRPS | ||
|---|---|---|---|
| Dataset 1 | Dataset 2 | Dataset 3 | |
| GRU-GPR | 382.62 | 539.07 | 177.90 |
| GRU-DeepAR | 307.30 | 440.29 | 152.99 |
| GRU-QR | 275.79 | 401.60 | 141.28 |
| GRU-NCQR | 270.49 | 389.40 | 138.42 |
| Models | Dataset 1 | Dataset 2 | Dataset 3 | |||
|---|---|---|---|---|---|---|
| RMSE (m3/s) | MAPE (%) | RMSE (m3/s) | MAPE (%) | RMSE (m3/s) | MAPE (%) | |
| GRU-NCQR | 949.98 | 5.86 | 1363.40 | 4.96 | 352.01 | 5.07 |
| MGM-NCQR | 933.01 | 5.30 | 1347.63 | 4.77 | 346.78 | 4.66 |
| SMGM-NCQR | 916.78 | 4.87 | 1324.00 | 4.54 | 338.20 | 4.54 |
| Models | Metrics | Dataset 1 | Dataset 2 | Dataset 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 90% | 80% | 70% | 90% | 80% | 70% | 90% | 80% | 70% | ||
| GRU-NCQR | PICP | 0.9448 | 0.8204 | 0.7127 | 0.9187 | 0.8292 | 0.7507 | 0.9641 | 0.8510 | 0.7379 |
| PINAW | 0.0801 | 0.0379 | 0.0369 | 0.0677 | 0.0417 | 0.0322 | 0.0714 | 0.0457 | 0.0355 | |
| CWC | 0.0801 | 0.0379 | 0.0369 | 0.0677 | 0.0417 | 0.0322 | 0.0714 | 0.0457 | 0.0355 | |
| MGM-NCQR | PICP | 0.9351 | 0.8412 | 0.7279 | 0.9215 | 0.8168 | 0.7410 | 0.9600 | 0.8524 | 0.7545 |
| PINAW | 0.0748 | 0.0478 | 0.0359 | 0.0638 | 0.0400 | 0.0310 | 0.0671 | 0.0429 | 0.0326 | |
| CWC | 0.0748 | 0.0478 | 0.0359 | 0.0638 | 0.0400 | 0.0310 | 0.0671 | 0.0429 | 0.0326 | |
| SMGM-NCQR | PICP | 0.9006 | 0.8204 | 0.7569 | 0.9229 | 0.8003 | 0.7066 | 0.9462 | 0.8234 | 0.7052 |
| PINAW | 0.0660 | 0.0435 | 0.0327 | 0.0601 | 0.0386 | 0.0298 | 0.0654 | 0.0407 | 0.0312 | |
| CWC | 0.0660 | 0.0435 | 0.0327 | 0.0601 | 0.0386 | 0.0298 | 0.0654 | 0.0407 | 0.0312 | |
| Models | CRPS | ||
|---|---|---|---|
| Dataset 1 | Dataset 2 | Dataset 3 | |
| GRU-NCQR | 270.49 | 389.40 | 138.42 |
| MGM-NCQR | 260.79 | 372.60 | 132.10 |
| SMGM-NCQR | 252.69 | 358.29 | 127.85 |
| Models | Training Time (s) | ||
|---|---|---|---|
| Dataset 1 | Dataset 2 | Dataset 3 | |
| GRU-NCQR | 255 | 198 | 225 |
| MGM-NCQR | 198 | 155 | 174 |
| SMGM-NCQR | 176 | 139 | 159 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhu, S.; Mo, L. A Novel Daily Runoff Probability Density Prediction Model Based on Simplified Minimal Gated Memory–Non-Crossing Quantile Regression and Kernel Density Estimation. Water 2023, 15, 3947. https://doi.org/10.3390/w15223947
Liu H, Zhu S, Mo L. A Novel Daily Runoff Probability Density Prediction Model Based on Simplified Minimal Gated Memory–Non-Crossing Quantile Regression and Kernel Density Estimation. Water. 2023; 15(22):3947. https://doi.org/10.3390/w15223947
Chicago/Turabian StyleLiu, Huaiyuan, Sipeng Zhu, and Li Mo. 2023. "A Novel Daily Runoff Probability Density Prediction Model Based on Simplified Minimal Gated Memory–Non-Crossing Quantile Regression and Kernel Density Estimation" Water 15, no. 22: 3947. https://doi.org/10.3390/w15223947
APA StyleLiu, H., Zhu, S., & Mo, L. (2023). A Novel Daily Runoff Probability Density Prediction Model Based on Simplified Minimal Gated Memory–Non-Crossing Quantile Regression and Kernel Density Estimation. Water, 15(22), 3947. https://doi.org/10.3390/w15223947





