Constraining Flood Forecasting Uncertainties through Streamflow Data Assimilation in the Tropical Andes of Peru: Case of the Vilcanota River Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Parsimonious Sub-Daily Hydrological Modeling
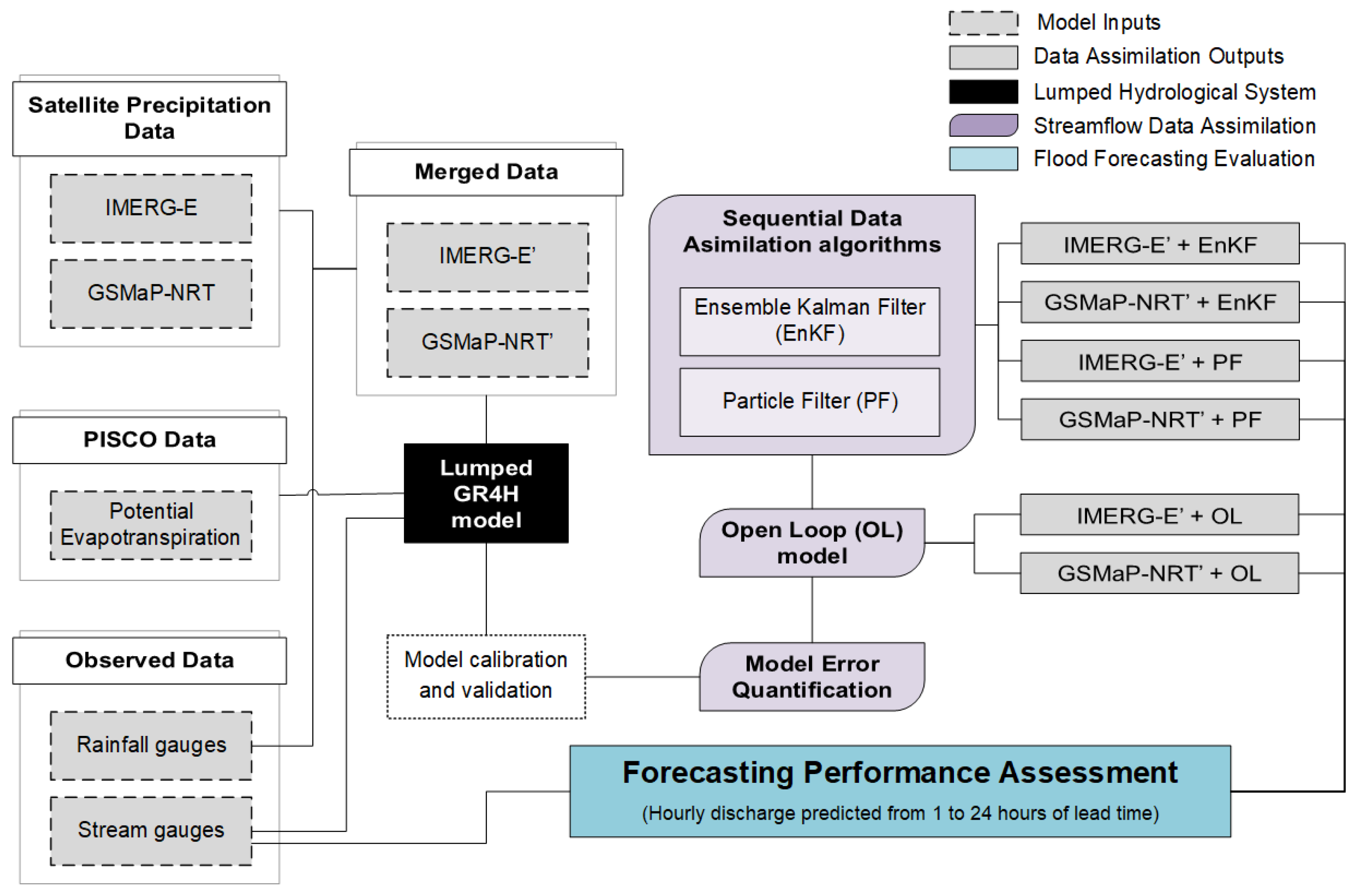
2.3. Design of Streamflow Data Assimilation Experiments
2.4. Quantification of Model Errors
2.5. Evaluation of Model Forecast
3. Results
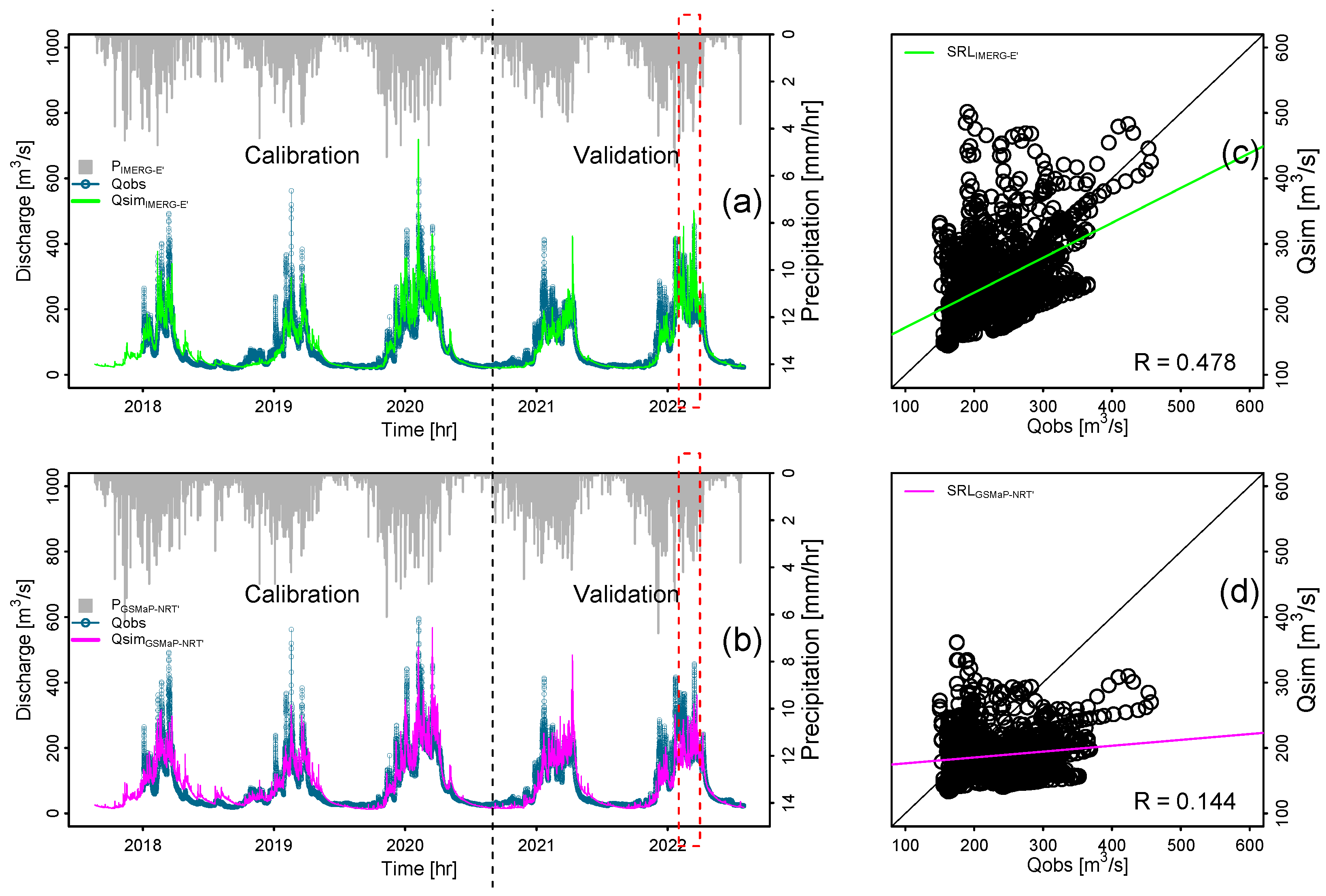
3.1. Model Calibration and Validation
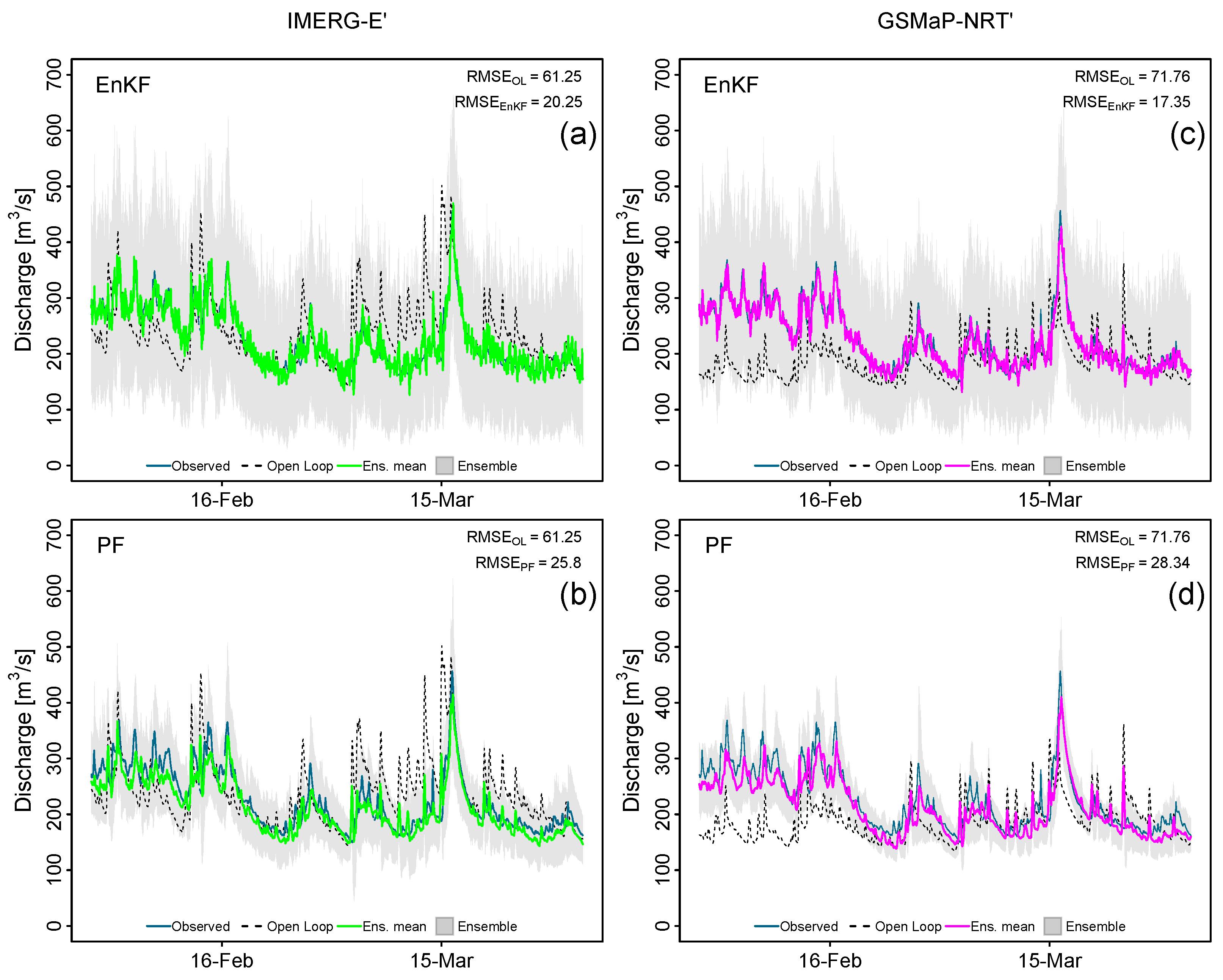
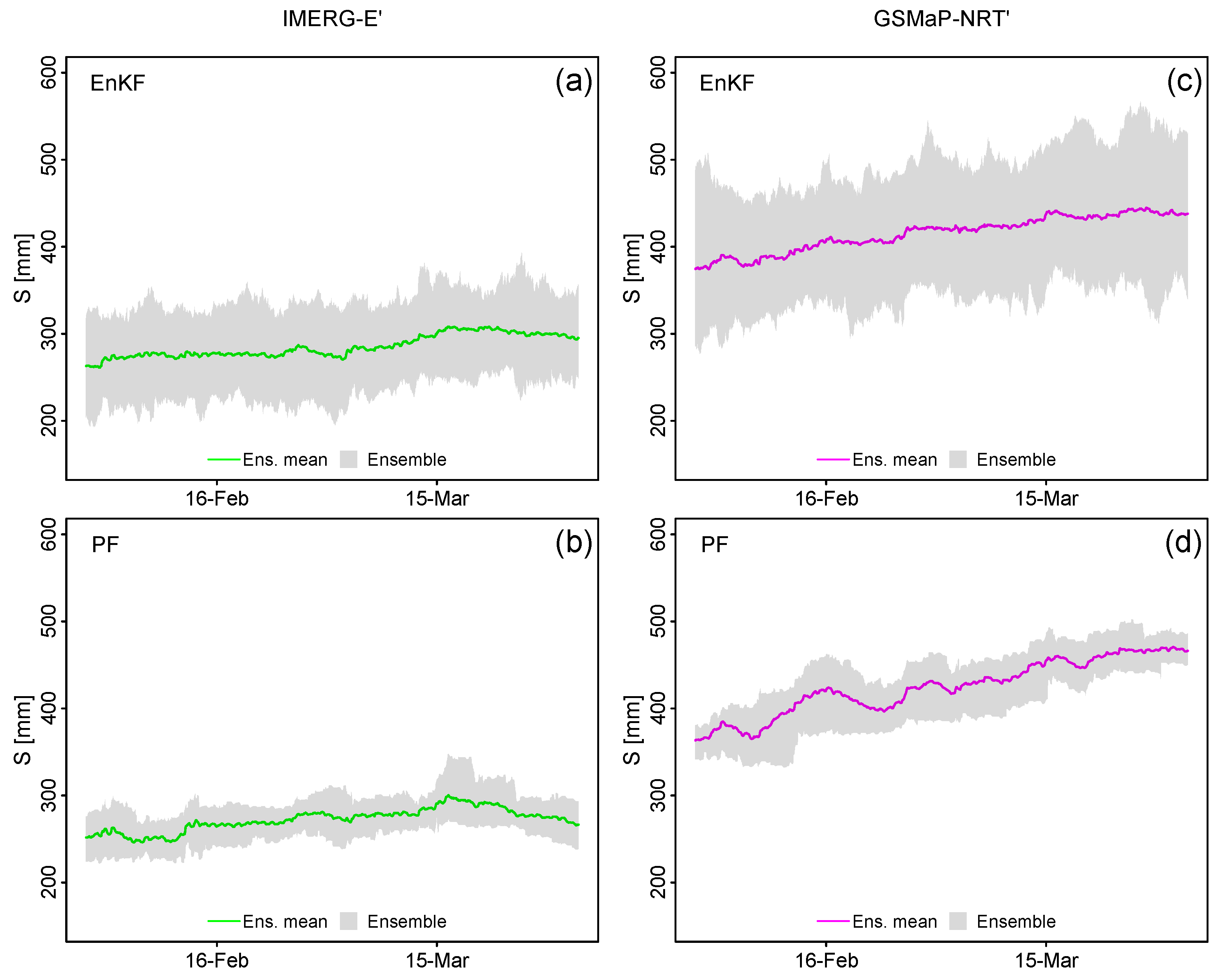
3.2. Estimation of Model Uncertainties in Streamflow Data Assimilation
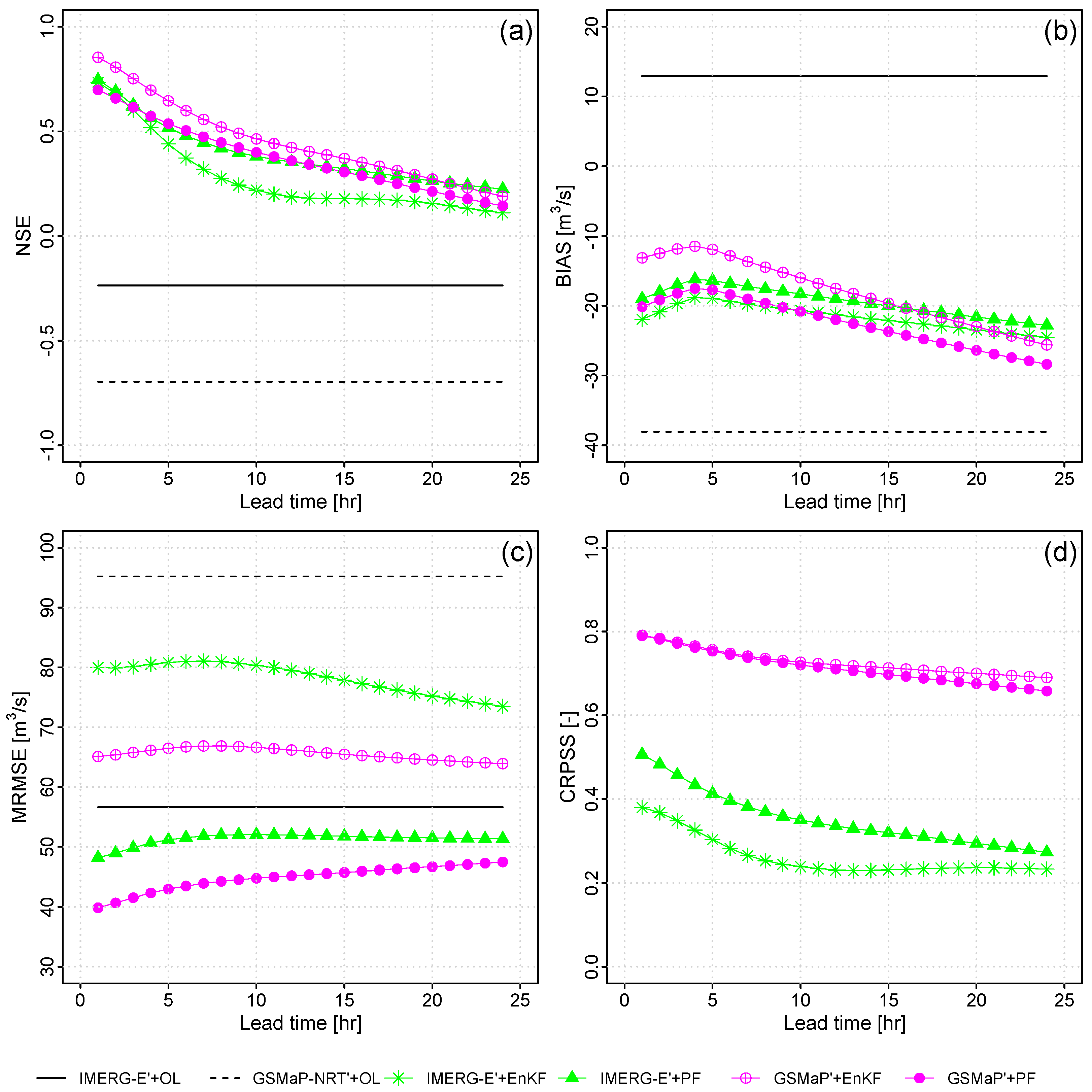
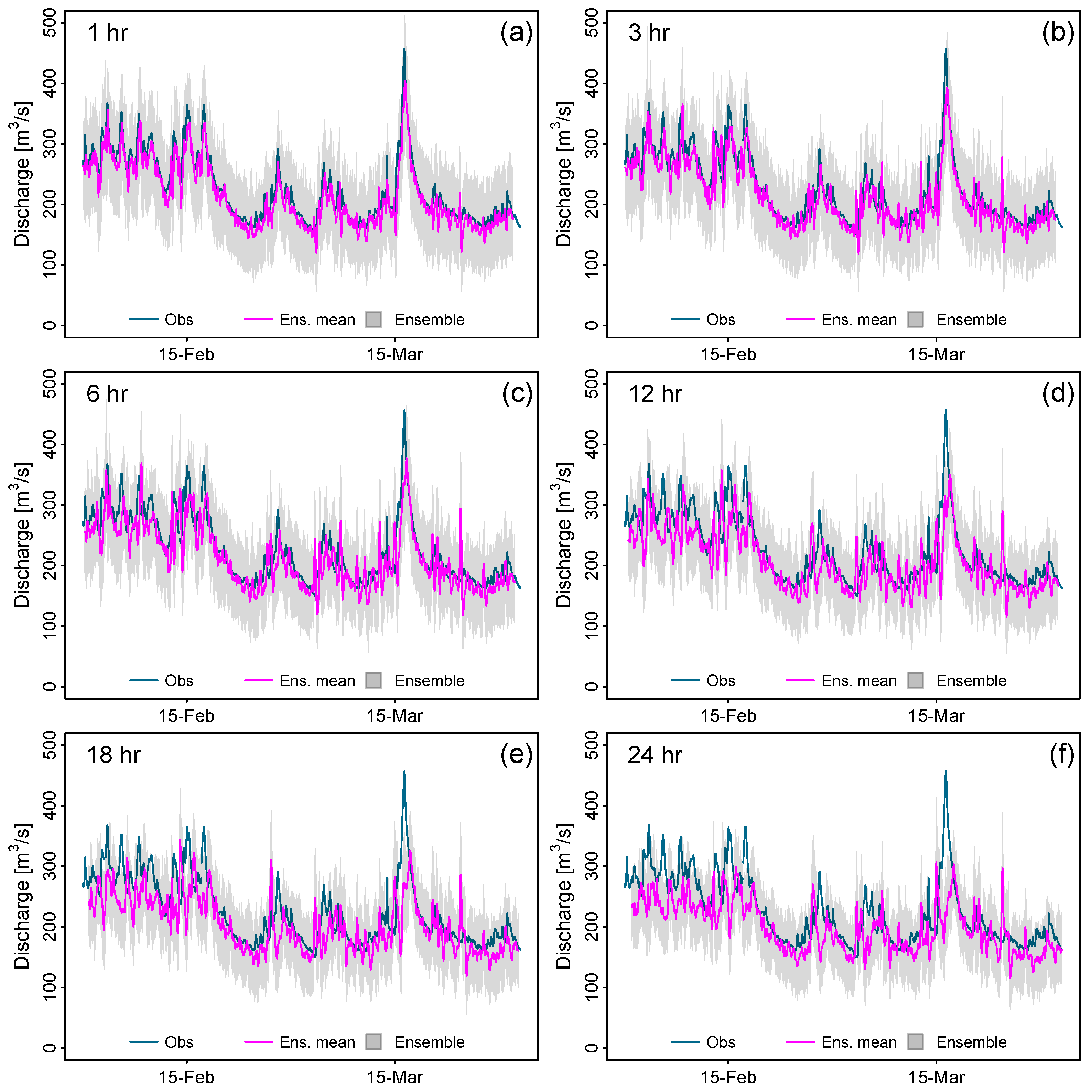
3.3. Forecasting Performance Assessment
4. Discussion
Limitations and Potential of Streamflow Data Assimilation in the Vilcanota River Basin
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BIAS | Error in observations and/or simulations. |
| BoxNSE | Nash–Sutcliffe Efficiency criterion with Box–Cox transformed values. |
| CRPS | Continuous Ranked Probability Score. |
| CRPSS | Continuous Ranked Probability Skill Score. |
| DA | Data Assimilation. |
| EnKF | Ensemble Kalman Filter. |
| GR4H | Génie Rural à 4 paramètres Horaire. |
| GSMaP-NRT | Global Satellite Mapping of Precipitation Near Real-Time product. |
| GSMaP-NRT’ | GSMaP-NRT product merged with pluviometric stations. |
| GSMaP-NRT’+EnKF | EnKF experiment applied to the hydrological model forced with GSMaP-NRT’. |
| GSMaP-NRT’+OL | Open Loop for the hydrological model forced with GSMaP-NRT’. |
| GSMaP-NRT’+PF | PF experiment applied to the hydrological model forced with GSMaP-NRT’. |
| IMERG-E | Integrated Multi-satellitE Retrievals for GPM Early Runs product. |
| IMERG-E’ | IMERG-E product merged with pluviometric stations. |
| IMERG-E’+EnKF | EnKF experiment applied to the hydrological model forced with IMERG-E’. |
| IMERG-E’+OL | Open Loop for the hydrological model forced with IMERG-E’. |
| IMERG-E’+PF | PF experiment applied to the hydrological model forced with IMERG-E’. |
| KGE | Kling-Gupta Efficiency criterion. |
| logNSE | Nash–Sutcliffe Efficiency criterion with logarithmic values. |
| MRMSE | Mean of Ensemble Root Mean Squared Error |
| NSE | Nash–Sutcliffe Efficiency criterion. |
| OL | Open Loop. |
| PF | Particle Filter. |
| RMSE | Root Mean square Error. |
| SM | Soil Moisture. |
References
- Poveda, G.; Espinoza, J.C.; Zuluaga, M.D.; Solman, S.A.; Garreaud, R.; van Oevelen, P.J. High Impact Weather Events in the Andes. Front. Earth Sci. Chin. 2020, 8. [Google Scholar] [CrossRef]
- Motschmann, A. Water Resource Risks in the Andes of Peru: An Integrative Perspective; University of Zurich: Zürich, Switzerland, 2021. [Google Scholar]
- Ávila, Á.; Guerrero, F.C.; Escobar, Y.C.; Justino, F. Recent Precipitation Trends and Floods in the Colombian Andes. Water 2019, 11, 379. [Google Scholar] [CrossRef]
- Pinos, J.; Orellana, D.; Timbe, L. Assessment of Microscale Economic Flood Losses in Urban and Agricultural Areas: Case Study of the Santa Bárbara River, Ecuador. Nat. Hazards 2020, 103, 2323–2337. [Google Scholar] [CrossRef]
- Höglund, S.; Rodin, L. Flood Simulation in the Colombian Andean Region Using UAV-Based LiDAR: Minor Field Study in Colombia; KTH Royal Institute of Technology: Stockholm, Sweden, 2023. [Google Scholar]
- Muñoz, P.; Orellana-Alvear, J.; Bendix, J.; Feyen, J.; Célleri, R. Flood Early Warning Systems Using Machine Learning Techniques: The Case of the Tomebamba Catchment at the Southern Andes of Ecuador. Hydrology 2021, 8, 183. [Google Scholar] [CrossRef]
- Wu, W.; Emerton, R.; Duan, Q.; Wood, A.W.; Wetterhall, F.; Robertson, D.E. Ensemble Flood Forecasting: Current Status and Future Opportunities. WIREs Water 2020, 7, e1432. [Google Scholar] [CrossRef]
- Drenkhan, F.; Carey, M.; Huggel, C.; Seidel, J.; Oré, M.T. The Changing Water Cycle: Climatic and Socioeconomic Drivers of Water-Related Changes in the Andes of Peru. Wiley Interdiscip. Rev. Water 2015, 2, 715–733. [Google Scholar] [CrossRef]
- Huggel, C.; Raissig, A.; Rohrer, M.; Romero, G.; Diaz, A.; Salzmann, N. How Useful and Reliable Are Disaster Databases in the Context of Climate and Global Change? A Comparative Case Study Analysis in Peru. Nat. Hazards Earth Syst. Sci. 2015, 15, 475–485. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Chavez, S.; Ronchail, J.; Junquas, C.; Takahashi, K.; Lavado, W. Rainfall Hotspots over the Southern Tropical Andes: Spatial Distribution, Rainfall Intensity, and Relations with Large-Scale Atmospheric Circulation. Water Resour. Res. 2015, 51, 3459–3475. [Google Scholar] [CrossRef]
- Llauca, H.; Leon, K.; Lavado-Casimiro, W. Construction of a Daily Streamflow Dataset for Peru Using a Similarity-Based Regionalization Approach and a Hybrid Hydrological Modeling Framework. J. Hydrol. Reg. Stud. 2023, 47, 101381. [Google Scholar] [CrossRef]
- Lavado-Casimiro, W.; Silvestre, E.; Pulache, W. Extreme Rainfall Trends around Cusco and Its Relationship with the Floods in January 2010; Revista Peruana Geo-Atmosferica: Cusco, Peru, 2010. [Google Scholar]
- Waldo, L.-C.; Juan Carlos, J.; Harold, L.; Karen, L.; Clara, O.; Alan, L.; Adrian, H.; Oscar, F.; Julia, A.; Pedro, R.; et al. ANDES: The First System for Flash Flood Monitoring and Forecasting in Peru. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020; p. 3759. [Google Scholar]
- Fan, Y. Uncertainty Quantification in Hydrologic Predictions: A Brief Review. J. Environ. Inform. Lett. 2019, 2, 48–56. [Google Scholar] [CrossRef]
- Gupta, A.; Govindaraju, R.S. Uncertainty Quantification in Watershed Hydrology: Which Method to Use? J. Hydrol. 2023, 616, 128749. [Google Scholar] [CrossRef]
- Segovia-Cardozo, D.A.; Bernal-Basurco, C.; Rodríguez-Sinobas, L. Tipping Bucket Rain Gauges in Hydrological Research: Summary on Measurement Uncertainties, Calibration, and Error Reduction Strategies. Sensors 2023, 23, 5385. [Google Scholar] [CrossRef] [PubMed]
- McMillan, H.K.; Westerberg, I.K.; Krueger, T. Hydrological Data Uncertainty and Its Implications. WIREs Water 2018, 5, e1319. [Google Scholar] [CrossRef]
- Saavedra, D.; Mendoza, P.A.; Addor, N.; Llauca, H.; Vargas, X. A Multi-objective Approach to Select Hydrological Models and Constrain Structural Uncertainties for Climate Impact Assessments. Hydrol. Process. 2021, 36, e14446. [Google Scholar] [CrossRef]
- Herrera, P.A.; Marazuela, M.A.; Hofmann, T. Parameter Estimation and Uncertainty Analysis in Hydrological Modeling. WIREs Water 2022, 9, e1569. [Google Scholar] [CrossRef]
- Panchanathan, A.; Ahrari, A.H.; Ghag, K.; Mustafa, S.M.T.; Haghighi, A.T.; Kløve, B.; Oussalah, M. An Overview of Approaches for Reducing Uncertainties in Hydrological Forecasting: Progress, and Challenges. Syst. Rev. 2023. Available online: https://www.researchsquare.com/article/rs-2802423/v1 (accessed on 26 October 2023).
- Rasmussen, J.; Madsen, H.; Jensen, K.H.; Refsgaard, J.C. Data Assimilation in Integrated Hydrological Modelling in the Presence of Observation Bias. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 8131–8173. [Google Scholar] [CrossRef]
- Avellaneda, P.M.; Ficklin, D.L.; Lowry, C.S.; Knouft, J.H.; Hall, D.M. Improving Hydrological Models with the Assimilation of Crowdsourced Data. Water Resour. Res. 2020, 56, e2019WR026325. [Google Scholar] [CrossRef]
- Boucher, M.-A.; Quilty, J.; Adamowski, J. Data Assimilation for Streamflow Forecasting Using Extreme Learning Machines and Multilayer Perceptrons. Water Resour. Res. 2020, 56, e2019WR026226. [Google Scholar] [CrossRef]
- Noh, S.J.; Lee, H.S.; Seo, D.J. Streamflow Data Assimilation for Hydrologic River Routing: Advances and Challenges. In Proceedings of the American Geophysical Union, Fall Meeting 2019, Washington, DC, USA, 9–13 December 2019; Volume 2019. pp. H31J–1853. [Google Scholar]
- Mazzoleni, M.; Noh, S.J.; Lee, H.; Liu, Y.; Seo, D.-J.; Amaranto, A.; Alfonso, L.; Solomatine, D.P. Real-Time Assimilation of Streamflow Observations into a Hydrological Routing Model: Effects of Model Structures and Updating Methods. Hydrol. Sci. J. 2018, 63, 386–407. [Google Scholar] [CrossRef]
- Li, Y.; Ryu, D.; Western, A.W.; Wang, Q.J. Assimilation of Stream Discharge for Flood Forecasting: Updating a Semidistributed Model with an Integrated Data Assimilation Scheme. Water Resour. Res. 2015, 51, 3238–3258. [Google Scholar] [CrossRef]
- Mendoza, P.A.; McPhee, J.; Vargas, X. Uncertainty in Flood Forecasting: A Distributed Modeling Approach in a Sparse Data Catchment. Water Resour. Res. 2012, 48, W09532. [Google Scholar] [CrossRef]
- Li, Y.; Ryu, D.; Western, A.W.; Wang, Q.J.; Robertson, D.E.; Crow, W.T. An Integrated Error Parameter Estimation and Lag-Aware Data Assimilation Scheme for Real-Time Flood Forecasting. J. Hydrol. 2014, 519, 2722–2736. [Google Scholar] [CrossRef]
- Bergeron, J.; Leconte, R.; Trudel, M.; Farhoodi, S. On the Choice of Metric to Calibrate Time-Invariant Ensemble Kalman Filter Hyper-Parameters for Discharge Data Assimilation and Its Impact on Discharge Forecast Modelling. Hydrology 2021, 8, 36. [Google Scholar] [CrossRef]
- Piazzi, G.; Thirel, G.; Perrin, C.; Delaigue, O. Sequential Data Assimilation for Streamflow Forecasting: Assessing the Sensitivity to Uncertainties and Updated Variables of a Conceptual Hydrological Model at Basin Scale. Water Resour. Res. 2021, 57, e2020WR028390. [Google Scholar] [CrossRef]
- Leach, J.M.; Coulibaly, P. An Extension of Data Assimilation into the Short-Term Hydrologic Forecast for Improved Prediction Reliability. Adv. Water Resour. 2019, 134, 103443. [Google Scholar] [CrossRef]
- Wang, S.; Ancell, B.C.; Huang, G.H.; Baetz, B.W. Improving Robustness of Hydrologic Ensemble Predictions through Probabilistic Pre- and Post-processing in Sequential Data Assimilation. Water Resour. Res. 2018, 54, 2129–2151. [Google Scholar] [CrossRef]
- Emery, C.M.; Biancamaria, S.; Boone, A.; Ricci, S.; Rochoux, M.C.; Pedinotti, V.; David, C.H. Assimilation of Wide-Swath Altimetry Water Elevation Anomalies to Correct Large-Scale River Routing Model Parameters. Hydrol. Earth Syst. Sci. 2020, 24, 2207–2233. [Google Scholar] [CrossRef]
- Wongchuig, S.C.; de Paiva, R.C.D.; Siqueira, V.; Collischonn, W. Hydrological Reanalysis across the 20th Century: A Case Study of the Amazon Basin. J. Hydrol. 2019, 570, 755–773. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Collischonn, W.; Bonnet, M.-P.; de Gonçalves, L.G.G.; Calmant, S.; Getirana, A.; Santos da Silva, J. Assimilating in Situ and Radar Altimetry Data into a Large-Scale Hydrologic-Hydrodynamic Model for Streamflow Forecast in the Amazon. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 2879–2925. [Google Scholar] [CrossRef]
- Cortés, G.; Girotto, M.; Margulis, S. Snow Process Estimation over the Extratropical Andes Using a Data Assimilation Framework Integrating MERRA Data and Landsat Imagery. Water Resour. Res. 2016, 52, 2582–2600. [Google Scholar] [CrossRef]
- Mount, N.J.; Maier, H.R.; Toth, E.; Elshorbagy, A.; Solomatine, D.; Chang, F.-J.; Abrahart, R.J. Data-Driven Modelling Approaches for Socio-Hydrology: Opportunities and Challenges within the Panta Rhei Science Plan. Hydrol. Sci. J. 2016, 61, 1192–1208. [Google Scholar] [CrossRef]
- Moine, N. Le Bassin Versant de Surface vu Par Le Souterrain: Une Voie d’amélioration Des Performances et Du Réalisme Des Modèles Pluie-Débit? Ph.D. Thesis, Université Pierre et Marie, Paris, France, 2008. [Google Scholar]
- Chancay, J.E.; Espitia-Sarmiento, E.F. Improving Hourly Precipitation Estimates for Flash Flood Modeling in Data-Scarce Andean-Amazon Basins: An Integrative Framework Based on Machine Learning and Multiple Remotely Sensed Data. Remote Sens. 2021, 13, 4446. [Google Scholar] [CrossRef]
- Caligiuri, S.; Camera, C.; Masetti, M.; Bruggeman, A.; Sofokleous, I. Testing GR4H Model Parameter Transferability for Extreme Events in Cyprus: Evaluation of a Cluster Analysis Approach. In Proceedings of the EGU General Assembly 2019, Vienna, Austria, 7–12 April 2019; Geophysical Research Abstracts. Volume 21. [Google Scholar]
- Basri, H.; Sidek, L.M.; Razad, A.Z.; Pokhrel, P. Hydrological Modelling of Surface Runoff for Temengor Reservoir Using GR4H Model. Int. J. Civ. Eng. Technol. 2019, 10, 29–40. [Google Scholar]
- Ayzel, G.; Heistermann, M. The Effect of Calibration Data Length on the Performance of a Conceptual Hydrological Model versus LSTM and GRU: A Case Study for Six Basins from the CAMELS Dataset. Comput. Geosci. 2021, 149, 104708. [Google Scholar] [CrossRef]
- Llauca, H.; Lavado-Casimiro, W.; León, K.; Jimenez, J.; Traverso, K.; Rau, P. Assessing Near Real-Time Satellite Precipitation Products for Flood Simulations at Sub-Daily Scales in a Sparsely Gauged Watershed in Peruvian Andes. Remote Sens. 2021, 13, 826. [Google Scholar] [CrossRef]
- Fernandez-Palomino, C.A.; Hattermann, F.F.; Krysanova, V.; Vega-Jácome, F.; Bronstert, A. Towards a More Consistent Eco-Hydrological Modelling through Multi-Objective Calibration: A Case Study in the Andean Vilcanota River Basin, Peru. Hydrol. Sci. J. 2021, 66, 59–74. [Google Scholar] [CrossRef]
- Aybar, C.; Fernández, C.; Huerta, A.; Lavado, W.; Vega, F.; Felipe-Obando, O. Construction of a High-Resolution Gridded Rainfall Dataset for Peru from 1981 to the Present Day. Hydrol. Sci. J. 2020, 65, 770–785. [Google Scholar] [CrossRef]
- Huerta, A.; Camacho, C.L.A.; Imfeld, N.; Correa, K. High-Resolution Grids of Daily Air Temperature for Peru-the New PISCOt v1. 2 Dataset. 2022. Available online: https://eartharxiv.org/repository/view/4864/ (accessed on 26 October 2023).
- Huerta, A.; Bonnesoeur, V.; Cuadros-Adriazola, J.; Gutierrez, L.; Ochoa-Tocachi, B.F.; Román-Dañobeytia, F.; Lavado-Casimiro, W. PISCOeo_pm, a Reference Evapotranspiration Gridded Database Based on FAO Penman-Monteith in Peru. Sci. Data 2022, 9, 328. [Google Scholar] [CrossRef]
- Dinku, T.; Hailemariam, K.; Maidment, R.; Tarnavsky, E.; Connor, S. Combined Use of Satellite Estimates and Rain Gauge Observations to Generate High-Quality Historical Rainfall Time Series over Ethiopia. Int. J. Climatol. 2014, 34, 2489–2504. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled Complex Evolution Approach for Effective and Efficient Global Minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart Low Flow Signature Metrics for an Improved Overall Performance Evaluation of Hydrological Models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the Choice of Calibration Metrics for “High-Flow” Estimation Using Hydrologic Models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Abbaszadeh, P.; Moradkhani, H. Sequential Data Assimilation for Real-Time Probabilistic Flood Inundation Mapping. Hydrol. Earth Syst. Sci. 2021, 25, 4995–5011. [Google Scholar] [CrossRef]
- Clark, M.P.; Rupp, D.E.; Woods, R.A.; Zheng, X.; Ibbitt, R.P.; Slater, A.G.; Schmidt, J.; Uddstrom, M.J. Hydrological Data Assimilation with the Ensemble Kalman Filter: Use of Streamflow Observations to Update States in a Distributed Hydrological Model. Adv. Water Resour. 2008, 31, 1309–1324. [Google Scholar] [CrossRef]
- Piazzi, G.; Delaigue, O. Ensemble-Based Data Assimilation with GR Hydrological Models (v. 0.1.3); HAL; R Foundation: Vienna, Austria, 2021; Available online: https://doi.org/hal-03301603 (accessed on 26 October 2023).
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual State–Parameter Estimation of Hydrological Models Using Ensemble Kalman Filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef]
- Reichle, R.H.; McLaughlin, D.B.; Entekhabi, D. Hydrologic Data Assimilation with the Ensemble Kalman Filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- Berg, D.; Bauser, H.H.; Roth, K. Covariance Resampling for Particle Filter—State and Parameter Estimation for Soil Hydrology. Hydrol. Earth Syst. Sci. 2019, 23, 1163–1178. [Google Scholar] [CrossRef]
- Jamal, A.; Linker, R. Covariance-Based Selection of Parameters for Particle Filter Data Assimilation in Soil Hydrology. Water 2022, 14, 3606. [Google Scholar] [CrossRef]
- He, X.; Lucatero, D.; Ridler, M.-E.; Madsen, H.; Kidmose, J.; Hole, Ø.; Petersen, C.; Zheng, C.; Refsgaard, J.C. Real-Time Simulation of Surface Water and Groundwater with Data Assimilation. Adv. Water Resour. 2019, 127, 13–25. [Google Scholar] [CrossRef]
- Wang, F.; Huang, G.H.; Fan, Y.; Li, Y.P. Development of a Disaggregated Multi-Level Factorial Hydrologic Data Assimilation Model. J. Hydrol. 2022, 610, 127802. [Google Scholar] [CrossRef]
- Nearing, G.S.; Klotz, D.; Frame, J.M. Data Assimilation and Autoregression for Using Near-Real-Time Streamflow Observations in Long Short-Term Memory Networks. Hydrol. Earth Syst. Sci. 2022, 26, 5493–5513. [Google Scholar] [CrossRef]
- De Sousa, E.R.; Hipsey, M.R.; Vogwill, R.I.J. Data Assimilation, Sensitivity Analysis and Uncertainty Quantification in Semi-Arid Terminal Catchments Subject to Long-Term Rainfall Decline. Front. Earth Sci. Chin. 2023, 10, 886304. [Google Scholar] [CrossRef]
- Mansanarez, V.; Renard, B.; Coz, J.L. Shift Happens! Adjusting Stage-discharge Rating Curves to Morphological Changes at Known Times. Water Resour. Res. 2019, 55, 2876–2899. [Google Scholar] [CrossRef]
- Arestegui, M.; Lavado, W.; Cisneros, A.; Madueño, G.; Almeida, C.; Millán, C.; Bazo, J.; Anicama, J. Exploration of Flood Lead-Times through River Level Monitoring: A Case Study from the Vilcanota River in Cusco, Peru. In Proceedings of the EGU General Assembly 2023, Online, 23–28 April 2023; p. 17570. [Google Scholar]
- Paul, J.D.; Buytaert, W.; Sah, N. A Technical Evaluation of Lidar-based Measurement of River Water Levels. Water Resour. Res. 2020, 56, e2019WR026810. [Google Scholar] [CrossRef]
- Llauca, H.; Lavado-Casimiro, W.; Montesinos, C.; Santini, W.; Rau, P. PISCO_HyM_GR2M: A Model of Monthly Water Balance in Peru (1981–2020). Water 2021, 13, 1048. [Google Scholar] [CrossRef]
- Condom, T.; Martínez, R.; Pabón, J.D.; Costa, F.; Pineda, L.; Nieto, J.J.; López, F.; Villacis, M. Climatological and Hydrological Observations for the South American Andes: In Situ Stations, Satellite, and Reanalysis Data Sets. Front. Earth Sci. Chin. 2020, 8, 92. [Google Scholar] [CrossRef]


| Type | Station | Abrev. | Longitude [°W] | Latitude [°S] | Elevation [m.a.s.l.] |
|---|---|---|---|---|---|
| Fluviometric | Pisac | PIS | 71.84 | 13.43 | 2791.65 |
| Pluviometric | Acjanaco Gore | AGR | 71.62 | 13.20 | 3466.11 |
| Calca | CAL | 71.96 | 13.33 | 2921.24 | |
| Casaccancha | CAS | 72.30 | 13.99 | 4033.16 | |
| Huayllabamba | HUA | 72.45 | 13.27 | 2976.55 | |
| Intihuatana M | INM | 72.56 | 13.17 | 1778.23 | |
| Machupicchu | MAC | 72.55 | 13.18 | 2399.80 | |
| Marcapata Gore | MAR | 70.90 | 13.50 | 1792.76 | |
| Qorihuayrachina | QOR | 72.43 | 13.22 | 2517.25 | |
| Salcca | SAL | 71.23 | 14.17 | 3920.10 | |
| San Pablo | SPB | 72.62 | 13.03 | 1228.11 | |
| Santo Tomas | STM | 72.10 | 14.45 | 3665.48 | |
| Sicuani | SIC | 71.24 | 14.24 | 3534.95 |
| Statistical Metric | Equation | Min, Max, Optimal | Emphasis |
|---|---|---|---|
| Logarithmic Nash–Sutcliffe Efficiency (logNSE) [-] | −∞,1,1 | Low flows [51] | |
| Nash–Sutcliffe Efficiency with Box–Cox transformation (BoxNSE) [-] | −∞,1,1 | Middle flows [26] | |
| Kling–Gupta Efficiency (KGE) [-] | −∞,1,1 | Variance and high flows [52] | |
| Bias (BIAS) [%] | 0,+∞,0 | Average trend of simulated flows [26] |
| Statistical Metric | Equation |
|---|---|
| Nash–Sutcliffe Efficiency (NSE) [-] | |
| Bias (BIAS) [m3/s] | |
| Mean of Ensemble Root Mean Squared Error (MRMSE) [m3/s] | |
| Continuous Ranked Probability Skill Score (CRPSS) [-] |
| Statistic Metric | Calibration | Validation | ||
|---|---|---|---|---|
| IMERG-E’ | GSMaP-NRT’ | IMERG-E’ | GSMaP-NRT’ | |
| logNSE | 0.875 | 0.792 | 0.878 | 0.786 |
| BoxNSE | 0.883 | 0.831 | 0.878 | 0.819 |
| KGE | 0.912 | 0.871 | 0.869 | 0.789 |
| BIAS | 0.003 | 0.003 | 0.016 | 0.029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Llauca, H.; Arestegui, M.; Lavado-Casimiro, W. Constraining Flood Forecasting Uncertainties through Streamflow Data Assimilation in the Tropical Andes of Peru: Case of the Vilcanota River Basin. Water 2023, 15, 3944. https://doi.org/10.3390/w15223944
Llauca H, Arestegui M, Lavado-Casimiro W. Constraining Flood Forecasting Uncertainties through Streamflow Data Assimilation in the Tropical Andes of Peru: Case of the Vilcanota River Basin. Water. 2023; 15(22):3944. https://doi.org/10.3390/w15223944
Chicago/Turabian StyleLlauca, Harold, Miguel Arestegui, and Waldo Lavado-Casimiro. 2023. "Constraining Flood Forecasting Uncertainties through Streamflow Data Assimilation in the Tropical Andes of Peru: Case of the Vilcanota River Basin" Water 15, no. 22: 3944. https://doi.org/10.3390/w15223944








