Figure 1.
Watershed situation of HuaYuankou station.
Figure 1.
Watershed situation of HuaYuankou station.
Figure 2.
Division of the HuaYuankou Station Dataset.
Figure 2.
Division of the HuaYuankou Station Dataset.
Figure 3.
Watershed situation of the LouDe station.
Figure 3.
Watershed situation of the LouDe station.
Figure 4.
Division of the LouDe Station Dataset.
Figure 4.
Division of the LouDe Station Dataset.
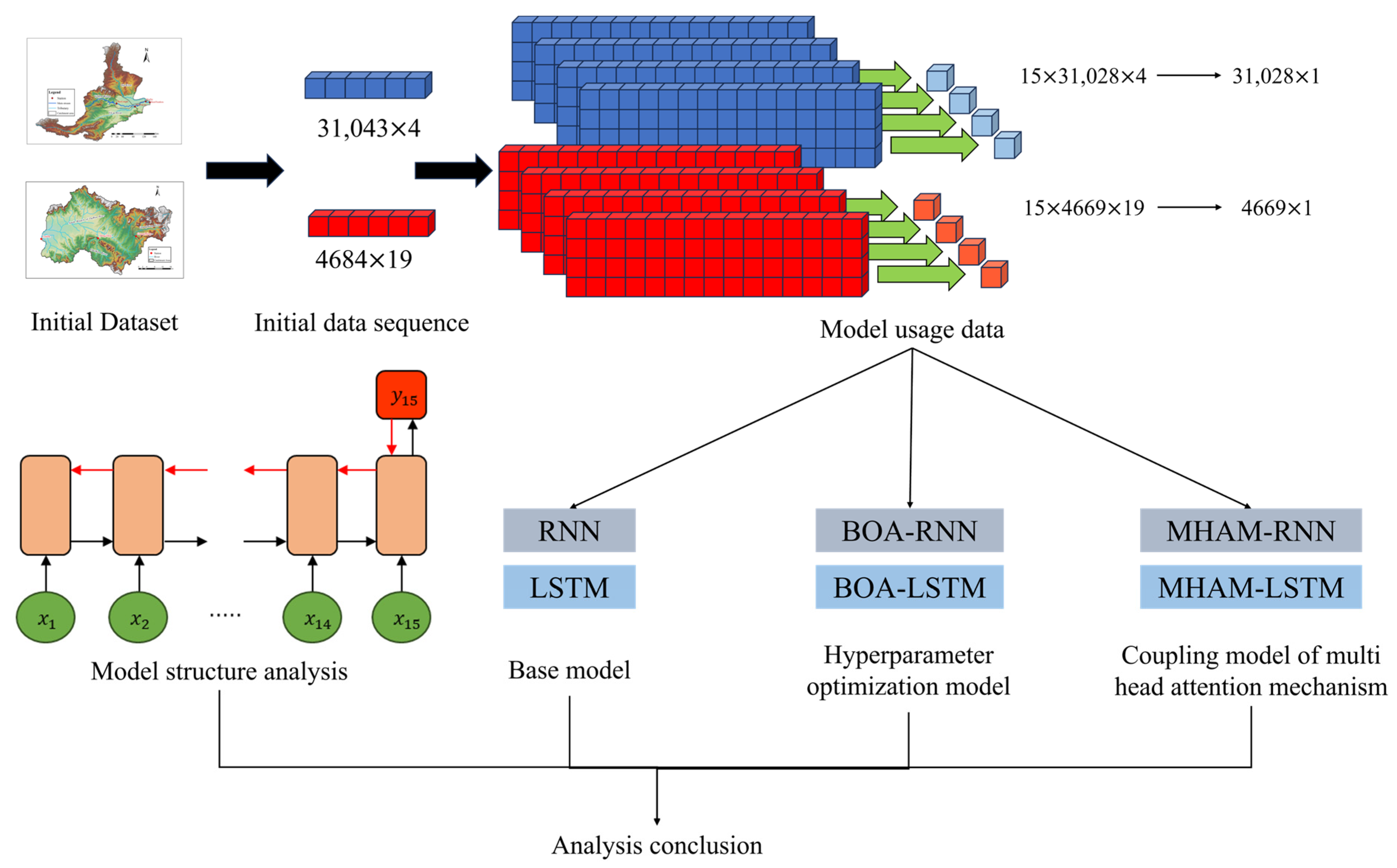
Figure 5.
Research Process Diagram (in the figure, 31,043 and 4684 represent the length of the flood sequence time obtained from the HuaYuankou station and the LouDe station; 4 and 19 represent the types of model input factors; 31, 028 and 4669 represent the length of the flood sequence used for model training, validation, and testing after removing Time step 15; 1 represents the type of the output target).
Figure 5.
Research Process Diagram (in the figure, 31,043 and 4684 represent the length of the flood sequence time obtained from the HuaYuankou station and the LouDe station; 4 and 19 represent the types of model input factors; 31, 028 and 4669 represent the length of the flood sequence used for model training, validation, and testing after removing Time step 15; 1 represents the type of the output target).
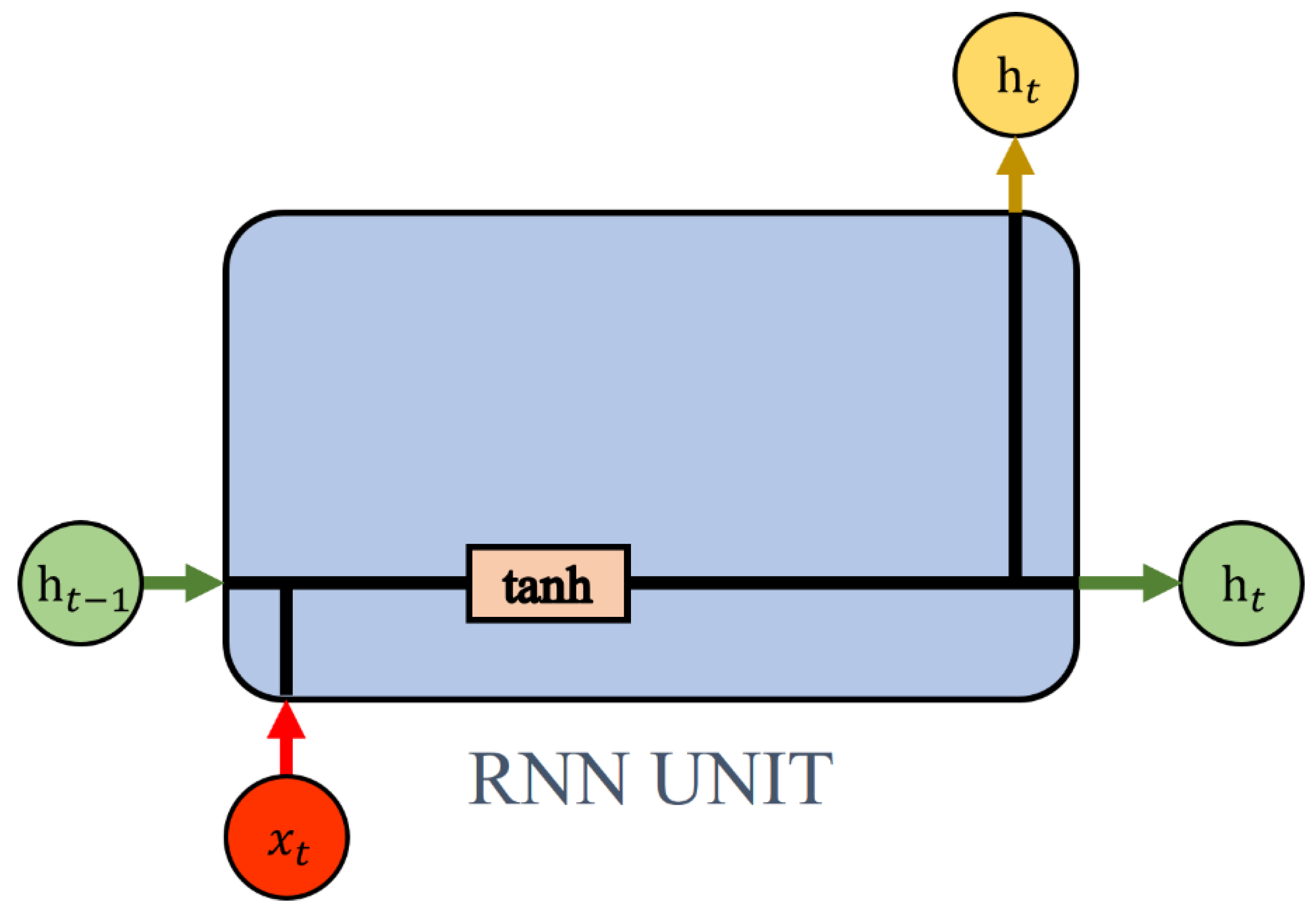
Figure 6.
RNN unit structure. In this figure, h stands for hidden state; x stands for input information; tanh is tangent activation; and stand for time.
Figure 6.
RNN unit structure. In this figure, h stands for hidden state; x stands for input information; tanh is tangent activation; and stand for time.
Figure 7.
LSTM unit structure. In this figure, c represents cell state; “F, I and O”, respectively, represent the forget gate, the input gate, and the output gate; represents pointwise addition; represents pointwise multiplication; represents sigmoid activation.
Figure 7.
LSTM unit structure. In this figure, c represents cell state; “F, I and O”, respectively, represent the forget gate, the input gate, and the output gate; represents pointwise addition; represents pointwise multiplication; represents sigmoid activation.
Figure 8.
Model Information Flow. In this figure, the unit can be an RNN unit or an LSTM unit. Linear is a linear layer, is output at time t.
Figure 8.
Model Information Flow. In this figure, the unit can be an RNN unit or an LSTM unit. Linear is a linear layer, is output at time t.
Figure 9.
MHAM coupled logic structure. In this figure, the unit can be an RNN unit or an LSTM unit.
Figure 9.
MHAM coupled logic structure. In this figure, the unit can be an RNN unit or an LSTM unit.
Figure 10.
Logical structure of the BOA coupling model. In this figure, the unit can be an RNN unit or an LSTM unit (1 represents the algorithm optimization process, and 2 represents the process where the model makes predictions based on the hyperparameters found by the algorithm.).
Figure 10.
Logical structure of the BOA coupling model. In this figure, the unit can be an RNN unit or an LSTM unit (1 represents the algorithm optimization process, and 2 represents the process where the model makes predictions based on the hyperparameters found by the algorithm.).
Figure 11.
Gradient propagation process of each batch of data in flood forecasting tasks. The black arrow represents the forward-propagation process; the red arrow represents the backpropagation process.
Figure 11.
Gradient propagation process of each batch of data in flood forecasting tasks. The black arrow represents the forward-propagation process; the red arrow represents the backpropagation process.
Figure 12.
Attention distribution of the model for test period data at the LouDe station.
Figure 12.
Attention distribution of the model for test period data at the LouDe station.
Figure 13.
Average performance of model experiment results.
Figure 13.
Average performance of model experiment results.
Figure 14.
Distribution of indicators during the testing period of RNN and LSTM models.
Figure 14.
Distribution of indicators during the testing period of RNN and LSTM models.
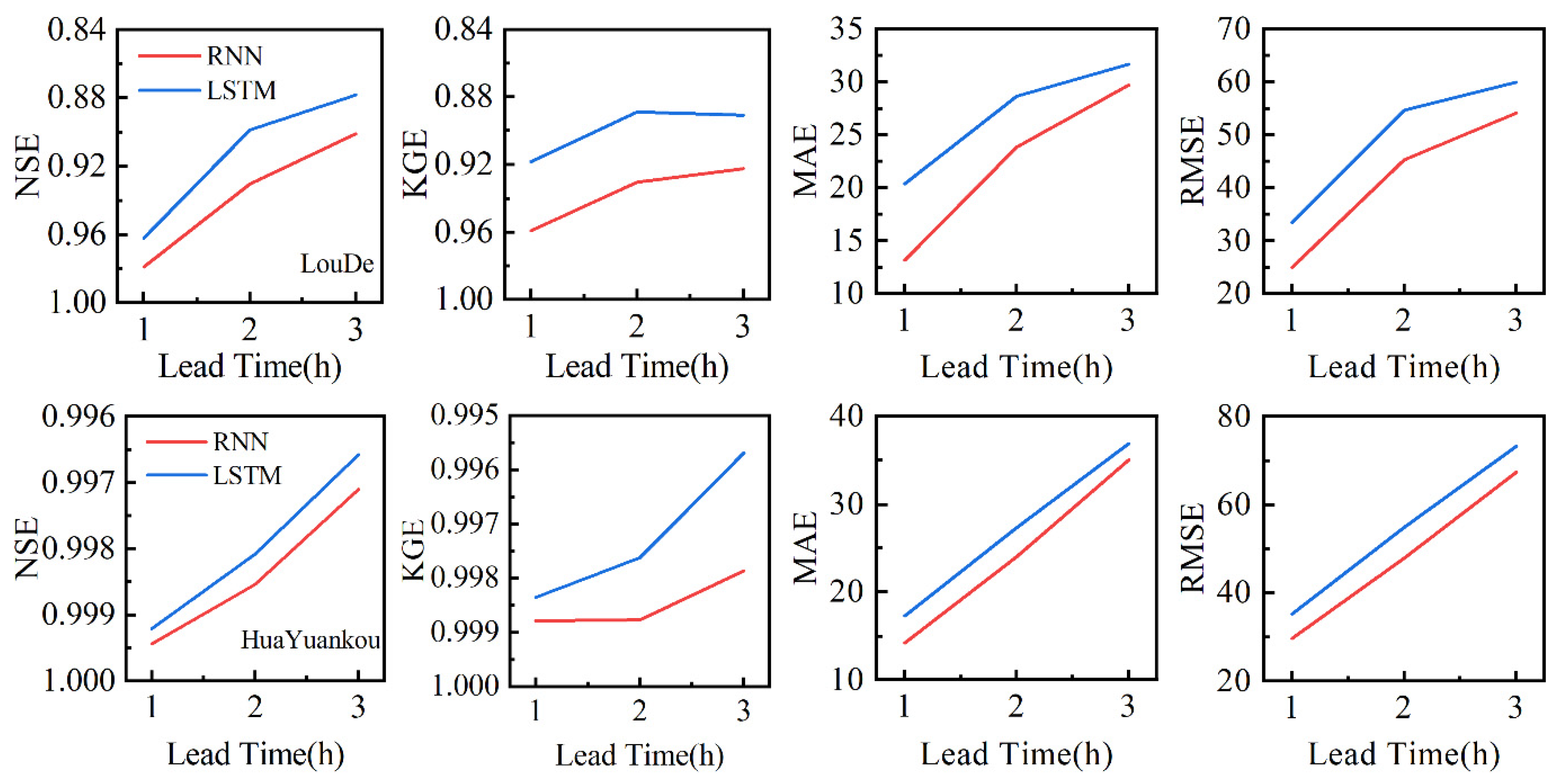
Figure 15.
The variation of average performance of RNN and LSTM models with lead time.
Figure 15.
The variation of average performance of RNN and LSTM models with lead time.
Figure 16.
Model predictive effects under different lead times of the LouDe station.
Figure 16.
Model predictive effects under different lead times of the LouDe station.
Figure 17.
Scatter plot of the model prediction performance at the LouDe station under different lead times (“✳” represents the distribution of data in observed and predicted values).
Figure 17.
Scatter plot of the model prediction performance at the LouDe station under different lead times (“✳” represents the distribution of data in observed and predicted values).
Figure 18.
Model predictive effects under different lead times of the HuaYuankou station.
Figure 18.
Model predictive effects under different lead times of the HuaYuankou station.
Figure 19.
Scatter plot of the model prediction performance at the HuaYuankou station under different lead times (“✳” represents the distribution of data in observed and predicted values).
Figure 19.
Scatter plot of the model prediction performance at the HuaYuankou station under different lead times (“✳” represents the distribution of data in observed and predicted values).
Figure 20.
Average performance of algorithm optimization model experimental results.
Figure 20.
Average performance of algorithm optimization model experimental results.
Figure 21.
Distribution of indicators during the testing period of BOA-RNN and BOA-LSTM models.
Figure 21.
Distribution of indicators during the testing period of BOA-RNN and BOA-LSTM models.
Figure 22.
Algorithm optimization model prediction effect of the Loude station during the testing period.
Figure 22.
Algorithm optimization model prediction effect of the Loude station during the testing period.
Figure 23.
Algorithm optimization model prediction effect of the HuaYuankou station during the testing period.
Figure 23.
Algorithm optimization model prediction effect of the HuaYuankou station during the testing period.
Figure 24.
Predicting average performance with a coupled attention mechanism model.
Figure 24.
Predicting average performance with a coupled attention mechanism model.
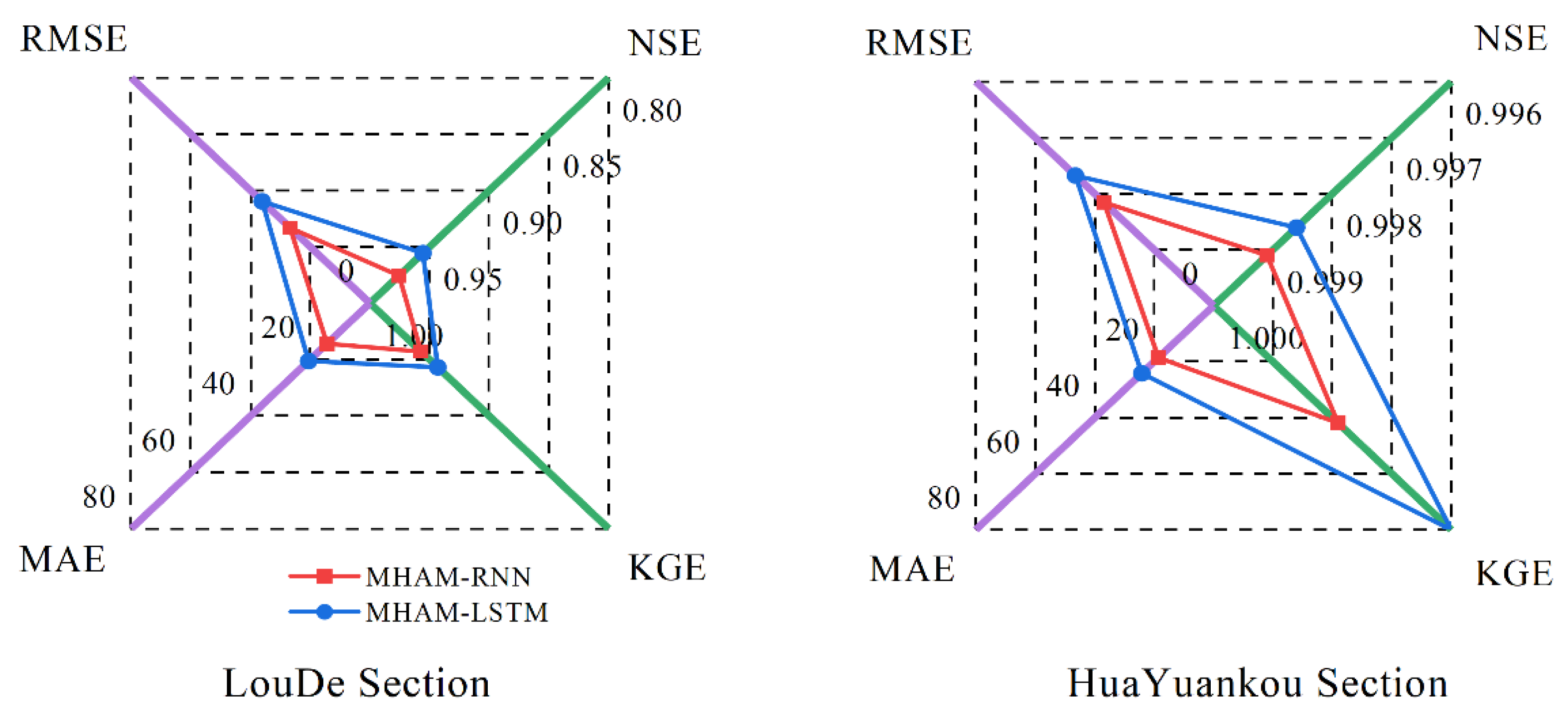
Figure 25.
Attention difference of the model for test period data.
Figure 25.
Attention difference of the model for test period data.
Table 1.
Algorithm optimization target details.
Table 1.
Algorithm optimization target details.
| Optimization Objectives | Optimization Scope | Reason for Selection |
|---|
| Learning rate | (1 × 10−4, 1 × 10−2) | Control model gradient descent |
| Hidden units | (10, 200) | Control model’s nonlinear
expression ability |
| L2 Regularization | (1 × 10−7, 1 × 10−3) | Avoid overfitting |
Table 2.
Model-related settings.
Table 2.
Model-related settings.
| Name | Setting | Reason |
|---|
| Learning rate | 1 × 10−3 | Beneficial for stable gradient descent |
| Hidden units | 128 | Sufficient nonlinear expression ability |
| L2 Regularization | 1 × 10−5 | Avoidable overfitting |
| Gradient descent algorithm | Adam | Stable effect |
| iterations | 1500 | Meet iteration requirements |
Table 3.
Average performance of model experiment results.
Table 3.
Average performance of model experiment results.
| Station | Model | NSE | KGE | MAE | RMSE |
| LouDe | RNN | 0.9789 | 0.9591 | 13.1555 | 24.9860 |
| LSTM | 0.9621 | 0.9184 | 20.4024 | 33.4670 |
| HuaYuankou | RNN | 0.9994 | 0.9988 | 14.2209 | 29.6959 |
| LSTM | 0.9992 | 0.9984 | 17.3051 | 35.2501 |
Table 4.
Average performance indicators of RNN and LSTM models under different lead times.
Table 4.
Average performance indicators of RNN and LSTM models under different lead times.
| Lead Time | Station | Model | NSE | KGE | MAE | RMSE |
|---|
| 2 h | LouDe | RNN | 0.9305 | 0.9305 | 23.8539 | 45.3195 |
| LSTM | 0.8988 | 0.8887 | 28.6722 | 54.6817 |
| HuaYuankou | RNN | 0.9985 | 0.9988 | 24.0427 | 47.8815 |
| LSTM | 0.9981 | 0.9976 | 27.3378 | 54.9296 |
| 3 h | LouDe | RNN | 0.9009 | 0.9225 | 29.7196 | 54.1151 |
| LSTM | 0.8783 | 0.8907 | 31.6699 | 59.9619 |
| HuaYuankou | RNN | 0.9971 | 0.9979 | 35.0459 | 67.4454 |
| LSTM | 0.9966 | 0.9957 | 36.9041 | 73.3273 |
Table 5.
Performance improvement effect of the RNN model compared to the LSTM model.
Table 5.
Performance improvement effect of the RNN model compared to the LSTM model.
| Lead Time | Station | NSE | KGE | MAE | RMSE |
| 2 h | LouDe | 3.53% | 4.70% | 16.80% | 17.12% |
| HuaYuankou | 0.04% | 0.12% | 12.05% | 12.83% |
| 3 h | LouDe | 2.57% | 3.57% | 6.16% | 9.75% |
| HuaYuankou | 0.05% | 0.22% | 5.04% | 8.02% |
Table 6.
Algorithm-selected model hyperparameters.
Table 6.
Algorithm-selected model hyperparameters.
| Model | Station | Learning Rate | Hidden Units | L2 Regularization |
|---|
| RNN | LouDe | 9.94721325044244 × 10−3 | 102 | 1.24128822320419 × 10−6 |
| HuaYuankou | 6.31430706313691 × 10−4 | 169 | 2.29751978936061 × 10−5 |
| LSTM | LouDe | 8.60162246721079 × 10−3 | 141 | 1.00331686970300 × 10−6 |
| HuaYuankou | 1.16040150867700 × 10−3 | 130 | 5.49314205875754 × 10−6 |
Table 7.
Average Performance of Algorithm Optimization Model Experimental Results.
Table 7.
Average Performance of Algorithm Optimization Model Experimental Results.
| Station | Model | NSE | KGE | MAE | RMSE |
|---|
| LouDe | BOA-RNN | 0.9819 | 0.9679 | 11.4860 | 23.1318 |
| BOA-LSTM | 0.9752 | 0.9607 | 13.4444 | 27.0929 |
| HuaYuankou | BOA-RNN | 0.9994 | 0.9988 | 14.5352 | 30.1463 |
| BOA-LSTM | 0.9993 | 0.9985 | 15.6075 | 32.1723 |
Table 8.
Changes in model performance after algorithm optimization.
Table 8.
Changes in model performance after algorithm optimization.
| Station | Model | NSE | KGE | MAE | RMSE |
|---|
| LouDe | BOA-RNN/RNN | 0.31% | 0.92% | 12.69% | 7.42% |
| BOA-LSTM/LSTM | 1.36% | 4.61% | 34.10% | 19.05% |
| HuaYuankou | BOA-RNN/RNN | 0.00% | 0.00% | −2.21% | −1.52% |
| BOA-LSTM/LSTM | 0.01% | 0.01% | 9.81% | 8.73% |
Table 9.
Predicting average performance with a coupled attention mechanism model.
Table 9.
Predicting average performance with a coupled attention mechanism model.
| Station | Model | NSE | KGE | MAE | RMSE |
|---|
| LouDe | MHAM-RNN | 0.9758 | 0.9569 | 14.2923 | 26.7232 |
| MHAM-LSTM | 0.9556 | 0.9433 | 20.4595 | 36.2084 |
| HuaYuankou | MHAM-RNN | 0.9991 | 0.9979 | 18.6464 | 36.9343 |
| MHAM-LSTM | 0.9986 | 0.9960 | 24.0945 | 46.4824 |
Table 10.
Changes in average performance indicators relative to the basic model.
Table 10.
Changes in average performance indicators relative to the basic model.
| Station | Model | NSE | KGE | MAE | RMSE |
|---|
| LouDe | MHAM-RNN/RNN | −0.32% | −0.23% | −8.64% | −6.95% |
| MHAM-LSTM/LSTM | −0.68% | 2.71% | −0.28% | −8.19% |
| HuaYuankou | MHAM-RNN/RNN | −0.03% | −0.09% | −31.12% | −24.38% |
| MHAM-LSTM/LSTM | −0.06% | −0.24% | −39.23% | −31.86% |
Table 11.
Model cost.
| Model | RNN | LSTM | BOA-RNN | BOA-LSTM | MHAM-RNN | MHAM-LSTM |
|---|
| Parameters | 19,201 | 76,417 | 19,201 | 76,417 | 68,737 | 125,953 |
| Time Cost(s) | 57.02 | 63.00 | -- | --- | 80.13 | 88.12 |