Modeling Morphodynamic Impacts and Optimization of Marine Hydrokinetic Arrays in Shallow Offshore Environments
Abstract
:1. Introduction
2. Background
2.1. MHK Types and Hydrodynamic Impacts
2.2. MHK Morphodynamic Impacts
3. Methods
3.1. Wave Climate Analyses
3.2. Numerical Model
3.3. Equilibrium Shoreface Bathymetry
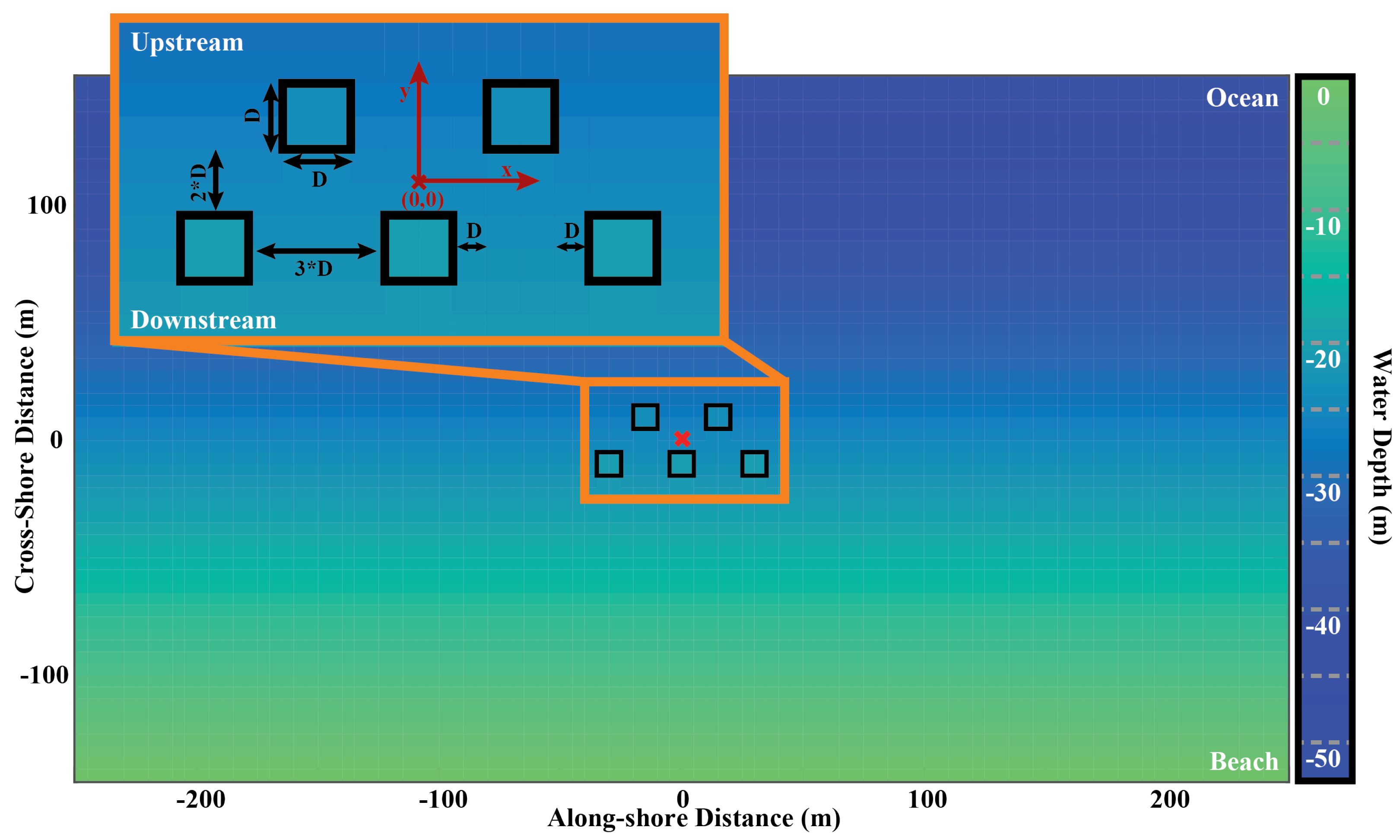
3.4. MHK Modeling on Equilibrium Bathymetry
4. Results
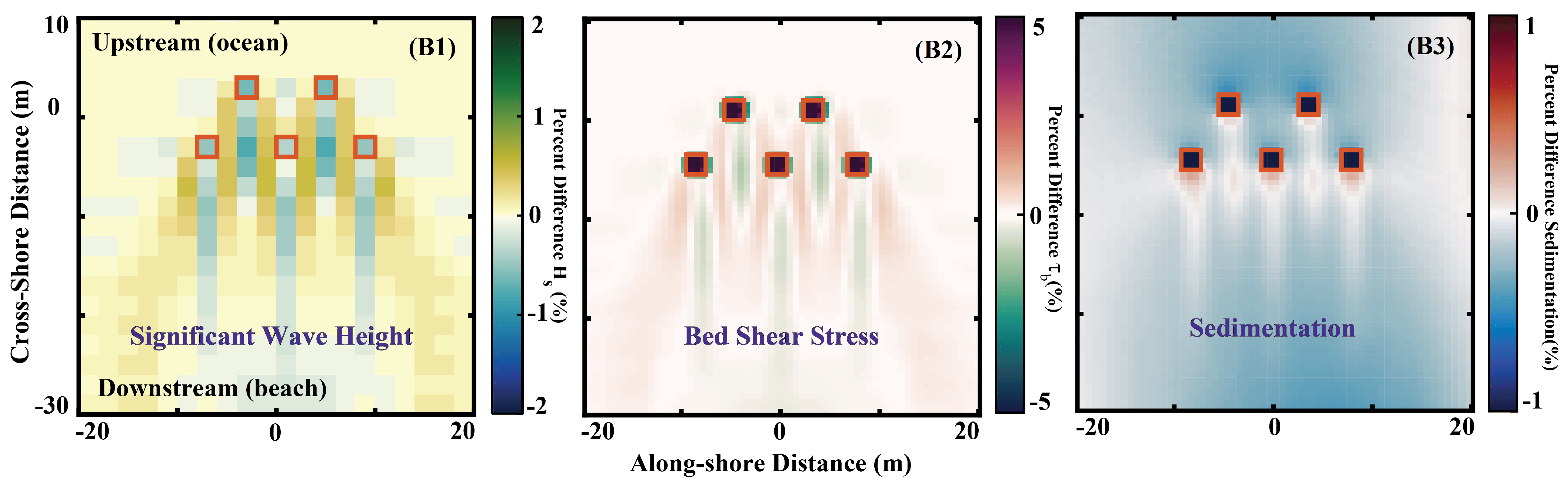
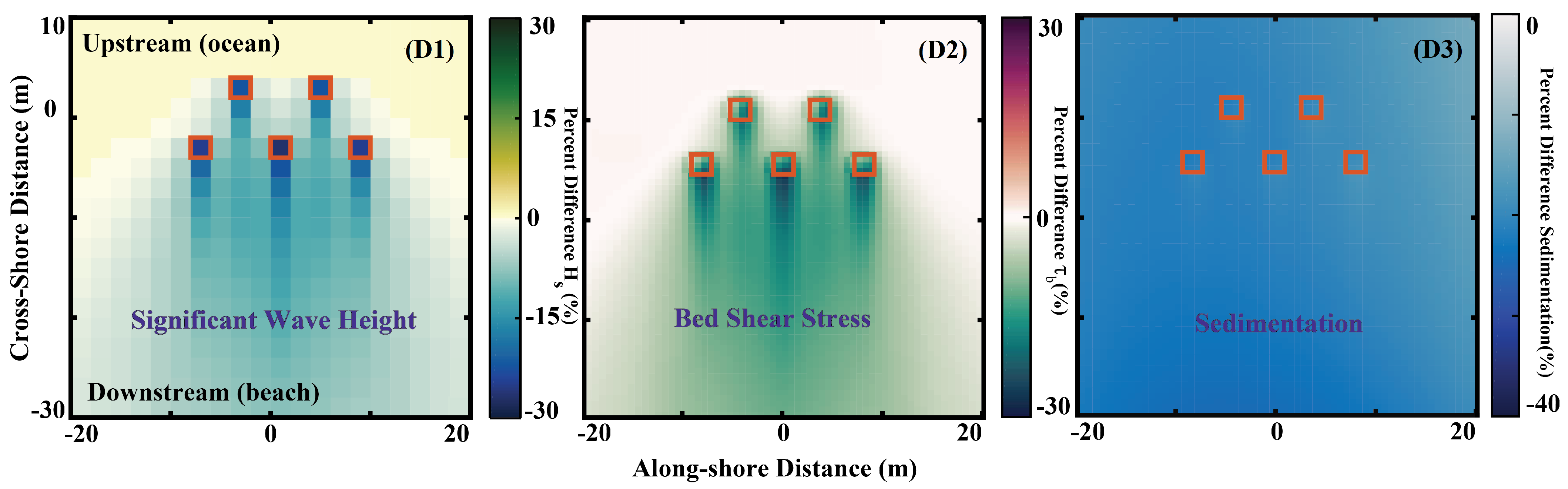
4.1. Morphodynamic Response to MHKs
4.1.1. Short-Term Morphologic Response
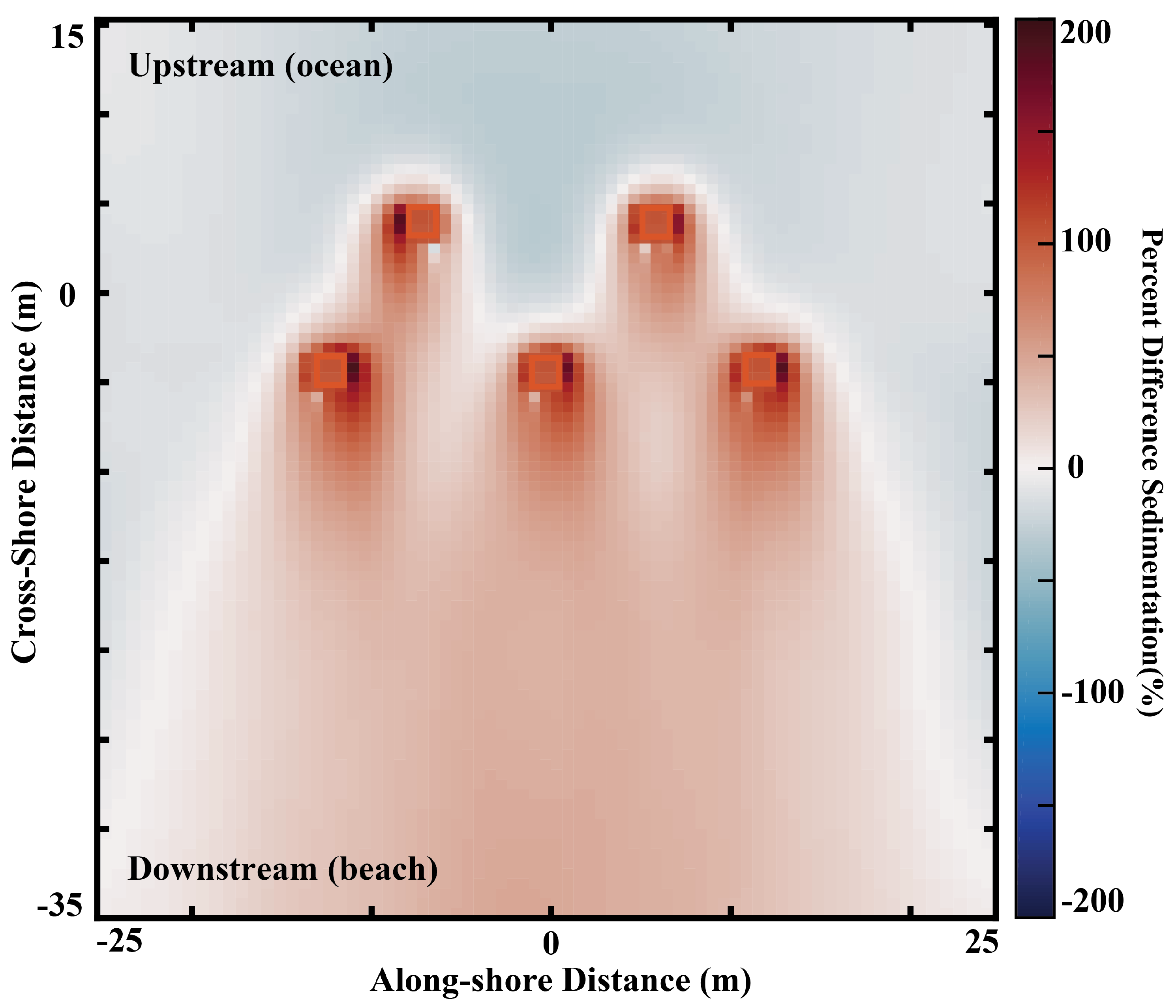
4.1.2. Long-Term Morphologic Response
4.2. Modeling Energy Dissipation
5. Discussion
5.1. Sensitivity Analysis: Array Scale
5.2. Sensitivity Analysis: Device Number and Spacing
6. Conclusions
- Energy absorption by MHK devices exerts a notable influence on the wave field and sedimentation, with a 30% energy uptake per device resulting in an increased sediment deposition, particularly downstream of the array.
- During extreme conditions, MHK-induced energy reduction significantly impacts the wave height and subsequent bed shear stress, altering the sedimentation pattern and leading to increased deposition around, over, and downstream of the devices.
- The pattern of morphodynamic response remains insensitive to array configurations, but the magnitude of this response displays sensitivity to various parameters.
- Larger arrays of turbines, such as those with 25 devices, are more susceptible to burial and instability for devices positioned downstream, especially during extreme events.
- Our study underscores the importance of deactivating MHK energy absorption during strong storm conditions to prevent substantial burial and potential escalation of maintenance costs. Conversely, deploying MHK devices during storms may offer coastal protection by reducing wave heights and energy.
- Lastly, increasing the spacing between MHK devices emerges as a crucial factor in minimizing the long-term risk of burial due to enhanced sedimentation around these devices.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shields, M.A.; Woolf, D.K.; Grist, E.P.; Kerr, S.A.; Jackson, A.C.; Harris, R.E.; Bell, M.C.; Beharie, R.; Want, A.; Osalusi, E.; et al. Marine renewable energy: The ecological implications of altering the hydrodynamics of the marine environment. Ocean Coast. Manag. 2011, 54, 2–9. [Google Scholar] [CrossRef]
- VanZwieten, J.; McAnally, W.; Ahmad, J.; Davis, T.; Martin, J.; Bevelhimer, M.; Cribbs, A.; Lippert, R.; Hudon, T.; Trudeau, M. In-stream hydrokinetic power: Review and appraisal. J. Energy Eng. 2015, 141, 1–16. [Google Scholar] [CrossRef]
- Güney, M.S.; Kaygusuz, K. Hydrokinetic energy conversion systems: A technology status review. Renew. Sustain. Energy Rev. 2010, 14, 2996–3004. [Google Scholar] [CrossRef]
- Laws, N.D.; Epps, B.P. Hydrokinetic energy conversion: Technology, research, and outlook. Renew. Sustain. Energy Rev. 2016, 57, 1245–1259. [Google Scholar] [CrossRef]
- Muljadi, E.; Yu, Y.H. Review of Marine Hydrokinetic Power Generation and Power Plant. Electr. Power Components Syst. 2015, 43, 1422–1433. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Review on power performance and efficiency of wave energy converters. Energies 2019, 12, 4329. [Google Scholar] [CrossRef]
- Nash, S.; Phoenix, A. A review of the current understanding of the hydro-environmental impacts of energy removal by tidal turbines. Renew. Sustain. Energy Rev. 2017, 80, 648–662. [Google Scholar] [CrossRef]
- Ahmadian, R.; Falconer, R.; Bockelmann-Evans, B. Far-field modelling of the hydro-environmental impact of tidal stream turbines. Renew. Energy 2012, 38, 107–116. [Google Scholar] [CrossRef]
- Gillibrand, P.A.; Walters, R.A.; McIlvenny, J. Numerical simulations of the effects of a tidal turbine array on near-bed velocity and local bed shear stress. Energies 2016, 9, 852. [Google Scholar] [CrossRef]
- Ramos, V.; Carballo, R.; Ringwood, J.V. Application of the actuator disc theory of Delft3D-FLOW to model far-field hydrodynamic impacts of tidal turbines. Renew. Energy 2019, 139, 1320–1335. [Google Scholar] [CrossRef]
- Ruehl, K.; Porter, A.; Chartrand, C.; Smith, H.; Chang, G.; Roberts, J. Development, Verification and Application of the SNL-SWAN Open Source Wave Farm Code. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Nash, S.; Olbert, A.I.; Hartnett, M. Towards a low-cost modelling system for optimising the layout of tidal turbine arrays. Energies 2015, 8, 13521–13539. [Google Scholar] [CrossRef]
- Plew, D.R.; Stevens, C.L. Numerical modelling of the effect of turbines on currents in a tidal channel—Tory Channel, New Zealand. Renew. Energy 2013, 57, 269–282. [Google Scholar] [CrossRef]
- Fallon, D.; Hartnett, M.; Olbert, A.; Nash, S. The effects of array configuration on the hydro-environmental impacts of tidal turbines. Renew. Energy 2014, 64, 10–25. [Google Scholar] [CrossRef]
- Li, X.; Li, M.; Jordan, L.B.; McLelland, S.; Parsons, D.R.; Amoudry, L.O.; Song, Q.; Comerford, L. Modelling impacts of tidal stream turbines on surface waves. Renew. Energy 2019, 130, 725–734. [Google Scholar] [CrossRef]
- Abanades, J.; Greaves, D.; Iglesias, G. Wave farm impact on the beach profile: A case study. Coast. Eng. 2014, 86, 36–44. [Google Scholar] [CrossRef]
- Bergillos, R.J.; López-Ruiz, A.; Medina-López, E.; Moñino, A.; Ortega-Sánchez, M. The role of wave energy converter farms on coastal protection in eroding deltas, Guadalfeo, southern Spain. J. Clean. Prod. 2018, 171, 356–367. [Google Scholar] [CrossRef]
- Ramírez-Mendoza, R.; Amoudry, L.O.; Thorne, P.D.; Cooke, R.D.; McLelland, S.J.; Jordan, L.B.; Simmons, S.M.; Parsons, D.R.; Murdoch, L. Laboratory study on the effects of hydro kinetic turbines on hydrodynamics and sediment dynamics. Renew. Energy 2018, 129, 271–284. [Google Scholar] [CrossRef]
- Neill, S.P.; Jordan, J.R.; Couch, S.J. Impact of tidal energy converter (TEC) arrays on the dynamics of headland sand banks. Renew. Energy 2012, 37, 387–397. [Google Scholar] [CrossRef]
- Robins, P.E.; Neill, S.P.; Lewis, M.J. Impact of tidal-stream arrays in relation to the natural variability of sedimentary processes. Renew. Energy 2014, 72, 311–321. [Google Scholar] [CrossRef]
- Neill, S.P.; Litt, E.J.; Couch, S.J.; Davies, A.G. The impact of tidal stream turbines on large-scale sediment dynamics. Renew. Energy 2009, 34, 2803–2812. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- van Rijn, L.C. Sediment transport, part II: Suspended load transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Soulsby, R. Dynamics of Marine Sands; Thomas Telford Services Limited: London, UK, 1997. [Google Scholar]
- Zaichik, L.; Alipchenkov, V.M.; Sinaiski, E.G. Particles in Turbulent Flows; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Martin-Short, R.; Hill, J.; Kramer, S.C.; Avdis, A.; Allison, P.A.; Piggott, M.D. Tidal resource extraction in the Pentland Firth, UK: Potential impacts on flow regime and sediment transport in the Inner Sound of Stroma. Renew. Energy 2015, 76, 596–607. [Google Scholar] [CrossRef]
- Haverson, D.; Bacon, J.; Smith, H.C.; Venugopal, V.; Xiao, Q. Modelling the hydrodynamic and morphological impacts of a tidal stream development in Ramsey Sound. Renew. Energy 2018, 126, 876–887. [Google Scholar] [CrossRef]
- Thiébot, J.; Bailly du Bois, P.; Guillou, S. Numerical modeling of the effect of tidal stream turbines on the hydrodynamics and the sediment transport - Application to the Alderney Race (Raz Blanchard), France. Renew. Energy 2015, 75, 356–365. [Google Scholar] [CrossRef]
- Auguste, C.; Nader, J.R.; Marsh, P.; Cossu, R.; Penesis, I. Variability of sediment processes around a tidal farm in a theoretical channel. Renew. Energy 2021, 171, 606–620. [Google Scholar] [CrossRef]
- Musa, M.; Hill, C.; Guala, M. Interaction between hydrokinetic turbine wakes and sediment dynamics: Array performance and geomorphic effects under different siting strategies and sediment transport conditions. Renew. Energy 2019, 138, 738–753. [Google Scholar] [CrossRef]
- Ortiz, A.C.; Ashton, A.D. Understanding the Timescales of Morphologic Evolution in the Crossshore and Long-shore of Sandy Wave-Dominated Coast. Geophys. Res. Lett. in preprint.
- Lesser, G.; Roelvink, J.; van Kester, J.; Stelling, G. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Roelvink, J.A. Coastal morphodynamic evolution techniques. Coast. Eng. 2006, 53, 277–287. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Swinkels, C.; Luijendijk, A.; Roelvink, D.; Bosboom, J.; Stive, M.; Walstra, D.J. Morphodynamic upscaling with the MORFAC approach: Dependencies and sensitivities. Coast. Eng. 2011, 58, 806–811. [Google Scholar] [CrossRef]
- Vlijm, R.J. Process-Based Modelling of Morphological Response to Submerged Breakwaters. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 2011. [Google Scholar]
- Wright, L.D.; Thom, B.G. Coastal depositional landforms: A morphodynamic approach. Prog. Phys. Geogr. Earth Environ. 1977, 1, 412–459. [Google Scholar] [CrossRef]
- Dissanayake, D.; Ranasinghe, R.; Roelvink, J. The morphological response of large tidal inlet/basin systems to relative sea level rise. Clim. Chang. 2012, 113, 253–276. [Google Scholar] [CrossRef]
- Booij, N.; Holthuijsen, L.; Ris, R. The“ SWAN” wave model for shallow water. In Coastal Engineering 1996: Proceedings of the Twenty-Fifth International Conference, September 2–6, 1996, the Peabody Hotel, Orlando, Florida (Proceedings of the Coastal Engineering Conference); Amer Society of Civil Engineers: Reston, VA, USA, 1997; pp. 668–676. [Google Scholar]
- Li, X.; Li, M.; McLelland, S.J.; Jordan, L.B.; Simmons, S.M.; Amoudry, L.O.; Ramirez-Mendoza, R.; Thorne, P.D. Modelling tidal stream turbines in a three-dimensional wave-current fully coupled oceanographic model. Renew. Energy 2017, 114, 297–307. [Google Scholar] [CrossRef]
- Yu, X.; Rosman, J.H.; Hench, J.L. Interaction of Waves with Idealized High-Relief Bottom Roughness. J. Geophys. Res. Ocean. 2018, 123, 3038–3059. [Google Scholar] [CrossRef]
- Davies, A. On the interaction between surface waves and undulations on the seabed. J. Mar. Res. 1982, 40, 331–368. [Google Scholar]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Gao, J.; Shi, H.; Zang, J.; Liu, Y. Mechanism analysis on the mitigation of harbor resonance by periodic undulating topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Ni, Y.L.; Teng, B. Bragg resonant reflection of water waves by a Bragg breakwater with porous rectangular bars on a sloping permeable seabed. Ocean Eng. 2021, 235, 109333. [Google Scholar] [CrossRef]
- Chang, G.; Ruehl, K.; Jones, C.; Roberts, J.; Chartrand, C. Numerical modeling of the effects of wave energy converter characteristics on nearshore wave conditions. Renew. Energy 2016, 89, 636–648. [Google Scholar] [CrossRef]
- Meire, D.W.S.A.; Kondziolka, J.M.; Nepf, H.M. Interaction between neighboring vegetation patches: Impact on flow and deposition. Water Resour. Res. 2014, 50, 3809–3825. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Z.; Lei, J.; Nepf, H. Vortex Structure and Sediment Deposition in the Wake behind a Finite Patch of Model Submerged Vegetation. J. Hydraul. Eng. 2018, 144, 04017065. [Google Scholar] [CrossRef]







| Mean Wave | Storm Conditions | |||
|---|---|---|---|---|
| (m) | (s) | (s) | (s) | |
| Mean Value | 1.5 | 8 | 6 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghadam, H.; Ortiz, A.C. Modeling Morphodynamic Impacts and Optimization of Marine Hydrokinetic Arrays in Shallow Offshore Environments. Water 2023, 15, 3884. https://doi.org/10.3390/w15223884
Moghadam H, Ortiz AC. Modeling Morphodynamic Impacts and Optimization of Marine Hydrokinetic Arrays in Shallow Offshore Environments. Water. 2023; 15(22):3884. https://doi.org/10.3390/w15223884
Chicago/Turabian StyleMoghadam, Hanieh, and Alejandra C. Ortiz. 2023. "Modeling Morphodynamic Impacts and Optimization of Marine Hydrokinetic Arrays in Shallow Offshore Environments" Water 15, no. 22: 3884. https://doi.org/10.3390/w15223884
APA StyleMoghadam, H., & Ortiz, A. C. (2023). Modeling Morphodynamic Impacts and Optimization of Marine Hydrokinetic Arrays in Shallow Offshore Environments. Water, 15(22), 3884. https://doi.org/10.3390/w15223884






