1. Introduction
Geographically Isolated Wetlands (GIWs) represent a unique group of depressional wetland areas that are entirely surrounded by upland regions, such as isolated marshes or cypress domes [
1,
2,
3]. These wetlands play a critical role in regional hydrology by capturing upland runoff and allowing for groundwater recharge, as well as providing for biodiversity, and water quality functions [
4]. GIWs are classified as isolated due to their limited hydrologic direct connectivity to surface waterways, such as streams or rivers, and they are equally likely in upland areas or low-lying areas [
4]. The Southwest Florida region is a coastal karst plain environment characterized by sinkholes with a shallow water table and a permeable limestone aquifer, leading to the formation of a hydrologically dense network of various waterbodies [
4]. Historically, wetlands covered more than 50% of Florida’s interior area before large scale development started in the middle of the last century [
5]. Many of these wetlands were ditched and drained over the last century for mosquito control and land development [
6]. Currently, wetlands cover around 29% of Florida’s area, with GIWs constituting a significant portion of this percentage [
4].
GIWs display a distinct seasonal behavior reflecting the wet and dry season of the region. In W-C Florida, water levels in GIWs typically decrease early in the dry season (ending in late spring, often leaving surface dry beds for months with a lowest groundwater level typically in May [
4]). However, as the wet season (June–August) progresses, water levels rise, inundating the surface typically in July, and peaking by September. This is a regular annual cycle for these wetlands [
4]. Together with corresponding groundwater level fluctuation, this cycle causes landscape runoff and resulting streamflow to be susceptible to flooding conditions about the peak of hurricane season [
4]. Thus, GIWs serve a strong surface storage attenuation and groundwater recharge function in the hydrology of much of Florida and Gulf coastal plain environment [
4].
GIWs are mostly classified based on the dominant vegetation cover, such as marsh, flatwoods or cypress dome wetlands [
4,
7,
8,
9]. Numerous studies of GIWs have investigated various aspects, including evapotranspiration (ET), groundwater recharge, biomass growth, water quality, and generally interactions between groundwater and surface water, storage capacity, and biochemistry [
10,
11,
12,
13,
14,
15]. Despite these investigations, research on quantifying their hydroperiod storage characteristics and measured discharges from these wetlands remains scarce [
16].
There is high variability in (and opinions about) the connectivity of isolated wetlands to downstream waterbodies. McDonough et al. [
16] documented the connectivity between GIWs and downstream discharges. During the wet season or extreme events, such as hurricanes, GIWs often become interconnected as water levels rise to the invert elevation, initiating downstream discharge and greatly increasing the effect drainage area [
4]. Lee et al. [
12] investigated the hydrologic responses of water levels in GIWs and resulting discharges at downstream gauge stations based on seasonal timescales and specific rainfall event timescales. They found that the lowest GIW water levels and streamflow were observed during the dry season, and a strong correlation was found between GIW water levels and downstream streamflow. In the wet season, when there is no rainfall for several days, GIW water levels fall rapidly, serving a valuable groundwater recharge function to the deep karst aquifer, and streamflow support is comparatively slower [
12]. Other observations suggest that GIWs lose water during the dry season due primarily to ET, often being supported by shallow groundwater flow. Except for extreme water levels exceeding individual invert, GIWs provide little water to the downstream channels [
12,
16,
17]. The correlation between upstream water levels and downstream discharges might indicate a connection to streamflow but this is probably only coincidental. Statistical frequency analysis of the downstream and upstream water levels indicates marked differences [
18]. Lee et al. [
12] did not include the quantification of discharges from GIWs in their investigation, highlighting the need for further research to better understand the role of GIWs in regional hydrology and flood management.
The wetland hydroperiod, defined as the duration per year that a wetland has standing water on its surface [
19], is critical for understanding the wetland’s hydrological function and seasonal patterns [
20]. In W-C Florida, cypress dome wetlands, one type of GIWs, have hydroperiods ranging from 215 to 325 days per year and are fully inundated for 5 to 20 days per year [
19]. During full inundation, wetlands become hydrologically connected to other water bodies through surface overflow [
21]. Additionally, GIW water level records during the wet season display threshold behaviors, indicating that GIWs have reached maximum capacity and have begun to discharge to other water bodies [
22]. Consequently, GIWs are hydrologically connected to downstream water bodies for at least a few days, potentially causing highly augmented streamflow at recording gauge stations during the wet season.
Wetland normal pool is a subjective level indicator defined by the inflection point on the cypress buttresses, water stains, and root crown height [
10,
23]. In this manner, normal pool refers to generally the highest 5–10% of pool elevations, not the average pool elevations, a condition where corresponding GIWs exceed their invert elevation and begin to discharge [
15]. Thus, inverts for GIWs are often discernable when their water levels reach the normal-pool height.
Establishing the stage–storage–discharge relationship for GIWs, which defines the water volume and discharge for each depth, is vital for modeling the hydrology of coastal plain environments [
24]. Stage–area and stage–volume relationships are typically determined through detailed bathymetry maps or by using simple geometric models [
14]. Simple geometric models require minimal field data to characterize area–depth and volume–depth relationships [
14]. Nilsson et al. [
14] examined the relationship between area, volume, and depth for different water bodies to develop volume–depth and area–depth relationships using available GIS data. Their investigation resulted in a dimensionless volume model developed by normalizing by full volume and depth and a resultant exponent (shape parameter) to describe the log-linear storage behavior.
Most available stage–discharge data originate from stage gauging station data [
25]. However, other empirical methods, such as Manning’s equation, assume streamflow as uniform open-channel flow with a fixed slope [
26]. These methods require channel property measurements, such as cross-section area, slope, and roughness coefficient [
26,
27,
28]. Channel property measurements are typically not available online and can be expensive to obtain, particularly for environments with thousands of GIWs, which limits the use of this method.
The dimensionless rating curve is commonly employed to establish a regional stage–discharge relationship for ungauged locations [
29]. Mueses et al. [
30] developed a dimensionless rating model for alluvial systems by normalizing the discharge and depth using the 10% daily discharge exceedance (
Q10) and the corresponding depth (
d10), respectively. However, the invert elevations for GIWs are relatively high compared to alluvial systems, and GIWs begin to discharge at water levels exceeding (less frequent than) the 10th percentile [
15,
23]. As a result, there is a high probability that the
Q10 for GIWs is zero, and the discharge must be normalized using extremely low probabilities, such as the 100-year storm discharge.
Mueses et al. [
30] discharge rating was developed relative to the invert elevation, while the storage model of Nilsson et al. [
14] was developed relative to the lowest ground surface of the wetland. To connect the two models, it is essential to determine the invert depth (or elevation) for GIW [
24]. The invert depth represents the elevation at which a water body initiates connection to other water bodies through surface flow.
To address the challenges in developing stage–discharge relationships for GIWs, further research is needed to refine the dimensionless rating curve approach for these systems. Considering the unique hydrologic characteristics of GIWs, a modified normalization method could be developed, accounting for the specific hydrologic drivers and landscape features of these environments. By combining the refined dimensionless rating curve with the improved stage–storage relationship derived from the investigation of the shape parameter, as proposed by Nilsson et al. [
14], a more accurate and reliable hydrologic model for GIWs can be established. This will ultimately contribute to the better understanding and management of these critical ecosystems, and their interactions with the surrounding landscape and downstream waterbodies.
In coastal plain environments such as W-C Florida, GIWs significantly influence the surface and groundwater wet season/dry season hydrologic response. Thus, the stage–storage–discharge relationship of these isolated wetlands is crucial when a regional hydrological model is needed. The objective of this study is to devise a method for creating the stage–storage–discharge relationship for GIWs, which can then serve as an input for hydrological models using readily available data sources, such as GIS coverages. This will enable the development of more accurate and reliable hydrologic models for GIWs, ultimately improving our understanding and management of these critical ecosystems and their interactions with surrounding landscapes and downstream waterbodies.
2. Methodology
The stage–storage–discharge relationship proposed for GIWs consists of three components: soil storage, bowl storage, and discharge. Soil storage refers to vadose zone storage, which extends from the groundwater ET extinction depth (the sum of root zone depth and capillary zone depth [
31]) to the dry bed of a wetland. Each component plays a significant role in water retention, groundwater recharge and wetland ET function in extended dry periods and the ultimate transition to discharge in the wet season. When water levels rise above the ground surface, wetlands exhibit bowl storage until reaching the upper limit, thereby providing flood attenuation and temporary surface water storage. Discharge occurs when water levels reach the invert elevation, regulating outflow and maintaining wetland water balance.
These three components can be estimated using the model of Nilsson et al. [
14], the model of Mueses et al. [
30], an integrated soil-storage model, and an invert relationship. The model of Mueses et al. [
30] characterizes the stage–discharge relationship, the model of Nilsson et al. [
14] describes bowl storage, the soil-storage model represents vadose zone storage during the dry season, and the invert relation couples the different stage references. Since the model of Mueses et al. [
30] defines stage–discharge behavior above the invert elevation, developing a technique to estimate the GIW invert elevation is key. Determining ground and top elevations of GIWs from GIS then becomes essential for estimating bowl storage and soil storage, which contributes to the overall understanding of wetland hydrology.
2.1. GIS Analyses
This study aimed to develop rating curve behavior for GIWs using commonly available GIS data, providing a cost-effective and efficient approach for hydrologic model analysis. It examined 35 unaltered GIWs with surveyed bed and invert elevations, as well as water level records, to understand GIW discharge and storage limitations and devise a method for determining rating characteristics. Also, the Southwest Florida Water Management District (SWFWMD) developed Advanced Interconnected Channel and Pond Routing (AdICPR) [
32] models for numerous watersheds in W-C Florida, which were employed to estimate GIW discharge and storage behaviors, (primarily during design flood conditions) providing additional data for this study.
ArcGIS was utilized to create 4.5 m (15 ft) buffers surrounding the 35 GIWs to analyze the surrounding topography and its influence on wetland hydrology. An investigation was conducted on buffers of varying distances to determine the optimal size; larger buffers began to encompass surrounding uplands and adjacent wetlands, while smaller ones did not adequately incorporate the resolution of the data and were affected by cover and digitization errors, leading to significant variance in the dataset. The Zonal Statistics as Table tool in ArcGIS, commonly employed for analyzing and summarizing spatial data, was employed to calculate statistics for the 4.5 m (15 ft) buffer using DEMs with 1.5 m horizontal resolution and 0.1 m > vertical accuracy (5 ft horizontal resolution, 0.32 ft > vertical accuracy). The input for this tool consisted of the DEMs and the 4.5 m (15 ft) buffer, while the output was a table displaying statistics for each buffer. The Zonal statistics function computed the mean, maximum, minimum, and various percentiles of exceedance for elevations within each zone. Subsequently, the surveyed invert elevations were compared to the mean from the Zonal Statistics results and linearly regressed, providing a reliable method for estimating (to 0.1 m) invert elevations of GIWs in the absence of field data.
The ground elevation of the GIW is required for estimating bowl storage in the model of Nilsson et al. [
14] and determining soil-storage model limitations. By overlaying GIS coverage of surveyed GIWs with the DEM, the minimum elevation within these GIWs can be estimated using the Zonal Statistics function. These data are then linearly regressed to assess the potential uncertainty of using minimum elevation as a proxy for bed elevation.
The top elevation of a wetland represents the maximum stage a wetland can achieve when fully submerged to the GIS area for the wetland (full depth for full wetland areal extent) and is an input for the model of Nilsson et al. [
14]. SWFWMD maintains GIS coverages of GIWs [
33] and has developed well-calibrated AdICPR flood models for many watersheds in the region. The stage–area relationship of the inundated region is input for each basin in the AdICPR models.
Overlaying GIW coverage onto the AdICPR model datasets allowed for the extraction of the stage–area relationship for specific basins containing a single GIW. The top elevations for 64 GIWs were then related to the 10th-percentile exceedance elevation from the Zonal Statistics tool results of the 4.5 m (15 ft) buffer and linearly regressed, providing a reliable method for estimating top elevations of GIWs in the absence of field data.
Studying the probabilities of discharging and the presence of visible bowl storage at one, ten, fifty, and ninety percentiles of daily exceedance water levels provides valuable insight into the hydrological behavior of GIWs under varying conditions. The study considered 35 natural, unaltered GIWs monitored twice a month by SWFWMD, with an average data length of 30 years. Drainage areas and cumulative wetland areas of GIWs were estimated from pre-developed AdICPR models and GIS coverages, and then related to the frequency of discharge to determine if these watershed characteristics influenced discharge behavior. The finding that watershed characteristics had no impact on (correlation to) discharge frequency highlights the need for further research into factors influencing the probability of discharge.
SWFWMD developed AdICPR models to estimate basin discharges during severe weather events of varying return periods, for flood risk assessment. Using GIS analysis to identify GIWs within these AdICPR models, peak discharges and stages during extreme rainfall events (100, 50, 25, 10, 5, and 2.33-year storms) were derived, enhancing the understanding of GIW response to extreme events.
2.2. Modified Non-Dimensional Discharge
According to the statistical analysis for monitored GIWs, these wetlands began discharging at or above the 10th-percentile daily exceedance water levels. As a result, a modified version of the model of Mueses et al. [
30] was developed. This modification involved normalizing discharges by the discharge resulting from the 100-year storm (
Q100), and normalizing depths by the depth of discharge resulting from the same storm (
d100). This produced a generalized, dimensionless rating model that can be applied to a broader range of GIWs:
where
Q is the model discharges (L
3/T),
is the discharge resulting from the 100-year storm (L
3/T),
d is the model flow depths (L),
is the depth of discharge resulting from the same 100-year storm (L), and
m is the exponent that describes the rating curve behavior.
AdICPR models were developed using a broad-crested weir assumption for the outlet, calculating the cross-sectional area of flow by integrating the cross-section profile derived from high-resolution DEM. Since cross-sectional areas of discharges were not included in AdICPR results, the equation was rearranged to solve for the cross-sectional area of Q100 (A100).
The hydraulic width of
Q100 (
W100) was determined by dividing the
A100 by
d100. The outlet shape was assumed to be triangular, based on an evaluation of cross-sectional profiles for numerous GIWs and verification from SWFWMD staff who surveyed the inverts. The side slope of the outlets (
Ss) was calculated by dividing
d100 by
W100.
where
Q100 and
d100 are previously defined,
is the weir coefficient from AdICPR models,
A100 is the cross-sectional area of
Q100 (L
2),
W100 is the hydraulic width of
Q100 (L), and
Ss is the side slope of the outlet (L/L).
To apply the dimensionless rating curve, methods for estimating Q100 and d100 are required. A linear regression model was developed to estimate Q100 using the drainage area (AD) and cumulative wetland area (AW) as predictor variables, considering the strong correlation to flow rate. Furthermore, to estimate d100, another linear regression model was created for A100, correlating A100 with AD and AW. By employing the median Ss and A100, d100 can be estimated, which is needed for developing the flow characteristics at the outlet.
2.3. Non-Dimensional Storage
Nilsson et al. [
14] developed a simple power model for estimating the bowl storage behavior of various waterbodies, including natural and man-made reservoirs, lakes, and wetlands. However, uncertainty was noted regarding the shape parameter (
n), which dictates the waterbody bowl storage behavior and has a significant impact on flood attenuation and water balance. To address this uncertainty, again the surveyed wetlands and AdICPR models were used to estimate
n for the 64 GIWs, covering a wide range of sizes, shapes, and geographical locations. Each basin within the AdICPR models had a stage–area relationship based on highly resolved DEM, and these relationships were utilized to estimate
n. The stage–area relationship was converted to a stage–volume using simple GIS average-area method, which estimates volume by averaging the area extents between two stages and then multiplying by the length between these stages, and fitted in the manner of [
14] to determine the GIW
n:
where
(L
3) is the wetland volume corresponding to pool depth h (L),
A0 (L
2) is the full wetland area,
h0 (L) is maximum wetland depth, and
n is a dimensionless shape parameter describing the geometric (and log-linear) relationship between volume and depth.
Soil storage represents the available storage in soil porosity (fillable space) and plays a critical role in regulating water availability and hydrological processes in wetlands. Soil characteristics, such as retention and effective porosity, and vegetation types in GIWs determine the depth of soil storage. The limit of available water for ET is the extinction depth, which comprises the capillary zone depth and root zone depth [
31]. Soil storage provides available water for plant ET uptake and gravity drainage with variable soil moisture content between the wilting point and saturation. While the interaction between the capillary zone and the root zone yields a complex relationship for extinction depth in natural settings, especially in GIWs with unique soils and hard-to-define root zones, employing a linear relationship based on a calibratable extinction depth offers valuable simplicity. Since the wetlands normally never go to extinction (or they since cease to be a viable wetland), this approach is particularly beneficial for describing dry-season hydroperiod storage (water table) behavior and reasonably describes the observed water level behavior in these systems [
34].
SMaxSoil is the full soil storage (L3), AW is the wetland area (L2), is the extinction depth, which is the sum of the intermediate capillary zone depth and root zone depth (L), is the saturation soil moisture content (L/L), and is the wilting-point soil moisture content, which is the soil moisture content at which wetland vegetation no longer extracts water from soil (L/L).
The model underwent verification by reproducing both the depth–storage rating and depth–discharge rating, and its outcomes were compared to the observed results from the AdICPR model. Using the proposed method to estimate wetland depth, combined with n and the GIS-derived wetland area, the bowl-storage GIWs were determined. These results were subsequently compared to those from the calibrated AdICPR model. Additionally, by employing the refined method from Mueses et al. [
30], rating curves were formulated using
AD,
AW, the average
m exponent, and
Ss. These curves were then compared against the stage–discharge data derived from AdICPR models for 100-, 50-, 25-, 10-, 5-, and 2.33-year storm events.
2.4. Aggregated GIWs
When constructing regional hydrologic models for extensive areal domains, such as those in W-C Florida, encompassing hundreds of watersheds each with hundreds of GIWs, addressing the hydrology of each individual GIW is impractical. The more feasible approach involves developing stage–storage–discharge relationships that capture the combined behavior (and average stage) of aggregated GIWs within each watershed, factoring in the individual characteristics of the GIWs under examination. To test this concept, assuming the 35 GIWs belong to a single watershed, the stage–storage–discharge relationship was developed for the aggregated GIW to assess the combined approach. The representative invert depth was estimated by calculating the area-weighted average of invert depths for all GIWs. The representative storage for each GIW is based on one depth-to-full pool and the combined wetland area. The same applies to the soil storage depth to groundwater of the GIWs. Furthermore, with the assistance of GIS coverages that provide information on vegetation and soil types, the representative extinction depth and the saturation and wilting points of soil moisture content for all GIWs can be estimated using an area-weighted-average method.
Lastly, by employing the model proposed by Mueses et al. [
30], the
Q100 linear regression model uses
AD and
Aw as independent variables, factoring in the representative average
d100 from water level records, area-weighted average invert, and average
m exponent, and a representative stage–discharge relationship for all GIWs can be established above the representative invert depth. Furthermore, using the model of Nilsson et al. [
14], taking into account the total area of GIWs, area-weighted average wetland depth, area-weighted or overall
n, a representative stage–storage relationship for bowl storage can be derived. By applying the soil storage model along with the total GIW area, area-weighted average extinction depth, and area-weighted average saturation and wilting point, a representative stage–storage relationship for soil storage can be devised.
3. Results and Discussion
3.1. DEM and Stage Uncertainty
As stated previously, the invert elevations of GIWs are relatively high, which impacts surface runoff connectivity to downstream areas. However, when the surveyed invert elevation of these wetlands was compared to zonal statistic results, the analysis revealed that the mean of a 4.5 m (15 ft) buffer provided the best representation of the invert elevation. This was used moving forward with defining the wetland invert elevations.
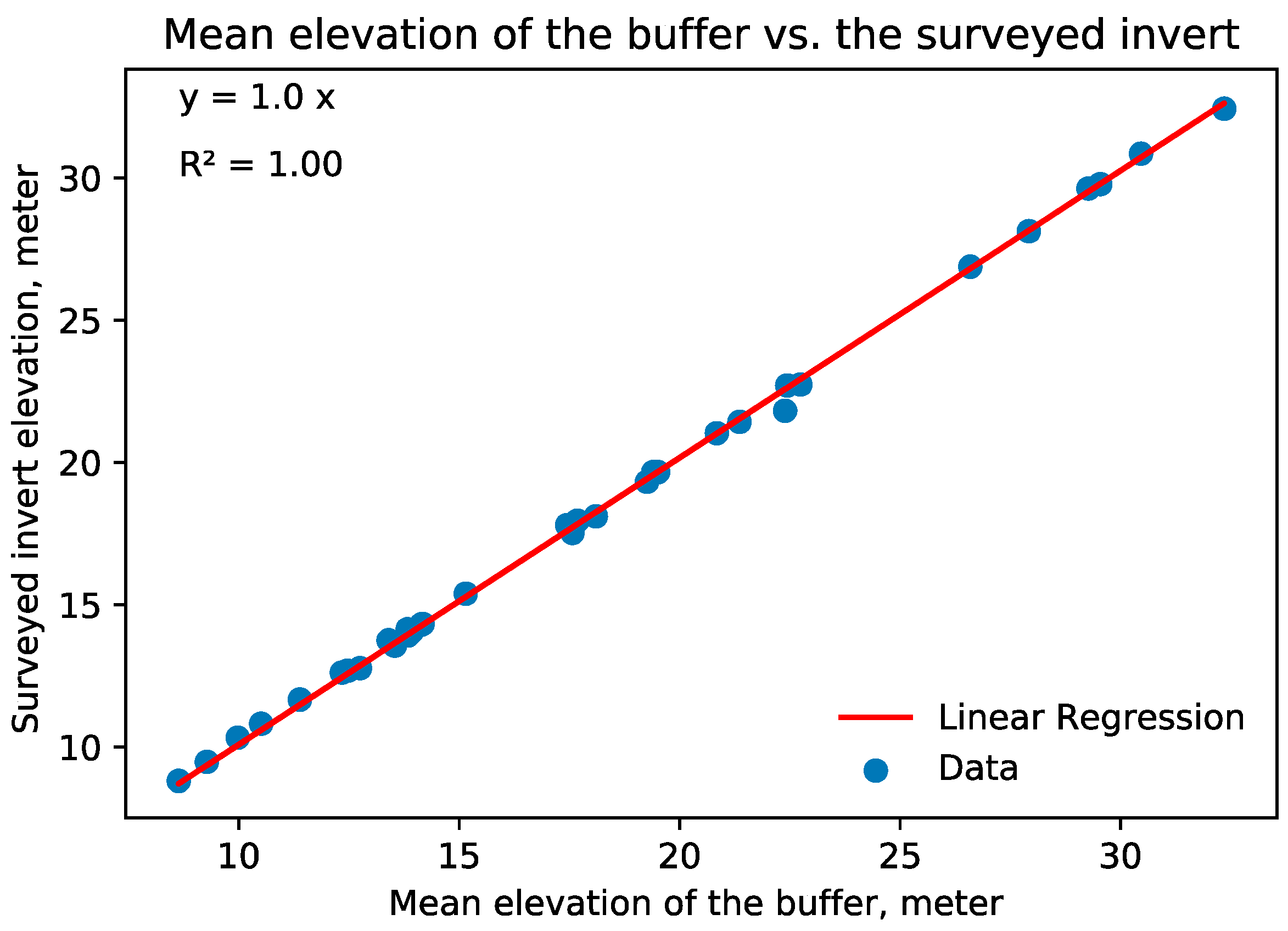
When the mean elevation of the wetland buffer was linearly regressed, the slope of the model was 1 m/1 m (45
, with a zero y-intercept and an R
2 of 1.0 (
Figure 1). This high R² value indicates an excellent fit between the model and the observed data. The root-mean-squared error, maximum and minimum errors, standard error, and standard deviation were 0.1 m (0.32 ft), 0.73 m (2.4 ft), −0.23 m (−0.77 ft), 0.03 m (0.1 ft), and 0.17 m (0.57 ft), respectively. These values provide an understanding of the variability within the model and the level of accuracy when estimating the invert elevation.
Although the minimum elevation of the 4.5 m (15 ft) buffer was intended to represent the invert elevation of natural GIWs, it deviated significantly from the observed invert elevation of the surveyed data. This discrepancy can be attributed to a combination of factors, including the resolution of the DEM, which provided a mean elevation value for every 2.32 m2 (25 ft2), and digitization issues in the GIW GIS coverages. Thus, the limitations of the DEM resolution likely led to inaccuracies in the representation of the invert as the lowest elevation within the buffer and, thus, the mean elevation is the best result. Meanwhile, digitization issues could arise from inaccuracies in the GIS data, problems with LiDAR, or misinterpretation of the terrain features. To improve the accuracy of the invert elevation estimation, future studies could consider using higher-resolution DEMs and refining GIS data.
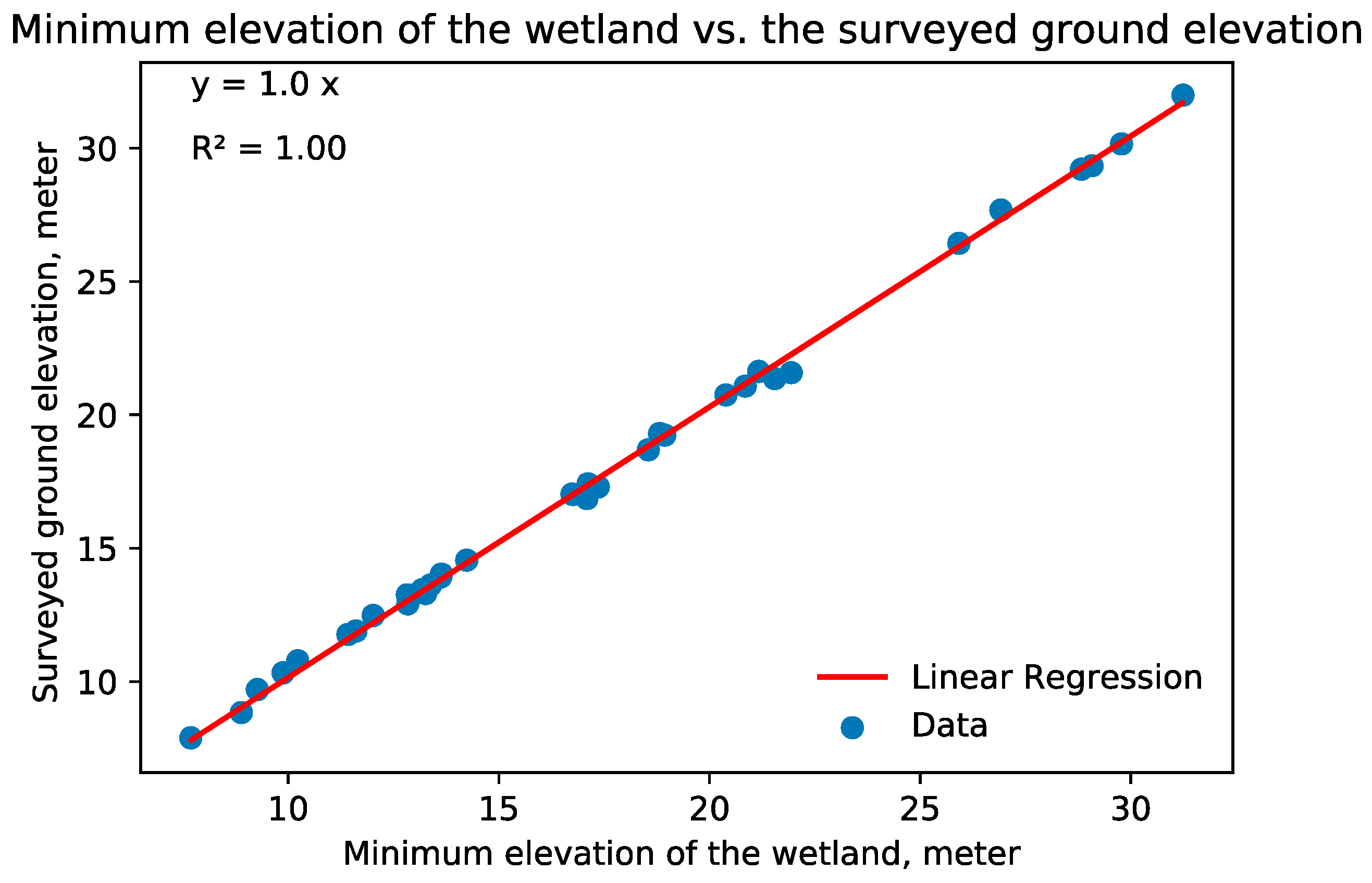
The minimum elevations within the GIW and the surveyed bottom ground elevation were linearly regressed, also producing a model with a 1 m/1 m slope, a zero y-intercept, and an R
2 of 1 (
Figure 2). The results indicated that the minimum elevation from the DEMs provided a good representation of the base ground elevation. The root-mean-squared error, maximum and minimum errors, standard error, and standard deviation were 0.18 m (0.61 ft), 0.66 m (2.2 ft), −0.4 m (−1.34 ft), 0.39 m (0.13 ft), and 0.24 m (0.79 ft), respectively. In a study conducted by Lee and Fouad [
35] for Tampa Bay Water to assess the accuracy of LiDAR elevations of wetland land surfaces, the results demonstrated that LiDAR could effectively represent the land-surface elevations of wetlands, with an intercept of 0.4 m (1.38 ft). This finding supports the notion that LiDAR-derived DEMs can be used as reliable data sources for wetland elevations to be used in the approach of Nilsson et al. [
14].
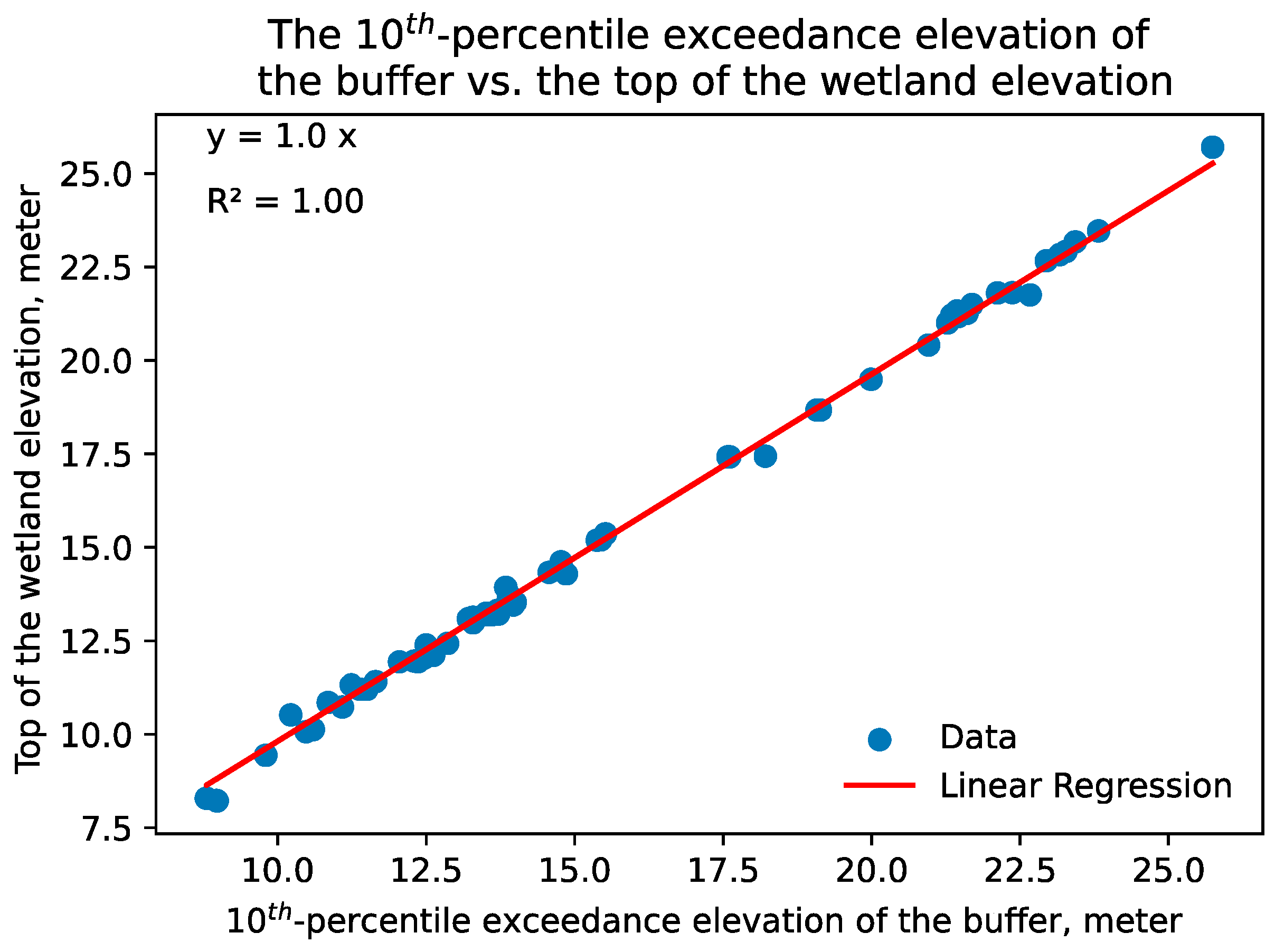
To estimate the full depth of a wetland for bowl-storage calculations, both the top and land surface elevations are required. The top of the GIWs was derived from surveyed data used in AdICPR model applications, then compared to various percentiles of exceedance elevations of the 4.5 m (15 ft) buffers. The 10th-percentile exceedance elevations and the calculated top of the wetland elevations were linearly regressed, producing a model with a 1 m/1 m slope, a zero y-intercept, and an R
2 of 1 (
Figure 3). The root-mean-squared error, maximum and minimum errors, standard error, and standard deviation were 0.21 m (0.69 ft), 1.14 m (3.79 ft), −0.6 m (−2 ft), 0.03 m (0.1 ft), and 0.25 m (0.83 ft), respectively. These findings suggest that the 10th-percentile exceedance elevation can be reliably used to estimate the upper morphological boundary (top-of-bank) of GIWs. Then, these top-of-bank values can be used for wetland depth and subsequent bowl storage calculations.
Considering the high R² value and the comparably low errors in the GIS analysis, it can be concluded that a 4.5 m (15 ft) buffer of DEMs with 1.5 m horizontal resolution and vertical accuracy < 0.1 m can be reliably used for estimating the top and bottom of the wetland, and invert elevation within GIWs, at least in the W-C Florida dataset investigated. Moreover, the minimum elevation observed in the wetland, obtained from the 1.5 m (5 feet) DEM, can serve as a reliable indicator for estimating the base ground elevation of GIWs. In general, the accuracy of the elevations is within 0.16 m (0.52 ft). Further investigation into the use of higher-resolution DEMs and the incorporation of additional remote sensing data sources could lead to even greater accuracy in predicting GIW elevations and, ultimately, more effective hydrological modeling.
3.2. Frequency Analysis Relative to Land Surface and Invert
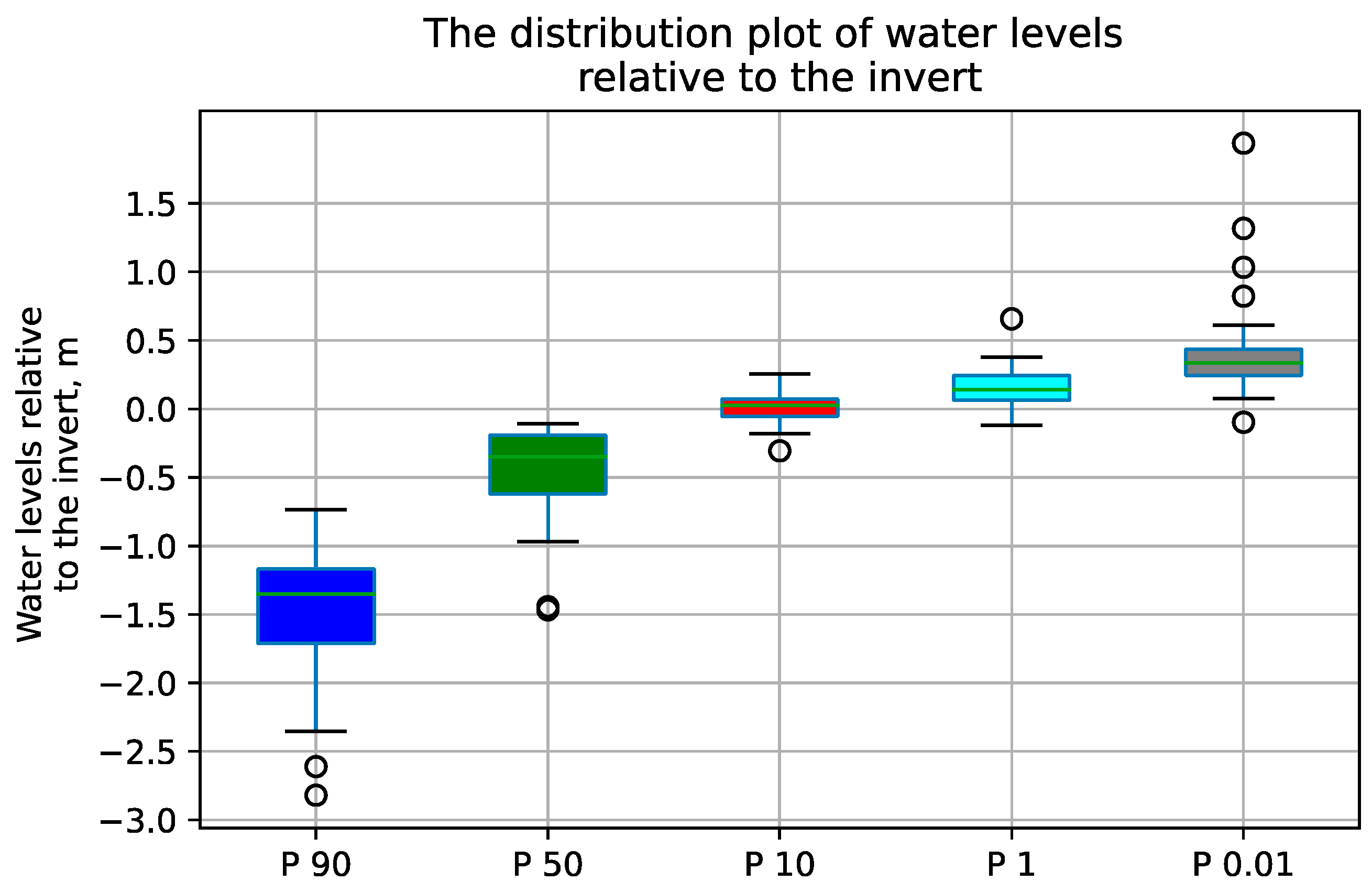
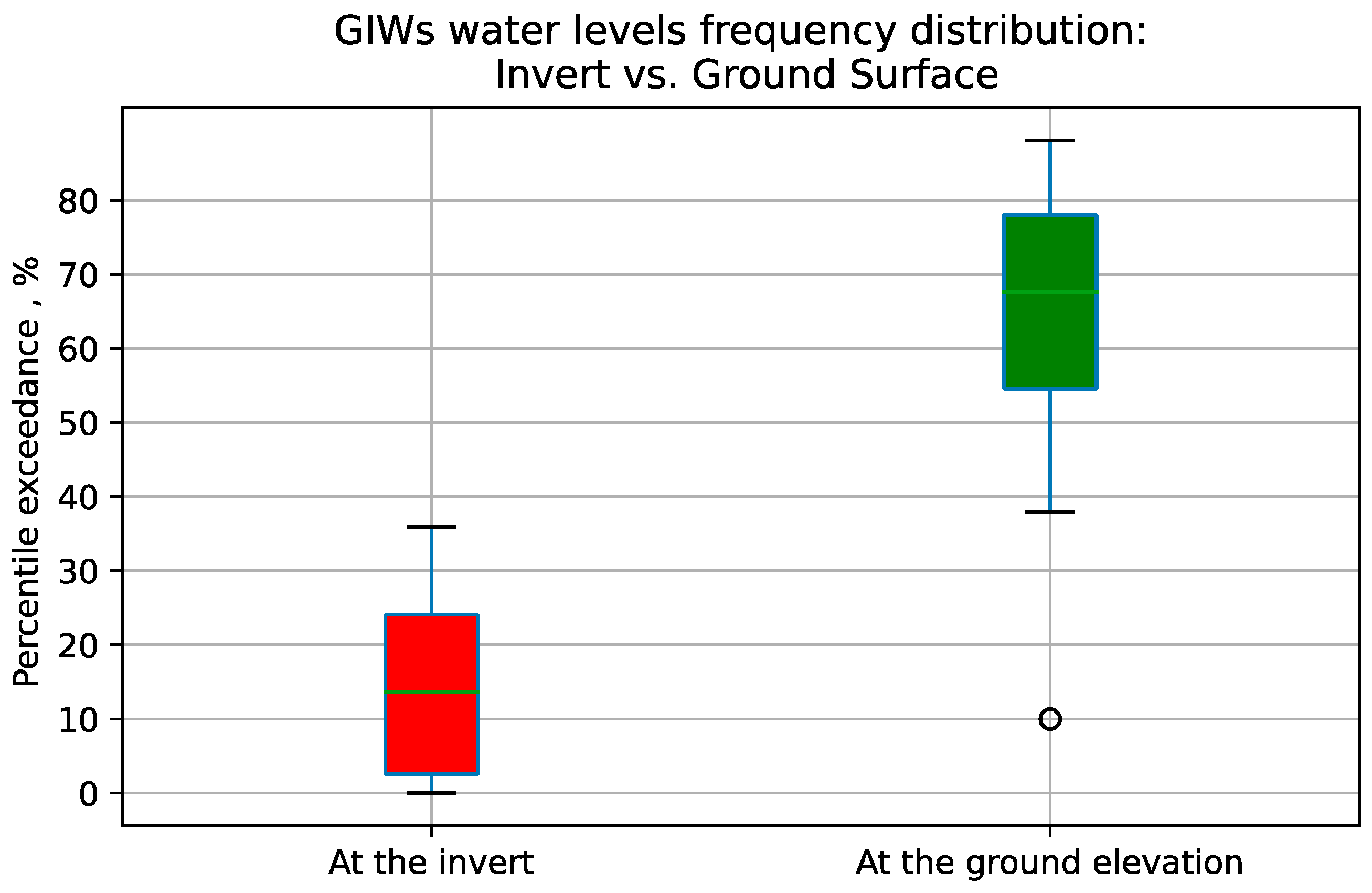
As mentioned earlier, the GIWs exhibit relatively high invert elevations, which can limit surface connectivity. The results of studying the discharge probability for the 35 monitored GIWs revealed that during the 10th- and 1st-percentile, daily exceedance water levels relative to the inverts (
d10 and
d1), respectively, and GIWs had discharge probabilities of 0.6 and 0.94, respectively. However, during the 50th-percentile daily exceedance water levels, relative to the invert (
d50), these GIWs exhibited statistically 0 probability of discharging (
Figure 4). Furthermore, the arithmetic mean, standard deviation, and maximum, and minimum discharging depths above the invert for the
d10 were 0.01 m (0.03 ft), 0.11 m (0.35 ft), 0.25 m (0.83 ft), and −0.3 m (−1 ft), respectively. The relatively small standard deviation of 0.11 m for the
d10 water levels underscores the close alignment between the average water level and the invert. This narrow spread of data around the mean of 0.01 m suggests that during the events, which occur approximately 10% of the time, the water levels remain very close to the invert (
Figure 4). Conversely, the arithmetic mean, standard deviation, maximum, and minimum discharge depths above the invert for the
d1 were 0.15 m (0.5 ft), 0.14 m (0.46 ft), 0.65 m (2.16 ft), and −0.12 m (−0.4 ft), respectively. With a standard deviation of 0.14 m, the
d1 demonstrates a greater dispersion of water levels relative to the invert than observed for the
d10. Furthermore, the arithmetic mean of 0.15 m indicates that during this less frequent event, the water levels typically remain higher than the invert by approximately 15 cm, further distinguishing these conditions from the more frequent ones captured by the
d10 (
Figure 4).
To further investigate the behavior of GIWs during extreme events, the 0.01-percentile daily exceedance was evaluated relative to the invert (
d0.01). The discharge probability was 0.97, and the arithmetic mean, standard deviation, maximum, and minimum of
d0.01 were 0.43 m (1.4 ft), 0.37 m (1.2 ft), 1.95 m (6.4 ft), and −0.09 m (−0.3 ft), respectively. These results indicate that, even during extreme events, some GIWs might lack surface connectivity (
Figure 4).
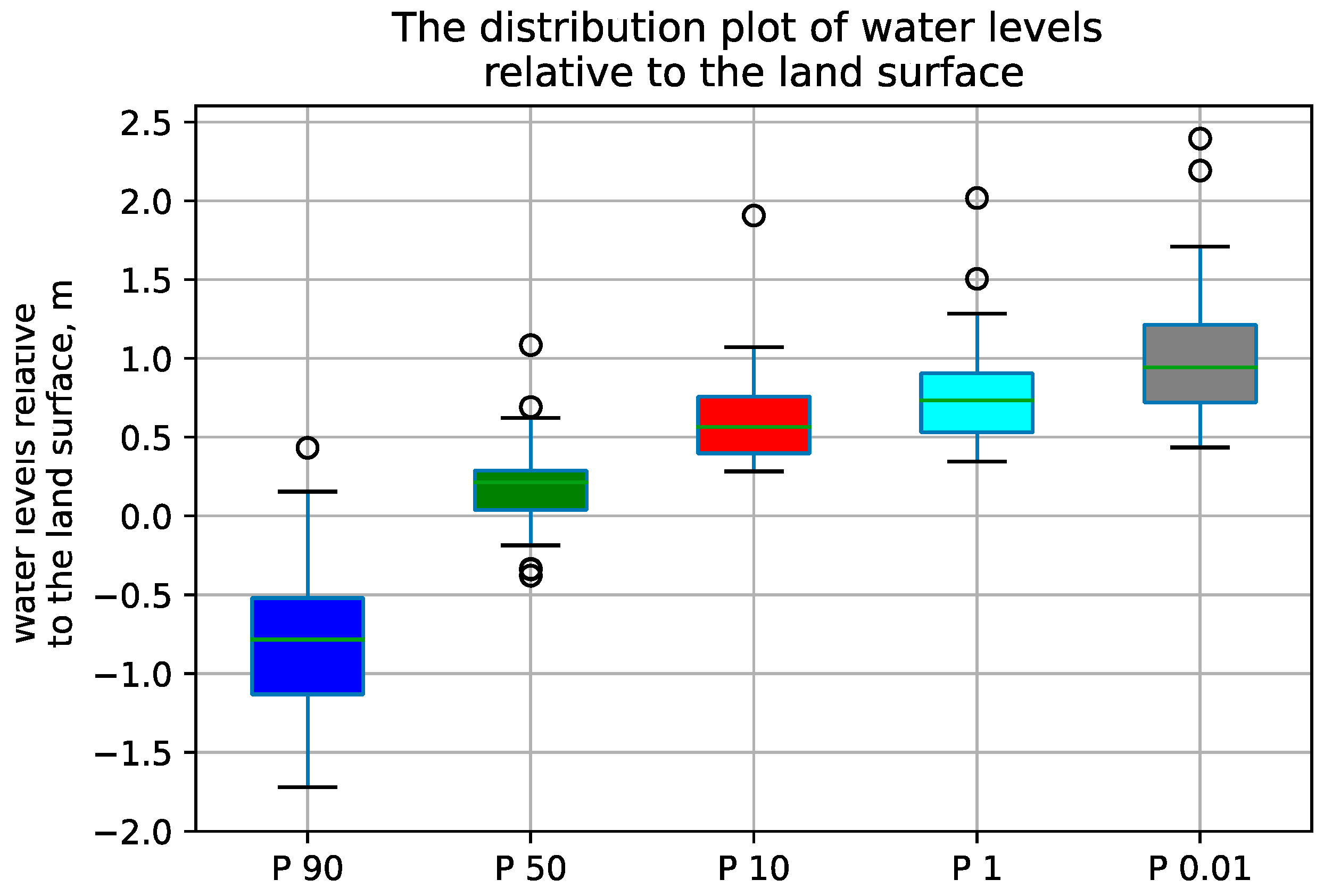
Analysis of water levels in GIWs relative to ground elevation shows a complex distribution across various percentile daily exceedance levels. These percentiles, specifically the 90th, 50th, 10th, 1st, and 0.01, offer distinctive insights into water level behavior in GIWs.
At the 90th-percentile exceedance (low levels), the average water level was −0.856 m (below land surface) with a standard deviation of 0.433 m. This indicates that under typical conditions, water levels in GIWs are well below the ground elevation and dependent on groundwater, demonstrating a moderate degree of variability (
Figure 5). The range from a maximum of 0.15 m to a minimum of −1.72 m further underscores that water levels typically fall well above the extinction depth for these GIWs, generally estimated to be around 2 m via soil moisture monitoring [
31]. As a consequence, it is evident that GIWs consistently facilitate groundwater ET for a substantial duration, amounting to a minimum of 328 days annually.
At the 50th-percentile daily exceedance, water levels were generally visible in the wetland with an average depth of approximately 0.17 m above ground elevation and a standard deviation of 0.288 m, indicating less variability than the 90th percentile. The range for this percentile suggests that under median conditions, GIWs can support an active aquatic ecosystem and open-water ET with typically above-ground water levels (
Figure 5).
The 10th-, 1st-, and 0.01-percentile (daily stage) exceedance, representing less-frequent water levels, showed averages of 0.63 m, 0.79 m, and 1.04 m, respectively, with corresponding standard deviations of 0.32 m, 0.35 m, and 0.44 m. These deviations suggest a high degree of variability during 0.01-percentile daily exceedance, which is not unexpected, as this percentile represents extreme water levels for GIWs (
Figure 5).
On average, for 14.8% of the year (54 days), the water levels of GIWs were at or above the invert, and for 65.1% of the year (238 days), the water levels of GIWs were at or below the ground surface (
Figure 6). These findings highlight the typical hydroperiod behavior of GIWs in W-C Florida, as emphasized in the study by Cameron et al. [
19].
The results above indicated that GIWs begin to establish downstream connectivity around the 10th-percentile daily exceedance water levels. Southwest Florida Water Management District (SWFWMD) monitors water levels in hundreds of wetlands, including GIWs. However, most of these wetlands do not have surveyed outlets. Establishing a relationship between water levels and invert elevations for GIWs would be useful for understanding and adequately incorporating their discharge behavior in hydrologic prediction models.
The 10th-percentile daily exceedance water levels and invert elevations were linearly regressed, resulting in a slope of 1 m/1 m with a zero y-intercept, a standard error of 0.11 m (0.36 ft), and an R
2 of 0.9997 (
Figure 7). This relationship can be helpful in estimating the outlet elevation of GIWs using only water level records, without the inconvenience of locating and surveying the outlet.
The characteristics of watersheds were examined to assess the influence on the frequency of GIW discharge, with a particular focus on factors such as drainage area and cumulative wetland area. A multi-variable linear regression model was employed to predict variables for percentile exceedance of invert elevation, considering the potential role of these factors in modulating the discharge frequency.
The analysis involved evaluating the p-values and R2 values to determine the significance of the relationships. The p-values for the drainage area (AD) (km2) and cumulative wetland area (AW) (km2) were 0.24 and 0.99, respectively (both > 0.05), indicating that these variables are statistically insignificant and, thus, do not have a substantial impact on the frequency of GIW discharge. Moreover, the R² value of 0.22 further implies a weak explanatory relationship, suggesting that other factors not examined in this study may play a more crucial role in determining the discharge frequency. Given these findings, future research may be beneficial examining additional watershed characteristics or exploring the potential interactions between various factors to better understand and predict the frequency of GIWs discharges.
3.3. Q100 and d100 Estimation
To establish an accurate stage–discharge relationship for GIWs using the modified approach by Mueses et al. [
30], essential parameters such as the discharge resulting from the 100-year storm
(Q100), the stage above the invert resulting from the 100-year storm
(d100), and the discharge exponent of Mueses et al. [
30] (
m) must be determined. To achieve this, a multi-variable linear regression model was employed. The application incorporated
AD and
AW as independent variables. The data were divided randomly into a training dataset (80%) and test dataset (20%). The training dataset was then used to predict
Q100 and
A100 values for GIWs, enabling the assessment of their respective relationships. Finally, the test dataset was evaluated against the developed models.
The results from the
Q100 and
A100 linear regression models revealed that the
AD exhibits a positive correlation with
Q100 and
A100, whereas the
AW demonstrates a negative correlation. This finding indicates that as the wetland area increases, the GIWs experience greater attenuation of flow, subsequently reducing both
Q100 and
A100 values (
Table 1). This insight is somewhat intuitive but nonetheless valuable for understanding the role of wetlands in flood mitigation, modeling, and water resource management.
Moreover, the statistical analysis showed the
p-values for
AD and
AW concerning
Q100 to be 2.26 × 10
−6 and 0.0011, respectively, indicating that both variables are statistically significant (
Table 1). The training and test R
2 values for this model were 0.76 and 0.82, respectively, signifying a moderately strong relationship between the independent variables and
Q100. Similarly, the
p-values for
AD and
AW in relation to
A100 were found to be 8.28 × 10
−7 and 0.0018, respectively, highlighting that these variables are also statistically significant. The training and test R² values for this model were 0.72 and 0.77, respectively, suggesting a moderately strong relationship as well; see
Table 1.
The outlet side slope, Ss, of the GIW, assuming a triangular cross-section, was used to define the relationship between the hydraulic width (W100) and d100. A comprehensive statistical analysis was conducted on Ss, yielding the following results: an average value of 0.022 m/m, a median value of 0.011, a maximum value of 0.19 m/m, a minimum value of 0.00025 m/m, and a standard deviation of 0.036 m/m. By employing the A100 value and the average Ss, it is possible to calculate the d100. This information allows for a more robust or alternative parameterization of the stage–discharge relationship, as well as the influence of the outlet side slope Ss on the cross section of the GIW outlet flow.
Since the average and median of Ss vary from each other and the average is impacted by outliers, the recommended Ss for W-C Florida is the median, as a basis for stage–discharge-relationship calibration. This approach enables a more accurate representation of the local conditions and provides an effective calibration knob for hydrological models. Using this information in modeling efforts will likely enhance the accuracy of predictions and support the development of more effective water-resource management in the region.
3.4. Mueses et al. [30], Discharge Exponent, m
The Mueses discharge exponent, m, defines the relationship between normalized discharge and normalized depth. To derive the m exponent, discharge and depths from various storm events (100, 50, 25, 10, 5, and 2.33 years) were normalized by Q100, and d100. Subsequently, the logarithm of the normalized values was calculated, and the slope of the best-fitting line through the data was used to find the m exponent. A statistical analysis was performed on the resultant m exponent, yielding a mean value of 2.45, a median of 2.45, a maximum of 4.11, a minimum of 0.6, a standard deviation of 0.65, and a standard error of 0.15. Given these results, it is recommended that the average m exponent be used to develop the stage–discharge relationship for GIWs in hydrological models in this area and perhaps in similar areas elsewhere. However, similar analysis could be used in other areas to glean a more representative value for m locally, tailored to the specific conditions of the region.
The GIW water level findings from the wetlands studied indicate that during extreme events, such as a 100-year storm event, GIWs contribute significantly to downstream flow. However, during more frequent events, such as 10th- and 1st-percentiles daily exceedance water levels, GIWs may or may not discharge, and their discharge rate is relatively small compared to that of alluvial wetlands for the same drainage area. This highlights the variable and unique hydrological behavior and significance of predicting GIW water levels and discharge in watershed modeling and water management.
3.5. Nilsson et al. [14], Shape Parameter, n
The storage or shape parameter of Nilsson et al. [
14],
n, represents the relationship between water depth and storage capacity in the waterbody. It serves as a simple quantitative measure to describe the geometric configuration, ultimately affecting the accumulation of wetland storage capacity. When
n is 1, the waterbody exhibits vertical (seawall) side slopes and a flat bottom, the simplest storage configuration requiring only the multiplication of the area by the depth. An
n of 2 generates a rotated triangular (conic) shape. Other values result in convex (
n > 2) and concave (1 <
n < 2) storage configurations with a typical 2.5 shape coefficient, referred to previously as roughly resembling the bottom of a margarita glass shape [
14].
This study examined 64 GIWs with surveyed bathymetry and calculated respective n to better understand the variability and best representation for these types of wetlands for cases where survey bathymetric data does not exist.
A comprehensive statistical analysis of surveyed GIWs, revealed a mean
n of 2.47, with a standard deviation of 0.93, a maximum 4.6, and a minimum of 1.12. Interestingly, the average
n of these 64 GIWs was slightly higher than the average reported by Nilsson et al. [
14] (2.3), perhaps an artifact of additional data and additional wetlands studied. As indicated above, an
n of 2.47 results in a GIW convex shape, with side slopes that are steepest near at the bottom and flatten towards the top. Results indicate using an
n value of 2.47 for GIWs to develop the stage–storage relationship for hydrological models in W-C Florida and potentially other environments will accurately represent the storage behavior from minimum to maximum water levels to generally within 0.1 m (<0.3 ft). This value accounts for the geometric configuration of waterbodies in this region but Nilsson et al. [
14] indicated that it worked equally well in wetlands in other settings. However, local site-specific
n values may be useful in calibrating particular model applications in other settings.
3.6. Soil Storage Model
Application of the soil storage model to estimate the available storage when the wetlands exhibit below ground water levels but are still supporting ET, infiltration, and groundwater exchange was not thoroughly tested for this study but has proven effective in representing wetland groundwater levels in other model applications [
34]. Since the GIWs experience prolonged (>100 days) dry bed conditions, representing the moisture dynamics and ET availability for this period is particularly relevant for understanding and modeling the hydrological processes in these periods [
31].
3.7. Testing Individual GIW Storage and Discharge Behavior
Employing the proposed method to estimate wetland depth, the average
n, together with the GIS-derived wetland area, the bowl storages of 64 GIWs were assessed and compared to the results obtained from the calibrated AdICPR model (
Figure 8). The calculated root-mean-square error was 8202 m
3 (6.6 acre-feet), accompanied by a mean absolute error of 4902 m
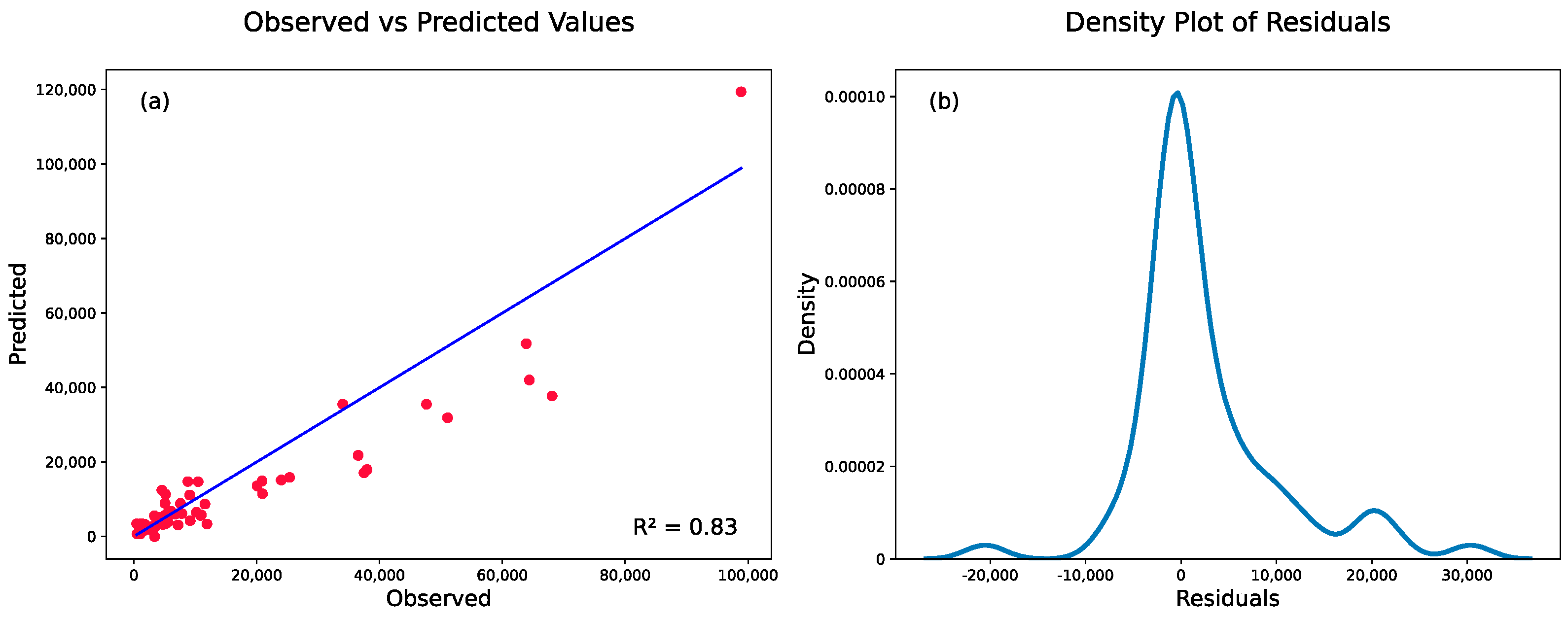
3 (3.97 acre-feet), and a mean absolute relative error of 55%. This methodology led to overpredictions of storage capacity in 48.4% of the instances, while underpredictions were observed in the remaining 51.6% of cases. Despite these discrepancies, the method shows promise for potential use in hydrological models with sufficient GIWs.
Figure 8a illustrates the model’s predictive performance in estimating storages using n = 2.47, employing a linear regression approach for comparison against observed data from AdICPR. This figure demonstrates the close alignment between observed values and model predictions. In
Figure 8b, the distribution of residuals is presented, providing insight into the model performance and (minimally observed) bias. The distribution of residuals further supports the accuracy of the model’s estimations.
Utilizing the modified version of Mueses et al. [
30], rating curves were developed for 22 GIWs and compared to the discharge and stage data obtained from AdICPR models for storm events with recurrence intervals of 100, 50, 25, 10, 5, and 2.33 years. The rating curves were derived using
AD,
AW, average
m exponent = 2.45, and median
Ss = 0.011. The results revealed a Root Mean Square Error of 0.44 m
3/s (15.5 ft
3/s) and a Mean Error of −0.022 m
3/s (−0.77 ft
3/s). The applied methodology resulted in overpredictions for 40% of the cases, while underpredictions were observed in the remaining 60%. These findings showcase the potential of the modified Mueses et al. [
30] approach for generating rating curves for GIWs and its suitability for further investigation and enhancement.
The primary objective of this study was to develop a method applicable to regional models for reproducing the average behavior of tens-hundreds of GIWs within a single basin. After verifying the accuracy of the proposed method in replicating the rating characteristics for each individual wetland, a representative stage–storage–discharge relationship accounting for the aggregated behavior of multiple GIWs was assessed.
3.8. Testing Aggregated Wetland Behavior
To use the modified version of the model of Mueses et al. [
30] for developing the stage–discharge relationship in aggregated wetlands, it is required to have
Q100,
d100, the
m exponent, and the invert depth for the combined watershed area and local conditions. The
Q100 can be calculated from the developed
Q100 linear regression model by summing combined
AD and
AW for all GIWs. Given the high variability in the
Ss and considering that our analysis of the
d0.01 shows an average of 0.43 m (1.4 ft) with a standard deviation of 0.37 m (1.2 ft), the average
d0.01 can be used as the
d100 for the representative stage–discharge relationship. Based on the local or published analysis of the
m exponent for GIWs, the average
m value, which is 2.45, can be used to define the representative stage–discharge relationship using the derived
d100. As previously demonstrated, the invert depth is the mean depth of the 15 ft buffer relative to ground elevation. Therefore, by performing an area-weighted average of the invert depths for all GIWs, a representative invert depth was obtained.
To test the approach, all GIWs were considered as a single aggregated GIW computational element, employing the area-weighted average method to estimate the max depth, , and and of the GIWs. An average n of 2.47 was used for the aggregated behavior of these GIWs. Utilizing n, and average overall soil storage parameters, the representative stage–storage that accounts for soil and bowl storage was derived.
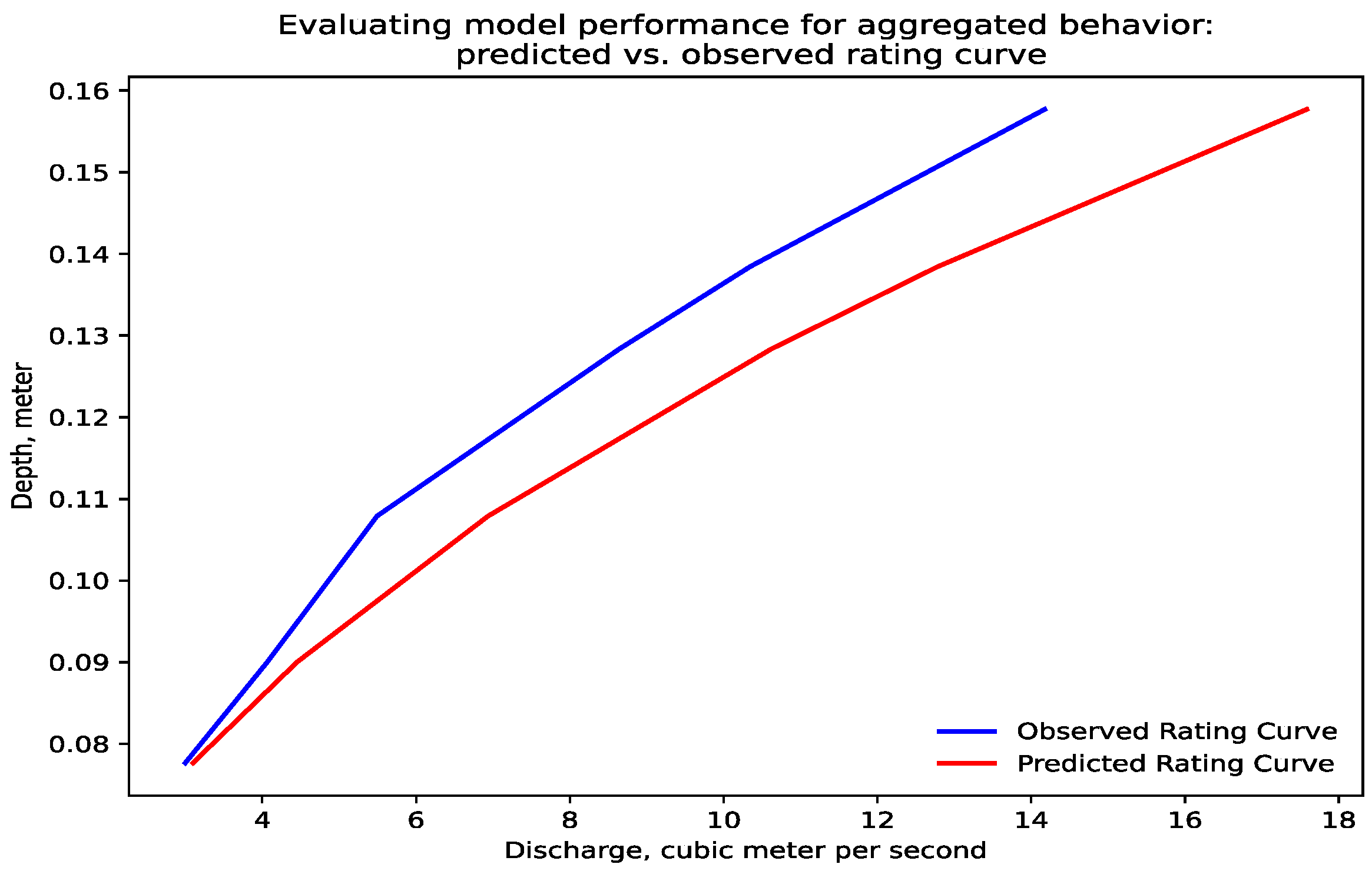
Figure 9 compares the predicted discharge rating of the aggregated GIW vs. the “observed” rating represented by the sum of the discharges from the individual GIWs. Note that the results compared favorably to the individual GIWs, with an RMSE of 1.8 m
3/s (15% relative error to observed discharges) for discharge. Also, for the same discharge, the RMSE error for stage is generally less than 10 cm and less than 10% relative error. In addition, the results of comparing the observed storage with the predicted bowl storage indicated an RMSE of 63,153 m
3, corresponding to a −7.2% relative error compared to the observed storages. This highlights the model effectiveness in predicting the overall behavior of aggregated GIWs. However, the error rate in predicting storage for individual wetlands was notably higher, at 55%. The model was specifically designed to capture the average behavior, which becomes more dominant in a population of tens to hundreds of GIWs, thereby enhancing the model’s performance in predicting general trends. These findings underscore the model suitability for regional-scale applications.
4. Conclusions and Summary
Geographically (and hydraulically) isolated wetlands (GIWs) play an important role in controlling the timing and magnitude of resultant streamflow and downstream water levels in coastal plain environments where they are prevalent. In W-C Florida, they make up a significant portion of the 29% surface area covered by wetlands and hydrography (waterways) and play a big role in groundwater recharge and flooding. Thus, describing the surface water capture, discharge, and groundwater recharge characteristics, as well as the transitional cycle to full wet-season contribution is critical. The procedure outlined proposes a relatively straightforward approach to develop a rating for hydrologic modeling of larger geographical areas (e.g., regional models of 10’s to 100’s of km2), often with limited site-specific bathymetric data. This approach defines GIS and pre-modeling spreadsheet analyses that can be developed to populate simulation models. However, it is not limited to larger areas and can be used whenever site-specific stage–storage–discharge data are lacking or need to be described by a few coefficients. It also defines methods to describe the rating for finite discretization where aggregation is required.
The approach extends and couples previous research methodologies [
14,
29], offering simplified key modeling coefficients (
m & n), and identifies depth and flow indexes (e.g.,
d100,
Q100) and an invert relation to fully define the range of rating for GIWs either individually or aggregated in a model discretization. These coefficients, when coupled with easily derivable physical attributes such as areas, slopes, and elevations, allow for the accurate simulation of storage, water level and downstream discharge, including flood behavior. The proposed method was tested against observational (surveyed) GIW data and data from well-calibrated models, and the results showed very tolerable errors for the stage (
10%), storage (
7%) and discharge (
15%).
The study also finds the relevant typical hydrologic (and hydroperiod) behavior of GIWs, at least applicable in W-C Florida and perhaps similar in other coastal plain environments, noting the period of inundation and standing water in these systems and the relative period-of-time levels exceeding the invert that are useful for understanding and managing these important ecosystems. A review of 35 available wetland long-term water level records indicates the period of standing-water level in these hydrologic features is approximately 65% of the time, with full-inundation (out to perimeter) water levels around 14.5% of the time and that level, previously referred to as normal pool by some wetland references [
15] roughly corresponding to the time period (or less) that they contribute to downstream streamflow (and flood flow). The study also suggests that for GIWs, due to the infrequent discharge nature, it is best to adapt the approach of Mueses et al. [
30] to work with 100 yr levels and flows instead of the 10% exceedance values advocated for alluvial systems.
Lastly, the GIS procedures to develop the required physical input data (elevations, wetland and drainage areas, and channel slopes) for GIWs were compared to surveyed data so that a measure of the error expectation could be quantified. Among the findings, it was concluded that, using 1.5 m DEMs, a 4.5 m buffer and mean elevation is far superior to a minimum elevation statistic for estimating the invert elevation of a GIW, at least in the low-gradient topography typical of W-C Florida and perhaps other coastal plain settings. Also, a minimum elevation statistic over the wetland area was reasonably accurate for defining the wetland bottom (dry bed) elevations. However, that would be subject to the accuracy and vertical resolution of the DEM in other applications.