A Finite Volume Method for a 2D Dam-Break Simulation on a Wet Bed Using a Modified HLLC Scheme
Abstract
:1. Introduction
2. Methods
2.1. Analytical Solution (Wet Bed)
2.2. Numerical Method
2.2.1. Time Approximation
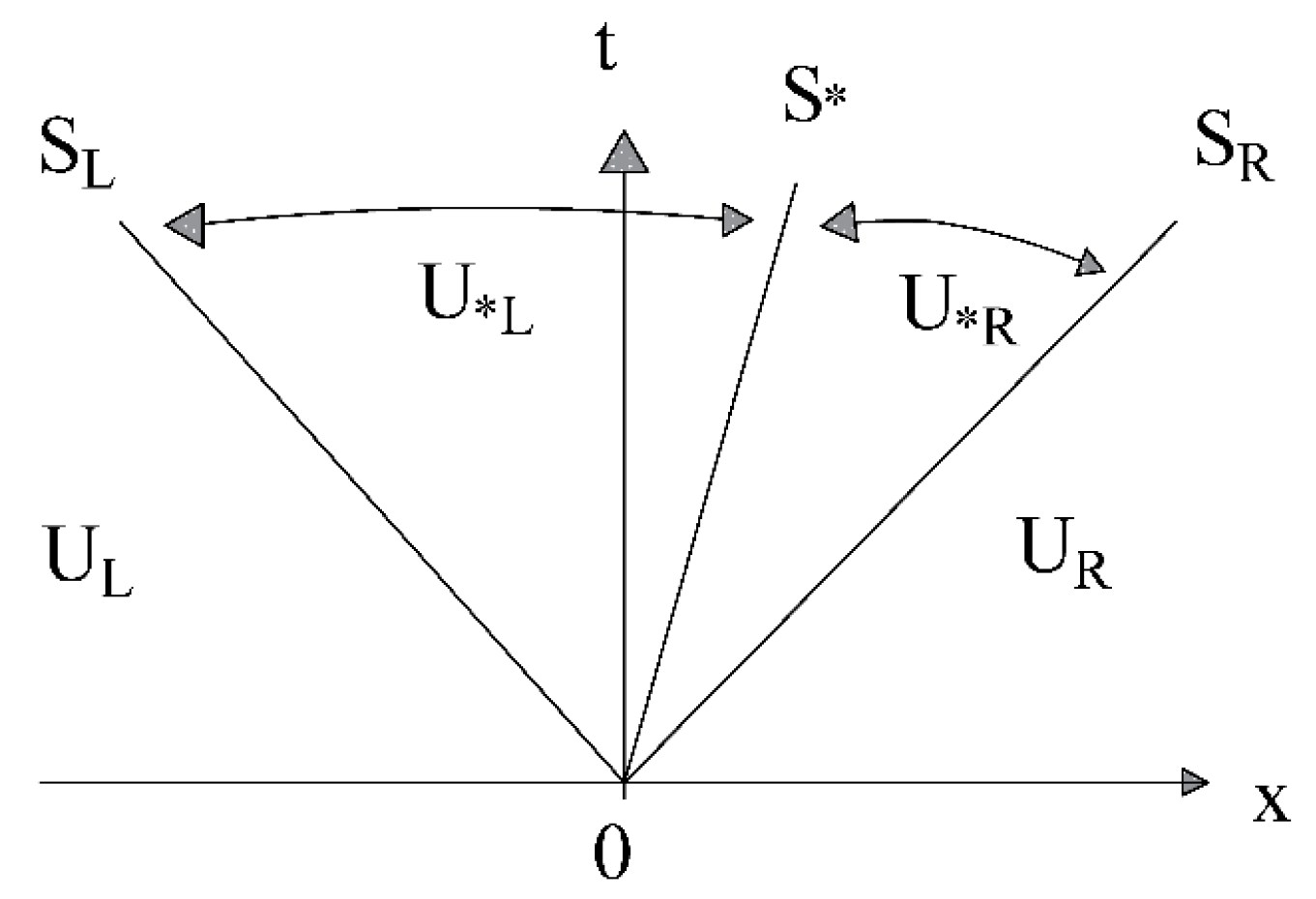
2.2.2. Approximate Solver Algorithm HLLC for Determination of Intercell Flux
- Determination of h:
- ii.
- Obtaining velocities of SL, SR, and :
- iii.
- Determination of :
- iv.
- Determination of and :
- v.
- Calculation of intercell flux :
2.2.3. Boundary Conditions
2.3. Model’s Verification
3. Results and Discussion
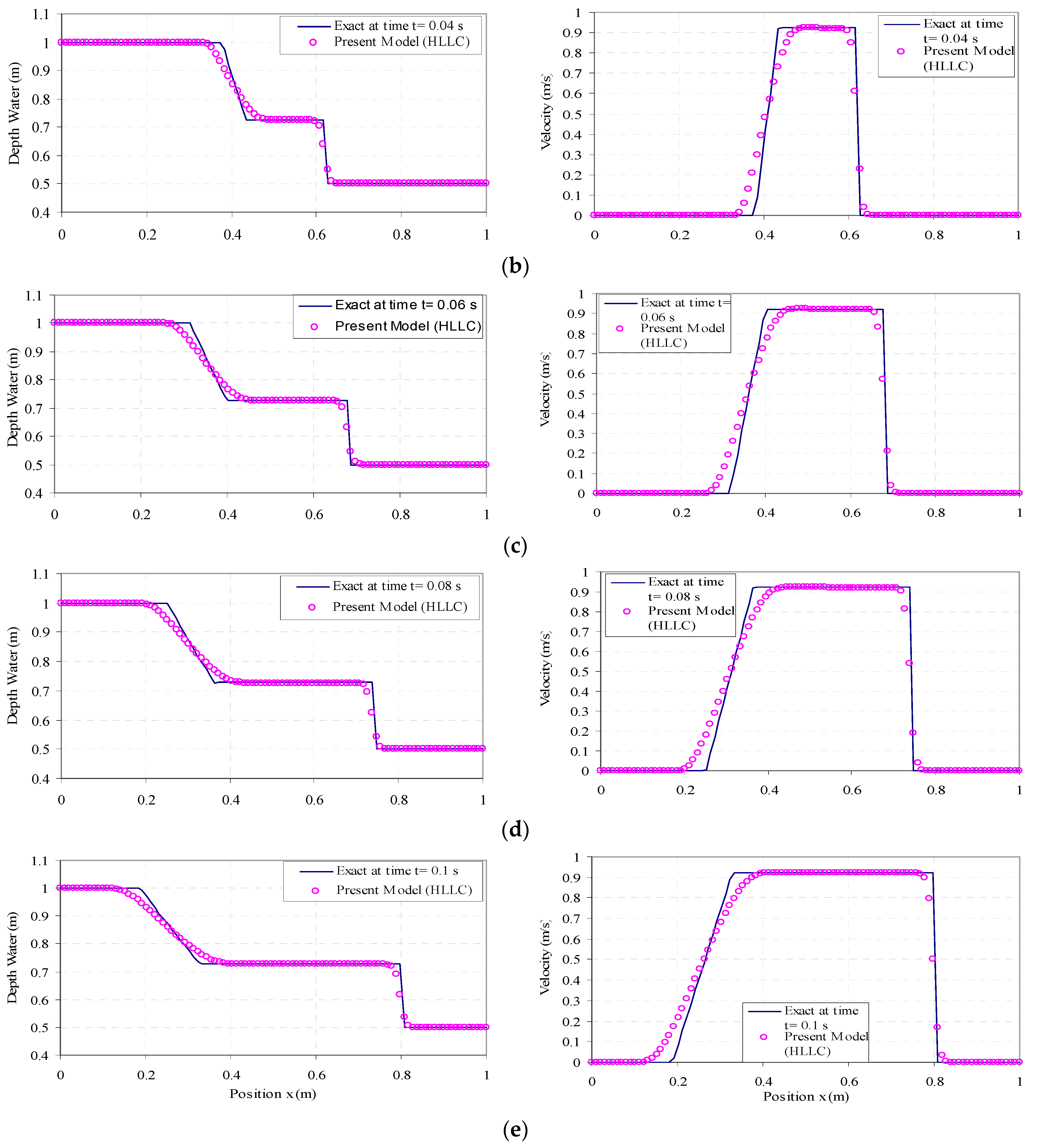
3.1. One-Dimensional (1D) Dam-Break Simulation
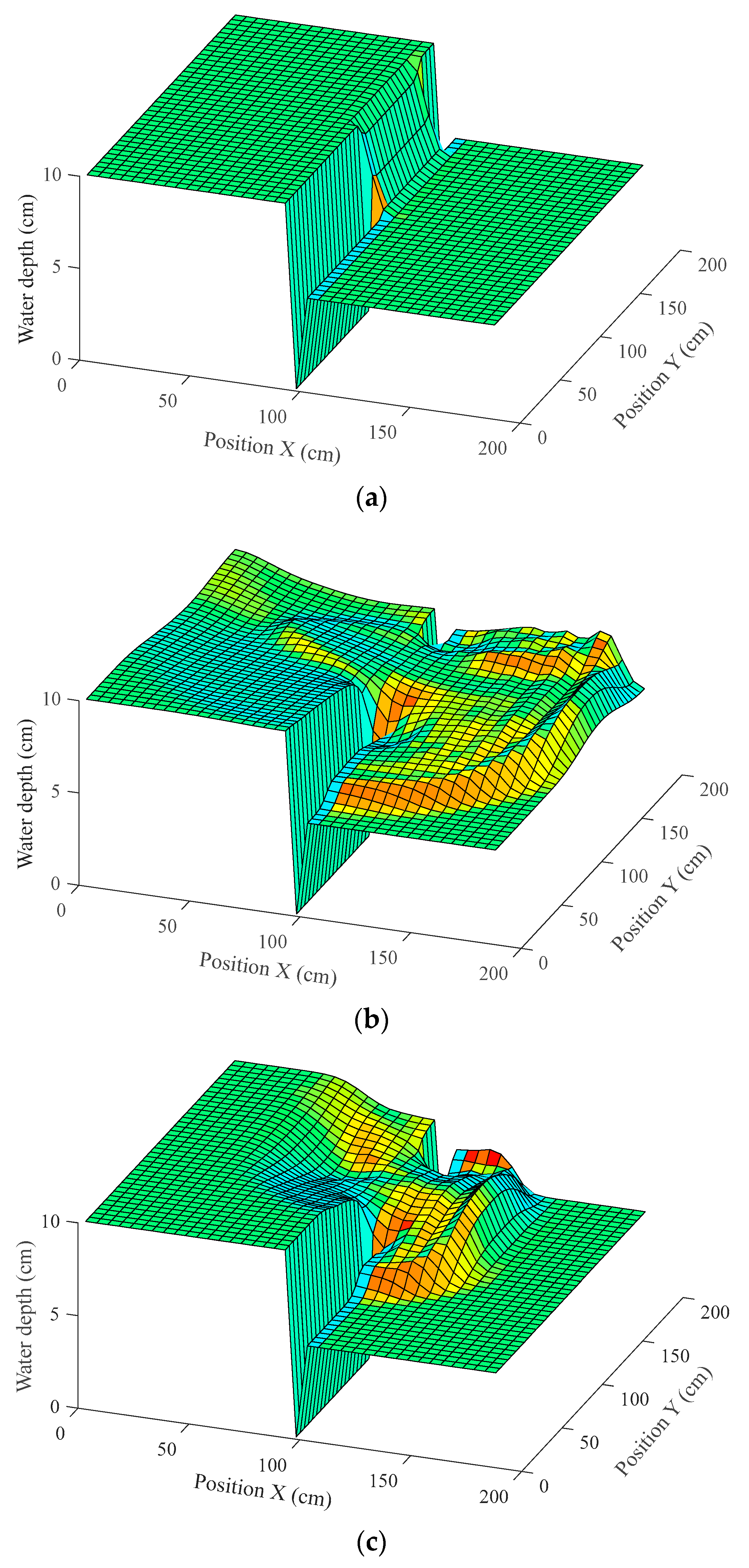
3.2. Two-Dimensional (2D) Dam Break
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Noori, R.; Ghiasi, B.; Sheikhian, H.; Adamowski, J.F. Estimation of the dispersion coefficient in natural rivers using a granular computing model. J. Hydraul. Eng. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Bagherzadeh, M.; Mousavi, F.; Manafpour, M.; Mirzaee, R.; Hoseini, K. Numerical simulation and application of soft computing in estimating vertical drop energy dissipation with horizontal serrated edge. Water Supply 2022, 22, 4676–4689. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Ge, L.; Tian, J.; Yin, Z.; Liu, M.; Zheng, W. Study on the thermospheric density distribution pattern during geomagnetic activity. Appl. Sci. 2023, 13, 5564. [Google Scholar] [CrossRef]
- Bouchaala, F.; Ali, M.Y.; Matsushima, J. Estimation of seismic attenuation in carbonate rocks using three different methods: Application on VSP data from Abu Dhabi oilfield. J. Appl. Geophys. 2016, 129, 79–91. [Google Scholar] [CrossRef]
- Xu, J.; Lan, W.; Ren, C.; Zhou, X.; Wang, S.; Yuan, J. Modeling of coupled transfer of water, heat and solute in saline loess considering sodium sulfate crystallization. Cold Reg. Sci. Technol. 2021, 189, 103335. [Google Scholar] [CrossRef]
- Panji, M.; Habibivand, M. Seismic analysis of semi-sine shaped alluvial hills above subsurface circular cavity. Earthq. Eng. Eng. Vib. 2020, 19, 903–917. [Google Scholar] [CrossRef]
- Panji, M.; Mojtabazadeh-Hasanlouei, S.; Fakhravar, A. Seismic ground response including underground horseshoe-shaped cavity. Transp. Infrastruct. Geotechnol. 2022, 9, 338–355. [Google Scholar] [CrossRef]
- Shafagh Loron, R.; Samadi, M.; Shamsai, A. Predictive explicit expressions from data-driven models for estimation of scour depth below ski-jump bucket spillways. Water Supply 2023, 23, 304–316. [Google Scholar] [CrossRef]
- Naganna, S.R.; Beyaztas, B.H.; Bokde, N.; Armanuos, A.M. On the evaluation of the gradient tree boosting model for groundwater level forecasting. Knowl. Based Eng. Sci. 2020, 1, 48–57. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Li, D.Q.; Tang, X.S.; Du, W. Predictive Models for Seismic Source Parameters Based on Machine Learning and General Orthogonal Regression Approaches. Bull. Seismol. Soc. Am. 2023. [Google Scholar] [CrossRef]
- Ghiasi, B.; Noori, R.; Sheikhian, H.; Zeynolabedin, A.; Sun, Y.; Jun, C.; Hamouda, M.; Bateni, S.M.; Abolfathi, S. Uncertainty quantification of granular computing-neural network model for prediction of pollutant longitudinal dispersion coefficient in aquatic streams. Sci. Rep. 2022, 12, 4610. [Google Scholar] [CrossRef]
- Samadi, M.; Sarkardeh, H.; Jabbari, E. Prediction of the dynamic pressure distribution in hydraulic structures using soft computing methods. Soft Comput. 2021, 25, 3873–3888. [Google Scholar] [CrossRef]
- Uyumaz, A.; Danandeh Mehr, A.; Kahya, E.; Erdem, H. Rectangular side weirs discharge coefficient estimation in circular channels using linear genetic programming approach. J. Hydroinform. 2014, 16, 1318–1330. [Google Scholar] [CrossRef]
- Pilotti, M.; Tomirotti, M.; Valerio, G.; Bacchi, B. Simplified Method for the Characterization of the Hydrograph Following a Sudden Partial Dam Break. J. Hydraul. Eng. 2010, 136, 693–704. [Google Scholar] [CrossRef]
- Hooshyaripor, F.; Tahershamsi, A.; Razi, S. Dam Break Flood Wave under Different Reservoir’s Capacities and Lengths. Sādhanā 2017, 42, 1557–1569. [Google Scholar] [CrossRef]
- Haltas, I.; Tayfur, G.; Elci, S. Two-Dimensional Numerical Modeling of Flood Wave Propagation in an Urban Area Due to Ürkmez Dam-Break, İzmir, Turkey. Nat. Hazards 2016, 81, 2103–2119. [Google Scholar] [CrossRef]
- Togun, H.; Sadeghinezhad, E.; Kazi, S.N. Navier-Stokes Equations and High-Resolutions: Advancements in Accurate Incompressible Flow Simulations. Knowl. Based Eng. Sci. 2023, 4, 51–59. [Google Scholar]
- Biscarini, C.; Di Francesco, S.; Manciola, P. CFD Modelling Approach for Dam Break Flow Studies. Hydrol. Earth Syst. Sci. 2010, 14, 705–718. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S. Dam-Break Flow in the Presence of Obstacle: Experiment and CFD Simulation. Eng. Appl. Comput. Fluid Mech. 2011, 5, 541–552. [Google Scholar] [CrossRef]
- Hooshyaripor, F.; Tahershamsi, A. Effect of Reservoir Side Slopes on Dam-Break Flood Waves. Eng. Appl. Comput. Fluid Mech. 2015, 9, 458–468. [Google Scholar] [CrossRef]
- Tahershamsi, A.; Hooshyaripor, F.; Razi, S. Reservoir’s Geometry Impact of Three Dimensions on Peak Discharge of Dam-Failure Flash Flood. Sci. Iran. 2018, 25, 1931–1942. [Google Scholar] [CrossRef]
- Pilotti, M.; Maranzoni, A.; Tomirotti, M.; Valerio, G. 1923 Gleno Dam Break: Case Study and Numerical Modeling. J. Hydraul. Eng. 2011, 137, 480–492. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Kocaman, S.; Guzel, H. Investigation of Dam-Break Flood Waves in a Dry Channel with a Hump. J. Hydro-Environ. Res. 2014, 8, 304–315. [Google Scholar] [CrossRef]
- Heniche, M.; Secretan, Y.; Boudreau, P.; Leclerc, M. A Two-Dimensional Finite Element Drying-Wetting Shallow Water Model for Rivers and Estuaries. Adv. Water Resour. 2000, 23, 359–372. [Google Scholar] [CrossRef]
- Yoshioka, H.; Unami, K.; Fujihara, M. A finite element/volume method model of the depth-averaged horizontally 2D shallow water equations. Int. J. Numer. Methods Fluids 2014, 75, 23–41. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical Resolution of Well-Balanced Shallow Water Equations with Complex Source Terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Pilotti, M.; Maranzoni, A.; Milanesi, L.; Tomirotti, M.; Valerio, G. Dam-Break Modeling in Alpine Valleys. J. Mt. Sci. 2014, 11, 1429–1441. [Google Scholar] [CrossRef]
- Liang, D.; Falconer, R.A.; Lin, B. Comparison between TVD-MacCormack and ADI-Type Solvers of the Shallow Water Equations. Adv. Water Resour. 2006, 29, 1833–1845. [Google Scholar] [CrossRef]
- Liang, D.; Lin, B.; Falconer, R.A. Simulation of Rapidly Varying Flow Using an Efficient TVD–MacCormack Scheme. Int. J. Numer. Methods Fluids 2007, 53, 811–826. [Google Scholar] [CrossRef]
- Parmas, B.; Vosoughifar, H.R. Novel Method of Boundary Condition of Dam-Break Phenomena Using Ghost-Particle SPH. Nat. Hazards 2016, 84, 897–910. [Google Scholar] [CrossRef]
- Vosoughifar, H.R.; Dolatshah, A.; Sadat Shokouhi, S.K. Discretization of Multidimensional Mathematical Equations of Dam Break Phenomena Using a Novel Approach of Finite Volume Method. J. Appl. Math. 2013, 2013, 642485. [Google Scholar] [CrossRef]
- Singh, J.; Altinakar, M.S.; Ding, Y. Two-Dimensional Numerical Modeling of Dam-Break Flows over Natural Terrain Using a Central Explicit Scheme. Adv. Water Resour. 2011, 34, 1366–1375. [Google Scholar] [CrossRef]
- Baghlani, A. Simulation of Dam-Break Problem by a Robust Flux-Vector Splitting Approach in Cartesian Grid. Sci. Iran. 2011, 18, 1061–1068. [Google Scholar] [CrossRef]
- Ferrari, A.; Fraccarollo, L.; Dumbser, M.; Toro, E.F.; Armanini, A. Three-Dimensional Flow Evolution after a Dam Break. J. Fluid Mech. 2010, 663, 456–477. [Google Scholar] [CrossRef]
- Aliparast, M. Two-Dimensional Finite Volume Method for Dam-Break Flow Simulation. Int. J. Sediment Res. 2009, 24, 99–107. [Google Scholar] [CrossRef]
- Ying, X.; Jorgeson, J.; Wang, S.S.Y. Modeling Dam-Break Flows Using Finite Volume Method on Unstructured Grid. Eng. Appl. Comput. Fluid Mech. 2009, 3, 184–194. [Google Scholar] [CrossRef]
- Kim, S.D.; Lee, B.J.; Lee, H.J.; Jeung, I.-S. Robust HLLC Riemann Solver with Weighted Average Flux Scheme for Strong Shock. J. Comput. Phys. 2009, 228, 7634–7642. [Google Scholar] [CrossRef]
- Loukili, Y.; Soulaimani, A. Numerical Tracking of Shallow Water Waves by the Unstructured Finite Volume WAF Approximation. Int. J. Comput. Methods Eng. Sci. Mech. 2007, 8, 75–88. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; Wiley and Sons Ltd.: Hoboken, NJ, USA, 2001; ISBN 0471987662. [Google Scholar]
- Hudson, J. Numerical Techniques for Morphodynamic Modeling. Ph.D. Thesis, University of Reading, Berkshire, UK, 2001. [Google Scholar]
- Liu, M.; Cao, W.; Fan, Z. Convergence and Stability of the Semi-Implicit Euler Method for a Linear Stochastic Differential Delay Equation. J. Comput. Appl. Math. 2004, 170, 255–268. [Google Scholar] [CrossRef]
- Harten, A.; Lax, P.D.; Leer, B. van On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Toro, E.F. Experimental and Numerical Assessment of the Shallow Water Model for Two-Dimensional Dam-Break Type Problems. J. Hydraul. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer Science & Business Media: Berlin, Germany, 2013; ISBN 3662034905. [Google Scholar]
- Yekta, A.H.A.; Banihashemi, M.A. A Godunov-type Fractional Semi-implicit Method Based on Staggered Grid for Dam-break Modeling. Int. J. Numer. Methods Fluids 2011, 67, 1291–1309. [Google Scholar] [CrossRef]
- Alcrudo, F.; Garcia-Navarro, P. A High-resolution Godunov-type Scheme in Finite Volumes for the 2D Shallow-water Equations. Int. J. Numer. Methods Fluids 1993, 16, 489–505. [Google Scholar] [CrossRef]
- Mingham, C.G.; Causon, D.M. High-Resolution Finite-Volume Method for Shallow Water Flows. J. Hydraul. Eng. 1998, 124, 605–614. [Google Scholar] [CrossRef]


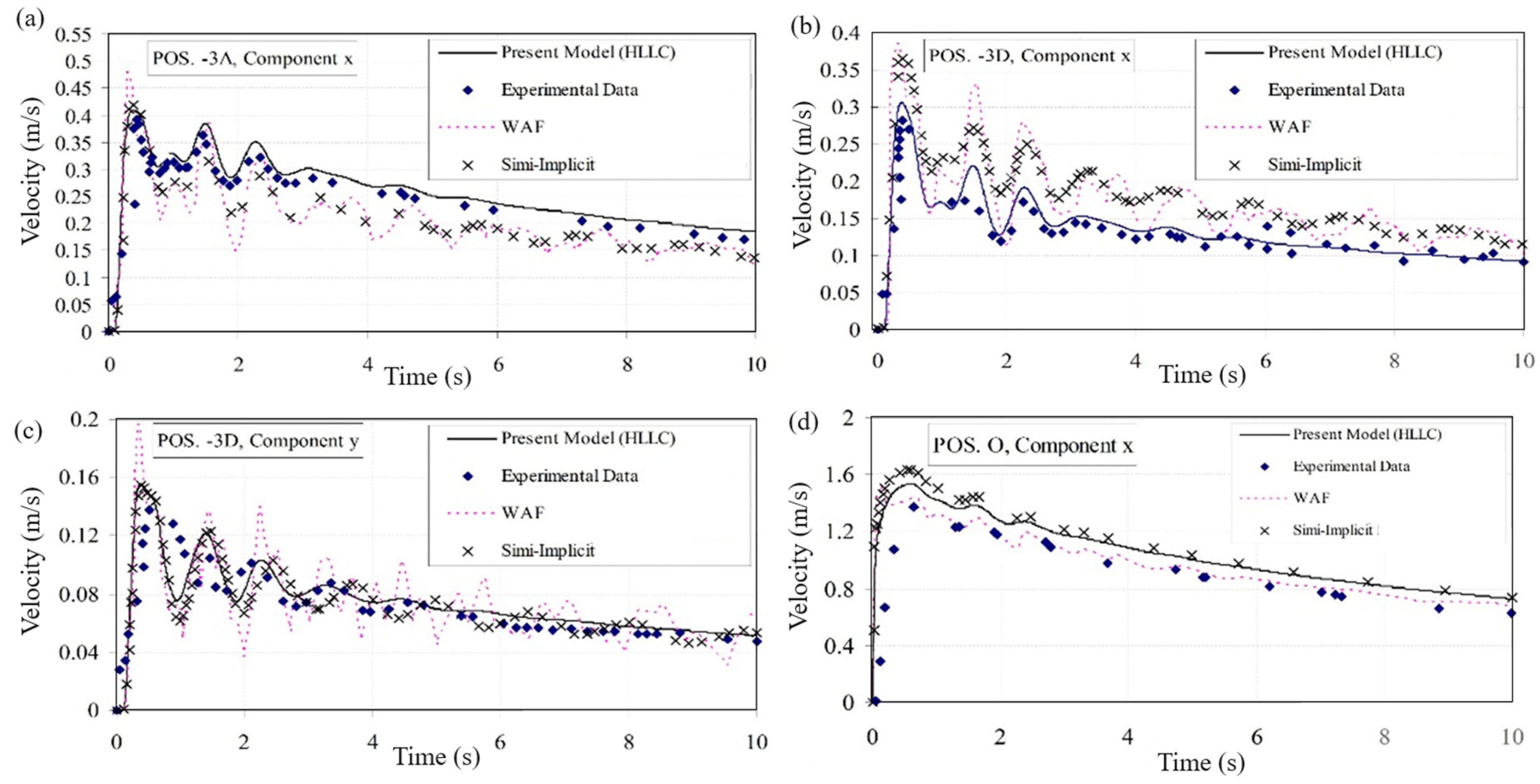


| t (s) | 0.02 | 0.04 | 0.06 | 0.08 | 0.1 |
|---|---|---|---|---|---|
| E1 (h) | −0.002 | −0.002 | −0.003 | −0.003 | −0.003 |
| E1 (u) | 0.03 | 0.007 | 0.001 | −0.001 | −0.003 |
| E2 (h) | 0.021 | 0.021 | 0.022 | 0.022 | 0.022 |
| E2 (u) | 0.02 | 0.143 | 0.117 | 0.01 | 0.094 |
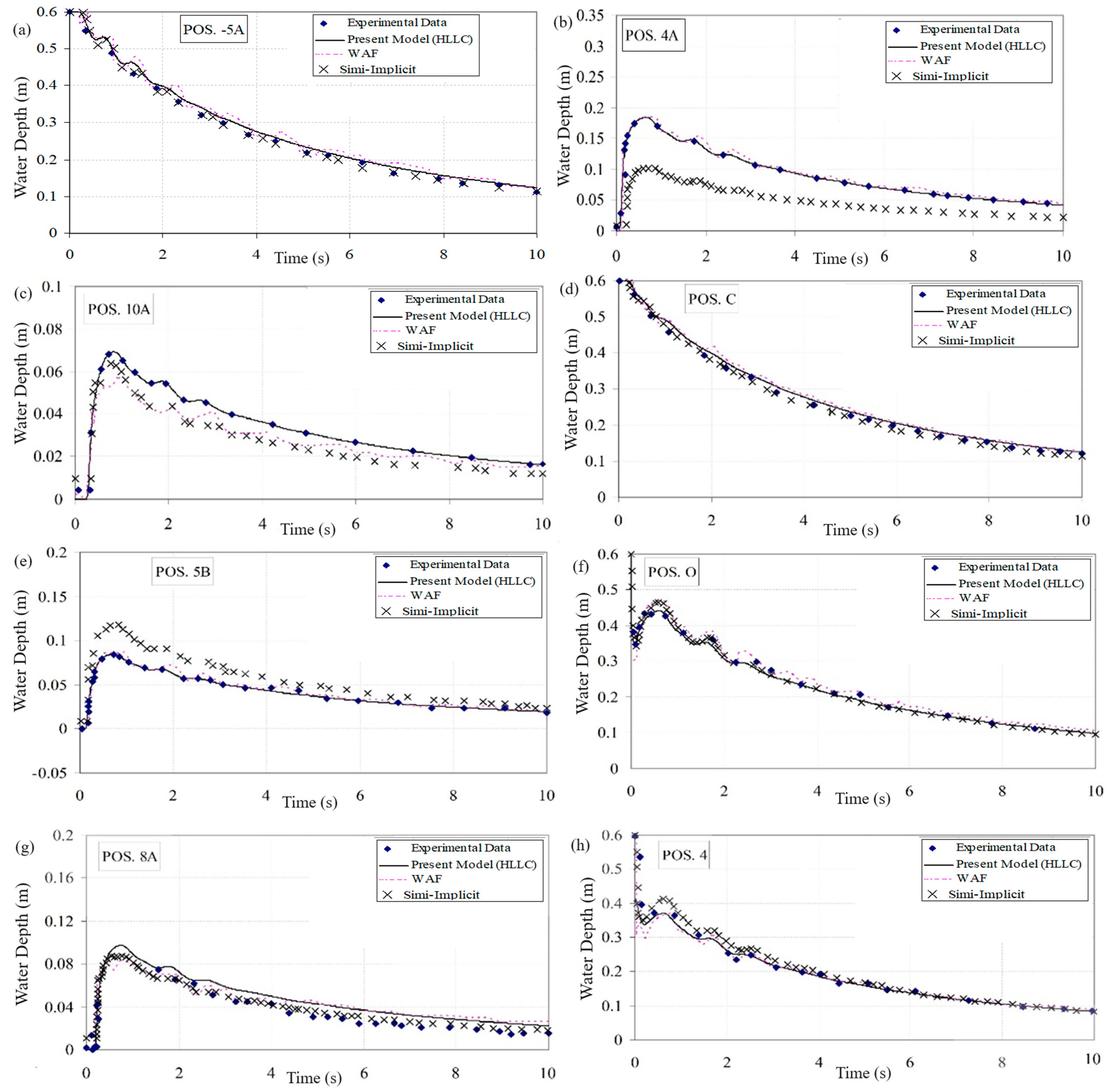
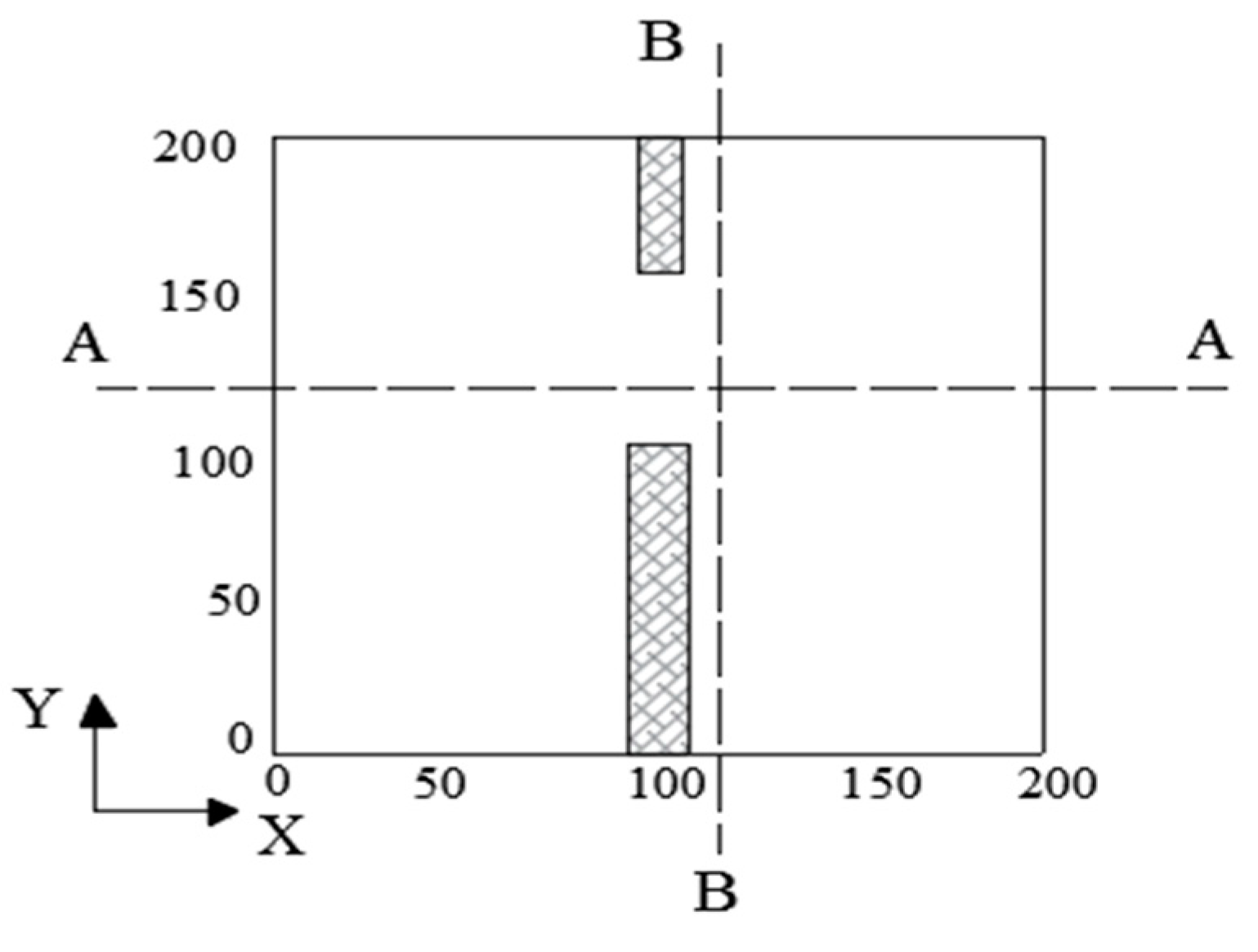
| Position | −5A | 4A | −4B | C | 4 | O | 5B | 8A | 9B | 10A | −3A | −3D |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x (m) | −820 | 322 | −845 | −520 | 0 | 0 | 454 | 722 | 802 | 1020 | −420 | −420 |
| y (m) | 0 | 0 | −500 | −600 | 150 | 0 | 250 | 0 | 450 | 0 | 0 | 200 |
| Point | HLLC | Semi-Implicit Method * | WAF Method ** |
|---|---|---|---|
| E2 (h) | E2 (h) | E2 (h) | |
| −5A | 0.054 | 0.042 | 0.06 |
| 4A | 0.356 | 0.645 | 0.351 |
| 10A | 0.294 | 0.137 | 0.124 |
| C | 0.035 | 0.027 | 0.041 |
| 5B | 0.434 | 0.298 | 0.434 |
| O | 0.15 | 0.131 | 0.149 |
| 8A | 0.341 | 0.323 | 0.359 |
| 4 | 0.034 | 0.003 | 0.045 |
| −4B | 0.042 | 0.013 | 0.039 |
| 9B | 0.188 | 0.257 | 0.136 |
| Point | Velocity Component | HLLC | Semi-Implicit Method * | WAF Method ** |
|---|---|---|---|---|
| E2 (u) | E2 (u) | E2 (u) | ||
| −3A | U | 0.392 | 0.148 | 0.203 |
| −3D | U | 0.222 | 0.181 | 0.231 |
| −3D | V | 0.206 | 0.29 | 0.364 |
| O | u | 0.361 | 0.465 | 0.389 |
| Downstream | Error Index | Experiment | Semi-Implicit Method * | WAF Method ** | |||
|---|---|---|---|---|---|---|---|
| A-A Cross-Section | B-B Cross-Section | A-A Cross-Section | B-B Cross-Section | A-A Cross-Section | B-B Cross-Section | ||
| Wet bed | E1 (h) | 0.102 | 0.0965 | 0.0876 | 0.067 | 0.0894 | 0.0876 |
| E2 (h) | 0.0112 | 0.0131 | 0.0128 | 0.0558 | 0.0086 | 0.0266 | |
| Dry bed | E1 (h) | 0.0456 | 0.0123 | - | - | 0.0567 | 0.0763 |
| E2 (h) | 0.0201 | 0.0114 | - | - | 0.0509 | 0.0661 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salamttalab, M.M.; Parmas, B.; Mustafa Alee, H.; Hooshyaripor, F.; Danandeh Mehr, A.; Vosoughifar, H.; Hosseini, S.A.; Maghrebi, M.; Noori, R. A Finite Volume Method for a 2D Dam-Break Simulation on a Wet Bed Using a Modified HLLC Scheme. Water 2023, 15, 3841. https://doi.org/10.3390/w15213841
Salamttalab MM, Parmas B, Mustafa Alee H, Hooshyaripor F, Danandeh Mehr A, Vosoughifar H, Hosseini SA, Maghrebi M, Noori R. A Finite Volume Method for a 2D Dam-Break Simulation on a Wet Bed Using a Modified HLLC Scheme. Water. 2023; 15(21):3841. https://doi.org/10.3390/w15213841
Chicago/Turabian StyleSalamttalab, Mohammad Milad, Behnam Parmas, Hedi Mustafa Alee, Farhad Hooshyaripor, Ali Danandeh Mehr, Hamidreza Vosoughifar, Seyed Abbas Hosseini, Mohsen Maghrebi, and Roohollah Noori. 2023. "A Finite Volume Method for a 2D Dam-Break Simulation on a Wet Bed Using a Modified HLLC Scheme" Water 15, no. 21: 3841. https://doi.org/10.3390/w15213841






