Numerical Modelling of Beach Profile Evolution with and without an Artificial Reef
Abstract
:1. Introduction
2. Methodology
2.1. Numerical Model
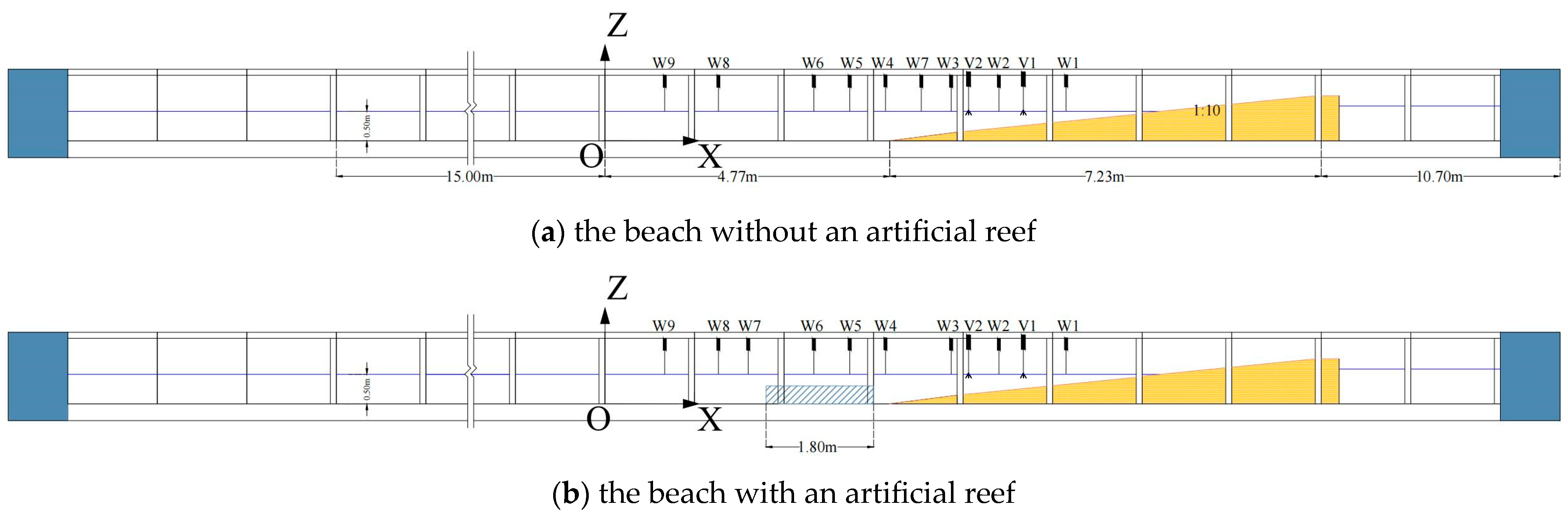
2.2. Parameter Setting
2.3. Validation
3. Results
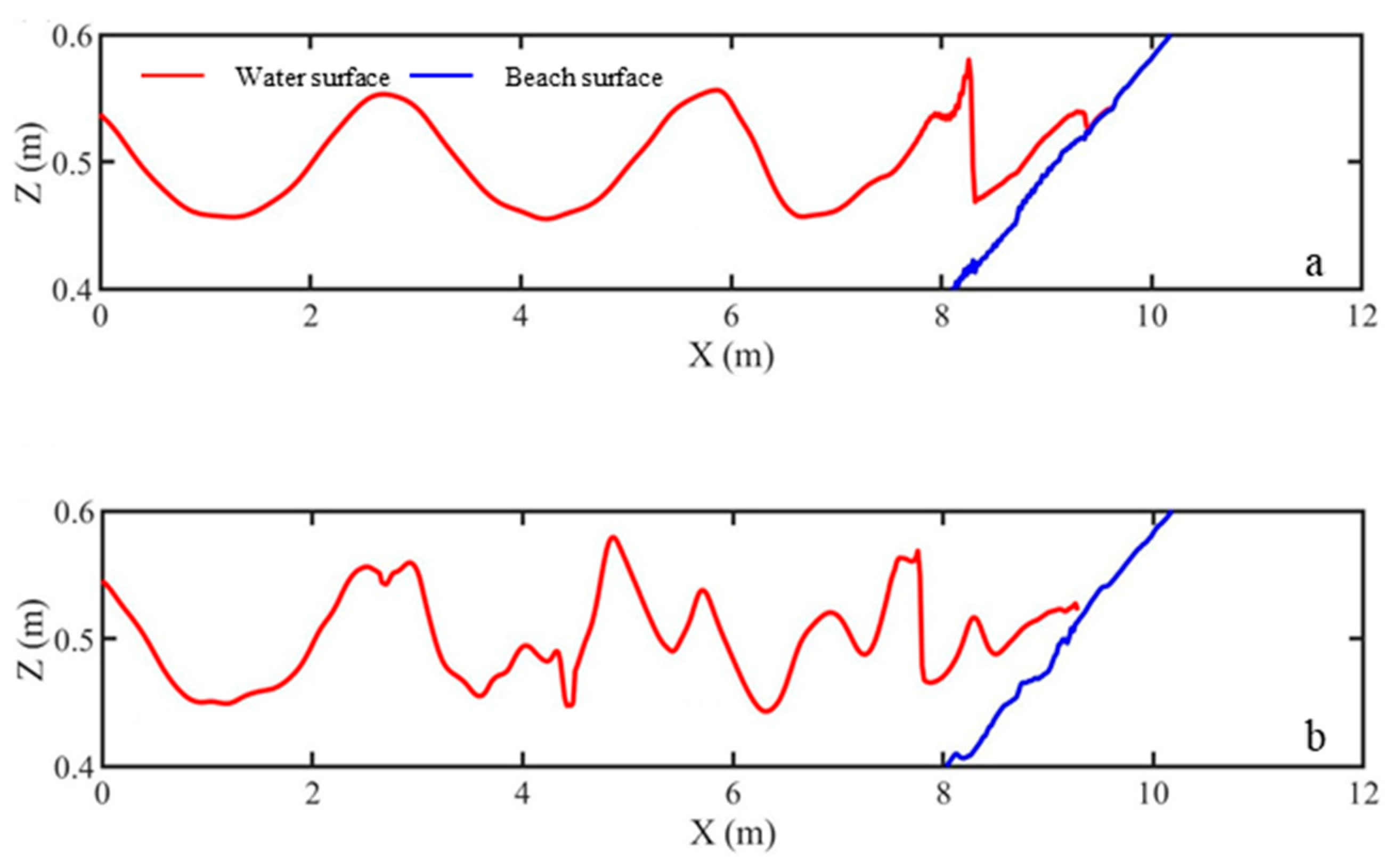
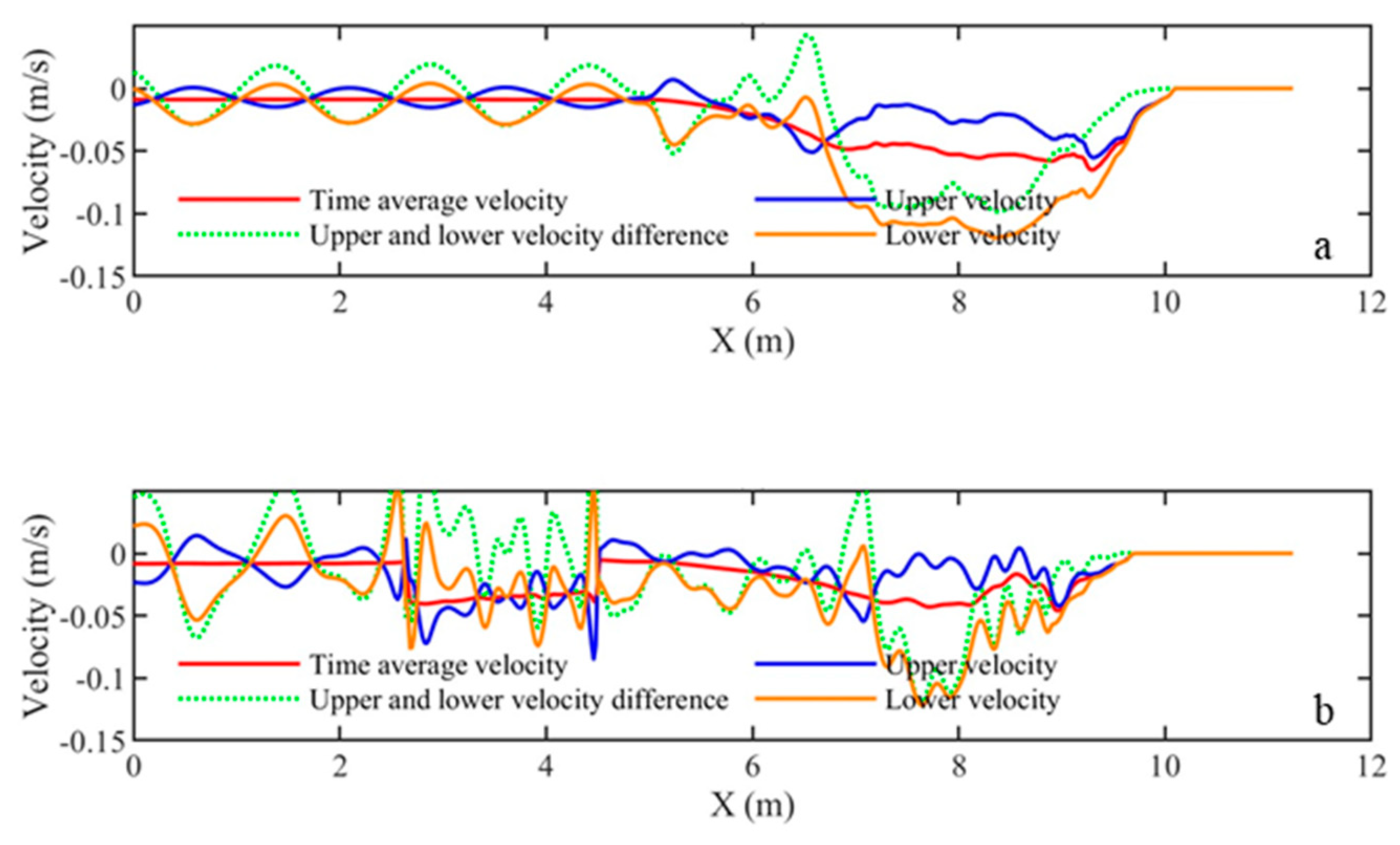
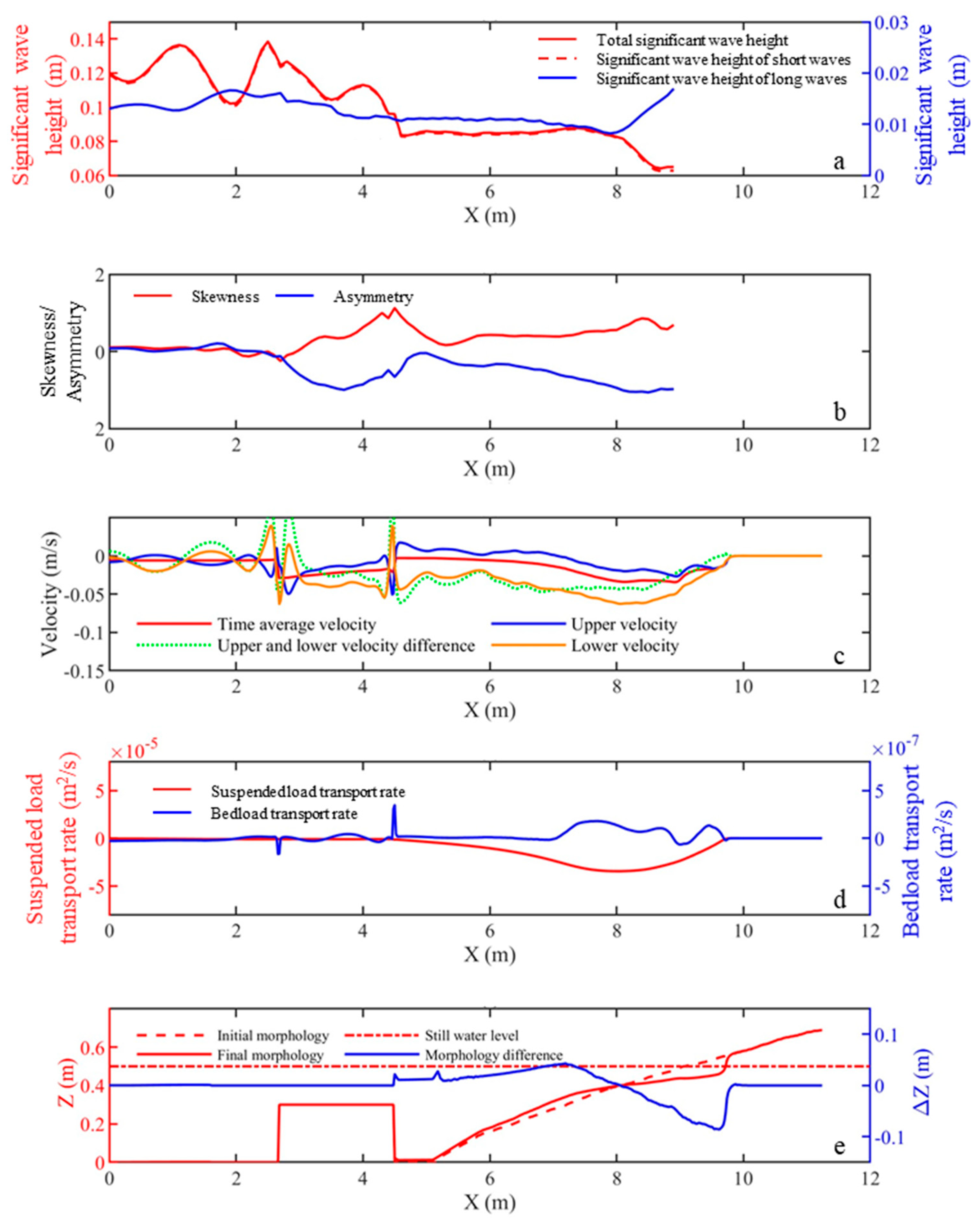
3.1. Hydrodynamic Characteristics
3.2. Sediment Transport
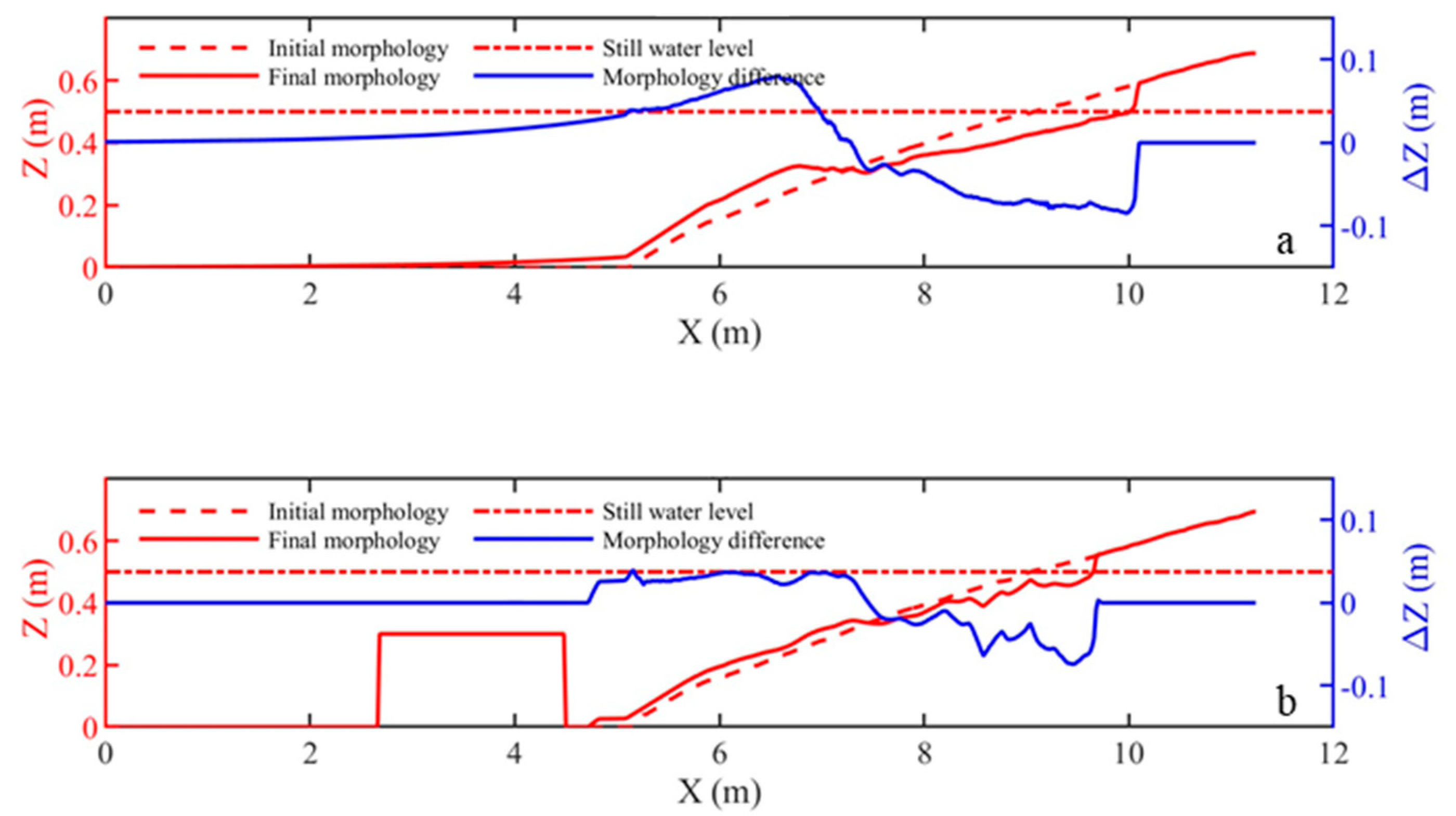
3.3. Morphological Evolution
4. Discussion
4.1. Irregular Wave Effects
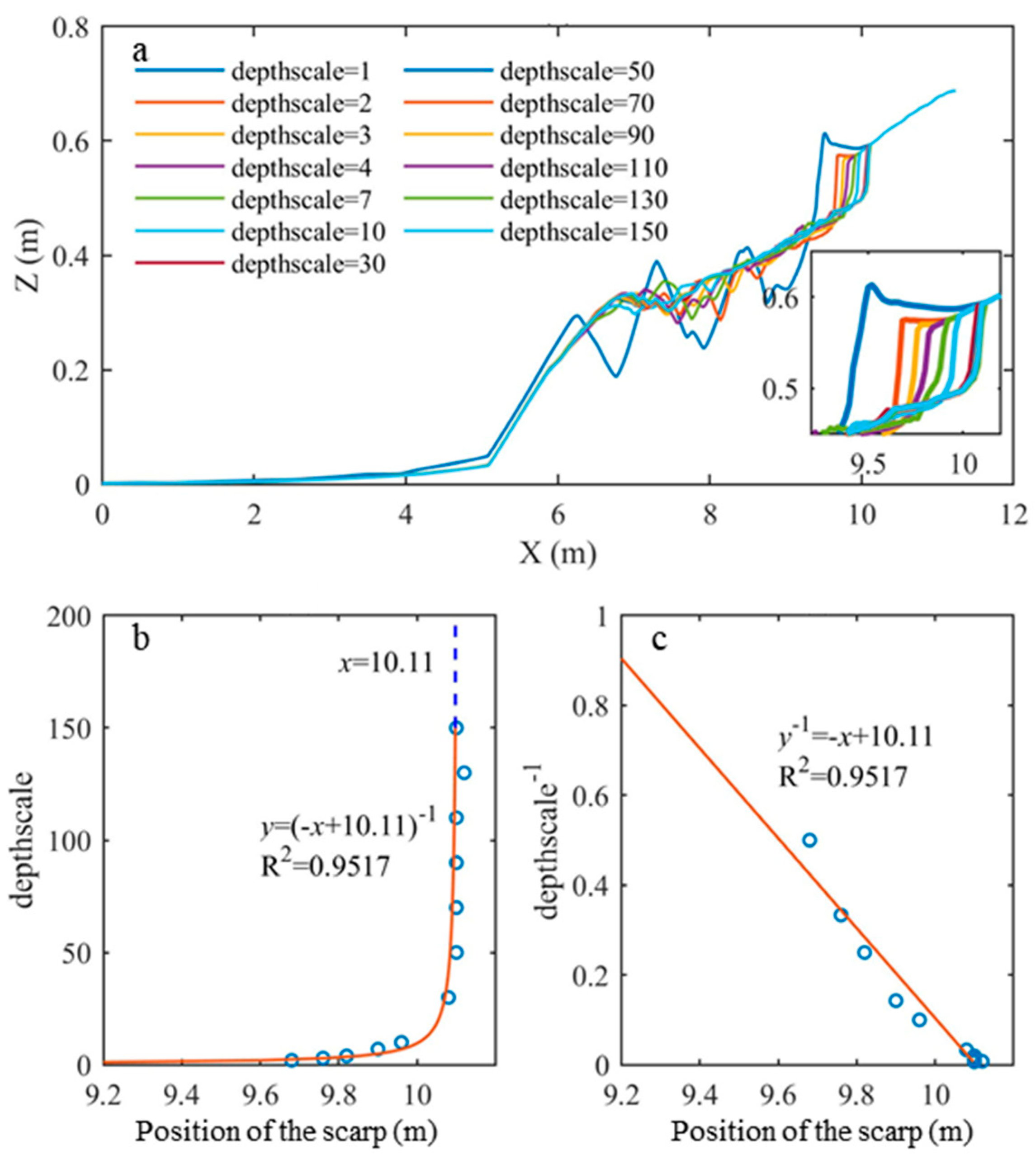
4.2. Sensitivity Analysis
5. Conclusions
- The artificial reef causes wave reflection and wave breaking further offshore, therefore, effectively attenuate waves;
- The intensive offshore flow plays a dominant role in suspended load transport, and the artificial reef decelerates local flow and reduces the offshore sediment transport by 51%;
- Regular waves transform the initial plane beach into a sandbar-trough-scarp profile, where the artificial reef reduces the total erosion amount per unit width by 53%;
- Over the artificial reef, wave skewness and asymmetry undergo a drastic change;
- Under irregular wave conditions, short waves contribute to the wave energy mainly. Meanwhile, standing wave effects due to wave reflection by the artificial reef decline considerably;
- Irregular waves transform the initial plane beach to a terrace-scarp profile, where the artificial reef shows good performances in protecting beach from excessive erosions under both regular and irregular wave conditions;
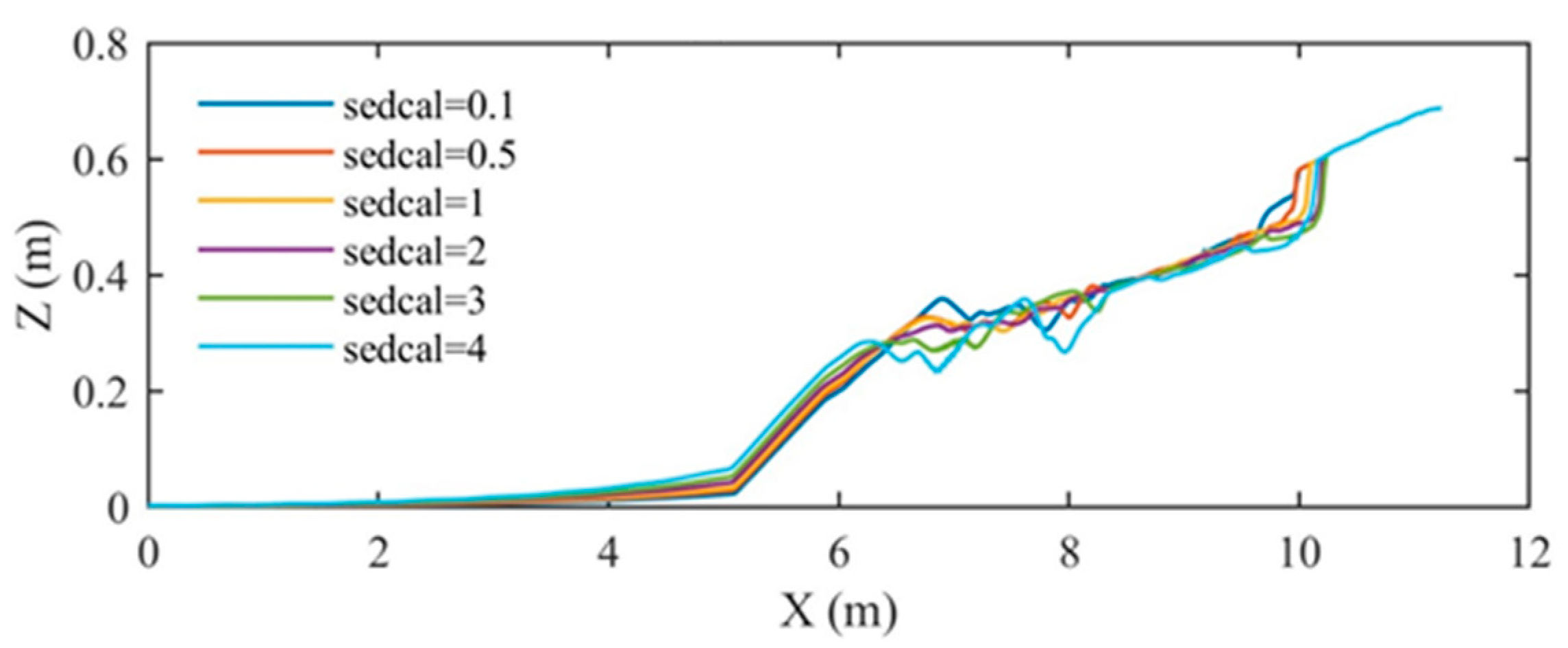
- In wave breaking area, the increase of maximum wave steepness criterium (maxbrsteep) may increase the wave height. With increasing water depth factor (depthscale), the scarp extends onshore until x = 10.11 m due to the limit of water level and uprush height. Increasing equilibrium sediment concentration factor (sedcal) extends the erosion area, but form the sandbar irregularly varying irregularly in shape.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vallam, S.; Annamalaisamy, S.S.; Ramesh, S.B. Sustainable hard and soft measures for coastal protection—Case studies along the Indian Coast. Mar. Georesour. Geotechnol. 2022, 40, 600–615. [Google Scholar]
- Ryzhakov, P.; Hermosilla, F.; Ubach, P.-A.; Oñate, E. Adaptive breakwaters with inflatable elements for coastal protection. Preliminary numerical estimation of their performance. Ocean Eng. 2022, 251, 110818. [Google Scholar] [CrossRef]
- Celli, D.; Li, Y.; Ong, C.M.; Di Risio, M. The role of submerged berms on the momentary liquefaction around conventional rubble mound breakwaters. Appl. Ocean Res. 2019, 85, 1–11. [Google Scholar]
- Semeoshenkova, V.; Newton, A. Overview of erosion and beach quality issues in three Southern European countries: Portugal, Spain and Italy. Ocean Coast. Manag. 2015, 118, 12–21. [Google Scholar] [CrossRef]
- Cantasano, N.; Boccalaro, F.; Ietto, F. Assessing of detached breakwaters and beach nourishment environmental impacts in Italy: A review. Environ. Monit. Assess. 2022, 195, 127. [Google Scholar] [CrossRef]
- Ma, Z.; Melville, D.S.; Liu, J.; Chen, Y.; Yang, H.; Ren, W.; Zhang, Z.; Piersma, T.; Li, B. Rethinking China’s new great wall. Science 2014, 346, 912–914. [Google Scholar] [CrossRef]
- Qi, H.S.; Liu, G.; Cai, F.; Zhu, J.; Liu, J.H.; Lei, G.; He, Y.Y.; Zheng, J.X.; Cao, H.M. Development trend and prospect of beach nourishment technology. J. Appl. Oceanogr. 2021, 40, 111–125. [Google Scholar]
- Schoonees, T.; Mancheño, G.A.; Scheres, B.; Bouma, T.J.; Silva, R.; Schlurmann, T.; Schüttrumpf, H. Hard structures for coastal protection, towards greener designs. Estuaries Coasts 2019, 42, 1709–1729. [Google Scholar]
- Elko, N.; Briggs, T.R.; Benedet, L.; Robertson, Q.; Thomson, G.; Webb, B.M.; Garvey, K. A century of U.S. beach nourishment. Ocean Coast. Manag. 2021, 199, 105406. [Google Scholar] [CrossRef]
- de Vriend, H.J.; van Koningsveld, M.; Aarninkhof, S.G.J.; de Vries, M.B.; Baptist, M.J. Sustainable hydraulic engineering through building with nature. J. Hydro-Environ. Res. 2015, 9, 159–171. [Google Scholar] [CrossRef]
- Dornhelm, R.B. The Coney Island public beach and boardwalk improvement of 1923. In Urban Beaches: Balancing Public Rights and Private Development; ASCE: Preston, VA, USA, 2003; pp. 52–63. [Google Scholar]
- Roest, B.; de Vries, S.; de Schipper, M.; Aarninkhof, S. Observed changes of a mega feeder nourishment in a coastal cell: Five years of Sand Engine morphodynamics. J. Mar. Sci. Eng. 2021, 9, 37. [Google Scholar]
- Aleixo, C.P.; Mendes, T.S.; Braz, S.T. Beach nourishment practice in mainland Portugal (1950–2017): Overview and retrospective. Ocean Coastal Manag. 2020, 192, 105211. [Google Scholar]
- Hamm, L.; Capobianco, M.; Dette, H.H.; Lechugad, A.; Spanhoffe, R.; Stive, M.J.F. A summary of European experience with shore nourishment. Coast. Eng. 2002, 47, 237–264. [Google Scholar]
- Bitan, M.; Zviely, D. Sand Beach Nourishment: Experience from the Mediterranean Coast of Israel. J. Mar. Sci. Eng. 2020, 8, 273. [Google Scholar] [CrossRef]
- Ali, A.; Abdullah, M.R.; Safuan, C.D.M.; Afiq-Firdaus, A.M.; Bachok, Z.; Akhir, M.F.M.; Latif, R.; Muhamad, A.; Seng, T.H.; Roslee, A.; et al. Side-scan sonar coupled with scuba diving observation for enhanced monitoring of benthic artificial reefs along the coast of Terengganu, Peninsular Malaysia. J. Mar. Sci. Eng. 2022, 10, 1309. [Google Scholar]
- David da Costa, I.; Luís da Silva, S.J.; Costa, L.L.; Lima, J.S.; Zalmon, I.R. Reproductive potential and production role of artificial reefs—Southeastern Brazil. Estuar. Coast. Shelf Sci. 2022, 265, 107710. [Google Scholar]
- Wang, G.; Wan, R.; Wang, X.X.; Zhao, F.F.; Lan, X.Z.; Cheng, H.; Tang, W.Y.; Guan, Q.L. Study on the influence of cut-opening ratio, cut-opening shape, and cut-opening number on the flow field of a cubic artificial reef. Ocean Eng. 2018, 162, 341–352. [Google Scholar]
- Nie, Z.; Zhu, L.; Xie, W.; Zhang, J.; Wang, J.; Jiang, Z.; Liang, Z. Research on the influence of cut-opening factors on flow field effect of artificial reef. Ocean Eng. 2022, 249, 110890. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, W.; Sun, L.; Zhao, F.; Long, X.; Wang, G. Studies on factors influencing hydrodynamic characteristics of plates used in artificial reefs. J. Ocean Univ. China 2019, 18, 193–202. [Google Scholar]
- Zheng, Y.; Kuang, C.; Zhang, J.; Gu, J.; Chen, K.; Liu, X. Current and turbulence characteristics of perforated box-type artificial reefs in a constant water depth. Ocean Eng. 2022, 244, 110359. [Google Scholar]
- Maslov, D.; Pereira, E.; Duarte, D.; Miranda, T.; Ferreira, V.; Tieppo, M.; Cruz, F.; Johnson, J. Numerical analysis of the flow field and cross section design implications in a multifunctional artificial reef. Ocean Eng. 2023, 272, 113817. [Google Scholar]
- Zhang, J.; Zhu, L.; Liang, Z.; Sun, L.; Nie, Z.; Wang, J.; Xie, W.; Jiang, Z. Numerical study of efficiency indices to evaluate the effect of layout mode of artificial reef unit on flow field. J. Mar. Sci. Eng. 2021, 9, 770. [Google Scholar]
- Xue, D.; Wang, C.; Huang, T.; Pan, Y.; Zhang, N.; Zhang, L. Flow field effects and physical stability of pyramidal artificial reef with different slope angles. Ocean Eng. 2023, 283, 115059. [Google Scholar]
- Zhou, P.; Gao, Y.; Zheng, S. Three-dimensional numerical simulation on flow behavior behind trapezoidal artificial reefs. Ocean Eng. 2022, 266, 112899. [Google Scholar]
- Jung, S.; Na, W.-B.; Kim, D. Rugosity and blocking indices of artificial reefs and their correlations with wake volume. Ocean Eng. 2022, 261, 112204. [Google Scholar]
- Shu, A.; Wang, M.; Qin, J.; Wang, S.; Zhu, F. The characteristics for flow field distribution and sediment incipient movement around the typical artificial reefs area in Bohai Bay. SHUILI XUEBAO 2020, 51, 1223–1233. [Google Scholar]
- Shu, A.; Qin, J.; Sun, T.; Yang, W.; Wang, M.; Zhu, J. Discussion on water and sediment dynamic characteristics and layout optimization of typical artificial reefs in Liaodong Bay of Bohai Sea. SHUILI XUEBAO 2022, 53, 43–53. [Google Scholar]
- Zhang, Q. Effects of Different Structures on Flow Resistance and Experiment on Local Scour of Artificial Reef. Master’s Thesis, Shanghai Ocean University, Shanghai, China, 13 May 2022. [Google Scholar]
- Tang, Y.; Wei, S.; Yang, M.; Wang, X.; Zhao, F. Experimental investigation of local scour around artificial reefs in steady currents. J. Ocean Univ. China 2022, 21, 445–456. [Google Scholar]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The state of the world’s beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar]
- Eelsalu, M.; Parnell, K.E.; Soomere, T. Sandy beach evolution in the low-energy microtidal Baltic Sea: Attribution of changes to hydrometerological forcing. Geomorphology 2022, 414, 108383. [Google Scholar]
- Wu, X. Numerical Modelling of Sediment Transport in an Artificial Reef Area. Ph.D. Thesis, Shanghai Ocean University, Shanghai, China, 20 May 2019. [Google Scholar]
- Vieira da Silva, G.; Hamilton, D.; Strauss, D.; Murray, T.; Tomlinson, R. Sediment pathways and morphodynamic response to a multi-purpose artificial reef—New insights. Coast. Eng. 2022, 171, 104027. [Google Scholar] [CrossRef]
- Schuh, E.; Grilli, A.R.; Groetsch, F.; Grilli, S.T.; Crowley, D.; Ginis, I.; Stempel, P. Assessing the morphodynamic response of a New England beach-barrier system to an artificial reef. Coast. Eng. 2023, 184, 104355. [Google Scholar]
- Yang, L.P.; Yang, S.P.; Zhang, Z.Y.; Zhu, J.L.; Shi, B. Experimental study on wave dissipation and beach protection by gravel dam and porous square reef: Taking Beidaihe West Beach as the example. Coastal Eng. 2022, 41, 223–232. [Google Scholar]
- Kuang, C.; Ma, Y.; Han, X.; Pan, S.; Zhu, L. Experimental observation on beach evolution process with presence of artificial submerged sand bar and reef. J. Mar. Sci. Eng. 2020, 8, 1019. [Google Scholar] [CrossRef]
- Ma, Y.; Kuang, C.; Han, X.; Niu, H.; Zheng, Y.; Shen, C. Experimental study on the influence of an artificial reef on cross-shore morphodynamic processes of a wave-dominated beach. Water 2020, 12, 2947. [Google Scholar] [CrossRef]
- Gharagozlou, A.; Dietrich, J.C.; Karanci, A.; Luettich, R.A.; Overton, M.F. Storm-driven erosion and inundation of barrier islands from dune to region-scales. Coast. Eng. 2020, 158, 103674. [Google Scholar] [CrossRef]
- Roelvink, D.; McCall, R.; Mehvar, S.; Nederhoff, K.; Dastgheib, A. Improving predictions of swash dynamics in Xbeach: The role of groupiness and incident-band runup. Coast. Eng. 2018, 134, 103–123. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; de Vries, J.V.T.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Cui, H.; Pietrzak, J.D.; Stelling, G.S. Optimal dispersion with minimized Poisson equations for non-hydrostatic free surface flows. Ocean Model. 2014, 81, 1–12. [Google Scholar]
- de Ridder, M.P.; Smit, P.B.; van Dongeren, A.; McCall, R.; Nederhoff, K.; Reniers, A.J.H.M. Efficient two-layer non-hydrostatic wave model with accurate dispersive behaviour. Coast. Eng. 2021, 164, 103808. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Stelling, G.; Zijlema, M. An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with applica-tion to wave propagation. Int. J. Numer. Methods Fluids 2003, 43, 1–23. [Google Scholar] [CrossRef]
- Lam, D.C.L.; Simpson, R.B. Centered differencing and the box scheme for diffusion convection problems. J. Comput. Phys. 1976, 22, 486–500. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Zou, Q.; Peng, Z. Evolution of wave shape over a low-crested structure. Coastal Eng. 2011, 58, 478–488. [Google Scholar] [CrossRef]
- Peng, Z.; Zou, Q.; Reeve, D.E.; Wang, B. Parameterisation and transformation of wave asymmetries over a low-crested breakwater. Coastal Eng. 2009, 56, 1123–1132. [Google Scholar] [CrossRef]
- Peng, Z.; Zou, Q.; Lin, P. A partial cell technique for modeling the morphological change and scour. Coastal Eng. 2018, 131, 88–105. [Google Scholar] [CrossRef]
- Ruessink, B.V.; Van Den Berg, T.J.J.; Van Rijn, L.C. Modeling sediment transport beneath skewed asymmetric waves above a plane bed. J. Geophys. Res. Oceans 2009, 114, 1–14. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, D.; Madsen, O.S. Seabed shear stress and bedload transport due to asymmetric and skewed waves. Coastal Eng. 2007, 54, 914–929. [Google Scholar] [CrossRef]
- Hoefel, F.; Elgar, S. Wave-induced sediment transport and sandbar migration. Science 2003, 299, 1885–1887. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. Coastal Eng. 1976, 1976, 828–845. [Google Scholar] [CrossRef]
- Dastgheib, A.; Martinez, C.; Udo, K.; Ranasinghe, R. Climate change driven shoreline change at Hasaki Beach Japan: A novel application of the Probabilistic Coastline Recession (PCR) model. Coast. Eng. 2021, 172, 104079. [Google Scholar] [CrossRef]
- Bonaldo, D.; Bucchignani, E.; Pomaro, A.; Ricchi, A.; Sclavo, M.; Carniel, S. Wind waves in the Adriatic Sea under a severe climate change scenario and implications for the coasts. Int. J. Clim. 2020, 40, 5389–5406. [Google Scholar] [CrossRef]
- Forgiarini, A.P.P.; de Figueiredo, S.A.; Calliari, L.J.; Goulart, E.S.; Marques, W.; Trombetta, T.B.; Oleinik, P.H.; Guimaraes, R.C.; Arigony-Neto, J.; Salame, C.C. Quantifying the geomorphologic and urbanization influence on coastal retreat under sea level rise. Estuar. Coast. Shelf Sci. 2019, 230, 106437. [Google Scholar] [CrossRef]
- Thepsiriamnuay, H.; Pumijumnong, N. Modelling Assessment of Sandy Beaches Erosion in Thailand. Environ. Nat. Resour. J. 2018, 17, 71–86. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Ranasinghe, R.; Mentaschi, L.; Plomaritis, T.A.; Athanasiou, P.; Luijendijk, A.; Feyen, L. Sandy coastlines under threat of erosion. Nat. Clim. Chang. 2020, 10, 260–263. [Google Scholar] [CrossRef]
- Bagheri, M.; Zaiton Ibrahim, Z.; Bin Mansor, S.; Abd Manaf, L.; Badarulzaman, N.; Vaghefi, N. Shoreline change analysis and erosion prediction using historical data of Kuala Terengganu, Malaysia. Environ. Earth Sci. 2019, 78, 1–21. [Google Scholar] [CrossRef]
- Frohlich, M.F.; Smith, T.F.; Fidelman, P.; Baldwin, C.; Jacobson, C.; Carter, R.B. Legal barriers to adaptive coastal management at a coastal erosion hotspot in Florianópolis, Brazil. Mar. Policy 2021, 127, 104436. [Google Scholar] [CrossRef]
- Yu, J.; Ding, Y.; Zhang, L.; Liu, P.; Fan, R. Erosion hotspot identified along the sandy coast of Shanwei: Characteristics and origin. Acta Oceanol. Sin. 2023, 42, 91–102. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Razmi, A.M.; Barry, D.A.; Yeganeh-Bakhtiary, A.; Zou, Q. Air-water two-phase flow modeling of turbulent surf and swash zone wave motions. Adv. Water Resour. 2010, 33, 1560–1574. [Google Scholar] [CrossRef]
- Lara, J.L.; Garcia, N.; Losada, I.J. RANS modelling applied to random wave interaction with submerged permeable structures. Coastal Eng. 2006, 53, 395–417. [Google Scholar] [CrossRef]
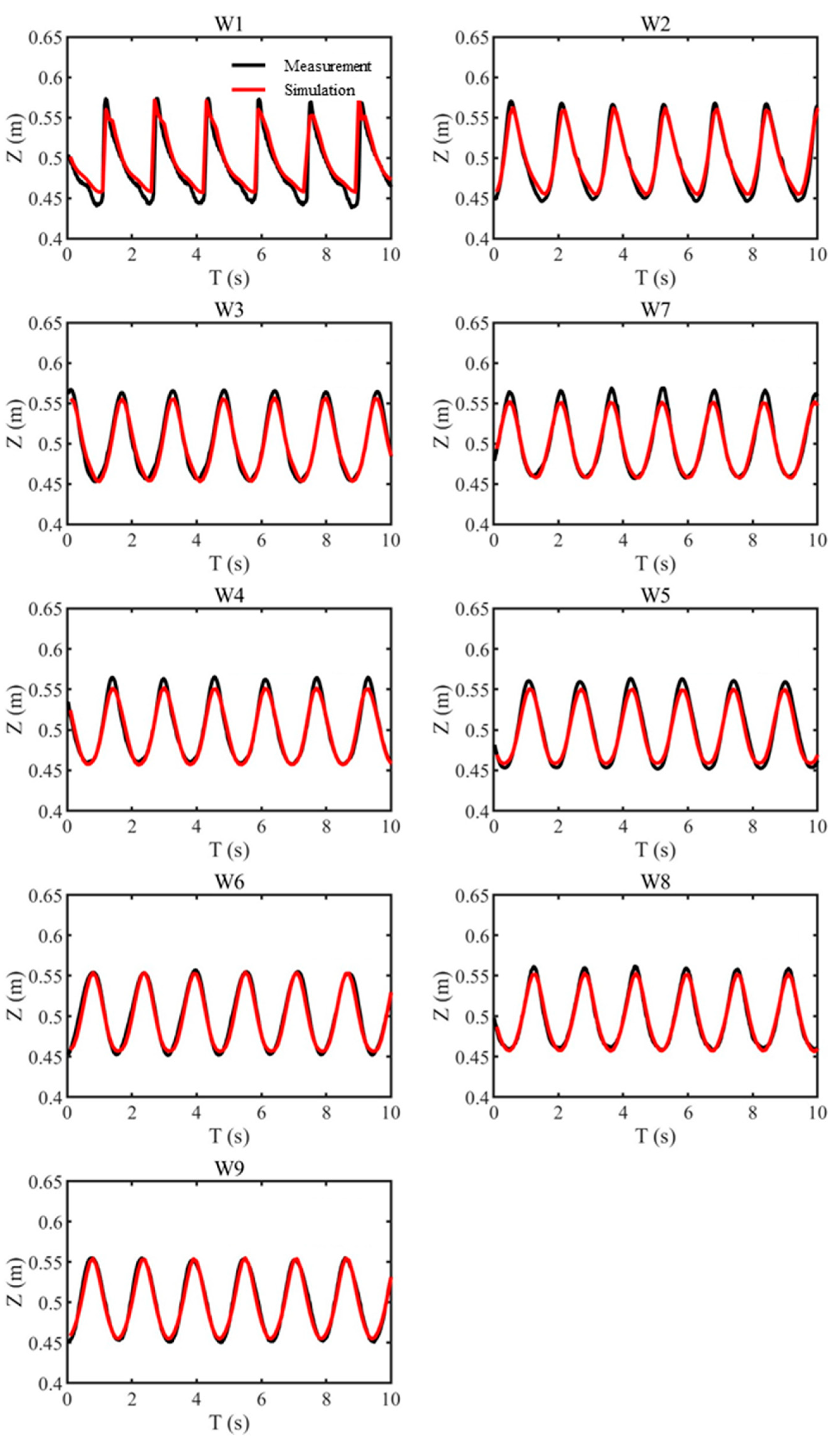
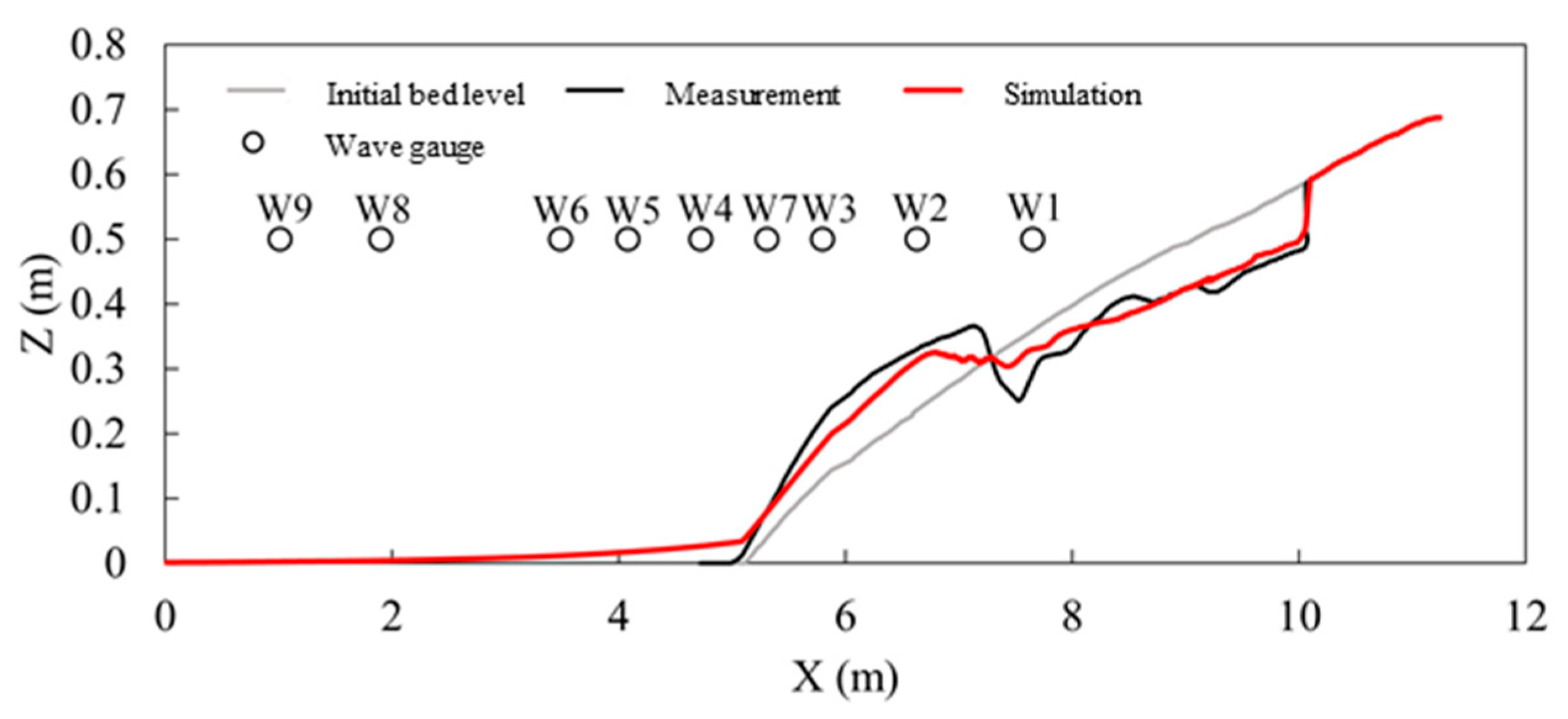



| Item | Position | d | Evaluation |
|---|---|---|---|
| Wave surface | W1 | 0.9421 | Excellent |
| Wave surface | W2 | 0.9917 | Excellent |
| Wave surface | W3 | 0.9925 | Excellent |
| Wave surface | W4 | 0.9936 | Excellent |
| Wave surface | W5 | 0.9905 | Excellent |
| Wave surface | W6 | 0.9942 | Excellent |
| Wave surface | W7 | 0.9921 | Excellent |
| Wave surface | W8 | 0.9966 | Excellent |
| Wave surface | W9 | 0.9955 | Excellent |
| Beach profile | 0.9953 | Excellent |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuang, C.; Fan, J.; Han, X.; Li, H.; Qin, R.; Zou, Q. Numerical Modelling of Beach Profile Evolution with and without an Artificial Reef. Water 2023, 15, 3832. https://doi.org/10.3390/w15213832
Kuang C, Fan J, Han X, Li H, Qin R, Zou Q. Numerical Modelling of Beach Profile Evolution with and without an Artificial Reef. Water. 2023; 15(21):3832. https://doi.org/10.3390/w15213832
Chicago/Turabian StyleKuang, Cuiping, Jiadong Fan, Xuejian Han, Hongyi Li, Rufu Qin, and Qingping Zou. 2023. "Numerical Modelling of Beach Profile Evolution with and without an Artificial Reef" Water 15, no. 21: 3832. https://doi.org/10.3390/w15213832
APA StyleKuang, C., Fan, J., Han, X., Li, H., Qin, R., & Zou, Q. (2023). Numerical Modelling of Beach Profile Evolution with and without an Artificial Reef. Water, 15(21), 3832. https://doi.org/10.3390/w15213832







