Performance Evaluation of Five Machine Learning Algorithms for Estimating Reference Evapotranspiration in an Arid Climate
Abstract
:1. Introduction
- ETo estimation using five ML (ID3, GB, RF, MLNN, and RBFNN) algorithms.
- Identifying an effective combination of meteorological inputs for ETo estimation.
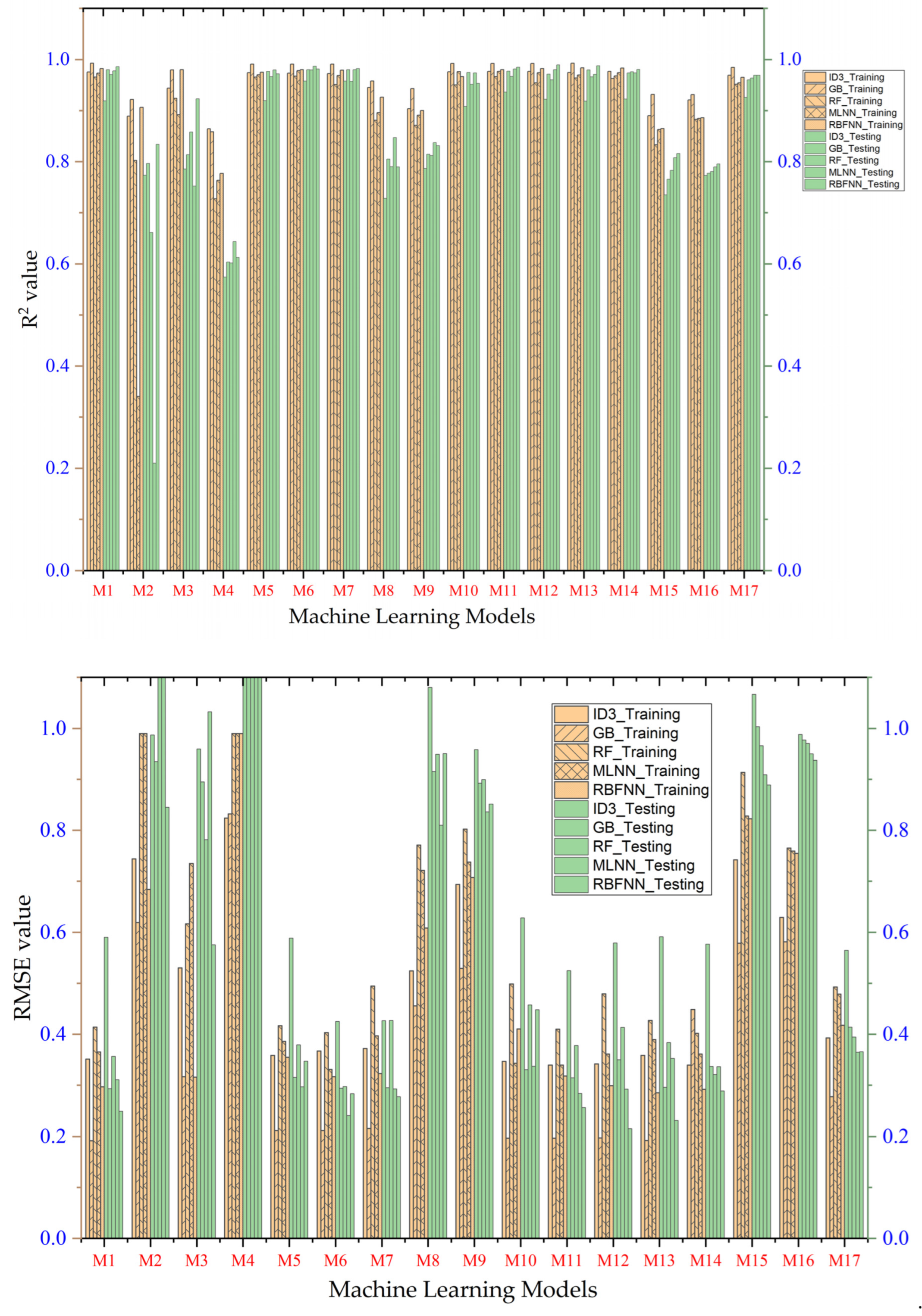
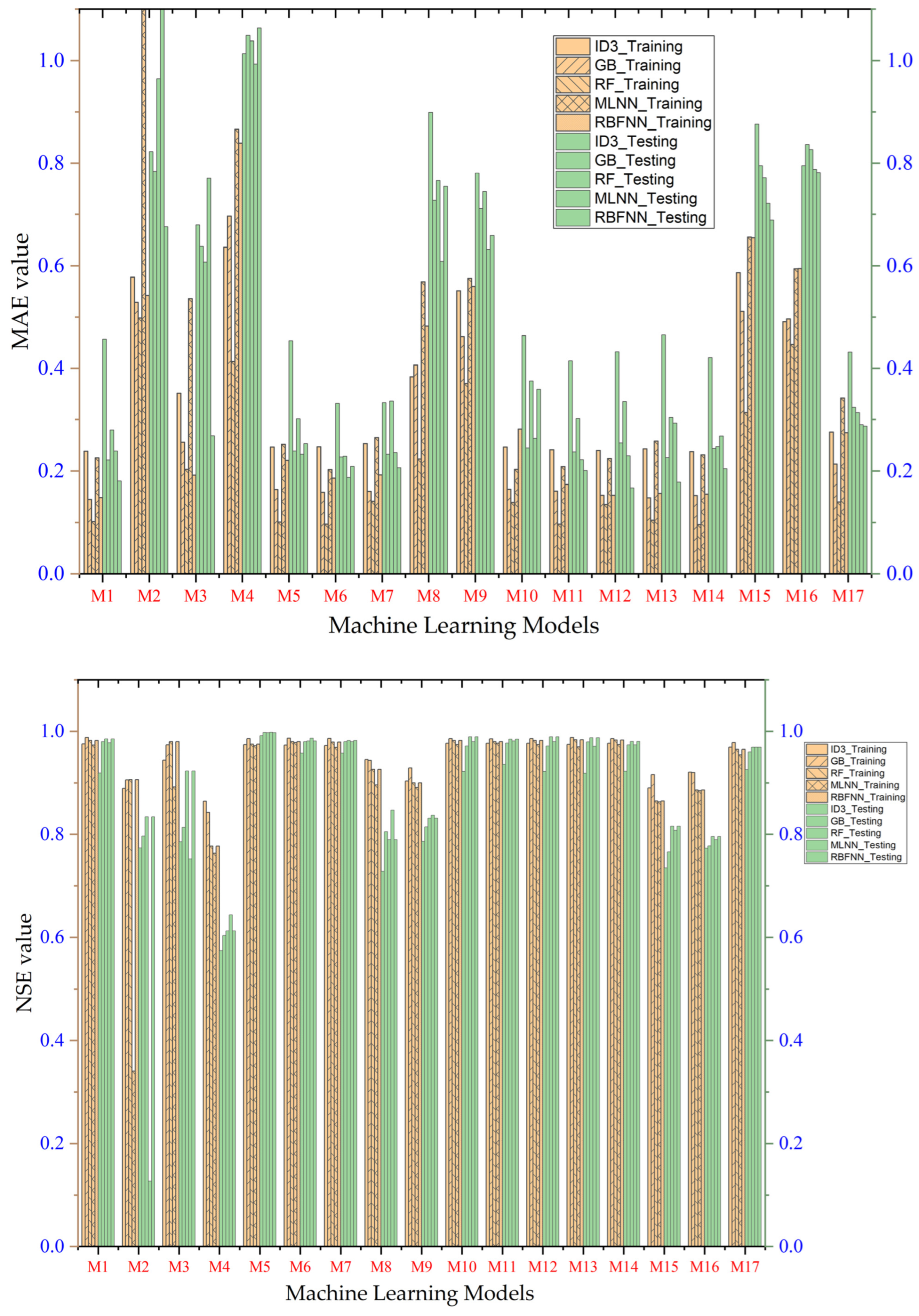
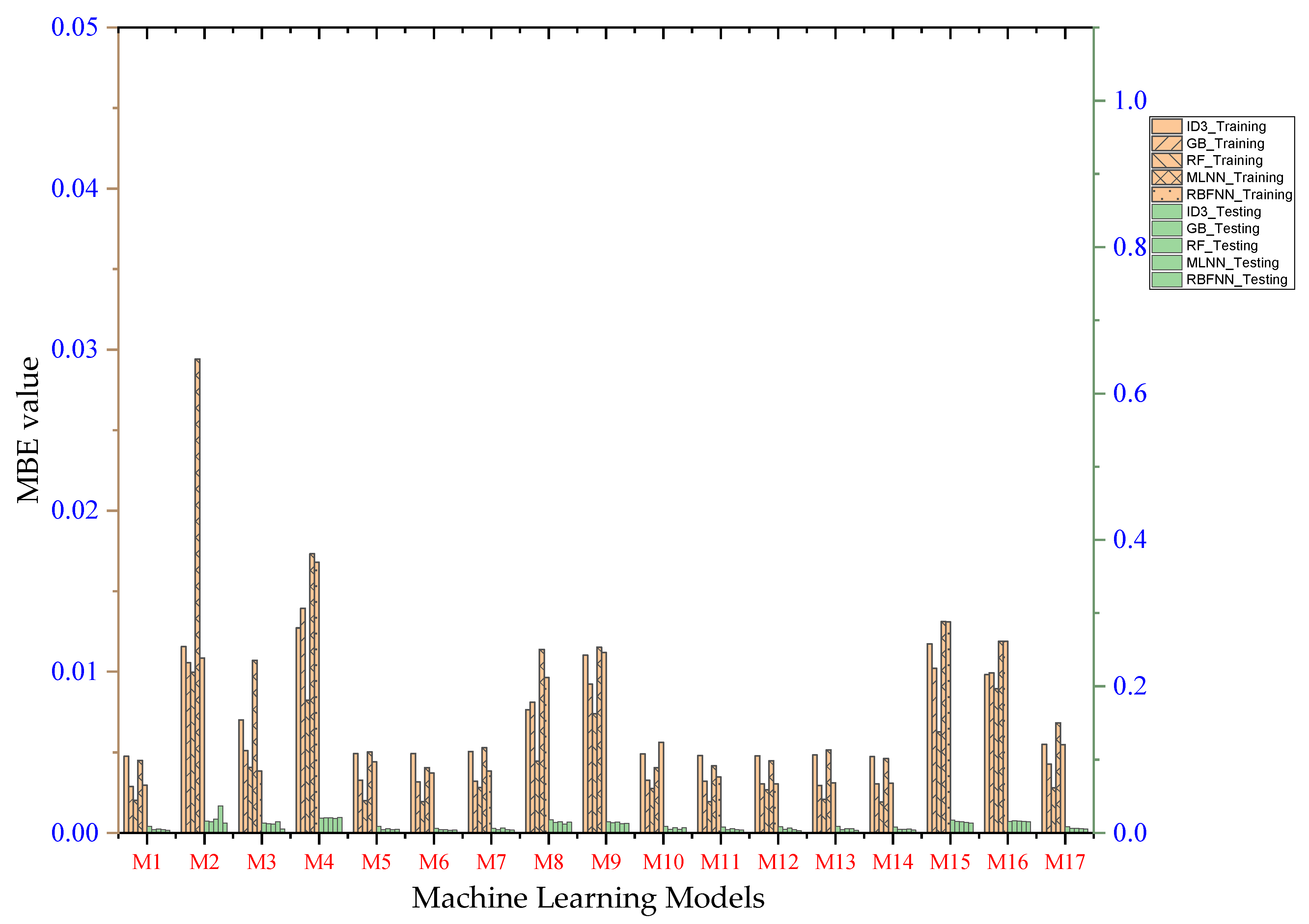
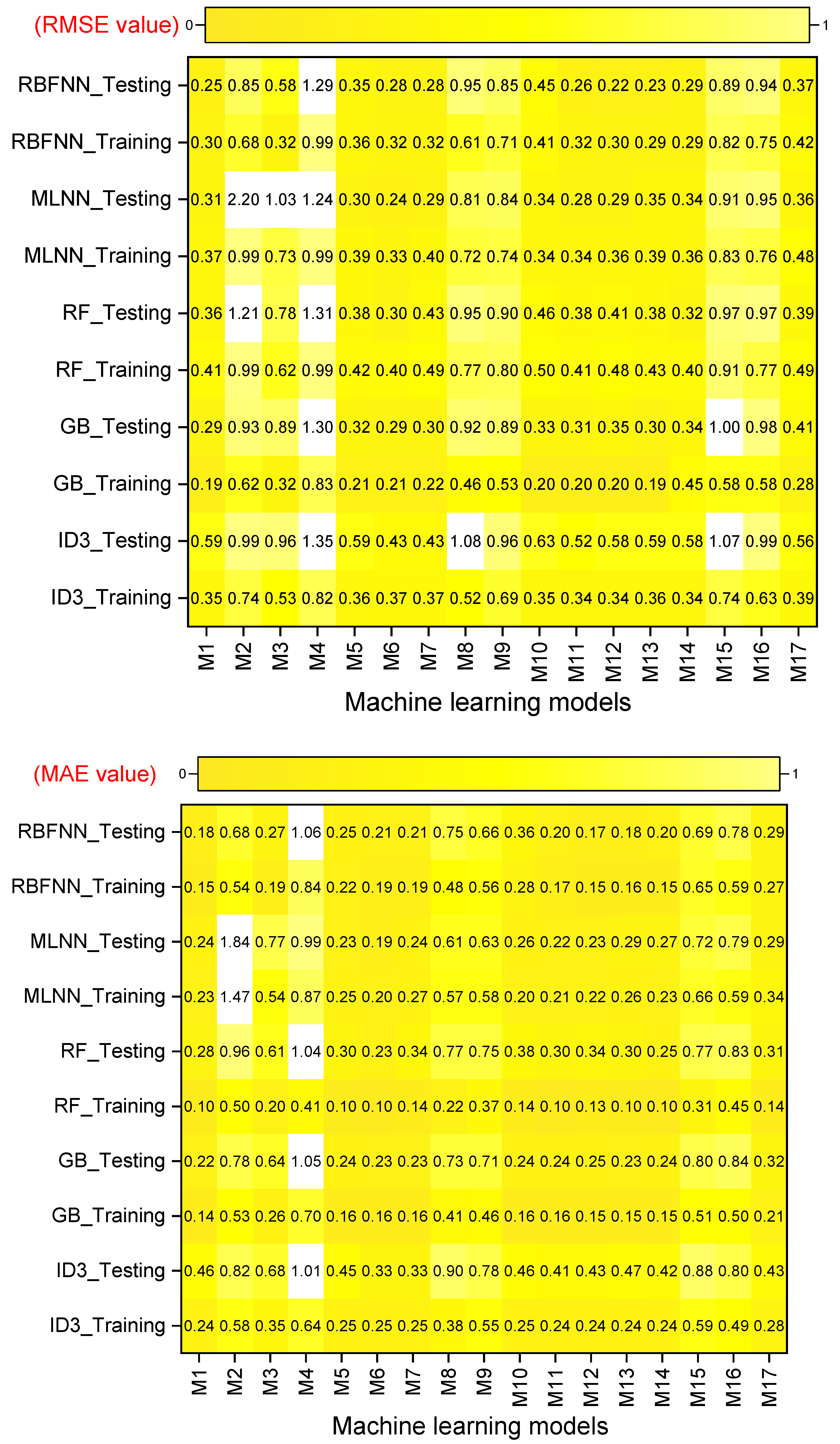
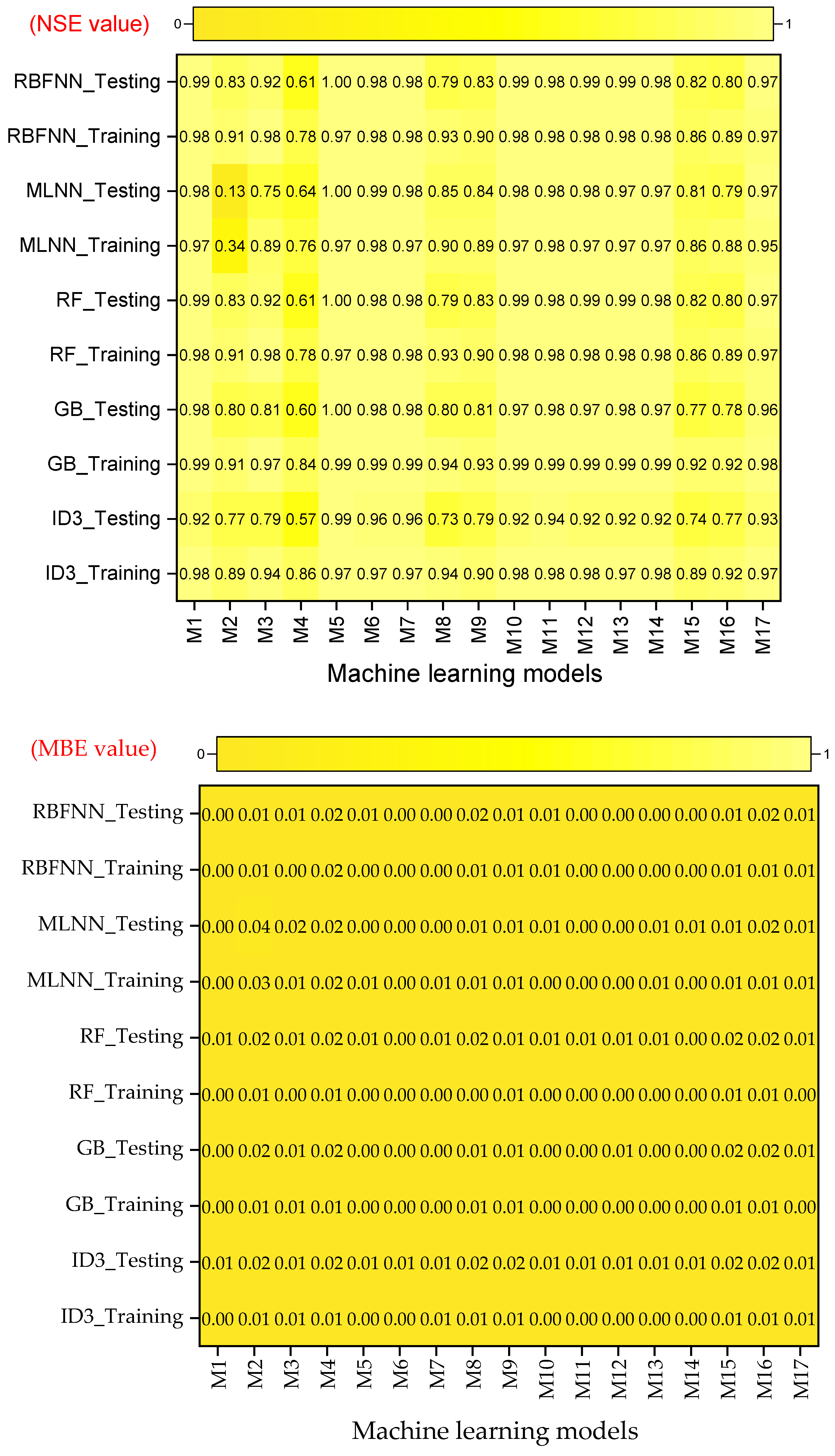
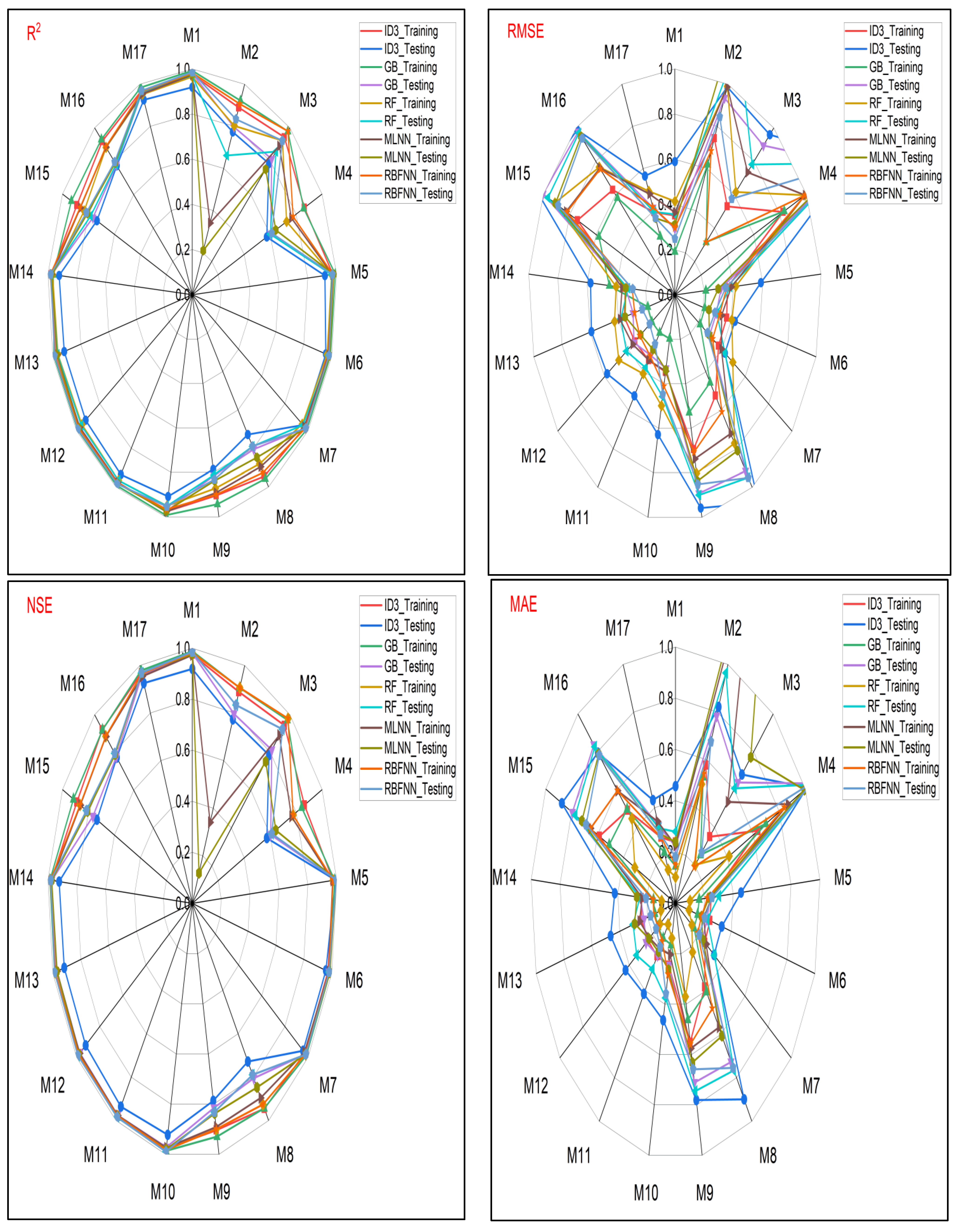
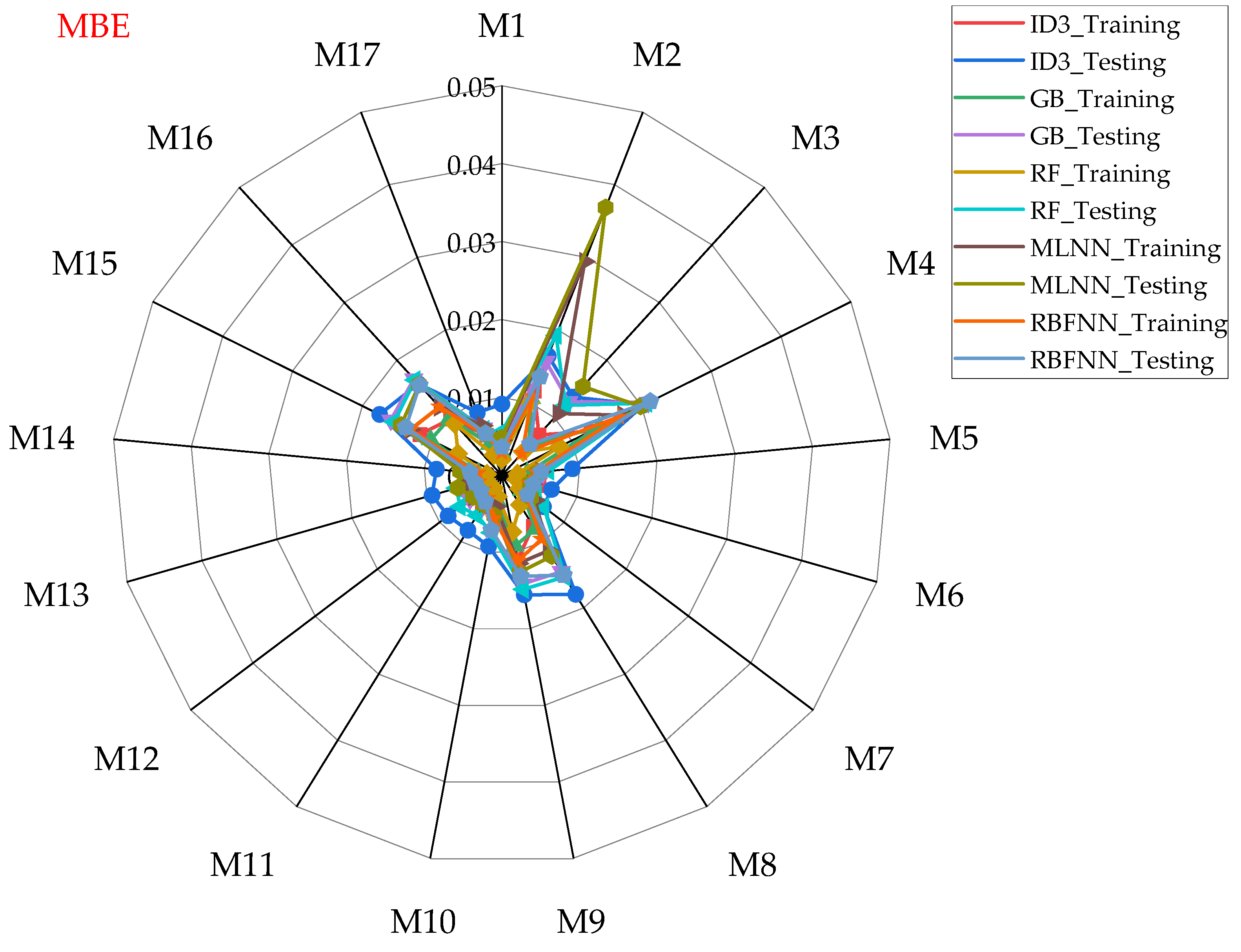
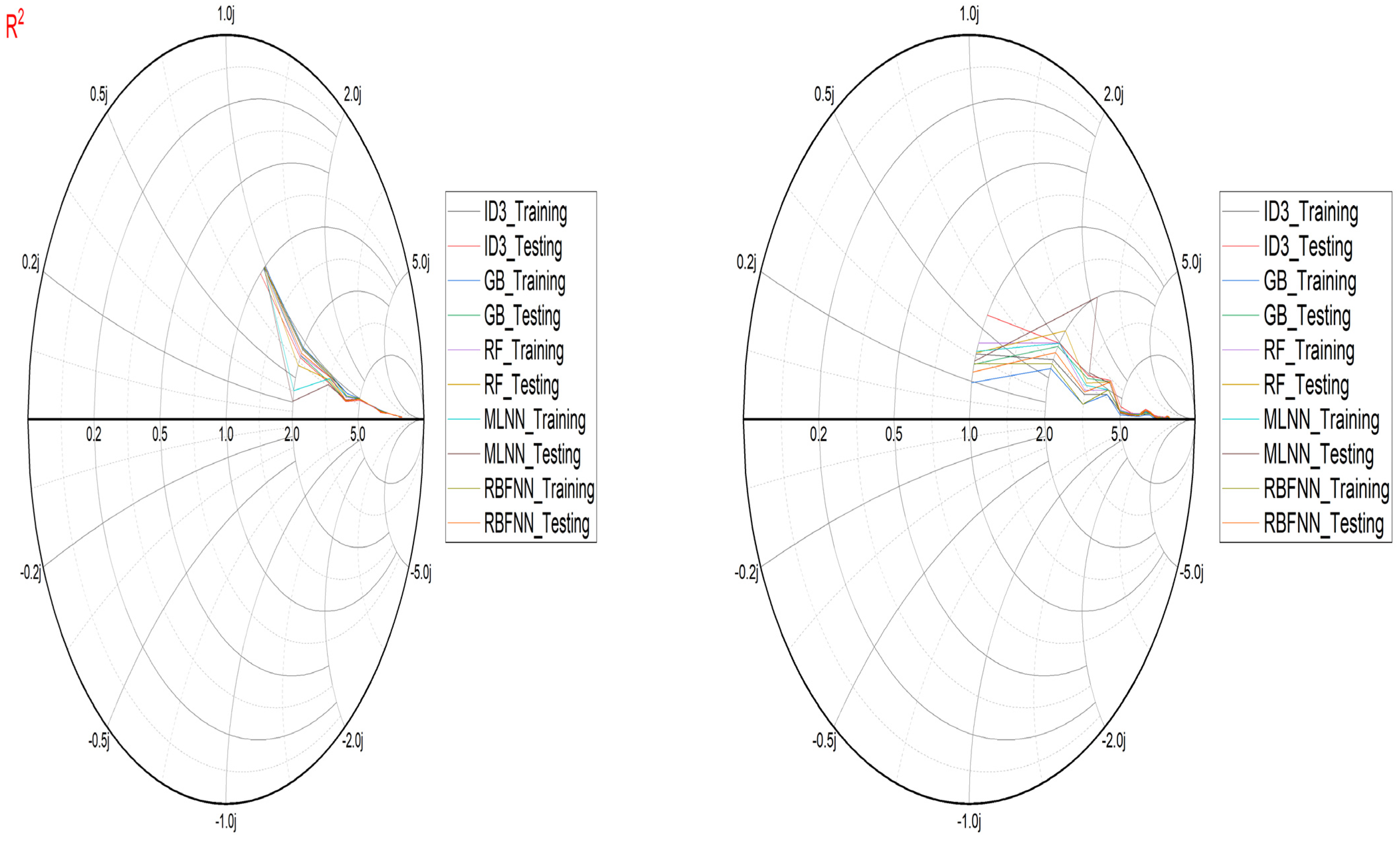
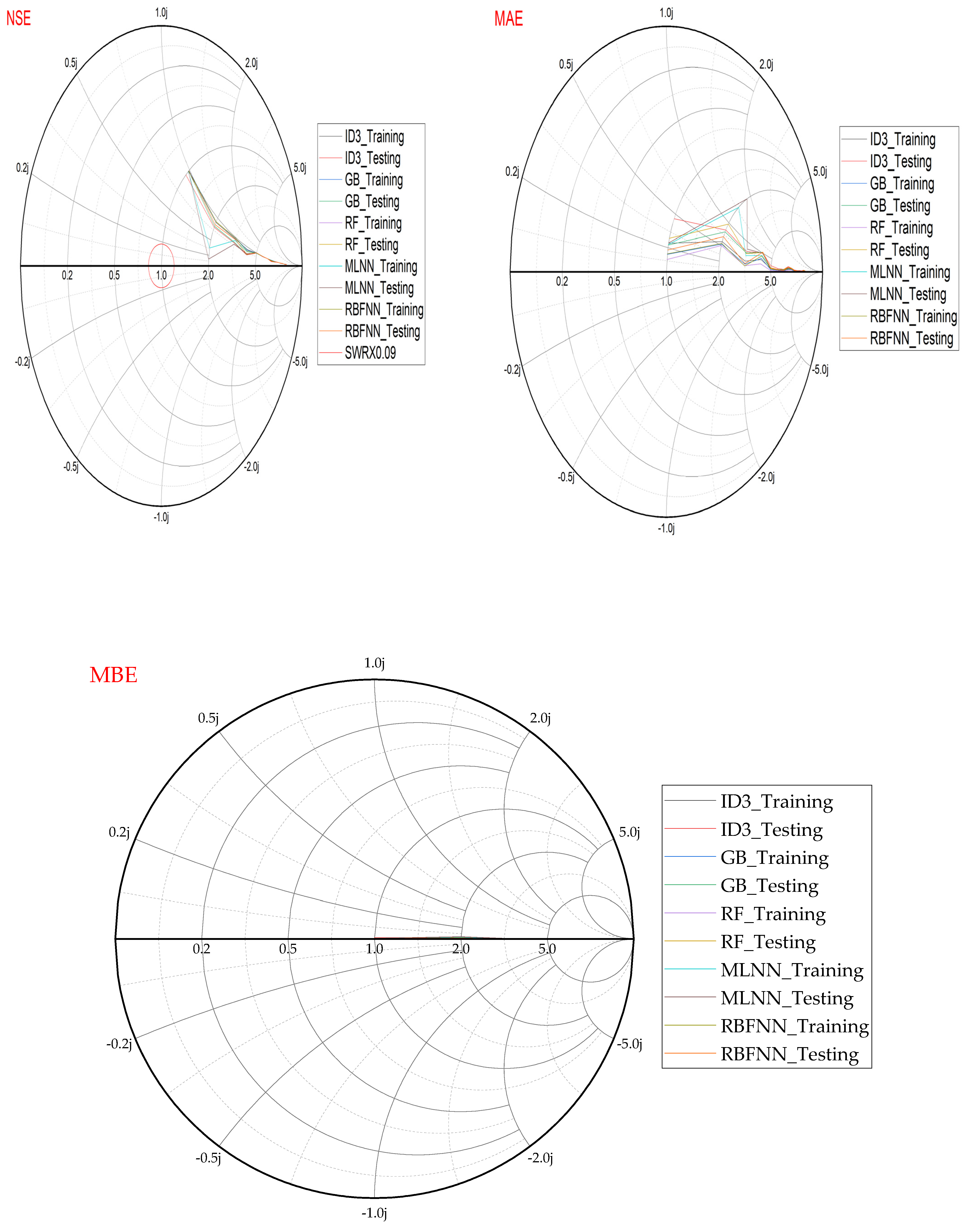
- Performance evaluation of ML algorithms through visualization (radar, heatmap, bullet, and Smith graphs) based on different statistical indices to determine the best one among them.
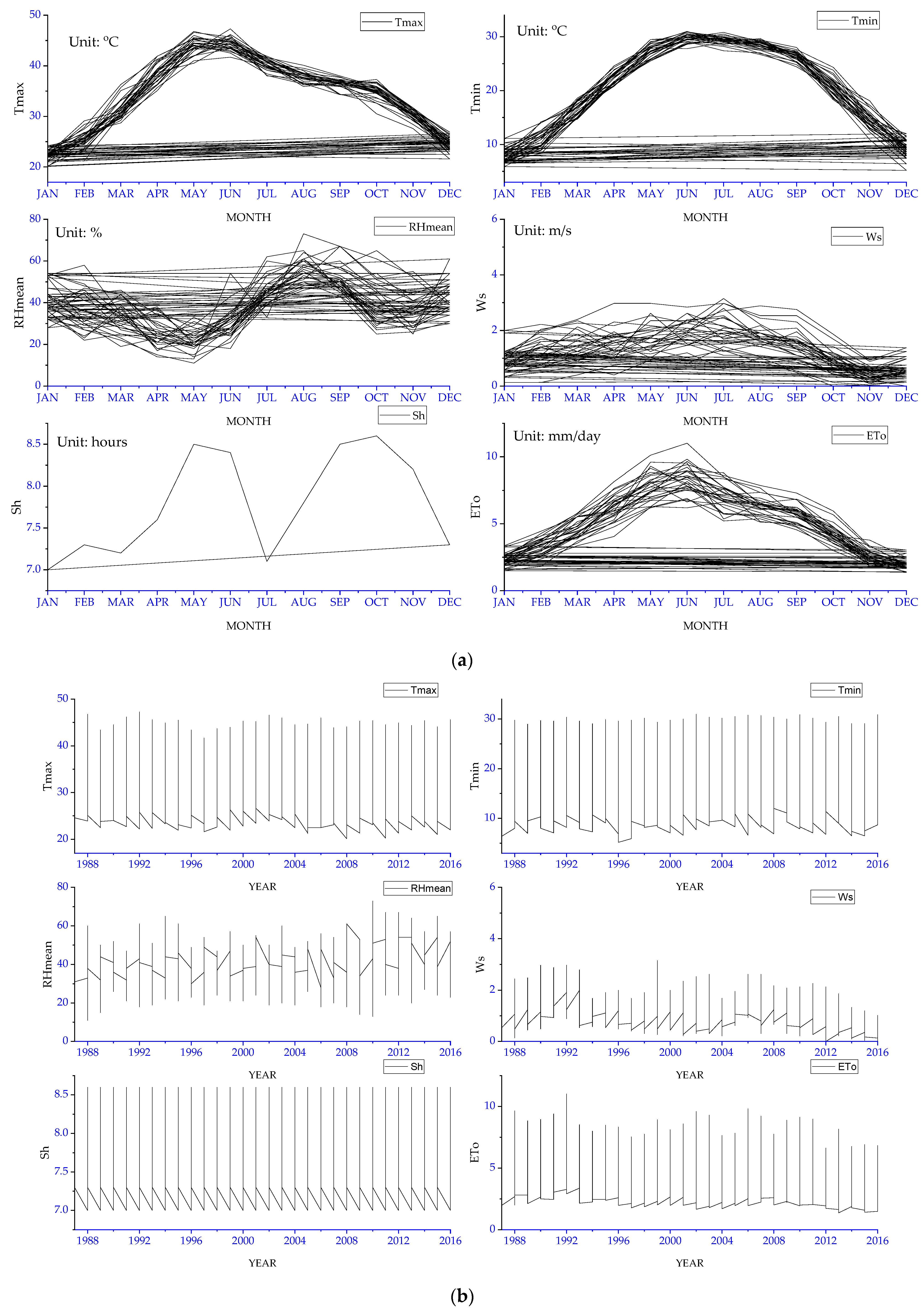
2. Study Area and Dataset
Physical–Geographical Conditions
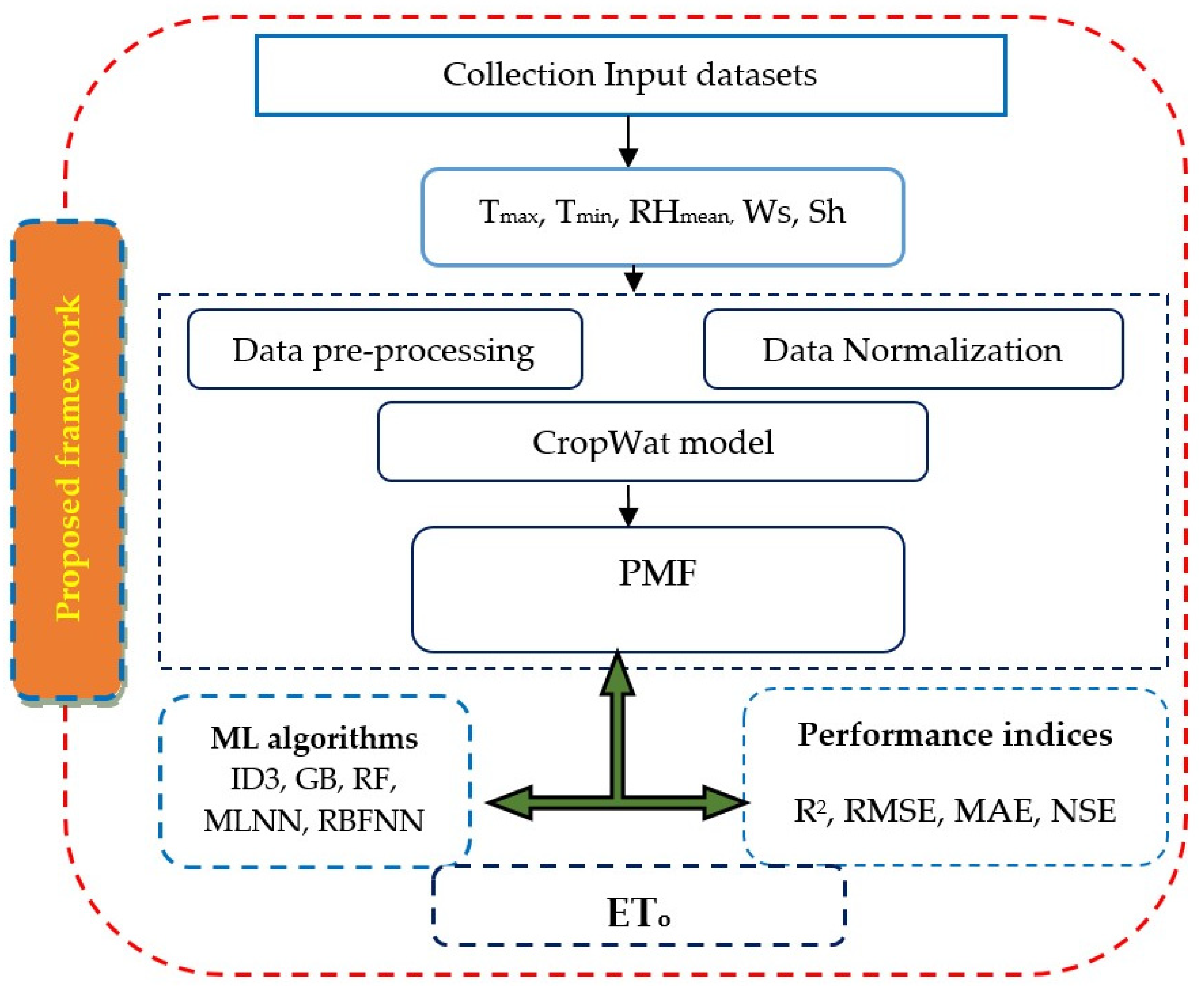
3. Study Methodology
3.1. PMF
3.2. Proposed ML Framework
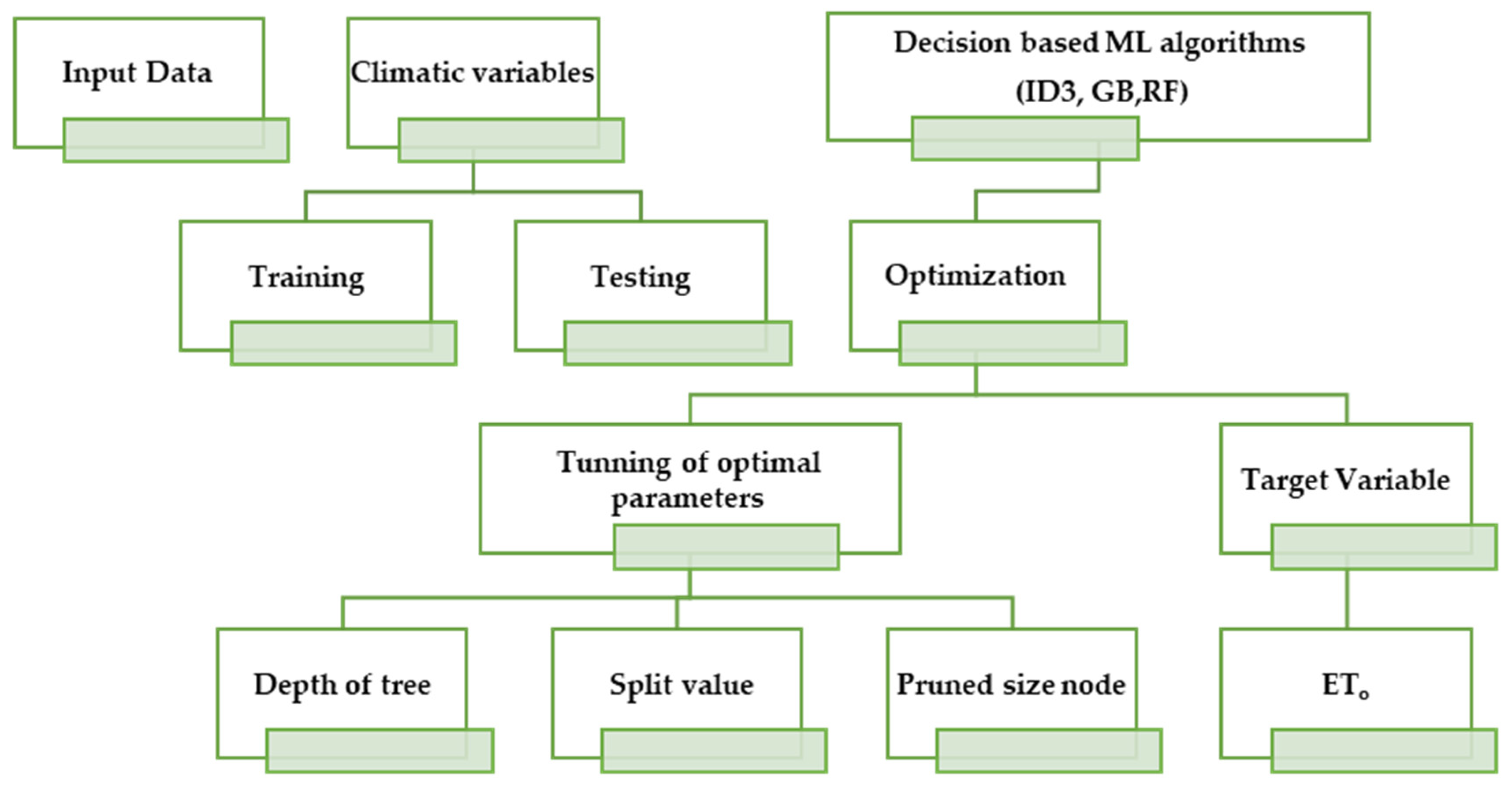
3.2.1. Iterative Dichotomizer (ID3)
3.2.2. Gradient Boosting (GB)
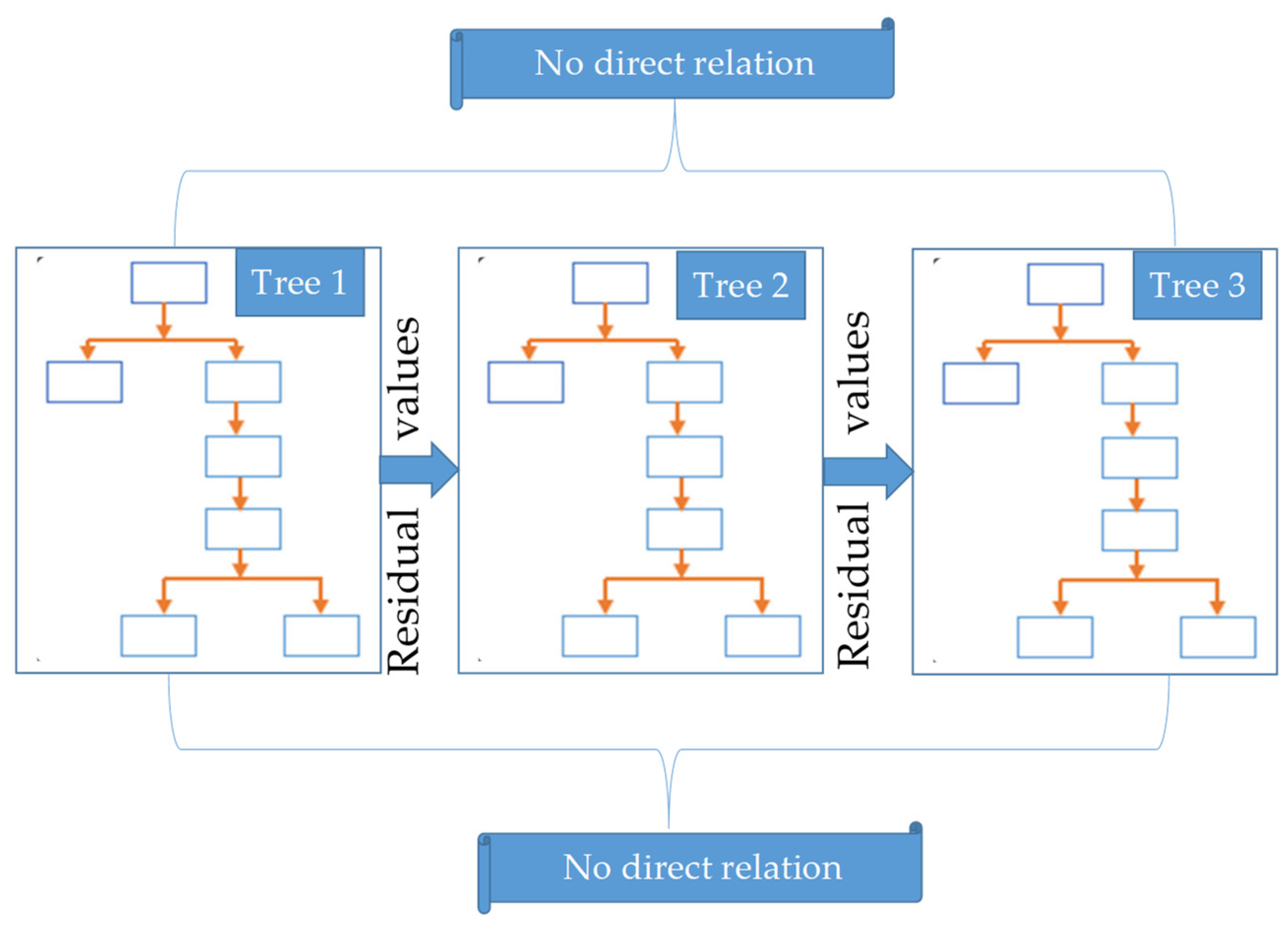
3.2.3. Random Forest (RF)
- Climatic variables were chosen as predictors/inputs.
- The sample data constituted 70% of the total dataset, separated using the randomization function.
- Analysis was performed using dataset (OOB), and residual values were stored separately.
- The ETo obtained from each tree as output was gathered and stored.
- The mean values of the output variable (ETo) were computed as a whole.
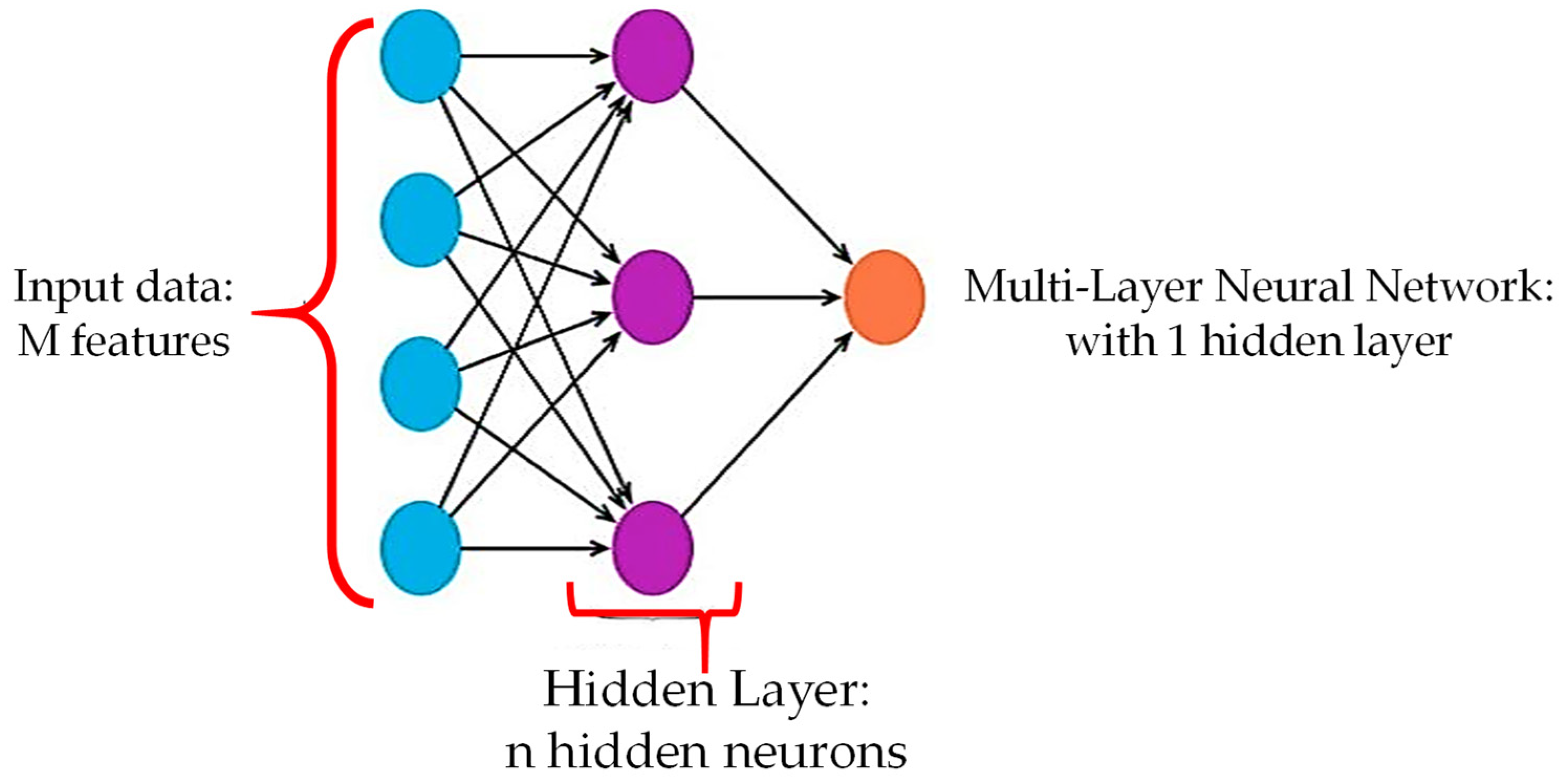
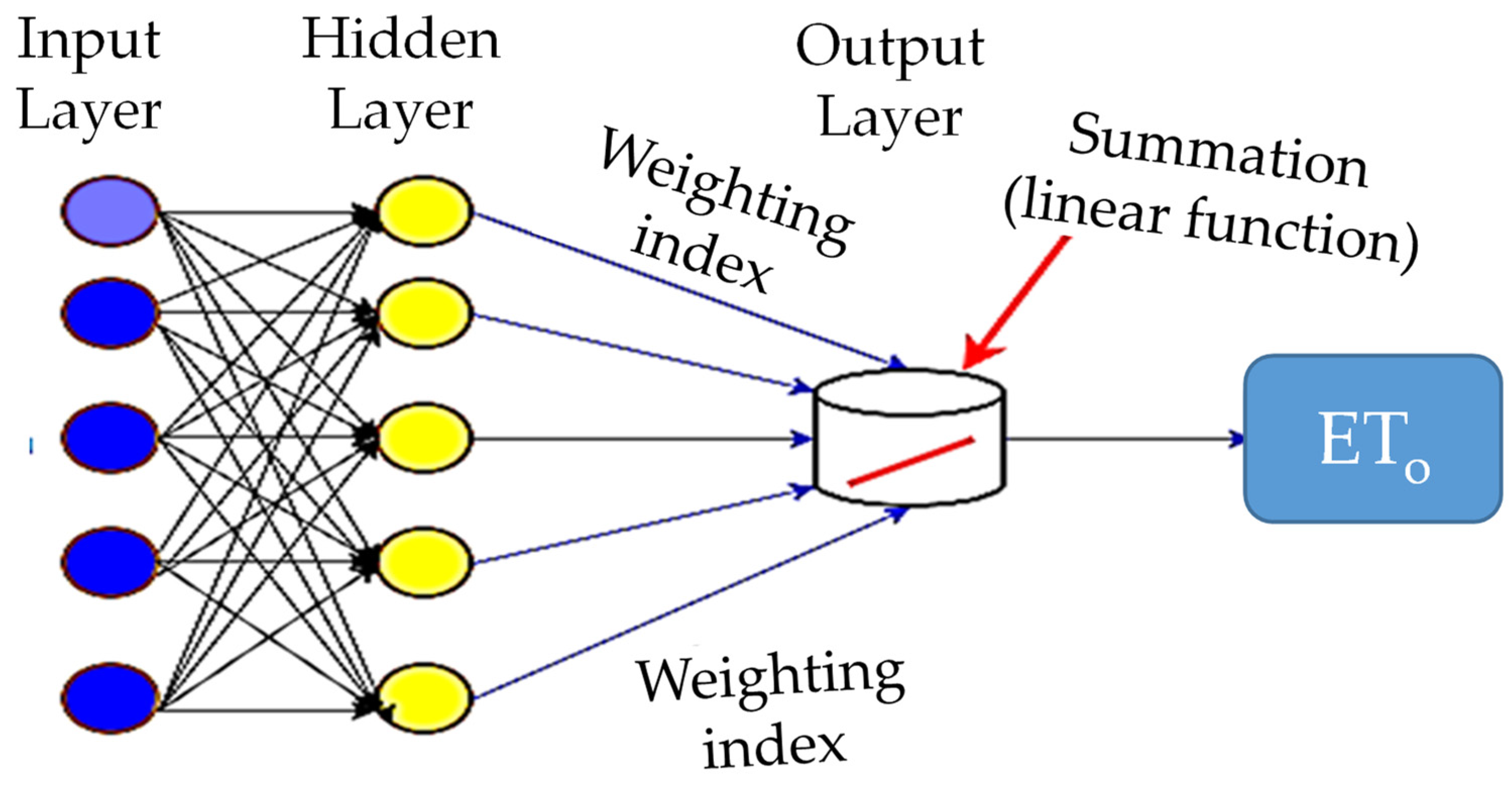
3.2.4. Multilayer Neural Network (MLNN)
- Climate-related input variables were chosen as predictors.
- Sigmoid and linear activation functions were used in the input-hidden and hidden-output layers.
- The weight connection between interconnected neurons was adjusted via the adoption of a back-propagation procedure.
- The kernel functions utilized were Traditional Conjugate Gradient (TCG) and Scaled Conjugate Gradient (SCG).
- The ETo was estimated as an output.
3.2.5. Radial Basis Function Neural Network (RBFNN)
3.2.6. Selection of Meteorological Input Combinations
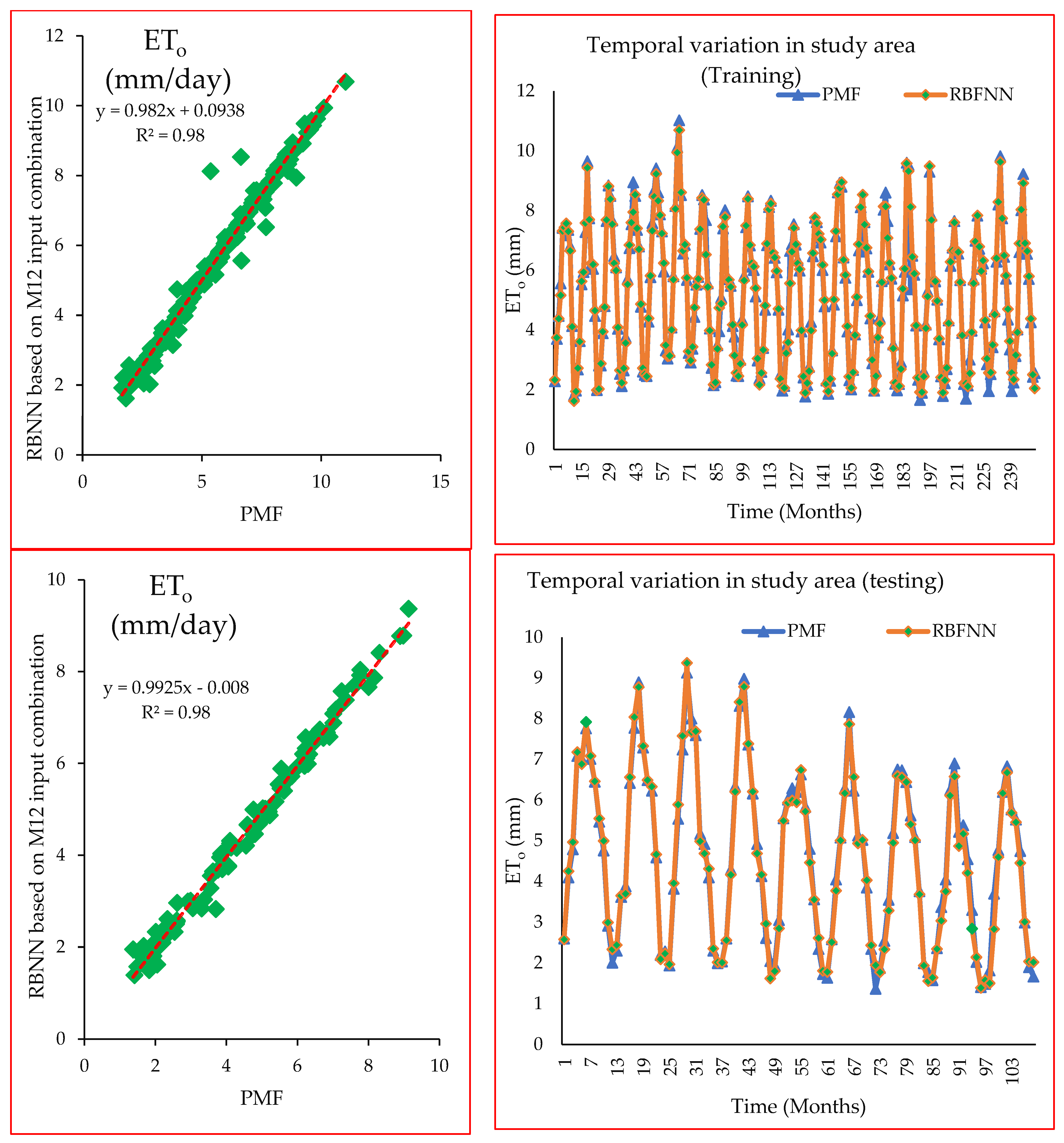
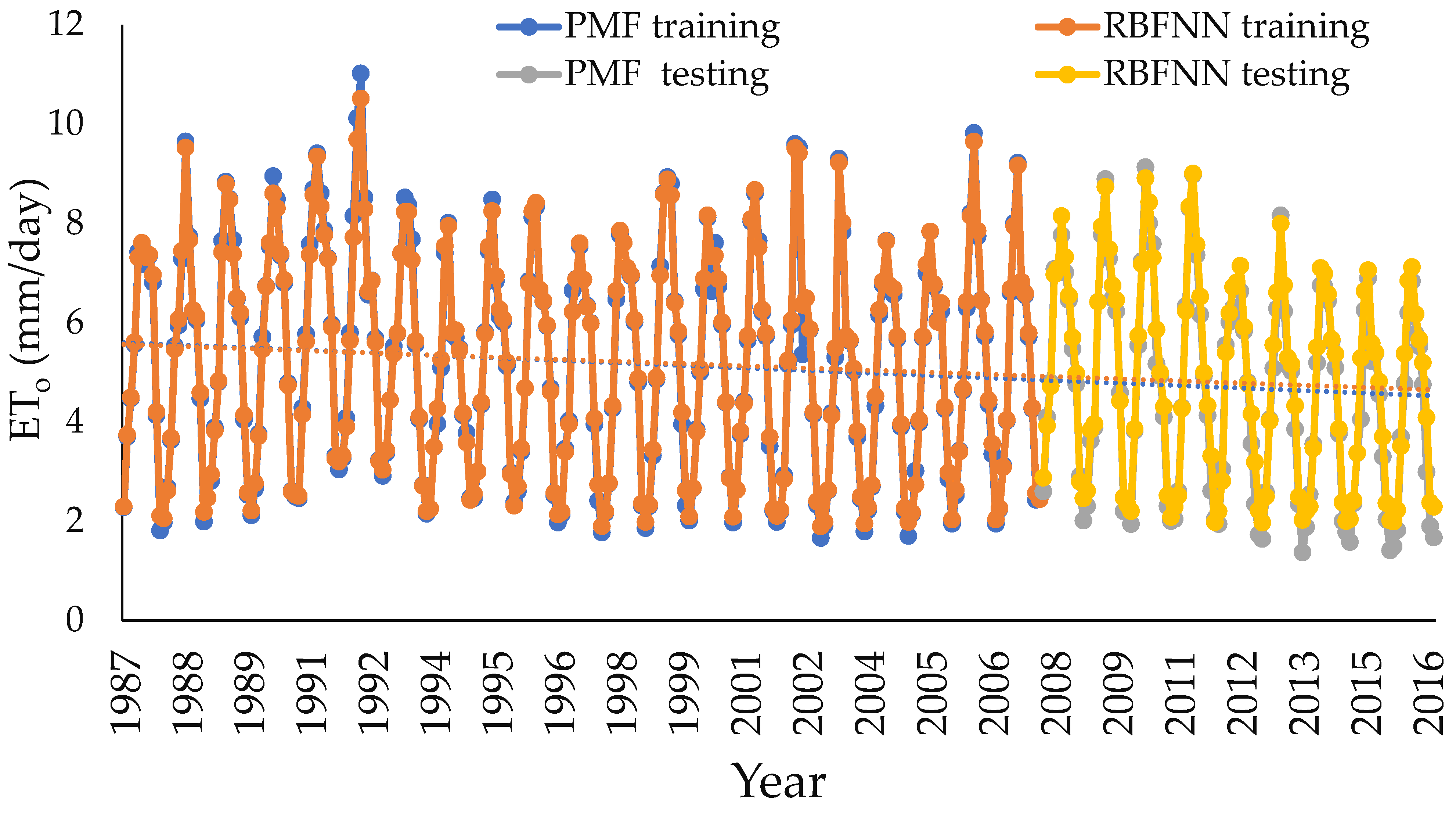
4. Study Results
5. Study Discussion
6. Conclusions
Limitations, Suggested Improvements, and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brasseur, G.P.; Jacob, D.; Schuck-Zöller, S. Climate Change 2001: Working Group II: Impacts, Adaptation and Vulnerability; Falkenmark and Lindh Quoted in UNEP/WMO; UNEP: Nairobi, Kenya, 2009. [Google Scholar]
- Fangmeier, D.D.; Elliot, W.J.; Workman, S.R.; Huffman, R.L.; Schwab, G.O. Soil and Water Conservation Engineering, 5th ed.; Thomson: Stamford, CT, USA, 2006. [Google Scholar]
- Gavilan, P.; Berengena, J.; Allen, R.G. Measuring versus estimating net radiation and soil heat flux: Impact on Penman–Monteith reference ET estimates in semiarid regions. Agric. Water Manag. 2007, 89, 275–286. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- López-Urrea, R.; De Santa Olalla, F.M.; Fabeiro, C.; Moratalla, A. Testing evapotranspiration equations using lysimeter observations in a semiarid climate. Agric. Water Manag. 2006, 85, 15–26. [Google Scholar] [CrossRef]
- Allen, R.G.; Walter, I.A.; Elliott, R.L.; Howell, T.A.; Itenfisu, D.; Jensen, M.E.; Snyder, R.L. The ASCE standardised reference evapotranspiration equation. In Task Committee on Standardization of Reference Evapotranspiration of the EWRI of the ASCE; ASCE: Reston, VI, USA, 2005. [Google Scholar]
- Başağaoğlu, H.; Chakraborty, D.; Winterle, J. Reliable Evapotranspiration Predictions with a Probabilistic Machine Learning Framework. Water 2021, 13, 557. [Google Scholar] [CrossRef]
- Chakraborty, D.; Başağaoğlu, H.; Winterle, J. Interpretable vs. noninterpretable machine learning models for data-driven hydro-climatological process modeling. Expert Syst. Appl. 2021, 170, 114498. [Google Scholar] [CrossRef]
- Ravindran, S.M.; Bhaskaran, S.K.M.; Ambat, S.K.N. A Deep Neural Network Architecture to Model Reference Evapotranspiration Using a Single Input Meteorological Parameter. Environ. Process. 2021, 8, 1567–1599. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhao, L.; Lin, A.; Qin, W.; Lu, Y.; Li, J.; Zhong, Y.; He, L. Exploring the potential of deep factorization machine and various gradient boosting models in modeling daily reference evapotranspiration in China. Arab. J. Geosci. 2020, 13, 1287. [Google Scholar] [CrossRef]
- Deo, R.C.; Wen, X.; Qi, F. A wavelet-coupled support vector machine model for forecasting global incident solar radiation using limited meteorological dataset. Appl. Energy 2016, 168, 568–593. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Hu, B.; Gong, W. Modeling and comparison of hourly photosynthetically active radiation in different ecosystems. Renew. Sustain. Energy Rev. 2015, 56, 436–453. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Salazar, G.; Zhu, Z.; Gong, W. Solar radiation prediction using different techniques: Model evaluation and comparison. Renew. Sustain. Energy Rev. 2016, 61, 384–397. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Software for estimating reference evapotranspiration using limited weather data. Comput. Electron. Agric. 2010, 71, 158–162. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P. Local calibration of the Hargreaves and Priestley–Taylor equations for estimating reference evapotranspiration in arid and cold climates of Iran based on the Penman–Monteith model. J. Hydrol. Eng. 2011, 16, 837–845. [Google Scholar] [CrossRef]
- Martí, P.; Royuela, A.; Manzano, J.; Palau-Salvador, G. Generalization of RET ANN Models through Data Supplanting. J. Irrig. Drain. Eng. 2010, 136, 161–174. [Google Scholar] [CrossRef]
- Rojas, J.P.; Sheffield, R.E. Evaluation of Daily Reference Evapotranspiration Methods as Compared with the ASCE-EWRI Penman-Monteith Equation Using Limited Weather Data in Northeast Louisiana. J. Irrig. Drain. Eng. 2013, 139, 285–292. [Google Scholar] [CrossRef]
- Sahoo, B.; Walling, I.; Deka, B.C.; Bhatt, B.P. Standardization of Reference Evapotranspiration Models for a Subhumid Valley Rangeland in the Eastern Himalayas. J. Irrig. Drain. Eng. 2012, 138, 880–895. [Google Scholar] [CrossRef]
- Shiri, J.; Nazemi, A.H.; Sadraddini, A.A.; Landeras, G.; Kisi, O.; Fard, A.F.; Marti, P. Comparison of heuristic and empirical approaches for estimating reference evapotranspiration from limited inputs in Iran. Comput. Electron. Agric. 2014, 108, 230–241. [Google Scholar] [CrossRef]
- Ehteram, M.; Singh, V.P.; Ferdowsi, A.; Mousavi, S.F.; Farzin, S.; Karami, H.; Mohd, N.S.; Afan, H.A.; Lai, S.H.; Kisi, O.; et al. An improved model based on the support vector machine and cuckoo algorithm for simulating reference evapotranspiration. PLoS ONE 2019, 14, e0217499. [Google Scholar] [CrossRef]
- Sayyahi, F.; Farzin, S.; Karami, H. Forecasting Daily and Monthly Reference Evapotranspiration in the Aidoghmoush Basin Using Multilayer Perceptron Coupled with Water Wave Optimization. Complexity 2021, 2021, 668375. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H.; Abghari, H. Utility of coactive neuro-fuzzy inference system for pan evaporation modeling in comparison with multilayer perceptron. Meteorol. Atmos. Phys. 2012, 116, 147–154. [Google Scholar] [CrossRef]
- Zakeri, M.S.; Mousavi, S.F.; Farzin, S.; Sanikhani, H. Modeling of Reference Crop Evapotranspiration in Wet and Dry Climates Using Data-Mining Methods and Empirical Equations. J. Soft Comput. Civ. Eng. 2022, 6, 1–28. [Google Scholar] [CrossRef]
- Fooladmand, H.R.; Zandilak, H.; Ravanan, M.H. Comparison of different types of Hargreaves equation for estimating monthly evapotranspiration in the south of Iran. Arch. Agron. Soil Sci. 2008, 54, 321–330. [Google Scholar] [CrossRef]
- George, B.A.; Reddy, B.R.S.; Raghuwanshi, N.S.; Wallender, W.W. Decision support system for estimating reference evapotranspiration. J. Irrig. Drain. Eng. 2002, 128, 1–10. [Google Scholar] [CrossRef]
- Sabziparvar, A.A.; Tabari, H. Regional estimation of reference evapotranspiration in arid and semiarid regions. J. Irrig. Drain. Eng. 2010, 136, 724–731. [Google Scholar] [CrossRef]
- Tabari, H. Evaluation of reference crop evapotranspiration equations in various climates. Water Resour. Manag. 2010, 24, 2311–2337. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V.P. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland. Water Resour. Manag. 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Anaraki, M.V.; Farzin, S.; Mousavi, S.-F.; Karami, H. Uncertainty Analysis of Climate Change Impacts on Flood Frequency by Using Hybrid Machine Learning Methods. Water Resour. Manag. 2021, 35, 199–223. [Google Scholar] [CrossRef]
- Farzin, S.; Anaraki, M.V. Modeling and predicting suspended sediment load under climate change conditions: A new hybridization strategy. J. Water Clim. Chang. 2021, 12, 2422–2443. [Google Scholar] [CrossRef]
- Kumar, M.; Bandyopadhyay, A.; Raghuwanshi, N.S.; Singh, R. Comparative study of conventional and artificial neural network-based ETo estimation models. Irrig. Sci. 2008, 26, 531–545. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R. Artificial neural networks approach in evapotranspiration modeling: A review. Irrig. Sci. 2010, 29, 11–25. [Google Scholar] [CrossRef]
- Landeras, G.; Ortiz-Barredo, A.; López, J.J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain). Agric. Water Manag. 2008, 95, 553–565. [Google Scholar] [CrossRef]
- Khoob, A.R. Comparative study of Hargreaves’s and artificial neural network’s methodologies in estimating reference evapotranspiration in a semiarid environment. Irrig. Sci. 2007, 26, 253–259. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H.; Fung, K.F. Recent Advances in Evapotranspiration Estimation Using Artificial Intelligence Approaches with a Focus on Hybridisation Techniques—A Review. Agronomy 2020, 10, 101. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Yang, L.; Deo, R.C.; Wen, X.; Si, J.; Xiao, S. Future Projection with an Extreme-Learning Machine and Support Vector Regression of Reference Evapotranspiration in a Mountainous Inland Watershed in North-West China. Water 2017, 9, 880. [Google Scholar] [CrossRef]
- Wen, X.; Si, J.; He, Z.; Wu, J.; Shao, H.; Yu, H. Support-Vector-Machine-Based Models for Modeling Daily Reference Evapotranspiration With Limited Climatic Data in Extreme Arid Regions. Water Resour. Manag. 2015, 29, 3195–3209. [Google Scholar] [CrossRef]
- Wang, S.; Fu, Z.-Y.; Chen, H.; Nie, Y.-P.; Wang, K.-L. Modeling daily reference ET in the karst area of northwest Guangxi (China) using gene expression programming (GEP) and artificial neural network (ANN). Theor. Appl. Climatol. 2016, 126, 493–504. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O.; Maroufpoor, E.; Yaseen, Z.M. Temperature-based modeling of reference evapotranspiration using several artificial intelligence models: Application of different modeling scenarios. Theor. Appl. Climatol. 2019, 135, 449–462. [Google Scholar] [CrossRef]
- Pour, O.M.R.; Piri, J.; Kisi, O. Comparison of SVM, ANFIS and GEP in modeling monthly potential evapotranspiration in an arid region (Case study: Sistan and Baluchestan Province, Iran). Water Supply 2019, 19, 392–403. [Google Scholar] [CrossRef]
- Wu, L.; Peng, Y.; Fan, J.; Wang, Y. Machine learning models for the estimation of monthly mean daily reference evapotranspiration based on cross-station and synthetic data. Hydrol. Res. 2019, 50, 1730–1750. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Shiri, J.; Nazemi, A.H.; Sadraddini, A.A.; Marti, P.; Fard, A.F.; Kisi, O.; Landeras, G. Alternative heuristics equations to the Priestley–Taylor approach: Assessing reference evapotranspiration estimation. Appl. Clim. 2019, 138, 831–848. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Kumar, A.; Souag-Gamane, D.; Kisi, O. Estimation of monthly reference evapotranspiration using novel hybrid machine learning approaches. Hydrol. Sci. J. 2019, 64, 1824–1842. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Filho, E.I.F. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM—A new approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kisi, O.; Zounemat-Kermani, M. Polynomial chaos expansion and response surface method for nonlinear modelling of reference evapotranspiration. Hydrol. Sci. J. 2019, 64, 720–730. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abdullahi, J. Multi-station artificial intelligence based ensemble modeling of reference evapotranspiration using pan evaporation measurements. J. Hydrol. 2019, 577, 123958. [Google Scholar] [CrossRef]
- Shiri, J. Modeling reference evapotranspiration in island environments: Assessing the practical implications. J. Hydrol. 2019, 570, 265–280. [Google Scholar] [CrossRef]
- Raza, A.; Hu, Y.; Shoaib, M.; Elnabi, M.K.A.; Zubair, M.; Nauman, M.; Syed, N.R. A Systematic Review on Estimation of Reference Evapotranspiration under Prisma Guidelines. Pol. J. Environ. Stud. 2021, 30, 5413–5422. [Google Scholar] [CrossRef]
- Kushwaha, N.L.; Rajput, J.; Elbeltagi, A.; Elnaggar, A.Y.; Sena, D.R.; Vishwakarma, D.K.; Mani, I.; Hussein, E.E. Data intelligence model and meta-heuristic algorithms-based pan evaporation modelling in two different agro-climatic zones: A case study from Northern India. Atmosphere 2021, 12, 1654. [Google Scholar] [CrossRef]
- Wu, L.; Peng, Y.; Fan, J.; Wang, Y.; Huang, G. A novel kernel extreme learning machine model coupled with K-means clustering and firefly algorithm for estimating monthly reference evapotranspiration in parallel computation. Agric. Water Manag. 2021, 245, 106624. [Google Scholar] [CrossRef]
- Roy, D.K.; Lal, A.; Sarker, K.K.; Saha, K.K.; Datta, B. Optimization algorithms as training approaches for prediction of reference evapotranspiration using adaptive neuro fuzzy inference system. Agric. Water Manag. 2021, 55, 107003. [Google Scholar] [CrossRef]
- Ahmadi, F.; Mehdizadeh, S.; Mohammadi, B.; Pham, Q.B.; Doan, T.N.C.; Vo, N.D. Application of an artificial intelligence technique enhanced with intelligent water drops for monthly reference evapotranspiration estimation. Agric. Water Manag. 2021, 244, 106622. [Google Scholar] [CrossRef]
- Sattari, M.T.; Apaydin, H.; Band, S.S.; Mosavi, A.; Prasad, R. Comparative analysis of kernel-based versus ANN and deep learning methods in monthly reference evapotranspiration estimation. Hydrol. Earth Syst. Sci. 2021, 25, 603–618. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Ghorbani, M.A.; Kashani, M.H.; Kisi, O.; Kim, S. The viability of co-active fuzzy inference system model for monthly reference evapotranspiration estimation: Case study of Uttarakhand State. Hydrol. Res. 2019, 50, 1623–1644. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. M5 model tree based modelling of reference evapotranspiration. Hydrol. Process. Int. J. 2009, 23, 1437–1443. [Google Scholar] [CrossRef]
- Vaz, P.J.; Schütz, G.; Guerrero, C.; Cardoso, P.J. Hybrid neural network based models for evapotranspiration prediction over limited weather parameters. IEEE Access 2022, 11, 963–976. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X.; Jiang, Y.; Sun, Z.; Liang, Y.; Hu, X.; Ruan, J. Hybrid machine learning approach for evapotranspiration estimation of fruit tree in agricultural cyber-physical systems. IEEE Trans. Cybern. 2022, 53, 5677–5691. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Raza, A.; Hu, Y.; Buttar, N.A.; Shoaib, M.; Saber, K.; Li, P.; Elbeltagi, A.; Ray, R.L. Development of Monthly Reference Evapotranspiration Machine Learning Models and Mapping of Pakistan—A Comparative Study. Water 2022, 14, 1666. [Google Scholar] [CrossRef]
- Tian, H.; Huang, N.; Niu, Z.; Qin, Y.; Pei, J.; Wang, J. Mapping Winter Crops in China with Multi-Source Satellite Imagery and Phenology-Based Algorithm. Remote Sens. 2019, 11, 820. [Google Scholar] [CrossRef]
- Wu, B.; Quan, Q.; Yang, S.; Dong, Y. A social-ecological coupling model for evaluating the human-water relationship in basins within the Budyko framework. J. Hydrol. 2023, 619, 129361. [Google Scholar] [CrossRef]
- Tian, H.; Pei, J.; Huang, J.; Li, X.; Wang, J.; Zhou, B.; Wang, L. Garlic and Winter Wheat Identification Based on Active and Passive Satellite Imagery and the Google Earth Engine in Northern China. Remote Sens. 2020, 12, 3539. [Google Scholar] [CrossRef]
- Qiu, D.; Zhu, G.; Lin, X.; Jiao, Y.; Lu, S.; Liu, J.; Chen, L. Dissipation and movement of soil water in artificial forest in arid oasis areas: Cognition based on stable isotopes. CATENA 2023, 228, 107178. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wu, X.; Xu, C.; Guo, S.; Chen, X. Toward Monitoring Short-Term Droughts Using a Novel Daily Scale, Standardized Antecedent Precipitation Evapotranspiration Index. J. Hydrometeorol. 2020, 21, 891–908. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Keim, B.D.; Konsoer, K.; Yin, Z.; Liu, M.; Zheng, W. Spatial and wavelet analysis of precipitation and river discharge during operation of the Three Gorges Dam, China. Ecol. Indic. 2023, 154, 110837. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Li, T.; Lu, S.; Yin, Z.; Liu, X.; Li, X.; Zheng, W. U-Net-STN: A Novel End-to-End Lake Boundary Prediction Model. Land 2023, 12, 1602. [Google Scholar] [CrossRef]
- Cheng, B.; Wang, M.; Zhao, S.; Zhai, Z.; Zhu, D.; Chen, J. Situation-Aware Dynamic Service Coordination in an IoT Environment. IEEE/ACM Trans. Netw. 2017, 25, 2082–2095. [Google Scholar] [CrossRef]
- Gao, C.; Hao, M.; Chen, J.; Gu, C. Simulation and design of joint distribution of rainfall and tide level in Wuchengxiyu Region, China. Urban Clim. 2021, 40, 101005. [Google Scholar] [CrossRef]
- Yin, Z.; Liu, Z.; Liu, X.; Zheng, W.; Yin, L. Urban heat islands and their effects on thermal comfort in the US: New York and New Jersey. Ecol. Indic. 2023, 154, 110765. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, L.; Zhong, X.; Yao, T.; Qi, J.; Wang, Y.; Xue, Y. Quantifying the major drivers for the expanding lakes in the interior Tibetan Plateau. Sci. Bull. 2022, 67, 474–478. [Google Scholar] [CrossRef]
- Yang, D.; Qiu, H.; Ye, B.; Liu, Y.; Zhang, J.; Zhu, Y. Distribution and Recurrence of Warming-induced ETo rogressive Thaw Slumps on the Central Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surf. 2023, 128, e2022JF007047. [Google Scholar] [CrossRef]
- Yuan, C.; Li, Q.; Nie, W.; Ye, C. A depth information-based method to enhance rainfall-induced landslide deformation area identification. Measurement 2023, 219, 113288. [Google Scholar] [CrossRef]
- Zhang, T.; Song, B.; Han, G.; Zhao, H.; Hu, Q.; Zhao, Y.; Liu, H. Effects of coastal wetland reclamation on soil organic carbon, total nitrogen, and total phosphorus in China: A meta-analysis. Land Degrad. Dev. 2023, 34, 3340–3349. [Google Scholar] [CrossRef]
- Kim, M.; Sung-hwan, M.; Ingoo, H. An Evolutionary Approach to the Combination of Multiple Classifiers to Predict a Stock Price Index. Earth Syst. Appl. 2006, 31, 241–247. [Google Scholar] [CrossRef]
- Estévez, J.; Pedro, G.; Joaquín, B. Sensitivity Analysis of a Penman–Monteith Type Equation to Estimate Reference Evapotranspiration in Southern Spain. Hydrol. Process. 2009, 23, 3342–3353. [Google Scholar] [CrossRef]
- Eslamian, S.; Saeid, S.; Alireza, G.; Zareian, M.J.; Alireza, F. Estimating Penman-Monteith Reference Evapotranspiration Using Artificial Neural Networks and Genetic Algorithm: A Case Study. Arab. J. Sci. Eng. 2012, 37, 935–944. [Google Scholar] [CrossRef]
- Sabino, M.; de Souza, A.P. Global Sensitivity of Penman–Monteith Reference Evapotranspiration to Climatic Variables in Mato Grosso, Brazil. Earth 2023, 4, 714–727. [Google Scholar] [CrossRef]

| Variables | Tmin | Tmax | RHmean | Ws | Sh |
|---|---|---|---|---|---|
| °C | °C | % | m/s | h | |
| Mean | 20.33 | 34.23 | 38.10 | 1.29 | 7.79 |
| Standard Error | 0.42 | 0.38 | 0.63 | 0.04 | 0.03 |
| Median | 21.50 | 35.90 | 37.00 | 1.24 | 7.70 |
| Mode | 29.10 | 25.70 | 33.00 | 1.11 | 7.30 |
| Standard Deviation | 7.96 | 7.23 | 11.88 | 0.67 | 0.59 |
| Sample Variance | 63.35 | 52.25 | 141.21 | 0.45 | 0.35 |
| Kurtosis | −1.39 | −1.10 | −0.52 | −0.40 | −1.65 |
| Skewness | −0.30 | −0.21 | 0.22 | 0.28 | 0.10 |
| Range | 25.80 | 27.20 | 62.00 | 3.15 | 1.60 |
| Minimum | 5.20 | 20.10 | 11.00 | 0.00 | 7.00 |
| Maximum | 31.00 | 47.30 | 73.00 | 3.15 | 8.60 |
| Sum | 7318.30 | 12,322.20 | 13,717.00 | 465.89 | 2805.00 |
| Count | 360.00 | 360.00 | 360.00 | 360.00 | 360.00 |
| Decision-Based ML Algorithm | Parametric Variables | ||
|---|---|---|---|
| Tree Numbers | Splitter | Node Size | |
| Iterative Dichotomizer (ID3) | 12 | 22 | 04 |
| Gradient Boosting (GB) | 14 | 26 | 06 |
| Random Forest (RF) | 18 | 29 | 08 |
| Input Combination | Symbol |
|---|---|
| Tmin, Tmax, RHmean, Ws, Sh | M1 |
| RHmean, Sh | M2 |
| RHmean, Sh, Ws | M3 |
| RHmean, Ws | M4 |
| Tmax,Tmin, Sh, Ws | M5 |
| Tmax, RHmean, Sh, Ws | M6 |
| Tmax, RHmean, Ws | M7 |
| Tmax, Tmin, RHmean, Sh | M8 |
| Tmean, RHmean, Sh | M9 |
| Tmin, RHmean, Ws | M10 |
| Tmin, RHmean, Sh, Ws | M11 |
| Tmean, RHmean, Ws | M12 |
| Tmax, Tmin, RHmean, Ws | M13 |
| Tmean, RHmean, N, Ws | M14 |
| Tmean, RHmean | M15 |
| Tmean, Sh | M16 |
| Tmean, Ws | M17 |
| Chosen Method | Climatic Variables | Aerodynamic Factors | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Tmin | Tmax | Tmean | RHmin | RHmax | RHmean | Ws | Sh | Rn, es, ea, emin, emax, Δ, G, and Ɣ | |
| PMF | ▀▀ | ▀▀ | ▀▀ | ▀▀ | ▀▀ | ▀▀ | ▀▀ | ▀▀ | ▀▀ |
| ML models | X | X | ▀▀ | X | X | ▀▀ | ▀▀ | X | X |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raza, A.; Fahmeed, R.; Syed, N.R.; Katipoğlu, O.M.; Zubair, M.; Alshehri, F.; Elbeltagi, A. Performance Evaluation of Five Machine Learning Algorithms for Estimating Reference Evapotranspiration in an Arid Climate. Water 2023, 15, 3822. https://doi.org/10.3390/w15213822
Raza A, Fahmeed R, Syed NR, Katipoğlu OM, Zubair M, Alshehri F, Elbeltagi A. Performance Evaluation of Five Machine Learning Algorithms for Estimating Reference Evapotranspiration in an Arid Climate. Water. 2023; 15(21):3822. https://doi.org/10.3390/w15213822
Chicago/Turabian StyleRaza, Ali, Romana Fahmeed, Neyha Rubab Syed, Okan Mert Katipoğlu, Muhammad Zubair, Fahad Alshehri, and Ahmed Elbeltagi. 2023. "Performance Evaluation of Five Machine Learning Algorithms for Estimating Reference Evapotranspiration in an Arid Climate" Water 15, no. 21: 3822. https://doi.org/10.3390/w15213822
APA StyleRaza, A., Fahmeed, R., Syed, N. R., Katipoğlu, O. M., Zubair, M., Alshehri, F., & Elbeltagi, A. (2023). Performance Evaluation of Five Machine Learning Algorithms for Estimating Reference Evapotranspiration in an Arid Climate. Water, 15(21), 3822. https://doi.org/10.3390/w15213822