A Review of Earth’s Surface Soil Moisture Retrieval Models via Remote Sensing
Abstract
:1. Introduction
2. Retrieval Model
2.1. Empirical Model
2.2. Semi-Empirical Model
2.3. Physical Model
2.4. Machine Learning

3. Future Perspective
3.1. Multi-Source Data Matching
3.2. Spatial–Temporal Resolution
3.3. Long Time Series, Low Latency
3.4. Model Accuracy and Meaning
4. Summary and Conclusions
- According to the acquisition of data sources and the characteristics of the study area, researchers select the appropriate model that makes the accuracy in a specific area satisfactory. Empirical model is widely used because of its few parameters and because it is easy to be obtained, but its accuracy is seriously restricted by the empirical data and it has no physical meaning. Semi-empirical model introduces physical meaning on the basis of empirical data and calibrates the coefficient from a certain theoretical formula by using empirical data, which improves the model’s scientificalness and interpretability to a certain extent. However, it is still subject to empirical data. A physical model is constructed in strict accordance with the laws of physics, containing complex formulas and a wide range of parameters for constraints. It has good model meaning, but because of the large number of parameters and the large amount of calculation, it is difficult to obtain some parameters directly, and the parameter values vary greatly in different regions; therefore, it cannot be applied to large-scale studies. Machine learning is the most rapidly developing model in recent years; by using computer technologies like artificial intelligence to process and train remote sensing data, the precision of large-scale research has been improved, the scope of application has been broadened, and the retrieval speed has been accelerated. However, similar to the empirical model, the model still lacks interpretability and the influence of the accuracy of training data cannot be ignored.
- At present, apart from the problems of the model itself, the characteristics of remote sensing data sources and terrain types also affect the retrieval accuracy. The relationship between SM and soil reflectance is uncertain due to the limitation of atmospheric conditions on optical data. The lack of penetration depth makes it difficult to precisely estimate the soil moisture in the root-zone layer. It is still inconvenient to eliminate the influence of the vegetation layer under the covered area. In addition, it is also a challenge to decrease the interference such as the angle of incidence of electromagnetic waves and surface roughness. Future optimization is suggested in the following aspects: multi-source data matching, spatial–temporal resolution, time series, latency, model accuracy, and meaning.
- The objective of this review is to provide readers with a more comprehensive introduction of the types and mechanisms of soil moisture retrieval models. At the same time, it should be emphasized that the applicability of the relevant model introduced in this review depends on the scope of the study area (space and time) and the availability of data. So far, there is no single model and data source that can be used as a common solution with high accuracy. In order to retrieve soil moisture more accurately and meet the actual demands, a growing number of scholars begin to consider multiple models to retrieve soil moisture. A common multi-source data and model retrieval flow chart is shown below (Figure 5).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anagnostopoulos, V.; Petropoulos, G.P.; Ireland, G.; Carlson, T.N. A modernized version of a 1D soil vegetation atmosphere transfer model for improving its future use in land surface interactions studies. Environ. Model. Softw. 2017, 90, 147–156. [Google Scholar] [CrossRef]
- Engman, E.T. Applications of microwave remote sensing of soil moisture for water resources and agriculture. Remote Sens. Environ. 1991, 35, 213–226. [Google Scholar] [CrossRef]
- Bolten, J.D.; Crow, W.T.; Jackson, T.J.; Zhan, X.; Jackson, T.J.; Reynolds, C.A. Evaluating the utility of remotely sensed soil moisture retrievals for operational agricultural drought monitoring. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 57–66. [Google Scholar] [CrossRef]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards improved spatio-temporal resolution soil moisture retrievals from the synergy of SMOS and MSG SEVIRI spaceborne observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar]
- Engman, E.T.; Chauhan, N. Status of microwave soil moisture measurements with remote sensing. Remote Sens. Environ. 1995, 51, 189–198. [Google Scholar] [CrossRef]
- Zhao, W.; Wen, F.P.; Cai, J.F. Methods, progresses, and challenges of passive microwave soil moisture spatial downscaling. Natl. Remote Sens. Bull. 2022, 26, 1699–1722. [Google Scholar] [CrossRef]
- Li, Z.L. Soil moisture retrieval from remote sensing measurements: Current knowledge and directions for the future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar]
- Petropoulos, G.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status, products and future trends. Phys. Chem. Earth 2015, 83–84, 36–56. [Google Scholar]
- Babaeian, E.; Sadeghi, M.; Jones, S.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, proximal, and satellite remote sensing of soil moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar]
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.; Crow, W.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.; et al. A roadmap for high-resolution satellite soil moisture applications confronting product characteristics with user requirements. Remote Sens. Environ. 2021, 252, 112162. [Google Scholar]
- Lobell, D.; Asner, G. Moisture effects on soil reflectance. Soil. Sci. Soc. Am. 2002, 66, 722–727. [Google Scholar] [CrossRef]
- Liu, W.; Baret, F.; Gu, X.; Zhang, B.; Tong, Q.; Zheng, L. Evaluation of methods for soil surface moisture estimation from reflectance data. Int. J. Remote Sens. 2003, 24, 2069–2083. [Google Scholar]
- Wang, J.X.; Pan, Y.Z.; Zhu, X.F.; Sun, Z.L. A review of researches on inversion of eigenvariance of soil water. J. Soil Sci. 2019, 56, 23–35. [Google Scholar] [CrossRef]
- Jiang, L.M.; Cui, H.Z.; Wang, G.X.; Yang, J.; Wang, J.; Pan, F.; Su, X.; Fang, X. Progress on Remote Sensing of Snow, Surface Soil Frozen/Thaw State and Soil Moisture. Remote Sens. Technol. Appl. 2020, 35, 1237–1262. [Google Scholar] [CrossRef]
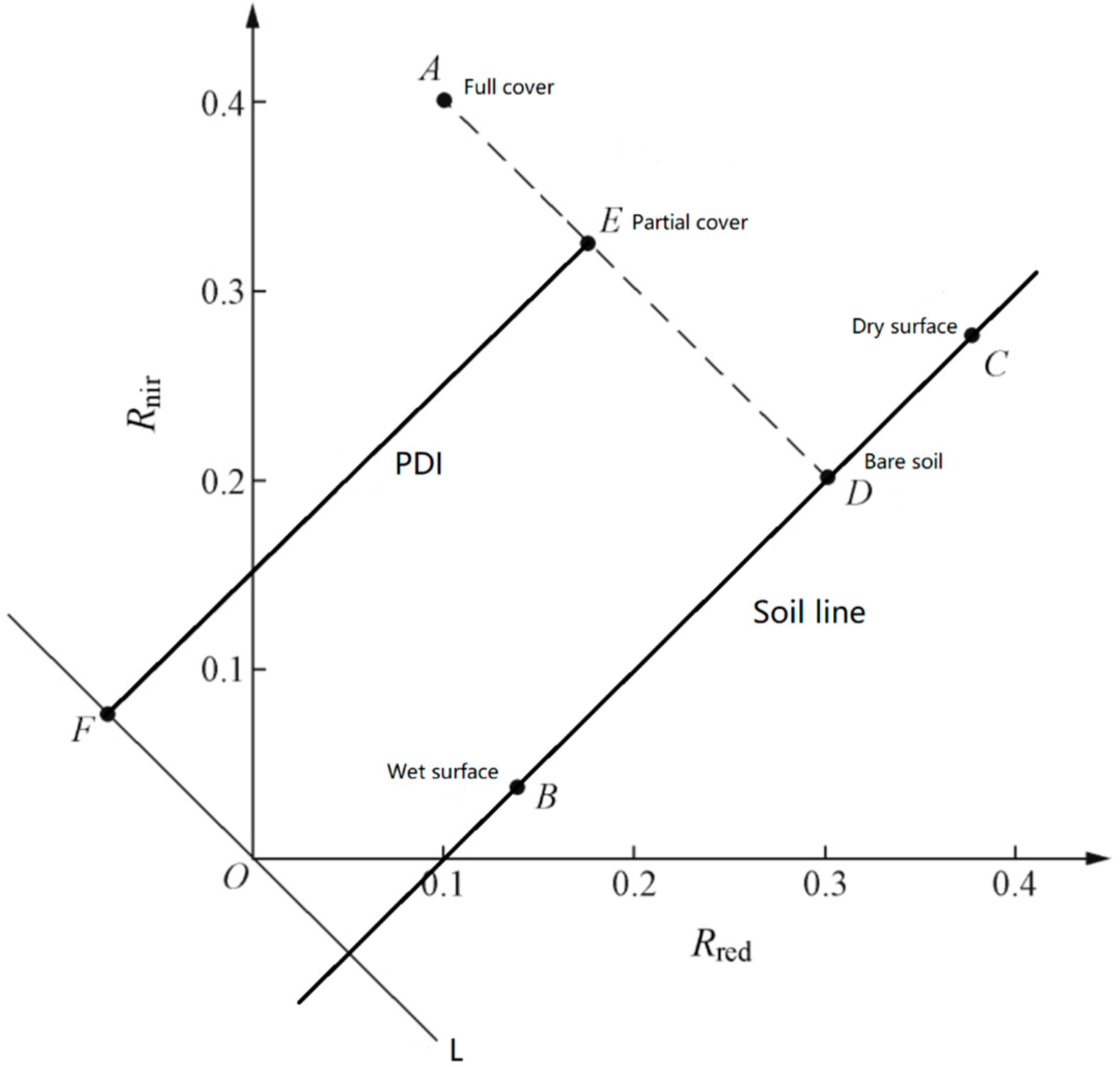
- Wang, L.; Qu, J. NMDI: A normalized multi-band drought index for monitoring soil and vegetation moisture with satellite remote sensing. Geophys. Res. Lett. 2007, 34, L20405. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Teyip, T.; Li, Z.L. Modified perpendicular drought index (MPDI): A real-time drought monitoring method. ISPRS J. Photogramm. Remote Sens. 2007, 62, 150–164. [Google Scholar]
- Yang, D.Y.; Yan, S.H.; Yang, Y.L.; Tian, M. Soil moisture retrieval based on multi-temporal GF-1 images. Sci. Technol. Eng. 2021, 21, 4540–4549. [Google Scholar]
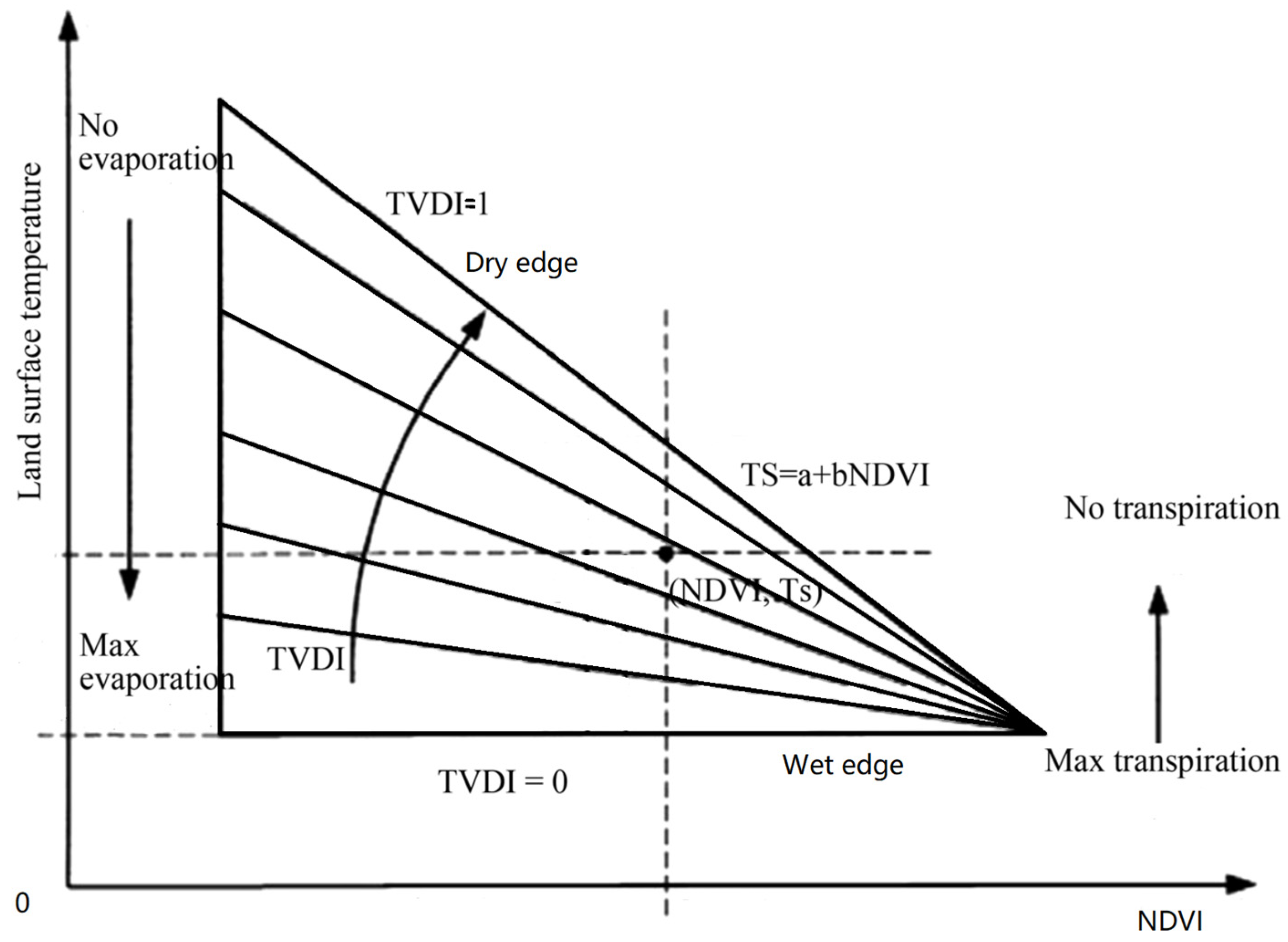
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Carlson, T. An Overview of the Triangle Method for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Holzman, M.; Rivas, R.; Piccolo, M. Geoinformation. Estimating soil moisture and the relationship with crop yield using surface temperature and vegetation index. Int. Appl. Earth Obs. Geoinf. 2014, 28, 181–192. [Google Scholar]
- Chen, J.; Wang, C.; Jiang, H.; Mao, L.; Yu, Z. Estimating soil moisture using Temperature–Vegetation Dryness Index (TVDI) in the Huang-huai-hai (HHH) plain. Int. J. Remote Sens. 2011, 32, 1165–1177. [Google Scholar] [CrossRef]
- Yuan, L.; Li, L.; Zhang, T.; Chen, L.; Zhao, J.; Hu, S.; Cheng, L.; Liu, W. Soil moisture estimation for the Chinese Loess Plateau using MODIS-derived ATI and TVDI. Remote Sens. 2020, 12, 3040. [Google Scholar] [CrossRef]
- Li, S.R.; Sun, Z. Analysis soil water content in Heihe river basin based on landsat—8 OLI TIRS. Geomat. Spat. Inf. Technol. 2021, 44, 159–163. [Google Scholar]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef]
- Dubois, P.C.; Van Zyl, J.; Engman, T. Measuring soil moisture with imaging Radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for Radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Wang, L.; Gong, H.L.; Pan, Y.; Miao, B.; Yang, J.; Cui, X. Retrieval of Soil Moisture in Typical Steppe of Xilinhot Based on Sentinel—1 SAR Data. J. Arid. Meteorol. 2019, 37, 979–986. [Google Scholar] [CrossRef]
- Xiong, Q.X.; Hu, P.M.; Ma, Y. Extracting the spatial distribution information of crop sub-surface waterlogging using antecedent precipitation index and sentinel-1A SAR data. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2021, 37, 175–183. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear Filtering and prediction problems. J. Fluids Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Bao, Y.S.; Lin, L.B.; Wu, S.Y.; Deng, K.A.K.; Petropoulos, G.P. Surface soil moisture retrievals over partially vegetated areas from the synergy of Sentinel-1 and Landsat 8 data using a modified water-cloud model. Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 76–85. [Google Scholar] [CrossRef]
- Xie, Y.; Yan, S.H.; Ma, Q.S.; Chen, N.C. Retrieval of soil moisture in vegetation covered area by SAR and optical image. Sci. Technol. Eng. 2021, 21, 3223–3230. [Google Scholar]
- Dabrowska-Zielinska, K.; Musial, J.; Malinska, A.; Budzynska, M.; Gurdak, R.; Kiryla, W.; Bartold, M.; Grzybowski, P. Soil Moisture in the Biebrza Wetlands retrieved from Sentinel-1 Imagery. Remote Sens. 2018, 10, 1979. [Google Scholar] [CrossRef]
- Cai, Q.K.; Li, E.J.; Tao, L.L.; Jiang, R.B. Farmland soil moisture retrieval using PROSAIL and water cloud model. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2018, 34, 117–123. [Google Scholar] [CrossRef]
- Sekertekin, A.; Marangoz, A.; Abdikan, S. ALOS-2 and Sentinel-1 SAR data sensitivity analysis to surface soil moisture over bare and vegetated agricultural fields. Comput. Electron. Agric. 2020, 171, 105303–105314. [Google Scholar]
- Lei, F.; Crow, W.T.; Kustas, W.P.; Dong, J.; Yang, Y.; Knipper, K.R.; Anderson, M.C.; Gao, F.; Notarnicola, C.; Greifeneder, F.; et al. Data assimilation of high-resolution thermal and radar remote sensing retrievals for soil moisture monitoring in a drip-irrigated vineyard. Remote Sens. Environ. 2020, 239, 111622. [Google Scholar] [CrossRef]
- He, L.; Qin, Q.M.; Ren, H.Z.; Du, J.; Meng, J.J.; Du, C. Soil moisture retrieval using multi-temporal Sentinel-1 SAR data in agricultural areas. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2016, 32, 142–148. [Google Scholar] [CrossRef]
- Rice, S.O. Reflection of electromagnetic waves from slightly rough surfaces. Commun. Pure Appl. Math. 1951, 4, 351–378. [Google Scholar] [CrossRef]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House, Inc.: Norwood, MA, USA, 1987; Volume 511. [Google Scholar]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Boisvert, J.B.; Gwyn, Q.H.J.; Chanzy, A.; Major, D.J.; Brisco, B.; Brown, R.J. Effect of surface soil moisture gradients on modelling radar backscattering from bare fields. Int. J. Remote Sens. 1997, 18, 153–170. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Yang, L.P.; Liu, F.; Li, Y.F.; Liu, J.; Li, G.Q.; Jin, M. Simulation of backscattering characteristics of bare surface based on the AIEM model in arid areas. J. Lanzhou Univ. Nat. Sci. 2019, 55, 176–182. [Google Scholar]
- Shi, J.C.; Jiang, L.M.; Zhang, L.X.; Chen, K.S.; Wigneron, J.P.; Chanzy, A. A Parameterized Multi-frequency-polarization Surface Emission Model. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2831–2841. [Google Scholar]
- Cui, H.Z.; Jiang, L.M.; Du, J.Y.; Zhao, S.; Wang, G.; Lu, Z.; Wang, J. Evaluation and Analysis of AMSR-2, SMOS, and SMAP Soil Moisture Products in the Genhe Area of China. J. Geophys. Res. Atmos. 2017, 122, 8650–8666. [Google Scholar] [CrossRef]
- Cui, H.Z.; Jiang, L.M.; Lu, Z.; Wang, G.; Wang, J. Improvement and Validation of QP Model. with Dual-Channel Soil. Moisture Retrieval Algorithm in Genhe, China. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Njoke, E.G.; Jackson, T.J.; Lakshni, V.; Chan, T.K.; Nghiem, S.V. Soil. Moisture Retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Lu, H.; Koike, T.; Fujii, H.; Tamagawa, K. Development of a Physicallybased Soil. Moisture Retrieval Algorithm for Spaceborne Passive Microwave Radiometers and Its Application to AMSR-E. J. Remote Sens. Soc. Jpn. 2009, 29, 253–262. [Google Scholar]
- Ulaby, F.T.; Sarabandi, K.; Mcdonald, K.; Whitt, M.; Dobson, M.C. Michigan Microwave Canopy Scattering Model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Owe, M.; De, J.R.; Holmes, T. Multi-sensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Wang, G.J.; Xue, F.; Chyi, D. Soil moisture retrievals from FY-3B satellite microwave brightness and comparative analyses over China. Trans. Atmos. Sci. 2018, 41, 113–125. (In Chinese) [Google Scholar] [CrossRef]
- Koike, T. Descriptions of GCOM-W1 AMSR2 Level 1R and Level 2 Algorithms; Earth Observation Research Center, Japan Aerospace Exploration Agency: Hatoyama, Japan, 2013; Chapter 8; pp. 107–115. Available online: http://suzaku.eorc.jaxa.jp/GCOM_W/data/doc/NDX-120015A.pdf (accessed on 1 August 2023).
- Li, P.X.; Liu, Z.Q.; Yang, J.; Sun, W.; Li, M.; Ren, Y. Soil. moisture retrieval of water wheat fields based on random forest regression using Quad-Polarimetric SAR images. Geomat. Inf. Sci. Wuhan. Univ. 2019, 44, 405–412. [Google Scholar] [CrossRef]
- Li, K.; Zhang, R.; Duan, J.L.; Jichao, L. Wide-area soil moisture retrieval using SAR images and multispectral data. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2020, 36, 134–140. [Google Scholar] [CrossRef]
- Wu, S.Y.; Bao, Y.S.; Li, Y.F.; Wu, Y. Joint retrieval of soil moisture from Sentinel-1 and Sentinel-2 remote sensing data based on neural network algorithm. Trans Atmos Sci. 2021, 44, 636–644. (In Chinese) [Google Scholar] [CrossRef]
- Yang, L.P.; Hou, C.L.; Su, Z.Q.; Bai, Y.X.; Wang, T.; Feng, R. Soil moisture inversion in arid areas by using machine learning and fully polarimetric SAR imagery. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2021, 37, 74–82, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Hachani, A.; Ouessar, M.; Paloscia, S.; Santi, E.; Pettinato, S. Soil moisture retrieval from Sentinel-1 acquisitions in an arid environment in Tunisia: Application of Artificial Neural Networks techniques. Int. J. Remote Sens. 2019, 40, 9159–9180. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Y.X.; Li, F.; He, L. Soil moisture retrieval using extremely randomized trees over the Shandian river basin. Natl. Remote Sens. Bull. 2021, 25, 941–951. [Google Scholar] [CrossRef]
- Guo, J.; Liu, J.; Ning, J.F.; Han, W.T. Construction and validation of soil moisture retrieval model in farmland based on Sentinel multi-source data. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2019, 35, 71–78, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Geng, D.Y.; Zhao, T.J.; Shi, J.C.; Hu, L.; Xu, H.X.; Hu, J.F. Surface microwave scattering model evaluation and soil moisture retrieval based on ground-based radar data. Natl. Remote Sens. Bull. 2021, 25, 929–940. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Yang, Y.; Ding, D.; Ding, F.; Dang, X.W. Multi-Parameter Inversion of AIEM by Using Bi-Directional Deep Neural Network. Remote Sens. 2022, 14, 3302. [Google Scholar] [CrossRef]
- Chen, S.D.; Zhang, L.; Guo, M.; Liu, X. Spatial Downscaling Methods of Soil. Moisture based on Multisource Remote Sensing Data and Its Application. Water 2019, 11, 1401. [Google Scholar] [CrossRef]
- Zhao, W.; SÁNchez, N.; Lu, H.; Li, A. A Spatial Downscaling Approach for the SMAP Passive Surface Soil. Moisture Product. Using. Random Forest Regression. J. Hydrol. 2018, 563, 1009–1024. [Google Scholar] [CrossRef]
- Liu, Y.X.Y.; Yang, Y.P. Advances in the Quality of Global Soil Moisture Products: A Review. Remote Sens. 2022, 14, 3741. [Google Scholar] [CrossRef]
- Ai, L.; Sun, S.Y.; Li, S.G.; Ma, H.Z. Research progress on the cooperative inversion of soil moisture using optical and SAR remote sensing. Remote Sens. Nat. Resour. 2021, 33, 10–18. [Google Scholar] [CrossRef]
- Alnaimy, M.A.; Elrys, A.S.; Zelenakova, M.; Pietrucha-Urbanik, K.; Merwad, A.-R.M. The Vital Roles of Parent Material in Driving Soil Substrates and Heavy Metals Availability in Arid Alkaline Regions: A Case Study from Egypt. Water 2023, 15, 2481. [Google Scholar] [CrossRef]


| Satellite Program | Spatial Resolution | Band | Temporal Resolution | Time Range | Publisher |
|---|---|---|---|---|---|
| SMOS | 25 KM | L | 1 d | 2 November 2009 ongoing | The European Space Agency (ESA) |
| ASCAT MetOp-B | 25 KM 50 KM | C | 1 d | 17 September 2012 ongoing | ESA |
| Terra-Sar | 2 M | X | 1 d | June 2007 ongoing | ESA |
| Sentinel-1 | 1 KM | C | 1 d | 3 April 2014 ongoing | ESA |
| SMAP | 36 KM | L | 1 d | 31 January 2015 ongoing | The National Aeronautics and Space Administration (NASA) |
| Satellite Program | Spatial Resolution | Band | Temporal Resolution | Time Range | Publisher |
|---|---|---|---|---|---|
| ERS-1 | 50 km × 50 km | C | 1 d | 17 July 1991–10 March 2000 | ESA |
| ERS-2 | 25 km × 25 km | C | 1 d | 21 April 1995–5 September 2011 | ESA |
| AMSR-E | 50 km | C, X | 1 d | 1 June 2002–4 October 2011 | NASA |
| AMSR-2 | 50 km | C, X | 1 d | 10 August 2012 ongoing | NASA |
| FY-3B | 25 km × 25 km | X | 1 d | 12 July 2011–19 August 2019 | China Meteorological Administration (CMA) |
| FY-3C | 25 km | X | 1 d | 29 May 2014 ongoing | CMA |
| Model | Advantages | Disadvantages |
|---|---|---|
| Empirical model |
|
|
| Semi-empirical model |
|
|
| Physical model |
|
|
| Machine learning |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhao, H.; Fan, J.; Wang, C.; Ji, X.; Jin, D.; Chen, J. A Review of Earth’s Surface Soil Moisture Retrieval Models via Remote Sensing. Water 2023, 15, 3757. https://doi.org/10.3390/w15213757
Wang Y, Zhao H, Fan J, Wang C, Ji X, Jin D, Chen J. A Review of Earth’s Surface Soil Moisture Retrieval Models via Remote Sensing. Water. 2023; 15(21):3757. https://doi.org/10.3390/w15213757
Chicago/Turabian StyleWang, Yuxuan, Hongli Zhao, Jinghui Fan, Chuan Wang, Xinyang Ji, Dingjian Jin, and Jianping Chen. 2023. "A Review of Earth’s Surface Soil Moisture Retrieval Models via Remote Sensing" Water 15, no. 21: 3757. https://doi.org/10.3390/w15213757
APA StyleWang, Y., Zhao, H., Fan, J., Wang, C., Ji, X., Jin, D., & Chen, J. (2023). A Review of Earth’s Surface Soil Moisture Retrieval Models via Remote Sensing. Water, 15(21), 3757. https://doi.org/10.3390/w15213757







