Numerical Study of Fluid–Solid Interaction in Elastic Sluice Based on SPH Method
Abstract
:1. Introduction
2. Numerical Model
2.1. Governing Equations
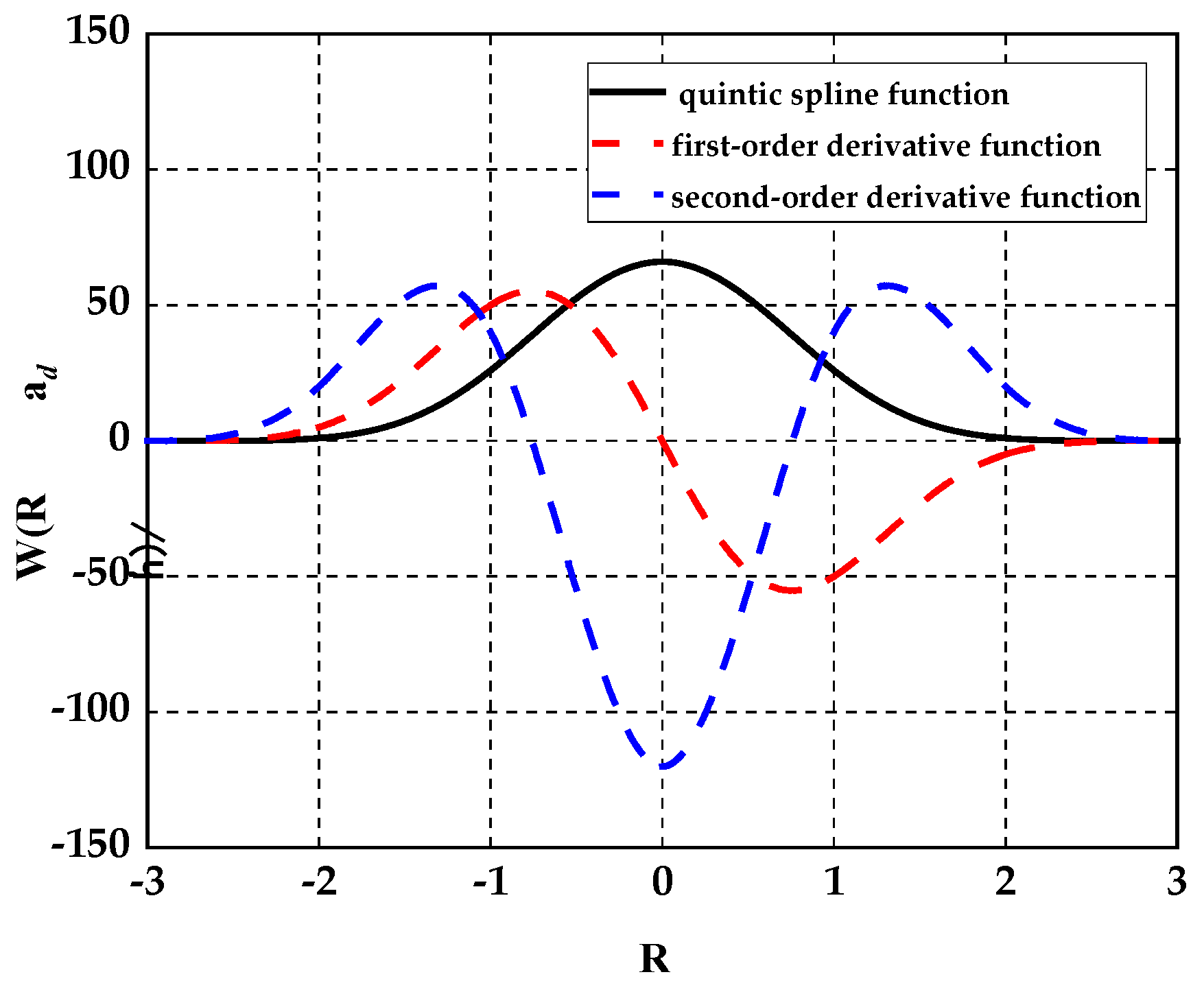
2.2. SPH Methodology
2.3. Particle Velocity Correction
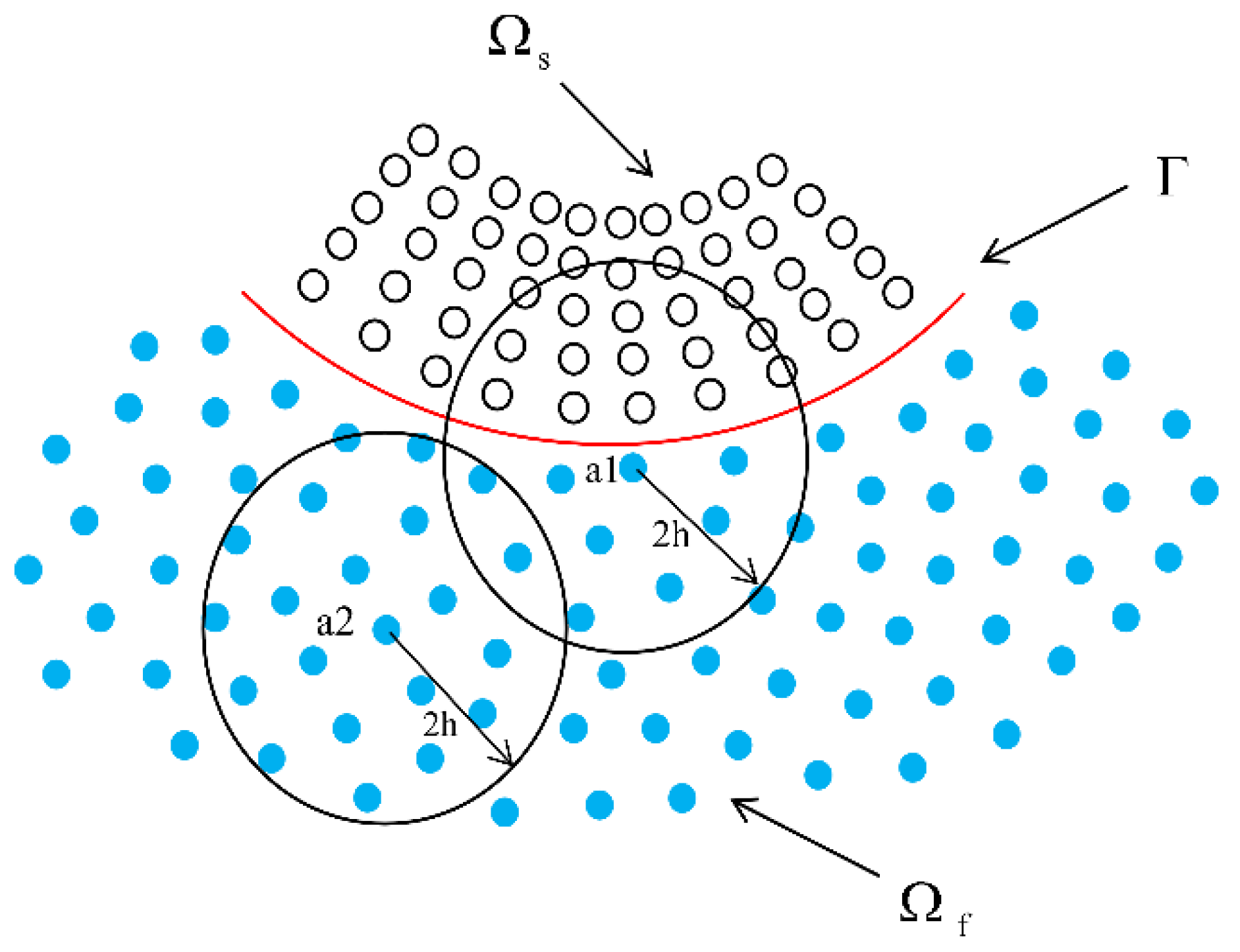
2.4. Flow–Solid Interface Treatment
2.4.1. Dynamic Interface Conditions
2.4.2. Motion Interface Conditions
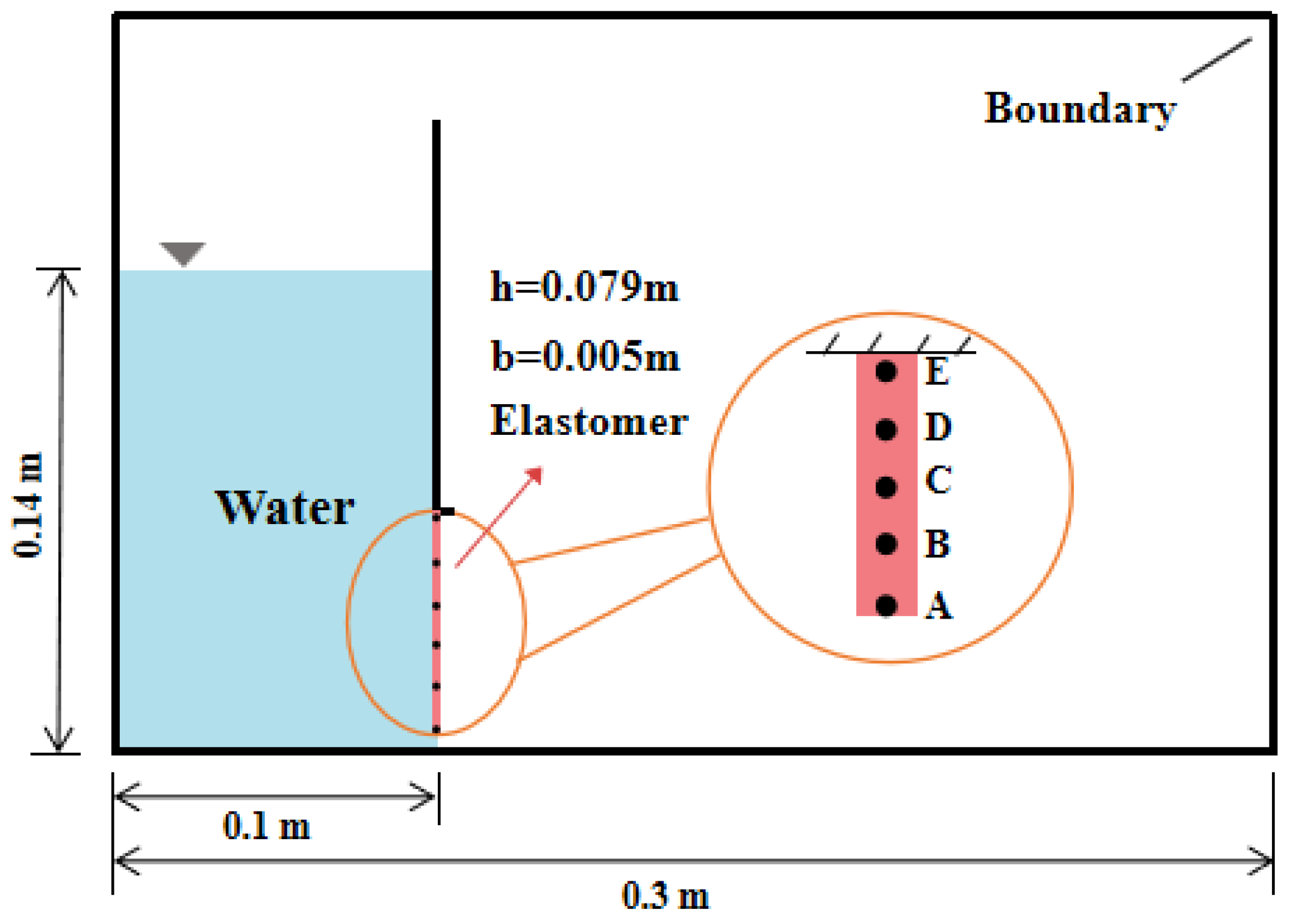
3. Model Validation
3.1. Comparison of Water Flow Patterns
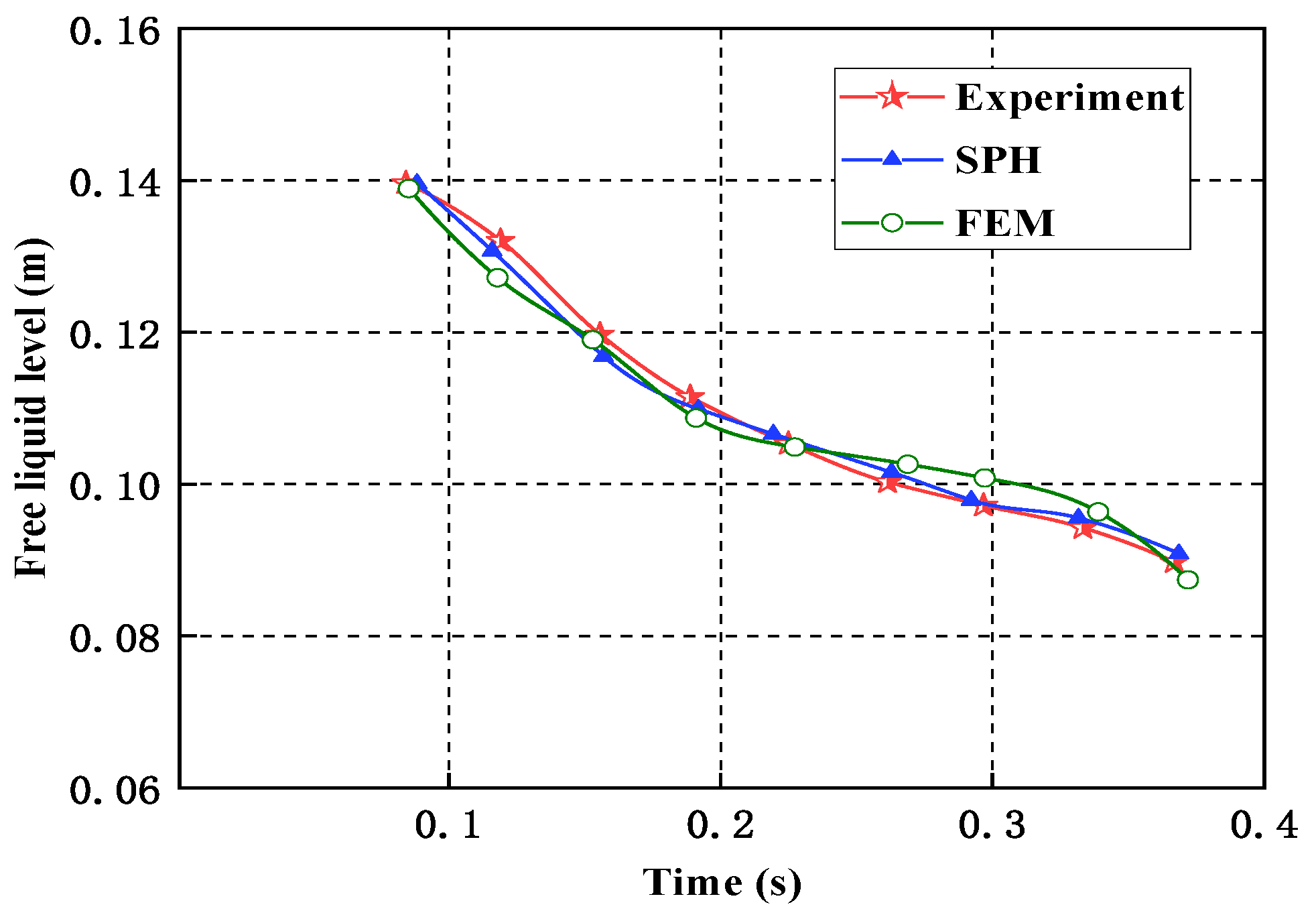
3.2. Comparison of Gate Opening and Free Liquid Level
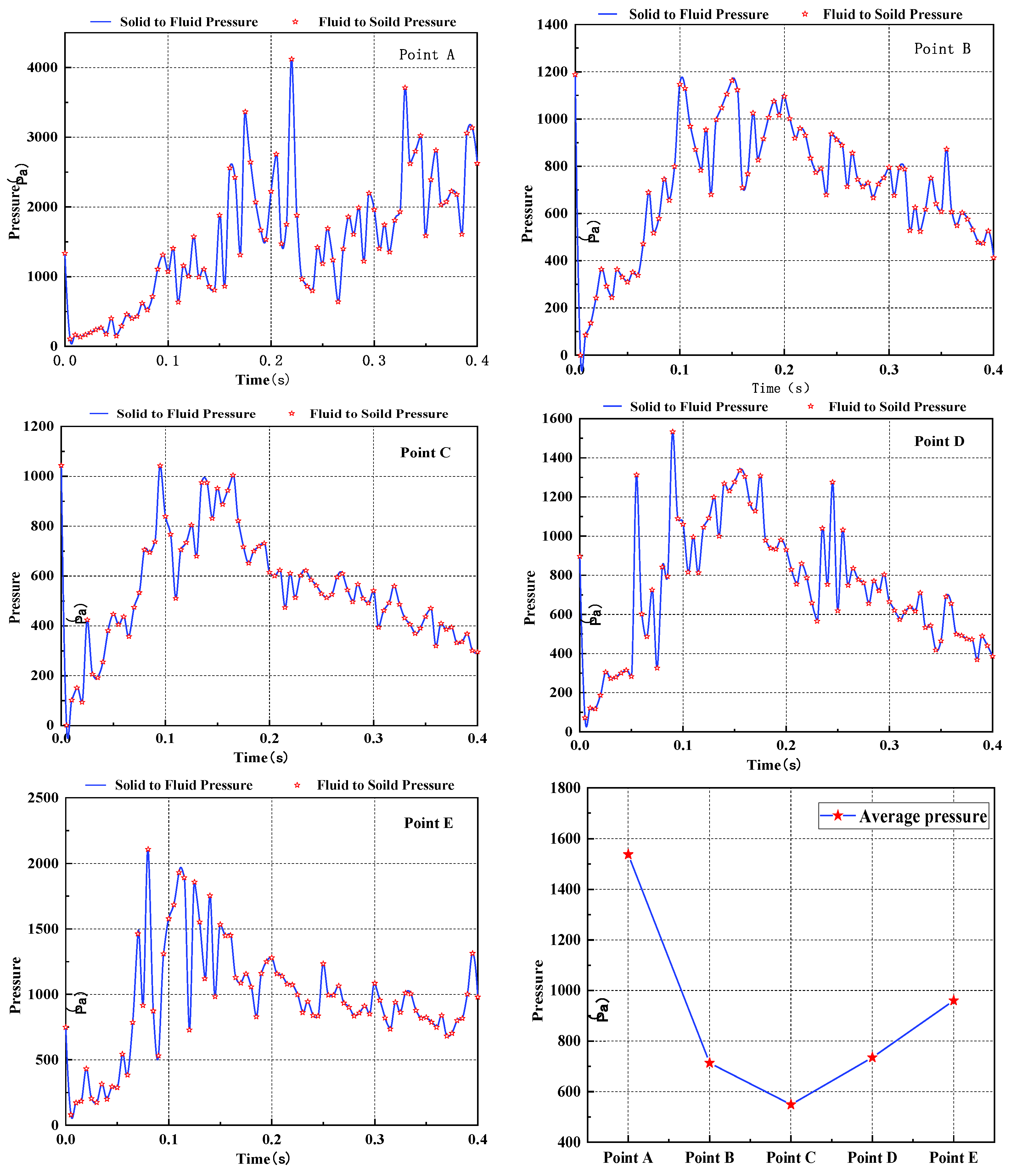
3.3. Fluid–Solid Pressure Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, M.; Zhang, Z. Smoothed particle hydrodynamics (sph) for modeling fluid-structure interactions. Sci. China Phys. Mech. Astron. 2019, 62, 1–38. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, B.; Ren, W. Aerodynamic load and structure stress analysis on hood of high-speed railway tunnel. Chin. J. Theor. Appl. Mech. 2017, 49, 48–54. [Google Scholar]
- Liu, J.; Bao, X.; Tan, H.; Wang, J.; Guo, D. Dynamical artificial boundary for fluid medium in wave motion problems. Chin. J. Theor. Appl. Mech. 2017, 49, 1418–1427. [Google Scholar]
- Du, T.; Wang, Y.; Huang, C.; Liao, L. Study on coupling effects of underwater launched vehicle. Chin. J. Theor. Appl. Mech. 2017, 49, 782–792. [Google Scholar]
- Chen, W.; Fu, Y.; Guo, S.; Jiang, C. Fluid-solid coupling and dynamic response of vortex-induced vibration of slender ocean cylinders. Adv. Mech. 2017, 47, 25–91. [Google Scholar]
- He, T.; Zhang, K.; Wang, T. AC-CBS-based partitioned semi-implicit coupling algorithm for fluid-structure interaction using stabilized second-order pressure scheme. Commun. Comput. Phys. 2017, 21, 1449–1474. [Google Scholar] [CrossRef]
- Zhou, D.; He, T.; Tu, J. A modified CBS finite element approach for fluid-structure interaction. Chin. J. Theor. Appl. Mech. 2012, 44, 494–504. [Google Scholar]
- Chen, W.; Ji, C.; Xu, W. Numerical investigation on the asymmetric vibration and symmetry hysteresis of flow-induced vibration of two side-by-side cylinders. Chin. J. Theor. Appl. Mech. 2015, 47, 731–739. [Google Scholar]
- Sun, X.; Zhang, J.; Huang, B. An application of the cbs scheme in the fluid-membrane interaction. Chin. J. Theor. Appl. Mech. 2013, 45, 787–791. [Google Scholar]
- Liu, Z.; Nan, S.; Shi, Y. Hemodynamic parameters analysis for coronary artery stenosis of intermediate severity model. Chin. J. Theor. Appl. Mech. 2017, 49, 1058–1064. [Google Scholar]
- Bazilevs, Y.; Calo, V.M.; Hughes, T.J.R.; Zhang, Y. Isogeometric fluid-structure interaction: Theory, algorithms, and computations. Comput. Mech. 2008, 43, 3–37. [Google Scholar] [CrossRef]
- Antona, R.; Vacondio, R.; Avesani, D.; Righetti, M.; Renzi, M. Towards a High Order Convergent ALE-SPH Scheme with Efficient WENO Spatial Reconstruction. Water 2021, 13, 2432. [Google Scholar] [CrossRef]
- Capasso, S.; Tagliafierro, B.; Viccione, G. Application of an SPH-DEM Coupled Model for Elastic Fluid–Structure Interaction. Environ. Sci. Proc. 2022, 21, 34. [Google Scholar]
- Zhang, A.M.; Ming, F.R.; Wang, S.P. Coupled SPHS-BEM method for transient fluid-structure interaction and applications in underwater impacts. Appl. Ocean. Res. 2013, 43, 223–233. [Google Scholar] [CrossRef]
- Wu, K.; Yang, D.M.; Wright, N. A coupled SPH-DEM model for fluid-structure interaction problems with free-surface flow and structural failure. Comput. Struct. 2016, 177, 141–161. [Google Scholar] [CrossRef]
- Raymond, S.J.; Jones, B.; Williams, J.R. A strategy to couple the material point method(MPM) and smoothed particle hydrodynamics (SPH) computational techniques. Comput. Part. Mech. 2018, 5, 49–58. [Google Scholar] [CrossRef]
- Liu, F.; Yu, Y.; Wang, Q.; Luo, Y. A coupled smoothed particle hydrodynamic and finite particle method: An efficient approach for fluid-solid interaction problems involving free-surface flow and solid failure. Eng. Anal. Bound. Elem. 2020, 118, 143–155. [Google Scholar] [CrossRef]
- Yao, X.; Huang, D. PD-SPH modeling and analysis of fluid-structure interaction problem. Eng. Mech. 2022, 39, 17–25. [Google Scholar]
- He, T. Numerical simulation of fluid-structure interaction strong coupling based on ALE finite element method. Chin. J. Mech. 2018, 50, 395–404. [Google Scholar]
- Boscheri, W.; Dumbser, M. A direct Arbitrary-Lagrangian–Eulerian ADER-WENO finite volume scheme on unstructured tetrahedral meshes for conservative and non-conservative hyperbolic systems in 3D. J. Comput. Phys. 2014, 275, 484–523. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Zhang, H.; Hao, Z.; Feng, Z. Application of lattice Boltzmann method in simulating droplet impact on liquid level. J. Hydraul. Eng. 2008, 39, 1316–1320. [Google Scholar]
- Wang, Z.; Li, D.; Hu, Y. An SPH stress correction algorithm and its application in free surface flow. Chin. J. Comput. Mech. 2017, 34, 101–105. [Google Scholar]
- Lu, W.; Fei, X.; Yang, Y. Improvement of the tensile instability in SPH scheme for the FEI (Fluid-Elastomer Interaction) problem. Eng. Anal. Bound. Elem. 2019, 106, 116–125. [Google Scholar]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Avesani, D.; Dumbser, M.; Chiogna, G.; Bellin, A. Analternative smooth particle hydrodynamics formulation to simulate chemotaxis in porous media. J. Math. Biol. 2017, 74, 1037–1058. [Google Scholar] [CrossRef] [PubMed]
- Ng, K.C.; Low, W.C.; Chen, H.; Tafuni, A.; Nakayama, A. A three-dimensional fluid-structure interaction model based on SPH and lattice-spring method for simulating complex hydroelastic problems. Ocean Eng. 2022, 260, 112026. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H.; Falahaty, H.; Shimizu, Y. An enhanced ISPH–SPH coupled method for simulation of incompressible fluid–elastic structure interactions. Comput. Phys. Commun. 2018, 232, 139–164. [Google Scholar] [CrossRef]
- Deng, L. Application of Variable-length Co-rotating Beam Element in Geometric Nonlinear Dynamic Analysis of Flexible Beam. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar]
- Meng, Z.-F.; Zhang, A.-M.; Yan, J.-L.; Wang, P.-P.; Khayyer, A. A hydroelastic fluid–structure interaction solver based on the iemann-SPH method. Comput. Methods Appl. Mech. Eng. 2022, 429, 110028. [Google Scholar]
- Rakhshaa, M.; Pazoukib, A.; Serbana, R.; Negrut, D. Using a half-implicit integration scheme for the SPH-based solution of fluid–solid interaction problems. Comput. Methods Appl. Mech. Eng. 2019, 345, 100–122. [Google Scholar] [CrossRef]
- Yilmaz, A.; Kocaman, S.; Demirci, M. Numerical modeling of the dam-break wave impact on elastic sluice gate: A new benchmark case for hydroelasticity problems. Ocean Eng. 2021, 231, 108870. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Progr. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Gray, J.P.; Monaghan, J.J.; Swift, R.P. SPH elastic dynamics. Comput. Methods Appl. Mech. Eng. 2001, 190, 6641–6662. [Google Scholar] [CrossRef]
- Antoci, C.; Gallati, M.; Sibilla, S. Numerical simulation of fluid-structure interaction by SPH. Comput. Struct. 2007, 85, 879–890. [Google Scholar] [CrossRef]
- Gallati, M.; Braschi, G. Simulazione Lagrangiana di flussi consuperficie libera in problemi di idraulica. L’acqua 2000, 5, 7–18. [Google Scholar]
- Vignjevic, R.; De Vuyst, T.; Campbell, J. The use of an homogeneous repulsive force for contact treatment in SPH. In Proceedings of the Fifth World Congress of Computational Mechanics WCCM V, Vienna, Austria, 7–12 July 2002. [Google Scholar]





| = 0.97 | = 0.93 | = 0.88 | |
|---|---|---|---|
| Similarity | 84.1% | 91.9% | 88.3% |
| Serial Number | Calculation Condition | Parameter Value |
|---|---|---|
| 1 | Particle spacing (m) | 0.001 |
| 2 | Number of particles in the water column | 17,997 |
| 3 | Number of elastomer particles | 1672 |
| 4 | Sidewall particle count | 2757 |
| 5 | Density of water (kg/m3) | 1000 |
| 6 | Density of elastic gate (kg/m3) | 1100 |
| 7 | Young’s modulus (N/m3) | 4.27 × 106 |
| 8 | Artificial stress factor (e,q) | 0.3 and 4 |
| 9 | Time step (s) | 5 × 10−6 |
| 10 | Physical time (s) | 0.4 |
| Numerical Method | SPH Method X Displacement | FEM Method X Displacement | SPH Method Y Displacement | FEM Method X Displacement |
|---|---|---|---|---|
| Similarity | 93.6% | 85.9% | 91.1% | 80.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, B.; Jiang, Q.; Hou, G.; Li, Z.; Liu, H. Numerical Study of Fluid–Solid Interaction in Elastic Sluice Based on SPH Method. Water 2023, 15, 3738. https://doi.org/10.3390/w15213738
Zhang J, Wang B, Jiang Q, Hou G, Li Z, Liu H. Numerical Study of Fluid–Solid Interaction in Elastic Sluice Based on SPH Method. Water. 2023; 15(21):3738. https://doi.org/10.3390/w15213738
Chicago/Turabian StyleZhang, Jianwei, Bingpeng Wang, Qi Jiang, Ge Hou, Zhirui Li, and Hongze Liu. 2023. "Numerical Study of Fluid–Solid Interaction in Elastic Sluice Based on SPH Method" Water 15, no. 21: 3738. https://doi.org/10.3390/w15213738





