Coordination of Flood Control under Urbanization on the Taihu Plain: Basin, City and Region Perspectives
Abstract
:1. Introduction
2. Materials and Methods
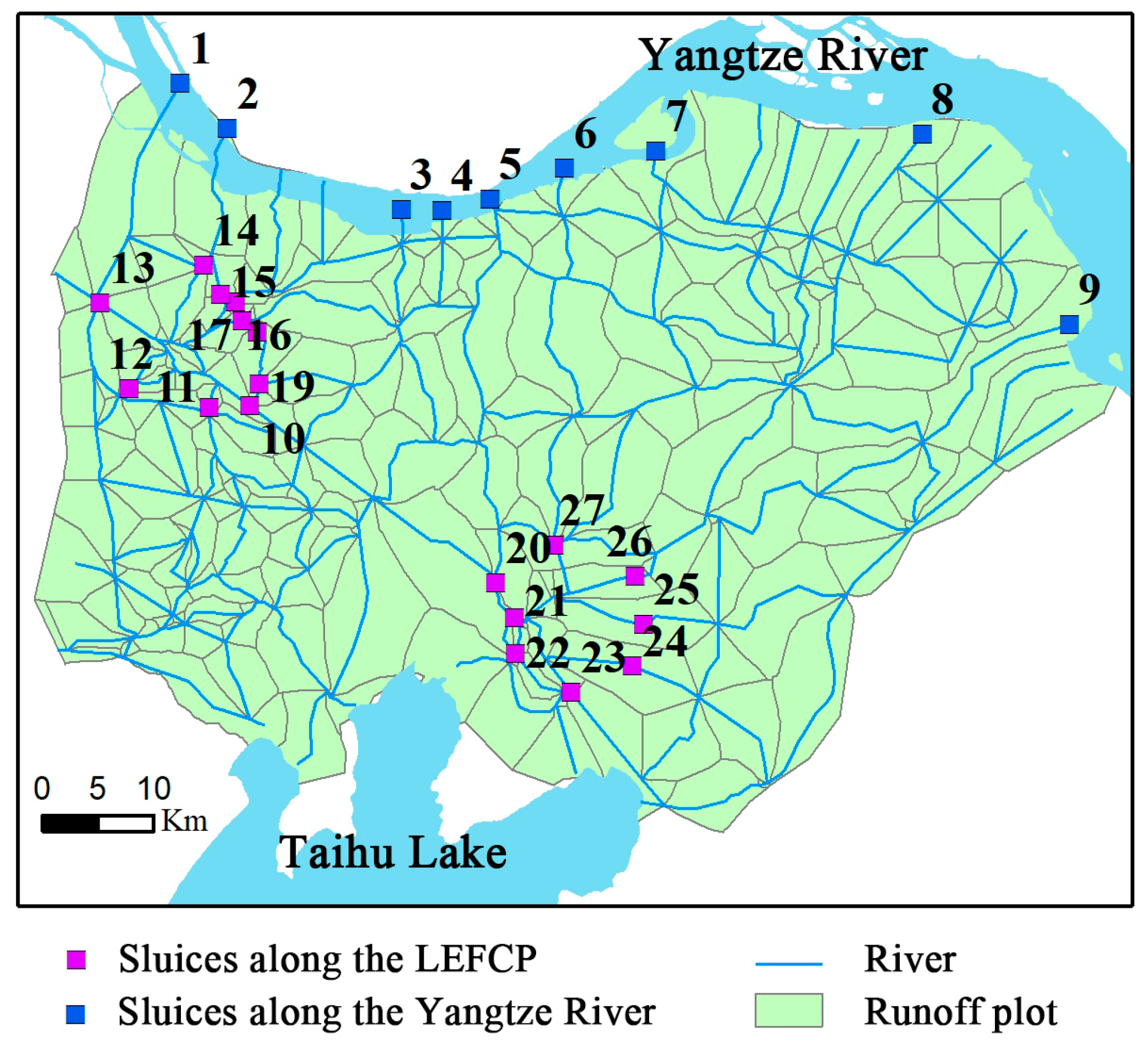
2.1. Study Area
2.2. Methods
2.2.1. Hydrodynamic Model
2.2.2. Flood Indicators
2.2.3. TOPSIS Coordination Evaluation Model
2.3. Data Description
3. Results
3.1. Modeling the Hydrological Process Based on a MIKE Model
3.1.1. Model Construction
3.1.2. Model Calibration and Validation
3.2. Simulation of Flood Characteristics under Different Scheduling Rules
3.2.1. Scheduling Scheme Scenarios
- (1)
- Scheme S0 refers to the present scheduling scheme.
- (2)
- Scheme S1 and Scheme S2 were urban optimal scheduling schemes, mainly examining the impact of controlled water level changes in the LEFCPs on the coordination of flood control.
- (3)
- Scheme S3 and Scheme S4 were the optimal scheduling schemes of the basin (water conservancy region), mainly examining the impact of controlled water level changes in sluices along the Yangtze River on the coordination of flood control.
- (4)
- Scheme S5, Scheme S6, Scheme S7, and Scheme S8 were the simultaneous optimal scheduling schemes of the city and basin, mainly examining the effect of combined optimal scheduling of the city and basin.
3.2.2. Flood Characteristics under Different Scheduling Rules
3.3. Coordination of Flood Control under Urbanization
3.3.1. Flood Control Coordination Assessment Index System and Weights
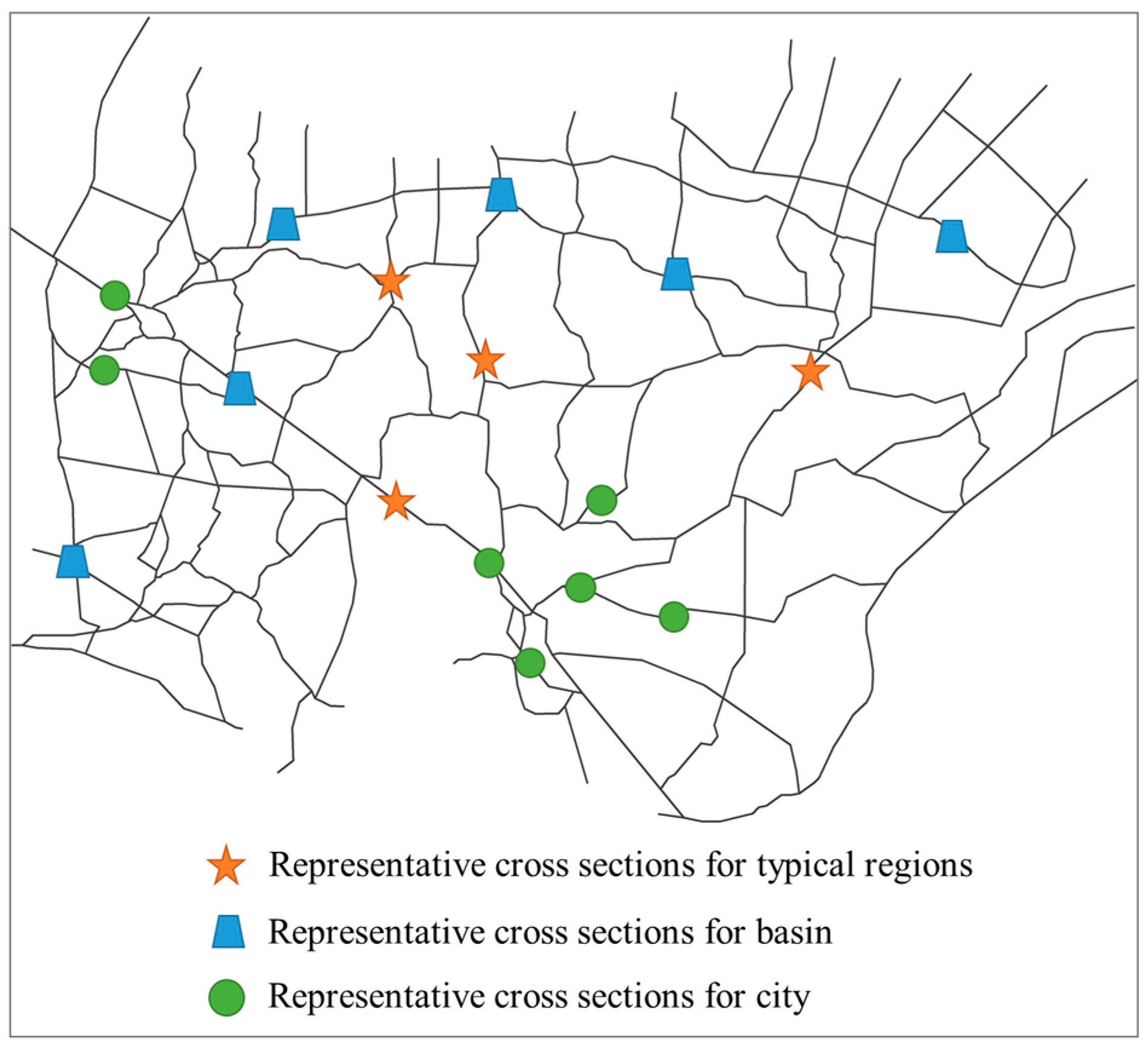
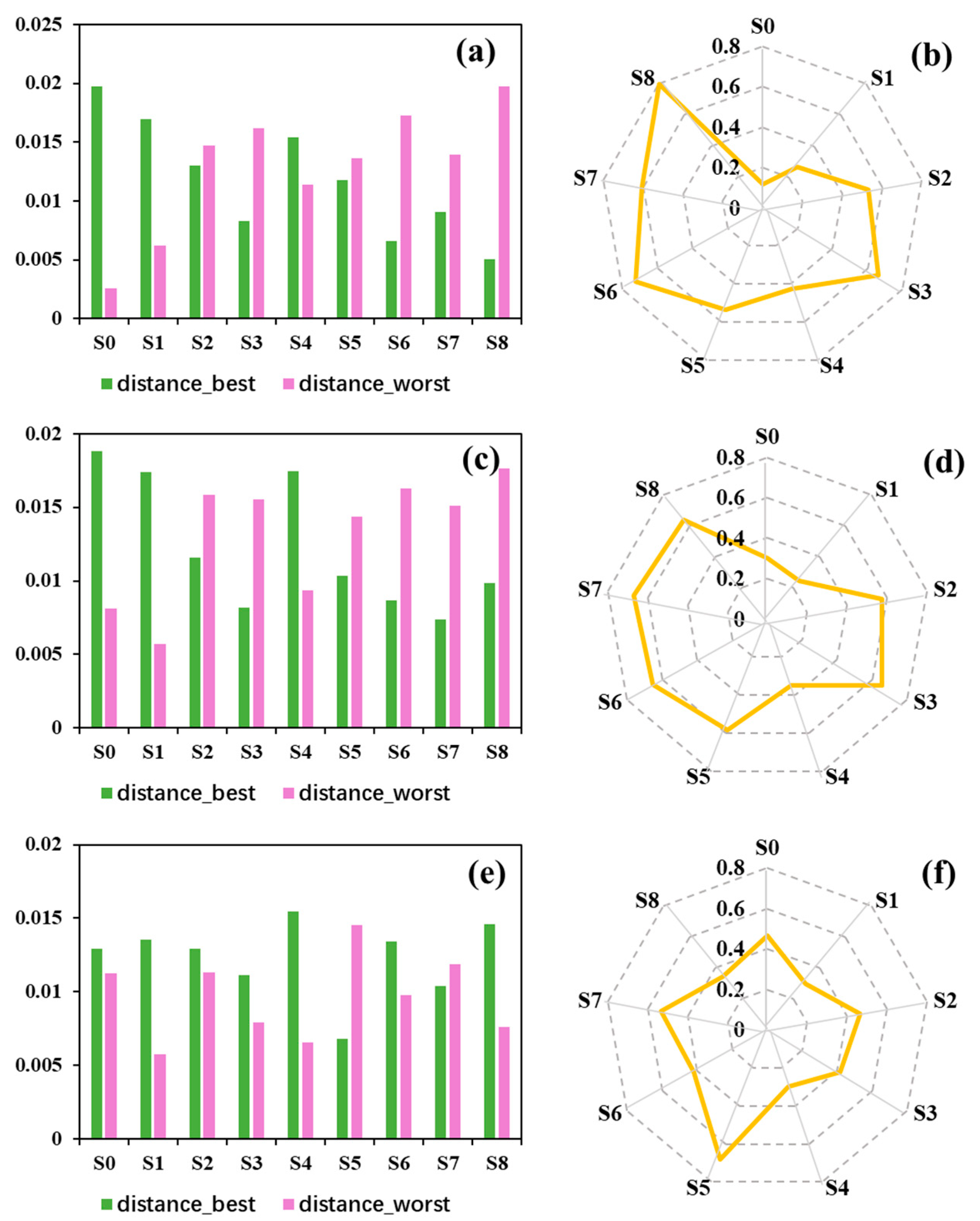
3.3.2. Flood Control Coordination between Basin and Regions
3.3.3. Flood Control Coordination between Basin and Cities
3.3.4. Flood Control Coordination between Regions and Cities
4. Discussion
4.1. Method Design
4.2. Limitations
4.3. Implication
5. Conclusions
- (1)
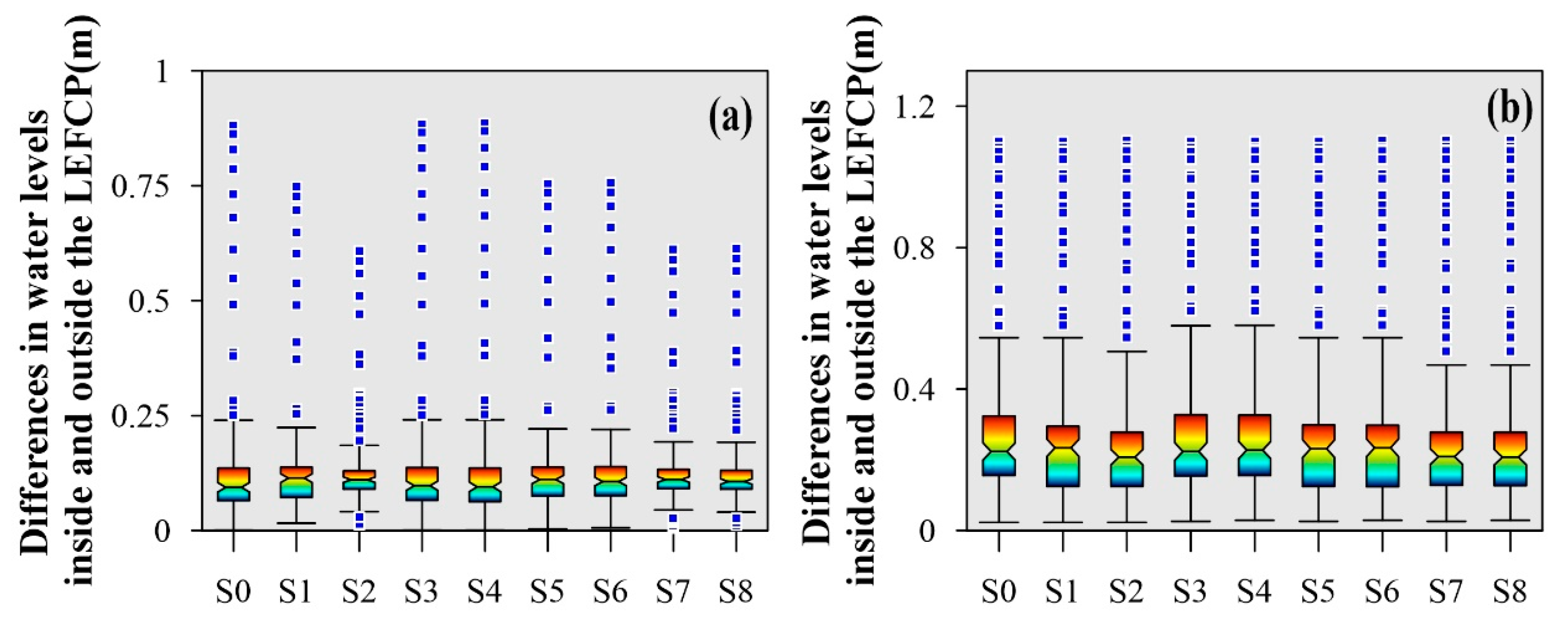
- Variations in Flood Characteristics under Different Flood Control Coordination Schemes: Schemes S2, S7, and S8 stand out by significantly reducing both the mean and maximum water level differences between the inner and outer urban areas. The flood characteristics of the flood processes under different scheduling rules varied slightly, especially the FI. With the exception of S4, the RCS means for the other models are higher than S0, and the highest RCS mean is for S5 at 1.022. The SFDC means for most scenarios are lower than S0, and the highest SFDC mean is for S5 at 0.305.
- (2)
- Effect of Different Scheduling Optimization Schemes on Flood Control Coordination at Various Levels: At the basin–region level, Scheme S8 significantly improved flood coordination, achieving a coordination coefficient of 0.68, compared to Scheme S0, which only scored 0.12. Moving to the basin–city level, Scheme S7 demonstrated notable progress with a coordination coefficient of 0.67, signifying a 0.37 improvement over Scheme S0, which scored 0.30. Finally, at the region-city level, Scheme S5 emerged as the most effective, attaining a coordination coefficient of 0.68, indicating a 0.22 improvement over Scheme S0, which scored 0.46. Overall, the optimal scheduling of cities and basins simultaneously had the most significant effect on enhancing coordination, followed by urban optimization schemes, while the effect of basin optimization schemes was relatively weaker.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Xu, Y.; Cai, X.; Tang, J.; Yang, L. Role of underlying surface, rainstorm and antecedent wetness condition on flood responses in small and medium sized watersheds in the Yangtze River Delta region, China. Catena 2021, 206, 105489. [Google Scholar] [CrossRef]
- Yin, J.; Gentine, P.; Zhou, S.; Sullivan, C.; Wang, R.; Zhang, Y.; Guo, S. Large increase in global storm runoff extremes driven by climate and anthropogenic changes. Nat. Commun. 2018, 9, 4389. [Google Scholar] [CrossRef]
- Winsemius, H.; Aerts, J.; Van Beek, L.; Bierkens, M.; Ward, P. Global drivers of future river flood risk. Nat. Clim. Chang. 2016, 6, 381–385. [Google Scholar] [CrossRef]
- Oddo, P.; Lee, B.; Garner, G.; Srikrishnan, V.; Reed, M.; Forest, E.; Keller, K. Deep uncertainties in sea-level rise and storm surge projections: Implications for coastal flood risk management. Risk Anal. 2020, 40, 153–168. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Liu, S.; Zhong, G.; Cai, Y. Flood Disaster and Flood Control Measurements in Shanghai. Nat. Hazards Rev. 2016, 18, B5016001. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis: Summary for Policymakers; Stocker, T.F., Qin, D., Plattner, G., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Liu, Y.; Huang, X.; Yang, H. An integrated approach to investigate the coupling coordination between urbanization and flood disasters in China. J. Clean. Prod. 2022, 375, 134191. [Google Scholar] [CrossRef]
- Harvey, G.; Thorne, C.; Cheng, X.; Evans, E.P.; Han, S.; Simm, J.D.; Wang, Y. Quantitative analysis of future flood risk in the Taihu Basin, China. J. Flood Risk Manag. 2009, 2, 85–100. [Google Scholar] [CrossRef]
- Cheng, X.; Evans, E.; Wu, H.; Thorne, C.; Han, S.; Simm, J.; Hall, J. A framework for long-term scenario analysis in the Taihu Bain, China. J. Flood Risk Manag. 2013, 6, 3–13. [Google Scholar] [CrossRef]
- Dey, P.; Mishra, A. Separating the impacts of climate change and human activities on streamflow: A review of methodologies and critical assumptions. J. Hydrol. 2017, 548, 278–290. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, L.; Tang, H. Prediction of the future flood severity in plain river network region based on numerical model: A case study. J. Hydrodyn. 2017, 29, 586–595. [Google Scholar] [CrossRef]
- Falter, D.; Dung, N.; Vorogushyn, S.; Schroeter, K.; Hundecha, Y.; Kreibich, H.; Apel, H.; Theisselmann, F.; Merz, B. Continuous, large-scale simulation model for flood risk assessments: Proof-of-concept. J. Flood Risk Manag. 2016, 9, 3–21. [Google Scholar] [CrossRef]
- Zhang, S.; Jing, Z.; Li, W.; Yi, Y.; Zhao, Y. Study of the flood control scheduling scheme for the Three Gorges Reservoir in a catastrophic flood. Hydrol. Process. 2018, 32, 1625–1634. [Google Scholar] [CrossRef]
- Jing, Z.; Zhang, R.; Bao, H.; Zhang, S. Joint flood control scheduling strategy of large cascade reservoirs: A case study of the cascade reservoirs in the upper reaches of the Yangtze River in China. J. Flood Risk Manag. 2022, 15, e12802. [Google Scholar] [CrossRef]
- Chen, W.; Wang, W.; Huang, G.; Wang, Z.; Lai, C.; Yang, Z. The capacity of grey infrastructure in urban flood management: A comprehensive analysis of grey infrastructure and the green-grey approach. Int. J. Disaster Risk Reduct. 2021, 54, 102045. [Google Scholar] [CrossRef]
- Bae, C.; Lee, D. Effects of low-impact development practices for flood events at the catchment scale in a highly developed urban area. Int. J. Disaster Risk Reduct. 2020, 44, 101412. [Google Scholar] [CrossRef]
- Macro, K.; Matott, L.; Rabideau, A.; Ghodsi, S.; Zhu, Z. OSTRICH-SWMM: A new multi-objective optimization tool for green infrastructure planning with SWMM. Environ. Model. Softw. 2019, 113, 42–47. [Google Scholar] [CrossRef]
- Yazdi, J.; Choi, H.; Kim, J. A methodology for optimal operation of pumping stations in urban drainage systems. J. Hydro-Environ. Res. 2016, 11, 101–112. [Google Scholar] [CrossRef]
- Ye, C.; Xu, Z.; Lei, X.; Zhang, R.; Chu, Q.; Li, P.; Ban, C. Assessment of the impact of urban water system scheduling on urban flooding by using coupled hydrological and hydrodynamic model in Fuzhou City, China. J. Environ. Manag. 2022, 321, 115935. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Q.; Li, W.; Sun, D.; Huang, F. Intensifier of urban economic resilience: Specialized or diversified agglomeration. PLoS ONE 2021, 16, 1–21. [Google Scholar] [CrossRef]
- Xu, Z.; Ye, C. Simulation of urban flooding/waterlogging processes: Principle, models and prospects. J. Hydraul. Eng. 2021, 52, 381–392. [Google Scholar]
- Elga, S.; Jan, B.; Okke, B. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, X.; Liang, S.; Zhu, B.; Yao, Y.; Meng, S.; Lu, C. Quantifying the response of potential flooding risk to urban growth in Beijing. Sci. Total Environ. 2020, 705, 135868. [Google Scholar] [CrossRef] [PubMed]
- Pumo, D.; Arnone, E.; Francipane, A.; Caracciolo, D.; Noto, L. Potential implications of climate change and urbanization on watershed hydrology. J. Hydrol. 2017, 554, 80–99. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, Y.; Chen, Y.; Xu, C.; Gao, Y.; Du, J. Hydrological response to urbanization at different spatio-temporal scales simulated by coupling of CLUE-S and the SWAT model in the Yangtze River Delta region. J. Hydrol. 2013, 485, 113–125. [Google Scholar] [CrossRef]
- Parvaze, S.; Khan, J.; Kumar, R.; Allaie, S. Flood forecasting in Jhelum river basin using integrated hydrological and hydraulic modeling approach with a real-time updating procedure. Clim. Dyn. 2022, 59, 2231–2255. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, H.; Zhang, H.; Du, G.; Zhou, J. Urban flood risk warning under rapid urbanization. Environ. Res. 2015, 139, 3–10. [Google Scholar] [CrossRef]
- Kalimisetty, S.; Singh, A.; Venkata, D.; Rao, V.; Mahammood, V. 1D and 2D model coupling approach for the development of operational spatial flood early warning system. Geocarto Int. 2021, 37, 4390–4405. [Google Scholar] [CrossRef]
- Mignot, E.; Paquier, A.; Haider, S. Modeling Floods in a Dense Urban Area Using 2D Shallow Water Equations. J. Hydrol. 2006, 327, 186–199. [Google Scholar] [CrossRef]
- Duan, H.; Gao, X. Flooding control and hydro-energy assessment for urban stormwater drainage systems under climate change. Water Resour. Manag. 2019, 33, 3523–3545. [Google Scholar] [CrossRef]
- Koudelak, P.; West, S. Sewerage network modelling in Latvia, use of InfoWorks CS and Storm Water Management Model 5 in Liepaja city. Water Environ. J. 2007, 22, 81–87. [Google Scholar] [CrossRef]
- Jayapadma, J.; Wickramaarachchi, T.; Silva, G.; Ishidaira, H.; Magome, J. Coupled hydrodynamic modelling approach to assess land use change induced flood characteristics. Environ. Monit. Assess. 2022, 194, 354. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Yu, Z.; Hua, J.; Kang, C.; Lin, Z. Spatial dependence of floods shaped by extreme rainfall under the influence of urbanization. Sci. Total Environ. 2023, 857, 159134. [Google Scholar] [CrossRef] [PubMed]
- Dhote, P.; Joshi, Y.; Rajib, A.; Thakur, P.; Nikam, B.; Aggarwal, S. Evaluating topography-based approaches for fast floodplain mapping in data-scarce complex-terrain regions: Findings from a Himalayan basin. J. Hydrol. 2023, 620, 129309. [Google Scholar] [CrossRef]
- Ghotbi, S.; Wang, D.; Singh, A.; Mayo, T.; Sivapalan, M. Climate and Landscape Controls of Regional Patterns of Flow Duration Curves Across Continental United States: Statistical Approach. Water Resour. Res. 2020, 56, 1–22. [Google Scholar] [CrossRef]
- Carrillo-Soto, G.A.; Cely, N.J.; Ayala-Ibarra, M.L. Hydrological similarity of catchments in the southern area of Colombian Andean region. J. Phys. Conf. Ser. 2019, 1388, 012042. [Google Scholar] [CrossRef]
- Deelstra, J.; Iital, A. The use of the flashiness index as a possible indicator for nutrient loss prediction in agricultural catchments. Boreal Environ. Res. 2008, 13, 209–221. [Google Scholar]
- Behzadian, M.; Otaghsara, S.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Shih, H.; Shyur, H.; Lee, E. An extension of TOPSIS for group decision making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
- Sabinaya, B.; Bhabagrahi, S.; Madan, K.; Bhuyan, M. A hybrid machine learning-based multi-DEM ensemble model of river cross-section extraction: Implications on streamflow routing. J. Hydrol. 2023, 625, 129951. [Google Scholar] [CrossRef]
- Ahmed, F. A hydrodynamic model for the Lower Rideau River. Nat. Hazards 2010, 55, 85–94. [Google Scholar] [CrossRef]
- Rahman, M.; Goel, N.; Arya, D. Development of the Jamuneswari Flood Forecasting System: Case Study in Bangladesh. J. Hydrol. Eng. 2012, 17, 1123–1140. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, C.; Xu, J.; Zhang, W.; She, L.; Zhang, Q.; Bao, R. Assessing the mechanism for flood control: A case of plain river network cities under extreme rainfalls. Environ. Sci. Pollut. Res. 2023, 30, 38076–38098. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, L.; Wang, Y. Research on Standard Syntaxis of Sub-basin Flood and Urban Drainage Based on Safety Margin Theory. J. Hohai Univ. Nat. Sci. 2023, 51, 150–156. (In Chinese) [Google Scholar]
- Zhong, G.; Liu, S.; Hu, Z. Analysis of influence on region flood control due to polder waterlogging drainage in Yangcheng and Dianmao area. Yangtze River 2017, 48, 9–14. (In Chinese) [Google Scholar]
- Wang, L. Research on Coordination of Flood Control in The Taihu Basin Under Rapid Urbanization. Ph.D. Dissertation, Nanjing Hydraulic Research Institute, Nanjing, China, 2019. (In Chinese). [Google Scholar]


| Indicator | Formula | Meaning | |
|---|---|---|---|
| SFDC | (5) | SFDC represents the flood process’s responsiveness to rainfall. Higher SFDC values indicate a more rapid response of the flooding process to rainfall. | |
| where w33% and w66% are the water level value at the 33rd and 66th percentile, respectively. | |||
| RCS | (6) | RCS quantifies the change in water level during the flood process. Larger RCS values imply a faster rate of water level rise, potentially leading to increased flood control pressure. | |
| where wp is the peak water level, w0 is the initial water level, and Δt is the interval from the initial water level to the peak water level. | |||
| FI | (7) | FI measures the degree of fluctuation in the flood process over time. Higher FI values indicate a greater degree of fluctuation in the flood process. | |
| where wi is the water level at the ith moment. | |||
| Schemes | Operation Rules of Sluices along the Yangtze River | Operation Rules of the LEFCPs |
|---|---|---|
| S0 | Changzhou > 4.0 m | Sanbaojie > 4.3 m |
| Wuxi > 3.6 m | ||
| Qingyang > 3.7 m | Nanmen > 3.8 m | |
| S1 | Changzhou > 4.0 m | Sanbaojie > 4.43 m |
| Wuxi > 3.6 m | ||
| Qingyang > 3.7 m | Nanmen > 4.0 m | |
| S2 | Changzhou > 4.00 m | Sanbaojie > 4.57 m |
| Wuxi > 3.6 m | ||
| Qingyang >3.7 m | Nanmen > 4.2 m | |
| S3 | Changzhou > 3.87 m | Sanbaojie > 4.3 m |
| Wuxi > 3.4 m | ||
| Qingyang > 3.53 m | Nanmen > 3.8 m | |
| S4 | Changzhou >3.73 m | Sanbaojie > 4.3 m |
| Wuxi > 3.2 m | ||
| Qingyang > 3.35 m | Nanmen > 3.8 m | |
| S5 | Changzhou > 3.87 m | Sanbaojie > 4.43 m |
| Wuxi > 3.4 m | ||
| Qingyang > 3.53 m | Nanmen > 4.0 m | |
| S6 | Changzhou >3.73 m | Sanbaojie > 4.43 m |
| Wuxi > 3.2 m | ||
| Qingyang > 3.35 m | Nanmen > 4.0 m | |
| S7 | Changzhou > 3.87 m | Sanbaojie > 4.57 m |
| Wuxi (da) > 3.4 m | ||
| Qingyang > 3.53 m | Nanmen > 4.2 m | |
| S8 | Changzhou >3.73 m | Sanbaojie > 4.57 m |
| Wuxi > 3.2 m | ||
| Qingyang > 3.35 m | Nanmen > 4.2 m |
| Indicators | Level | Weights | Direction | Normalized Value of Each Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | ||||
| FI | Basin | 0.187 | Negative | 0.333 | 0.331 | 0.335 | 0.334 | 0.330 | 0.335 | 0.333 | 0.335 | 0.334 |
| Region | 0.255 | Negative | 0.295 | 0.297 | 0.353 | 0.355 | 0.299 | 0.342 | 0.347 | 0.345 | 0.357 | |
| RCS | Basin | 0.195 | Negative | 0.309 | 0.333 | 0.306 | 0.330 | 0.358 | 0.308 | 0.358 | 0.333 | 0.359 |
| Region | 0.146 | Negative | 0.338 | 0.331 | 0.337 | 0.332 | 0.327 | 0.337 | 0.329 | 0.334 | 0.335 | |
| SFDC | Basin | 0.062 | Negative | 0.333 | 0.336 | 0.315 | 0.319 | 0.341 | 0.405 | 0.310 | 0.306 | 0.324 |
| Region | 0.155 | Negative | 0.320 | 0.332 | 0.315 | 0.334 | 0.346 | 0.320 | 0.347 | 0.334 | 0.350 | |
| Indicators | Level | Weights | Direction | Normalized Value of Each Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | ||||
| FI | Basin | 0.173 | Negative | 0.333 | 0.331 | 0.335 | 0.334 | 0.330 | 0.335 | 0.333 | 0.335 | 0.334 |
| City | 0.236 | Negative | 0.295 | 0.297 | 0.353 | 0.355 | 0.299 | 0.342 | 0.347 | 0.345 | 0.357 | |
| RCS | Basin | 0.180 | Negative | 0.309 | 0.333 | 0.306 | 0.330 | 0.358 | 0.308 | 0.358 | 0.333 | 0.359 |
| City | 0.114 | Negative | 0.327 | 0.330 | 0.330 | 0.334 | 0.332 | 0.330 | 0.335 | 0.341 | 0.341 | |
| SFDC | Basin | 0.096 | Negative | 0.302 | 0.306 | 0.314 | 0.345 | 0.308 | 0.356 | 0.360 | 0.380 | 0.319 |
| City | 0.201 | Positive | 0.354 | 0.329 | 0.355 | 0.329 | 0.314 | 0.352 | 0.315 | 0.332 | 0.316 | |
| Indicators | Level | Weights | Direction | Normalized Value of Each Indicator | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | ||||
| FI | Region | 0.180 | Negative | 0.338 | 0.331 | 0.337 | 0.332 | 0.327 | 0.337 | 0.329 | 0.334 | 0.335 |
| City | 0.077 | Negative | 0.333 | 0.336 | 0.315 | 0.319 | 0.341 | 0.405 | 0.310 | 0.306 | 0.324 | |
| RCS | Region | 0.192 | Negative | 0.320 | 0.332 | 0.315 | 0.334 | 0.346 | 0.320 | 0.347 | 0.334 | 0.350 |
| City | 0.153 | Negative | 0.327 | 0.330 | 0.330 | 0.334 | 0.332 | 0.330 | 0.335 | 0.341 | 0.341 | |
| SFDC | Region | 0.128 | Negative | 0.302 | 0.306 | 0.314 | 0.345 | 0.308 | 0.356 | 0.360 | 0.380 | 0.319 |
| City | 0.270 | Positive | 0.354 | 0.329 | 0.355 | 0.329 | 0.314 | 0.352 | 0.315 | 0.332 | 0.316 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, M.; Kang, C.; Yu, Z.; Zhang, X. Coordination of Flood Control under Urbanization on the Taihu Plain: Basin, City and Region Perspectives. Water 2023, 15, 3723. https://doi.org/10.3390/w15213723
Lu M, Kang C, Yu Z, Zhang X. Coordination of Flood Control under Urbanization on the Taihu Plain: Basin, City and Region Perspectives. Water. 2023; 15(21):3723. https://doi.org/10.3390/w15213723
Chicago/Turabian StyleLu, Miao, Congxuan Kang, Zhihui Yu, and Xiuhong Zhang. 2023. "Coordination of Flood Control under Urbanization on the Taihu Plain: Basin, City and Region Perspectives" Water 15, no. 21: 3723. https://doi.org/10.3390/w15213723





