Synchronized Structure and Teleconnection Patterns of Meteorological Drought Events over the Yangtze River Basin, China
Abstract
:1. Introduction
2. Study Area and Data
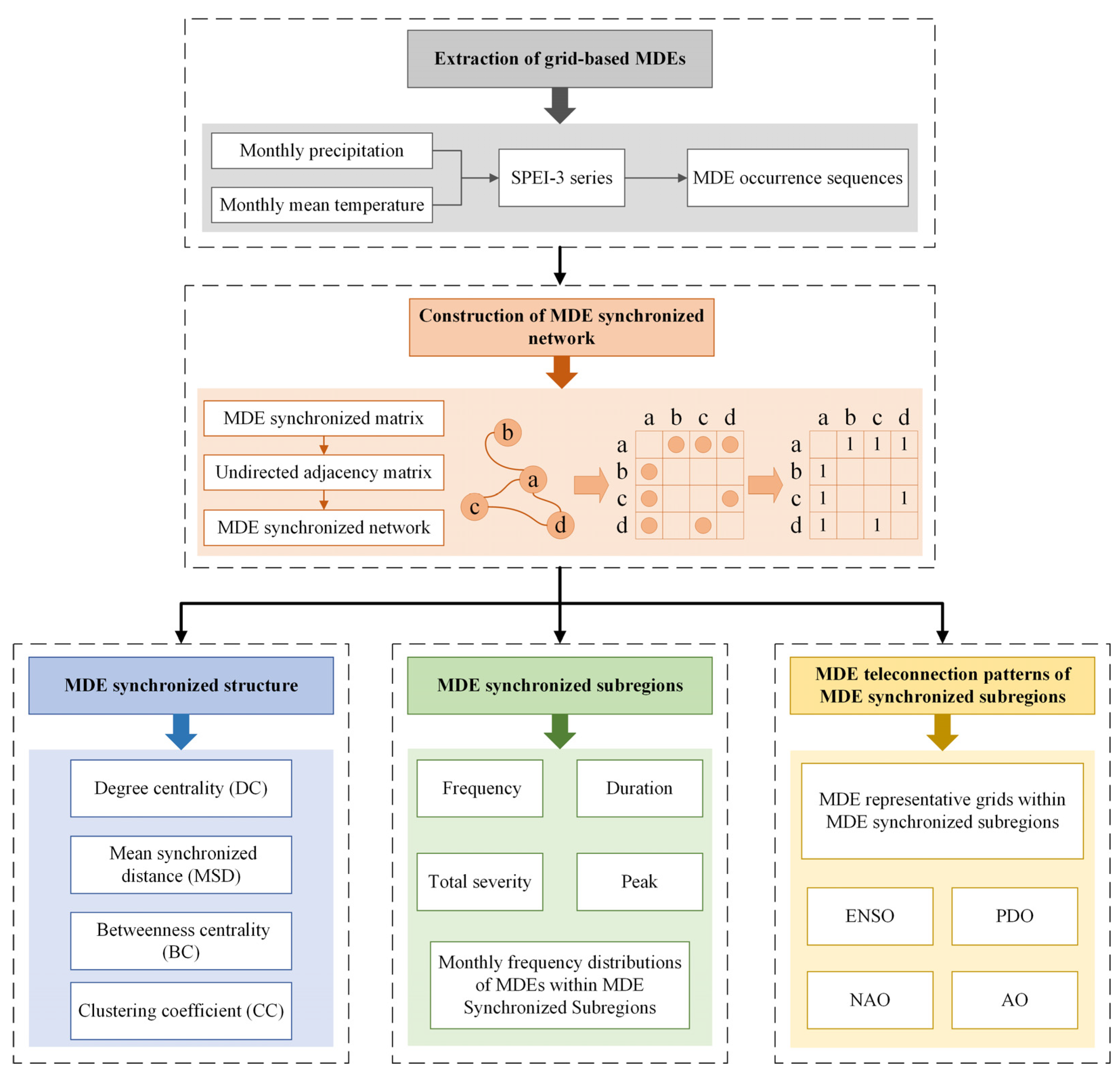
3. Methodology
3.1. Extraction of Grid-Based MDEs and Relevant MDE Characteristics over the YRB by Run Theory
3.2. Calculation of the MDE Synchronized Matrix over the YRB by Event Synchronization (ES)
3.3. Construction of the MDE Synchronized Network over the YRB by a Complex Network (CN)
3.4. Quantification of MDEs’ Synchronized Structure over the YRB by Network-Based Metrics
- (1)
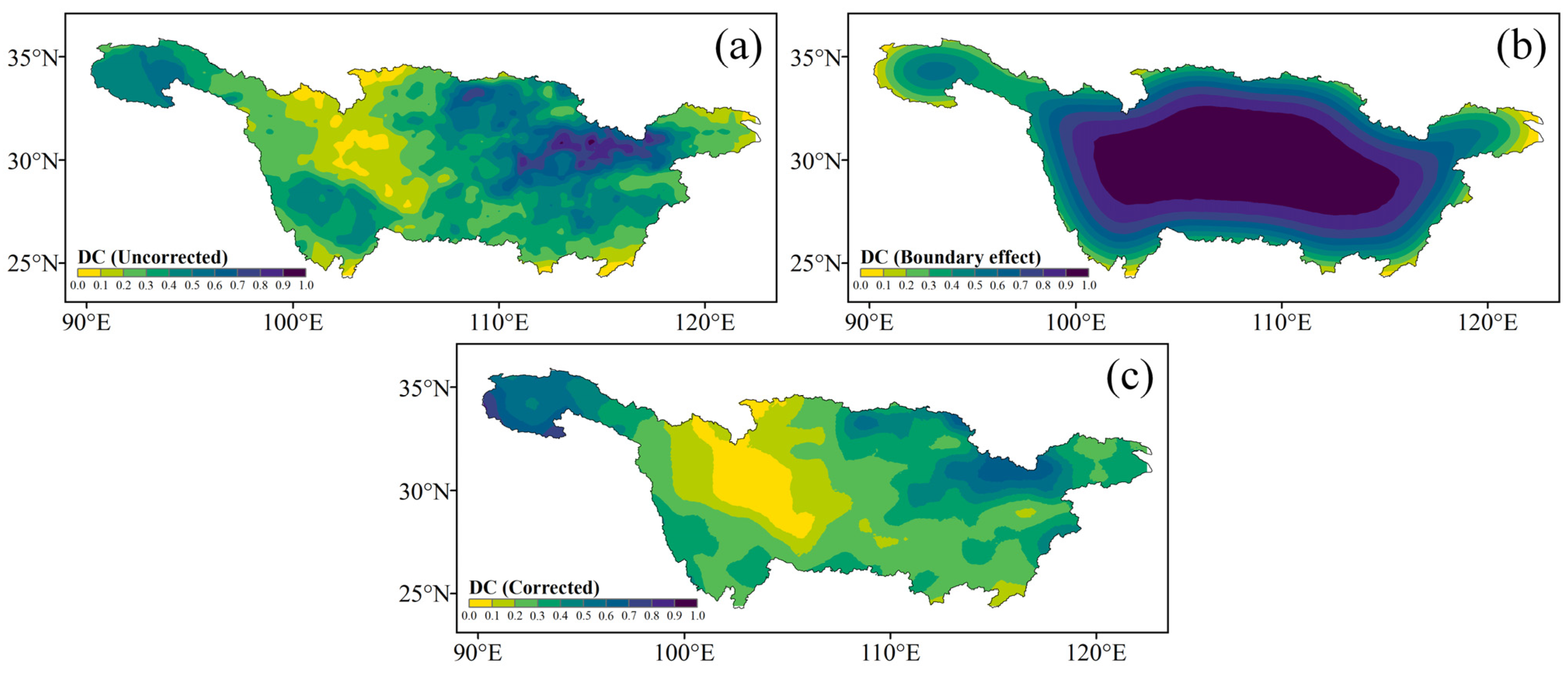
- Degree ki measures the number of edges that node i has in the network; these connected nodes make up the adjacent nodes of node i. Degree centrality DCi is the normalized result of ki, which is formulated as follows:
- (2)
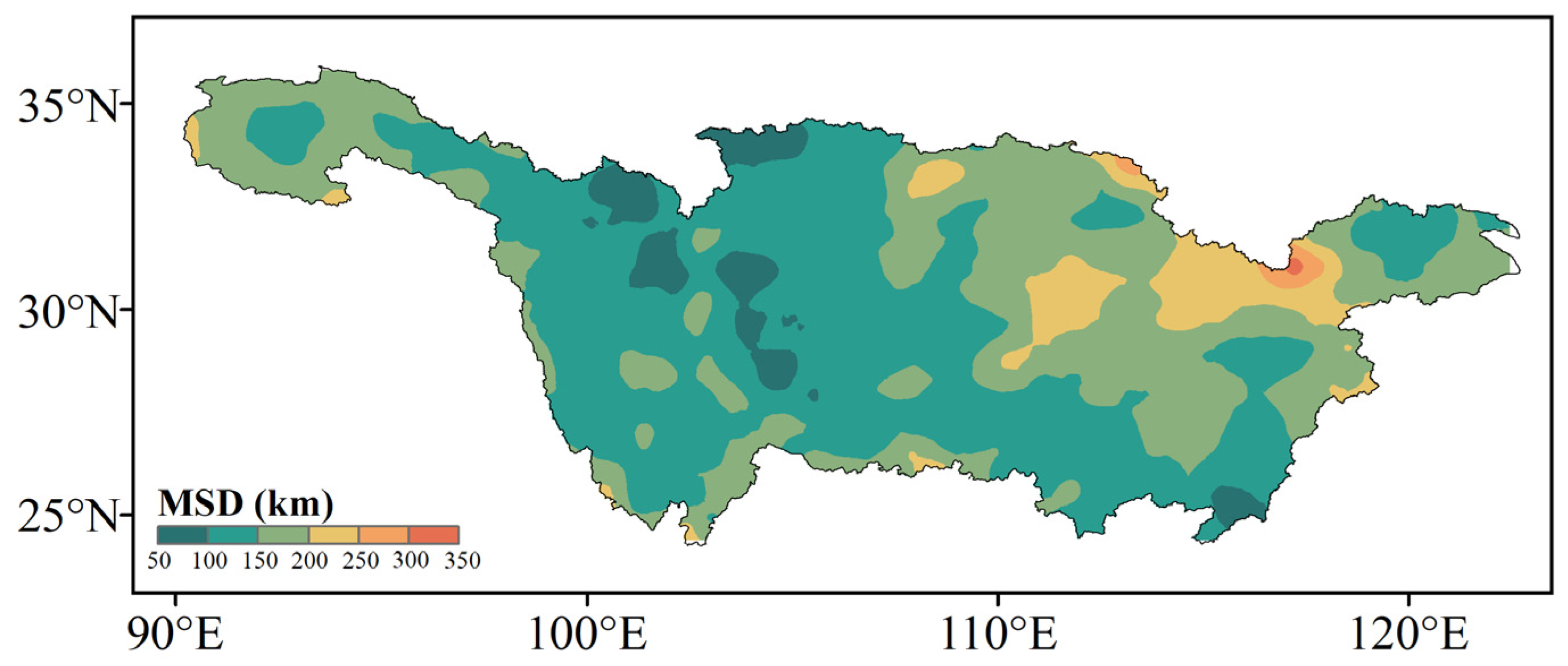
- MSD represents the average geographic distance between a node and its adjacent nodes in the network. MSDi can be mathematically expressed as follows:
- (3)
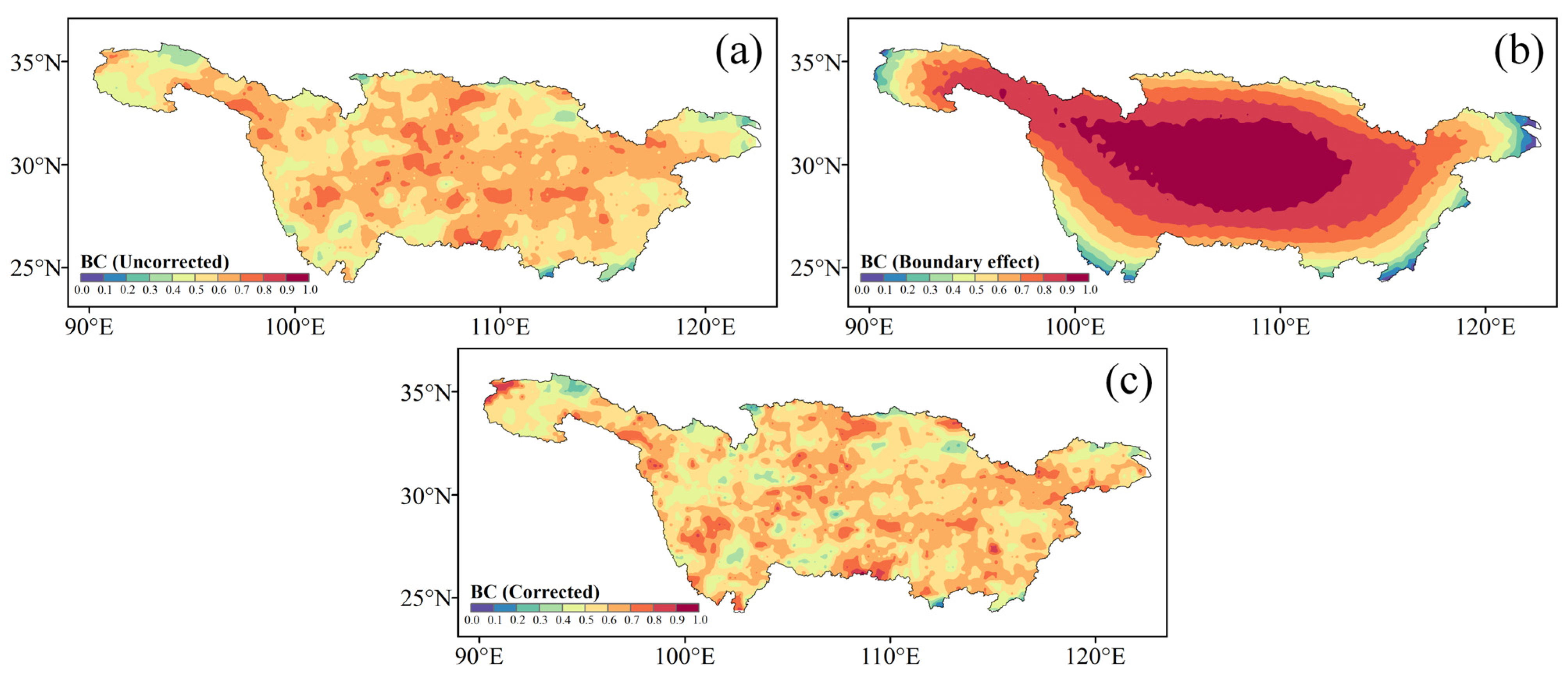
- BC is a metric that identifies nodes that act as intermediaries or bridges in the network. BCi is defined as the proportion of the shortest path number between node pairs passing through node i to the total number of the shortest paths of these node pairs in the network, which is shown as follows:
- (4)
- The CC of a node measures the proportion of its neighbors that are also connected to one another, which is defined as follows:
3.5. Partitioning of MDE Synchronized Subregions within the YRB by the Leiden Algorithm
3.6. Identification of MDE Representative Grids in MDE Synchronized Subregions by the Z − P Space Approach
3.7. Evaluation of MDE Teleconnection Patterns of MDE Synchronized Subregions by Wavelet Coherence Analysis (WCA)
4. Results and Discussion
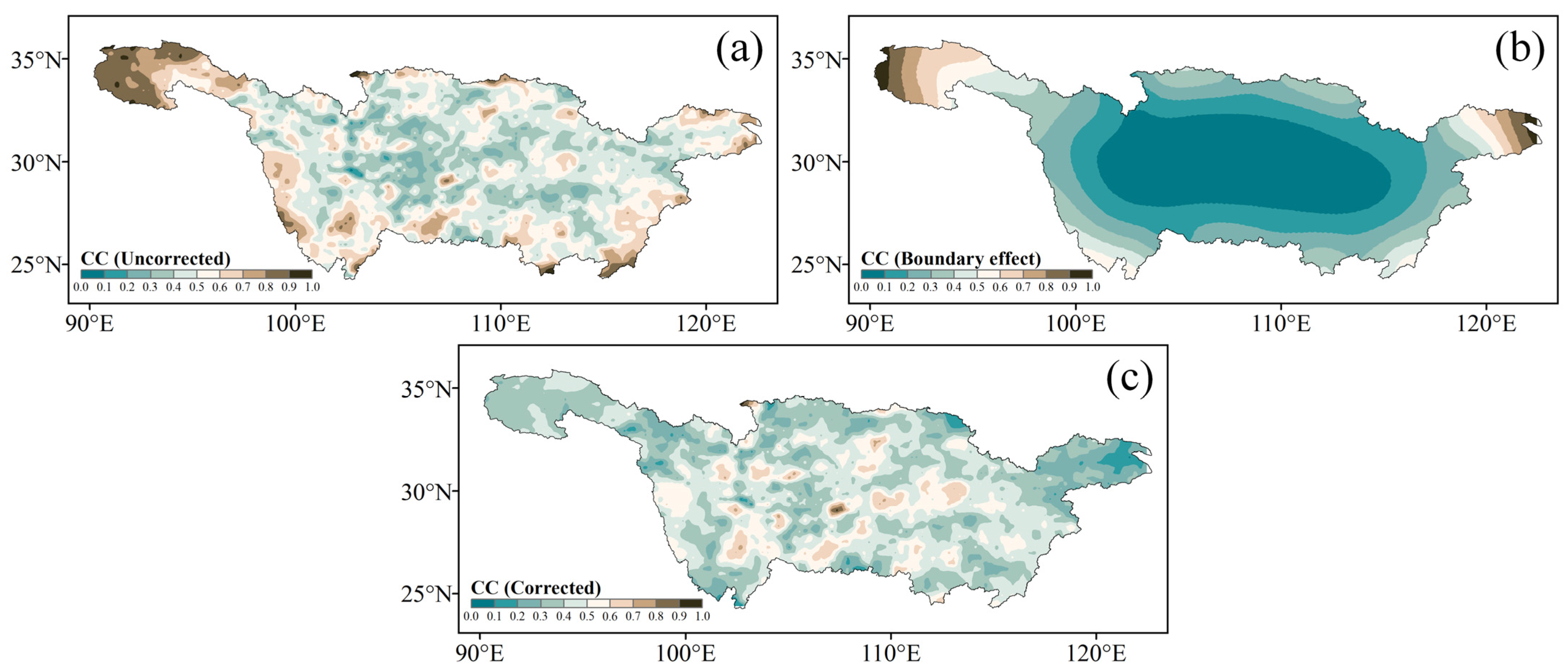
4.1. MDEs’ Synchronized Structure over the YRB
4.2. Synchronized Subregions and Representative Grids of MDEs within the YRB
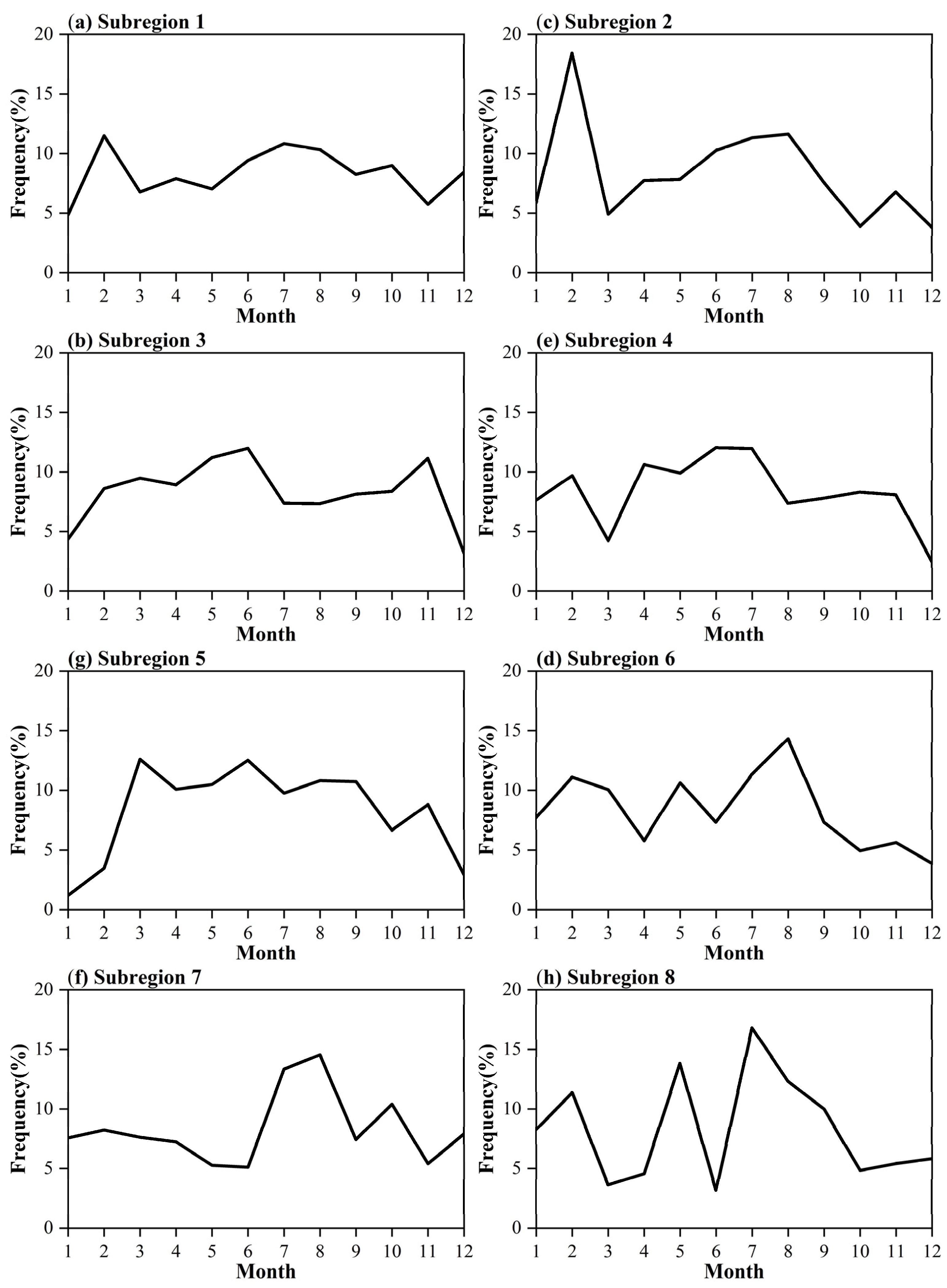
4.3. MDE Characteristics of MDE Synchronized Subregions
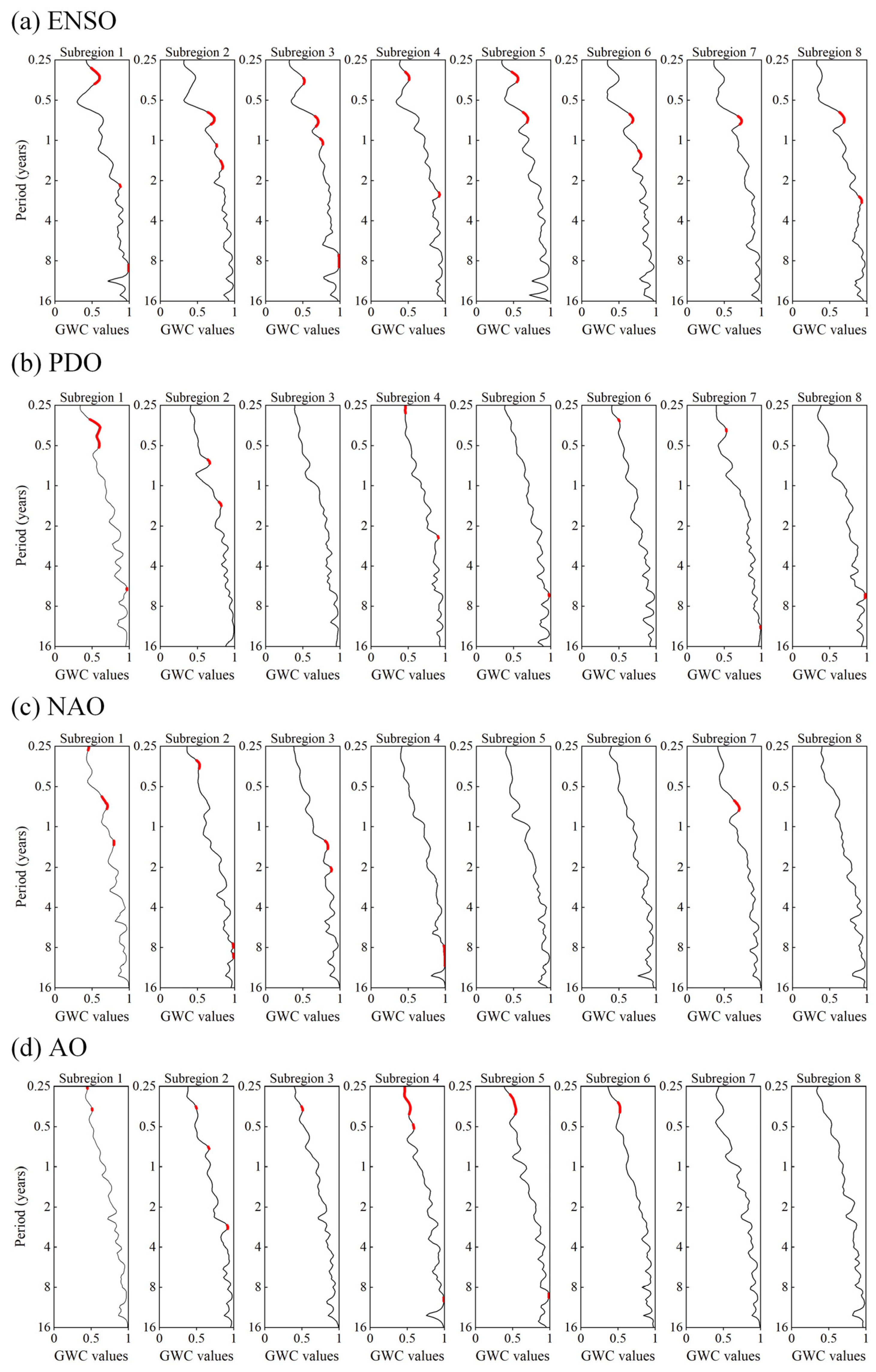
4.4. MDE Teleconnection Patterns of MDE Synchronized Subregions
5. Conclusions
- ●
- The northeastern portion of the YRB exhibits significant MDE synchronization, as evidenced by its high DC and MSD values. These characteristics make this region more susceptible to experiencing widespread MDEs. Conversely, specific areas in the upper reaches, characterized by low DC and MSD values, suggest a higher likelihood of localized MDE occurrences. The BC results highlight the propagation of synchronous MDEs along two main pathways: the central pathway and the eastern pathway. These two pathways display relatively low MDE spatial coherence, as indicated by the low CC values.
- ●
- The YRB is partitioned into eight MDE synchronized subregions, and the spatial ranges of the individual subregions are consistent with the MDE synchronized scales identified from the DC and MSD results. Each subregion exhibits distinct characteristics in terms of the frequency, duration, total severity, and peak of MDEs, as well as distinct MDE temporal frequency distributions. Among these subregions, Subregion 3 in the southeast experiences the fewest MDEs, while Subregion 1 in the southwest has the highest MDE duration value and the strongest MDE total severity value. Additionally, Subregions 3, 5, 6, and 7 in the southeast and north show relatively low MDE peak values. In Subregions 1–7, the season with the highest MDE frequency gradually shifts from winter to summer, while Subregion 8 in the northwest exhibits greater month-to-month fluctuations in the MDEs’ temporal frequency.
- ●
- The MDE synchronized subregions exhibit significant variability in MDE teleconnection patterns at multiple timescales. ENSO exerts a strong influence on MDEs in all subregions, whereas the influence effects from other teleconnection factors (i.e., the PDO, NAO, and AO) are relatively weaker. Specifically, the PDO shows a significant association with MDEs in all subregions except for Subregion 3 in the southeast, the NAO displays a significant influence on the MDEs in the southern subregions of the YRB (Subregions 1, 2, and 3), and the AO has a more pronounced influence on the MDEs in the northern subregions of the YRB (Subregions 4, 5, and 6).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little Change in Global Drought over the Past 60 Years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E.; Dai, A.; Van der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global Warming and Changes in Drought. Nat. Clim. Chang. 2014, 4, 17–22. [Google Scholar] [CrossRef]
- Zhao, R.; Sun, H.; Xing, L.; Li, R.; Li, M. Effects of Anthropogenic Climate Change on the Drought Characteristics in China: From Frequency, Duration, Intensity, and Affected Area. J. Hydrol. 2023, 617, 129008. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Boulange, J.; Do, H.X.; Gosling, S.N.; Grillakis, M.G.; Koutroulis, A.G.; Leonard, M.; Liu, J.; Schmied, H.M.; Papadimitriou, L.; et al. Globally Observed Trends in Mean and Extreme River Flow Attributed to Climate Change. Science 2021, 371, 1159–1162. [Google Scholar] [CrossRef]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human Contribution to More-Intense Precipitation Extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Foroumandi, E.; Nourani, V.; Huang, J.J.; Moradkhani, H. Drought Monitoring by Downscaling GRACE-Derived Terrestrial Water Storage Anomalies: A Deep Learning Approach. J. Hydrol. 2023, 616, 128838. [Google Scholar] [CrossRef]
- Foroumandi, E.; Nourani, V.; Kantoush, S.A. Investigating the Main Reasons for the Tragedy of Large Saline Lakes: Drought, Climate Change, or Anthropogenic Activities? A Call to Action. J. Arid. Environ. 2022, 196, 104652. [Google Scholar] [CrossRef]
- Bevacqua, E.; Zappa, G.; Lehner, F.; Zscheischler, J. Precipitation Trends Determine Future Occurrences of Compound Hot–Dry Events. Nat. Clim. Chang. 2022, 12, 350–355. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mishra, A.K. Increase in Compound Drought and Heatwaves in a Warming World. Geophys. Res. Lett. 2021, 48, e2020GL090617. [Google Scholar] [CrossRef]
- Zscheischler, J.; Seneviratne, S.I. Dependence of Drivers Affects Risks Associated with Compound Events. Sci. Adv. 2017, 3, e1700263. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; Van den Hurk, B.J.J.M.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future Climate Risk from Compound Events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Singh, J.; Ashfaq, M.; Skinner, C.; Anderson, W.; Singh, D. Amplified Risk of Spatially Compounding Droughts during Co-Occurrences of Modes of Natural Ocean Variability. NPJ Clim. Atmos. Sci. 2021, 4, 7. [Google Scholar] [CrossRef]
- Xia, J.; Chen, J.; She, D.X. Impacts and Countermeasures of Extreme Drought in the Yangtze River Basin in 2022. J. Hydraul. Eng. 2022, 53, 1143–1153. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.; Sivapalan, M.; et al. Twenty-Three Unsolved Problems in Hydrology (UPH)—A Community Perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Wen, X.; Tu, Y.; Tan, Q.; Li, W.; Fang, G.; Ding, Z.; Wang, Z. Construction of 3D Drought Structures of Meteorological Drought Events and Their Spatio-Temporal Evolution Characteristics. J. Hydrol. 2020, 590, 125539. [Google Scholar] [CrossRef]
- Apurv, T.; Cai, X. Drought Propagation in Contiguous U.S. Watersheds: A Process-Based Understanding of the Role of Climate and Watershed Properties. Water Resour. Res. 2020, 56, e2020WR027755. [Google Scholar] [CrossRef]
- Herrera-Estrada, J.E.; Satoh, Y.; Sheffield, J. Spatiotemporal Dynamics of Global Drought. Geophys. Res. Lett. 2017, 44, 2254–2263. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A. Review of Complex Networks Application in Hydroclimatic Extremes with an Implementation to Characterize Spatio-Temporal Drought Propagation in Continental USA. J. Hydrol. 2017, 555, 600–620. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Multivariate Drought Index: An Information Theory Based Approach for Integrated Drought Assessment. J. Hydrol. 2015, 526, 164–182. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Peña-Angulo, D.; Murphy, C.; López-Moreno, J.I.; Tomas-Burguera, M.; Dominguez-Castro, F.; Tian, F.; Eklundh, L.; Cai, Z.; Alvarez-Farizo, B.; et al. The Complex Multi-Sectoral Impacts of Drought: Evidence from a Mountainous Basin in the Central Spanish Pyrenees. Sci. Total Environ. 2021, 769, 144702. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, Z.; Singh, V.P.; Zhang, Y.; Feng, S.; Xu, Y.; Hao, F. Drought Propagation under Global Warming: Characteristics, Approaches, Processes, and Controlling Factors. Sci. Total Environ. 2022, 838, 156021. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Hejazi, M.; Cai, X.; Valocchi, A.J. Climate Change Impact on Meteorological, Agricultural, and Hydrological Drought in Central Illinois. Water Resour. Res. 2011, 47, W09527. [Google Scholar] [CrossRef]
- Li, L.; Zhao, L.; Ge, J.; Yang, P.; Wu, F. Investigating Drought Propagation Time, Relationship, and Drivers in Perennial River Basins of China. Water 2022, 14, 2812. [Google Scholar] [CrossRef]
- Zhu, K.; Xu, Y.; Lu, F.; Sun, X.; Gao, M.; Han, X.; Li, D.; Jiang, M. Spatio-Temporal Evolution and Propagation of Meteoro-Hydrological Drought in Yalong River Basin. Water 2023, 15, 1025. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Begueria, S.; Lopez-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- Liu, Q.; Zhang, S.; Zhang, H.; Bai, Y.; Zhang, J. Monitoring Drought Using Composite Drought Indices Based on Remote Sensing. Sci. Total Environ. 2020, 711, 134585. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Spatiotemporal Characteristics of Drought in Serbia. J. Hydrol. 2014, 510, 110–123. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A Review of Drought Concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X. Spatiotemporal Trends of Dryness/Wetness Duration and Severity: The Respective Contribution of Precipitation and Temperature. Atmos. Res. 2019, 216, 176–185. [Google Scholar] [CrossRef]
- Gonzalez-Hidalgo, J.; Vicente-Serrano, S.; Pena-Angulo, D.; Salinas, C.; Tomas-Burguera, M.; Begueria, S. High-Resolution Spatio-Temporal Analyses of Drought Episodes in the Western Mediterranean Basin (Spanish Mainland, Iberian Peninsula). Acta Geophys. 2018, 66, 381–392. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, X.; Chen, N.; Li, B.; Ma, H.; Xu, L.; Li, R.; Niyogi, D. Drought Propagation Modification after the Construction of the Three Gorges Dam in the Yangtze River Basin. J. Hydrol. 2021, 603, 127138. [Google Scholar] [CrossRef]
- Tijdeman, E.; Blauhut, V.; Stoelzle, M.; Menzel, L.; Stahl, K. Different Drought Types and the Spatial Variability in Their Hazard, Impact, and Propagation Characteristics. Nat. Hazards Earth Syst. Sci. 2022, 22, 2099–2116. [Google Scholar] [CrossRef]
- Palazzolo, N.; Peres, D.J.; Bonaccorso, B.; Cancelliere, A. A Probabilistic Analysis of Drought Areal Extent Using SPEI-Based Severity-Area-Frequency Curves and Reanalysis Data. Water 2023, 15, 3141. [Google Scholar] [CrossRef]
- Mondal, S.; Mishra, A.; Leung, R.; Cook, B. Global Droughts Connected by Linkages between Drought Hubs. Nat. Commun. 2023, 14, 144. [Google Scholar] [CrossRef] [PubMed]
- Konapala, G.; Mondal, S.; Mishra, A. Quantifying Spatial Drought Propagation Potential in North America Using Complex Network Theory. Water Resour. Res. 2022, 58, e2021WR030914. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H. Statistical Physics Approaches to the Complex Earth System. Phys. Rep. 2021, 896, 1–84. [Google Scholar] [CrossRef] [PubMed]
- Jha, V.; Gujrati, A.; Singh, R. Complex Network Theoretic Assessment of Precipitation-Driven Meteorological Drought in India: Past and Future. Int. J. Climatol. 2022, 42, 3274–3289. [Google Scholar] [CrossRef]
- Gao, C.; Liu, L.; Zhang, S.; Xu, Y.-P.; Wang, X.; Tang, X. Spatiotemporal Patterns and Propagation Mechanism of Meteorological Droughts over Yangtze River Basin and Pearl River Basin Based on Complex Network Theory. Atmos. Res. 2023, 292, 106874. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Guerreiro, S.B.; Nicholson, A.; Liang, Q.; Quinn, P.; Zhang, L.; He, B.; Yin, J.; Fowler, H.J. Climate Change Impacts on Yangtze River Discharge at the Three Gorges Dam. Hydrol. Earth Syst. Sci. 2017, 21, 1911–1927. [Google Scholar] [CrossRef]
- Sun, F.; Mejia, A.; Zeng, P.; Che, Y. Projecting Meteorological, Hydrological and Agricultural Droughts for the Yangtze River Basin. Sci. Total Environ. 2019, 696, 134076. [Google Scholar] [CrossRef]
- Chen, J.; Wan, S.; Henebry, G.; Qi, J.; Gutman, G.; Sun, G.; Kappas, M. (Eds.) Dryland East Asia: Land Dynamics amid Social and Climate Change; Walter de Gruyter: Berlin, Germany, 2013. [Google Scholar]
- Huang, T.; Xu, L.; Fan, H. Drought Characteristics and Its Response to the Global Climate Variability in the Yangtze River Basin, China. Water 2018, 11, 13. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, H.; Huang, J.; Yuan, Y. Prediction of Multi-Scale Meteorological Drought Characteristics over the Yangtze River Basin Based on CMIP6. Water 2022, 14, 2996. [Google Scholar] [CrossRef]
- Tian, F.; Yang, J.; Liu, L.; Wu, J. Progress of Research on the Conception, Characteristic, and Influencing Factors of Drought Propagation from the Perspective of Geographic Sciences. Prog. Geogr. 2022, 548, 202–205. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X. A gridded daily observation dataset over China region and comparison with the other datasets. Chin. J. Geophys. 2013, 56, 1102–1111. [Google Scholar] [CrossRef]
- Yang, J.; Chang, J.; Wang, Y.; Li, Y.; Hu, H.; Chen, Y.; Huang, Q.; Yao, J. Comprehensive Drought Characteristics Analysis Based on a Nonlinear Multivariate Drought Index. J. Hydrol. 2018, 557, 651–667. [Google Scholar] [CrossRef]
- Zeng, P.; Sun, F.; Liu, Y.; Wang, Y.; Li, G.; Che, Y. Mapping Future Droughts under Global Warming across China: A Combined Multi-Timescale Meteorological Drought Index and SOM-Kmeans Approach. Weather. Clim. Extrem. 2021, 31, 100304. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Kreuz, T.; Grassberger, P. Event Synchronization: A Simple and Fast Method to Measure Synchronicity and Time Delay Patterns. Phys. Rev. E 2002, 66, 041904. [Google Scholar] [CrossRef]
- Agarwal, A.; Marwan, N.; Maheswaran, R.; Ozturk, U.; Kurths, J.; Merz, B. Optimal Design of Hydrometric Station Networks Based on Complex Network Analysis. Hydrol. Earth Syst. Sci. 2020, 24, 2235–2251. [Google Scholar] [CrossRef]
- Wiedermann, M.; Donges, J.F.; Kurths, J.; Donner, R.V. Mapping and Discrimination of Networks in the Complexity-Entropy Plane. Phys. Rev. E 2017, 96, 042304. [Google Scholar] [CrossRef]
- Boers, N.; Bookhagen, B.; Marwan, N.; Kurths, J.; Marengo, J. Complex Networks Identify Spatial Patterns of Extreme Rainfall Events of the South American Monsoon System. Geophys. Res. Lett. 2013, 40, 4386–4392. [Google Scholar] [CrossRef]
- Mondal, S.; Mishra, A.K.; Leung, L.R. Spatiotemporal Characteristics and Propagation of Summer Extreme Precipitation Events over United States: A Complex Network Analysis. Geophys. Res. Lett. 2020, 47, e2020GL088185. [Google Scholar] [CrossRef]
- Malik, N.; Bookhagen, B.; Marwan, N.; Kurths, J. Analysis of Spatial and Temporal Extreme Monsoonal Rainfall over South Asia Using Complex Networks. Clim. Dyn. 2012, 39, 971–987. [Google Scholar] [CrossRef]
- Barnett, L.; Di Paolo, E.; Bullock, S. Spatially Embedded Random Networks. Phys. Rev. E 2007, 76, 056115. [Google Scholar] [CrossRef] [PubMed]
- Rheinwalt, A.; Marwan, N.; Kurths, J.; Werner, P.; Gerstengarbe, F.-W. Boundary Effects in Network Measures of Spatially Embedded Networks. In Proceedings of the 2012 SC Companion: High Performance Computing, Networking Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 500–505. [Google Scholar]
- Wiedermann, M.; Donges, J.F.; Kurths, J.; Donner, R.V. Spatial Network Surrogates for Disentangling Complex System Structure from Spatial Embedding of Nodes. Phys. Rev. E 2016, 93, 042308. [Google Scholar] [CrossRef]
- Fortunato, S.; Hric, D. Community Detection in Networks: A User Guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
- Traag, V.A.; Waltman, L.; Van Eck, N.J. From Louvain to Leiden: Guaranteeing Well-Connected Communities. Sci. Rep. 2019, 9, 5233. [Google Scholar] [CrossRef]
- Kurths, J.; Agarwal, A.; Shukla, R.; Marwan, N.; Rathinasamy, M.; Caesar, L.; Krishnan, R.; Merz, B. Unravelling the Spatial Diversity of Indian Precipitation Teleconnections via a Non-Linear Multi-Scale Approach. Nonlinear Process. Geophys. 2019, 26, 251–266. [Google Scholar] [CrossRef]
- Halverson, M.; Fleming, S. Complex Network Theory, Streamflow, and Hydrometric Monitoring System Design. Hydrol. Earth Syst. Sci. 2015, 19, 3301–3318. [Google Scholar] [CrossRef]
- Agarwal, A.; Marwan, N.; Maheswaran, R.; Merz, B.; Kurths, J. Quantifying the Roles of Single Stations within Homogeneous Regions Using Complex Network Analysis. J. Hydrol. 2018, 563, 802–810. [Google Scholar] [CrossRef]
- Guimera, R.; Amaral, L.A.N. Cartography of Complex Networks: Modules and Universal Roles. J. Stat. Mech. Theory Exp. 2005, 2005, P02001. [Google Scholar] [CrossRef]
- Peters, D.P.; Pielke Sr, R.A.; Bestelmeyer, B.T.; Allen, C.D.; Munson-McGee, S.; Havstad, K.M. Cross-Scale Interactions, Nonlinearities, and Forecasting Catastrophic Events. Proc. Natl. Acad. Sci. USA 2004, 101, 15130–15135. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.; Wang, B.; Yan, Y.; Hao, Y.; Zhang, M. Characterizing Effects of Monsoons and Climate Teleconnections on Precipitation in China Using Wavelet Coherence and Global Coherence. Clim. Dyn. 2019, 52, 5213–5228. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Partal, T.; Küçük, M. Long-Term Trend Analysis Using Discrete Wavelet Components of Annual Precipitations Measurements in Marmara Region (Turkey). Phys. Chem. Earth Parts A/B/C 2006, 31, 1189–1200. [Google Scholar] [CrossRef]




| Teleconnection Factors | Time Frame | Data Source | Access Date |
|---|---|---|---|
| ENSO | 1961–2021 | http://www.esrl.noaa.gov/psd/data/correlation/nina34.data | 22 October 2023 |
| PDO | 1961–2021 | http://www.ncdc.noaa.gov/teleconnections/pdo/ | 22 October 2023 |
| NAO | 1961–2021 | https://www.ncdc.noaa.gov/teleconnections/nao/ | 22 October 2023 |
| AO | 1961–2021 | https://www.ncdc.noaa.gov/teleconnections/ao/ | 22 October 2023 |
| Subregion | Frequency | Duration | Total Severity | Peak |
|---|---|---|---|---|
| 1 | 17.8 | 4.4 | −44.1 | −2.6 |
| 2 | 18.3 | 3.9 | −38.8 | −2.5 |
| 3 | 16.1 | 3.9 | −36.3 | −2.8 |
| 4 | 17.8 | 3.8 | −36.5 | −2.6 |
| 5 | 18.1 | 3.7 | −38.2 | −3.4 |
| 6 | 17.8 | 3.9 | −38.5 | −2.9 |
| 7 | 18.2 | 3.8 | −36.5 | −2.8 |
| 8 | 18.0 | 4.0 | −41.2 | −2.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Gao, C.; Zhu, Z.; Tang, X.; Zhang, D.; Zhang, S. Synchronized Structure and Teleconnection Patterns of Meteorological Drought Events over the Yangtze River Basin, China. Water 2023, 15, 3707. https://doi.org/10.3390/w15213707
Liu L, Gao C, Zhu Z, Tang X, Zhang D, Zhang S. Synchronized Structure and Teleconnection Patterns of Meteorological Drought Events over the Yangtze River Basin, China. Water. 2023; 15(21):3707. https://doi.org/10.3390/w15213707
Chicago/Turabian StyleLiu, Lei, Chao Gao, Zhanliang Zhu, Xiongpeng Tang, Dongjie Zhang, and Silong Zhang. 2023. "Synchronized Structure and Teleconnection Patterns of Meteorological Drought Events over the Yangtze River Basin, China" Water 15, no. 21: 3707. https://doi.org/10.3390/w15213707
APA StyleLiu, L., Gao, C., Zhu, Z., Tang, X., Zhang, D., & Zhang, S. (2023). Synchronized Structure and Teleconnection Patterns of Meteorological Drought Events over the Yangtze River Basin, China. Water, 15(21), 3707. https://doi.org/10.3390/w15213707






