Flux Vector Splitting Method of Weakly Compressible Water Navier-Stokes Equation and Its Application
Abstract
:1. Introduction
2. Control Equation and Flux Vector Splitting Method
2.1. Weakly Compressible Water N-S Equation
2.2. Flux Vector Splitting Method
3. Results and Discussion
3.1. Validation of Water Hammer
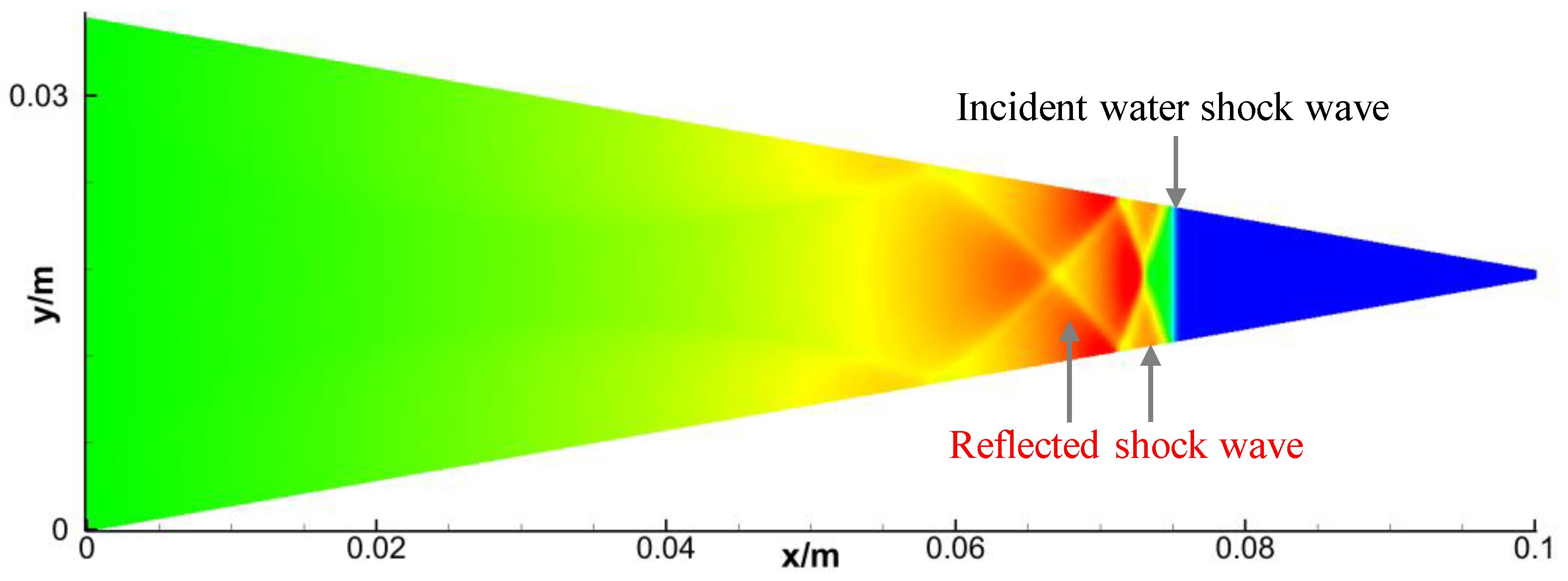
3.2. Validation of Pulse Hydraulic Fracturing
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Wave speed, m/s | u | Streamwise velocity, m/s |
| A | Slope in linear model, J/kg | v | Normal velocity, m/s |
| B | Intercept in linear model, Pa | x | Streamwise coordinate, m |
| d | Pipe diameter, m | y | Normal coordinate, m |
| e | Internal energy per unit mass, J/kg | U | Conservative flux |
| H | Width of the wedge, m | F | Flow flux in x direction |
| L | Length of the pipe, m | G | Flow flux in y direction |
| p | Water pressure, Pa | γ | Specific heat ratio |
| R | Gas constant | λ | Eigenvalues of matrix A |
| t | Time, s | η | Eigenvalues of matrix B |
| T | Water temperature, K | ρ | Fluid density, kg/m3 |
References
- Jia, X.Y.; Wang, S.S.; Xu, J. Nonlinear characteristics and corrections of near-field underwater explosion shock waves. Phys. Fluids 2022, 34, 046108. [Google Scholar] [CrossRef]
- MacCormack, R.W. The effect of viscosity in hypervelocity impact cratering. AIAA Paper 1969, 40, 69–354. [Google Scholar]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Wan, W.Y.; Huang, W.R. Water hammer simulation of a series pipe system using the MacCormack time marching scheme. Acta Mech. 2018, 229, 3143–3160. [Google Scholar] [CrossRef]
- Li, H.; Huang, B.X. Pulse supercharging phenomena in a water-filled pipe and a universal prediction model of optimal pulse frequency. Phys. Fluids 2022, 34, 106108. [Google Scholar] [CrossRef]
- Li, H.; Huang, B.X. Pulsating pressurization of two-phase fluid in a pipe filled with water and a little gas. Phys. Fluids 2023, 35, 046111. [Google Scholar]
- Li, H.; Huang, B.X.; Xu, H.H. The optimal sine pulse frequency of pulse hydraulic fracturing for reservoir stimulation. Water 2022, 14, 3189. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-osciallatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 87–89. [Google Scholar]
- Li, Y.H. Equation of state of water and sea water. J. Geophys. Res. 1967, 72, 2665–2678. [Google Scholar] [CrossRef]
- Shyue, K.M. An efficient shock-capturing algorithm for compressible multicomponent problems. J. Comput. Phys. 1998, 142, 208–242. [Google Scholar] [CrossRef]
- Métayer, O.L.; Massoni, J.; Saurel, R. Modelling evaporation fronts with reactive Riemann solvers. J. Comput. Phys. 2005, 205, 567–610. [Google Scholar] [CrossRef]
- Beig, S.A.; Johnsen, E. Maintaining interface equilibrium conditions in compressible multiphase flows using interface capturing. J. Comput. Phys. 2015, 302, 548–566. [Google Scholar] [CrossRef]
- Li, X.J.; Zhang, C.J.; Wang, X.H.; Yan, H.H. Numerical study on the effect of equations of state of water on underwater explosions. Eng. Mech. 2014, 31, 46–52. (In Chinese) [Google Scholar]
- Yu, J.; Pan, J.J.; Wang, H.K.; Mao, H.B. A γ-based model interface capturing method to near-field underwater explosion (undex) simulation. J. Ship Mech. 2015, 19, 641–653. [Google Scholar]
- Zhang, A.M.; Li, S.M.; Cui, P.; Li, S.; Liu, Y.L. A unified theory for bubble dynamics. Phys. Fluids 2023, 35, 033323. [Google Scholar] [CrossRef]
- John, D.; Anderson, J.R. Computational Fluid Dynamic: The Basics with Applications; McGraw-Hill, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Henrych, J. Explosion Dynamics and Its Applications; Science Press: Beijing, China, 1987; pp. 152–160. (In Chinese) [Google Scholar]
- Wu, Q.; Wang, K.; Kong, D.C.; Zhang, J.Y.; Liu, T.T. Numerical simulation of subsonic and transonic water entry with compressibility effect considered. Ocean Eng. 2023, 281, 114984. [Google Scholar] [CrossRef]
- Chakravarthy, S.R. The Split Coefficient Matrix Method for Hyperbolic Systems of Gas Dynamic Equations. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1980. [Google Scholar]
- Steger, J.; Warming, R.F. Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods. J. Comput. Phys. 1981, 40, 263–293. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Vtkovsk, J. Developments in unsteady pipe flow friction modelling. J. Hydraul. Res. 2001, 39, 249–257. [Google Scholar] [CrossRef]
- Zhai, C.; Yu, X.; Xiang, X.W.; Li, Q.G.; Wu, S.L.; Xu, J.Z. Experimental study of pulsating water pressure propagation in CBM reservoirs during pulse hydraulic fracturing. J. Nat. Gas Sci. Eng. 2015, 25, 15–22. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Ghias, R.; Mittal, R.; Dong, H. A sharp interface immersed boundary method for compressible viscous flows. J. Comput. Phys. 2007, 225, 528–553. [Google Scholar] [CrossRef]
- Eliasson, V.; Mello, M.; Rosakis, A.J.; Dimotakis, P.E. Experimental investigation of converging shocks in water with various confinement materials. Shock Waves 2010, 20, 395–408. [Google Scholar] [CrossRef]
- Wang, C.X.; Qiu, S.; Eliasson, V. Investigation of shock wave focusing in water in a logarithmic spiral duct, Part 1: Weak coupling. Ocean Eng. 2015, 102, 174–184. [Google Scholar] [CrossRef]
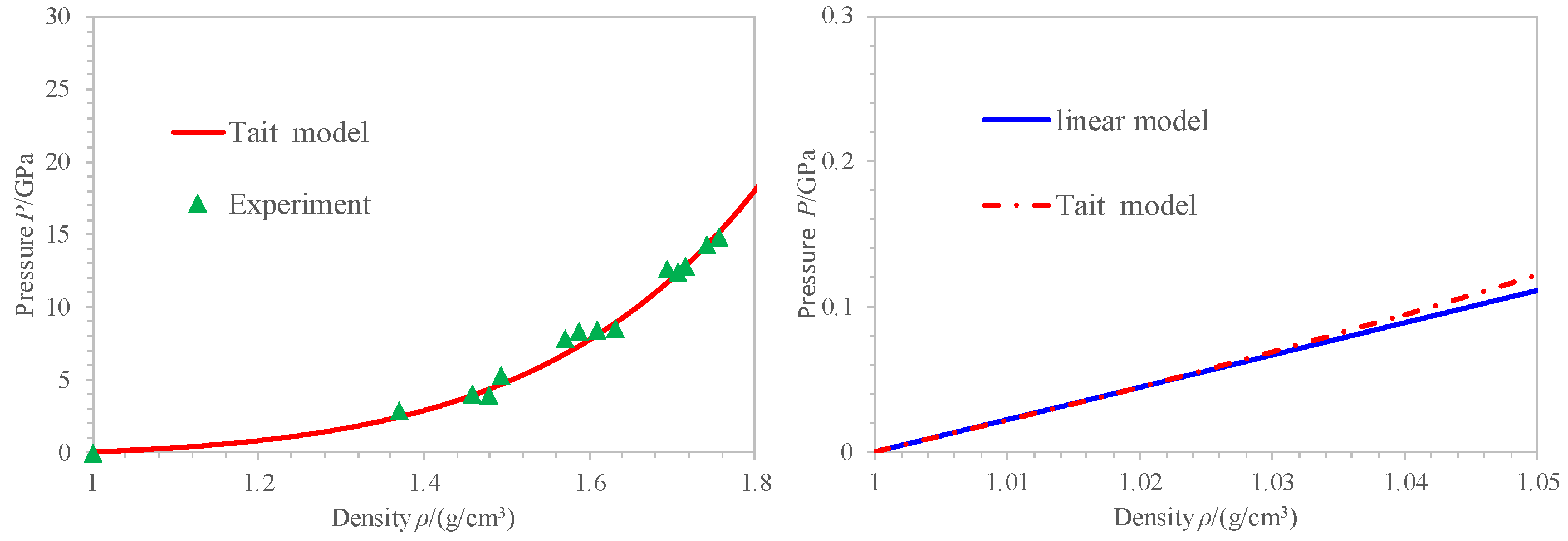
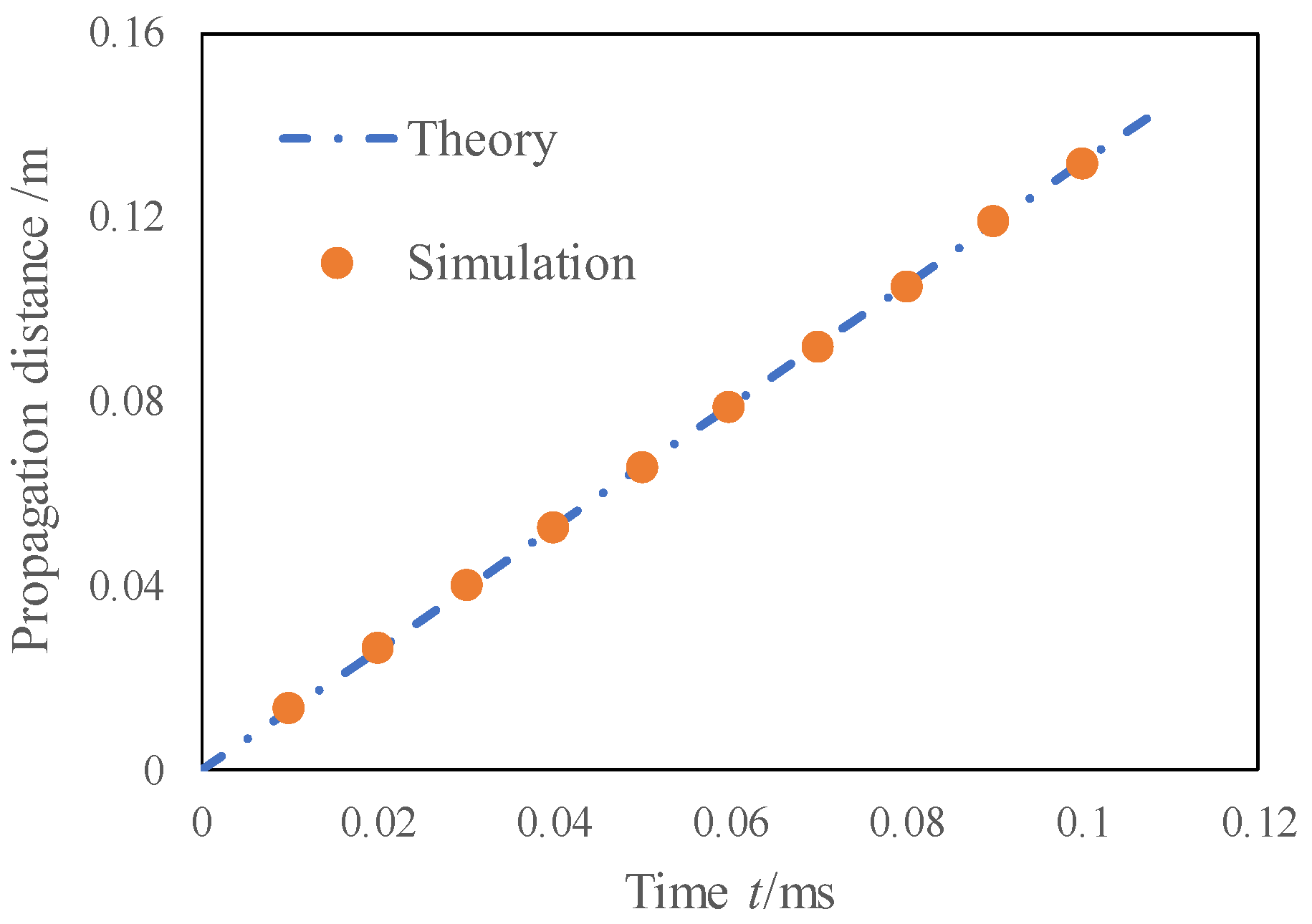
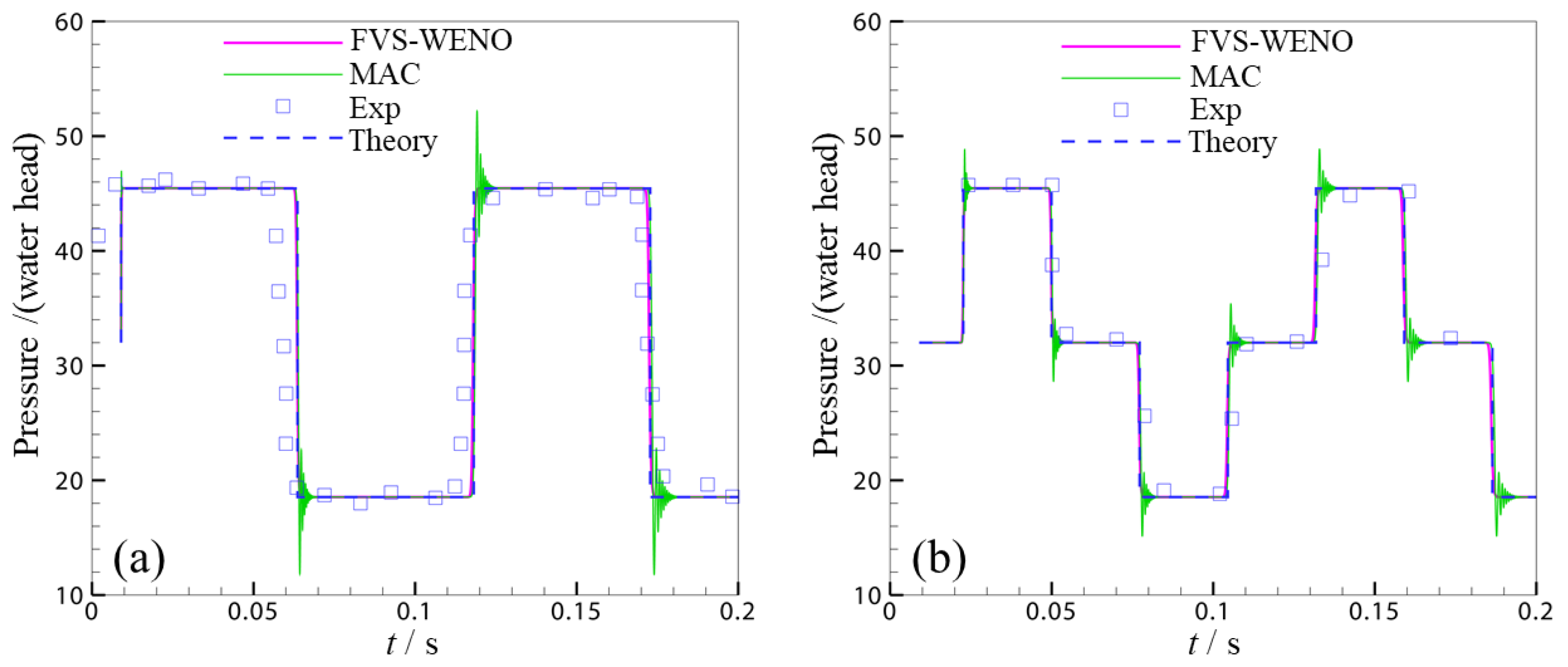
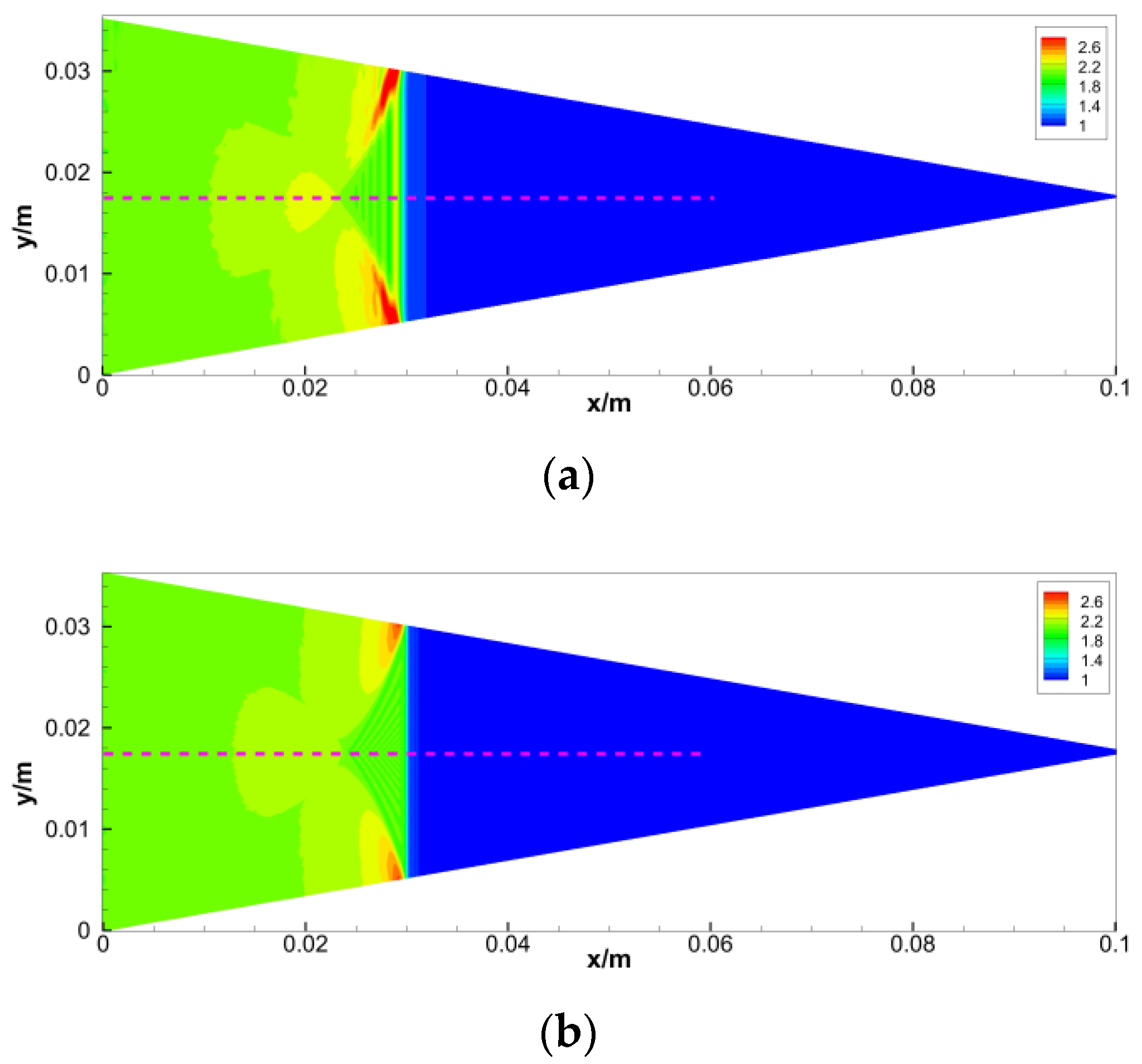


| Parameter | Value |
|---|---|
| Pipe length/(m) | 36 |
| Flow velocity/(m/s) | 0.1 |
| Initial pressure/(water head, m) | 32 |
| Water temperature/(°C) | 15.4 |
| Wave speed/(m/s) | 1319 |
| Closure time of valve/(s) | 0.009 |
| Grid number | 1000 |
| Parameter | Value |
|---|---|
| Wedge length/(m) | 0.1 |
| Wedge width/(m) | 0.03527 |
| Wedge angle/(°) | 20 |
| Initial pressure/(MPa) | 1 |
| Pulse pressure/(MPa) | 2 |
| Wave speed/(m/s) | 1491 |
| Grid number Nx | 1600 |
| Grid number Ny | 564 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Huang, B. Flux Vector Splitting Method of Weakly Compressible Water Navier-Stokes Equation and Its Application. Water 2023, 15, 3699. https://doi.org/10.3390/w15203699
Li H, Huang B. Flux Vector Splitting Method of Weakly Compressible Water Navier-Stokes Equation and Its Application. Water. 2023; 15(20):3699. https://doi.org/10.3390/w15203699
Chicago/Turabian StyleLi, Heng, and Bingxiang Huang. 2023. "Flux Vector Splitting Method of Weakly Compressible Water Navier-Stokes Equation and Its Application" Water 15, no. 20: 3699. https://doi.org/10.3390/w15203699





