Changes in Magnitude and Shifts in Timing of Australian Flood Peaks
Abstract
:1. Introduction
Objectives and Scientific Questions
- What is the seasonality of flood events across Australia? Our analyses focus on basic seasonality, its time of occurrence after rainfall and spatial distribution across drainage divisions covering different hydroclimatic regions.
- Can we detect changes in the seasonal cycle of flood occurrence over the past 50 years?
- Are there any monotonic trends in flood magnitude across Australia over the past 50 years? (A monotonic trend is one, which is either constantly increasing or decreasing.)
- Are the changes in seasonality and flood magnitude with time statistically significant at the regional scale across Australia?
2. Catchments Data and Methodology
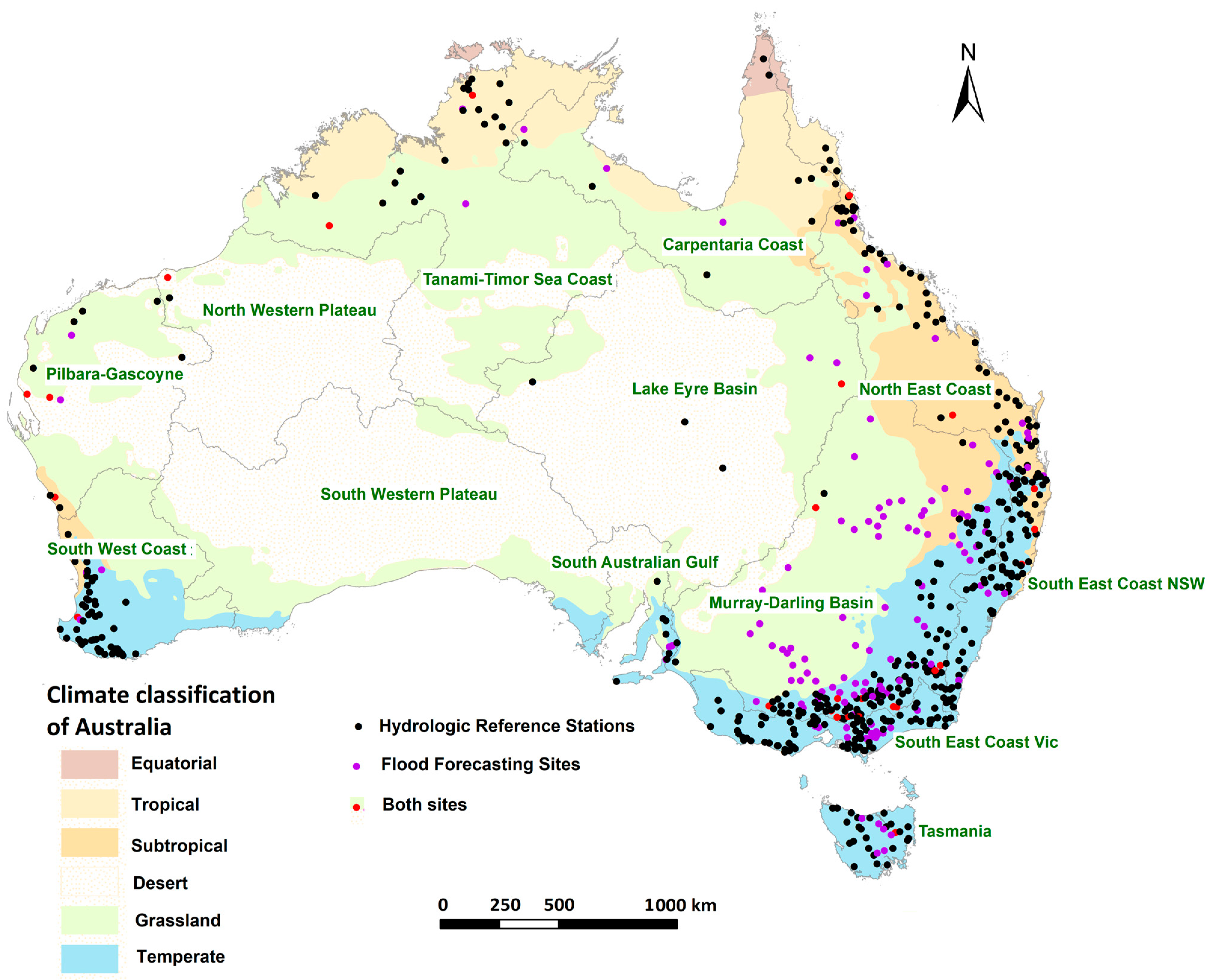
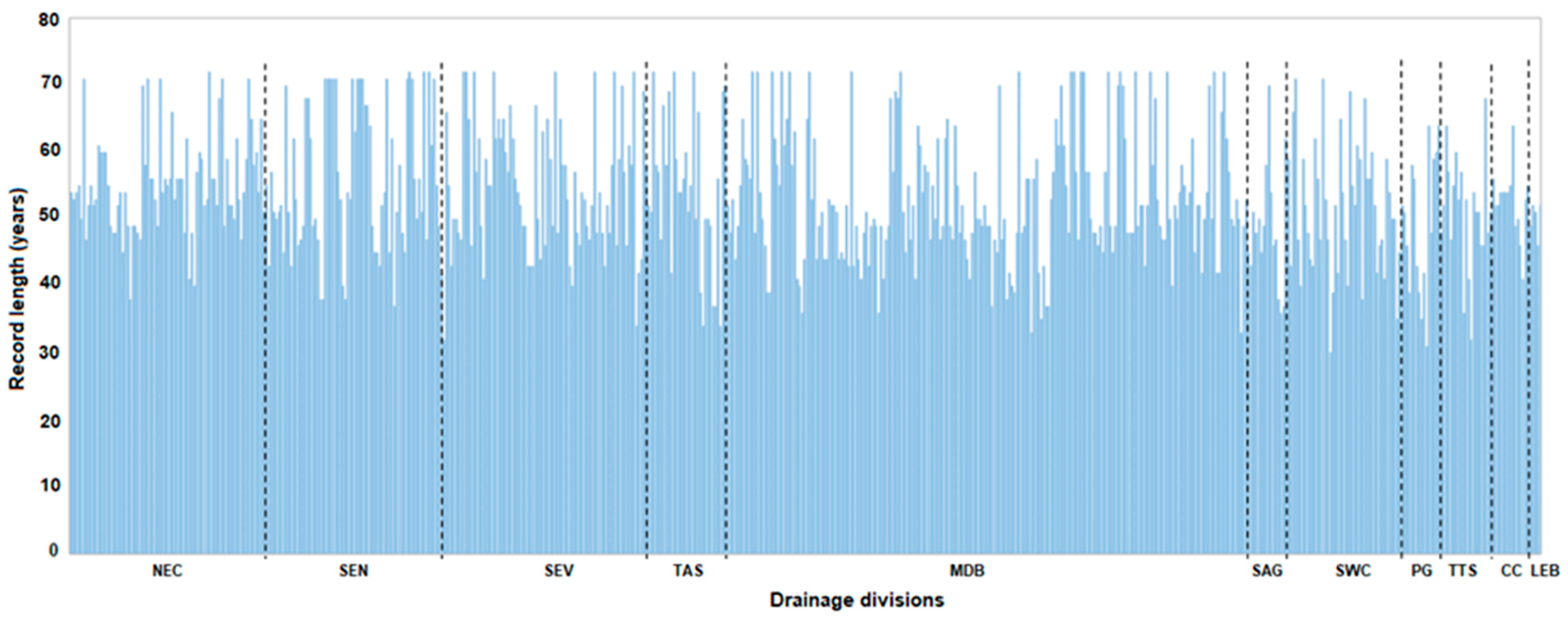
2.1. Catchments and Data
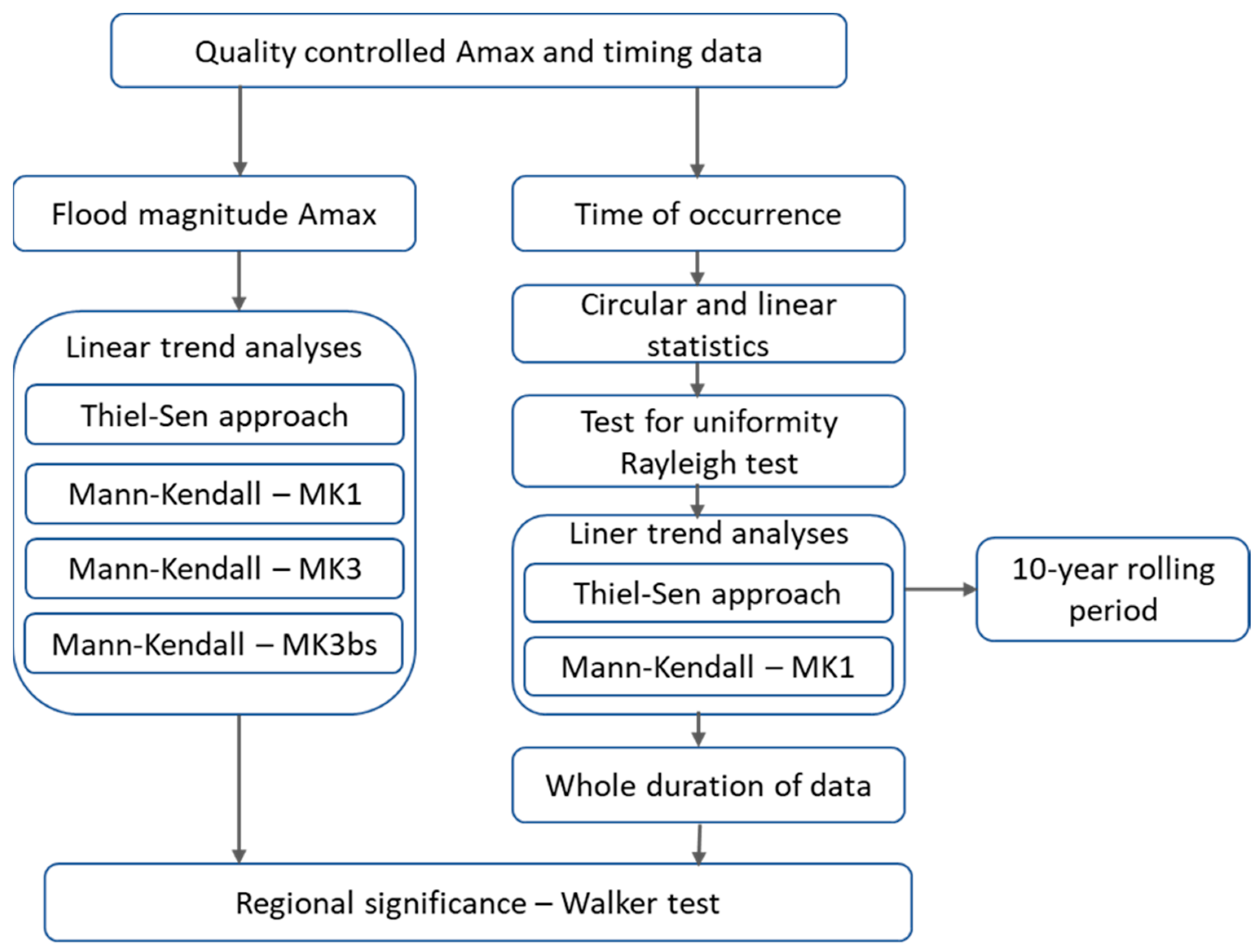
2.2. Analytical Methodology
2.3. Identifying Flood Thresholds and Timings
2.4. Monotonic Trend and Change Analyses: Amax
2.5. Shifts in Seasonality and Timing
2.5.1. Circular Statistics
2.5.2. Linear Statistics
2.5.3. Estimating Trends
2.6. Test for Regional Significance
3. Results
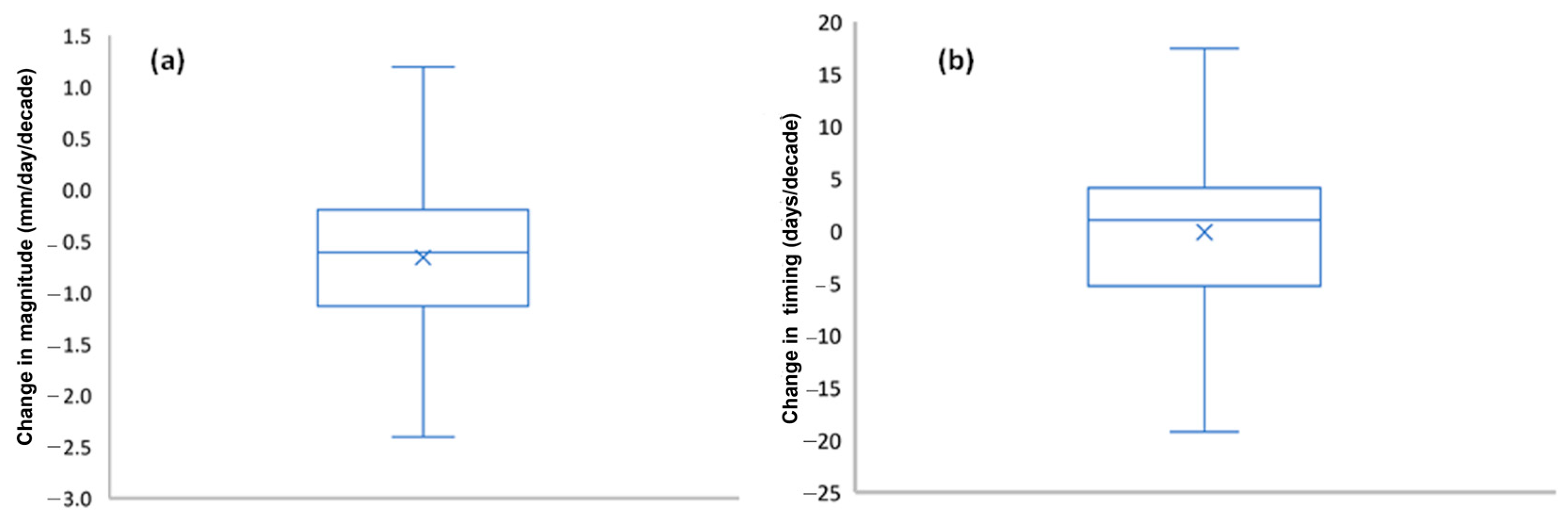
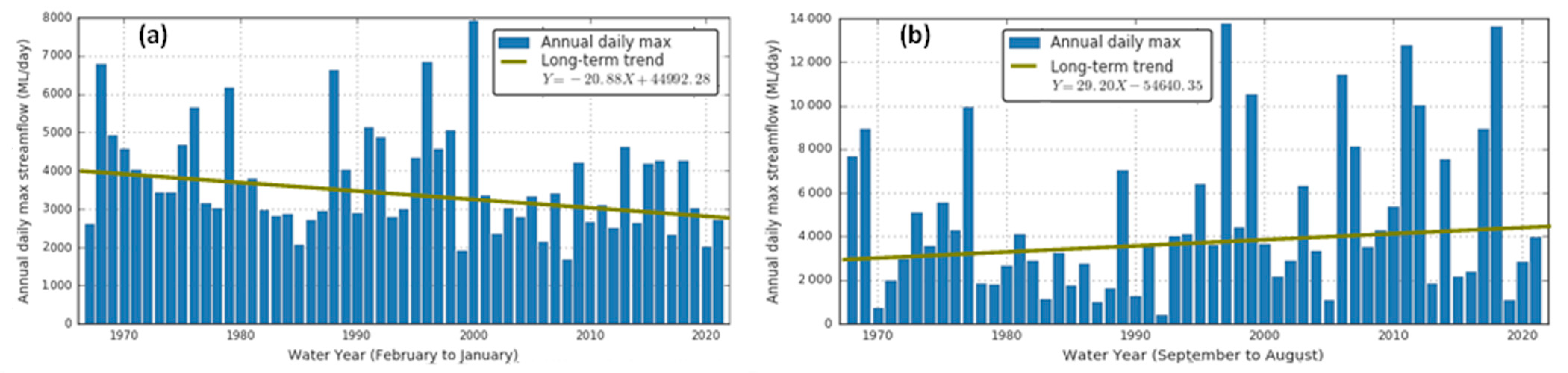
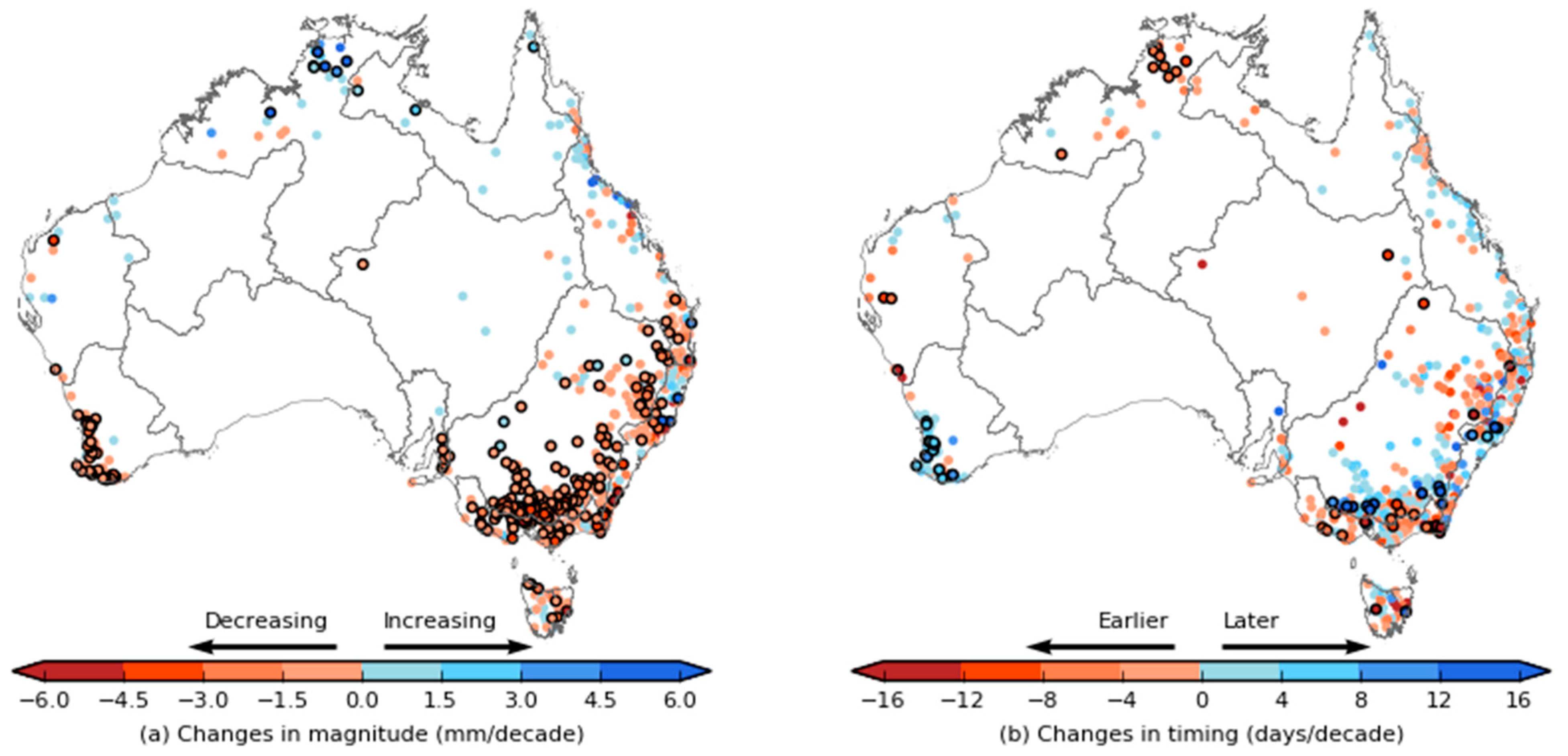
3.1. Trends in Amax Magnitude
3.2. Trends and Timing of Flood Peaks
3.2.1. Water Year
3.2.2. Test for Circular Uniformity
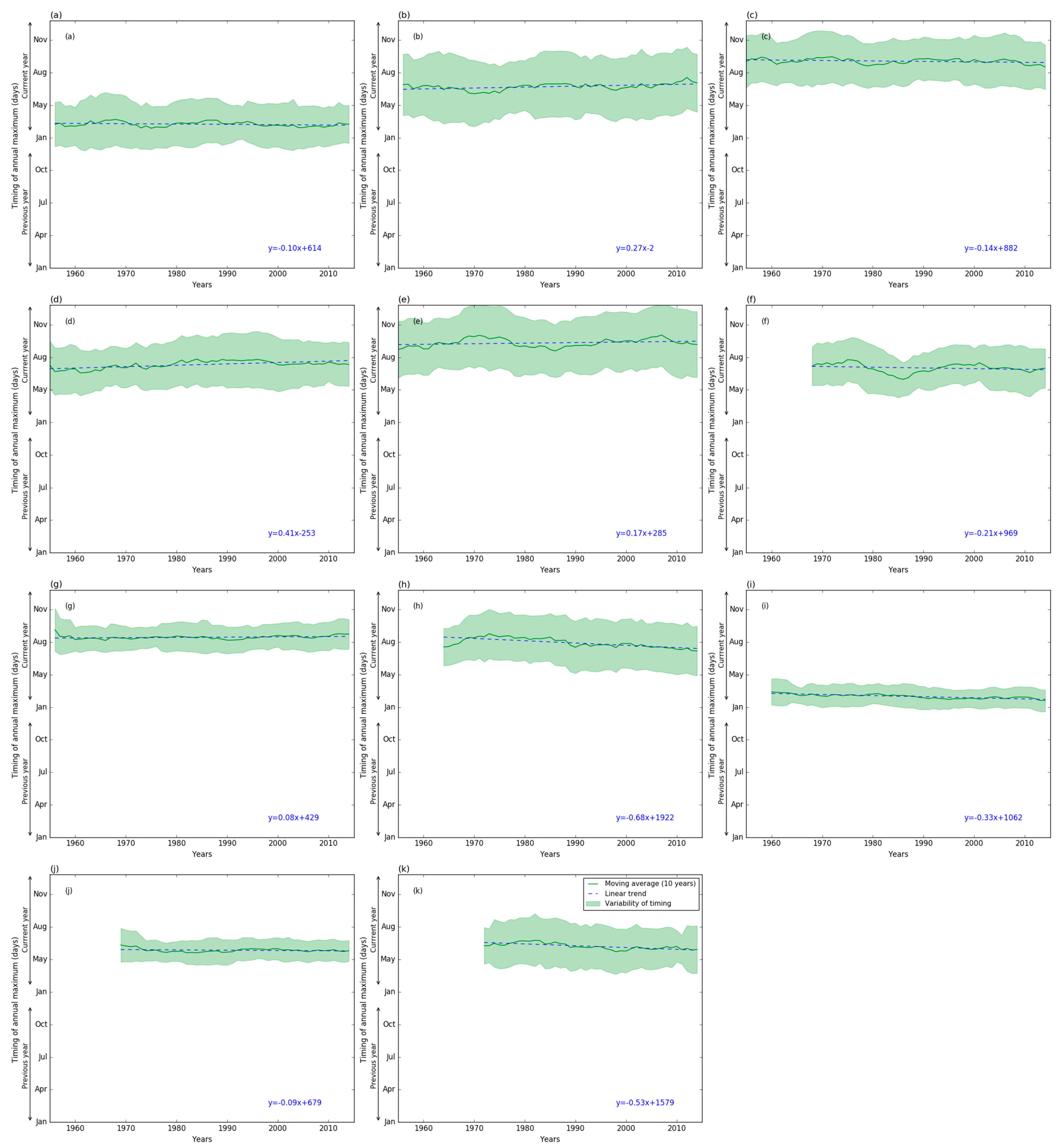
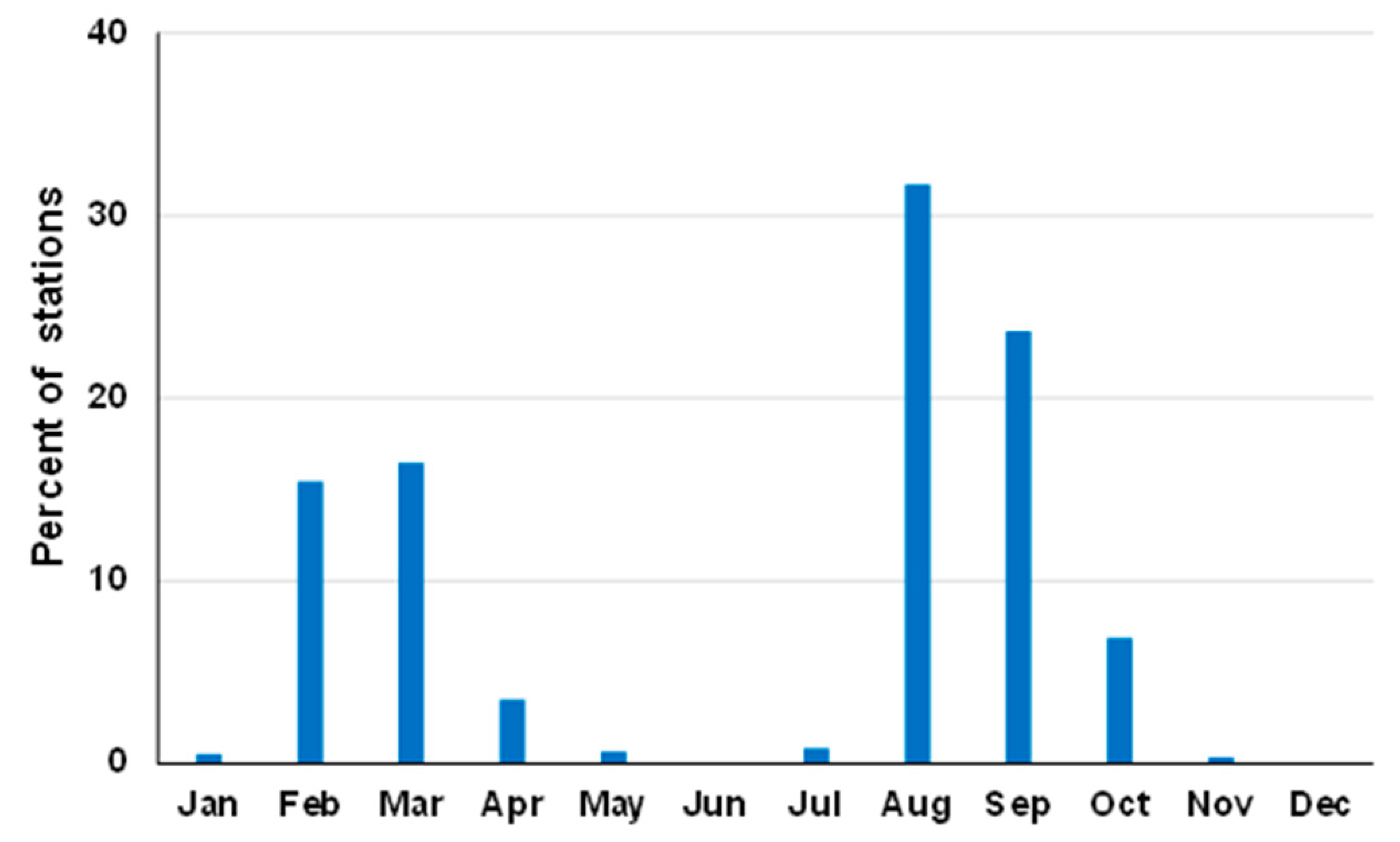
3.2.3. Timing of Amax Peaks
3.2.4. Trends in Timing
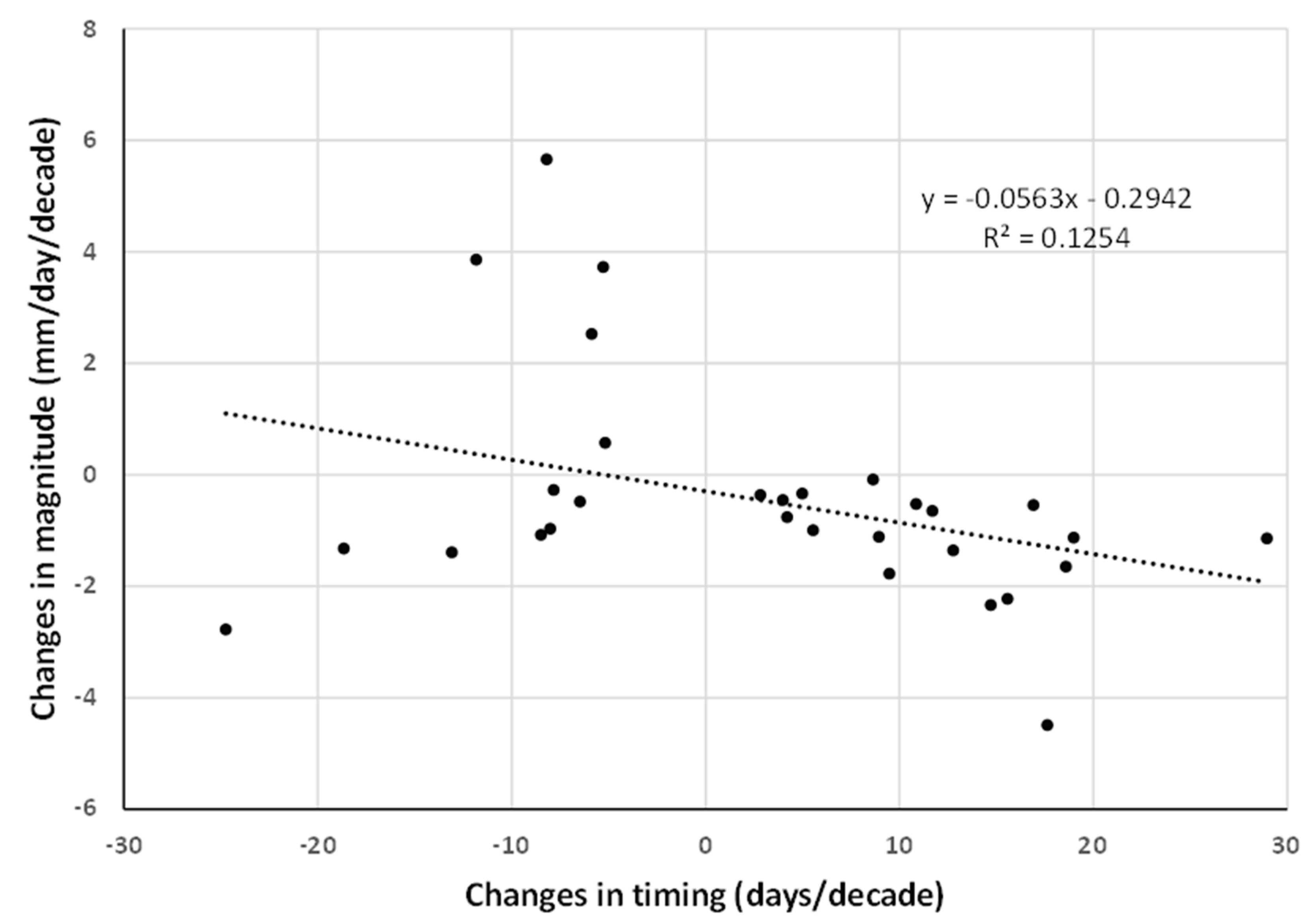
3.2.5. Trends in Magnitude
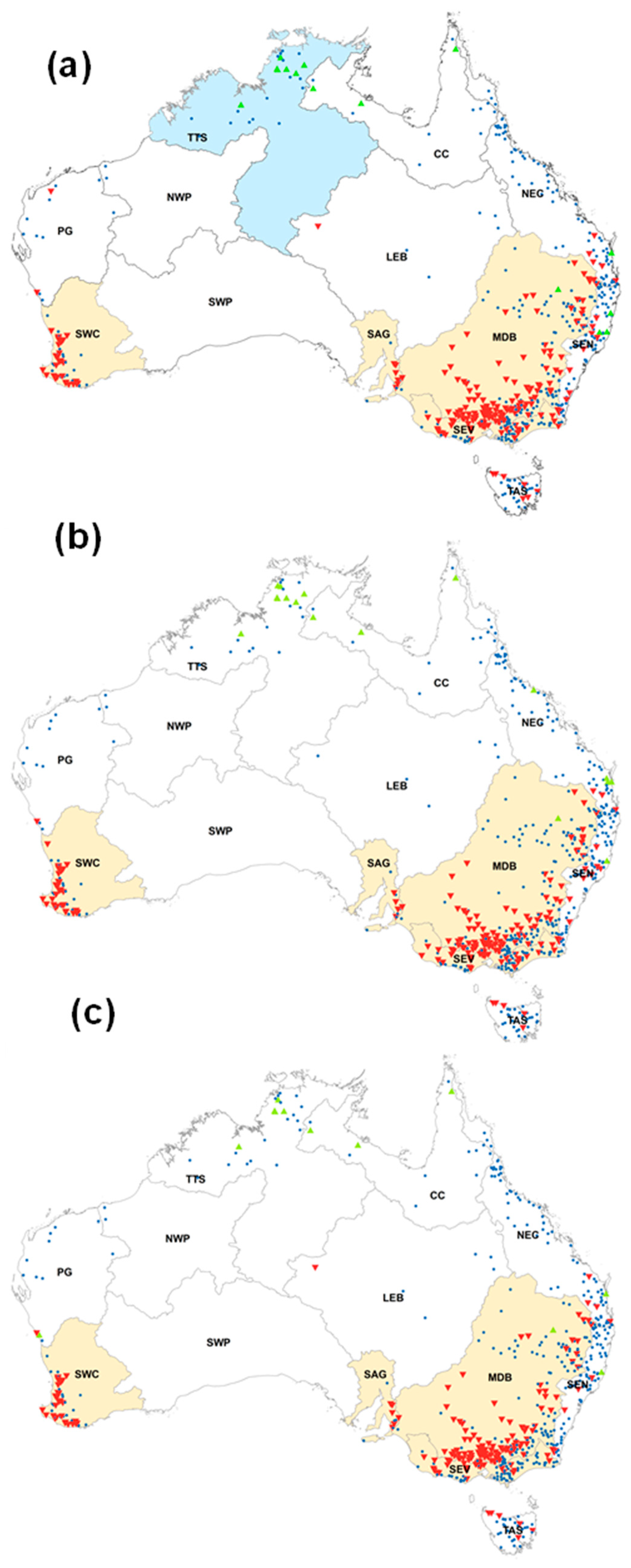
3.3. Regional Significance
Amax Magnitude, Seasonality and Timing
4. Discussion
4.1. Consistency and Enrichment
4.2. Statistical Tests
4.3. Flood Peak Generation, Rainfall and Climate Change
4.3.1. Northern Australia
4.3.2. Coastal NSW and Murray–Darling Basin
4.3.3. Southern Australia
4.4. Future Research
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Long-Term Temporal Variation in Flood Timing: All Drainage Divisions
References
- Balica, S.F.; Popescu, I.; Beevers, L.; Wright, N.G. Parametric and Physically Based Modelling Techniques for Flood Risk and Vulnerability Assessment: A Comparison. Environ. Model. Softw. 2013, 41, 84–92. [Google Scholar] [CrossRef]
- Doocy, S.; Daniels, A.; Murray, S.; Kirsch, T.D. The Human Impact of Floods: A Historical Review of Events 1980-2009 and Systematic Literature Review. PLoS Curr. 2013, 5, 31. [Google Scholar] [CrossRef] [PubMed]
- UNDP. Reducing Disaster Risk: A Challenge for Development—A Global Report; UNDP: New York, NY, USA, 2004; ISBN 9211261600. [Google Scholar]
- Guha-Sapir, D.; Checchi, F. Science and Politics of Disaster Death Tolls. BMJ 2018, 362, k4005. [Google Scholar] [CrossRef]
- Allan, R.P.; Soden, B.J. Atmospheric Warming and the Amplification of Precipitation Extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef] [PubMed]
- Song, X.M.; Zhang, J.Y.; Zhan, C.S.; Liu, C.Z. Review for Impacts of Climate Change and Human Activities on Water Cycle. Shuili Xuebao/J. Hydraul. Eng. 2013, 44, 779–790. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). IPCC Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change. In The Special Report on Global Warming of 1.5 °C (SR15) (Ipcc—Sr15); IPCC: Geneva, Switzerland, 2018; Volume 2, pp. 17–20. [Google Scholar]
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global Flood Risk under Climate Change. Nat. Clim. Change 2013, 3, 816–821. [Google Scholar] [CrossRef]
- Gado, T.A.; Van Nguyen, V.T. An At-Site Flood Estimation Method in the Context of Nonstationarity I. A Simulation Study. J. Hydrol. 2016, 535, 710–721. [Google Scholar] [CrossRef]
- Vormoor, K.; Lawrence, D.; Schlichting, L.; Wilson, D.; Wong, W.K. Evidence for Changes in the Magnitude and Frequency of Observed Rainfall vs. Snowmelt Driven Floods in Norway. J. Hydrol. 2016, 538, 33–48. [Google Scholar] [CrossRef]
- Ahn, K.H.; Palmer, R.N. Use of a Nonstationary Copula to Predict Future Bivariate Low Flow Frequency in the Connecticut River Basin. Hydrol. Proc. 2016, 30, 3518–3532. [Google Scholar] [CrossRef]
- Daneshkhah, A.; Remesan, R.; Chatrabgoun, O.; Holman, I.P. Probabilistic Modeling of Flood Characterizations with Parametric and Minimum Information Pair-Copula Model. J. Hydrol. 2016, 540, 469–487. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Ouarda, T.B.M.J. Trends in the Timing and Magnitude of Floods in Canada. J. Hydrol. 2009, 375, 471–480. [Google Scholar] [CrossRef]
- Coughlan De Perez, E.; Van Den Hurk, B.; Van Aalst, M.K.; Jongman, B.; Klose, T.; Suarez, P. Forecast-Based Financing: An Approach for Catalyzing Humanitarian Action Based on Extreme Weather and Climate Forecasts. Nat. Hazards Earth Syst. Sci. 2015, 15, 895–904. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Kelly, S. The Use of Coastal Reservoirs and SPP Strategy to Provide Sufficient High Quality Water to Coastal Communities. J. Geosci. Environ. Prot. 2015, 3, 80–92. [Google Scholar] [CrossRef]
- Zhang, X.S.; Amirthanathan, G.E.; Bari, M.A.; Laugesen, R.M.; Shin, D.; Kent, D.M.; MacDonald, A.M.; Turner, M.E.; Tuteja, N.K. How Streamflow Has Changed across Australia since the 1950s: Evidence from the Network of Hydrologic Reference Stations. Hydrol. Earth Syst. Sci. 2016, 20, 3947–3965. [Google Scholar] [CrossRef]
- Castellarin, A.; Burn, D.H.; Brath, A. Assessing the Effectiveness of Hydrological Similarity Measures for Flood Frequency Analysis. J. Hydrol. 2001, 241, 270–285. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G.; Merz, R.; Gutknecht, D. Linking Flood Frequency to Long-Term Water Balance: Incorporating Effects of Seasonality. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Beurton, S.; Thieken, A.H. Seasonality of Floods in Germany. Hydrol. Sci. J. 2009, 54, 62–76. [Google Scholar] [CrossRef]
- Smith, I.N.; Timbal, B. Links between Tropical Indices and Southern Australian Rainfall. Int. J. Climatol. 2012, 32, 33–40. [Google Scholar] [CrossRef]
- IPCC. Global Warming of 1.5 C—Summary for Poliymakers; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Do, H.X.; Gudmundsson, L.; Leonard, M.; Westra, S. The Global Streamflow Indices and Metadata Archive (GSIM)—Part 1: The Production of a Daily Streamflow Archive and Metadata. Earth Syst. Sci. Data 2018, 10, 765–785. [Google Scholar] [CrossRef]
- Xuan Do, H.; Zhao, F.; Westra, S.; Leonard, M.; Gudmundsson, L.; Eric Stanislas Boulange, J.; Chang, J.; Ciais, P.; Gerten, D.; Gosling, S.N.; et al. Historical and Future Changes in Global Flood Magnitude—Evidence from a Model-Observation Investigation. Hydrol. Earth Syst. Sci. 2020, 24, 1543–1564. [Google Scholar] [CrossRef]
- Do, H.X.; Westra, S.; Leonard, M.; Gudmundsson, L. Global-Scale Prediction of Flood Timing Using Atmospheric Reanalysis. Water Resour. Res. 2020, 56, WR024945. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Leonard, M.; Do, H.X.; Westra, S.; Seneviratne, S.I. Observed Trends in Global Indicators of Mean and Extreme Streamflow. Geophys. Res. Lett. 2019, 46, 756–766. [Google Scholar] [CrossRef]
- Wasko, C.; Sharma, A. Global Assessment of Flood and Storm Extremes with Increased Temperatures. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wasko, C.; Nathan, R.; Peel, M.C. Trends in Global Flood and Streamflow Timing Based on Local Water Year. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Lee, D.; Ward, P.; Block, P. Defining High-Flow Seasons Using Temporal Streamflow Patterns from a Global Model. Hydrol. Earth Syst. Sci. 2015, 19, 4689–4705. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing Climate Shifts Timing of European Floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef] [PubMed]
- Parajka, J.; Kohnová, S.; Bálint, G.; Barbuc, M.; Borga, M.; Claps, P.; Cheval, S.; Dumitrescu, A.; Gaume, E.; Hlavčová, K.; et al. Seasonal Characteristics of Flood Regimes across the Alpine-Carpathian Range. J. Hydrol. 2010, 394, 78–89. [Google Scholar] [CrossRef]
- Macdonald, N.; Sangster, H. High-Magnitude Flooding across Britain since AD 1750. Hydrol. Earth Syst. Sci. 2017, 21, 1631–1650. [Google Scholar] [CrossRef]
- Köplin, N.; Schädler, B.; Viviroli, D.; Weingartner, R. Seasonality and Magnitude of Floods in Switzerland under Future Climate Change. Hydrol. Proc. 2014, 28, 2567–2578. [Google Scholar] [CrossRef]
- Dhakal, N.; Palmer, R.N. Changing River Flood Timing in the Northeastern and Upper Midwest United States: Weakening of Seasonality over Time? Water 2020, 12, 1951. [Google Scholar] [CrossRef]
- Villarini, G. On the Seasonality of Flooding across the Continental United States. Adv. Water Resour. 2016, 87, 80–91, ISBN 0309170815002. [Google Scholar] [CrossRef]
- Slater, L.J.; Villarini, G. Recent Trends in U.S. Flood Risk. Geophys. Res. Lett. 2016, 43, 121. [Google Scholar] [CrossRef]
- Lecce, S.A. Spatial Variations in the Timing of Annual Floods in the Southeastern United States. J. Hydrol. 2000, 235, 151–169. [Google Scholar] [CrossRef]
- Ye, S.; Li, H.Y.; Leung, L.R.; Guo, J.; Ran, Q.; Demissie, Y.; Sivapalan, M. Understanding Flood Seasonality and Its Temporal Shifts within the Contiguous United States. J. Hydrometeorol. 2017, 18, 1997–2009. [Google Scholar] [CrossRef]
- Henstra, D.; Thistlethwaite, J. Climate Change, Floods, and Municipal Risk Sharing in Canada; Institute on Municipal Finance & Governance: Toronto, ON, Canada, 2017; ISBN 9780772709745. [Google Scholar]
- Burn, D.H. Catchment Similarity for Regional Flood Frequency Analysis Using Seasonality Measures. J. Hydrol. 1997, 202, 212–230. [Google Scholar] [CrossRef]
- Beauchamp, M.; Assani, A.A.; Landry, R.; Massicotte, P. Temporal Variability of the Magnitude and Timing of Winter Maximum Daily Flows in Southern Quebec (Canada). J. Hydrol. 2015, 529, 410–417. [Google Scholar] [CrossRef]
- Mediero, L.; Santillán, D.; Garrote, L.; Granados, A. Detection and Attribution of Trends in Magnitude, Frequency and Timing of Floods in Spain. J. Hydrol. 2014, 517, 1072–1088. [Google Scholar] [CrossRef]
- Mostofi Zadeh, S.; Burn, D.H.; O’Brien, N. Detection of Trends in Flood Magnitude and Frequency in Canada. J. Hydrol. Reg. Stud. 2020, 28, 100673. [Google Scholar] [CrossRef]
- Queensland Floods Commission of Inquiry. Queensland Floods Commission of Inquiry Publishes Final Report; Queensland Government: Queensland, Australia, 2012.
- Hendon, H.H.; Lim, E.P.; Nguyen, H. Seasonal Variations of Subtropical Precipitation Associated with the Southern Annular Mode. J. Clim. 2014, 27, 3446–3460. [Google Scholar] [CrossRef]
- Lewis, S.C.; Karoly, D.J. Anthropogenic Contributions to Australia’s Record Summer Temperatures of 2013. Geophys. Res. Lett. 2013, 40, 3705–3709. [Google Scholar] [CrossRef]
- Ishak, E.; Rahman, A. Examination of Changes in Flood Data in Australia. Water 2019, 11, 1734. [Google Scholar] [CrossRef]
- Johnson, F.; White, C.J.; van Dijk, A.; Ekstrom, M.; Evans, J.P.; Jakob, D.; Kiem, A.S.; Leonard, M.; Rouillard, A.; Westra, S. Natural Hazards in Australia: Floods. Clim. Change 2016, 139, 21–35. [Google Scholar] [CrossRef]
- Wasko, C.; Nathan, R. Influence of Changes in Rainfall and Soil Moisture on Trends in Flooding. J. Hydrol. 2019, 575, 432–441. [Google Scholar] [CrossRef]
- Sharma, A.; Wasko, C.; Lettenmaier, D.P. If Precipitation Extremes Are Increasing, Why Aren’t Floods? Water Resour. Res. 2018, 54, 8545–8551. [Google Scholar] [CrossRef]
- Amirthanathan, E.; Bari, M.A.; Woldemeskel, F.; Narendra, K.; Feikema, P.M. Regional Significance of Historical Trends and Step Changes in Australian Streamflow. Hydrol. Earth Syst. Sci. 2023, 27, 229–254. [Google Scholar] [CrossRef]
- Bureau of Meteorology. National Arrangements for Flood Forecasting and Warning; Melbourne: Melbourne, Australia, 2018. [Google Scholar]
- Stern, H.; De Hoedt, G.; Ernst, J. Objective Classification of Australian Climates. Aust. Meteorol. Mag. 2000, 49, 87–96. [Google Scholar]
- Atkinson, R.; Power, R.; Lemon, D.; O’Hagan, R.G.; Dee, D.; Kinny, D. The Australian Hydrological Geospatial Fabric—Development Methodology and Conceptual Architecture; CSIRO: Canberra, Australia, 2008; p. 57. [Google Scholar]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global Pattern of Trends in Streamflow and Water Availability in a Changing Climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Theil, H. A rank-Invariant Method of Linear and Polynomial Regression Analysis, Part I. In Henri Theil’s Contributions to Economics and Econometrics; Advanced Studies in Theoretical and Applied Econometrics; Springer: Dordrecht, The Netherland, 1950. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Grififin: London, UK, 1975; ISBN 978-0195208375. [Google Scholar]
- Mann, H.B. Non-Parametric Test Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Wilks, D.S. On “Field Significance” and the False Discovery Rate. J. Appl. Meteorol. Climatol. 2006, 45, 1181–1189. [Google Scholar] [CrossRef]
- Mostofi Zadeh, S.; Durocher, M.; Burn, D.H.; Ashkar, F. Pooled Flood Frequency Analysis: A Comparison Based on Peaks-Over-Threshold and Annual Maximum Series. Hydrol. Sci. J. 2019, 64, 121–136. [Google Scholar] [CrossRef]
- Burn, D.H.; Whitfield, P.H. Changes in Flood Events Inferred from Centennial Length Streamflow Data Records. Adv. Water Resour. 2018, 121, 333–349. [Google Scholar] [CrossRef]
- Bačová-Mitková, V.; Onderka, M. Analýza Extrémnych Hydrologických Situácii na Dunaji Využitim Metódy Pot. J. Hydrol. Hydromech. 2010, 58, 88–101. [Google Scholar] [CrossRef]
- Bezak, N.; Brilly, M.; Šraj, M. Comparaison Entre les Méthodes de Dépassement de Seuil et du Maximum Annuel Pour les Analyses de Fréquence des Crues. Hydrol. Sci. J. 2014, 59, 959–977. [Google Scholar] [CrossRef]
- Mangini, W.; Viglione, A.; Hall, J.; Hundecha, Y.; Ceola, S.; Montanari, A.; Rogger, M.; Salinas, J.L.; Borzì, I.; Parajka, J. Detection of Trends in Magnitude and Frequency of Flood Peaks across Europe. Hydrol. Sci. J. 2018, 63, 493–512. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Singh, R.D.; Berndtsson, R.; Panda, S.N. Flood Analysis Using Generalized Logistic Models in Partial Duration Series. J. Hydrol. 2012, 420–421, 59–71. [Google Scholar] [CrossRef]
- Lang, M.; Ouarda, T.B.M.J.; Bobée, B. Towards Operational Guidelines for Over-Threshold Modeling. J. Hydrol. 1999, 225, 103–117. [Google Scholar] [CrossRef]
- Solari, S.; Losada, M.A. A Unified Statistical Model for Hydrological Variables Including the Selection of Threshold for the Peak over Threshold Method. Water Resour. Res. 2012, 48, WR011475. [Google Scholar] [CrossRef]
- Dey, R.; Lewis, S.C.; Arblaster, J.M.; Abram, N.J. A Review of Past and Projected Changes in Australia’s Rainfall. Wiley Interdiscip. Rev. Clim. Change 2019, 10, e577. [Google Scholar] [CrossRef]
- Nicholls, N.; Drosdowsky, W.; Lavery, B. Australian Rainfall Variability and Change. Weather 1997, 52, 66–72. [Google Scholar] [CrossRef]
- Poff, N.L.R.; Olden, J.D.; Pepin, D.M.; Bledsoe, B.P. Placing Global Stream Flow Variability in Geographic and Geomorphic Contexts. River Res. Appl. 2006, 22, 149–166. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s Rho Tests for Detecting Monotonic Trends in Hydrological Series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Önöz, B.; Bayazit, M. The Power of Statistical Tests for Trend Detection. Turk. J. Eng. Environ. Sci. 2003, 27, 247–251. [Google Scholar]
- Abdul Aziz, O.I.; Burn, D.H. Trends and Variability in the Hydrological Regime of the Mackenzie River Basin. J. Hydrol. 2006, 319, 282–294. [Google Scholar] [CrossRef]
- Birsan, M.V.; Molnar, P.; Burlando, P.; Pfaundler, M. Streamflow Trends in Switzerland. J. Hydrol. 2005, 314, 312–329. [Google Scholar] [CrossRef]
- Dixon, H.; Lawler, D.M.; Shamseldin, A.Y. Streamflow Trends in Western Britain. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of Statistical Analysis in Climate. In Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1995; pp. 11–26. [Google Scholar]
- Kundzewicz, Z.W.; Robson, A. Detecting Trend and Other Changes in Hydrological Data; WMO: Geneva, Switzerland, 2000; ISBN WCDMP-45. [Google Scholar]
- Gumbel, E.J. The Return Period of Flood Flows. Ann. Math. Stat. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Von Mises, R. Uber die “Ganzzahligkeit” der Atomgewicht und Verwandte Fragen. Phys. Z. 1918, 19, 490–500. [Google Scholar]
- Berghuijs, W.R.; Woods, R.A.; Hutton, C.J.; Sivapalan, M. Dominant Flood Generating Mechanisms across the United States. Geophys. Res. Lett. 2016, 43, 4382–4390. [Google Scholar] [CrossRef]
- Dhakal, N.; Jain, S.; Gray, A.; Dandy, M.; Stancioff, E. Nonstationarity in Seasonality of Extreme Precipitation: A Nonparametric Circular Statistical Approach and Its Application. Water Resour. Res. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Rutkowska, A.; Kohnová, S.; Banasik, K. Probabilistic Properties of the Date of Maximum River Flow, an Approach Based on Circular Statistics in Lowland, Highland and Mountainous Catchment. Acta Geophys. 2018, 66, 755–768. [Google Scholar] [CrossRef]
- Fisher, N.I. Statistical Analysis of Circular Data; Cambridge UP: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Mardia, K.; Jupp, P. Directional Statistics, 1st ed.; Wiley and Sons: Hoboken, NJ, USA, 2008; ISBN 9780470316979. [Google Scholar]
- Zhang, Q.; Gu, X.; Singh, V.P.; Shi, P.; Luo, M. Timing of Floods in Southeastern China: Seasonal Properties and Potential Causes. J. Hydrol. 2017, 552, 732–744. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Dudley, R.W. Changes in the Timing of Winter-Spring Streamflows in Eastern North America, 1913–2002. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Gumbel, E.J. Probability-Interpretation of the Observed Return-Periods of Floods. Eos. Trans. Am. Geophys. Union 1941, 22, 836–850. [Google Scholar] [CrossRef]
- Court, A. Some New Statistical Techniques in Geophysics. Adv. Geophys. 1952, 1, 45–85. [Google Scholar] [CrossRef]
- Petrow, T.; Merz, B. Trends in Flood Magnitude, Frequency and Seasonality in Germany in the Period 1951–2002. J. Hydrol. 2009, 371, 129–141. [Google Scholar] [CrossRef]
- Svensson, C.; Kundzewicz, Z.W.; Maurer, T. Trend Detection in River Flow Series: 2. Flood and Low-Flow Index Series. Hydrol. Sci. J. 2005, 50, 1–824. [Google Scholar] [CrossRef]
- Sagarika, S.; Kalra, A.; Ahmad, S. Evaluating the Effect of Persistence on Long-Term Trends and Analyzing Step Changes in Streamflows of the Continental United States. J. Hydrol. 2014, 517, 36–53. [Google Scholar] [CrossRef]
- Ishak, E.; Rahman, A.; Westra, S.; Sharma, A.; Kuczera, G. Trend Analysis of Australian Annual Maximum Flood Data: Exploring Relationship with Climate and Catchment Characteristics. In Proceedings of the Hydrology and Water Resources Symposium 2014, HWRS 2014—Conference Proceedings, Perth, Australia, 24–27 February 2014. [Google Scholar]
- Zhang, S.X.; Bari, M.; Amirthanathan, G.; Kent, D.; MacDonald, A.; Shin, D. Hydrologic Reference Stations to Monitor Climate-Driven Streamflow Variability and Trends. In Proceedings of the Hydrology and Water Resources Symposium 2014, HWRS 2014—Conference Proceedings, Perth, Australia, 24–27 February 2014; pp. 1048–1055. [Google Scholar]
- Fang, G.; Yang, J.; Li, Z.; Chen, Y.; Duan, W.; Amory, C.; De Maeyer, P. Shifting in the Global Flood Timing. Sci. Rep. 2022, 12, 1–9. [Google Scholar] [CrossRef]
- Villarini, G.; Serinaldi, F.; Smith, J.A.; Krajewski, W.F. On the Stationarity of Annual Flood Peaks in the Continental United States during the 20th Century. Water Resour. Res. 2009, 45, W08417. [Google Scholar] [CrossRef]
- Rice, J.S.; Emanuel, R.E.; Vose, J.M.; Nelson, S.A.C. Their Relationships with Watershed Spatial Characteristics. Water Resour. Res. 2015, 51, 6262–6275. [Google Scholar] [CrossRef]
- Asadieh, B.; Krakauer, N.Y.; Fekete, B.M. Historical Trends in Mean and Extreme Runoff and Streamflow Based on Observations and Climate Models. Water 2016, 8, 189. [Google Scholar] [CrossRef]
- Mallakpour, I.; Villarini, G. Analysis of Changes in the Magnitude, Frequency, and Seasonality of Heavy Precipitation over the Contiguous USA. Theor. Appl. Climatol. 2017, 130, 345–363. [Google Scholar] [CrossRef]
- Guerreiro, S.B.; Fowler, H.J.; Barbero, R.; Westra, S.; Lenderink, G.; Blenkinsop, S.; Lewis, E.; Li, X.F. Detection of Continental-Scale Intensification of Hourly Rainfall Extremes. Nat. Clim. Change 2018, 8, 803–807. [Google Scholar] [CrossRef]
- Alfieri, L.; Lorini, V.; Hirpa, F.A.; Harrigan, S.; Zsoter, E.; Prudhomme, C.; Salamon, P. A Global Streamflow Reanalysis for 1980–2018. J. Hydrol. X 2020, 6, 100049. [Google Scholar] [CrossRef]
- Do, H.X.; Westra, S.; Leonard, M. A Global-Scale Investigation of Trends in Annual Maximum Streamflow. J. Hydrol. 2017, 552, 28–43. [Google Scholar] [CrossRef]
- Lins, H.F.; Slack, J.R. Streamflow Trends in the United States. Geophys. Res. Lett. 1999, 26, 227–230. [Google Scholar] [CrossRef]
- Alexander, L.V.; Arblaster, J.M. Historical and Projected Trends in Temperature and Precipitation Extremes in Australia in Observations and CMIP5. Weather Clim. Extrem. 2017, 15, 34–56. [Google Scholar] [CrossRef]
- Jakob, D.; Walland, D. Variability and Long-Term Change in Australian Temperature and Precipitation Extremes. Weather Clim. Extrem. 2016, 14, 36–55. [Google Scholar] [CrossRef]
- CSIRO. BoM State of the Climate 2018—CSIRO-BOM-Dec2018; CSIRO: Canberra, Australia, 2018. [Google Scholar]
- Bao, J.; Sherwood, S.C.; Alexander, L.V.; Evans, J.P. Future Increases in Extreme Precipitation Exceed Observed Scaling Rates. Nat. Clim. Change 2017, 7, 128–132. [Google Scholar] [CrossRef]
- Ho, M.; Nathan, R.; Wasko, C.; Vogel, E.; Sharma, A. Projecting Changes in Flood Event Runoff Coefficients under Climate Change. J. Hydrol. 2022, 615, 128689. [Google Scholar] [CrossRef]
- Visser, J.B.; Wasko, C.; Sharma, A.; Nathan, R. Eliminating the Hook in Precipitation Temperature Scaling. J. Clim. 2021, 1, 1–42. [Google Scholar] [CrossRef]
- Mitchell, J.F.B. The “Greenhouse” Effect and Climate Change. Rev. Geophys. 1989, 27, 115–139. [Google Scholar] [CrossRef]
- Rotstayn, L.D.; Jeffrey, S.J.; Collier, M.A.; Dravitzki, S.M.; Hirst, A.C.; Syktus, J.I.; Wong, K.K. Aerosol- and Greenhouse Gas-Induced Changes in Summer Rainfall and Circulation in the Australasian Region: A Study Using Single-Forcing Climate Simulations. Atmos. Chem. Phys. 2012, 12, 6377–6404. [Google Scholar] [CrossRef]
- Lin, Z.; Li, Y. Remote Influence of the Tropical Atlantic on the Variability and Trend in North West Australia Summer Rainfall. J. Clim. 2012, 25, 2408–2420. [Google Scholar] [CrossRef]
- Clark, S.; Reeder, M.J.; Jakob, C. Rainfall Regimes over Northwestern Australia. Q. J. R. Meteorol. Soc. 2018, 144, 458–467. [Google Scholar] [CrossRef]
- Nguyen, H.; Timbal, B. Changes in the Hadley Circulation and Its Implication for Sub-Tropical Climate. In Proceedings of the AMOS 18th Annual Conference: Connections in the Climate System: General Information, Programme and Abstracts Handbook: University of New South Wales, Sydney, Australia, 31 January–3 February 2012. [Google Scholar]
- Wasko, C.; Nathan, R.; Peel, M.C. Changes in Antecedent Soil Moisture Modulate Flood Seasonality in a Changing Climate. Water Resour. Res. 2020, 56, e2019WR026300. [Google Scholar] [CrossRef]
- Brown, J.R.; Moise, A.F.; Colman, R.A. Projected Increases in Daily to Decadal Variability of Asian-Australian Monsoon Rainfall. Geophys. Res. Lett. 2017, 44, 5683–5690. [Google Scholar] [CrossRef]
- Timbal, B.; Drosdowsky, W. The Relationship between the Decline of Southeastern Australian Rainfall and the Strengthening of the Subtropical Ridge. Int. J. Climatol. 2012, 33, 1021–1034. [Google Scholar] [CrossRef]
- Whan, K.; Timbal, B.; Lindesay, J. Linear and Nonlinear Statistical Analysis of the Impact of Sub-Tropical Ridge Intensity and Position on South-East Australian Rainfall. Int. J. Climatol. 2014, 34, 326–342. [Google Scholar] [CrossRef]
- Stein, L.; Pianosi, F.; Woods, R. Event-Based Classification for Global Study of River Flood Generating Processes. Hydrol. Proc. 2020, 34, 1514–1529. [Google Scholar] [CrossRef]
- Fowler, K.; Peel, M.; Peterson, T.; Saft, M.; Band, L.; Bonotto, G.; Cartwright, I.; Chiew, F.; Daly, E.; Dharmadi, S.; et al. Explaining Changes in Rainfall-Runoff Relationships during and after Australia’s Millennium Drought: A Community Perspective. Hydrol. Earth Syst. Sci. Discuss. 2022, 26, 6073–6120. [Google Scholar] [CrossRef]
- CSIRO. Phase1_SynthesisReport.pdf; CSIRO: Canberra, Australia, 2010. [Google Scholar]
- Bari, M.A.; Charles, S.P.; Kitsios, A.; Coppolina, M.; Boniecka, L. Streamflow Reduction Due to Projected Climate Change in the Southwest of Western Australia—A Review. Geophys. Res. Abstr. 2008, 10, 2099–2100. [Google Scholar]
- Haylock, M.; Nicholls, N. Trends in Extreme Rainfall Indices for an Updated High Quality Data Set for Australia, 1910–1998. Int. J. Climatol. 2000, 20, 1533–1541. [Google Scholar] [CrossRef]
- Bari, M.A.; Smith, N.; Ruprecht, J.K.; Boyd, B.W. Changes in Streamflow Components Following Logging and Regeneration in the Southern Forest of Western Australia. Hydrol. Proc. 1996, 10, 447–461. [Google Scholar] [CrossRef]
- Silberstein, R.P.; Aryal, S.K.; Durrant, J.; Pearcey, M.; Braccia, M.; Charles, S.P.; Boniecka, L.; Hodgson, G.A.; Bari, M.A.; Viney, N.R.; et al. Climate Change and Runoff in South-Western Australia. J. Hydrol. 2012, 475, 441–455. [Google Scholar] [CrossRef]
- Grose, M.R.; Bhend, J.; Argueso, D.; Ekström, M.; Dowdy, A.J.; Hoffmann, P.; Evans, J.P.; Timbal, B. Comparison of Various Climate Change Projections of Eastern Australian Rainfall. Aust. Meteorol. Oceanogr. J. 2015, 65, 72–89. [Google Scholar] [CrossRef]
- White, C.J.; Sanabria, A.; Corney, S.; Grose, M.; Holz, G.; Bennett, J.; Cechet, R.; Bindoff, N.L. Modelling Extreme Events in a Changing Climate Using Regional Dynamically-Downscaled Climate Projections. In Proceedings of the Modelling for Environment’s Sake: Proceedings of the 5th Biennial Conference of the International Environmental Modelling and Software Society, iEMSs 2010, Ottawa, QN, Canada, 1 July 2010. [Google Scholar]
- Bennett, J.C.; Ling, F.L.N.; Post, D.A.; Grose, M.R.; Corney, S.P.; Graham, B.; Holz, G.K.; Katzfey, J.J.; Bindoff, N.L. High-Resolution Projections of Surface Water Availability for Tasmania, Australia. Hydrol. Earth Syst. Sci. 2012, 16, 1287–1303. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Bari, M.A.; Kabir, A.; Hasan, M.M.; Woldemeskel, F.M.; Gamage, N.; Sunter, P.D.; Zhang, X.S.; Robertson, D.E.; Bennett, J.C.; et al. Development of a National 7-Day Ensemble Streamflow Forecasting Service for Australia. Hydrol. Earth Syst. Sci. 2022, 26, 4801–4821. [Google Scholar] [CrossRef]



| Code | Drainage Division (No. of Stations) | Monotonic Trend * (+/−) | Timing +/− | ||
|---|---|---|---|---|---|
| Mk1 | Mk3 | Mk3bs | |||
| NEC | North East Coast (77) | 1/5 | 4/3 | 1/4 | 0/0 |
| SEN | South East Coast NSW (68) | 3/11 | 1/11 | 1/6 | 4/1 |
| SEV | South East Coast Vic (88) | 0/34 | 0/33 | 0/26 | 1/12 |
| TAS | Tasmania (31) | 0/7 | 0/5 | 0/6 | 2/1 |
| MDB | Murray–Darling Basin (212) | 1/115 | 1/85 | 1/99 | 10/6 |
| SAG | South Australian Gulf (12) | 1/7 | 1/5 | 1/6 | 0/0 |
| SWC | South West Coast (53) | 0/31 | 0/32 | 0/30 | 14/0 |
| PG | Pilbara–Gascoyne (12) | 0/2 | 0/1 | 1/1 | 0/3 |
| TTS | Tanami–Timor Sea Coast (22) | 6/0 | 7/0 | 4/0 | 0/10 |
| CC | Carpentaria Coast (13) | 3/0 | 3/0 | 3/0 | 0/0 |
| LEB | Lake Eyre Basin (6) | 0/1 | 0/0 | 0/1 | 0/1 |
| NWP | North Western Plateau (2) | 0/0 | 0/0 | 0/0 | 0/0 |
| SWP | South Western Plateau (0) | -- | -- | -- | |
| Total (596) | 15/213 | 17/175 | 12/179 | 31/34 | |
| Drainage Division | Drainage Division (No. of Stations) | Magnitude | Timing | ||
|---|---|---|---|---|---|
| Mk1 | Mk3 | Mk3bs | Mk1 | ||
| NEC | North East Coast (77) | ||||
| SEN | South East Coast NSW (68) | ||||
| SEV | South East Coast Vic (88) | √ | √ | √ | |
| TAS | Tasmania (31) | ||||
| MDB | Murray–Darling Basin (212) | √ | √ | √ | |
| SAG | South Australian Gulf (12) | √ | √ | √ | |
| SWC | South West Coast (53) | √ | √ | √ | |
| PG | Pilbara–Gascoyne (12) | ||||
| TTS | Tanami–Timor Sea Coast (22) | √ | |||
| CC | Carpentaria Coast (13) | ||||
| LEB | Lake Eyre Basin (6) | ||||
| NWP | North Western Plateau (2) | ||||
| SWP | South Western Plateau (0) | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bari, M.A.; Amirthanathan, G.E.; Woldemeskel, F.M.; Feikema, P.M. Changes in Magnitude and Shifts in Timing of Australian Flood Peaks. Water 2023, 15, 3665. https://doi.org/10.3390/w15203665
Bari MA, Amirthanathan GE, Woldemeskel FM, Feikema PM. Changes in Magnitude and Shifts in Timing of Australian Flood Peaks. Water. 2023; 15(20):3665. https://doi.org/10.3390/w15203665
Chicago/Turabian StyleBari, Mohammed Abdul, Gnanathikkam Emmanuel Amirthanathan, Fitsum Markos Woldemeskel, and Paul Martinus Feikema. 2023. "Changes in Magnitude and Shifts in Timing of Australian Flood Peaks" Water 15, no. 20: 3665. https://doi.org/10.3390/w15203665





