Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
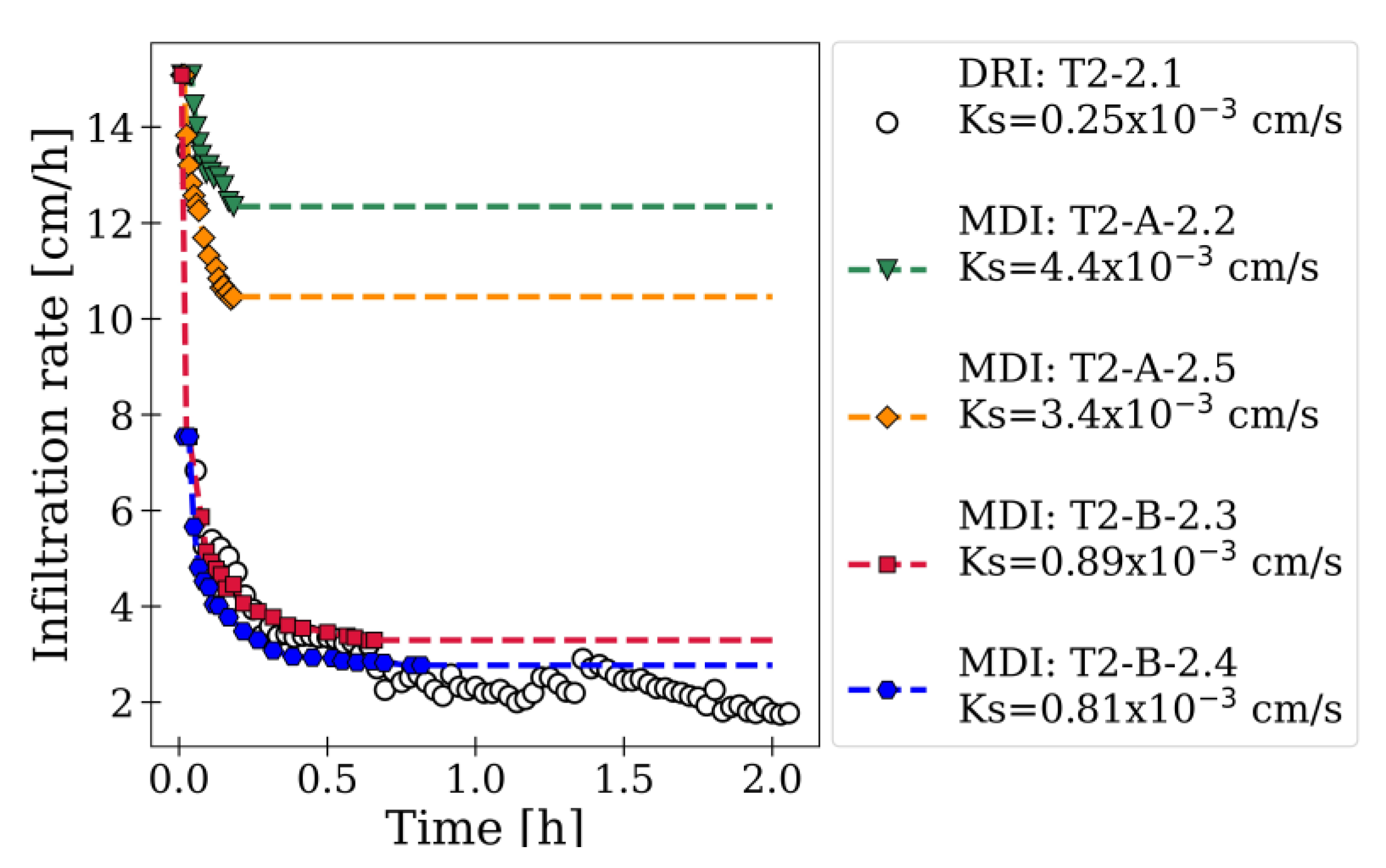
3.1. Infiltration Measurement Results
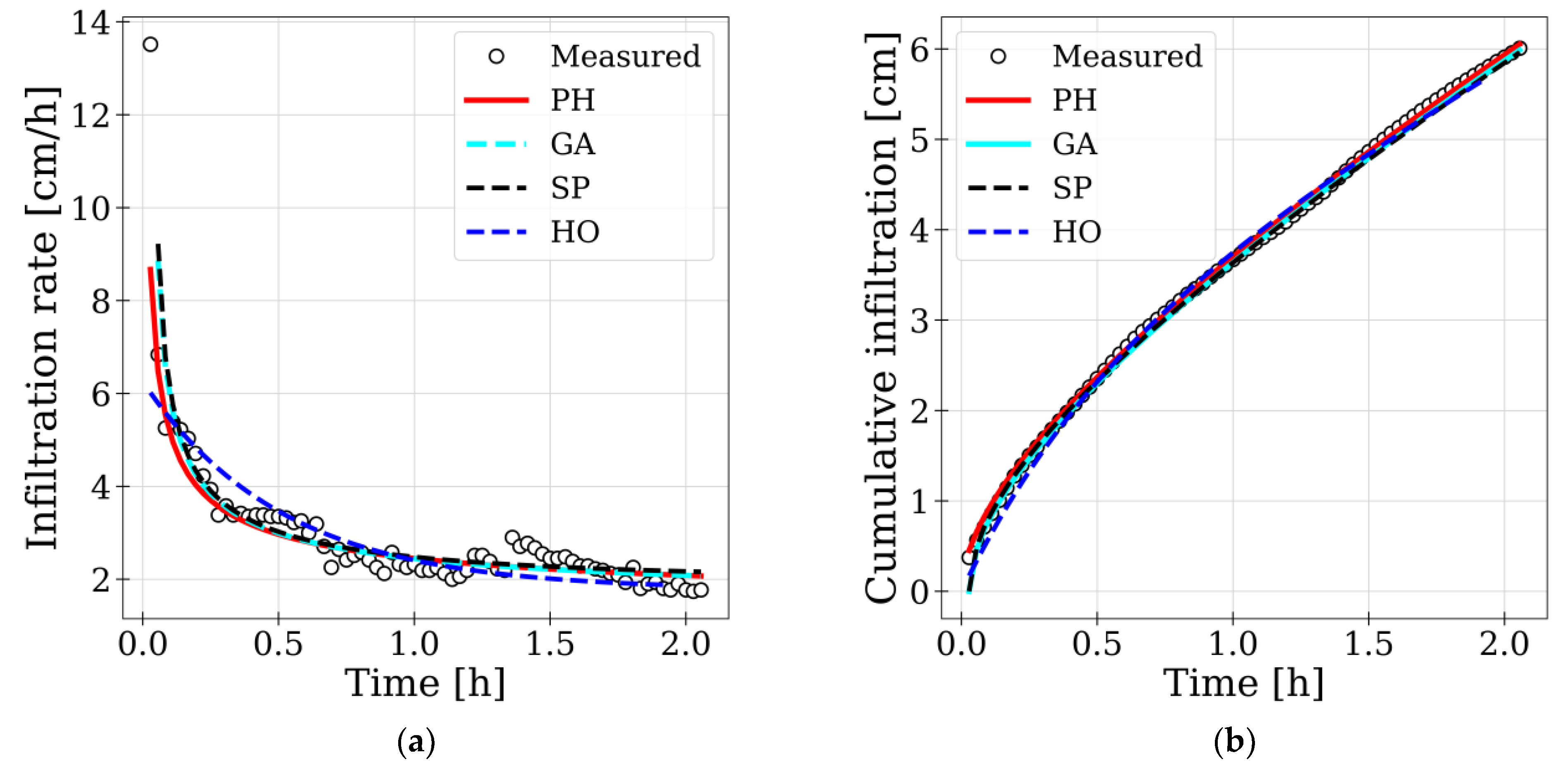
3.2. Infiltration Modeling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chithra, S.V.; Harindranathan Nair, M.V.; Amaranth, A.; Anjana, N.S. Impacts of Impervious Surfaces on the Environment. Int. J. Eng. Sci. Invent. 2015, 4, 27–31. [Google Scholar]
- Deska, I.; Mrowiec, M.; Ociepa, E.; Michniewski, M. Impact of the Hydrogel Amendment and the Dry Period Duration on the Green Roof Retention Capacity. Ecol. Chem. Eng. S 2020, 27, 357–371. [Google Scholar] [CrossRef]
- Brilly, M.; Rusjan, S.; Vidmar, A. Monitoring the Impact of Urbanisation on the Glinscica Stream. Phys. Chem. Earth 2006, 31, 1089–1096. [Google Scholar] [CrossRef]
- Miller, J.D.; Hess, T. Urbanisation Impacts on Storm Runoff along a Rural-Urban Gradient. J. Hydrol. 2017, 552, 474–489. [Google Scholar] [CrossRef]
- Rezaei, A.R.; Ismail, Z.B.; Niksokhan, M.H.; Ramli, A.H.; Sidek, L.M.; Dayarian, M.A. Investigating the Effective Factors Influencing Surface Runoff Generation in Urbacatchments—A Review. Desalination Water Treat. 2019, 164, 276–292. [Google Scholar] [CrossRef]
- Ponting, J.; Kelly, T.J.; Verhoef, A.; Watts, M.J.; Sizmur, T. The Impact of Increased Flooding Occurrence on the Mobility of Potentially Toxic Elements in Floodplain Soil—A Review. Sci. Total Environ. 2021, 754, 142040. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, X.; Jin, X.; Jin, P. Characteristics of Overflow Pollution from Combined Sewer Sediment: Formation, Contribution and Regulation. Chemosphere 2022, 298, 134254. [Google Scholar] [CrossRef]
- Barron, O.V.; Donn, M.J.; Barr, A.D. Urbanisation and Shallow Groundwater: Predicting Changes in Catchment Hydrological Responses. Water Resour. Manag. 2013, 27, 95–115. [Google Scholar] [CrossRef]
- Passarello, M.C.; Sharp, J.M.; Pierce, S.A. Estimating Urban-Induced Artificial Recharge: A Case Study for Austin, TX. Environ. Eng. Geosci. 2012, 18, 25–36. [Google Scholar] [CrossRef]
- Grischek, T.; Nestler, W. Urban Groundwater in Dresen, Germany. Hydrogeol. J. 1996, 4, 48–63. [Google Scholar] [CrossRef]
- Rose, S.; Peters, N.E. Effects of Urbanization on Streamflow in the Atlanta Area (Georgia, USA): A Comparative Hydrological Approach. Hydrol. Process 2001, 15, 1441–1457. [Google Scholar] [CrossRef]
- Minnig, M.; Moeck, C.; Radny, D.; Schirmer, M. Impact of Urbanization on Groundwater Recharge Rates in Dübendorf, Switzerland. J. Hydrol. 2018, 563, 1135–1146. [Google Scholar] [CrossRef]
- Zeng, F.; Ma, M.G.; Di, D.R.; Shi, W.Y. Separating the Impacts of Climate Change and Human Activities on Runoff: A Review of Method and Application. Water 2020, 12, 2201. [Google Scholar] [CrossRef]
- Fortier, C.; Mailhot, A. Climate Change Impact on Combined Sewer Overflows. J. Water Resour. Plan. Manag. 2015, 141, 04014073. [Google Scholar] [CrossRef]
- Tavakol-Davani, H.; Goharian, E.; Hansen, C.H.; Tavakol-Davani, H.; Apul, D.; Burian, S.J. How Does Climate Change Affect Combined Sewer Overflow in a System Benefiting from Rainwater Harvesting Systems? Sustain. Cities Soc. 2016, 27, 430–438. [Google Scholar] [CrossRef]
- Fu, X.; Hopton, M.E.; Wang, X. Assessment of Green Infrastructure Performance through an Urban Resilience Lens. J. Clean. Prod. 2021, 289, 125146. [Google Scholar] [CrossRef]
- Zabret, K.; Šraj, M. Rainfall Interception by Urban Trees and Their Impact on Potential Surface Runoff. Clean 2019, 47, 1800327. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Sample-Lord, K.; Wadzuk, B.; Traver, R. Temporal and Spatial Variation of Infiltration in Urban Green Infrastructure. Hydrol. Process 2020, 34, 1016–1034. [Google Scholar] [CrossRef]
- Davis, A.P.; Hunt, W.F.; Traver, R.G.; Clar, M. Bioretention Technology: Overview of Current Practice and Future Needs. J.Environ.Eng. 2009, 135, 109–117. [Google Scholar] [CrossRef]
- Raška, P.; Bezak, N.; Ferreira, C.S.S.; Kalantari, Z.; Banasik, K.; Bertola, M.; Bourke, M.; Cerdà, A.; Davids, P.; Madruga de Brito, M.; et al. Identifying Barriers for Nature-Based Solutions in Flood Risk Management: An Interdisciplinary Overview Using Expert Community Approach. J. Environ. Manag. 2022, 310, 114725. [Google Scholar] [CrossRef]
- Štajdohar, M.; Brilly, M.; Šraj, M. The Influence of Sustainable Measures on Runoff Hydrograph from an Urbanized Drainage Area. Acta Hydrotech. 2016, 29, 145–162. [Google Scholar]
- Yang, Y.; Chui, T.F.M. Hydrologic Performance Simulation of Green Infrastructures: Why Data-Driven Modelling Can Be Useful? In New Trends in Urban Drainage Modelling, Proceedings of the 11th International Conference on Urban Drainage Modelling (UDM), Palermo, Italy, 23–26 September, 2018; Mannina, G., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 480–484. [Google Scholar]
- Chowdary, V.M.; Rao, M.D.; Jaiswal, C.S. Study of Infiltration Process under Different Experimental Conditions. Agric. Water Manag. 2006, 83, 69–78. [Google Scholar] [CrossRef]
- Söderberg, M.H. Measuring Soil Infiltration Rates in Cultivated Land. Master’s Thesis, Stockholm University, Stockholm, Sweden, 2015. [Google Scholar]
- Mubarak, I.; Angulo-Jaramillo, R.; Mailhol, J.C.; Ruelle, P.; Khaledian, M.; Vauclin, M. Spatial Analysis of Soil Surface Hydraulic Properties: Is Infiltration Method Dependent? Agric. Water Manag. 2010, 97, 1517–1526. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, H.S.; White, E.A. Surface Soil Hydraulic Properties in Four Soil Series under Different Land Uses and Their Temporal Changes. Catena 2008, 73, 180–188. [Google Scholar] [CrossRef]
- Stolte, J.; Van Venrooij, B.; Zhang, G.; Trouwborst, K.O.; Liu, G.; Ritsema, C.J.; Hessel, R. Land-Use Induced Spatial Heterogeneity of Soil Hydraulic Properties on the Loess Plateau in China. Catena 2003, 54, 59–75. [Google Scholar] [CrossRef]
- Kumar, S.; Sekhar, M.; Reddy, D.V.; Mohan Kumar, M.S. Estimation of Soil Hydraulic Properties and Their Uncertainty: Comparison between Laboratory and Field Experiment. Hydrol. Process 2010, 24, 3426–3435. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R.; Regalado, C.M.; Álvarez-Benedi, J.; Bartoli, F. Field Evaluation of the New Philip-Dunne Permeameter for Measuring Saturated Hydraulic Conductivity. Soil. Sci. 2002, 167, 9–24. [Google Scholar] [CrossRef]
- Ronayne, M.J.; Houghton, T.B.; Stednick, J.D. Field Characterization of Hydraulic Conductivity in a Heterogeneous Alpine Glacial Till. J. Hydrol. 2012, 458–459, 103–109. [Google Scholar] [CrossRef]
- Ghosh, B.; Pekkat, S. A Critical Evaluation of Measurement Induced Variability in Infiltration Characteristics for a River Sub-Catchment. Measurement 2019, 132, 47–59. [Google Scholar] [CrossRef]
- Radinja, M.; Vidmar, I.; Atanasova, N.; Mikoš, M.; Šraj, M. Determination of Spatial and Temporal Variability of Soil Hydraulic Conductivity for Urban Runoff Modelling. Water 2019, 11, 941. [Google Scholar] [CrossRef]
- Bodhinayake, W.; Cheng Si, B.; Noborio, K. Determination of Hydraulic Properties in Sloping Landscapes from Tension and Double-Ring Infiltrometers. Vadose Zone J. 2004, 3, 964–970. [Google Scholar]
- Angulo-Jaramillo, R.; Vandervaere, J.-P.; Âphanie Roulier, S.; Thony, J.-L.; Gaudet, J.-P.; Vauclin, M. Field Measurement of Soil Surface Hydraulic Properties by Disc and Ring Infitrometers A Review and Recent Developments. Soil. Tillage Res. 2000, 55, 1–29. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. Rainfall Infiltration Modeling: A Review. Water 2018, 10, 1873. [Google Scholar] [CrossRef]
- Mishra, S.K.; Tyagi, J.V.; Singh, V.P. Comparison of Infiltration Models. Hydrol. Process 2003, 17, 2629–2652. [Google Scholar] [CrossRef]
- Šraj, M.; Dirnbek, L.; Brilly, M. The Influence of Effective Rainfall on Modeled Runoff Hydrograph. J. Hydrol. Hydromech. 2010, 58, 3–14. [Google Scholar] [CrossRef]
- Žlebnik, L. Pleistocene Deposits of the Kranj, Sora and Ljubljana Fields. Geologija 1971, 14, 5–51. (In Slovene) [Google Scholar]
- Premru, U. Geological Map of SFRJ 1: 100000 Sheet Ljubljana. Geologija 1974, 17, 497–499. [Google Scholar]
- Drobne, F.; Mencej, Z.; Brilly, M. Review and Additions to the Expert Basis for Determining the Water Protection Zones of Current and Prospective Water Sources for the City of Ljubljana and Its Surroundings; Interpreter for Maps of Water Protection Zones: Ljubljana, Slovenia, 1997. (In Slovene) [Google Scholar]
- Prestor, J.; Urbanc, J.; Janža, M.; Peternel Rikanovič, R.; Bizjak, M.; Medič, M.; Strojan, M. Review and Additions to the Expert Basis for Determining the Protection Zones of Water Resources for the Central Drinking Water Supply System in the City of Ljubljana—Ljubljansko Polje; Geological Survey of Slovenia: Ljubljana, Slovenia, 2002. (In Slovene) [Google Scholar]
- ARSO ARSO Meteorological Achive. Available online: https://meteo.arso.gov.si/met/sl/archive/ (accessed on 15 December 2022).
- Ritchey, E.L.; Mcgrath, J.M.; Gehring, D. Determining Soil Texture by Feel. Agric. Nat. Resour. Publ. Coop. Ext. Serv. 2015, 1, 1–4. [Google Scholar]
- Klocke, N.L.; Fischbach, P.E. G84-690 Estimating Soil Moisture by Appearance and Feel; Historical Materials from University of Nebraska-Lincoln Extension: Lincoln, NE, USA, 1984. [Google Scholar]
- Smith, R.E. Infiltration Theory for Hydrologic Applications; American Geophysical Union: Washington, DC, USA, 2002; ISBN 0875903193. [Google Scholar]
- Standard D3385-09; Standard Test Method for Infiltration Rate of Soils in Field Using Double-Ring Infiltrometer. ASTM: West Conshohocken, PA, USA, 2009.
- Arriaga, F.J.; Kornecki, T.S.; Balkcom, K.S.; Raper, R.L. A Method for Automating Data Collection from a Double-Ring Infiltrometer under Falling Head Conditions. Soil. Use Manag. 2010, 26, 61–67. [Google Scholar] [CrossRef]
- USDA. Soil Survey Field and Laboratory Methods Manual, Soil Survey Investigations Report No. 51; Version 2; USDA: Washington, DC, USA, 2014. [Google Scholar]
- Reynolds, W.D.; Elrick, D.E. Ponded Infiltration From a Single Ring: I. Analysis of Steady Flow. Soil. Sci. Soc. Am. J. 1990, 54, 1233–1241. [Google Scholar] [CrossRef]
- Youngs, E.G.; Leeds-Harrison, P.B.; Elrick, D.E. The Hydraulic Conductivity of Low Permeability Wet Soils Used as Landfill Lining and Capping Material: Analysis of Pressure Infiltrometer Measurements. Soil. Technol. 1995, 8, 153–160. [Google Scholar] [CrossRef]
- Elrick, D.E.; Reynolds, W.D.; Tan, K.A. Hydraulic Conductivity Measurements in the Unsaturated Zone Using Improved Well Analyses. Groundw. Monit. Remediat. 1989, 9, 184–193. [Google Scholar] [CrossRef]
- Decagon Devices. METER Group Mini Disk Infiltrometer—User’s Manual; Decagon Devices Inc.: Pullman, WA, USA, 2021. [Google Scholar]
- Dohnal, M.; Dusek, J.; Vogel, T. Improving Hydraulic Conductivity Estimates from Minidisk Infiltrometer Measurements for Soils with Wide Pore-Size Distributions. Soil. Sci. Soc. Am. J. 2010, 74, 804–811. [Google Scholar] [CrossRef]
- Zhang, R. Infiltration Models for the Disk Infiltrometer. Soil Sci. Soc. Am. J. 1996, 61, 1597–1603. [Google Scholar] [CrossRef]
- Philip, J.R. The Theory of Infiltration: 4. Sorptivity and Algebraic Infiltration Equations. Soil. Sci. 1957, 84, 257–264. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability Distributions of Soil Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Bátková, K.; Miháliková, M.; Matula, S. Hydraulic Properties of a Cultivated Soil in Temperate Continental Climate Determined by Mini Disk Infiltrometer. Water 2020, 12, 843. [Google Scholar] [CrossRef]
- Kutilek, M.; Nielsen, D.R. Soil Hydrology; Schweizerbart Science Publishers: Stuttgart, Germany, 1992; ISBN 9783510653874. [Google Scholar]
- Fodor, N.; Sándor, R.; Orfanus, T.; Lichner, L.; Rajkai, K. Evaluation Method Dependency of Measured Saturated Hydraulic Conductivity. Geoderma 2011, 165, 60–68. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies in Soil Physics: Part 1. The Flow of Air and Water through Soils. J. Agric. Sci. 1911, 4, 11–24. [Google Scholar]
- Smith, R.E.; Parlange, J.-Y. A Parameter-Efficient Hydrologic Infiltration Model. Water Resour. Res. 1978, 14, 533–538. [Google Scholar] [CrossRef]
- Horton, R.E. Analysis of Runoff-Plat Experiments with Varying Infiltration-Capacity. Rep. Pap. 1939, 20, 693–711. [Google Scholar] [CrossRef]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks—A Publishing Format for Reproducible Computational Workflows. In Proceedings of the Positioning and Power in Academic Publishing: Players, Agents and Agendas—Proceedings of the 20th International Conference on Electronic Publishing, ELPUB 2016, Göttingen, Germany, 7–9 June 2016; pp. 87–90. [Google Scholar]
- Turner, E.R. Comparison of Infiltration Equations and Their Field Validation with Rainfall Simulation. Master Thesis, University of Maryland, College Park, MD, USA, 2006. [Google Scholar]
- Farid, H.U.; Mahmood-Khan, Z.; Ahmad, I.; Shakoor, A.; Anjum, M.N.; Iqbal, M.M.; Mubeen, M.; Asghar, M. Estimation of Infiltration Models Parameters and Their Comparison to Simulate the Onsite Soil Infiltration Characteristics. Int. J. Agric. Biol. Eng. 2019, 12, 84–91. [Google Scholar] [CrossRef]
- Lili, M.; Bralts, V.F.; Yinghua, P.; Han, L.; Tingwu, L. Methods for Measuring Soil Infiltration: State of the Art. Int. J. Agric. Biol. Eng. 2008, 1, 22–30. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Hopkins, I.; Guo, L.; Lin, H. Dynamics of Infiltration Rate and Field-Saturated Soil Hydraulic Conductivity in a Wastewater- Irrigated Cropland. Water 2019, 11, 1632. [Google Scholar] [CrossRef]
- Turner, D.P.; Sumner, M.E. The Influence of Initial Soil Moisture Content on Field Measured Infiltration Rates. Water SA 1978, 4, 1–8. [Google Scholar]
- Fatehnia, M.; Tawfiq, K.; Ye, M. Estimation of Saturated Hydraulic Conductivity from Double-Ring Infiltrometer Measurements. Eur. J. Soil. Sci. 2016, 67, 135–147. [Google Scholar] [CrossRef]
- Fan, G.; Han, Y.; Song, M. Experimental Study on the Reasonable Inbuilt-Ring Depth of Soil One-Dimensional Infiltration Experiment in Field. In Proceedings of the Computer and Computing Technologies in Agriculture V, CCTA 2011, IFIP Advances in Information and Communication Technology, Beijing, China, 29–31 October 2011; Springer: Berlin/Heidelberg, Germany, 2012; Volume 368, pp. 427–436. [Google Scholar]
- De Jonge, L.W.; Jacobsen, O.H.; Moldrup, P. Soil Water Repellency: Effects of Water Content, Temperature, and Particle Size. Soil. Sci. Soc. Am. J. 1999, 63, 437–442. [Google Scholar] [CrossRef]
- Leelamanie, D.A.L.; Karube, J. Effects of Organic Compounds, Water Content and Clay on the Water Repellency of a Model Sandy Soil. Soil. Sci. Plant Nutr. 2007, 53, 711–719. [Google Scholar] [CrossRef]
- Akan, A.O.; Houghtalen, R.J. Urban Hydrology, Hydraulics, and Stormwater Quality: Engineering Applications and Computer Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 0471431583. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Saxton, K.E. Estimation of Soil Water Properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Rawls, W.J.; Asce, M.; Brakensiek, D.L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- USDA Soil. Survey Manual; USDA Soil: Waverly, IA, USA, 2017. [Google Scholar]
- Lu, N.; Likos, W.J. Rate of Capillary Rise in Soil. J. Geotech. Geoenviron. Eng. 2004, 130, 646–650. [Google Scholar] [CrossRef]
- Oleszczuk, R.; Truba, M. The Analysis of Some Physical Properties of Drained Peat-Moorsh Soil Layers. Ann. Wars. Univ. Life Sci.-SGGW. Land. Reclam. 2013, 45, 41–48. [Google Scholar] [CrossRef]
- Aldrees, A.; Nachabe, M. Capillary Length and Field Capacity in Draining Soil Profiles. Water Resour. Res. 2019, 55, 4499–4507. [Google Scholar] [CrossRef]
- Lehmann, P.; Bickel, S.; Wei, Z.; Or, D. Physical Constraints for Improved Soil Hydraulic Parameter Estimation by Pedotransfer Functions. Water Resour. Res. 2020, 56, e2019WR025963. [Google Scholar] [CrossRef]
- Elrick, D.E.; Reynolds, W.D. Methods for Analyzing Constant-Head Well Permeameter Data. Soil. Sci. Soc. Am. J. 1992, 56, 320–323. [Google Scholar] [CrossRef]
- Di Prima, S.; Stewart, R.D.; Castellini, M.; Bagarello, V.; Abou Najm, M.R.; Pirastru, M.; Giadrossich, F.; Iovino, M.; Angulo-Jaramillo, R.; Lassabatere, L. Estimating the Macroscopic Capillary Length from Beerkan Infiltration Experiments and Its Impact on Saturated Soil Hydraulic Conductivity Predictions. J. Hydrol. 2020, 589, 125159. [Google Scholar] [CrossRef]

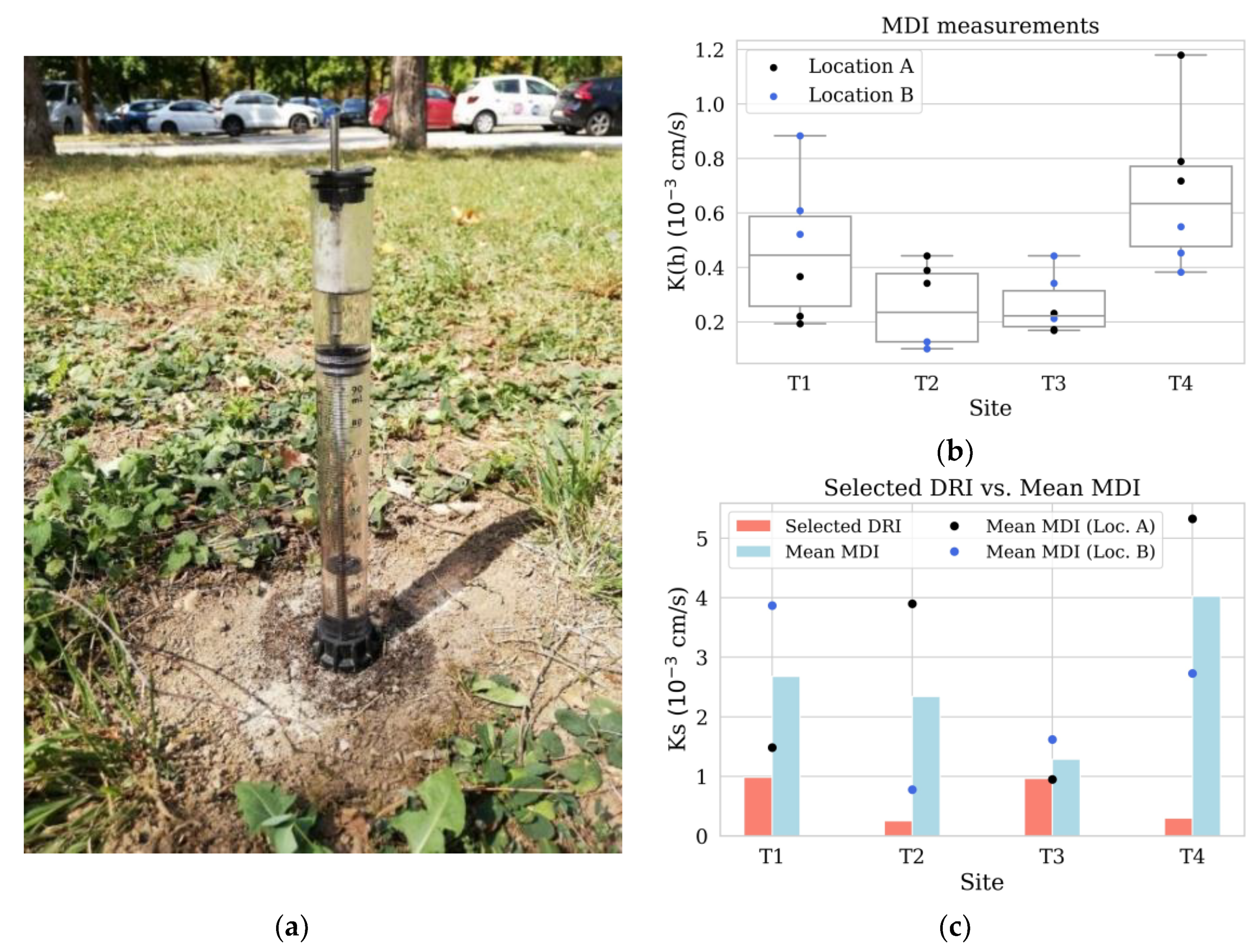
| Site | Soil Texture [43] | Moisture [44] | Sun Exposure | Vegetation |
|---|---|---|---|---|
| T1 | sandy loam | moist | mostly shaded | dense grass |
| T2 | sandy clay loam | slightly moist | sunlit | dense grass |
| T3 | sandy clay loam | moist | mostly shaded | dense grass |
| T4 | sandy loam | dry | sunlit | sparsely grown grass |
| Infiltration Model | Infiltration Rate | |
|---|---|---|
| Green-Ampt | (7) | |
| Smith-Parlange | (8) | |
| Horton | (9) | |
| Philip | (10) | |
| Infiltration Model | Cumulative Infiltration | |
| Green-Ampt | (11) | |
| Smith-Parlange | (12) | |
| Horton | (13) | |
| Philip | (14) | |
| Abbreviation | Parameter | Unit |
| potential infiltration rate (capacity) after time of ponding () | (cm/s) | |
| cumulative infiltration | (cm) | |
| time | (s) | |
| saturated water content | (-) | |
| initial water content | (-) | |
| average suction across the wetting front | (cm) | |
| saturated hydraulic conductivity | (cm/s) | |
| initial hydraulic conductivity | (cm/s) | |
| capillary length scale | (cm) | |
| dimensionless Smith-Parlange coefficient (usually 0.8–0.85) | (-) | |
| sorptivity | () | |
| soil dependent dimensionless Philip coefficient | (-) | |
| initial infiltration capacity | (cm/s) | |
| final constant infiltration rate | (cm/s) | |
| Horton dimensionless coefficient that depends on the initial water content and the application rate | (-) |
| Site | No. | Loc. | Soil Type | KsDRI (Equation (1)) [10−3 cm/s] | KsDRI* [10−3 cm/s] | K(h)MDI (Equation (3)) [10−3 cm/s] | KsMDI (Equation (6)) [10−3 cm/s] | K(h)MDI /KsDRI* | KsMDI/ KsDRI* | CV of K(h)MDI [%] Loc./Site | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | D1.1 | SL | 2.99 * | 0.98 | |||||||
| D1.2 | 0.98 | ||||||||||
| M1.1 | T1-A | SL | 0.19 (0.05) | 1.08 | 0.19 (0.05) | 1.10 | 35.9 | 56.2 | |||
| M1.3 | 0.22 (0.05) | 1.22 | 0.22 (0.05) | 1.24 | |||||||
| M1.4 | 0.37 (0.09) | 2.15 | 0.38 (0.09) | 2.18 | |||||||
| M1.2 | T1-B | SL | 0.61 (0.15) | 3.37 | 0.62 (0.15) | 3.42 | 28.1 | ||||
| M1.5 | 0.88 (0.21) | 5.18 | 0.90 (0.21) | 5.26 | |||||||
| M1.6 | 0.52 (0.12) | 3.06 | 0.53 (0.12) | 3.11 | |||||||
| T2 | D2.1 | SCL | 0.25 | 0.25 | |||||||
| M2.1 | T2-A | CL | 0.39 (0.16) | 3.88 | 1.56 (0.64) | 15.35 | 13.0 | 60.1 | |||
| M2.2 | 0.44 (0.18) | 4.42 | 1.76 (0.72) | 17.48 | |||||||
| M2.5 | 0.34 (0.14) | 3.40 | 1.36 (0.56) | 13.45 | |||||||
| M2.3 | T2-B | SCL | 0.13 (0.04) | 0.89 | 0.52 (0.16) | 3.51 | 12.5 | ||||
| M2.4 | 0.13 (0.03) | 0.81 | 0.52 (0.12) | 3.20 | |||||||
| M2.6 | 0.10 (0.03) | 0.65 | 0.40 (0.12) | 2.55 | |||||||
| T3 | D3.1 | SCL | 2.39 * | 0.97 | |||||||
| D3.2 | 0.83 | ||||||||||
| D3.3 | 1.10 | ||||||||||
| M3.1 | T3-A | SCL | 0.17 (0.04) | 1.06 | 0.18 (0.04) | 1.10 | 18.9 | 41.7 | |||
| M3.2 | 0.23 (0.03) | 0.70 | 0.24 (0.03) | 0.73 | |||||||
| M3.4 | 0.17 (0.04) | 1.09 | 0.18 (0.04) | 1.13 | |||||||
| M3.3 | T3-B | SCL | 0.44 (0.05) | 1.34 | 0.45 (0.05) | 1.39 | 34.7 | ||||
| M3.5 | 0.21 (0.06) | 1.35 | 0.22 (0.06) | 1.40 | |||||||
| M3.6 | 0.34 (0.09) | 2.18 | 0.35 (0.09) | 2.26 | |||||||
| T4 | D4.1 | SL | 0.18 | 0.30 | |||||||
| D4.2 | 0.41 | ||||||||||
| M4.1 | T4-A | SL | 0.79 (0.19) | 4.56 | 2.63 (0.63) | 15.26 | 27.7 | 42.6 | |||
| M4.2 | 1.18 (0.28) | 6.95 | 3.93 (0.93) | 23.26 | |||||||
| M4.5 | 0.72 (0.17) | 4.46 | 2.40 (0.57) | 14.93 | |||||||
| M4.3 | T4-B | SL | 0.45 (0.11) | 2.65 | 1.50 (0.37) | 8.87 | 18.2 | ||||
| M4.4 | 0.55 (0.13) | 3.28 | 1.83 (0.43) | 10.98 | |||||||
| M4.6 | 0.38 (0.09) | 2.25 | 1.27 (0.30) | 7.53 | |||||||
| Parameter | Green-Ampt | Smith-Parlange | Philip |
|---|---|---|---|
| 0.42 (0.39–0.44) | 0.56 (0.53–0.58) | 0.33 (0.14–0.42) | |
| 0.27 (0.27–0.45) | 0.29 (0.28–0.41) | / | |
| 8.5 (4.5–9.5) | / | / | |
| / | 5.0 (5.0–7.0) | / | |
| / | 0.022 (0.008–0.025) | / | |
| / | / | 0.69 (0.58–0.86) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svetina, J.; Prestor, J.; Šraj, M. Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia. Water 2023, 15, 3635. https://doi.org/10.3390/w15203635
Svetina J, Prestor J, Šraj M. Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia. Water. 2023; 15(20):3635. https://doi.org/10.3390/w15203635
Chicago/Turabian StyleSvetina, Janja, Joerg Prestor, and Mojca Šraj. 2023. "Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia" Water 15, no. 20: 3635. https://doi.org/10.3390/w15203635






