Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
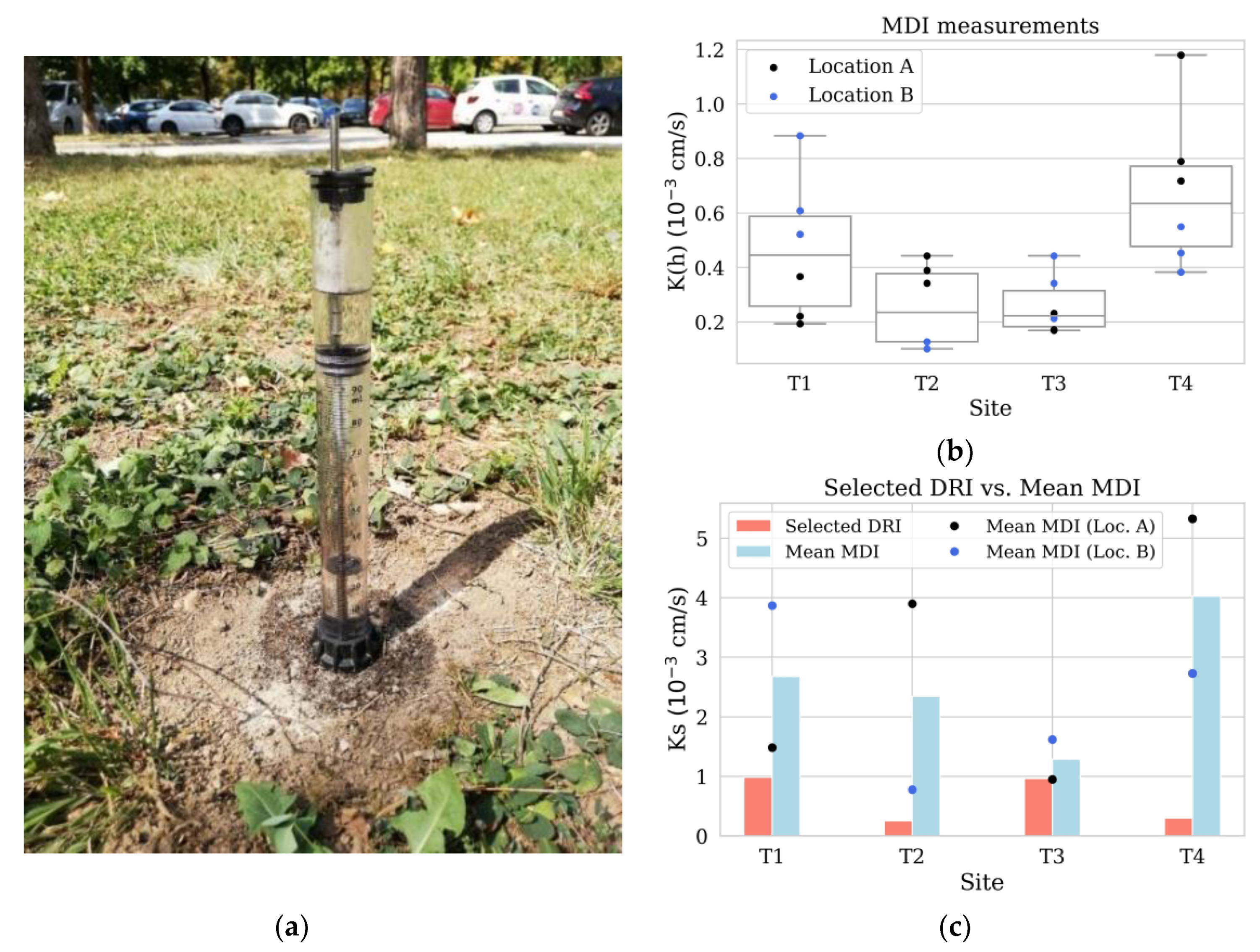
3.1. Infiltration Measurement Results
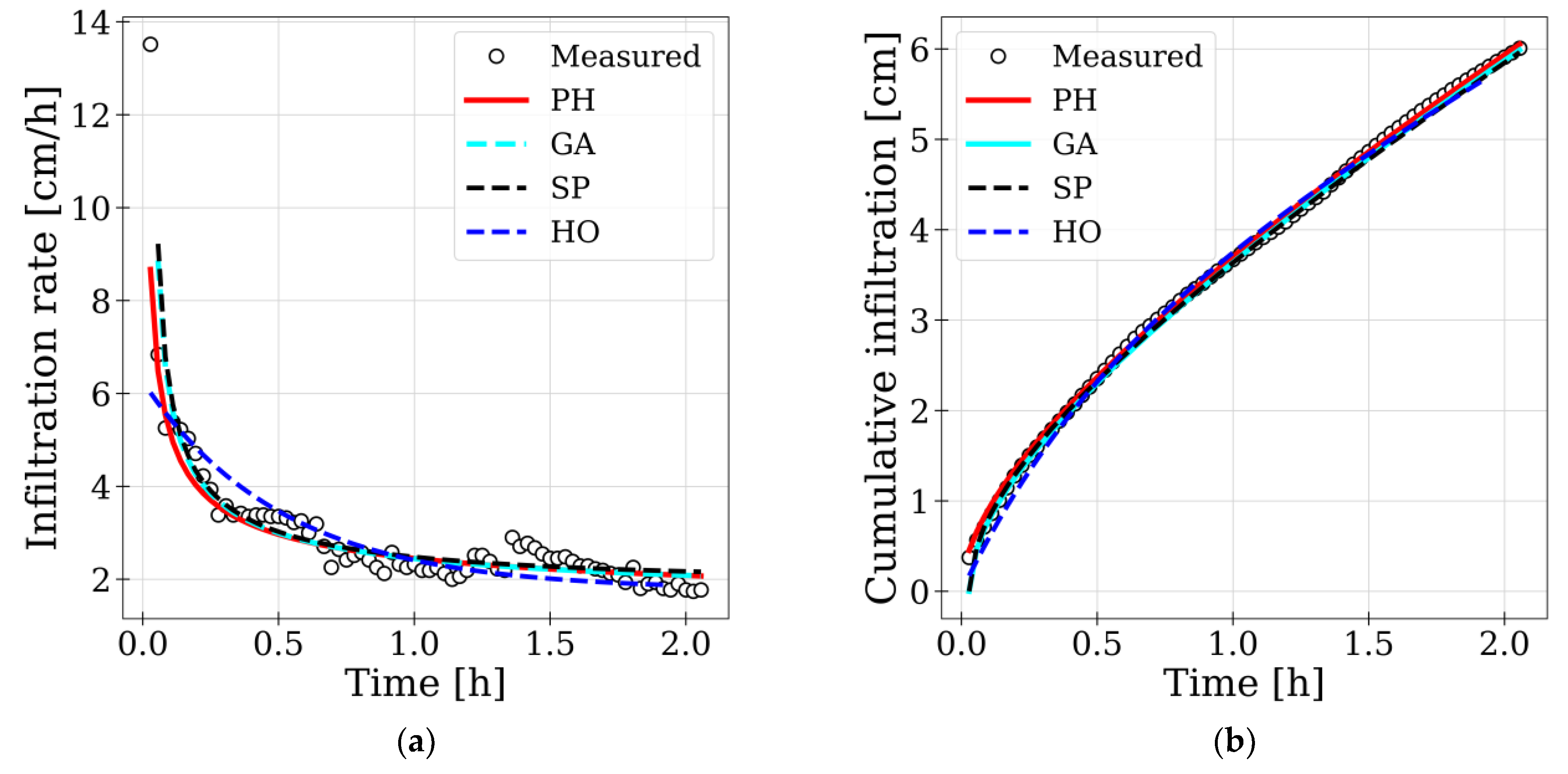
3.2. Infiltration Modeling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chithra, S.V.; Harindranathan Nair, M.V.; Amaranth, A.; Anjana, N.S. Impacts of Impervious Surfaces on the Environment. Int. J. Eng. Sci. Invent. 2015, 4, 27–31. [Google Scholar]
- Deska, I.; Mrowiec, M.; Ociepa, E.; Michniewski, M. Impact of the Hydrogel Amendment and the Dry Period Duration on the Green Roof Retention Capacity. Ecol. Chem. Eng. S 2020, 27, 357–371. [Google Scholar] [CrossRef]
- Brilly, M.; Rusjan, S.; Vidmar, A. Monitoring the Impact of Urbanisation on the Glinscica Stream. Phys. Chem. Earth 2006, 31, 1089–1096. [Google Scholar] [CrossRef]
- Miller, J.D.; Hess, T. Urbanisation Impacts on Storm Runoff along a Rural-Urban Gradient. J. Hydrol. 2017, 552, 474–489. [Google Scholar] [CrossRef]
- Rezaei, A.R.; Ismail, Z.B.; Niksokhan, M.H.; Ramli, A.H.; Sidek, L.M.; Dayarian, M.A. Investigating the Effective Factors Influencing Surface Runoff Generation in Urbacatchments—A Review. Desalination Water Treat. 2019, 164, 276–292. [Google Scholar] [CrossRef]
- Ponting, J.; Kelly, T.J.; Verhoef, A.; Watts, M.J.; Sizmur, T. The Impact of Increased Flooding Occurrence on the Mobility of Potentially Toxic Elements in Floodplain Soil—A Review. Sci. Total Environ. 2021, 754, 142040. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, X.; Jin, X.; Jin, P. Characteristics of Overflow Pollution from Combined Sewer Sediment: Formation, Contribution and Regulation. Chemosphere 2022, 298, 134254. [Google Scholar] [CrossRef]
- Barron, O.V.; Donn, M.J.; Barr, A.D. Urbanisation and Shallow Groundwater: Predicting Changes in Catchment Hydrological Responses. Water Resour. Manag. 2013, 27, 95–115. [Google Scholar] [CrossRef]
- Passarello, M.C.; Sharp, J.M.; Pierce, S.A. Estimating Urban-Induced Artificial Recharge: A Case Study for Austin, TX. Environ. Eng. Geosci. 2012, 18, 25–36. [Google Scholar] [CrossRef]
- Grischek, T.; Nestler, W. Urban Groundwater in Dresen, Germany. Hydrogeol. J. 1996, 4, 48–63. [Google Scholar] [CrossRef]
- Rose, S.; Peters, N.E. Effects of Urbanization on Streamflow in the Atlanta Area (Georgia, USA): A Comparative Hydrological Approach. Hydrol. Process 2001, 15, 1441–1457. [Google Scholar] [CrossRef]
- Minnig, M.; Moeck, C.; Radny, D.; Schirmer, M. Impact of Urbanization on Groundwater Recharge Rates in Dübendorf, Switzerland. J. Hydrol. 2018, 563, 1135–1146. [Google Scholar] [CrossRef]
- Zeng, F.; Ma, M.G.; Di, D.R.; Shi, W.Y. Separating the Impacts of Climate Change and Human Activities on Runoff: A Review of Method and Application. Water 2020, 12, 2201. [Google Scholar] [CrossRef]
- Fortier, C.; Mailhot, A. Climate Change Impact on Combined Sewer Overflows. J. Water Resour. Plan. Manag. 2015, 141, 04014073. [Google Scholar] [CrossRef]
- Tavakol-Davani, H.; Goharian, E.; Hansen, C.H.; Tavakol-Davani, H.; Apul, D.; Burian, S.J. How Does Climate Change Affect Combined Sewer Overflow in a System Benefiting from Rainwater Harvesting Systems? Sustain. Cities Soc. 2016, 27, 430–438. [Google Scholar] [CrossRef]
- Fu, X.; Hopton, M.E.; Wang, X. Assessment of Green Infrastructure Performance through an Urban Resilience Lens. J. Clean. Prod. 2021, 289, 125146. [Google Scholar] [CrossRef]
- Zabret, K.; Šraj, M. Rainfall Interception by Urban Trees and Their Impact on Potential Surface Runoff. Clean 2019, 47, 1800327. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Sample-Lord, K.; Wadzuk, B.; Traver, R. Temporal and Spatial Variation of Infiltration in Urban Green Infrastructure. Hydrol. Process 2020, 34, 1016–1034. [Google Scholar] [CrossRef]
- Davis, A.P.; Hunt, W.F.; Traver, R.G.; Clar, M. Bioretention Technology: Overview of Current Practice and Future Needs. J.Environ.Eng. 2009, 135, 109–117. [Google Scholar] [CrossRef]
- Raška, P.; Bezak, N.; Ferreira, C.S.S.; Kalantari, Z.; Banasik, K.; Bertola, M.; Bourke, M.; Cerdà, A.; Davids, P.; Madruga de Brito, M.; et al. Identifying Barriers for Nature-Based Solutions in Flood Risk Management: An Interdisciplinary Overview Using Expert Community Approach. J. Environ. Manag. 2022, 310, 114725. [Google Scholar] [CrossRef]
- Štajdohar, M.; Brilly, M.; Šraj, M. The Influence of Sustainable Measures on Runoff Hydrograph from an Urbanized Drainage Area. Acta Hydrotech. 2016, 29, 145–162. [Google Scholar]
- Yang, Y.; Chui, T.F.M. Hydrologic Performance Simulation of Green Infrastructures: Why Data-Driven Modelling Can Be Useful? In New Trends in Urban Drainage Modelling, Proceedings of the 11th International Conference on Urban Drainage Modelling (UDM), Palermo, Italy, 23–26 September, 2018; Mannina, G., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 480–484. [Google Scholar]
- Chowdary, V.M.; Rao, M.D.; Jaiswal, C.S. Study of Infiltration Process under Different Experimental Conditions. Agric. Water Manag. 2006, 83, 69–78. [Google Scholar] [CrossRef]
- Söderberg, M.H. Measuring Soil Infiltration Rates in Cultivated Land. Master’s Thesis, Stockholm University, Stockholm, Sweden, 2015. [Google Scholar]
- Mubarak, I.; Angulo-Jaramillo, R.; Mailhol, J.C.; Ruelle, P.; Khaledian, M.; Vauclin, M. Spatial Analysis of Soil Surface Hydraulic Properties: Is Infiltration Method Dependent? Agric. Water Manag. 2010, 97, 1517–1526. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, H.S.; White, E.A. Surface Soil Hydraulic Properties in Four Soil Series under Different Land Uses and Their Temporal Changes. Catena 2008, 73, 180–188. [Google Scholar] [CrossRef]
- Stolte, J.; Van Venrooij, B.; Zhang, G.; Trouwborst, K.O.; Liu, G.; Ritsema, C.J.; Hessel, R. Land-Use Induced Spatial Heterogeneity of Soil Hydraulic Properties on the Loess Plateau in China. Catena 2003, 54, 59–75. [Google Scholar] [CrossRef]
- Kumar, S.; Sekhar, M.; Reddy, D.V.; Mohan Kumar, M.S. Estimation of Soil Hydraulic Properties and Their Uncertainty: Comparison between Laboratory and Field Experiment. Hydrol. Process 2010, 24, 3426–3435. [Google Scholar] [CrossRef]
- Muñoz-Carpena, R.; Regalado, C.M.; Álvarez-Benedi, J.; Bartoli, F. Field Evaluation of the New Philip-Dunne Permeameter for Measuring Saturated Hydraulic Conductivity. Soil. Sci. 2002, 167, 9–24. [Google Scholar] [CrossRef]
- Ronayne, M.J.; Houghton, T.B.; Stednick, J.D. Field Characterization of Hydraulic Conductivity in a Heterogeneous Alpine Glacial Till. J. Hydrol. 2012, 458–459, 103–109. [Google Scholar] [CrossRef]
- Ghosh, B.; Pekkat, S. A Critical Evaluation of Measurement Induced Variability in Infiltration Characteristics for a River Sub-Catchment. Measurement 2019, 132, 47–59. [Google Scholar] [CrossRef]
- Radinja, M.; Vidmar, I.; Atanasova, N.; Mikoš, M.; Šraj, M. Determination of Spatial and Temporal Variability of Soil Hydraulic Conductivity for Urban Runoff Modelling. Water 2019, 11, 941. [Google Scholar] [CrossRef]
- Bodhinayake, W.; Cheng Si, B.; Noborio, K. Determination of Hydraulic Properties in Sloping Landscapes from Tension and Double-Ring Infiltrometers. Vadose Zone J. 2004, 3, 964–970. [Google Scholar]
- Angulo-Jaramillo, R.; Vandervaere, J.-P.; Âphanie Roulier, S.; Thony, J.-L.; Gaudet, J.-P.; Vauclin, M. Field Measurement of Soil Surface Hydraulic Properties by Disc and Ring Infitrometers A Review and Recent Developments. Soil. Tillage Res. 2000, 55, 1–29. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. Rainfall Infiltration Modeling: A Review. Water 2018, 10, 1873. [Google Scholar] [CrossRef]
- Mishra, S.K.; Tyagi, J.V.; Singh, V.P. Comparison of Infiltration Models. Hydrol. Process 2003, 17, 2629–2652. [Google Scholar] [CrossRef]
- Šraj, M.; Dirnbek, L.; Brilly, M. The Influence of Effective Rainfall on Modeled Runoff Hydrograph. J. Hydrol. Hydromech. 2010, 58, 3–14. [Google Scholar] [CrossRef][Green Version]
- Žlebnik, L. Pleistocene Deposits of the Kranj, Sora and Ljubljana Fields. Geologija 1971, 14, 5–51. (In Slovene) [Google Scholar]
- Premru, U. Geological Map of SFRJ 1: 100000 Sheet Ljubljana. Geologija 1974, 17, 497–499. [Google Scholar]
- Drobne, F.; Mencej, Z.; Brilly, M. Review and Additions to the Expert Basis for Determining the Water Protection Zones of Current and Prospective Water Sources for the City of Ljubljana and Its Surroundings; Interpreter for Maps of Water Protection Zones: Ljubljana, Slovenia, 1997. (In Slovene) [Google Scholar]
- Prestor, J.; Urbanc, J.; Janža, M.; Peternel Rikanovič, R.; Bizjak, M.; Medič, M.; Strojan, M. Review and Additions to the Expert Basis for Determining the Protection Zones of Water Resources for the Central Drinking Water Supply System in the City of Ljubljana—Ljubljansko Polje; Geological Survey of Slovenia: Ljubljana, Slovenia, 2002. (In Slovene) [Google Scholar]
- ARSO ARSO Meteorological Achive. Available online: https://meteo.arso.gov.si/met/sl/archive/ (accessed on 15 December 2022).
- Ritchey, E.L.; Mcgrath, J.M.; Gehring, D. Determining Soil Texture by Feel. Agric. Nat. Resour. Publ. Coop. Ext. Serv. 2015, 1, 1–4. [Google Scholar]
- Klocke, N.L.; Fischbach, P.E. G84-690 Estimating Soil Moisture by Appearance and Feel; Historical Materials from University of Nebraska-Lincoln Extension: Lincoln, NE, USA, 1984. [Google Scholar]
- Smith, R.E. Infiltration Theory for Hydrologic Applications; American Geophysical Union: Washington, DC, USA, 2002; ISBN 0875903193. [Google Scholar]
- Standard D3385-09; Standard Test Method for Infiltration Rate of Soils in Field Using Double-Ring Infiltrometer. ASTM: West Conshohocken, PA, USA, 2009.
- Arriaga, F.J.; Kornecki, T.S.; Balkcom, K.S.; Raper, R.L. A Method for Automating Data Collection from a Double-Ring Infiltrometer under Falling Head Conditions. Soil. Use Manag. 2010, 26, 61–67. [Google Scholar] [CrossRef]
- USDA. Soil Survey Field and Laboratory Methods Manual, Soil Survey Investigations Report No. 51; Version 2; USDA: Washington, DC, USA, 2014. [Google Scholar]
- Reynolds, W.D.; Elrick, D.E. Ponded Infiltration From a Single Ring: I. Analysis of Steady Flow. Soil. Sci. Soc. Am. J. 1990, 54, 1233–1241. [Google Scholar] [CrossRef]
- Youngs, E.G.; Leeds-Harrison, P.B.; Elrick, D.E. The Hydraulic Conductivity of Low Permeability Wet Soils Used as Landfill Lining and Capping Material: Analysis of Pressure Infiltrometer Measurements. Soil. Technol. 1995, 8, 153–160. [Google Scholar] [CrossRef]
- Elrick, D.E.; Reynolds, W.D.; Tan, K.A. Hydraulic Conductivity Measurements in the Unsaturated Zone Using Improved Well Analyses. Groundw. Monit. Remediat. 1989, 9, 184–193. [Google Scholar] [CrossRef]
- Decagon Devices. METER Group Mini Disk Infiltrometer—User’s Manual; Decagon Devices Inc.: Pullman, WA, USA, 2021. [Google Scholar]
- Dohnal, M.; Dusek, J.; Vogel, T. Improving Hydraulic Conductivity Estimates from Minidisk Infiltrometer Measurements for Soils with Wide Pore-Size Distributions. Soil. Sci. Soc. Am. J. 2010, 74, 804–811. [Google Scholar] [CrossRef]
- Zhang, R. Infiltration Models for the Disk Infiltrometer. Soil Sci. Soc. Am. J. 1996, 61, 1597–1603. [Google Scholar] [CrossRef]
- Philip, J.R. The Theory of Infiltration: 4. Sorptivity and Algebraic Infiltration Equations. Soil. Sci. 1957, 84, 257–264. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability Distributions of Soil Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Bátková, K.; Miháliková, M.; Matula, S. Hydraulic Properties of a Cultivated Soil in Temperate Continental Climate Determined by Mini Disk Infiltrometer. Water 2020, 12, 843. [Google Scholar] [CrossRef]
- Kutilek, M.; Nielsen, D.R. Soil Hydrology; Schweizerbart Science Publishers: Stuttgart, Germany, 1992; ISBN 9783510653874. [Google Scholar]
- Fodor, N.; Sándor, R.; Orfanus, T.; Lichner, L.; Rajkai, K. Evaluation Method Dependency of Measured Saturated Hydraulic Conductivity. Geoderma 2011, 165, 60–68. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies in Soil Physics: Part 1. The Flow of Air and Water through Soils. J. Agric. Sci. 1911, 4, 11–24. [Google Scholar]
- Smith, R.E.; Parlange, J.-Y. A Parameter-Efficient Hydrologic Infiltration Model. Water Resour. Res. 1978, 14, 533–538. [Google Scholar] [CrossRef]
- Horton, R.E. Analysis of Runoff-Plat Experiments with Varying Infiltration-Capacity. Rep. Pap. 1939, 20, 693–711. [Google Scholar] [CrossRef]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks—A Publishing Format for Reproducible Computational Workflows. In Proceedings of the Positioning and Power in Academic Publishing: Players, Agents and Agendas—Proceedings of the 20th International Conference on Electronic Publishing, ELPUB 2016, Göttingen, Germany, 7–9 June 2016; pp. 87–90. [Google Scholar]
- Turner, E.R. Comparison of Infiltration Equations and Their Field Validation with Rainfall Simulation. Master Thesis, University of Maryland, College Park, MD, USA, 2006. [Google Scholar]
- Farid, H.U.; Mahmood-Khan, Z.; Ahmad, I.; Shakoor, A.; Anjum, M.N.; Iqbal, M.M.; Mubeen, M.; Asghar, M. Estimation of Infiltration Models Parameters and Their Comparison to Simulate the Onsite Soil Infiltration Characteristics. Int. J. Agric. Biol. Eng. 2019, 12, 84–91. [Google Scholar] [CrossRef]
- Lili, M.; Bralts, V.F.; Yinghua, P.; Han, L.; Tingwu, L. Methods for Measuring Soil Infiltration: State of the Art. Int. J. Agric. Biol. Eng. 2008, 1, 22–30. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Hopkins, I.; Guo, L.; Lin, H. Dynamics of Infiltration Rate and Field-Saturated Soil Hydraulic Conductivity in a Wastewater- Irrigated Cropland. Water 2019, 11, 1632. [Google Scholar] [CrossRef]
- Turner, D.P.; Sumner, M.E. The Influence of Initial Soil Moisture Content on Field Measured Infiltration Rates. Water SA 1978, 4, 1–8. [Google Scholar]
- Fatehnia, M.; Tawfiq, K.; Ye, M. Estimation of Saturated Hydraulic Conductivity from Double-Ring Infiltrometer Measurements. Eur. J. Soil. Sci. 2016, 67, 135–147. [Google Scholar] [CrossRef]
- Fan, G.; Han, Y.; Song, M. Experimental Study on the Reasonable Inbuilt-Ring Depth of Soil One-Dimensional Infiltration Experiment in Field. In Proceedings of the Computer and Computing Technologies in Agriculture V, CCTA 2011, IFIP Advances in Information and Communication Technology, Beijing, China, 29–31 October 2011; Springer: Berlin/Heidelberg, Germany, 2012; Volume 368, pp. 427–436. [Google Scholar]
- De Jonge, L.W.; Jacobsen, O.H.; Moldrup, P. Soil Water Repellency: Effects of Water Content, Temperature, and Particle Size. Soil. Sci. Soc. Am. J. 1999, 63, 437–442. [Google Scholar] [CrossRef]
- Leelamanie, D.A.L.; Karube, J. Effects of Organic Compounds, Water Content and Clay on the Water Repellency of a Model Sandy Soil. Soil. Sci. Plant Nutr. 2007, 53, 711–719. [Google Scholar] [CrossRef][Green Version]
- Akan, A.O.; Houghtalen, R.J. Urban Hydrology, Hydraulics, and Stormwater Quality: Engineering Applications and Computer Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 0471431583. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Saxton, K.E. Estimation of Soil Water Properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Rawls, W.J.; Asce, M.; Brakensiek, D.L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- USDA Soil. Survey Manual; USDA Soil: Waverly, IA, USA, 2017. [Google Scholar]
- Lu, N.; Likos, W.J. Rate of Capillary Rise in Soil. J. Geotech. Geoenviron. Eng. 2004, 130, 646–650. [Google Scholar] [CrossRef]
- Oleszczuk, R.; Truba, M. The Analysis of Some Physical Properties of Drained Peat-Moorsh Soil Layers. Ann. Wars. Univ. Life Sci.-SGGW. Land. Reclam. 2013, 45, 41–48. [Google Scholar] [CrossRef]
- Aldrees, A.; Nachabe, M. Capillary Length and Field Capacity in Draining Soil Profiles. Water Resour. Res. 2019, 55, 4499–4507. [Google Scholar] [CrossRef]
- Lehmann, P.; Bickel, S.; Wei, Z.; Or, D. Physical Constraints for Improved Soil Hydraulic Parameter Estimation by Pedotransfer Functions. Water Resour. Res. 2020, 56, e2019WR025963. [Google Scholar] [CrossRef]
- Elrick, D.E.; Reynolds, W.D. Methods for Analyzing Constant-Head Well Permeameter Data. Soil. Sci. Soc. Am. J. 1992, 56, 320–323. [Google Scholar] [CrossRef]
- Di Prima, S.; Stewart, R.D.; Castellini, M.; Bagarello, V.; Abou Najm, M.R.; Pirastru, M.; Giadrossich, F.; Iovino, M.; Angulo-Jaramillo, R.; Lassabatere, L. Estimating the Macroscopic Capillary Length from Beerkan Infiltration Experiments and Its Impact on Saturated Soil Hydraulic Conductivity Predictions. J. Hydrol. 2020, 589, 125159. [Google Scholar] [CrossRef]

| Site | Soil Texture [43] | Moisture [44] | Sun Exposure | Vegetation |
|---|---|---|---|---|
| T1 | sandy loam | moist | mostly shaded | dense grass |
| T2 | sandy clay loam | slightly moist | sunlit | dense grass |
| T3 | sandy clay loam | moist | mostly shaded | dense grass |
| T4 | sandy loam | dry | sunlit | sparsely grown grass |
| Infiltration Model | Infiltration Rate | |
|---|---|---|
| Green-Ampt | (7) | |
| Smith-Parlange | (8) | |
| Horton | (9) | |
| Philip | (10) | |
| Infiltration Model | Cumulative Infiltration | |
| Green-Ampt | (11) | |
| Smith-Parlange | (12) | |
| Horton | (13) | |
| Philip | (14) | |
| Abbreviation | Parameter | Unit |
| potential infiltration rate (capacity) after time of ponding () | (cm/s) | |
| cumulative infiltration | (cm) | |
| time | (s) | |
| saturated water content | (-) | |
| initial water content | (-) | |
| average suction across the wetting front | (cm) | |
| saturated hydraulic conductivity | (cm/s) | |
| initial hydraulic conductivity | (cm/s) | |
| capillary length scale | (cm) | |
| dimensionless Smith-Parlange coefficient (usually 0.8–0.85) | (-) | |
| sorptivity | () | |
| soil dependent dimensionless Philip coefficient | (-) | |
| initial infiltration capacity | (cm/s) | |
| final constant infiltration rate | (cm/s) | |
| Horton dimensionless coefficient that depends on the initial water content and the application rate | (-) |
| Site | No. | Loc. | Soil Type | KsDRI (Equation (1)) [10−3 cm/s] | KsDRI* [10−3 cm/s] | K(h)MDI (Equation (3)) [10−3 cm/s] | KsMDI (Equation (6)) [10−3 cm/s] | K(h)MDI /KsDRI* | KsMDI/ KsDRI* | CV of K(h)MDI [%] Loc./Site | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | D1.1 | SL | 2.99 * | 0.98 | |||||||
| D1.2 | 0.98 | ||||||||||
| M1.1 | T1-A | SL | 0.19 (0.05) | 1.08 | 0.19 (0.05) | 1.10 | 35.9 | 56.2 | |||
| M1.3 | 0.22 (0.05) | 1.22 | 0.22 (0.05) | 1.24 | |||||||
| M1.4 | 0.37 (0.09) | 2.15 | 0.38 (0.09) | 2.18 | |||||||
| M1.2 | T1-B | SL | 0.61 (0.15) | 3.37 | 0.62 (0.15) | 3.42 | 28.1 | ||||
| M1.5 | 0.88 (0.21) | 5.18 | 0.90 (0.21) | 5.26 | |||||||
| M1.6 | 0.52 (0.12) | 3.06 | 0.53 (0.12) | 3.11 | |||||||
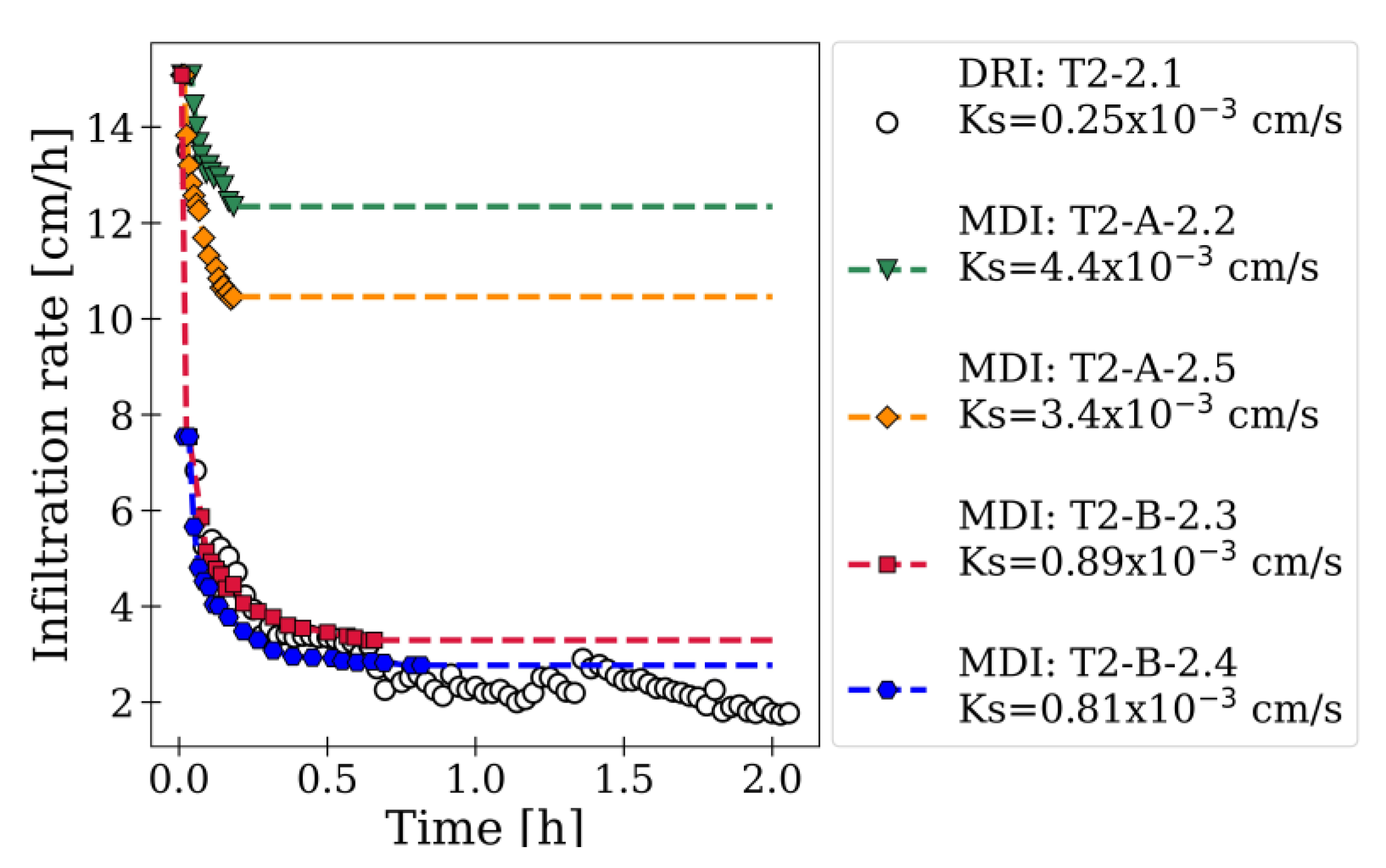
| T2 | D2.1 | SCL | 0.25 | 0.25 | |||||||
| M2.1 | T2-A | CL | 0.39 (0.16) | 3.88 | 1.56 (0.64) | 15.35 | 13.0 | 60.1 | |||
| M2.2 | 0.44 (0.18) | 4.42 | 1.76 (0.72) | 17.48 | |||||||
| M2.5 | 0.34 (0.14) | 3.40 | 1.36 (0.56) | 13.45 | |||||||
| M2.3 | T2-B | SCL | 0.13 (0.04) | 0.89 | 0.52 (0.16) | 3.51 | 12.5 | ||||
| M2.4 | 0.13 (0.03) | 0.81 | 0.52 (0.12) | 3.20 | |||||||
| M2.6 | 0.10 (0.03) | 0.65 | 0.40 (0.12) | 2.55 | |||||||
| T3 | D3.1 | SCL | 2.39 * | 0.97 | |||||||
| D3.2 | 0.83 | ||||||||||
| D3.3 | 1.10 | ||||||||||
| M3.1 | T3-A | SCL | 0.17 (0.04) | 1.06 | 0.18 (0.04) | 1.10 | 18.9 | 41.7 | |||
| M3.2 | 0.23 (0.03) | 0.70 | 0.24 (0.03) | 0.73 | |||||||
| M3.4 | 0.17 (0.04) | 1.09 | 0.18 (0.04) | 1.13 | |||||||
| M3.3 | T3-B | SCL | 0.44 (0.05) | 1.34 | 0.45 (0.05) | 1.39 | 34.7 | ||||
| M3.5 | 0.21 (0.06) | 1.35 | 0.22 (0.06) | 1.40 | |||||||
| M3.6 | 0.34 (0.09) | 2.18 | 0.35 (0.09) | 2.26 | |||||||
| T4 | D4.1 | SL | 0.18 | 0.30 | |||||||
| D4.2 | 0.41 | ||||||||||
| M4.1 | T4-A | SL | 0.79 (0.19) | 4.56 | 2.63 (0.63) | 15.26 | 27.7 | 42.6 | |||
| M4.2 | 1.18 (0.28) | 6.95 | 3.93 (0.93) | 23.26 | |||||||
| M4.5 | 0.72 (0.17) | 4.46 | 2.40 (0.57) | 14.93 | |||||||
| M4.3 | T4-B | SL | 0.45 (0.11) | 2.65 | 1.50 (0.37) | 8.87 | 18.2 | ||||
| M4.4 | 0.55 (0.13) | 3.28 | 1.83 (0.43) | 10.98 | |||||||
| M4.6 | 0.38 (0.09) | 2.25 | 1.27 (0.30) | 7.53 | |||||||
| Parameter | Green-Ampt | Smith-Parlange | Philip |
|---|---|---|---|
| 0.42 (0.39–0.44) | 0.56 (0.53–0.58) | 0.33 (0.14–0.42) | |
| 0.27 (0.27–0.45) | 0.29 (0.28–0.41) | / | |
| 8.5 (4.5–9.5) | / | / | |
| / | 5.0 (5.0–7.0) | / | |
| / | 0.022 (0.008–0.025) | / | |
| / | / | 0.69 (0.58–0.86) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svetina, J.; Prestor, J.; Šraj, M. Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia. Water 2023, 15, 3635. https://doi.org/10.3390/w15203635
Svetina J, Prestor J, Šraj M. Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia. Water. 2023; 15(20):3635. https://doi.org/10.3390/w15203635
Chicago/Turabian StyleSvetina, Janja, Joerg Prestor, and Mojca Šraj. 2023. "Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia" Water 15, no. 20: 3635. https://doi.org/10.3390/w15203635
APA StyleSvetina, J., Prestor, J., & Šraj, M. (2023). Infiltration Measurements during Dry Conditions in an Urban Park in Ljubljana, Slovenia. Water, 15(20), 3635. https://doi.org/10.3390/w15203635








