Empirical Formula to Calculate Ionic Strength of Limnetic and Oligohaline Water on the Basis of Electric Conductivity: Implications for Limnological Monitoring
Abstract
1. Introduction
2. Materials and Methods
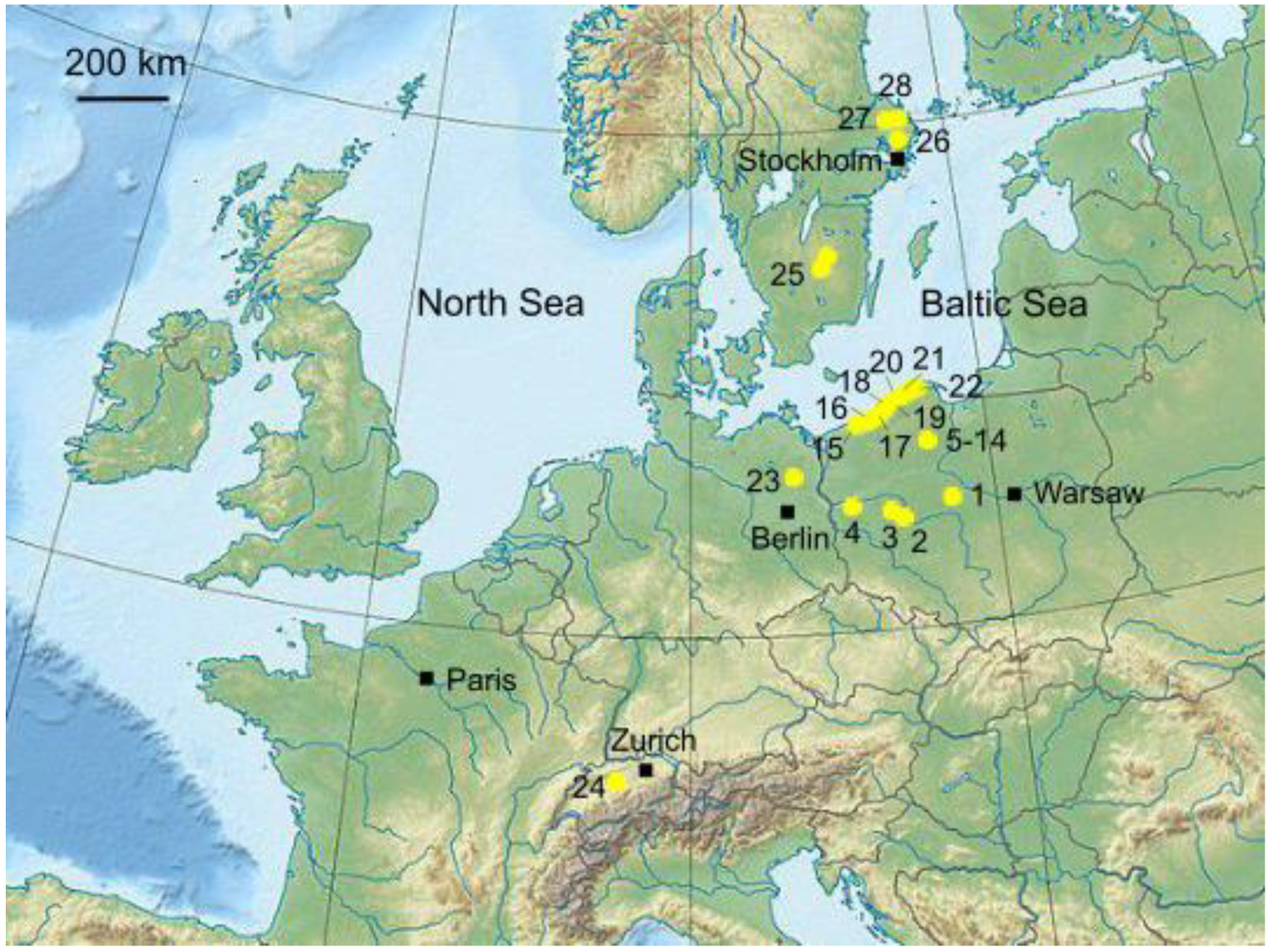
2.1. Data Collection
2.2. Water Analyses
2.3. Chemical Calculations
2.4. Model Development
2.5. Model Validation
3. Results and Discussion
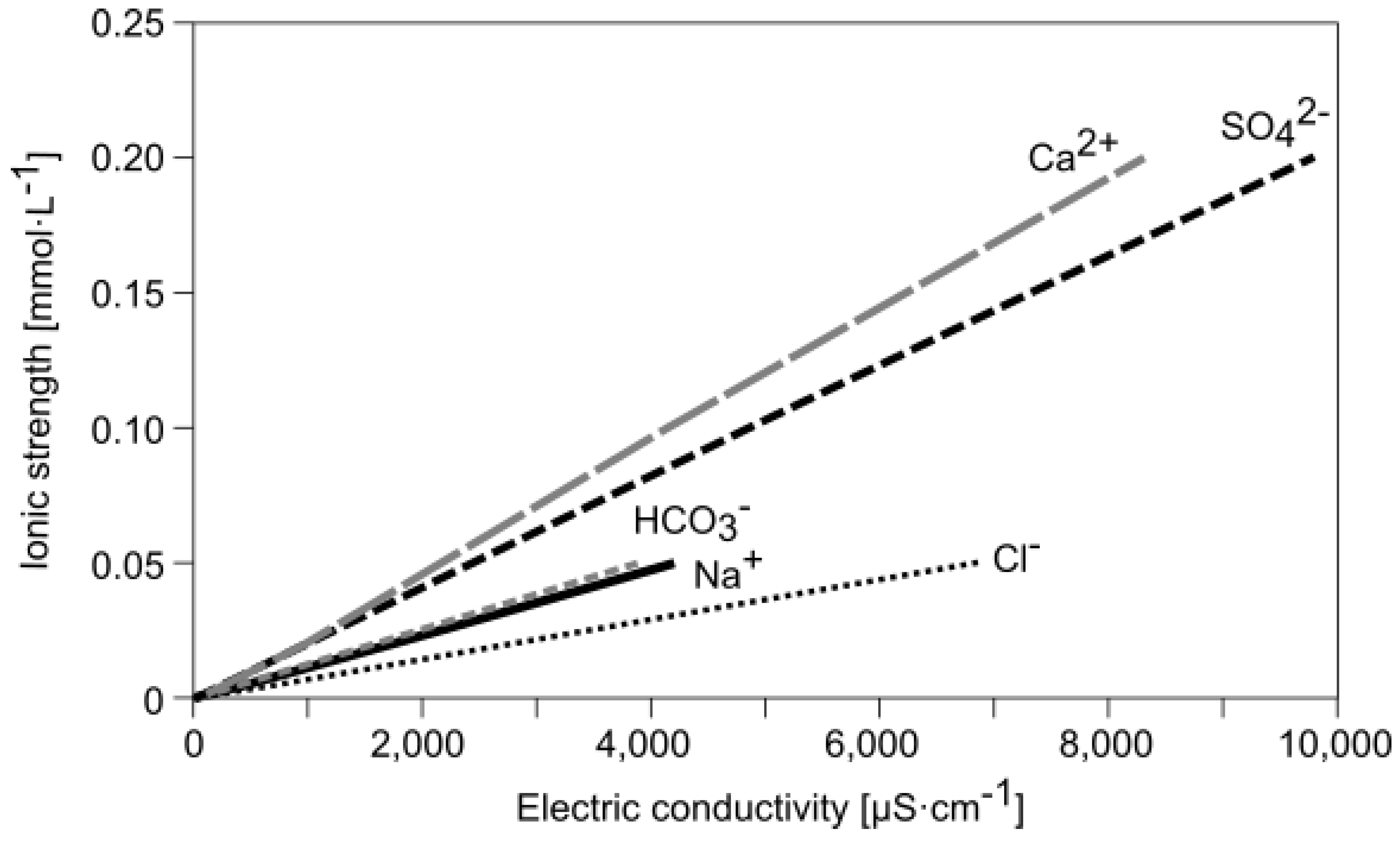
3.1. Data Characterization
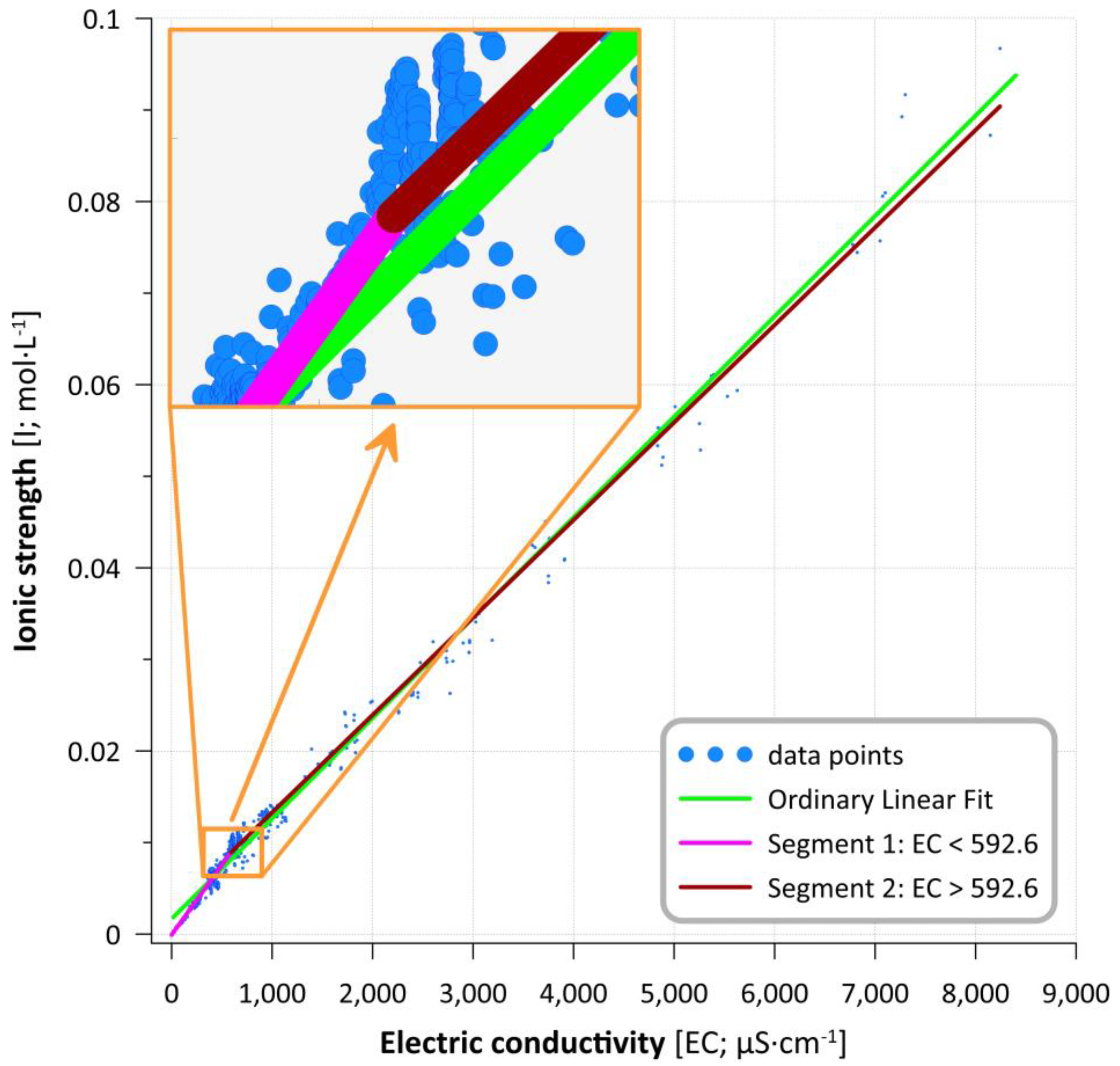
3.2. Modeling Results
3.3. Model Validation
3.4. Potential Implications of the Model
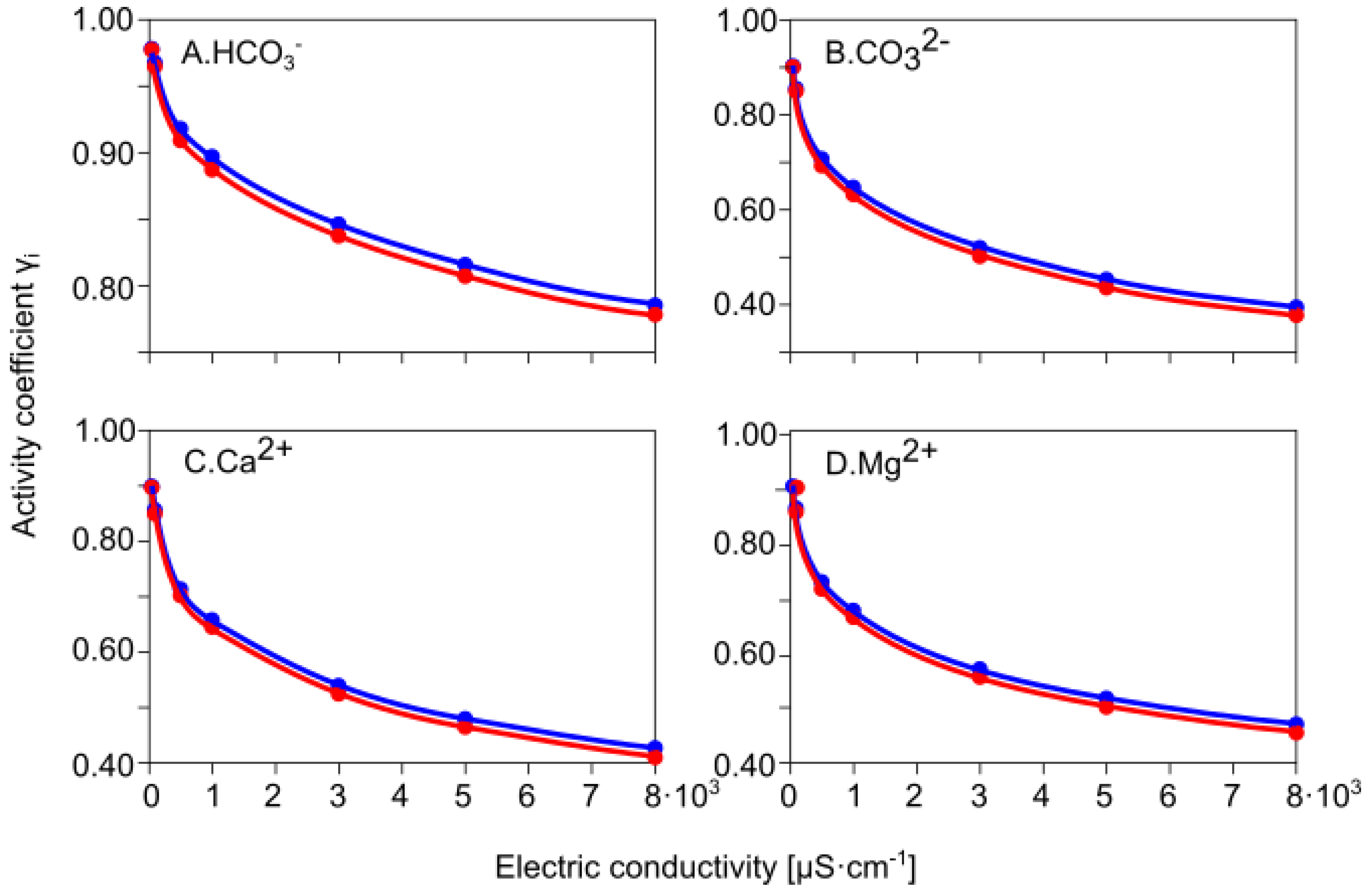
3.4.1. Calculating γ Activity Coefficients for Major Ions
3.4.2. Calculating Carbonate Saturation of Lake Water
3.4.3. Screening of Spatial Distribution of pCO2 in Lakes
3.4.4. Temporal Changes in pCO2 in Lakes
3.4.5. Spatial CO2 Distribution in Lakes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Woolway, R.I.; Benjamin, M.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Bartosiewcz, M.; Przytulska, A.; Lapierre, J.F.; Laurion, I.; Lehmann, M.F.; Maranger, R. Hot tops, cold bottoms: Synergistic climate warming and shielding effects increase carbon burial in lakes. Limnol. Oceanogr. Lett. 2019, 4, 132–144. [Google Scholar] [CrossRef]
- Cheng, J.; Xu, L.; Jiang, M.; Jiang, J.; Xu, Y. Warming Increases Nitrous Oxide Emission from the Littoral Zone of Lake Poyang, China. Sustainability 2020, 12, 5674. [Google Scholar] [CrossRef]
- Guo, M.; Zhuang, Q.; Tan, Z.; Shurpali, N.; Juutinen, S.; Kortelainen, P.; Martikainen, P.J. Rising methane emissions from boreal lakes due to increasing ice-free days. Environ. Res. Lett. 2020, 15, 064008. [Google Scholar] [CrossRef]
- Hofmann, H. Spatiotemporal distribution patterns of dissolved methane in lakes: How accurate are the current estimations of the diffusive flux path? Geophys. Res. Lett. 2013, 40, 2779–2784. [Google Scholar] [CrossRef]
- del Sontro, S.; Beaulieu, J.J.; Downing, J.A. Greenhouse gas emissions from lakes and impoundments: Upscaling in the face of global change. Limnol. Oceanogr. 2018, 3, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, R.J. Mechanisms controlling world water chemistry. Science 1970, 170, 1088–1090. [Google Scholar] [CrossRef]
- Wu, T.; Zhu, G.; Zhu, M.; Xu, H.; Zhang, Y.; Qin, B. Use of conductivity to indicate long-term changes in pollution processes in Lake Taihu, a large shallow lake. Environ. Sci. Poll. Res. 2020, 27, 21376–21385. [Google Scholar] [CrossRef]
- Groleau, A.; Sarazin, G.; Vinçon-Leite, B.; Tassin, B.; Quiblier-Llobéras, C. Tracing calcite precipitation with specific conductance in a hard water Alpine lake (Lake Bourget). Water Res. 2000, 34, 4151–4160. [Google Scholar] [CrossRef]
- Escoffier, N.; Perolo, P.; Many, G.; Tofield Pasche, N.; Perga, M.-E. Fine-scale dynamics of calcite precipitation in a large hardwater lake. Sci. Total Environ. 2023, 864, 160699. [Google Scholar] [CrossRef]
- Kester, D.R.; Pytkowicz, R.M. Magnesium sulfate association at 25 °C in synthetic seawater. Limnol. Oceanogr. 1968, 13, 670–674. [Google Scholar] [CrossRef]
- Stumm, W.; Morgan, J.J. Aquatic Chemistry, Chemical Equilibria and Rates in Natural Waters, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1981; 780p. [Google Scholar]
- Griffin, R.A.; Jurniak, J.J. Estimation of activity coefficients from the electrical conductivity of natural aquatic system and soil extracts. Soil Sci. 1973, 116, 26–30. [Google Scholar] [CrossRef]
- Polemio, M.; Bufo, S.; Paoletti, S. Evaluation of ionic strength and salinity of groundwaters: Effect of the ionic composition. Geochim. Cosmochim. Acta 1980, 44, 809–814. [Google Scholar] [CrossRef]
- Simón, M.; García, I. Physico-chemical properties of the soil-saturation extracts: Estimation from electrical conductivity. Geoderma 1999, 90, 99–109. [Google Scholar] [CrossRef]
- Tchobanoglous, G.; Burton, F.L.; Stensel, H.D. Wastewater Engineering Treatment and Reuse, 4th ed.; McGraw-Hill Education: Boston, MA, USA, 2003; 920p. [Google Scholar]
- McCleskey, R.B.; Nordstrom, D.K.; Ryan, J.N.; Ball, J.W. A new method of calculating electrical conductivity with applications to natural waters. Geochim. Cosmochim. Acta 2012, 77, 369–382. [Google Scholar] [CrossRef]
- Ponnamperuna, P.N.; Tianco, E.M.; Loy, T.A. Ionic strength of the solutions of flooded soils and other natural aqueous solutions from specific conductance. Soil Sci. 1966, 102, 408–413. [Google Scholar] [CrossRef]
- Lind, C.J. Specific conductance as a means of estimating ionic strength. U.S. Geol. Survey Prof. Papers 1970, 700-D, D272–D280. [Google Scholar]
- Anonymous, J. Symposium on the Classification of Brackish Waters. Venice, 8–14 April 1958. The Venice System for the classification of marine waters according to salinity. Limnol. Oceanogr. 1958, 3, 346–347. [Google Scholar] [CrossRef]
- Pawlowicz, R. Calculating the conductivity of natural waters. Limnol. Oceanogr. Methods 2008, 6, 489–501. [Google Scholar] [CrossRef]
- McNeil, V.H.; Cox, M.E. Relationship between conductivity and analysed composition in a large set of natural surface-water samples, Queensland, Australia. Environ. Geol. 2000, 39, 1325–1333. [Google Scholar] [CrossRef]
- Marandi, A.; Polikarpus, M.; Jõeleht, A. A new approach for describing the relationship between electrical conductivity and major anion concentration in natural waters. Appl. Geochem. 2013, 38, 103–109. [Google Scholar] [CrossRef]
- ISO9963-1:2001; Jakość Wody—Oznaczanie Zasadowości—Część 1: Oznaczanie Zasadowości Ogólnej i Zasadowości Wobec Fenoloftaleiny. 23 April 2001; 10p. Available online: https://sklep.pkn.pl/pn-en-iso-9963-1-2001p.html (accessed on 1 October 2023).
- Bentley, E.M.; Lee, G.F. Determination of calcium in natural water by atomic absorption spectrophotometry. Environ. Sci. Technol. 1967, 1, 721–724. [Google Scholar] [CrossRef] [PubMed]
- Borges, A.V.; Delille, B.; Schiettecatte, L.-S.; Gazeau, F.; Abril, G.; Frankignoulle, M. Gas transfer velocities of CO2 in three European estuaries (Randers Fjord, Scheldt, and Thames). Limnol. Oceanogr. 2004, 49, 1630–1641. [Google Scholar] [CrossRef]
- Cole, J.J.; Prairie, Y.T. Dissolved CO2. In Encyclopedia of Inland Waters; Likens, G.E., Ed.; Elsevier: Oxford, UK, 2009; Volume 2, pp. 30–34. [Google Scholar]
- Balmer, M.; Downing, J. Carbon dioxide concentrations in eutrophic lakes: Undersaturation implies atmospheric uptake. Inland Waters 2011, 1, 125–132. [Google Scholar] [CrossRef]
- Henley, S.F.; Annett, A.L.; Ganeshram, R.S.; Carson, D.S.; Weston, K.; Crosta, X.; Tait, A.; Dougans, J.; Fallick, A.E.; Clarke, A. Factors influencing the stable carbon isotopic composition of suspended and sinking organic matter in the coastal Antarctic sea ice environment. Biogeosciences 2012, 9, 1137–1157. [Google Scholar] [CrossRef]
- Raymond, P.A.; Hartmann, J.; Lauerwald, R.; Sobek, S.; McDonald, C.; Hoover, M.; Butman, D.; Striegl, R.; Mayorga, E.; Humborg Ch Kortelainen, P.; et al. Global carbon dioxide emissions from inland waters. Nature 2013, 503, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Hastie, A.; Lauerwald, R.; Weyhenmeyer, G.; Sobek, S.; Verpoorter, C.; Regnier, P. CO2 evasion from boreal lakes: Revised estimate, drivers of spatial variability, and future projections. Glob. Change Biol. 2018, 24, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Kelts, K.; Hsü, K.J. Freshwater carbonate sedimentation. In Lakes Chemistry Geology Physics; Lerman, A., Ed.; Springer: New York, NY, USA, 1978; pp. 295–323. [Google Scholar]
- Abril, G.; Bouillon, S.; Darchambeau, F.; Teodoru, C.R.; Marwick, T.R.; Tamooh, F.; Ochieng Omengo, F.; Geeraert, N.; Deirmendjian, L.; Polsenaere, P.; et al. Large overestimation of pCO2 calculated from pH and alkalinity in acidic, organic-rich freshwaters. Biogeosciences 2015, 12, 67–78. [Google Scholar] [CrossRef]
- Berner, R.A. Principles of Chemical Sedimentology; McGraw-Hill: New York, NY, USA, 1971; 240p. [Google Scholar]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Muggeo, V.M.R. Estimating regression models with unknown break-points. Stat. Med. 2003, 22, 3055–3071. [Google Scholar] [CrossRef]
- Muggeo, V.M.R. Segmented: An R package to fit regression models with broken-line relationships. R News 2008, 8, 20–25. [Google Scholar]
- Muggeo, V.M.R. Package ‘Segmented’. 2022. Available online: https://pypi.org/project/segmented/ (accessed on 1 October 2023).
- Muggeo, V.M.R. Selecting Number of Breakpoints in Segmented Regression: Implementation in the R Package Segmented. 2020. Available online: https://www.researchgate.net/publication/343737604_Selecting_number_of_breakpoints_in_segmented_regression_implementation_in_the_R_package_segmented (accessed on 1 October 2023).
- Vrieze, S.I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 2012, 17, 228–243. [Google Scholar] [CrossRef] [PubMed]
- Aho, K.; Derryberry, D.W.; Peterson, T. Model selection for ecologists: The worldviews of AIC and BIC. Ecology 2014, 95, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y. Can the strengths of AIC and BIC be shared? A conflict between model identification and regression estimation. Biometrika 2005, 92, 937–950. Available online: https://www.jstor.org/stable/20441246 (accessed on 1 October 2023). [CrossRef]
- Davies, R.B. Hypothesis testing when a nuisance parameter is present only under the alternatives. Biometrika 1987, 74, 33–43. [Google Scholar] [CrossRef]
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K. Cluster: Cluster Analysis Basics and Extensions, R package version 2.1.4. 2022.
- Apolinarska, K.; Pleskot, K.; Pełechata, A.; Migdałek, M.; Siepak, M.; Pełechaty, M. The recent deposition of laminated sediments in highly eutrophic Lake Kierskie, western Poland: 1 year pilot study of limnological monitoring and sediment traps. J. Paleolimnol. 2020, 63, 283–304. [Google Scholar] [CrossRef]
- Kemp, A. Organic carbon and nitrogen in the surface sediments of Lakes Ontario, Erie and Huron. J. Sediment. Res. 1971, 41, 537–548. [Google Scholar] [CrossRef]
- Cleveland, W.S. Robust Locally Weighted Regression and Smoothing Scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Woszczyk, M.; Schubert, C.J. Greenhouse gas emissions from Baltic coastal lakes. Sci. Total Environ. 2021, 755, 143500. [Google Scholar] [CrossRef]
- Stawecki, K.; Zdanowski, B.; Pyka, J.P. Long-term changes in post-cooling water loads from power plants and thermal and oxygen conditions in stratified lakes. Arch. Pol. Fish. 2013, 21, 331–342. [Google Scholar]
- Tylmann, W.; Szpakowska, K.; Ohlendorf, C.; Woszczyk, M.; Zolitschka, B. Conditions for deposition of annually laminated sediments in small meromictic lakes: A case study of Lake Suminko (northern Poland). J. Paleolimnol. 2012, 47, 55–70. [Google Scholar] [CrossRef]
- Schilder, J.; Bastviken, D.; van Hardenbroek, M.; Kankaala, P.; Rinta, P.; Stötter, P.; Heiri, O. Spatial heterogeneity and lake morphology affect diffusive greenhouse gas emission estimates of lakes. Geophys. Res. Lett. 2013, 40, 5752–5756. [Google Scholar] [CrossRef]
- Loken, L.C.; Crawford, J.C.; Schramm, P.J.; Stadler, P.; Desai, A.R.; Stanley, E.H. Large spatial and temporal variability of carbon ioxide and methane in a eutrophic lake. J. Geophys. Res. Biogeosci. 2019, 124, 2248–2266. [Google Scholar] [CrossRef]
- Dragon, K.; Górski, J. Identification of groundwater chemistry origins in a regional aquifer system (Wielkopolska region, Poland). Environ. Earth Sci. 2015, 73, 153–2167. [Google Scholar] [CrossRef]
- Kasperczyk, L.; Modelska, M.; Staśko, S. Pollution indicators in groundwater of two agricultural catchments in Lower Silesia (Poland). Geosci. Rec. 2016, 3, 18–29. [Google Scholar] [CrossRef][Green Version]
- Michalska, G. Zróżnicowanie właściwości fizykochemicznych wód podziemnych w zlewni Chwalimskiego Potoku (górna Parsęta, Pomorze Zachodnie. In Funkcjonowanie i Monitoring Geoekosystemów z Uwzględnieniem Zanieczyszczeń Powietrza; Jóźwiak, M., Kowalkowski, A., Eds.; Biblioteka Monitoringu Środowiska: Kielce, Poland, 2001; pp. 305–320. [Google Scholar]
- Motyka, J.; Gradziński, M.; Różkowski, K.; Górny, A. Chemistry of cave water in Smocza Jama, city of Kraków, Poland. Ann. Soc. Geol. Pol. 2005, 75, 189–198. [Google Scholar]
- Sojka, M.; Choiński, A.; Ptak, M.; Siepak, M. The Variability of lake water chemistry in the Bory Tucholskie National Park (Northern Poland). Water 2020, 12, 394. [Google Scholar] [CrossRef]
- Fölster, J.; Johnson, R.K.; Futter, M.N.; Wilander, A. The Swedish monitoring of surface waters: 50 Years of adaptive monitoring. Ambio 2014, 43, 3–18. [Google Scholar] [CrossRef] [PubMed]
- Gíslason, S.R.; Snorrason, Á.; Ingvarsson, G.B.; Sigfússon, B.; Eiríksdóttir, E.S.; Elefsen, S.Ó.; Hardardóttir, J.; Þorláksdóttir, S.B.; Torssander, P. Chemical Composition, Discharge and Suspended Matter of Rivers in North-Western Iceland; The Database of the Science Institute, University of Iceland: Reykjavik, Iceland; Hydrological Service of the National Energy Authority: Reykjavik, Iceland, 2006; RH-07-2006; 51p. [Google Scholar]
- Maciejewska, E.; Chmiel, S.; Furtak, T. Zróżnicowanie składu chemicznego wód rzecznych i podziemnych w Roztoczańskim Parku Narodowym. In Wody na Obszarach Chronionych; Partyka, J., Pociask-Karteczka, J., Eds.; Instytut Geografii i Gospodarki Przestrzennej UJ, Ojcowski Park Narodowy, Komisja Hydrologiczna PTG: Kraków, Poland, 2008; pp. 221–227. [Google Scholar]
- Małek, S.; Gawęda, T. Charakterystyka chemiczna wód powierzchniowych zlewni Potok Dupniański w Beskidzie Śląskim. Sylwan 2005, 2, 29–36. [Google Scholar]
- Żelazny, M. Czasowo-Przestrzenna Zmienność cech Fizykochemicznych wód Tatrzańskiego Parku Narodowego; Instytut Geografii i Gospodarki Przestrzennej Uniwersytetu Jagiellońskiego: Kraków, Poland, 2012. [Google Scholar]
- Jenks, G.F. The Data Model Concept in Statistical Mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Jasiewicz, J.; Zawiska, I.; Rzodkiewicz, M.; Woszczyk, M. Interpretative Machine Learning as a Key in Recognizing the Variability of Lakes Trophy Patterns. Quaest. Geogr. 2022, 41, 127–146. [Google Scholar] [CrossRef]
- Woszczyk, M.; Spychalski, W.; Lutyńska, M.; Cieśliński, R. Temporal trend in the intensity of subsurface saltwater ingressions to coastal Lake Sarbsko (northern Poland) during the last few decades. IOP Conf. Ser. Earth Environ. Sci. 2010, 9, 012013. [Google Scholar] [CrossRef]
- Woszczyk, M.; Bechtel, A.; Cieśliński, R. Interactions between microbial degradation of sedimentary organic matter and lake hydrodynamics in shallow water bodies: Insights from Lake Sarbsko (northern Poland). J. Limnol. 2011, 70, 293–304. [Google Scholar] [CrossRef]
- Schubert, C.J.; Lucas, F.S.; Durisch-Kaiser, E.; Stierli, R.; Diem, T.; Scheidegger, O.; Vazquez, F.; Müller, B. Oxidation and emission of methane in a monomictic lake (Rotsee, Switzerland). Aquat. Sci. 2010, 72, 455–466. [Google Scholar] [CrossRef]

| Lake Mineralisation | EC | ti | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| μS·cm−1 | Na+ | Ca2+ | Mg2+ | K+ | HCO3− | SO42− | Cl− | NO3− | Dival. Ions | Monoval. Ions | |
| Weak | <200 | 0.13 | 0.25 | 0.10 | 0.03 | 0.14 | 0.17 | 0.18 | 0.01 | 0.48 | 0.52 |
| Moderate | 200–750 | 0.07 | 0.32 | 0.09 | 0.01 | 0.27 | 0.12 | 0.11 | 0.00 | 0.46 | 0.54 |
| High | 750–2250 | 0.17 | 0.16 | 0.09 | 0.02 | 0.12 | 0.10 | 0.34 | 0.00 | 0.65 | 0.35 |
| Very high | >2250 | 0.27 | 0.04 | 0.07 | 0.01 | 0.03 | 0.05 | 0.53 | 0.00 | 0.84 | 0.16 |
| Conductivity [μS·cm−1] | This Study | Ponnamperuna [18] # | Griffin and Jurniak [13] & | Tchobanoglous et al. [16] * |
|---|---|---|---|---|
| <250 | 1.1 | 13.1 | −8.1 | 14.8 |
| 250–500 | 2.1 | 8.9 | −11.5 | 10.7 |
| 500–1000 | −3.5 | 11.0 | −9.8 | 12.7 |
| 1000–2500 | −12.6 | 11.3 | −9.6 | 13.0 |
| 2500–5000 | 6.6 | 51.1 | 22.7 | 53.4 |
| 5000–7500 | −6.9 | 34.5 | 9.3 | 36.6 |
| >7500 | −17.8 | 20.4 | −2.2 | 22.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woszczyk, M.; Stach, A.; Nowosad, J.; Zawiska, I.; Bigus, K.; Rzodkiewicz, M. Empirical Formula to Calculate Ionic Strength of Limnetic and Oligohaline Water on the Basis of Electric Conductivity: Implications for Limnological Monitoring. Water 2023, 15, 3632. https://doi.org/10.3390/w15203632
Woszczyk M, Stach A, Nowosad J, Zawiska I, Bigus K, Rzodkiewicz M. Empirical Formula to Calculate Ionic Strength of Limnetic and Oligohaline Water on the Basis of Electric Conductivity: Implications for Limnological Monitoring. Water. 2023; 15(20):3632. https://doi.org/10.3390/w15203632
Chicago/Turabian StyleWoszczyk, Michał, Alfred Stach, Jakub Nowosad, Izabela Zawiska, Katarzyna Bigus, and Monika Rzodkiewicz. 2023. "Empirical Formula to Calculate Ionic Strength of Limnetic and Oligohaline Water on the Basis of Electric Conductivity: Implications for Limnological Monitoring" Water 15, no. 20: 3632. https://doi.org/10.3390/w15203632
APA StyleWoszczyk, M., Stach, A., Nowosad, J., Zawiska, I., Bigus, K., & Rzodkiewicz, M. (2023). Empirical Formula to Calculate Ionic Strength of Limnetic and Oligohaline Water on the Basis of Electric Conductivity: Implications for Limnological Monitoring. Water, 15(20), 3632. https://doi.org/10.3390/w15203632








