Study on Characteristics of Water Level Variations and Water Balance of the Largest Lake in the Qinghai-Tibet Plateau
Abstract
:1. Introduction
2. Study Area, Data and Methods
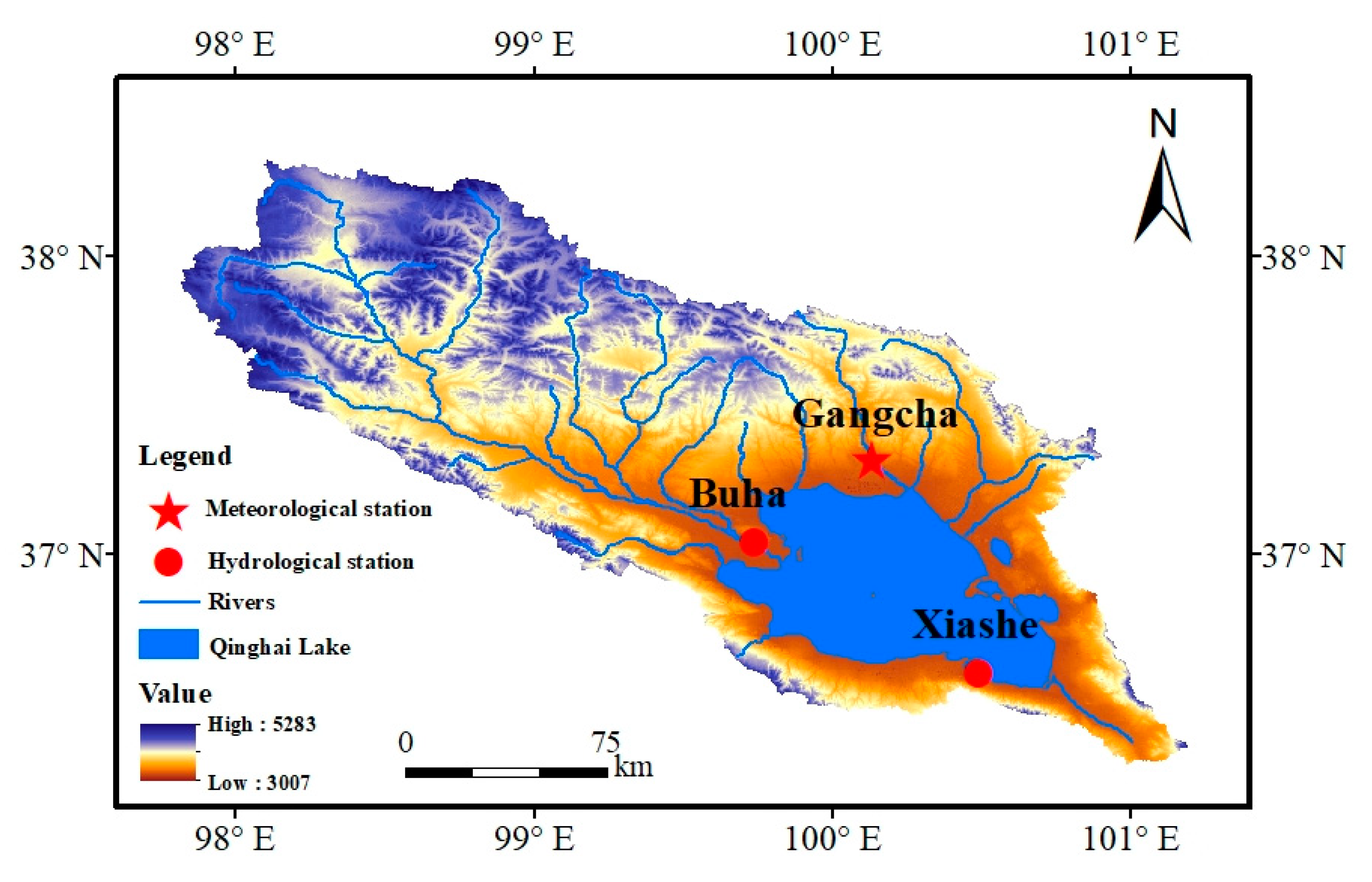
2.1. Study Area
2.2. Data
2.2.1. Gangcha Meteorological Station Data
2.2.2. CMFD Meteorological Data
2.2.3. Hydrographic Station Data
2.3. Methods
2.3.1. Penman–Monteith Equation
2.3.2. Water Balance Equation
2.3.3. Mann-Kendall Test Method
2.3.4. Sen’s Slope Analysis
2.3.5. Ridge Regression
2.3.6. Correlation Analysis
3. Results and Discussions
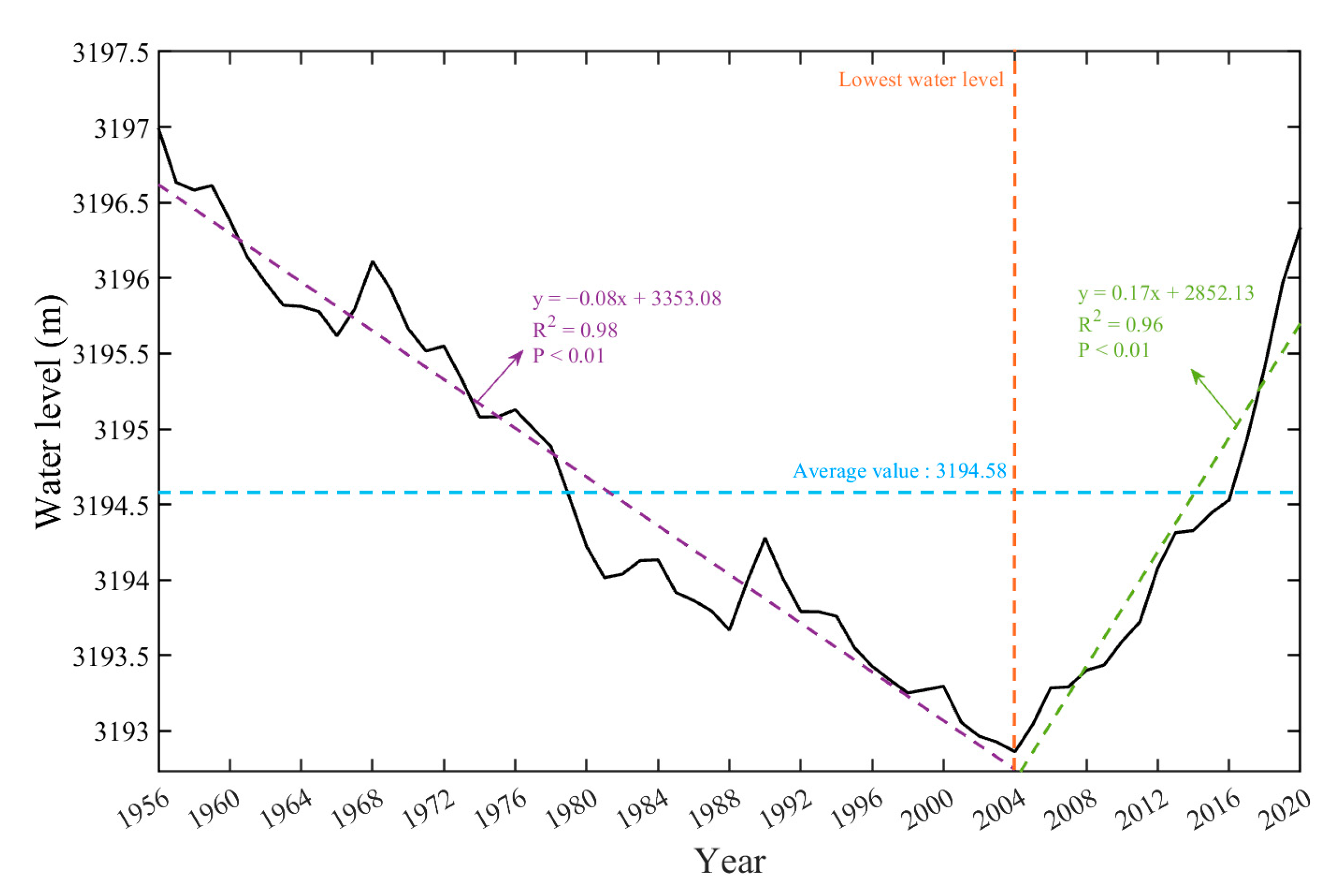
3.1. Interannual Variation Characteristics of Water Level in Qinghai Lake
3.2. Variations in Annual Water Level Difference in Qinghai Lake
3.3. Characteristics of Fixed-Month Water Level Difference at Qinghai Lake
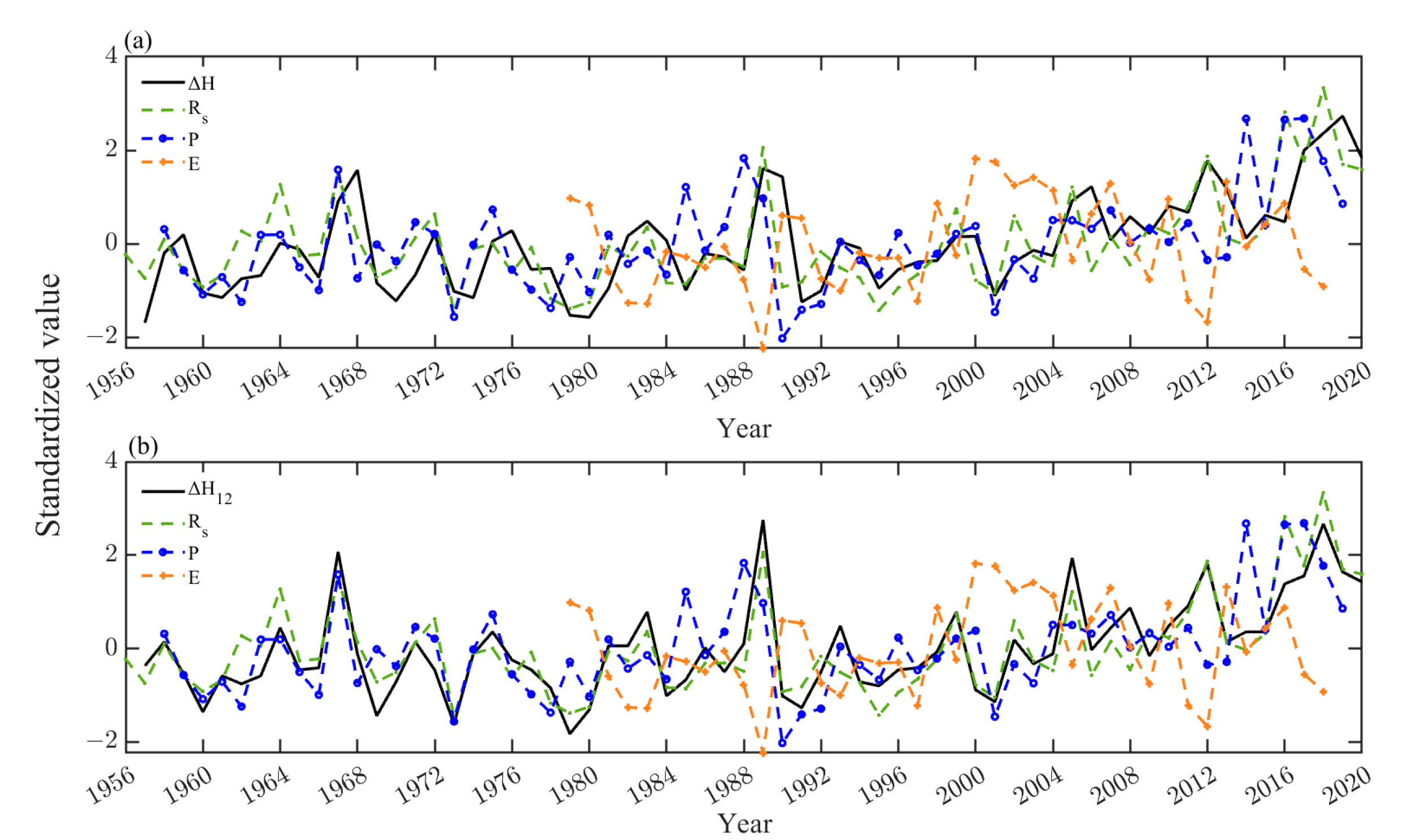
3.4. Influence of Water Balance Components on Water Level of Qinghai Lake
3.5. Contributions of Water Balance Components to the Interannual Evolution of Qinghai Lake Water Level
3.6. Contributions of Meteorological Variables to the Interannual Evolution of Qinghai Lake Water Level
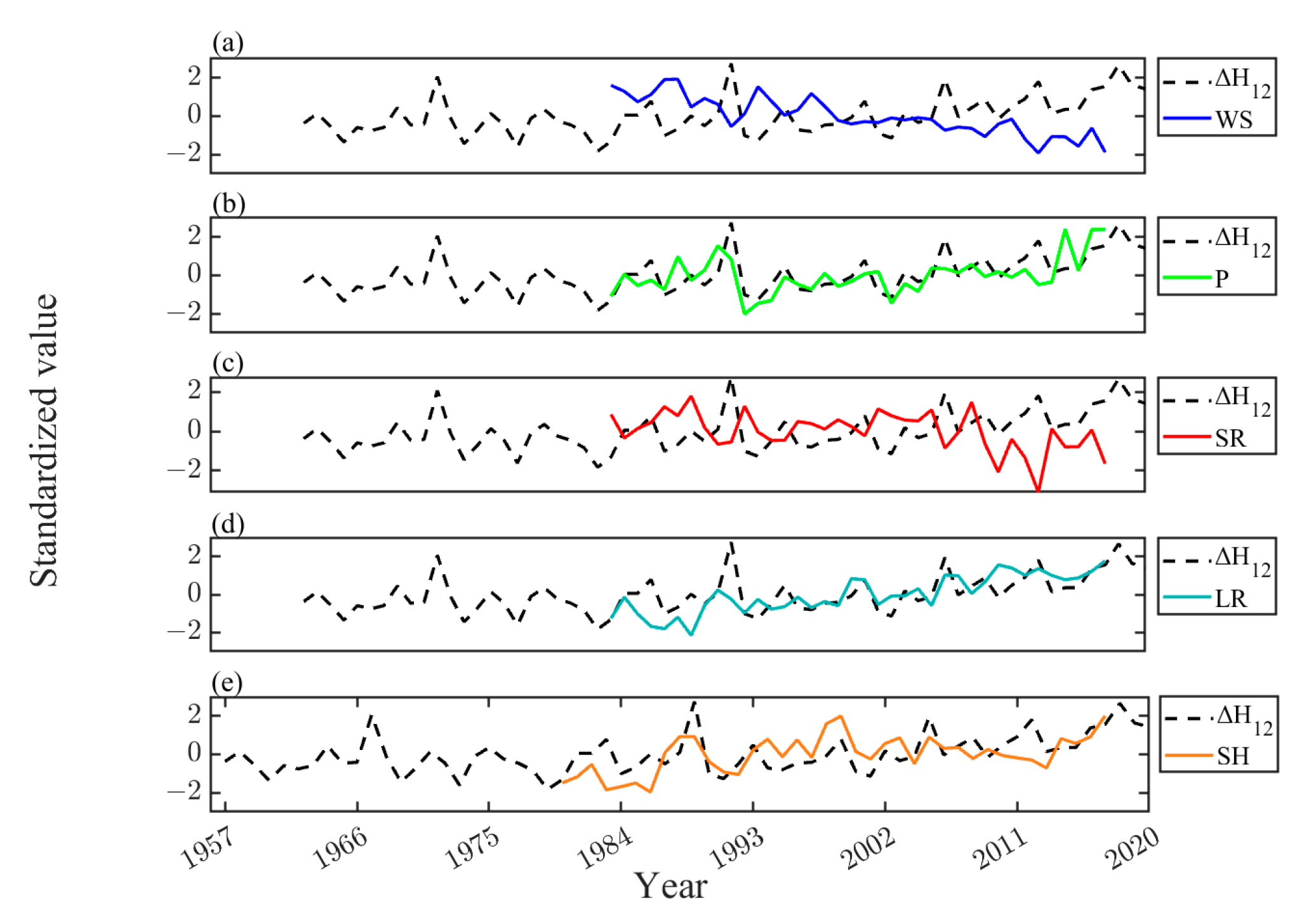
3.7. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Chang, J.; Xu, C.Y.; Zhou, Y.; Wu, Y.; Chen, X.; Jiang, S.; Duan, Z. The response of lake area and vegetation cover variations to climate change over the Qinghai-Tibetan Plateau during the past 30 years. Sci. Total Environ. 2018, 635, 443–451. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Li, Q.; Liu, X.; Wen, D. Hydrological characteristics of Qinghai Lake, 1956–2017. J. Hydrol. 2020, 41, 27–33. [Google Scholar] [CrossRef]
- Yang, K.; Ye, B.; Zhou, D.; Wu, B.; Foken, T.; Qin, J.; Zhou, Z. Response of hydrological cycle to recent climate changes in the Tibetan Plateau. Clim. Chang. 2011, 109, 517–534. [Google Scholar] [CrossRef]
- Kuang, X.; Jiao, J.J. Review on climate change on the Tibetan Plateau during the last half century. J. Geophys. Res. Atmos. 2016, 121, 3979–4007. [Google Scholar] [CrossRef]
- Duan, A.M.; Xiao, Z.X. Does the climate warming hiatus exist over the Tibetan Plateau? Sci. Rep. 2015, 5, 13711. [Google Scholar] [CrossRef] [PubMed]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Long, D.; Li, X.; Li, X.; Han, P.; Zhao, F.; Hong, Z.; Wang, Y.; Tian, F. Remote sensing retrieval of water storage changes and underlying climatic mechanisms over the Tibetan Plateau during 2000—2020. Adv. Water Sci. 2022, 33, 375–389. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased mass over the Tibetan Plateau: From lakes or glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, L.; Ouyang, Z. Ecosystem services valuation of Qinghai Lake. Ying Yong Sheng Tai Xue Bao 2015, 26, 3137–3144. [Google Scholar] [CrossRef]
- Han, Y.; Yu, D.; Chen, K.; Yang, H. Spatial distribution characteristics of temperature and precipitation trend in Qinghai Lake Basin from 2000 to 2018. Arid Land Geogr. 2022, 45, 999–1009. [Google Scholar]
- Dai, Y.; Wang, X.; Ma, G.; Hou, Y.; Li, D. Diversity characteristics of waterfowl community in Qinghai Lake National Nature Reserve. For. Ecol. Manag. 2018, 02, 74–80. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.; Liu, T.; Li, Y.; Yang, Y. Analysis of Qinghai Lake’s water level changes and water balance analysis from 1956 to 2019. J. China Hydrol. 2021, 41, 91–96. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, J.; Luo, J.; Guo, G.; Li, B. Analysis on the causes of Qinghai Lake water level changes and prediction of its future trends. Ecol. Environ. Sci. 2021, 30, 1482–1491. [Google Scholar] [CrossRef]
- Zhao, L.; Simon Wang, S.Y.; Meyer, J. Interdecadal climate variations controlling the water level of Lake Qinghai over the Tibetan Plateau. J. Hydrometeorol. 2017, 18, 3013–3025. [Google Scholar] [CrossRef]
- Li, L.; Shen, H.; Liu, C.; Jiao, R. Response of water level fluctuation to climate warming and wetting scenarios and its mechanism on Qinghai Lake. Clim. Chang. Res. 2020, 16, 600–608. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, G.; Jia, Z.; Song, X.; Wang, x. Study on the shoreline evolution of Qinghai Lake and its socioeconomic impact under the Background of global climate change. Plateau Sci. Res. 2021, 5, 1–10. [Google Scholar] [CrossRef]
- Wang, L.; Mao, X.; Song, X.; Tang, W.; Wang, W.; Yu, H.; Deng, Y.; Zhang, Z.; Zhang, Z.; Zhou, H. How rising water levels altered ecosystem provisioning services of the area around Qinghai Lake from 2000 to 2020: An InVEST-RF-GTWR combined method. Land 2022, 11, 1570. [Google Scholar] [CrossRef]
- Hao, M.; Zhu, H.; Xiong, X.; He, Y.; Ao, H.; Yu, G.; Wu, C.; Liu, G.; Luo, Z.; Liu, J.; et al. Analysis on the distribution and origin of cladophora in the nearshore water of Qinghai Lake. Acta Hydrobiol. Sin. 2020, 44, 1152–1158. [Google Scholar]
- Hou, P.; Weidman, R.P.; Liu, Q.; Li, H.; Duan, L.; Zhang, X.; Liu, F.; Gao, Y.; Xu, J.; Li, H.; et al. Recent water-level fluctuations, future trends and their eco-environmental impacts on Lake Qinghai. J. Environ. Manag. 2023, 333, 117461. [Google Scholar] [CrossRef]
- Coe, M.T.; Birkett, C.M. Calculation of river discharge and prediction of lake height from satellite radar altimetry: Example for the Lake Chad basin. Water Resour. Res. 2004, 40, W10205.1–W10205.11. [Google Scholar] [CrossRef]
- Coe, M.T.; Foley, J.A. Human and natural impacts on the water resources of the Lake Chad basin. J. Geophys. Res. Atmos. 2001, 106, 3349–3356. [Google Scholar] [CrossRef]
- Foroumandi, E.; Nourani, V.; Kantoush, S.A. Investigating the main reasons for the tragedy of large saline lakes: Drought, climate change, or anthropogenic activities? A call to action. J. Arid Environ. 2022, 196, 104652. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, M.; Xie, Z.; Li, J.; Ma, M.; Lai, P.; Wang, J. Quantifying the Contributions of Climate Change and Human Activities to Water Volume in Lake Qinghai, China. Remote Sens. 2021, 14, 99. [Google Scholar] [CrossRef]
- Wang, X.; Gao, B. Study on the change of water balance and its influence on lake level in Qinghai Lake. J. Hydroelectr. Eng. 2021, 40, 60–70. [Google Scholar] [CrossRef]
- Chang, B.; He, K.-N.; Li, R.-J.; Sheng, Z.-P.; Wang, H. Linkage of climatic factors and human activities with water level fluctuations in Qinghai Lake in the northeastern Tibetan Plateau, China. Water 2017, 9, 552. [Google Scholar] [CrossRef]
- Cui, B.L.; Li, X.Y. Stable isotopes reveal sources of precipitation in the Qinghai Lake Basin of the northeastern Tibetan Plateau. Sci. Total Environ. 2015, 527–528, 26–37. [Google Scholar] [CrossRef] [PubMed]
- Cui, B.L.; Li, X.Y. The impact of climate changes on water level of Qinghai Lake in China over the past 50 years. Hydrol. Res. 2016, 47, 532–542. [Google Scholar] [CrossRef]
- Fang, J.; Li, G.; Rubinato, M.; Ma, G.; Zhou, J.; Jia, G.; Yu, X.; Wang, H. Analysis of long-term water level variations in Qinghai Lake in China. Water 2019, 11, 2136. [Google Scholar] [CrossRef]
- Li, X.; Zhang, T.; Yang, D.; Wang, G.; He, Z.; Li, L. Research on lake water level and its response to watershed climate change in Qinghai Lake from 1961 to 2019. Front. Environ. Sci 2023, 11, 1130443. [Google Scholar] [CrossRef]
- Zhang, M.; Song, Y.; Dong, H. Hydrological trend of Qinghai Lake over the last 60 years: Driven by climate variations or human activities? J. Water Clim. Chang. 2019, 10, 524–534. [Google Scholar] [CrossRef]
- Zhu, H.; Xiong, X.; Ao, H.; Wu, C.; He, Y.; Hu, Z.; Liu, G. Cladophora reblooming after half a century: Effect of climate change-induced increases in the water level of the largest lake in Tibetan Plateau. Environ. Sci. Pollut. Res. 2020, 27, 42175–42181. [Google Scholar] [CrossRef] [PubMed]
- Cui, B.L.; Li, X.Y. Characteristics of stable isotopes and hydrochemistry of river water in the Qinghai Lake Basin, northeast Qinghai-Tibet Plateau, China. Environ. Earth 2015, 73, 4251–4263. [Google Scholar] [CrossRef]
- Fan, C.; Song, C.; Li, W.; Liu, K.; Cheng, J.; Fu, C.; Chen, T.; Ke, L.; Wang, J. What drives the rapid water-level recovery of the largest lake (Qinghai Lake) of China over the past half century? J. Hydrol. 2021, 593, 125921. [Google Scholar] [CrossRef]
- Zhang, G.; Duan, S. Lakes as sentinels of climate change on the Tibetan Plateau. All Earth 2021, 33, 161–165. [Google Scholar] [CrossRef]
- Su, D.; Hu, X.; Wen, L.; Lyu, S.; Gao, X.; Zhao, L.; Li, Z.; Du, J.; Kirillin, G. Numerical study on the response of the largest lake in China to climate change. Hydrol. Earth Syst. Sci. 2019, 23, 2093–2109. [Google Scholar] [CrossRef]
- Cao, J.; Yao, X.; Jin, H.; Zhang, T.; Gao, Y.; Zhang, D.; Zhao, Q. Spatiotemporal variation of ice thickness of Lake Qinghai derived from field measurements and model simulation. J. Lake Sci. 2021, 33, 607–621. [Google Scholar]
- Yi, W.; Li, X.; Cui, B.; Ma, Y. Climate change and impact on water level of the Qinghai Lake watershed. J. Arid Meteorol. 2010, 28, 375–383. [Google Scholar]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C.K. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Zhang, G. Qinghai Lake Hydrology and Climate Data (1956–2020). 2021. Available online: https://www.tpdc.ac.cn/zh-hans/data/12cb9320-e6ba-4938-a9ac-5b0ebb656825 (accessed on 10 October 2023).
- Zhou, J.; Wang, L.; Zhang, Y.; Guo, Y.; Li, X.; Liu, W. Exploring the water storage changes in the largest lake (Selin Co) over the Tibetan Plateau during 2003–2012 from a basin-wide hydrological modeling. Water Resour. Res. 2015, 51, 8060–8086. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Yang, N. The unique role of ridge regression analysis in solving multicollinearity problems. New Theor. Explor. 2004, 3, 1–2. [Google Scholar] [CrossRef]
- Wang, R.; Niu, Z. Characteristics of lake temperature variation and its response to climate change in China. China Environ. Sci. 2020, 40, 780–788. [Google Scholar] [CrossRef]
- Li, L.; Shi, X.; Shen, H.; Dai, S.; Xiao, J. Cause of water level fluctuation in Qinghai Lake from 1960 to 2009 and its future trend forecasting. J. Nat. Resour. 2011, 26, 1566–1574. [Google Scholar]
- Li, L.; Zhu, X.; Wang, Z.; Wang, Q. Impacting factors and changing tendency of water level in Qinghai Lake in recent 42 years. J. Desert Res. 2005, 25, 689–696. [Google Scholar]
- Jin, Z.; Zhang, F.; Wang, H.; Bai, A.; Qiu, X. Analysis of reasons for the continuous rise of Qinghai Lake water level since 2005. J. Environ. Sci. 2013, 4, 1355–1362. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Qi, Y.; Lian, X.; Zhang, J.; Yang, R.; Zhang, M. Effects of climate change and land use/cover change on the volume of the Qinghai Lake in China. J. Arid. Land 2022, 14, 245–261. [Google Scholar] [CrossRef]


| PY | CY | PY | CY | PY | CY | PY | CY | |
|---|---|---|---|---|---|---|---|---|
| P | ||||||||
| E | −0.16 | −0.09 | −0.05 | |||||
| P | E | |||
|---|---|---|---|---|
| 1979–2004 | 379.8 | 340 | 904.9 | 719.8 |
| 2004–2018 | 449.3 | 610 | 907.8 | 1059.3 |
| Variation | 69.5 | 270 | 2.9 | 339.6 |
| Variables | Correlation Coefficient | Contribution Rate (%) |
|---|---|---|
| WS | 33 | |
| AT | - | |
| SH | 2 | |
| AP | - | |
| SR | 27 | |
| LR | 11 | |
| P | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Wen, L.; Wang, M.; Long, X.; Shu, L.; Yang, L. Study on Characteristics of Water Level Variations and Water Balance of the Largest Lake in the Qinghai-Tibet Plateau. Water 2023, 15, 3614. https://doi.org/10.3390/w15203614
Zheng J, Wen L, Wang M, Long X, Shu L, Yang L. Study on Characteristics of Water Level Variations and Water Balance of the Largest Lake in the Qinghai-Tibet Plateau. Water. 2023; 15(20):3614. https://doi.org/10.3390/w15203614
Chicago/Turabian StyleZheng, Jingyuan, Lijuan Wen, Mengxiao Wang, Xiao Long, Lele Shu, and Liuyiyi Yang. 2023. "Study on Characteristics of Water Level Variations and Water Balance of the Largest Lake in the Qinghai-Tibet Plateau" Water 15, no. 20: 3614. https://doi.org/10.3390/w15203614






