Projection and Uncertainty Analysis of Future Temperature Change over the Yarlung Tsangpo-Brahmaputra River Basin Based on CMIP6

Abstract

Accurate predictions of future climate change are significant to both human social production and development. Accordingly, the changes in the daily maximum (T_max) and minimum temperatures (T_min) in the Yarlung Tsangpo-Brahmaputra River Basin (YBRB), along with its three sub-regions (Tibetan Plateau—TP, Himalayan Belt—HB, and Floodplain—FP) were evaluated here using the Bayesian model average (BMA) results from nine climate models in the CMIP6 under four future scenarios, and the corresponding uncertainty of the projected results was analyzed. The results showed the following: (1) The BMA can simulate the T_max and T_min of the YBRB well. (2) Future T_max and T_min over the YBRB exhibited an overall fluctuating upward trend. Even under the most ideal sustainable development scenario examined (SSP126), the average T_max (T_min) over the YBRB was projected to increase by 3.53 (3.38) °C by the end of this century. (3) Although the future changes in the YBRB are predicted to fall below the global average, the future temperature difference in the YBRB will increase further. (4) The uncertainty increased with prediction time, while spatially, the regions with the uncertainty were the TP > HB > FP. These findings can provide a reference for the YBRB climate change adaptation strategies.

1. Introduction

Global climate change is increasingly accepted as fact, as the Sixth Assessment Report of the United Nations Intergovernmental Panel on Climate Change (IPCC) has confirmed that the average global surface temperature in the first two decades of the 21st century (2001–2020) increased by 0.99 °C relative to the global surface temperature during the Industrial Revolution (1850–1900) [1]. Under warmer global temperatures, certain natural disasters (storms, floods, heatwaves, droughts, and fires) are expected to occur more frequently [2,3], significantly impacting agriculture, social economy, human well-being, etc. [4,5,6,7,8], and potentially increasing global conflicts [9,10]. Similar to other parts of the world, significant warming has been observed on and around the Tibetan Plateau in recent decades. Studies have shown that the increased melting of glaciers and snow cover caused by warming in this Third Polar Region will continue to threaten water supply security throughout Asia [11,12]. Daily maximum (T_max) and minimum temperatures (T_min) are fundamental metrics in climate change research and important indicators of extreme climate events. Accordingly, reasonable assessments of future T_max and T_min values are beneficial for predicting the impact of extreme climate events across all sectors, informing national climate policies, as well as maintaining the stability of regional ecosystems and socioeconomic development.

Global climate models are important tools for climate science research [13,14], capable of explaining past climate change and predicting future climate [15]. Since 1995, the Working Group on Coupled Models of the World Climate Research Programme has initiated and organized six Coupled Model Intercomparison Projects. The Coupled Model Intercomparison Project (CMIP) seeks to better understand past, present, and future climate changes caused by natural, unforced, or radiative forcing in multi-model environments [16]. Since its inception, the CMIP has made significant contributions to various IPCC assessment reports [1,17,18,19]. Elsewhere, Song et al. [20] used 20 climate models from the Fifth Coupled Model Intercomparison Project (CMIP5) to predict warmer global surface air temperatures under higher emission scenarios. Zhao et al. [21] employed the CMIP5 multi-model to simulate climate change across typical arid and semi-arid regions of the world, revealing the stronger capacity of the multi-model ensemble (MME) mean compared to any individual model. However, one of the important problems is that there are large uncertainties in using global climate models for the prediction or projection of future climate. Multi-model weighting based on performance indicators has been found to reduce the uncertainty of predicted results [22,23,24,25,26,27,28]. Specifically, Bayesian model averaging (BMA) has been shown to be less uncertain than either single model or MME results [29,30,31].

The Yarlung Tsangpo-Brahmaputra River is an important international river in Asia, which spans multiple countries (China, India, Bhutan, and Bangladesh), and maintains great potential for hydropower along with other abundant water resources. The geography of the Yarlung Tsangpo-Brahmaputra River Basin (YBRB) is diverse, the climate is complex, and climate change has already had a significant impact on the local hydrology and ecology. Accordingly, predicting future regional climate change across the YBRB is of great significance to all countries in the basin [32]. So far, The YBRB has been partially studied regarding climate change. Shi et al. [33] used a high-resolution regional climate model (RegCM3) simulation to study future climate change under the A1B scenario of the IPCC Special Report on Emissions Scenarios. Immerzeel [34] predicted future YBRB temperature, precipitation, and hydrological cycles using six climate model datasets (2002–2100) under two scenarios via a multiple linear regression model. The CMIP has entered its sixth phase (CMIP6), characterized by higher spatial resolution models, improved physical parameterization schemes, as well as new Earth system processes and components [16,35,36]; yet, the basin-scale study of the YBRB under CMIP6 remains lacking.

Accordingly, this study conducted the following work in the YBRB using the most common CMIP6 climate model data. Based on historical data (1961–2014), a Bayesian model was trained, and the BMA’s ability to simulate the T_max and T_min over the YBRB test period (2005–2014) was evaluated. Each model was evaluated according to the weight coefficient obtained during the optimal training period. Based on the observational data and BMA prediction results, the changing trends of the T_max and T_min in the YBRB historical (1961–2014) and future periods (2015–2100) were acquired. Additionally, the changing trend and increase in the T_max and T_min of the YBRB were discussed over different periods. Lastly, the quantitative uncertainty of the predicted results was discussed to provide a scientific basis for the YBRB climate change adaptation strategies and decision making.

2. Materials and Methods

2.1. Study Area

The Yarlung Tsangpo-Brahmaputra River spans 2900 km in China, India, Bhutan, and Bangladesh, comprising a drainage area of 53,000 km² [37,38]. It originates from the Jamayangzong Glacier in Tibet, and its upstream region is the Yarlung Tsangpo River. It is the fifth largest river in China and the highest river in the world, with an average altitude > 4000 m. After entering India, the river is known as the Brahmaputra River; within the territory of Bangladesh, it joins with the Ganges and the Jamuna River and flows into the Bay of Bengal [32]. The seasonal distribution of precipitation within the YBRB is highly uneven, with the period from June to September accounting for 60%–70% of the total annual precipitation [39]. Furthermore, heavy and concentrated precipitation events lead to frequent flooding in the lower YBRB [40]. The majority of monthly mean T_max values are recorded in June–July; whereas monthly mean T_min occur in December–January. Annual temperature differences can be as high as 40 °C, with a strong differential between the upper and lower reaches, and obvious vertical changes [41]. There are 10 different climate types within the YBRB which vary significantly by region. The overall pattern—dry and cold on the plateau, dry and hot in the mountains, and warm and wet on the plains—is strongly influenced by the division of the Himalayas [42,43].

Considering the vast territory and substantial topographic differences across the YBRB, the simulation effects of climate models vary regionally. In accordance with the physical geographical zoning method of Immerzeel [34], this study divided the YBRB into three sub-regions for spatial analysis: the Tibetan Plateau (TP, elevation ≥ 3500 m), the Himalayan Belt (HB, elevation 100~3500 m), and the Floodplain (FP, elevation ≤ 100 m; Figure 1).

2.2. Materials

Based on the availability of the CMIP6 climate model data and its frequency of use (Table S1), nine climate model data sets were selected under four shared socioeconomic pathway (SSP) scenarios: SSP126, SSP245, SSP370, and SSP585 (see O’Neill et al. [44] for further background on SSPs).

Table 1. Basic information of the 9 CMIP6 climate models.

No.	Model	Country/Region	Resolution
1	ACCESS-ESM1-5	Australia	1.88° × 1.24°
2	BCC-CSM2-MR	China	1.13° × 1.13°
3	CanESM5	Canada	2.81° × 2.81°
4	CMCC-CM2-SR5	Italy	1.25° × 0.94°
5	EC-Earth3-Veg	Europe	0.70° × 7.20°
6	GFDL-ESM4	America	1.00° × 1.00°
7	IPSL-CM6A-LR	France	2.50° × 1.26°
8	MIROC6	Japan	1.41° × 1.41°
9	MRI-ESM2-0	Japan	1.13° × 1.13°

shows the basic information of the selected 9 models, with greater detail listed on the CMIP6 website (https://esgf-node.llnl.gov/projects/cmip6/. Accessed on 15 May 2022). The selected climate model data included daily T_max and T_min data from the historical climate simulation experiment (1961–2014) and future emission scenario experiment (2015–2100). Owing to differences in the spatial resolution among the climate models, the bilinear interpolation method was used to resample all the model resolutions to 0.25° × 0.25° [45,46]. Reference daily observation data from the historical period were used with the bias-corrected PGF-V3 (Princeton Global Forcings) T_max and T_min data from Ji et al. [47]. The PGF-V3 dataset coverage maintained a similar resolution (0.25° × 0.25°) and was sufficiently long for inclusion in the present study (1948–2016) [47].

2.3. BMA Estimation

The BMA method was used here to fuse the CMIP6 multi-model data (daily T_max and T_min) for predicting future temperature changes across the YBRB and evaluating its uncertainty. In contrast to a single optimal model, the BMA assigns a weight to each model and determines the final predicted value using the weighted average, thereby producing more reliable predicted values. An average BMA forecast can be calculated via Equation (1):

$$E\left[p\left(\left.y\right|f_1,\dots f_K\right)\right]=\sum _{k=1}^K{\omega }_k(a_k+b_k{f}_k)$$

(1)

where y is the predicted variable,$f_k$ is the $k$th model prediction, and $p\left(\left.y\right|f_1,\dots f_K\right)$ means the corresponding conditional probability density function. When the study variable is temperature, $\left.y\right|f_k$ approximately follows a normal distribution with an expectation of $a_k+b_k{f}_k$ [29]. If the variable has not yet been bias-corrected, $a_k+b_k{f}_k$ can be seen as a simple bias correction process, and can also be considered as a simple form of model output statistics [48,49]. $a_k$ and $b_k$ can be obtained using a linear regression. ${\mathsf{\omega }}_k$ can be obtained using the maximum likelihood estimation principle [50] and expectation maximization algorithm [51] alongside the training period dataset. Further details about the BMA method can be found in Raftery et al. [29].

Lastly, the BMA future estimate $\tilde{\mathsf{\Delta }}T$ is calculated using Equation (2):

$$\tilde{\mathsf{\Delta }}T=\sum _{k=1}^K{\omega }_k\mathsf{\Delta }{T}_k$$

(2)

where $\mathsf{\Delta }{T}_k$ is the mean temperature change of the $k$th model over the next 20 years compared to the reference period (1995–2014).

2.4. Evaluation Metrics of Ensemble Mean

The root mean square error (RMSE) and anomaly correlation coefficient (ACC) were used to test the BMA simulation results. The RMSE was used to measure the deviation between the simulated and real values: the smaller the RMSE value, the better the BMA simulation effect (Equation (3)):

$$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(y_i-o_i\right)}^2}$$

(3)

where $N$ is the total amount of data obtained, $y_i$ is the BMA simulation result, and $o_i$ is the observed value.

Alternatively, ACC also represents the degree of similarity between the simulated and observed value, with a greater correlation coefficient indicating a stronger relationship (Equation (4)):

$$ACC=\frac{1}{N}\sum _{i=1}^N(\left(y_i-\stackrel{-}{y}\right)\left(o_i-\stackrel{-}{o}\right)/\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(y_i-\stackrel{-}{y}\right)}^2}\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(o_i-\stackrel{-}{o}\right)}^2}$$

(4)

where $\stackrel{-}{y}$ is the average BMA simulation result value, and $\stackrel{-}{o}$ is the observational average.

2.5. Uncertainty Estimation

Pennell and Reichler [52] found that multi-model weighting results are dependent upon the modes that comprise the modal set (i.e., the effective modes); therefore, the effective mode number ($M_{eff}$) was introduced into the calculation of the difference between modes $\delta \mathsf{\Delta }T$ (Equations (5) and (6)):

$$M_{eff}=1/\sum _{k=1}^K{\omega }_k^2,$$

(5)

$$\delta \mathsf{\Delta }T=\sqrt{\frac{M_{eff}}{M_{eff}-1}}.{\left[\sum _{k=1}^K{\omega }_k{\left(\mathsf{\Delta }{T}_k-\tilde{\mathsf{\Delta }}T\right)}^2\right]}^{1/2}$$

(6)

The model interval deviation $\delta \mathsf{\Delta }T$ can be used to characterize the uncertainty of BMA results, where the greater the value, the higher the uncertainty and lower the reliability of the predicted result.

2.6. Determine the Optimal Training Period

When constructing a Bayesian model, it is necessary to divide historical multi-model and observation data series into training and test periods, and evaluate the overall effects on the latter to select the optimal model. Here, different training period lengths were explored, and the performance of the model was judged based on the RMSE and ACC between the BMA estimate and test period observations. Finally, 28 and 20 years were selected as the optimal training periods for the T_max and T_min, respectively (see Text S1 in Supporting Information).

3. Results and Discussion

3.1. Evaluation of BMA Simulation

The performances of the T_max and T_min simulated by the optimal BMA model in the YBRB were evaluated and compared with those of the MME and single model (Figure 2, the closer it is to the top right corner, the better the simulation).

The RMSE of the BMA-simulated T_max over the YBRB was 1.75 °C, notably lower than that of the MME or the nine single models (1.81–2.29 °C; Figure 2a). The higher ACC of the T_max simulated by the BMA for the YBRB (0.93) compared to that of the MME and nine single models (0.88–0.92) further supported its predictive superiority. By sub-region, the T_max RMSE for the TP and HB simulated by the BMA were 1.99 °C and 1.75 °C, respectively, lower than that of the MME and nine single models (TP: 2.05–2.71 °C, HB:1.78–2.41 °C). Comparatively, the T_max RMSE for the FP simulated by the BMA (2.02 °C) was slightly larger than that of the MME (2.00 °C) and CanESM5 (1.98 °C), but smaller than that of the other eight models (2.13–2.56 °C). The T_max ACC for the TP, HB, and FP simulated by the BMA were 0.94, 0.89, and 0.82, respectively, higher than those of the MME and nine models (TP: 0.88–0.92, HB: 0.76–0.88, FP: 0.63–0.80). By comparing the performances across the three regions, it was revealed that the T_max simulated by the BMA was better in the HB than in the TP or FP.

The RMSE of the T_min simulated by the BMA for the YBRB was 2.07 °C, lower than that of the MME and the nine models (2.13–3.32 °C); the ACC of the T_min simulated by the BMA for the YBRB (0.95) was also higher than that of the MME or the nine single models (0.87–0.94; Figure 2b). By sub-region, the T_min RMSE for the TP and HB simulated by the BMA was 2.53 °C and 1.85 °C, respectively, lower than those of the MME and nine models (TP: 2.61–4.11 °C, HB: 1.87–2.62 °C). The BMA-derived ACC of the T_min (2.00 °C) was slightly larger than that of the MME (1.99 °C), but less than that of the other nine models (2.19–2.76 °C). By region, the ACC of the T_min for the TP, HB, and FP were 0.95, 0.95, and 0.94, respectively, greater than that of the MME and the nine models (TP: 0.84–0.93, HB: 0.89–0.93, FP: 0.87–0.92). Ultimately, when comparing the performance of the overall region and different sub-regions, the T_min values simulated by the BMA were superior to the MME and the other individual models, particularly over the TP and FP compared to the HB region (consistent with the T_max).

In general, the BMA effectively improved the climate model predictions of the T_max and T_min over the YBRB; thus, the BMA-based CMIP6 multi-model set was recommended for future T_max and T_min change predictions across this region.

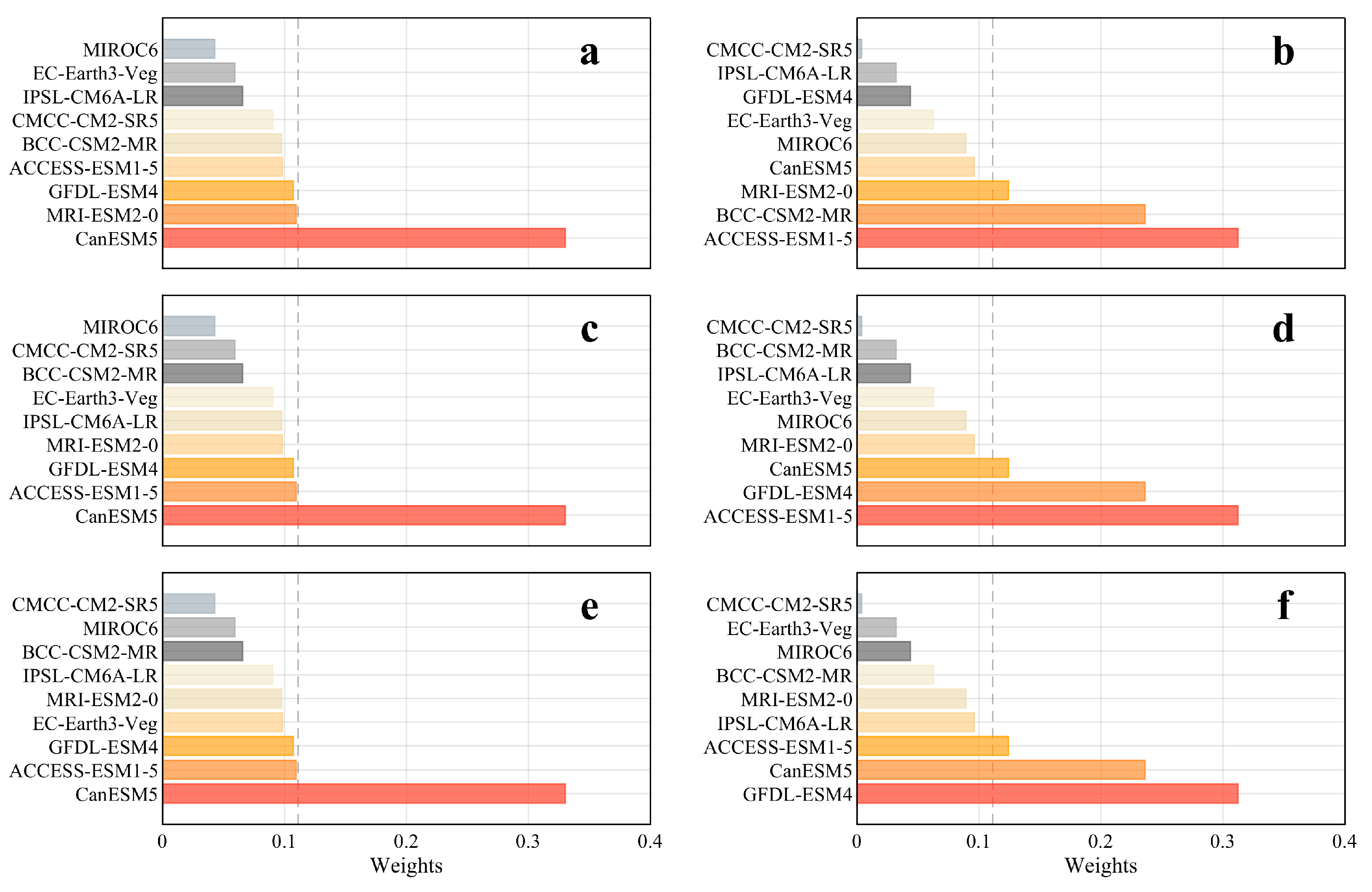
3.2. Evaluation of Weighted Model Performance

Model weights reflect their relative contribution to the ensemble average results during the training period, where increased weights equate to each model’s stronger forecasting ability. Figure 3 shows the weight distribution comparison for the nine climate model components across each YBRB sub-region throughout the optimal training period. For T_max, the top three climate model results were CanESM5 > ACCESS-ESM1-5 > GFDL-ESM4 among the three sub-regions. The average weight of the three sub-regions was ≥ 0.35, far exceeding the equal weight value of 0.11. Comparatively, the worst-performing model was MIROC6, with sub-equal weights across all three sub-regions of the YBRB, averaging ≥ 0.02. The top T_min simulation models were ACCESS-ESM1-5 > GFDL-ESM4 > MRI-ESM2-0. For ACCESS-ESM1-5, the weights of the TP (0.27) and HB (0.25) reached their maximum values, far exceeding the equal weight of 0.11; however, the simulation effect on the FP was relatively poor (0.14; GFDL-ESM4 was the top-performing model for the FP). For T_min, the poorest performing model was CMC-CM2-SR5, with all sub-region weights lower than the equal weights (averaging ≥ 0.01).

Namely, the ACCESS-ESM1-5 and CanESM5 models performed the best for T_max and T_min over the YBRB; whereas CMC-CM2-SR5 produced the poorest simulation effects. For the performance of ACCESS-ESM1-5, Lun et al. [53] evaluated the ability of 24 CMIP6 climate models to simulate the TP temperature, also revealing the superiority of ACCESS-ESM1-5. It indicated that the ACCESS-ESM1-5 should be preferred when the CMIP6 model is used to study the temperature, T_max and T_min of the TP and its surrounding areas. In addition, the same climate model produced distinct simulation effects across different variables, such as T_max and T_min. Zhu and Yang [54] used CMIP5 and CMIP6 data to simulate historical TP temperatures and precipitation, and found that the same climate model had different simulation effects on temperatures and precipitation. Hence, it is advisable to assess climate models specifically for the study area and variables when selecting them.

3.3. Spatiotemporal Distribution of Future YBRB Temperature Changes

According to the principle of the BMA method, the expected maximization algorithm can be used to obtain the estimated values of each model parameter throughout the optimal training period. To this end, the BMA-projected T_max and T_min values for the future period (2015–2100) were calculated via Equation (1). In accordance with the IPCC Sixth Assessment Report, the future period was divided into the near- (2021–2040), mid- (2041–2060), and long-term (2081–2100) [1]. Figure 4 and Figure 5 reflect the overall change trends of the annual mean T_max and T_min across the YBRB, respectively, as projected by the BMA under different climate scenarios. Over the period from 2015 to 2100, the growth rate of the BMA-predicted T_min under the SSP245, SSP370, and SSP585 scenarios was higher than that of the T_max; whereas these rates were similar in the SSP126 emission scenario. When comparing the growth rates of different sub-regions, it was found that the future T_max and T_min growth rates predicted by the BMA showed similar characteristics under the four scenarios; that is, the fastest growing region was the TP, followed by the HB and the FP. This finding further corroborates the discovery made by Immerzeel [34], which indicates that the growth rate of future YBRB temperatures exhibits significant spatial variations, with higher regional altitudes experiencing faster temperature growth. It was also found that the increase in the development scenario intensity led to stronger growth rates of T_max over the YBRB throughout the 21st century, with these differences becoming more extrapolated towards the latter end of this era (Figure 4). For T_min, the rate of increase did not particularly increase with the development scenario intensities until the mid- and long-term periods (Figure 5).

Figure 6 and Figure 7 present the predicted spatial patterns of annual surface T_max and T_min from the BMA over the YBRB across the near- (2021–2040), mid- (2041–2060), and long-term periods (2081–2100) relative to the reference period (1995–2014) under SSP126, SSP245, SSP370, and SSP585, respectively. By sub-region, the TP displayed the most significant future increase in T_max, followed by the HB and the FP. Comparatively, there was no significant difference observed for T_min by sub-region. In addition, with the increase in radiative forcing, the change amplitudes of T_max and T_min over the YBRB showed an overall increasing trend, especially among scenarios over the mid- and long-terms. According to the Sixth Assessment Report of the IPCC and the results of this study [1], when compared with the historical reference period (1995–2014), the global temperatures (T_max; T_min over the YBRB) in the near term will increase by 0.7, 0.7, 0.7, and 0.8 °C (0.58, 0.61, 0.54, and 0.69 °C; 0.18, 0.47, −0.01, and 0.09 °C) under scenarios SSP126, SSP245, SSP370, and SSP585, respectively; whereas those across the mid- and long-terms will increase by 1.0, 1.3, 1.4, and 1.7 °C (0.91, 1.09, 1.15, and 1.51 °C; 0.52, 0.99, 0.68, and 1.04 °C) and 1.2, 2.0, 3.1, and 4.0 °C (1.09, 1.82, 2.64, and 3.53 °C; 0.61, 1.77, 2.46, and 3.38 °C), respectively.

Notably, the future increases in T_max and T_min over the YBRB both fell below the global averages; however, the increase (decrease) in T_max (T_min) over the TP was greater (lesser) than these averages, indicating that the importance of spatial differentiation over the YBRB in the future. Additionally, the increase in future T_min over the YBRB was lower than that of T_max, indicating a larger temperature difference in the future. The significant increase in T_max is expected to intensify glacier and snow melting, leading to an escalated risk of water-related disasters such as glacial lake outburst floods and ice avalanches [55]. Conversely, the summer peak flows will increase, posing a greater flood threat to downstream areas [56,57]. From a water resources perspective, while the immediate effect of ice and snow melting may temporarily increase runoff, the long-term reduction in ice and snow water storage will ultimately lead to decreased runoff, thereby jeopardizing the food security of approximately 26 million people in downstream regions [58]. In summary, the temperature changes will exacerbate the transboundary water security risks in the YBRB.

3.4. Uncertainty in Future Temperature Projections

Uncertainty is inevitable during predictions of climate change [59,60], as future impacts on climate (whether man-made or natural) are inherently complex [61]. Accordingly, for projections to be applicable to future climate mitigation and strategic planning, it is necessary to quantify model uncertainty. To this end, model deviation can be used to assess the BMA climate projections [62], where the greater the deviation between the models (i.e., the larger the difference between them in simulating the T_max and T_min), the greater the uncertainty and lower the reliability of the predicted results. Figure 8 shows the uncertainty of the BMA-projected YBRB temperature changes over the near-, mid-, and long-term under the four future development scenarios. It was found that the uncertainty of the T_max was smaller than that of the T_min. Further, within the same region under the same scenario, the uncertainty of the two temperature variables increased with the forecast time. Across different regions, the TP displayed the largest uncertainty, followed by the HB and the FP. The strong uncertainty associated with the TP region may be related to the complex cryosphere environment. For example, albedo feedback is distorted owing to extensive snow cover over the plateau, potentially leading to large uncertainties in regional future climate projections [33].

Additionally, uncertainty within the predicted results may also be related to model selection. Here, nine climate models were chosen for incorporation in BMA modeling, while intentionally excluding other CMIP6 models. Although this selection was made according to the frequency of use in existing studies (see Table S1 in Supporting Information), these assessments were based only on statistical results, and other models with potentially excellent performances across the study area may have been excluded. In future climate projections, further consideration should be given to using improved and more comprehensive climate model data to further reduce data uncertainty.

Nevertheless, the BMA multi-modal ensemble method produces decreased uncertainty compared with the traditional MME results and single models [29,30,31], as was confirmed in the present study (Section 3.1). While improving model algorithms and accuracies should be sought after, the remaining uncertainty must not deter those working on climate impact, mitigation, and adaptation from making critical decisions [63].

4. Conclusions

Taking the YBRB as a study area, the T_max and T_min performances over a historical period (2005–2014) were evaluated using nine CMIP6 climate models based on the BMA, and the aggregate average data fusion of the T_max and T_min under four future scenarios (SSP126, SSP245, SSP370, and SSP585) was performed according to the corresponding weight coefficients. On this basis, future changes in the T_max and T_min were estimated, and the following conclusions were drawn:

(1)

By comparing the performances of the T_max and T_min via the RMSE and ACC, the BMA-simulation effect on the T_max and T_min was deemed superior to that of the MME or individual models. Regional comparisons further revealed that the BMA could better simulate the T_max and T_min over the HB versus the TP or FP. By comparing the model weights, it was found that CanESM5 and ACCESS-ESM1-5 were the top performers for the T_max and T_min, respectively.

(2)

According to the BMA prediction results, the T_max and T_min over the YBRB during 2015–2100 fluctuated upwards under each of the four scenarios, with their respective warming rates increasing with scenario intensity. Under the most ideal sustainable development scenario (SSP126), the increase in the T_max over the near-, mid-, and long-terms will reach 0.58, 0.91, and 1.09 °C across the YBRB; whereas the increases of the T_min will reach 0.18, 0.52, and 0.61 °C, respectively. Under the high emissions scenario (SSP585), the increases in the T_max (T_min) over the near-, mid-, and long-terms are 0.69 (0.09), 1.51 (1.04), and 3.53 (3.38) °C, respectively. Although the overall future increases in the T_max and T_min are predicted to fall below global averages, the spatial differentiation of temperature in the upper and lower reaches of the basin will be more obvious.

(3)

The uncertainty of the future T_max was smaller than that of the T_min according to the BMA-derived results. In general, uncertainty increased with the prediction time, while spatially, the regions with the uncertainty were the TP > HB > FP.

In general, the BMA simulations outperformed traditional ensemble averages and individual models, which will lead to significant improvements for climatic projections over the YBRB. The inevitable and ongoing uncertainties should not affect our macro-cognition of the future temperature change characteristics across the YBRB. Further assessment to reduce the uncertainty of the estimated results is part of our future work.