Numerical Study of the Influence of Horizontal Spatial Distribution of Macropores on Water Infiltration
Abstract
:1. Introduction
2. Materials and Methods
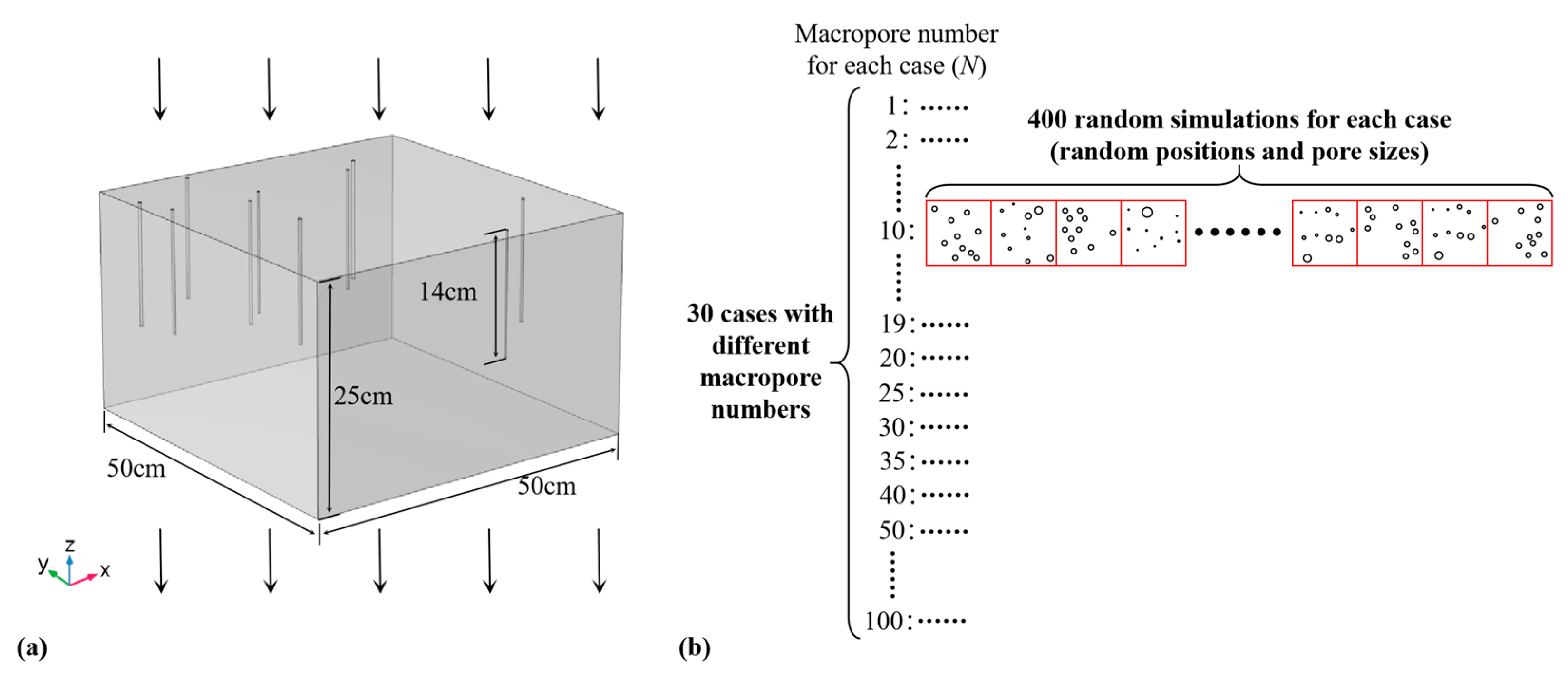
2.1. Modeling Scheme
2.2. COMSOL Simulation
2.3. Statistical Parameters for Characterizing Macropore Position
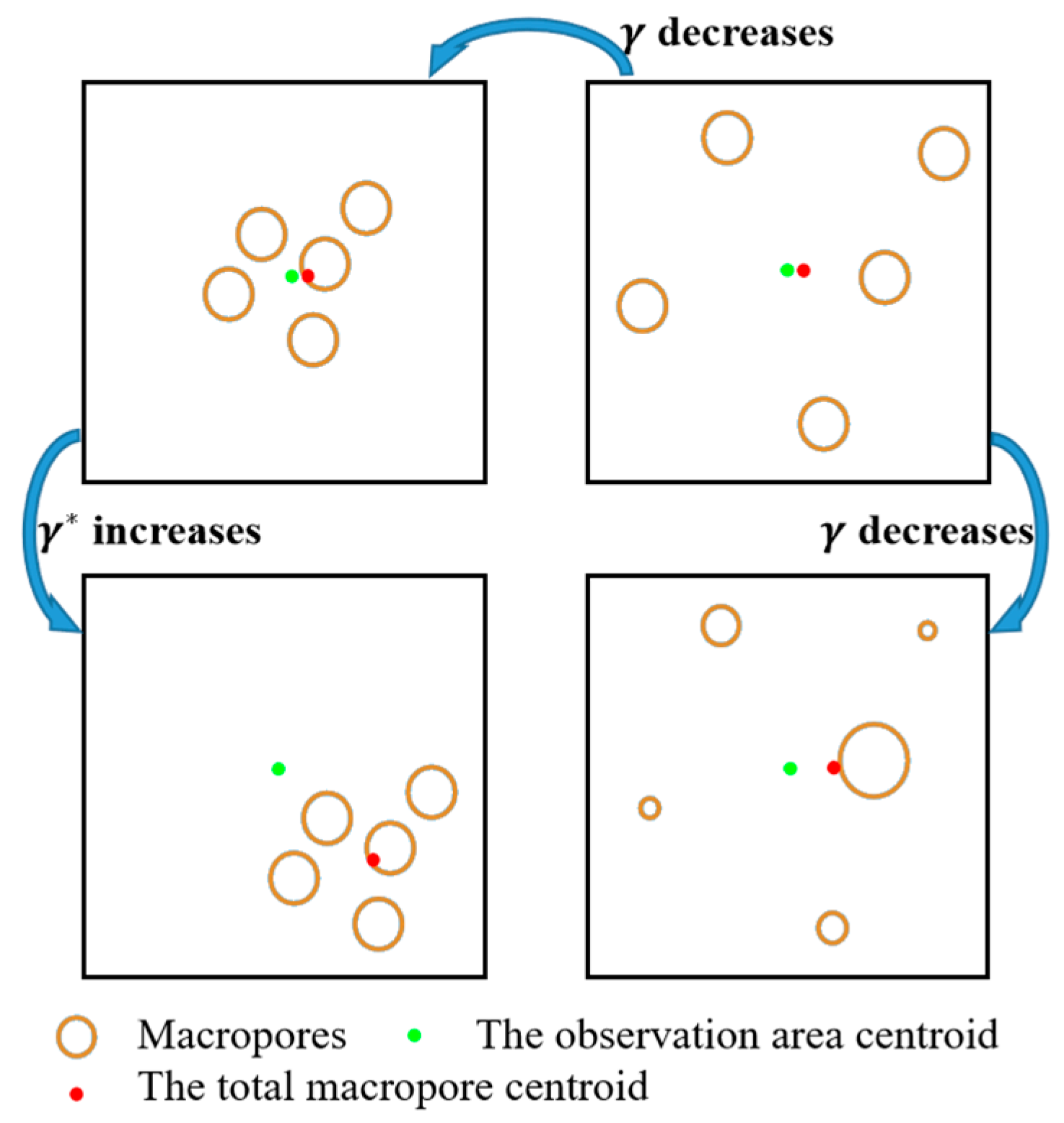
2.3.1. Spatial Dispersion, (Position Relationship among Macropores)
2.3.2. Spatial Deviation, (Position Relationship between the Macropores and Observation Area)
3. Results and Discussion
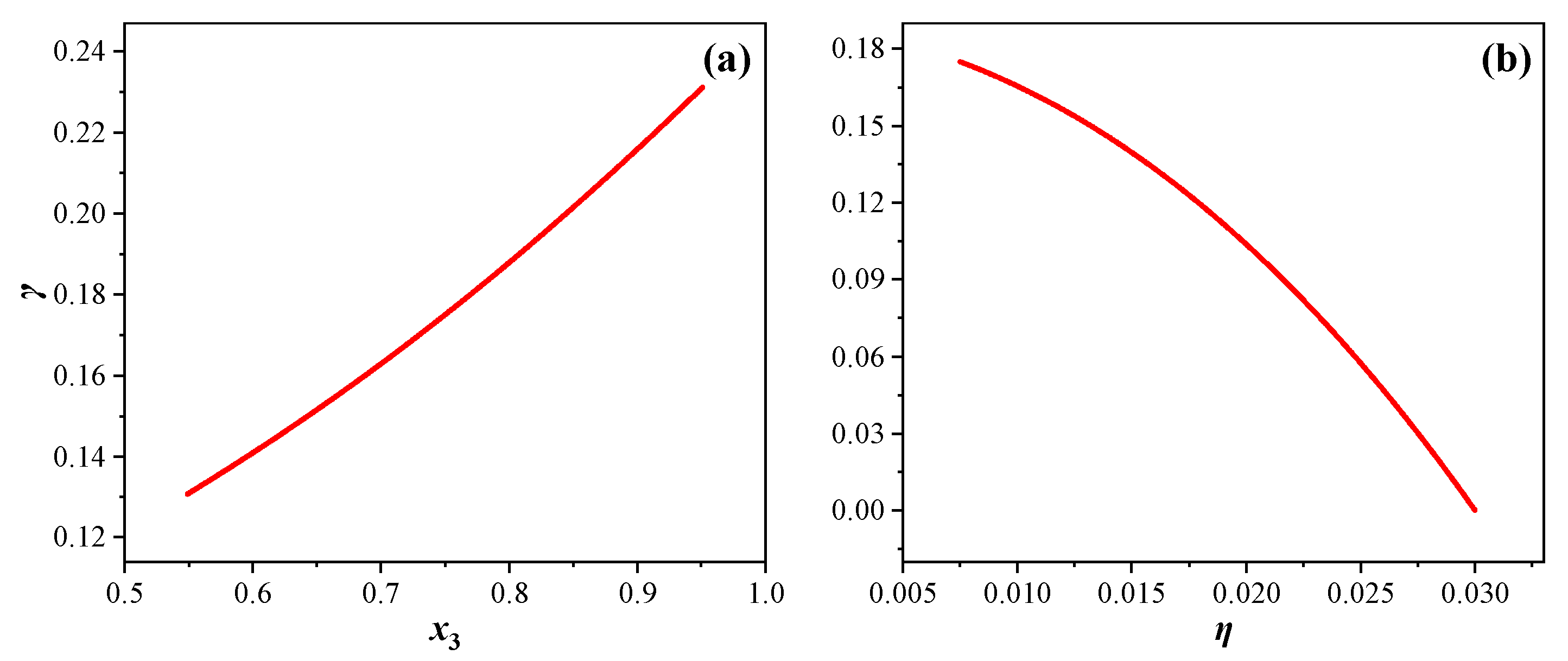
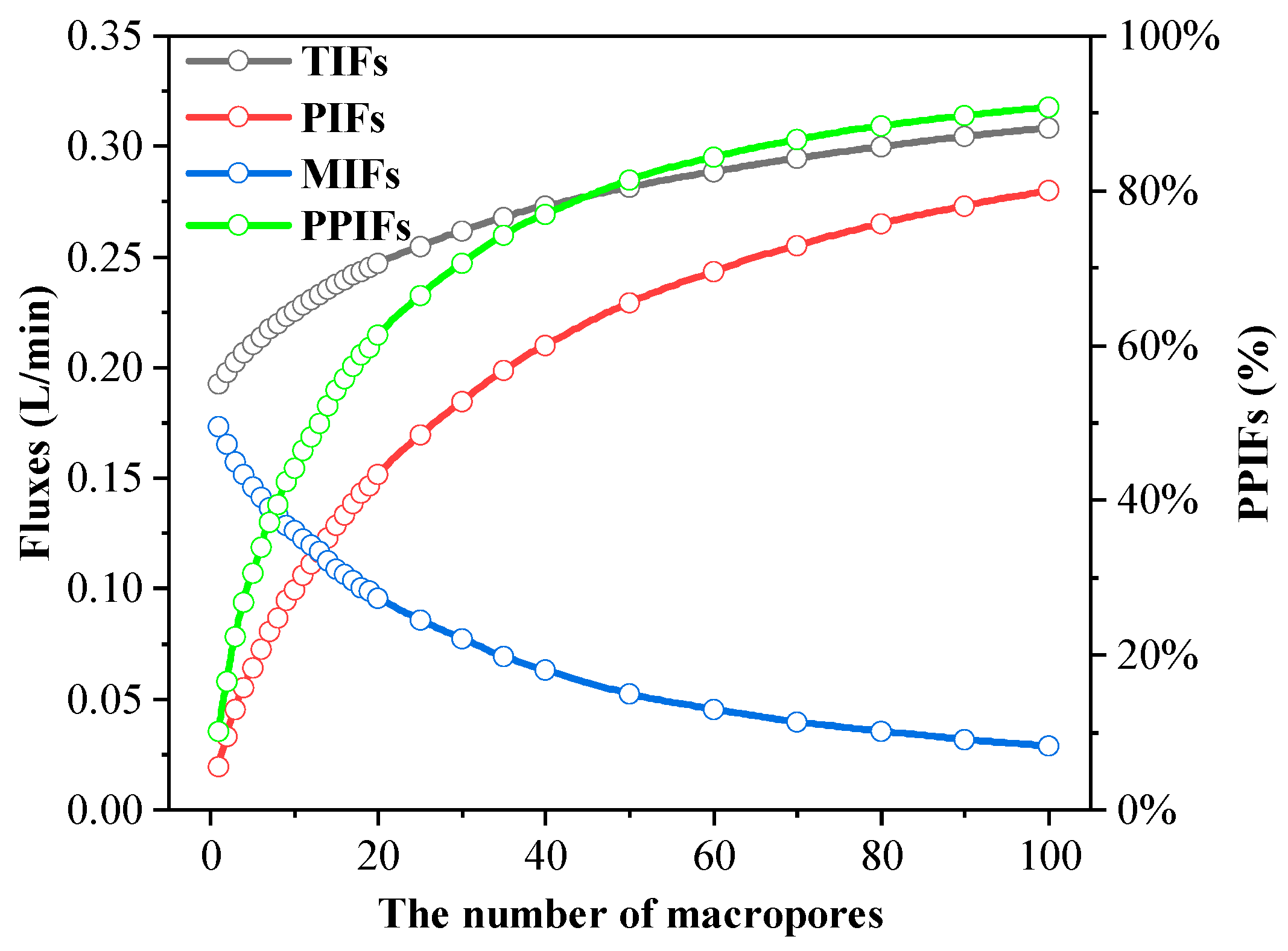
3.1. The Effect of Macropore Number
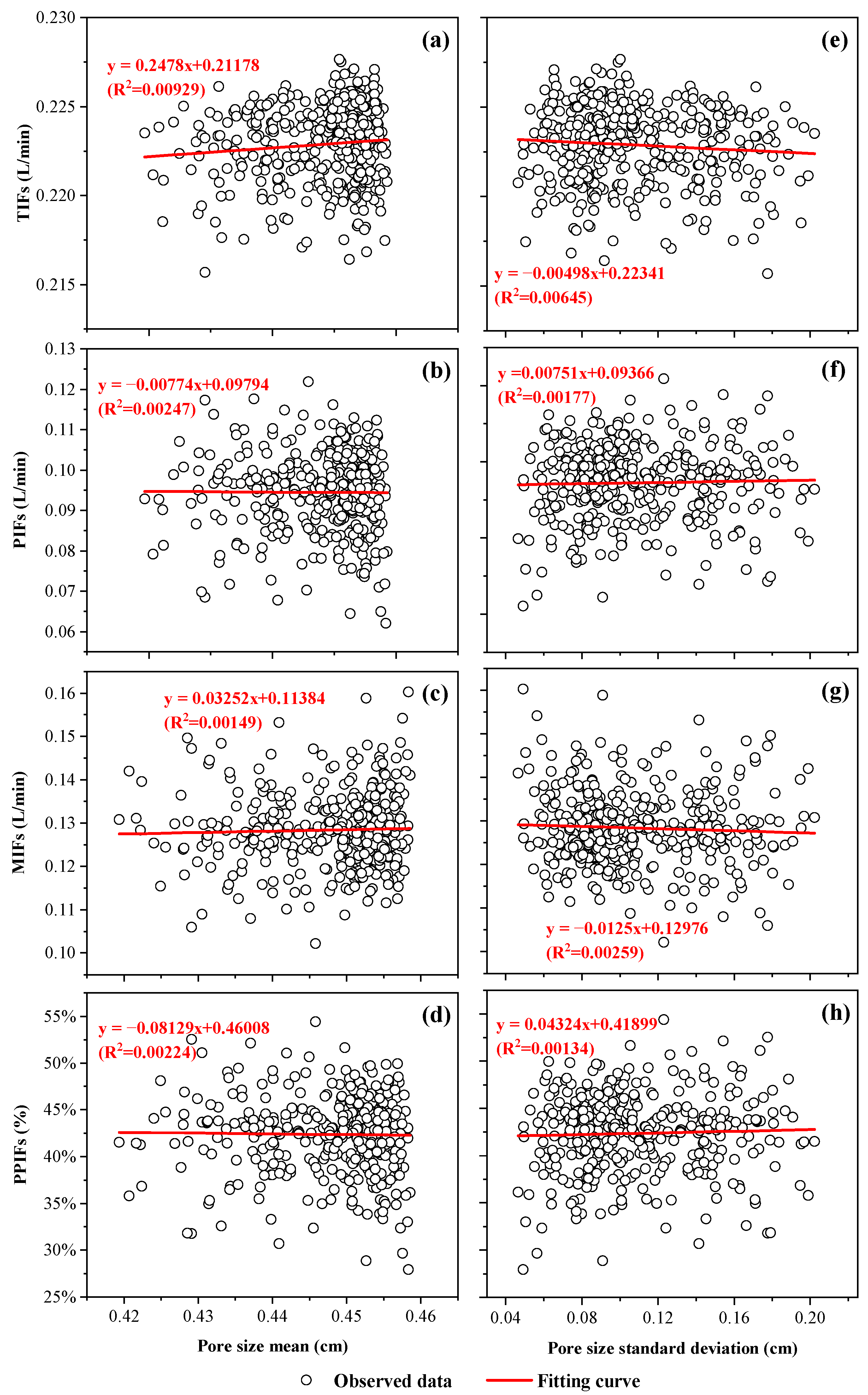
3.2. The Effect of Pore Size
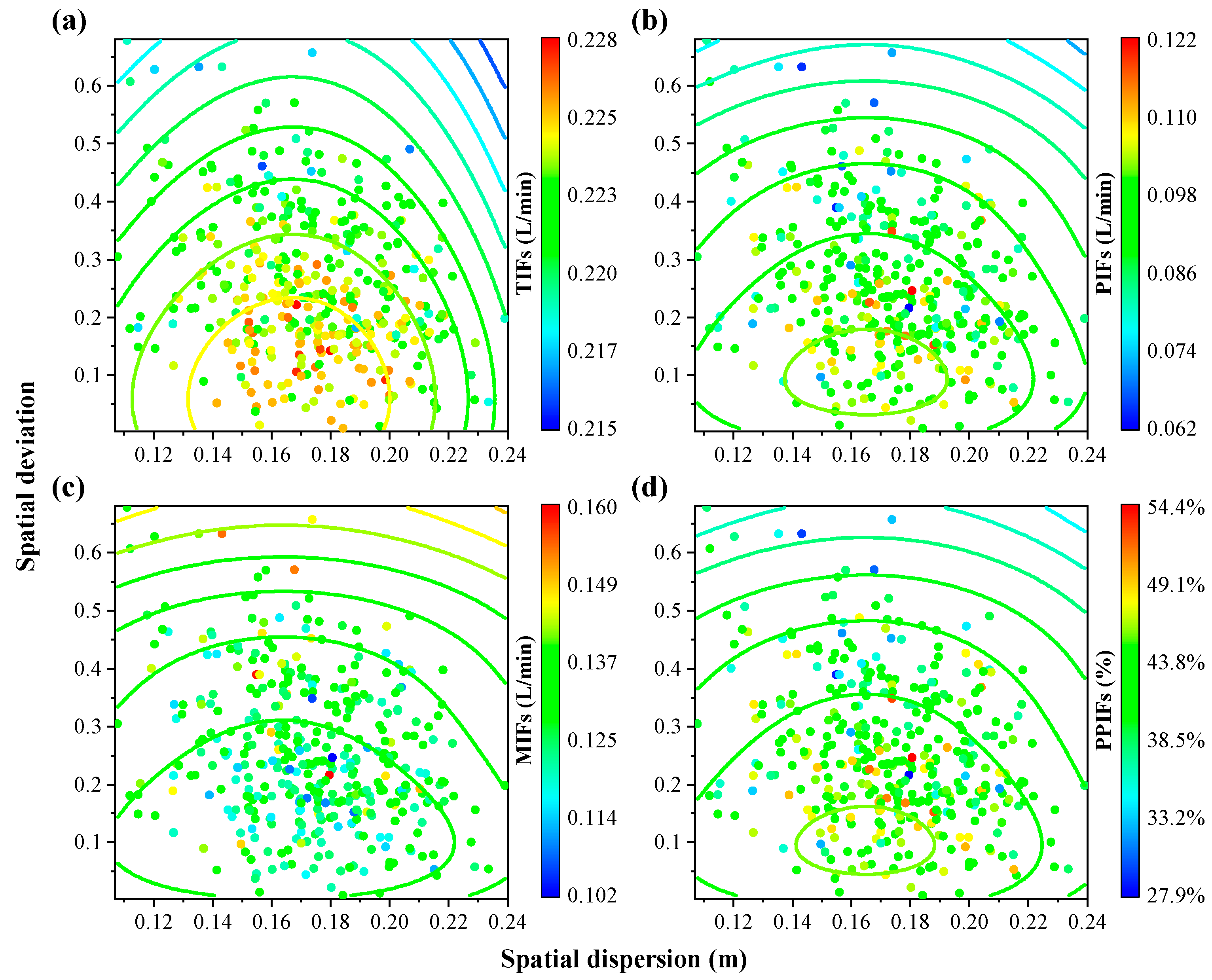
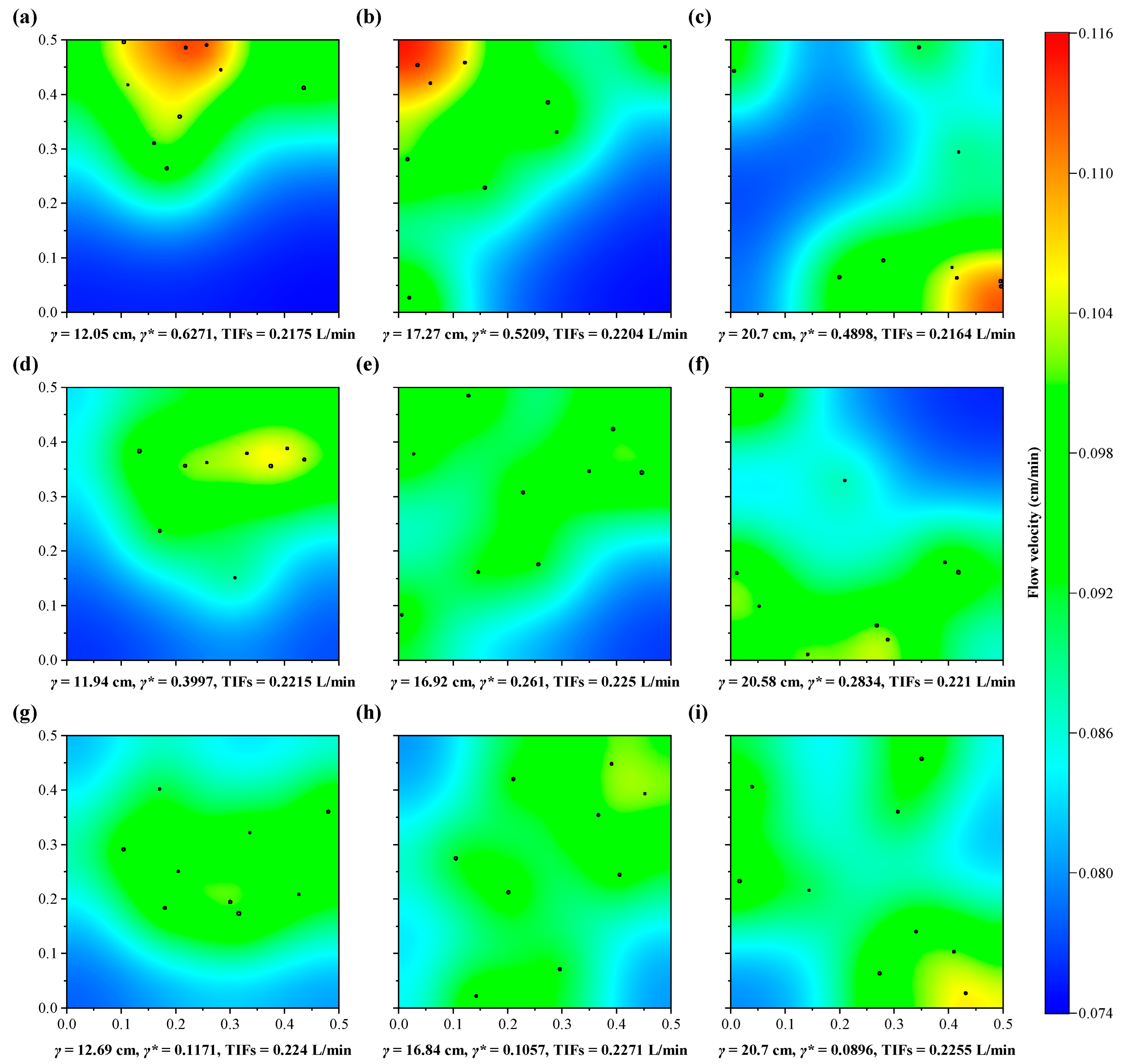
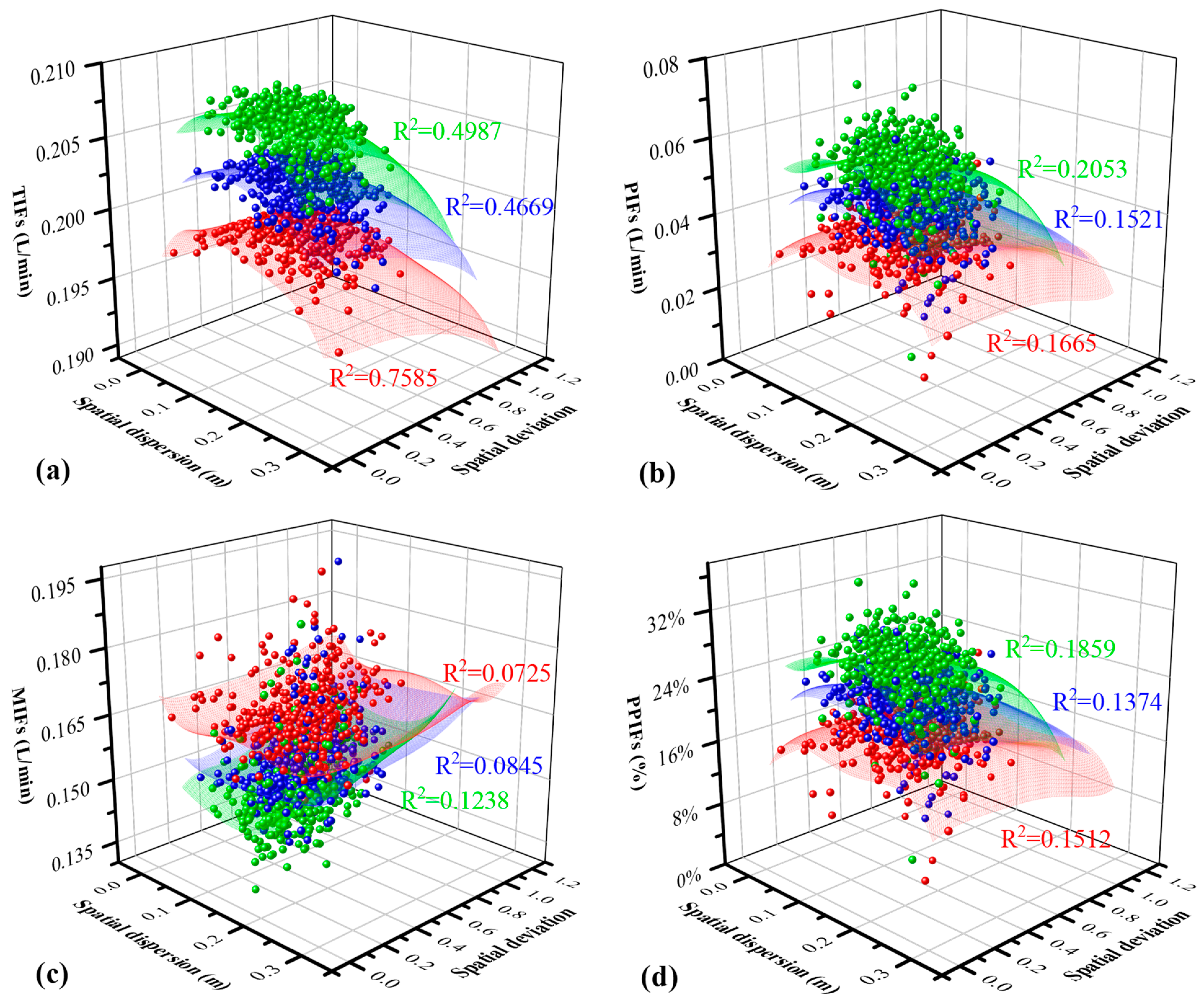
3.3. The Effect of Macropore Position
3.4. Comparison between Number and Position Effects
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Generation Approach for Random Pore Sizes and Positions
Appendix B. Spatial Dispersion (Weighted Mean Distance)
Appendix B.1. Case 1: When the Distance among Macropores Increases
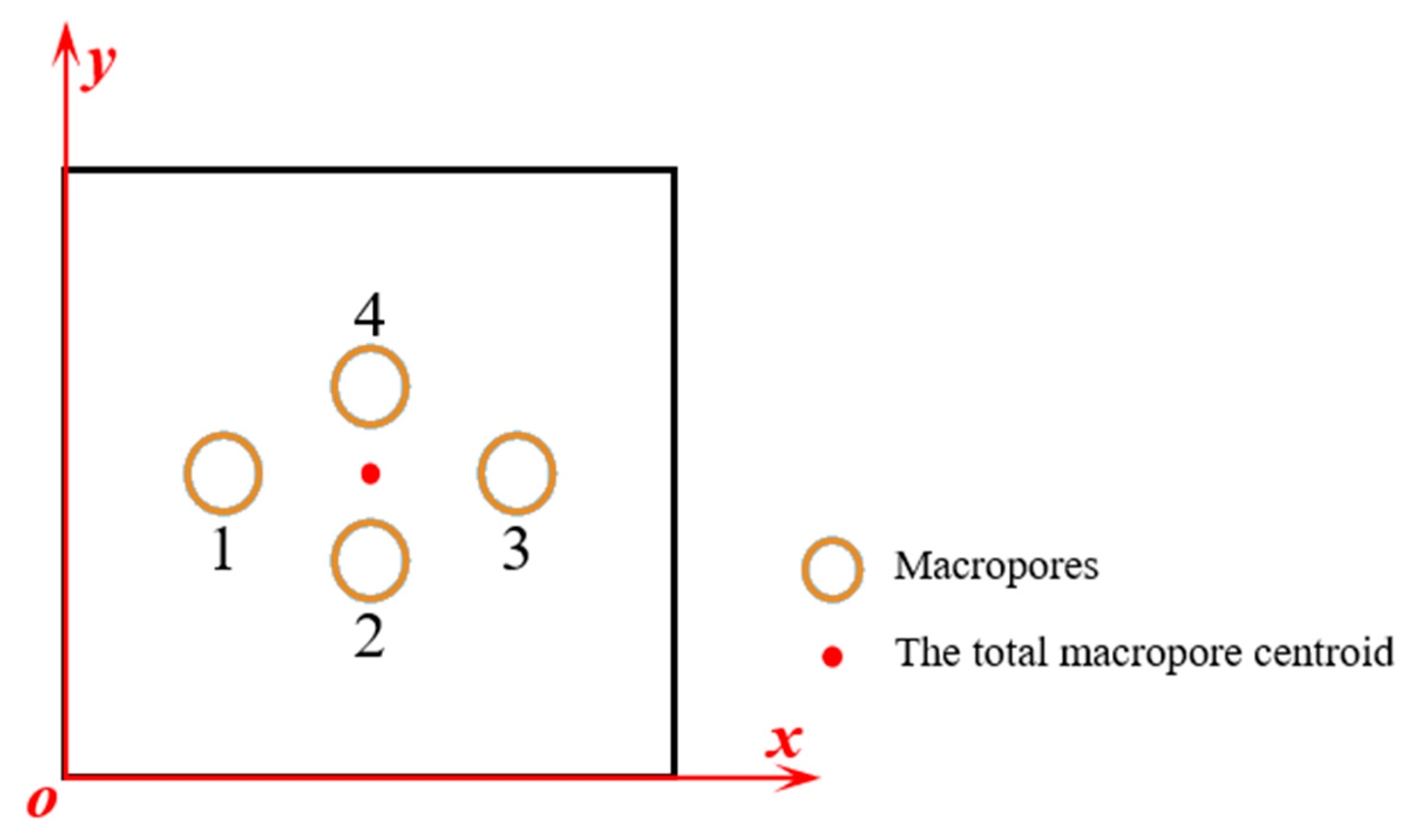
Appendix B.2. Case 2: When the Macroporosity Is Concentrated in One Macropore
References
- Beven, K.; Germann, P. Macropores and water flow in soils. Water Resour. Res. 1982, 18, 1311–1325. [Google Scholar] [CrossRef]
- Jarvis, N.; Koestel, J.; Larsbo, M. Understanding preferential flow in the vadose zone: Recent advances and future prospects. Vadose Zone J. 2016, 15, 1–11. [Google Scholar] [CrossRef]
- Jarvis, N.J. A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality. Eur. J. Soil Sci. 2020, 71, 279–302. [Google Scholar] [CrossRef]
- Koestel, J.; Larsbo, M. Imaging and quantification of preferential solute transport in soil macropores. Water Resour. Res. 2014, 50, 4357–4378. [Google Scholar] [CrossRef]
- Luxmoore, R.J.; Jardine, P.M.; Wilson, G.V.; Jones, J.R.; Zelazny, L.W. Physical and chemical controls of preferred path flow through a forested hillslope. Geoderma 1990, 46, 139–154. [Google Scholar] [CrossRef]
- Raimbault, J.; Peyneau, P.; Courtier-Murias, D.; Bigot, T.; Roca, J.G.; Béchet, B.; Lassabatère, L. Investigating the impact of exit effects on solute transport in macroporous media. Hydrol. Earth Syst. Sci. 2021, 25, 671–683. [Google Scholar] [CrossRef]
- Abou Najm, M.R.; Jabro, J.D.; Iversen, W.M.; Mohtar, R.H.; Evans, R.G. New method for the characterization of three-dimensional preferential flow paths in the field. Water Resour. Res. 2010, 46, W02503. [Google Scholar] [CrossRef]
- Gackiewicz, B.; Lamorski, K.; Kochiieru, M.; Sławiński, C.; Hsu, S.; Chang, L. Hybrid modelling of saturated water flow in percolating and non-percolating macroporous soil media. Geoderma 2022, 406, 115467. [Google Scholar] [CrossRef]
- Yi, J.; Yang, Y.; Liu, M.; Hu, W.; Lou, S.; Zhang, H.; Zhang, D. Characterising macropores and preferential flow of mountainous forest soils with contrasting human disturbances. Soil Res. 2019, 57, 601–614. [Google Scholar] [CrossRef]
- Allaire, S.E.; Roulier, S.; Cessna, A.J. Quantifying preferential flow in soils: A review of different techniques. J. Hydrol. 2009, 378, 179–204. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Steenhuis, T.S.; Nam, K. Movement of heavy metals in soil through preferential flow paths under different rainfall intensities. CLEAN-Soil Air Water 2008, 36, 984–989. [Google Scholar] [CrossRef]
- Smet, S.; Beckers, E.; Plougonven, E.; Léonard, A.; Degré, A. Can the pore scale geometry explain soil sample scale hydrodynamic properties? Front. Environ. Sci. 2018, 6, 20. [Google Scholar] [CrossRef]
- Pierret, A.; Capowiez, Y.; Belzunces, L.; Moran, C.J. 3D reconstruction and quantification of macropores using X-ray computed tomography and image analysis. Geoderma 2002, 106, 247. [Google Scholar] [CrossRef]
- Bastardie, F.; Capowiez, Y.; de Dreuzy, J.R.; Cluzeau, D. X-ray tomographic and hydraulic characterization of burrowing by three earthworm species in repacked soil cores. Appl. Soil Ecol. 2003, 24, 3–16. [Google Scholar] [CrossRef]
- Luo, L.; Lin, H.; Halleck, P. Quantifying soil structure and preferential flow in intact soil using X-ray computed tomography. Soil Sci. Soc. Am. J. 2008, 72, 1058–1069. [Google Scholar] [CrossRef]
- Peth, S.; Horn, R.; Beckmann, F.; Donath, T.; Fischer, J.; Smucker, A.J.M. Three-dimensional quantification of intra-aggregate pore-space features using synchrotron-radiation-based microtomography. Soil Sci. Soc. Am. J. 2008, 72, 897–907. [Google Scholar] [CrossRef]
- Saravanathiiban, D.S.; Kutay, M.E.; Khire, M.V. Effect of macropore tortuosity and morphology on preferential flow through saturated soil: A Lattice Boltzmann study. Comput. Geotech. 2014, 59, 44–53. [Google Scholar] [CrossRef]
- Allaire, S.E.; Gupta, S.C.; Nieber, J.; Moncrief, J.F. Role of macropore continuity and tortuosity on solute transport in soils—1. Effects of initial and boundary conditions. J. Contam. Hydrol. 2002, 58, 299–321. [Google Scholar] [CrossRef]
- Luo, L.; Lin, H.; Schmidt, J. Quantitative relationships between soil macropore characteristics and preferential flow and transport. Soil Sci. Soc. Am. J. 2010, 74, 1929–1937. [Google Scholar] [CrossRef]
- Hu, X.; Li, Z.-C.; Li, X.-Y.; Liu, L.-Y. Quantification of soil macropores under alpine vegetation using computed tomography in the Qinghai Lake Watershed, NE Qinghai–Tibet Plateau. Geoderma 2016, 264, 244–251. [Google Scholar] [CrossRef]
- Zhang, J.; Wen, N.; Sun, Q.; Horton, R.; Liu, G. The effect of macropore morphology of actual anecic earthworm burrows on water infiltration: A COMSOL simulation. J. Hydrol. 2023, 618, 129261. [Google Scholar] [CrossRef]
- Cheik, S.; Bottinelli, N.; Minh, T.T.; Doan, T.T.; Jouquet, P. Quantification of three dimensional characteristics of macrofauna macropores and their effects on soil hydraulic conductivity in Northern Vietnam. Front. Environ. Sci. 2019, 7, 31. [Google Scholar] [CrossRef]
- Müller, K.; Katuwal, S.; Young, I.; McLeod, M.; Moldrup, P.; de Jonge, L.W.; Clothier, B. Characterising and linking X-ray CT derived macroporosity parameters to infiltration in soils with contrasting structures. Geoderma 2018, 313, 82–91. [Google Scholar] [CrossRef]
- Rasse, D.P.; Smucker, A.J.M.; Santos, D. Alfalfa root and shoot mulching effects on soil hydraulic properties and aggregation. Soil Sci. Soc. Am. J. 2000, 64, 725–731. [Google Scholar] [CrossRef]
- Meurer, K.; Barron, J.; Chenu, C.; Coucheney, E.; Fielding, M.; Hallett, P.; Herrmann, A.M.; Keller, T.; Koestel, J.; Larsbo, M.; et al. A framework for modelling soil structure dynamics induced by biological activity. Glob. Chang. Biol. 2020, 26, 5382–5403. [Google Scholar] [CrossRef]
- Porre, R.J.; van Groenigen, J.W.; De Deyn, G.B.; de Goede, R.G.M.; Lubbers, I.M. Exploring the relationship between soil mesofauna, soil structure and N2O emissions. Soil Biol. Biochem. 2016, 96, 55–64. [Google Scholar] [CrossRef]
- Chen, L.; Ghorbani, J.; Zhang, C.; Dutta, T.T.; Kodikara, J. A novel unified model for volumetric hardening and water retention in unsaturated soils. Comput. Geotech. 2021, 140, 104446. [Google Scholar] [CrossRef]
- Ghorbani, J.; Chen, L.; Kodikara, J.; Carter, J.P.; McCartney, J.S. Memory repositioning in soil plasticity models used in contact problems. Comput. Mech. 2022, 71, 385–408. [Google Scholar] [CrossRef]
- Capowiez, Y.; Bottinelli, N.; Sammartino, S.; Michel, E.; Jouquet, P. Morphological and functional characterisation of the burrow systems of six earthworm species (Lumbricidae). Biol. Fertil. Soils 2015, 51, 869–877. [Google Scholar] [CrossRef]
- Xin, P.; Yu, X.; Lu, C.; Li, L. Effects of macro-pores on water flow in coastal subsurface drainage systems. Adv. Water Resour. 2016, 87, 56–67. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, J.; Chen, Y.; Zhang, H.; Zhang, F.; Yao, J. Study of soil macropore spatial structure based on stand spatial structure analysis method. Trans. Chin. Soc. Agric. Mach. 2015, 46, 174–186. [Google Scholar] [CrossRef]
- Weiler, M.; Naef, F. Simulating surface and subsurface initiation of macropore flow. J. Hydrol. 2003, 273, 139–154. [Google Scholar] [CrossRef]
- Droogers, P.; Stein, A.; Bouma, J.; de Boer, G. Parameters for describing soil macroporosity derived from staining patterns. Geoderma 1998, 83, 293–308. [Google Scholar] [CrossRef]
- Li, L.; Gu, Z.; Xu, W.; Tan, Y.; Fan, X.; Tan, D. Mixing mass transfer mechanism and dynamic control of gas-liquid-solid multiphase flow based on VOF-DEM coupling. Energy 2023, 272, 127015. [Google Scholar] [CrossRef]
- Li, L.; Xu, W.; Tan, Y.; Yang, Y.; Yang, J.; Tan, D. Fluid-induced vibration evolution mechanism of multiphase free sink vortex and the multi-source vibration sensing method. Mech. Syst. Signal. Process. 2023, 189, 110058. [Google Scholar] [CrossRef]
- Xing, K.; Qian, J.; Ma, L.; Ma, H.; Zhao, W. Characterizing the scaling coefficient ω between viscous and inertial permeability of fractures. J. Hydrol. 2021, 593, 125920. [Google Scholar] [CrossRef]
- Xing, K.; Qian, J.; Zhao, W.; Ma, H.; Ma, L. Experimental and numerical study for the inertial dependence of non-Darcy coefficient in rough single fractures. J. Hydrol. 2021, 603, 127148. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, B.X.; Ye, M. Numerical modeling and sensitivity analysis of seawater intrusion in a dual-permeability coastal karst aquifer with conduit networks. Hydrol. Earth Syst. Sci. 2018, 22, 221–239. [Google Scholar] [CrossRef]
- Lepore, B.J.; Morgan, C.L.S.; Norman, J.M.; Molling, C.C. A mesopore and matrix infiltration model based on soil structure. Geoderma 2009, 152, 301–313. [Google Scholar] [CrossRef]
- Bronstert, A.; Niehoff, D.; Schiffler, G.R. Modelling infiltration and infiltration excess: The importance of fast and local processes. Hydrol. Process. 2023, 37, e14875. [Google Scholar] [CrossRef]
- Sheng, F.; Liu, H.; Wang, K.; Zhang, R.; Tang, Z. Investigation into preferential flow in natural unsaturated soils with field multiple-tracer infiltration experiments and the active region model. J. Hydrol. 2014, 508, 137–146. [Google Scholar] [CrossRef]
- Herbst, M.; Diekkrüger, B. The influence of the spatial structure of soil properties on water balance modeling in a microscale catchment. Phys. Chem. Earth. Parts A/B/C 2002, 27, 701–710. [Google Scholar] [CrossRef]
- Herbst, M.; Diekkrüger, B.; Vanderborght, J. Numerical experiments on the sensitivity of runoff generation to the spatial variation of soil hydraulic properties. J. Hydrol. 2006, 326, 43–58. [Google Scholar] [CrossRef]
- Zhou, T.; Xin, P.; Li, L.; Barry, D.A.; Šimůnek, J. Effects of large macropores on soil evaporation in salt marshes. J. Hydrol. 2020, 584, 124754. [Google Scholar] [CrossRef]
- Liu, G.; Li, B.; Hu, K.; van Genuchten, M.T. Simulating the gas diffusion coefficient in macropore network images: Influence of soil pore morphology. Soil Sci. Soc. Am. J. 2006, 70, 1252–1261. [Google Scholar] [CrossRef]
- Rosenbom, A.E.; Binning, P.J.; Aamand, J.; Dechesne, A.; Smets, B.F.; Johnsen, A.R. Does microbial centimeter-scale heterogeneity impact MCPA degradation in and leaching from a loamy agricultural soil? Sci. Total Environ. 2014, 472, 90–98. [Google Scholar] [CrossRef]
- Wen, N.; Zhang, J.; Zeng, H.; Liu, G.; Horton, R. In-situ tin casting combined with three-dimensional scanner to quantify anecic earthworm burrows. Vadose Zone J. 2022, 21, e20198. [Google Scholar] [CrossRef]
- Anderson, B.; Newman, M.A.; Grim Ii, P.A.; Hardin, J.M. A Monte Carlo simulation framework for reject inference. J. Oper. Res. Soc. 2022, 74, 1133–1149. [Google Scholar] [CrossRef]
- Mallants, D.; Jacques, D.; Vanclooster, M.; Diels, J.; Feyen, J. A atochastic approach to simulate water flow in a macroporous soil. Geoderma 1996, 70, 299–324. [Google Scholar] [CrossRef]
- Liu, G.; Si, B.C. Soil ice content measurement using a heat pulse probe method. Can. J. Agric. Sci. 2011, 91, 235–246. [Google Scholar] [CrossRef]
- Shao, W.; Bogaard, T.; Bakker, M. How to use COMSOL Multiphysics for coupled dual-permeability hydrological and slope stability modeling. Procedia Earth Planet. Sci. 2014, 9, 83–90. [Google Scholar] [CrossRef]
- Zhu, H.; Tang, H.; Cheng, Y.; Li, Z.; Qiu, J.; Tong, L. Electrostatic separation of pea proteins assisted by COMSOL simulation. J. Food Eng. 2022, 335, 111175. [Google Scholar] [CrossRef]
- Yu, X.; Song, M.; Wang, Z. Simulation and verification of effect of arc duration on arc temperature based on COMSOL. Machines 2023, 11, 289. [Google Scholar] [CrossRef]
- Sang, Y.; Liu, G.; Horton, R. Wind effects on soil thermal properties measured by the dual-probe heat pulse method. Soil Sci. Soc. Am. J. 2020, 84, 414–424. [Google Scholar] [CrossRef]
- Feehley, C.E.; Zheng, C.; Molz, F.J. A dual-domain mass transfer approach for modeling solute transport in heterogeneous aquifers: Application to the Macrodispersion Experiment (MADE) site. Water Resour. Res. 2000, 36, 2501–2515. [Google Scholar] [CrossRef]
- Hakoun, V.; Comolli, A.; Dentz, M. Upscaling and prediction of Lagrangian velocity dynamics in heterogeneous porous media. Water Resour. Res. 2019, 55, 3976–3996. [Google Scholar] [CrossRef]
- Ma, L.; Gao, D.; Qian, J.; Han, D.; Xing, K.; Ma, H.; Deng, Y. Multiscale fractures integrated equivalent porous media method for simulating flow and solute transport in fracture-matrix system. J. Hydrol. 2023, 617, 128845. [Google Scholar] [CrossRef]
- Hou, X.; Fan, H. Study on rainfall infiltration characteristics of unsaturated fractured soil based on COMSOL Multiphysics. Rock Soil Mech. 2022, 43, 563–572. [Google Scholar] [CrossRef]
- Zhou, Y.; Liang, X.; Ma, E.; Chen, K.; Zhang, J.; Zhang, Y.-K. Effect of unsaturated flow on groundwater-river interactions induced by flood event in riparian zone. J. Hydrol. 2023, 620, 129405. [Google Scholar] [CrossRef]
- Akay, O.; Fox, G.A.; Šimůnek, J. Numerical simulation of flow dynamics during macropore–subsurface drain interactions using HYDRUS. Vadose Zone J. 2008, 7, 909–918. [Google Scholar] [CrossRef]
- Xin, P.; Jin, G.; Li, L.; Barry, D.A. Effects of crab burrows on pore water flows in salt marshes. Adv. Water Resour. 2009, 32, 439–449. [Google Scholar] [CrossRef]
- Cai, H.; Zhang, Q.; Ye, G.; Lu, L.; Wu, C.; Ji, F. Investigation on strong vertical permeability and micro-pore characteristics of Jinan red clay using X-ray micro-tomography. Environ. Earth Sci. 2023, 82, 122. [Google Scholar] [CrossRef]
- Luo, L.; Lin, H.; Li, S. Quantification of 3-D soil macropore networks in different soil types and land uses using computed tomography. J. Hydrol. 2010, 393, 53–64. [Google Scholar] [CrossRef]
- Scheibe, T.D.; Perkins, W.A.; Richmond, M.C.; McKinley, M.I.; Romero-Gomez, P.D.J.; Oostrom, M.; Wietsma, T.W.; Serkowski, J.A.; Zachara, J.M. Pore-scale and multiscale numerical simulation of flow and transport in a laboratory-scale column. Water Resour. Res. 2015, 51, 1023–1035. [Google Scholar] [CrossRef]
- Veeraraghavan, P. The G-convexity and the G-centroids of composite graphs. Mathematics 2020, 8, 1927. [Google Scholar] [CrossRef]
- Yan, H.; Tao, J.; Dong, L. Analysis on the centroid offset of coupling beam in array-composite resonator due to process variations. Sens. Mater. 2018, 30, 2727–2745. [Google Scholar] [CrossRef]
- Cey, E.E.; Rudolph, D.L. Field study of macropore flow processes using tension infiltration of a dye tracer in partially saturated soils. Hydrol. Process. 2009, 23, 1768–1779. [Google Scholar] [CrossRef]
- Arora, B.; Mohanty, B.P.; McGuire, J.T. Inverse estimation of parameters for multidomain flow models in soil columns with different macropore densities. Water Resour. Res. 2011, 47, W04512. [Google Scholar] [CrossRef]
- Meng, C.; Niu, J.; Li, X.; Luo, Z.; Du, X.; Du, J.; Lin, X.; Yu, X. Quantifying soil macropore networks in different forest communities using industrial computed tomography in a mountainous area of North China. J. Soils Sediments 2016, 17, 2357–2370. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, K.; Zhou, H.; Lin, H.; Li, D.; Peng, X. Linking saturated hydraulic conductivity and air permeability to the characteristics of biopores derived from X-ray computed tomography. J. Hydrol. 2019, 571, 1–10. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, T.; Duan, L.; Chen, Z.; Wang, Y.; Li, Y.; Zhao, X.; Wang, G.; Singh, V.P. Processes of preferential flow in a eurasian steppe under different scenarios. J. Hydrol. 2022, 612, 128166. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Z. Dye tracer infiltration technique to investigate macropore flow paths in Maka Mountain, Yunnan Province, China. J. Cent. South Univ. 2016, 23, 2101–2109. [Google Scholar] [CrossRef]
- Akhtar, M.S.; Stüben, D.; Norra, S.; Memon, M. Soil structure and flow rate-controlled molybdate, arsenate and chromium(III) transport through field columns. Geoderma 2011, 161, 126–137. [Google Scholar] [CrossRef]
- Torrentó, C.; Prasuhn, V.; Spiess, E.; Ponsin, V.; Melsbach, A.; Lihl, C.; Glauser, G.; Hofstetter, T.B.; Elsner, M.; Hunkeler, D. Adsorbing vs. nonadsorbing tracers for assessing pesticide transport in arable soils. Vadose Zone J. 2017, 17, 1–18. [Google Scholar] [CrossRef]
- Xie, S.; Wen, Z.; Jakada, H. A new model approach for reactive solute transport in dual-permeability media with depth-dependent reaction coefficients. J. Hydrol. 2019, 577, 123946. [Google Scholar] [CrossRef]
- Larsbo, M.; Koestel, J.; Jarvis, N. Relations between macropore network characteristics and the degree of preferential solute transport. Hydrol. Earth Syst. Sci. 2014, 18, 5255–5269. [Google Scholar] [CrossRef]
- Akay, O.; Fox, G.A. Experimental investigation of direct connectivity between macropores and subsurface drains during infiltration. Soil Sci. Soc. Am. J. 2007, 71, 1600–1606. [Google Scholar] [CrossRef]
- Alberti, D.R.; Cey, E.E. Evaluation of macropore flow and transport using three-dimensional simulation of tension infiltration experiments. Vadose Zone J. 2011, 10, 603–617. [Google Scholar] [CrossRef]
- Jarvis, N.; Larsbo, M.; Koestel, J. Connectivity and percolation of structural pore networks in a cultivated silt loam soil quantified by X-ray tomography. Geoderma 2017, 287, 71–79. [Google Scholar] [CrossRef]
- Julich, S.; Kreiselmeier, J.; Scheibler, S.; Petzold, R.; Schwärzel, K.; Feger, K.-H. Hydraulic properties of forest soils with stagnic conditions. Forests 2021, 12, 1113. [Google Scholar] [CrossRef]
- Jačka, L.; Walmsley, A.; Kovář, M.; Frouz, J. Effects of different tree species on infiltration and preferential flow in soils developing at a clayey spoil heap. Geoderma 2021, 403, 115372. [Google Scholar] [CrossRef]
- Hellner, Q.; Koestel, J.; Ulén, B.; Larsbo, M.; Goss, M. Effects of tillage and liming on macropore networks derived from X-ray tomography images of a silty clay soil. Soil Use Manag. 2018, 34, 197–205. [Google Scholar] [CrossRef]
- Lucas, M.; Schlüter, S.; Vogel, H.-J.; Vetterlein, D. Soil structure formation along an agricultural chronosequence. Geoderma 2019, 350, 61–72. [Google Scholar] [CrossRef]
- Pagenkemper, S.K.; Athmann, M.; Uteau, D.; Kautz, T.; Peth, S.; Horn, R. The effect of earthworm activity on soil bioporosity—Investigated with X-ray computed tomography and endoscopy. Soil Tillage Res. 2015, 146, 79–88. [Google Scholar] [CrossRef]
- Ahmadi, A.; Chitsazan, M.; Mirzaee, S.Y.; Nadri, A. The effects of influence radius and drawdown cone on the areas related to the protection of water wells. J. Hydrol. 2023, 617, 129001. [Google Scholar] [CrossRef]
- Li, L.; Hou, X.; Li, Y. A finite element method for calculating the influence radius of foundation pit dewatering. Rock Soil Mech. 2021, 42, 574–580. [Google Scholar] [CrossRef]
- Liu, H.-B.; Zhou, J.-Q.; Li, C.; Tan, J.; Hou, D. Semi-empirical models for predicting stable water inflow and influence radius of a tunnel considering non-Darcian effect. J. Hydrol. 2023, 621, 129574. [Google Scholar] [CrossRef]
- Budhathoki, S.; Lamba, J.; Srivastava, P.; Malhotra, K.; Way, T.R.; Katuwal, S. Temporal and spatial variability in 3D soil macropore characteristics determined using X-ray computed tomography. J. Soils Sediments 2022, 22, 1263–1277. [Google Scholar] [CrossRef]
- Hallam, J.; Berdeni, D.; Grayson, R.; Guest, E.J.; Holden, J.; Lappage, M.G.; Prendergast-Miller, M.T.; Robinson, D.A.; Turner, A.; Leake, J.R.; et al. Effect of earthworms on soil physico-hydraulic and chemical properties, herbage production, and wheat growth on arable land converted to ley. Sci. Total Environ. 2020, 713, 136491. [Google Scholar] [CrossRef]
- Lipiec, J.; Turski, M.; Hajnos, M.; Świeboda, R. Pore structure, stability and water repellency of earthworm casts and natural aggregates in loess soil. Geoderma 2015, 243–244, 124–129. [Google Scholar] [CrossRef]
- Van Groenigen, J.W.; Van Groenigen, K.J.; Koopmans, G.F.; Stokkermans, L.; Vos, H.M.J.; Lubbers, I.M. How fertile are earthworm casts? A meta-analysis. Geoderma 2019, 338, 525–535. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Huan, X.; Qian, J.; Xing, Y. Numerical Study of the Influence of Horizontal Spatial Distribution of Macropores on Water Infiltration. Water 2023, 15, 3593. https://doi.org/10.3390/w15203593
Zhang R, Huan X, Qian J, Xing Y. Numerical Study of the Influence of Horizontal Spatial Distribution of Macropores on Water Infiltration. Water. 2023; 15(20):3593. https://doi.org/10.3390/w15203593
Chicago/Turabian StyleZhang, Ruigang, Xiaoxiang Huan, Jiazhong Qian, and Yueqing Xing. 2023. "Numerical Study of the Influence of Horizontal Spatial Distribution of Macropores on Water Infiltration" Water 15, no. 20: 3593. https://doi.org/10.3390/w15203593
APA StyleZhang, R., Huan, X., Qian, J., & Xing, Y. (2023). Numerical Study of the Influence of Horizontal Spatial Distribution of Macropores on Water Infiltration. Water, 15(20), 3593. https://doi.org/10.3390/w15203593





