Analysis of Water-Surface Oscillations Upstream of a Double-Right-Angled Bend with Incoming Supercritical Flow
Abstract
:1. Introduction
- What are the effects of altering the approaching flow and Froude number on the upstream water elevation of the DRAB, and how can the maximum water depth upstream of the DRAB be estimated?
- Can the existing analytical/empirical equations used to predict the backwater effect be applied to the DRAB configuration?
- What are the flow conditions that induce water-surface oscillations upstream of the DRAB?
- What are the dominant frequencies characterizing these oscillations, and is there an empirical formula for estimating these dominant frequencies?
2. Methodology
2.1. Experimental Setup
2.2. Experimental Runs
2.2.1. Main Assumptions
- The channel is non-erodible with a fixed bed.
- The channel is a prismatic, constant-width rectangular section.
- All runs were conducted with a constant width (W) of 100 mm and a constant DRAB length (L) of 300 mm (i.e., bend length to width ratio L/W = 3).
- The width through turns is equal to the bed width of the upstream and downstream reaches (b/W = 1).
- All turns within the DRAB are perfectly sharp turns (r = 0, b/2r = ∞) (where r is the radius of curvature of the turns).
- The slopes of all reaches remain constant for each run but vary across different runs.
- All runs were conducted under approaching flow conditions classified as low supercritical flow conditions (1.03 < Fn < 2.63).
- The Manning n roughness varies with the water depth, and the depth-averaged value is approximately 0.008 s/m1/3.
2.2.2. Work Flow
- Adjust the flume bed slope, turn on the pump, and adjust the flow to the required value.
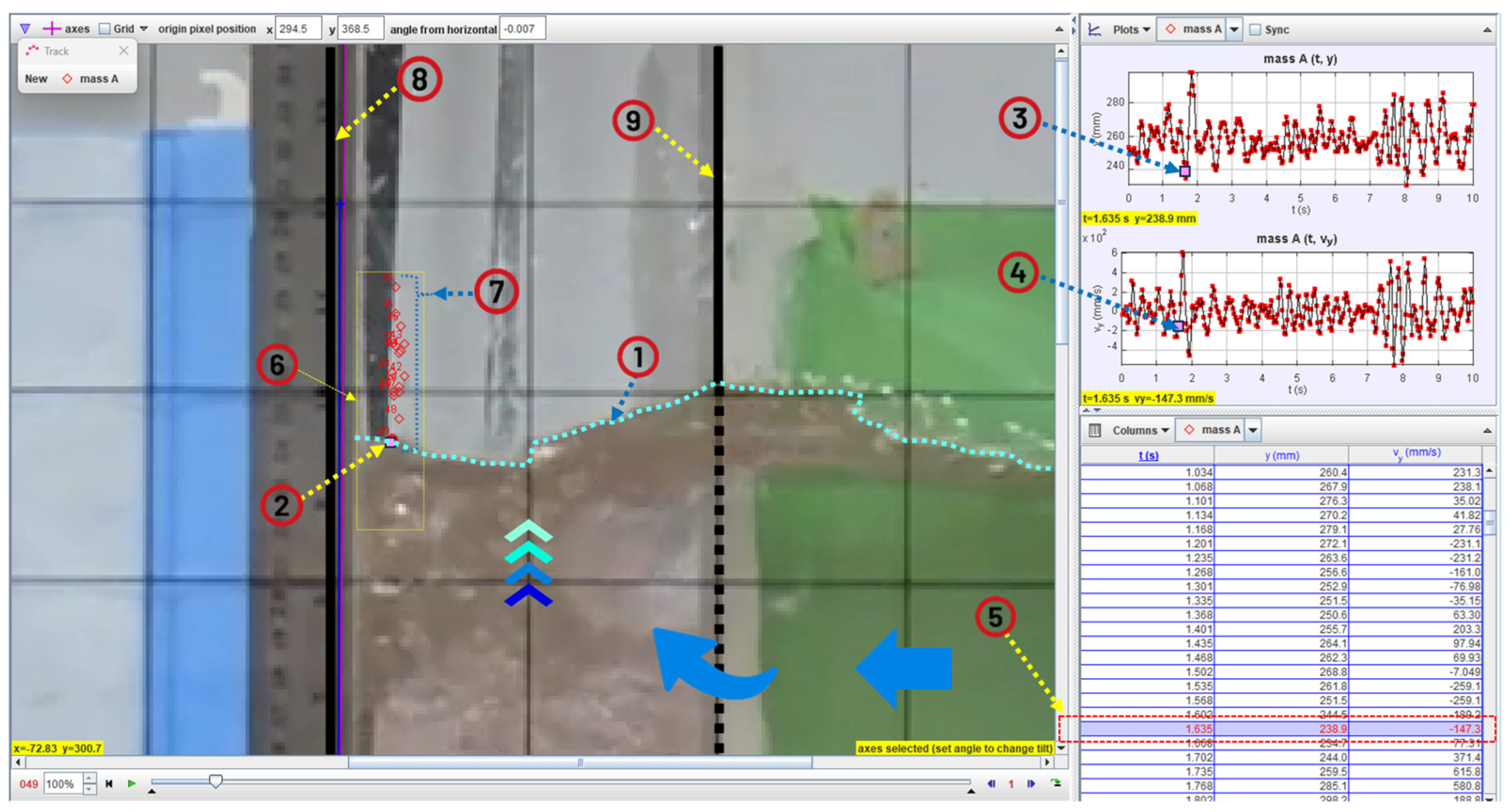
- Wait for a few minutes to reach stationary flow conditions, then start video recording using sampling rate of 30 fps. Export recorded videos and open them in the Tracker software. Adjust axes, scale, and apply suitable filters (if necessary) to ensure a clear water interface. Then, perform auto-tracking for the water-surface upstream of the DRAB. The recording duration should be at least 10 s to obtain sufficient time series data for spectral power analysis. Export time series data of water-surface elevation and vertical velocity and save them to CSV format. Perform power spectral analysis for the water-surface elevation time series data and plot the corresponding power–spectral density curve on a log–log scale using the signal processing toolbox in MATLAB. An m-script was prepared to automate the analysis process (Appendix A).
- Based on the obtained spectral power density curve, identify the dominant frequency and the slope of the higher frequency data.
- Conduct dimensional analysis to identify the relevant π-terms affecting the dominant frequency of the water-surface oscillation upstream of the DRAB. Employ the least squares approach to obtain the best fitting formula for data measurements.
2.3. Digital Cameras
2.4. Video Tracking Packages
2.5. Measurement of Temporal Variation in Water-Surface Elevation
3. Hydraulic Analysis of Supercritical Flow through DRAB
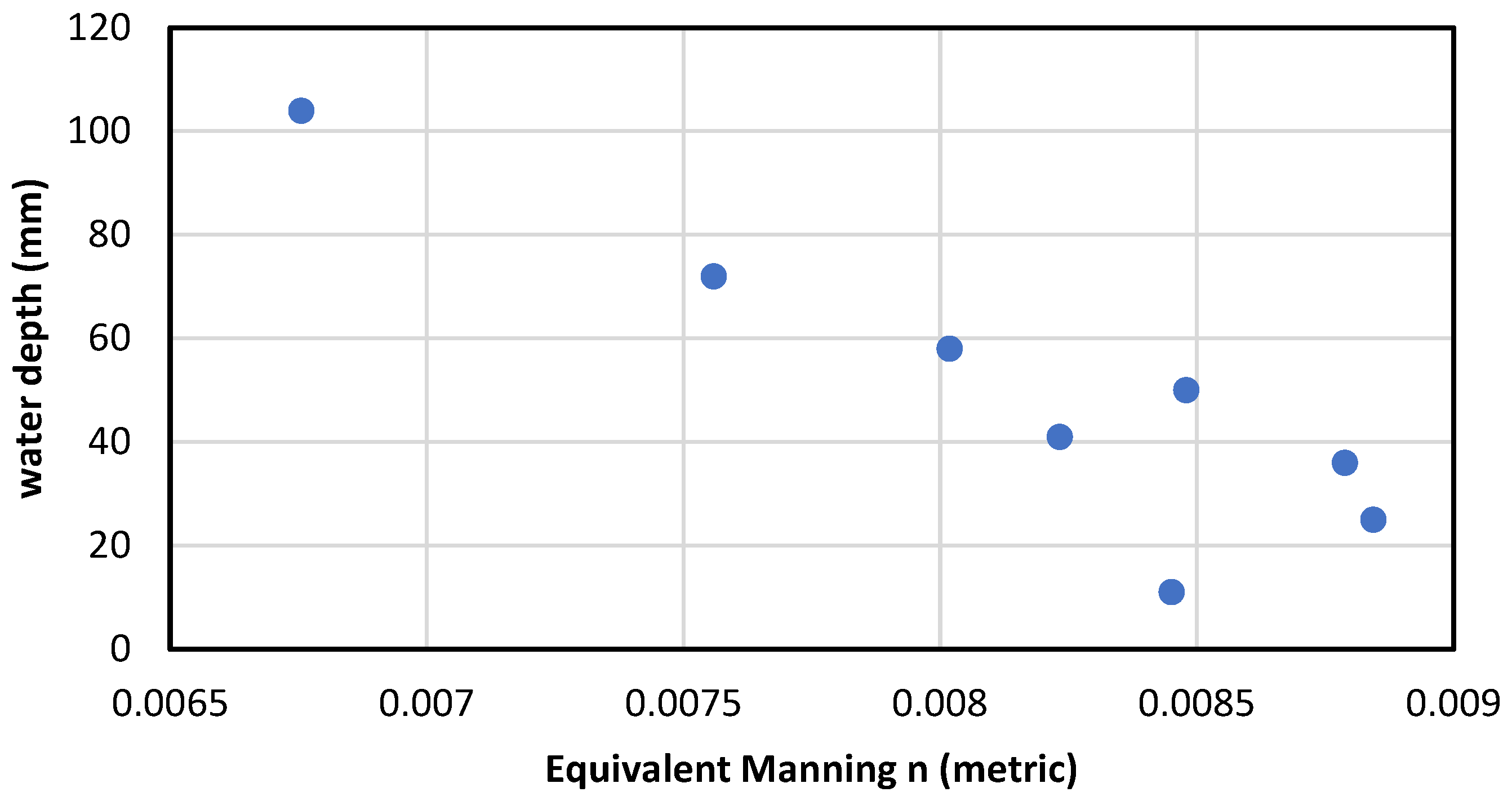
3.1. Estimation of the Equivalent Manning Coefficient
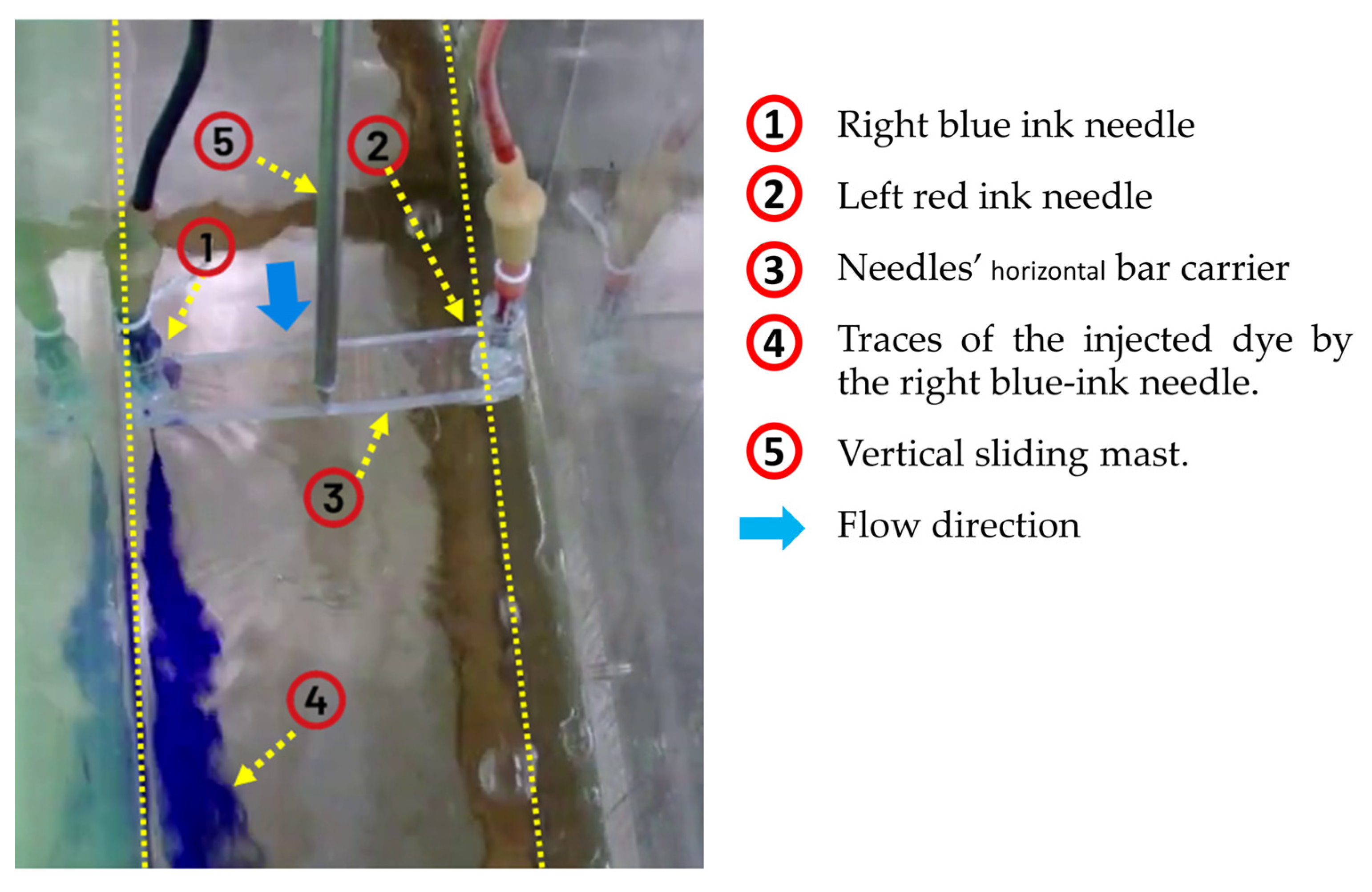
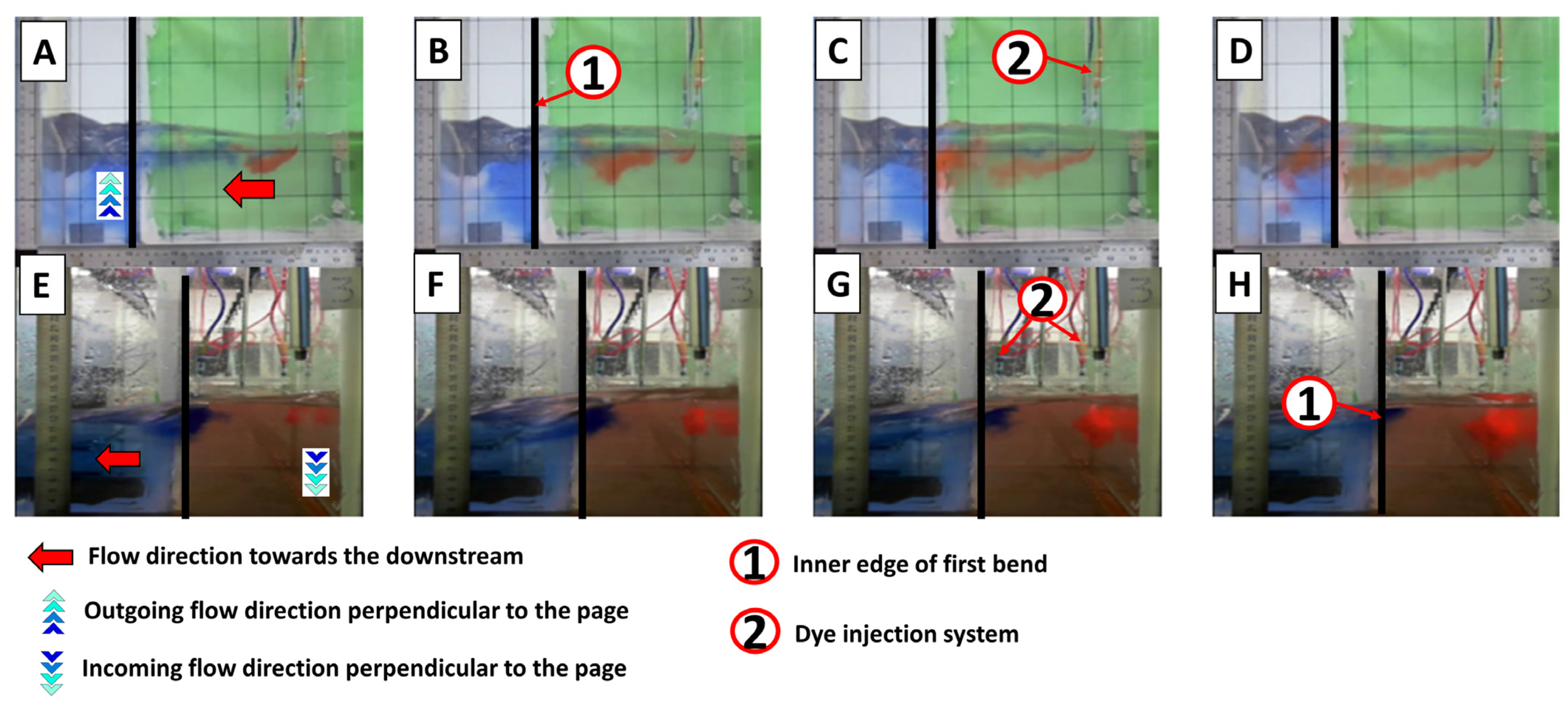
3.2. Visual Analysis
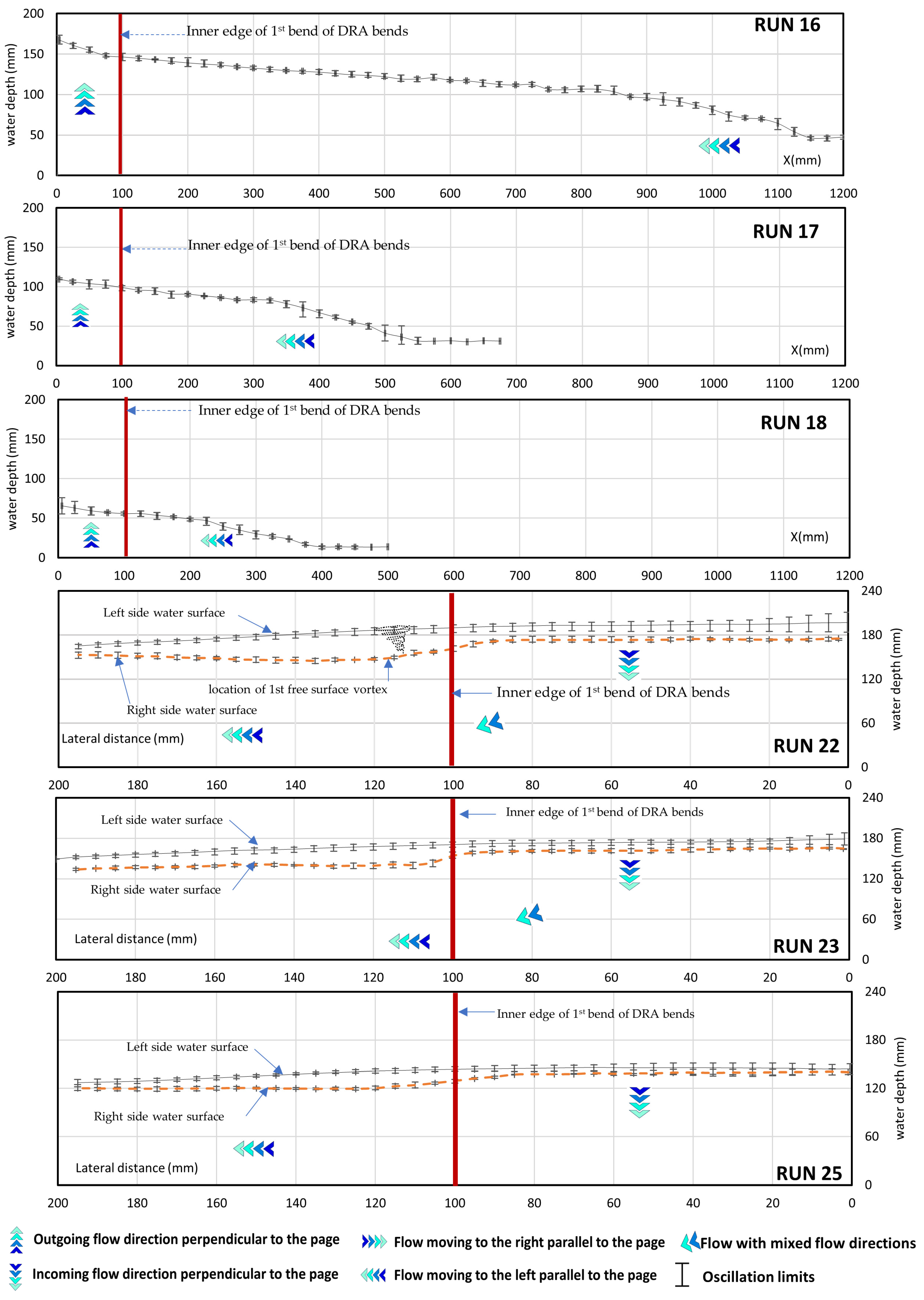
3.3. Spatial Variations in Water Surface
3.4. Water Oscillation Analysis
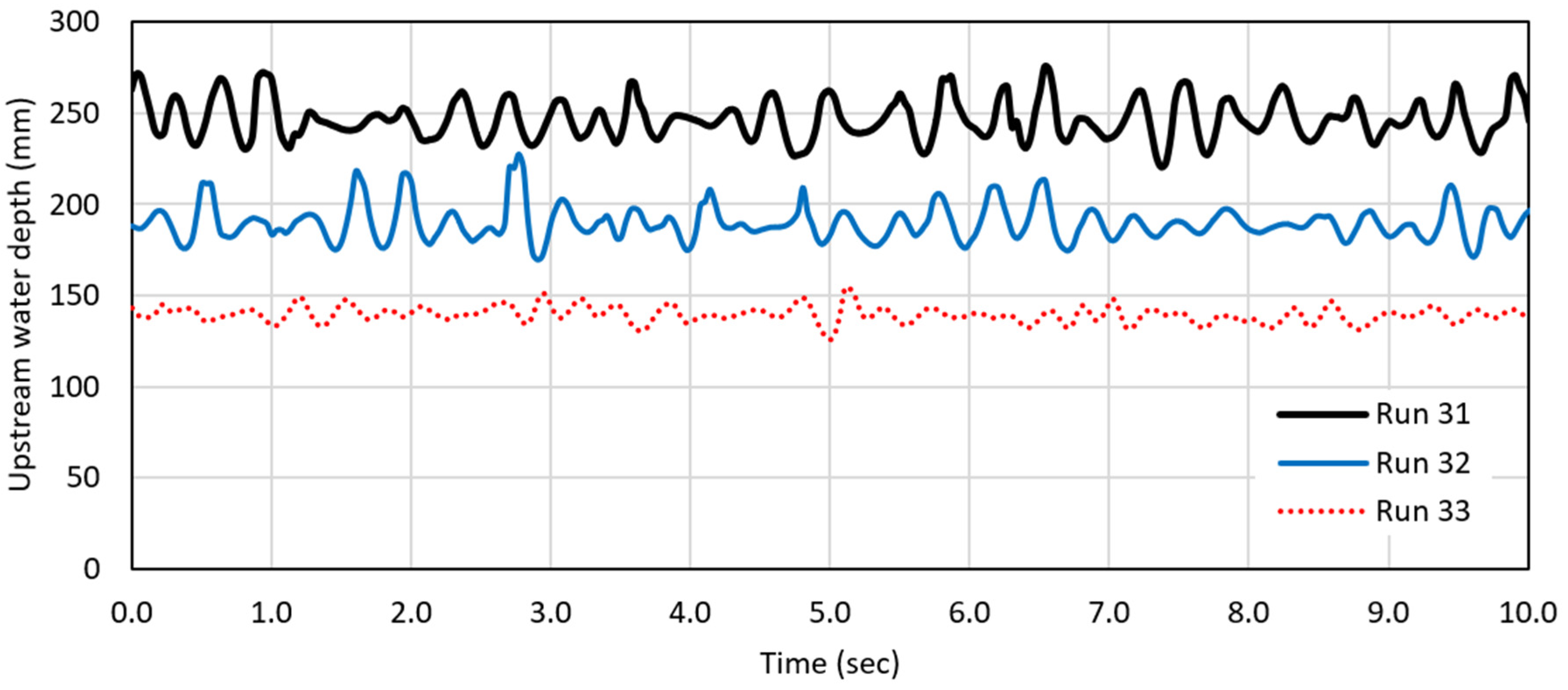
3.4.1. Time Series Analysis
3.4.2. Power Spectral Analysis
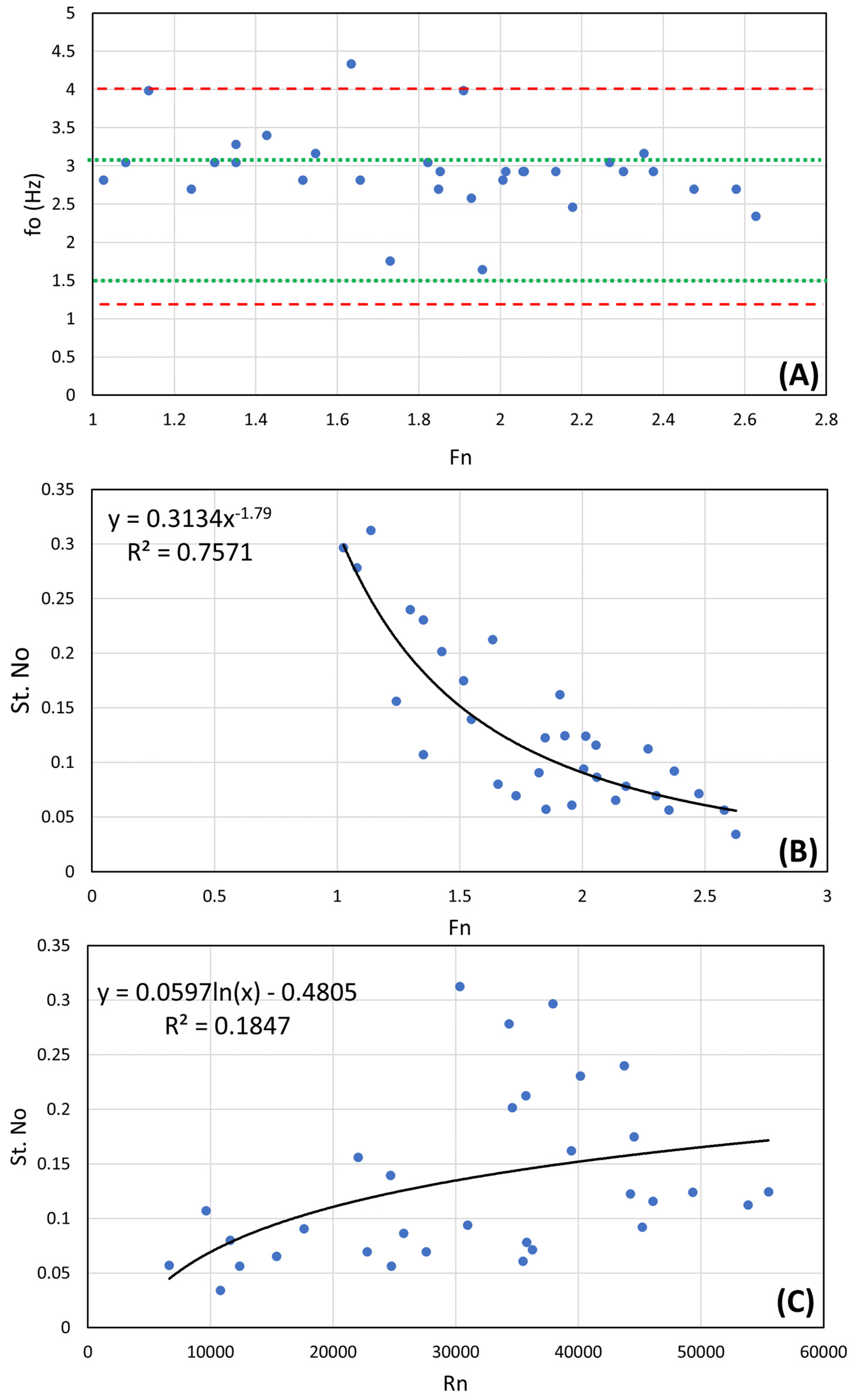
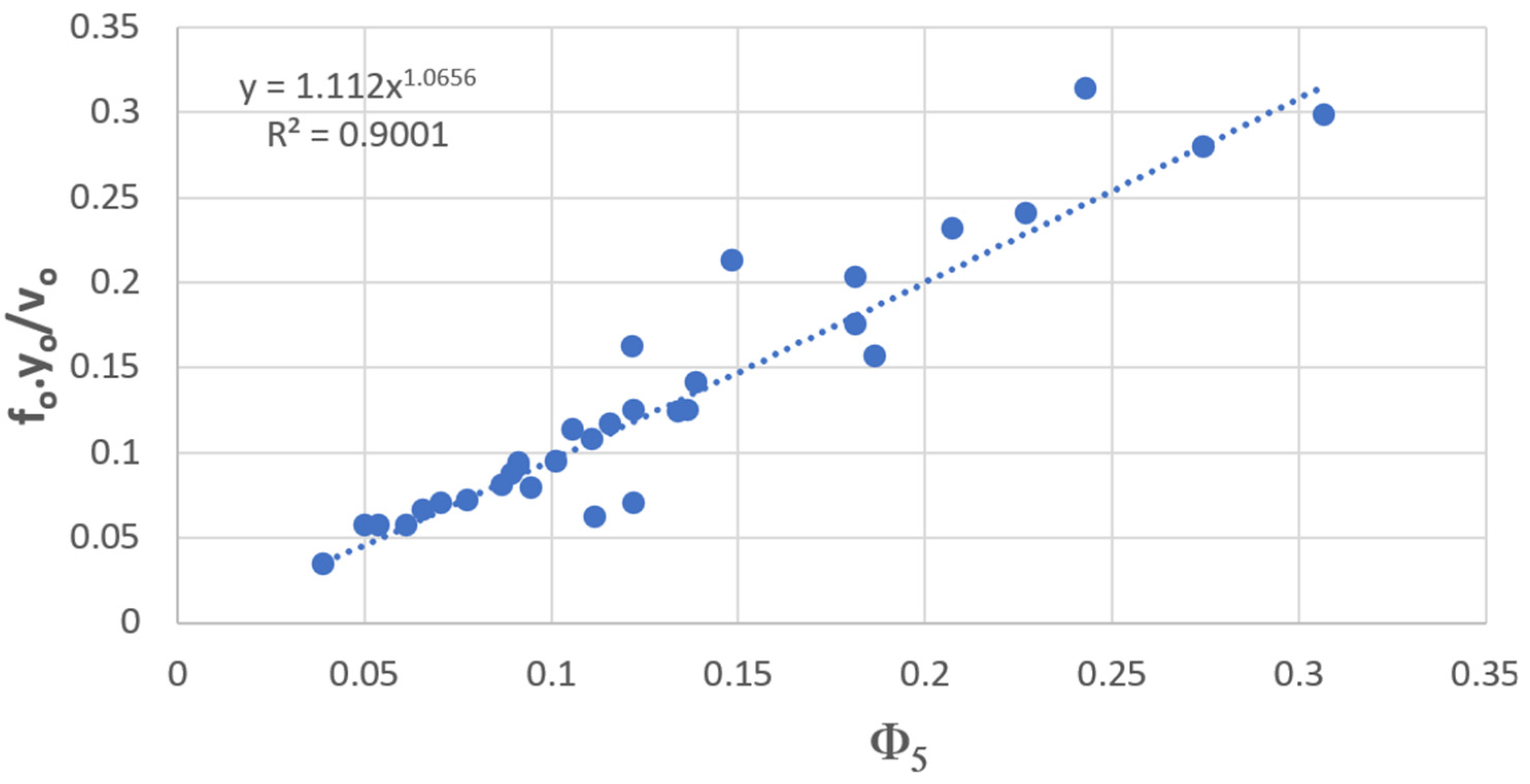
3.5. Regression Frequency Formulas Based on Dimensional Analysis
4. Results and Discussion
4.1. Oscillation of Water Level Upstream DRAB
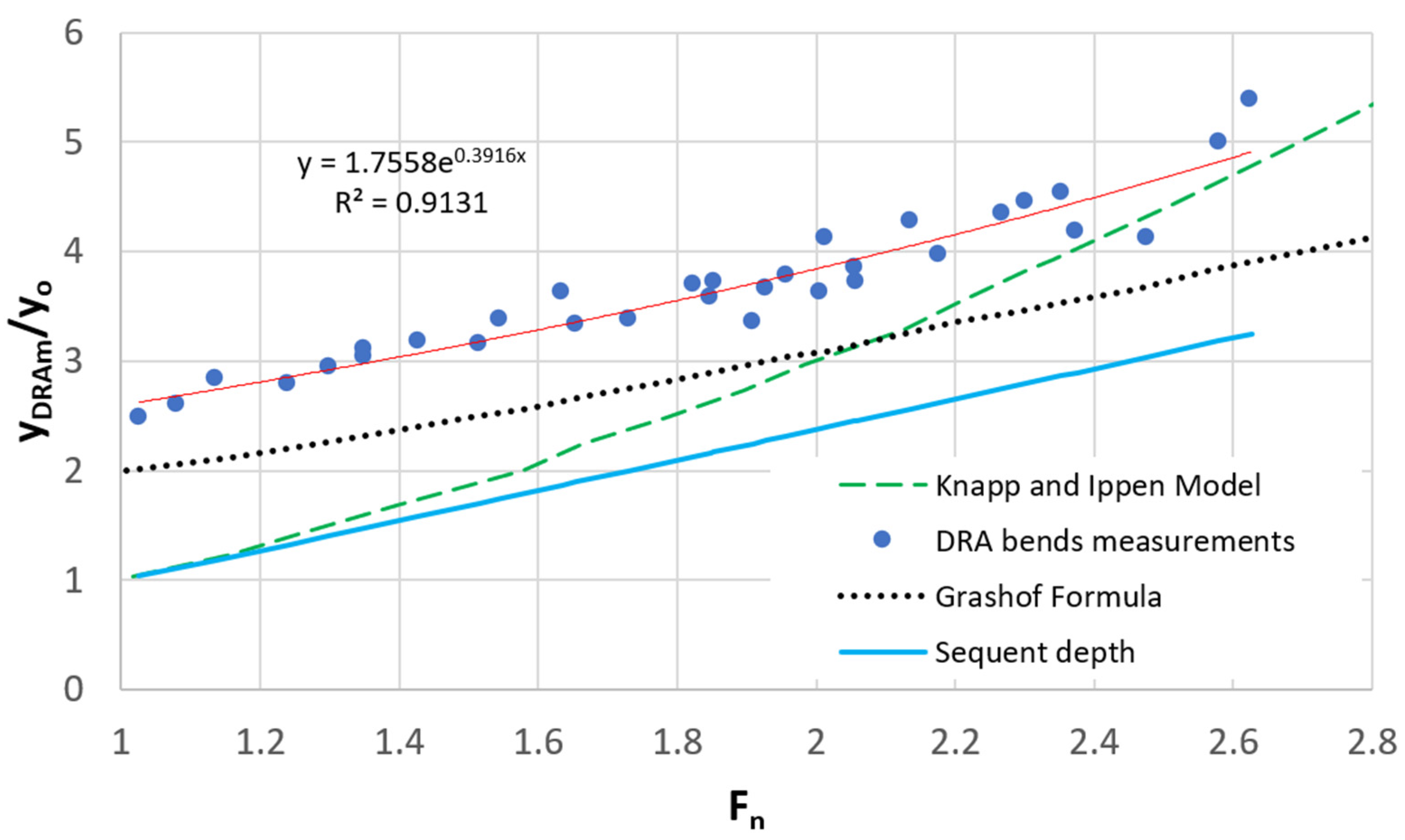
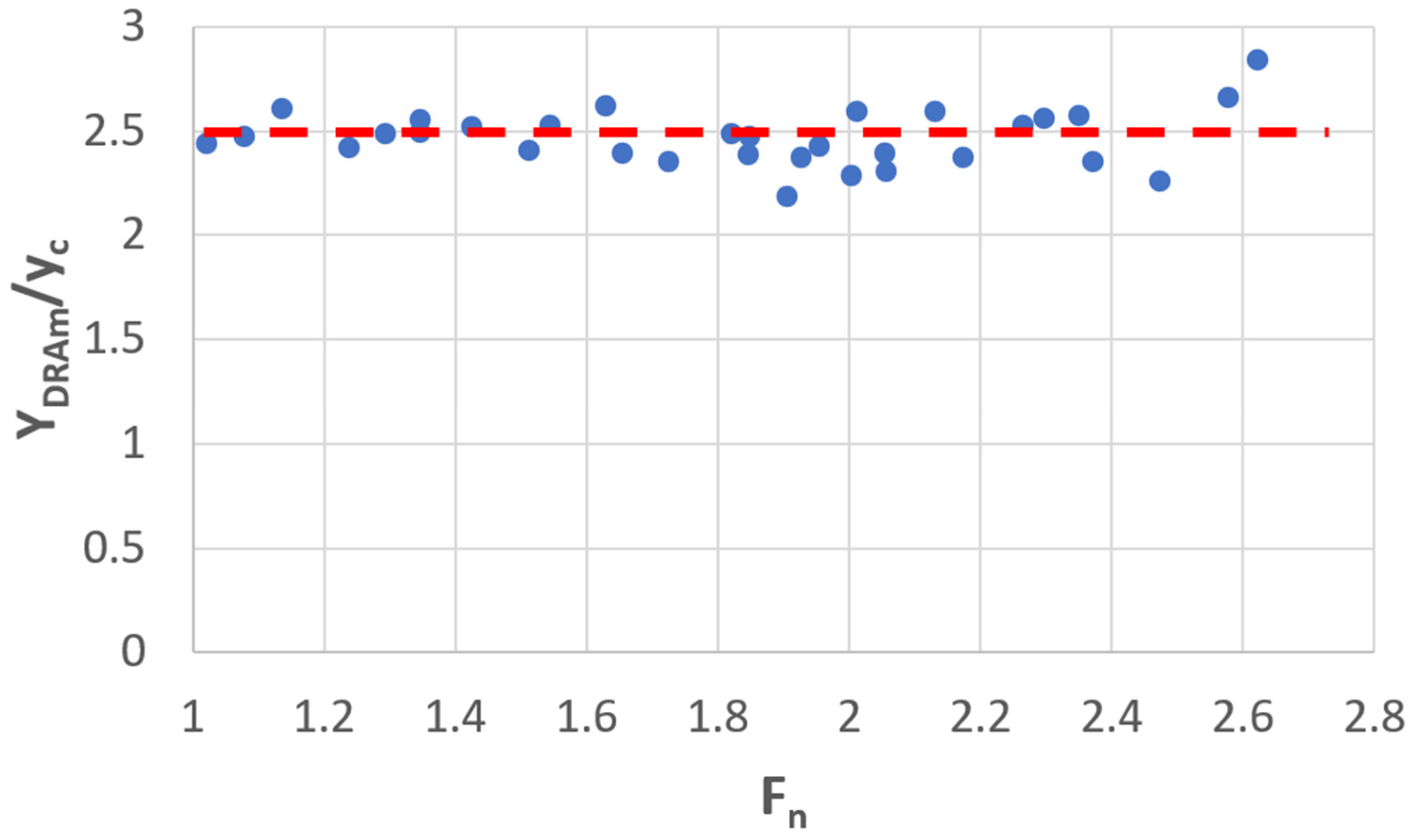
4.2. Water Depth Upstream of DRAB
4.3. Limitations and Outlook
- The experimental runs were conducted for a specific geometry of the DRAB, where the spacing length between the two bends is three times its width (L/W = 3). It is important to note that altering the L/W ratio could lead to the occurrence of “trans-critical flow conversion” earlier within the distance between the two bends. Consequently, supercritical cross waves might be present not only in the downstream reach but also within the gap between the two bends.
- Another limitation is that all the runs were conducted with a channel bed bend–width ratio (b/W) equal to unity. By reducing the b/W ratio, oblique hydraulic jumps may potentially form inside the gap between the two bends, contrary to the observations made in this study. The influence of different L/W or b/W ratios warrants further investigation in future work.
- The study focused solely on DRABs in channels with a rectangular section. However, in trapezoidal channels, the local flow regime can exhibit a mixture of subcritical and supercritical flow at the same cross-section, introducing additional complexities, three-dimensionality, and water depth oscillations. The investigation of DRABs in trapezoidal channels presents a challenging yet important task for future research.
- The experimental runs were limited to approaching flows categorized as low supercritical flow conditions (1.03 ≤ Fn ≤ 2.63). In cases of very high supercritical flow conditions (Fn ≥ 6), the formation of humped non-stationary waves with sustained supercritical flow throughout the bends, without the formation of hydraulic jumps, might be expected.
- Furthermore, the present analysis did not consider the effect of an erodible channel with a movable bed, which could be a significant aspect for future exploration.
5. Conclusions
- The flow through the DRAB is characterized by high complexity and three-dimensionality. The approaching supercritical flow in the upstream reach undergoes a conversion to subcritical flow through the formation of a hydraulic jump upstream of the DRAB. This hydraulic jump was consistently observed in all experimental runs (1.03 ≤ Fn ≤ 2.63).
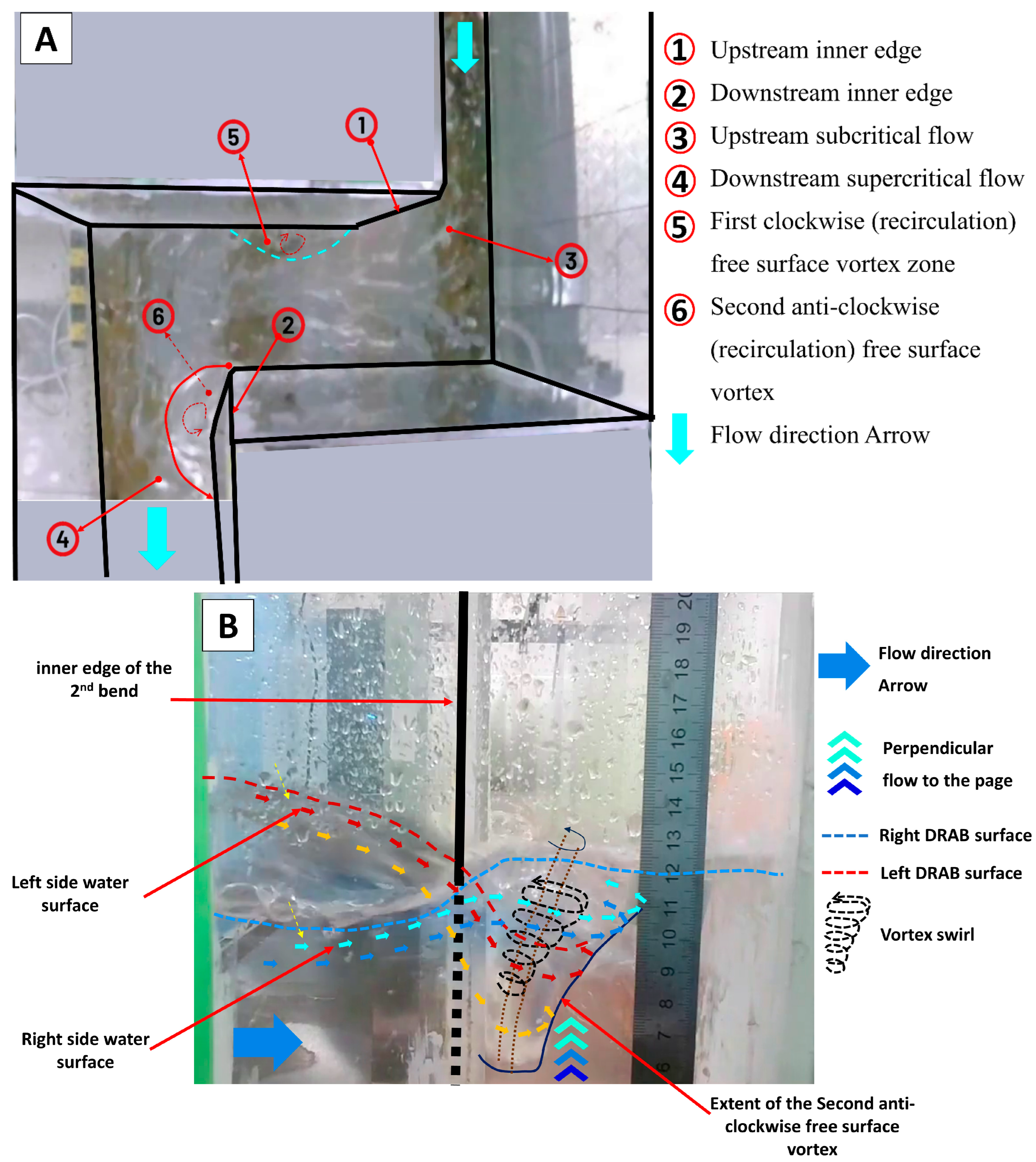
- The dye injection experiments provided valuable insights, showing the formation of a secondary anticlockwise swirl flow just upstream of the DRAB. This flow pattern contributes to water set-up (superelevation) along the left (outer) side of the water surface compared to the right (inner) side of the upstream reach.
- A non-intrusive video tracking system via a set of 5 cameras was used to record the spatial and temporal variations in water surface upstream, within, and downstream of the DRAB.
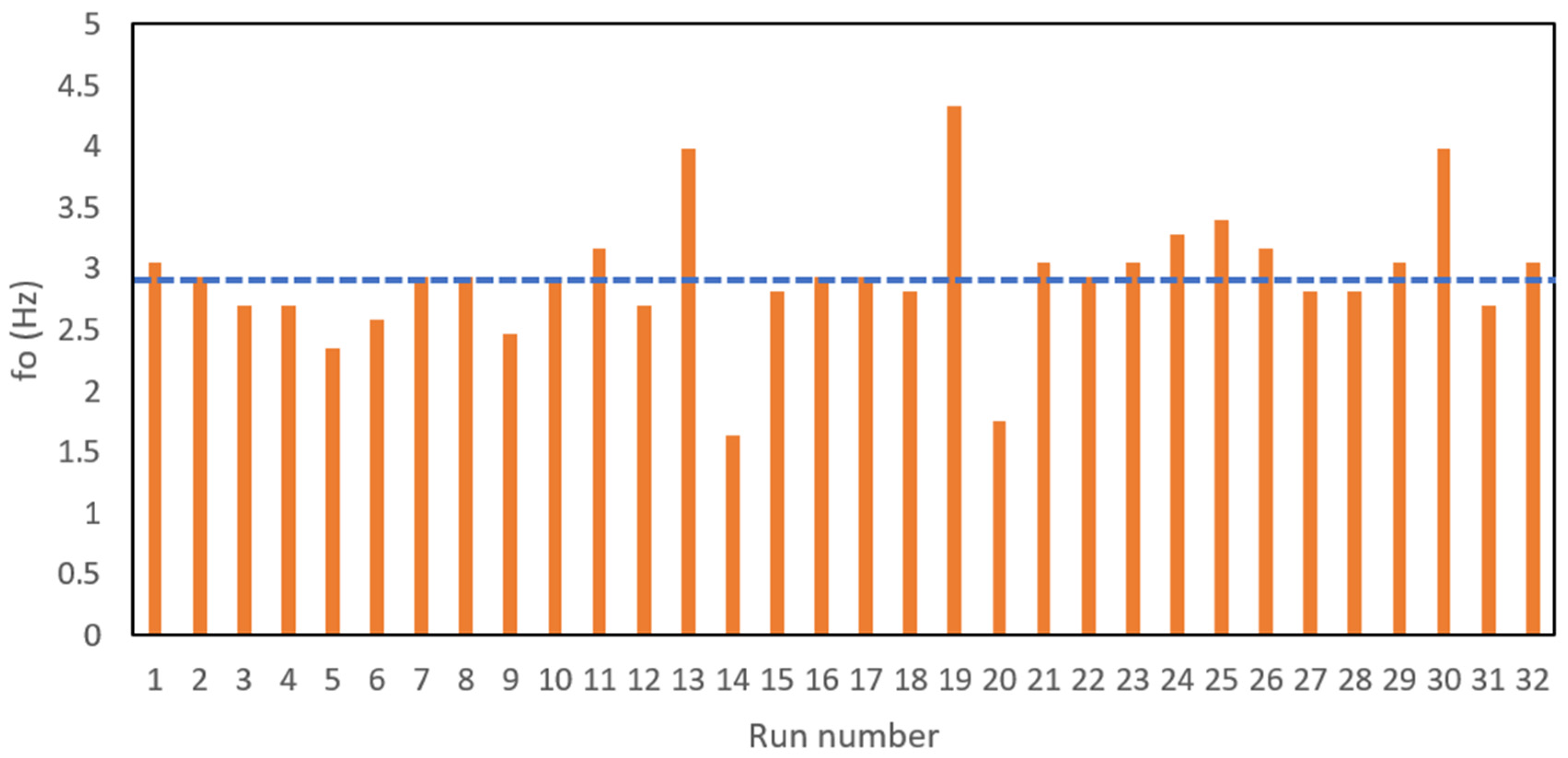
- Spectral analysis was used to identify the dominant frequencies of water-surface fluctuations upstream of the DRAB. It is noted that the dominant frequencies span a range of 1.4 to 4.4 Hz (with an average of 3 Hz). This range is slightly higher than the recorded values (by previous researchers) at the end of different hydraulic jump types. The marginal increase in the measured frequencies upstream of the DRAB suggests the presence of dual sources contributing to the water-surface oscillations at the DRAB. The primary source is the hydraulic jump, while the secondary source probably stems from the additional instability induced by the secondary spiral flow that is developed by the action of the centrifugal force just upstream of the first bend and the crosswaves generated far upstream at the asymmetric contraction of the channel inlet.
- Due to the sharp 90-degree bends in the DRAB, two distinct free vortex structures were observed. The first vortex is shallow in depth, rotates clockwise, and exists along the inner side of the junction and downstream of the upstream inner edge. The second vortex is comparatively deeper, rotates anticlockwise, and lies just downstream of the downstream inner edge along the inner side of the second bend. As the flow progresses through the DRAB, the subcritical flow is influenced by the formation of these two free vortices, resulting in a transition to trans-critical flow and eventually supercritical flow, with pronounced cross waves at the junction outlet in the downstream reach.
- The Strouhal number corresponding to the water-surface oscillations upstream of the DRAB is found to be strongly dependent on the Froude number and weakly dependent on the Reynolds number. A decrease in the supercritical Froude number leads to an increase in the Strouhal number, indicating that the highest water-surface oscillations are associated with critical flow conditions.
- The recorded water surface and dominant frequencies data set for the DRAB problem could be used for calibration and verification of CFD models. These data not only enable a rigorous comparison between the CFD model’s predictions and measured time-averaged values, but they could also provide a new basis for a higher level of model calibrations in which the measurements of the dominant frequency of fluctuations are compared against CFD model outputs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| b | channel bed width [L] |
| c1, c2, c3 | coefficients of regression Equations (5)–(9), Table 3 |
| CFD | computational fluid dynamics |
| CHU | conveyance heading up upstream DRAB [L] |
| DRAB | double-right-angled bend |
| fo | dominant frequency [1/T] |
| fps | number of recorded frames per second [1/T] |
| Fn | Froude number [1] |
| g | the acceleration of gravity (L/T2) |
| L | length of DRAB as per Figure 1d |
| n | Manning roughness coefficient [T/L1/3] |
| O.S.P. | open-source physics project |
| Q | water flow rate [L3/T] |
| Ro | hydraulic radius for normal water depth [L] |
| Rn | Reynolds number [1] |
| R2 | coefficient of determination for a given regression [1] |
| So | channel bed slope [1] |
| St | Strouhal number [1] |
| Vo | cross-sectional averaged velocity assuming uniform flow (L/T) |
| W | width of the DRAB, Figure 1d |
| WSO | water-surface oscillation |
| WSP | water-surface profile |
| yo | normal depth [L] |
| yt | tail water depth [L] |
| time averaged water depth upstream DRAB [L] | |
| maximum instantaneous water depth upstream DRAB [L] | |
| ν | kinematic viscosity of water (L2/T) |
| Φ1 to Φ5 | regression functions, Equations (5)–(9), Table 3 |
Appendix A. MATLAB Code
References
- Chong, N.B. Numerical simulation of supercritical flow in open channel. Comput. Methods Appl. Mech. Eng. 2006, 3, 269–289. [Google Scholar]
- Stockstill, R.L. Hydraulic Design of Channels Conveying Supercritical Flow. Urban Flood Damage Reduction and Channel Restoration Demonstration Program for Arid and Semi-Arid Regions. 2006. Available online: https://www.researchgate.net/publication/235103810_Hydraulic_Design_of_Channels_Conveying_Supercritical_Flow/related (accessed on 26 July 2023).
- Defina, A.; Viero, D.P. Open channel flow through a linear contraction. Phys. Fluids 2010, 22, 036602. [Google Scholar] [CrossRef]
- Viero, D.P.; Lazzarin, T.; Peruzzo, P.; Defina, A. Supercritical flow overpassing forward-or backward-facing steps non-orthogonal to the flow direction. Phys. Fluids 2023, 35, 036604. [Google Scholar] [CrossRef]
- Han, S.S.; Ramamurthy, A.S.; Biron, P.M. Characteristics of flow around open channel 90 bends with vanes. J. Irrig. Drain. Eng. 2011, 137, 668–676. [Google Scholar] [CrossRef]
- Ippen, A.T.; Knapp, R.T. A study of high-velocity flow in curved channels of rectangular cross-section. Eos Trans. Am. Geophys. Union 1936, 17, 516–521. [Google Scholar] [CrossRef]
- Reinauer, R.; Hager, W.H. Supercritical bend flow. J. Hydraul. Eng. 1997, 123, 208–218. [Google Scholar] [CrossRef]
- Reinauer, R.; Hager, W.H. Supercritical flow in chute contraction. J. Hydraul. Eng. 1998, 124, 55–64. [Google Scholar] [CrossRef]
- Reinauer, R.; Hager, W.H. Supercritical flow behind chute piers. J. Hydraul. Eng. 1994, 120, 1292–1308. [Google Scholar] [CrossRef]
- Reinauer, R.; Hager, W.H. Shockwave in air-water flows. Int. J. Multiph. Flow 1996, 22, 1255–1263. [Google Scholar] [CrossRef]
- Ghaeini-Hessaroeyeh, M.; Tahershamsi, A.; Namin, M.M. Numerical modelling of supercritical flow in rectangular chute bends. J. Hydraul. Res. 2011, 49, 685–688. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P. Two-dimensional dam break flow simulation. Int. J. Numer. Methods Fluids 2000, 33, 35–57. [Google Scholar] [CrossRef]
- Valiani, A.; Caleffi, V. Brief analysis of shallow water equations suitability to numerically simulate supercritical flow in sharp bends. J. Hydraul. Eng. 2005, 131, 912–916. [Google Scholar] [CrossRef]
- Souli, H.; Ahattab, J.; Agoumi, A. Investigating Supercritical Bended Flow Using Physical Model and CFD. Model. Simul. Eng. 2023, 2023, 5542589. [Google Scholar] [CrossRef]
- Soares Frazao, S.; Zech, Y. Dam break in channels with 90 degrees bend. J. Hydraul. Eng. 2002, 128, 956. [Google Scholar] [CrossRef]
- Dian-Guang, M.A.; Lei, W.; Jun-yi, Y. Water Level Fluctuation Patterns in Restricted Intermediate Navigable Channels with Different Lock Emptying Processes. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 826, p. 012044. [Google Scholar]
- Wan, Z.; Li, Y.; An, J.; Wang, X.; Cheng, L.; Liao, Y. Exploring water-level fluctuation amplitude in an approach channel under the regulation of a dual cascade hydro-plant in the dry season. Water Supply 2022, 22, 4159–4175. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, Y.; Ji, D.; Yang, Z.; Tan, J.; Hu, H.; Lorke, A. Discharge and water level fluctuations in response to flow regulation in impounded rivers: An analytical study. J. Hydrol. 2020, 590, 125519. [Google Scholar] [CrossRef]
- Ohomoto, T.; Nirakawa, R.; Watanabe, K. Interaction between Water Surface Oscillations and Large Eddies in an Open Channel with Spur Dikes. In Proceedings of the 31st IAHR Congress, Seoul, Republic of Korea, 1 January 2005; CD-Rom. Volume 1, pp. 347–348. [Google Scholar]
- Meile, T.; Boillat, J.L.; Schleiss, A.J. Water-surface oscillations in channels with axi-symmetric cavities. J. Hydraul. Res. 2011, 49, 73–81. [Google Scholar] [CrossRef]
- Zhao, K.; Cheng, N.S.; Huang, Z. Experimental study of free-surface fluctuations in open-channel flow in the presence of periodic cylinder arrays. J. Hydraul. Res. 2014, 52, 465–475. [Google Scholar] [CrossRef]
- Viero, D.P.; Pradella, I.; Defina, A. Free surface waves induced by vortex shedding in cylinder arrays. J. Hydraul. Res. 2017, 55, 16–26. [Google Scholar] [CrossRef]
- Hager, W.H. Energy Dissipators and Hydraulic Jump; Kluwer Academic Publishers, Water Science and Technology Library: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Jesudhas, V.; Murzyn, F.; Balachandar, R. IDDES Evaluation of Oscillating Hydraulic Jumps. In E3S Web of Conferences; EDP Sciences: Paris, France, 2018; Volume 40, p. 05067. [Google Scholar]
- De Leo, A.; Ruffini, A.; Postacchini, M.; Colombini, M.; Stocchino, A. The effects of hydraulic jumps instability on a natural river confluence: The case study of the Chiaravagna River (Italy). Water 2020, 12, 2027. [Google Scholar] [CrossRef]
- Wang, H.; Chanson, H. Experimental study of turbulent fluctuations in hydraulic jumps. J. Hydraul. Eng. 2015, 141, 04015010. [Google Scholar] [CrossRef]
- Lennon, J.M.; Hill, D. Particle image velocity measurements of undular and hydraulic jumps. J. Hydraul. Eng. 2006, 132, 1283–1294. [Google Scholar] [CrossRef]
- Murzyn, F.; Chanson, H. Free-surface fluctuations in hydraulic jumps: Experimental observations. Exp. Therm. Fluid Sci. 2009, 33, 1055–1064. [Google Scholar] [CrossRef]
- Nikon, CoolPix P600 Digital Camera, User Manual. Available online: https://www.bhphotovideo.com/lit_files/104252.pdf (accessed on 27 January 2023).
- Sony Cyber-Shot DSC-RX100 Digital Camera, User Manual. Available online: https://manuals.plus/wp-content/sideloads/cyber-shot-dsc-rx100-manual-original.pdf (accessed on 27 January 2023).
- Microsoft LifeCam Studio WebCam, Data Sheet, Rev.1606A. 2016. Available online: https://download.microsoft.com/download/0/9/5/0952776D-7A26-40E1-80C4-76D73FC729DF/TDS_LifeCamStudio.pdf (accessed on 27 January 2023).
- Eadkhong, T.; Rajsadorn, R.; Jannual, P.; Danworaphong, S. Rotational dynamics with Tracker. Eur. J. Phys. 2012, 33, 615. [Google Scholar] [CrossRef]
- Elgamal, M.; Abdel-Mageed, N.; Helmy, A.; Ghanem, A. Hydraulic performance of sluice gate with unloaded upstream rotor. Water SA 2017, 43, 563–572. [Google Scholar] [CrossRef]
- Brown, D. Tracker Introduction to Video Modeling (AAPT 2010). Portland, Oregon. 2010. Available online: http://www.compadre.org/Repository/document/ServeFile.cfm?ID=10188&DocID=1749 (accessed on 24 December 2022).
- Brown, D. Autotracker. 2010. Available online: https://physlets.org/tracker/help/autotracker.html (accessed on 24 December 2022).
- Elgamal, M.; Fouli, H. Sediment removal from dam reservoirs using syphon suction action. Arab. J. Geosci. 2020, 13, 943. [Google Scholar] [CrossRef]
- Elgamal, M.; Kriaa, K.; Farouk, M. Drainage of a water tank with pipe outlet loaded by a passive rotor. Water 2021, 13, 1872. [Google Scholar] [CrossRef]
- Lazzarin, T.; Viero, D.P.; Defina, A.; Cozzolino, L. Flow under vertical sluice gates: Flow stability at large gate opening and disambiguation of partial dam-break multiple solutions. Phys. Fluids 2023, 35, 024114. [Google Scholar] [CrossRef]
- Blanckaert, K.D.V.H.; De Vriend, H.J. Secondary flow in sharp open-channel bends. J. Fluid Mech. 2004, 498, 353–380. [Google Scholar] [CrossRef]
- Lazzarin, T.; Viero, D.P. Curvature-induced secondary flow in 2D depth-averaged hydro-morphodynamic models: An assessment of different approaches and key factors. Adv. Water Resour. 2023, 171, 104355. [Google Scholar] [CrossRef]
- Yunus, A.C. Fluid Mechanics: Fundamentals and Applications (Si Units); Tata McGraw Hill Education Private Limited: Noida, India, 2010. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics, Classical Textbook Reissue; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Liggett, J.A. Fluid Mechanics; McGraw-Hill Inc.: New York, NY, USA, 1994. [Google Scholar]



| Run No # | Ditch Setup | Experiment Scope | Slope (%) | Water Flow Q (L/s) | Rn | Fn | Remarks | |
|---|---|---|---|---|---|---|---|---|
| Straight | DRAB | |||||||
| 1 | ✓ | R | 1 | 0.56 | 4622 | 1.56 | ||
| 2 | ✓ | R | 1 | 1.94 | 12,296 | 1.49 | ||
| 3 | ✓ | R | 1 | 3.06 | 18,088 | 1.45 | ||
| 4 | ✓ | R | 1 | 3.89 | 21,825 | 1.53 | ||
| 5 | ✓ | R | 1 | 5 | 25,208 | 1.44 | ||
| 6 | ✓ | R | 1 | 6.39 | 30,028 | 1.48 | ||
| 7 | ✓ | R | 1 | 9.17 | 37,278 | 1.50 | ||
| 8 | ✓ | R | 1 | 16.11 | 52,219 | 1.53 | ||
| 9 | ✓ | R | 0.2 | 1.39 | 8830 | 1.05 | ||
| 10 | ✓ | R | 0.2 | 2.78 | 15,449 | 1.14 | ||
| 11 | ✓ | R | 0.2 | 4.17 | 20,421 | 1.14 | ||
| 12 | ✓ | DT | 2 | 5.28 | 30,599 | 2.23 | Right injection | |
| 13 | ✓ | DT | 2 | 5.28 | 30,599 | 2.23 | Right & Left injection | |
| 14 | ✓ | WSO | 2.5 | 12.78 | 53,848 | 2.27 | ||
| 15 | ✓ | WSO | 2.5 | 9.44 | 45,225 | 2.38 | ||
| 16 | ✓ | WSP/O | 2.5 | 6.67 | 36,242 | 2.48 | ||
| 17 | ✓ | WSP/O | 2.5 | 3.89 | 24,766 | 2.58 | ||
| 18 | ✓ | WSP/O | 2.5 | 1.39 | 10,821 | 2.63 | ||
| 19 | ✓ | WSO | 2 | 15 | 55,513 | 1.93 | ||
| 20 | ✓ | WSO | 2 | 11.94 | 49,334 | 2.01 | ||
| 21 | ✓ | WSO | 2 | 10.56 | 46,079 | 2.06 | ||
| 22 | ✓ | WSP | 2 | 8.89 | 41,707 | 2.11 | ||
| 23 | ✓ | WSP | 2 | 7.5 | 37,593 | 2.16 | ||
| 24 | ✓ | WSP/O | 2 | 6.94 | 35,805 | 2.18 | ||
| 25 | ✓ | WSP | 2 | 5.83 | 31,945 | 2.22 | ||
| 26 | ✓ | WSP/O | 2 | 3.61 | 22,777 | 2.30 | ||
| 27 | ✓ | WSP/O | 2 | 1.67 | 12,395 | 2.35 | ||
| 28 | ✓ | WSO | 1.67 | 10.56 | 44,249 | 1.85 | ||
| 29 | ✓ | WSO | 1.67 | 8.61 | 39,433 | 1.91 | ||
| 30 | ✓ | WSO | 1.67 | 7.22 | 35,476 | 1.96 | ||
| 31 | ✓ | WSO | 1.67 | 5.83 | 30,973 | 2.01 | ||
| 32 | ✓ | WSO | 1.67 | 4.44 | 25,774 | 2.06 | ||
| 33 | ✓ | WSO | 1.67 | 2.22 | 15,376 | 2.14 | ||
| 34 | ✓ | WSO | 1.25 | 12.22 | 44,545 | 1.52 | ||
| 35 | ✓ | WSO | 1.25 | 8.06 | 35,707 | 1.63 | ||
| 36 | ✓ | WSO | 1.25 | 5.28 | 27,598 | 1.73 | ||
| 37 | ✓ | WSO | 1.25 | 2.78 | 17,645 | 1.82 | ||
| 38 | ✓ | WSO | 1.25 | 0.83 | 6642 | 1.85 | ||
| 39 | ✓ | WSO | 1 | 13.33 | 43,735 | 1.3 | ||
| 40 | ✓ | WSO | 1 | 11.11 | 40,159 | 1.35 | ||
| 41 | ✓ | WSO | 1 | 8.33 | 34,632 | 1.43 | ||
| 42 | ✓ | WSO | 1 | 4.72 | 24,690 | 1.55 | ||
| 43 | ✓ | WSO | 1 | 1.67 | 11,610 | 1.66 | ||
| 44 | ✓ | WSO | 0.67 | 12.5 | 37,925 | 1.03 | ||
| 45 | ✓ | WSO | 0.67 | 10 | 34,347 | 1.08 | ||
| 46 | ✓ | WSO | 0.67 | 7.78 | 30,354 | 1.14 | ||
| 47 | ✓ | WSO | 0.67 | 4.44 | 22,060 | 1.24 | ||
| 48 | ✓ | WSO | 0.67 | 1.39 | 9634 | 1.35 | ||
| Camera No. | Model | Type | Sensor | Max Resolution (MP) | Max Frame Rate (fps) | Zoom (Optical) | Measured Parameter |
|---|---|---|---|---|---|---|---|
| 1 | Nikon, CoolPix P600 | Bridge-DSLR styled | 1/2.3” BSI-CMOS | 16 | 120 | 60X | Water surface upstream of bends |
| 2 | Sony Cyber-Shot DSC-RX100 | Point-and-shoot | 1” CMOS | 20.1 | 1000 | 3.6X | Spatial variation in water surface downstream of bends |
| 3 and 4 | Microsoft-Life Cam Studio | Webcam | CMOS | 5 | 30 | 3X | Lateral water-surface profiles throughout the two bends |
| 5 | Kiosk High Speed Webcams | Webcam | 1/3” CMOS | 2 | 260 | 10X | Top view for water features extent |
| Regression Formula | Function | Equation No | Coefficients | R2 | ||
|---|---|---|---|---|---|---|
| c1 | c2 | c3 | ||||
| 1 | Φ1 | 5 | 42.22809 | −0.4635 | −0.71255 | 0.784 |
| 2 | Φ2 | 6 | 0.081352 | 0.026588 | −1.08519 | 0.743 |
| 3 | Φ3 | 7 | 0.003221 | 0.441993 | −0.66306 | 0.74 |
| 4 | Φ4 | 8 | 0.003678 | 0.424442 | −1.54091 | 0.897 |
| 5 | Φ5 | 9 | 0.777935 | 0.85343 | 1.13919 | 0.9001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgamal, M.; Chaouachi, L.; Farouk, M.; Helmi, A.M. Analysis of Water-Surface Oscillations Upstream of a Double-Right-Angled Bend with Incoming Supercritical Flow. Water 2023, 15, 3570. https://doi.org/10.3390/w15203570
Elgamal M, Chaouachi L, Farouk M, Helmi AM. Analysis of Water-Surface Oscillations Upstream of a Double-Right-Angled Bend with Incoming Supercritical Flow. Water. 2023; 15(20):3570. https://doi.org/10.3390/w15203570
Chicago/Turabian StyleElgamal, Mohamed, Lotfi Chaouachi, Mohamed Farouk, and Ahmed M. Helmi. 2023. "Analysis of Water-Surface Oscillations Upstream of a Double-Right-Angled Bend with Incoming Supercritical Flow" Water 15, no. 20: 3570. https://doi.org/10.3390/w15203570
APA StyleElgamal, M., Chaouachi, L., Farouk, M., & Helmi, A. M. (2023). Analysis of Water-Surface Oscillations Upstream of a Double-Right-Angled Bend with Incoming Supercritical Flow. Water, 15(20), 3570. https://doi.org/10.3390/w15203570







