Study on Spatiotemporal Transport Characteristics of Soil Moisture in Layered Heterogeneous Vadose Zone Based on HYDRAS-3D
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. In Situ Test of Moisture Transport in Heterogeneous Media
3. Model Building
3.1. Basic Equation for Soil Moisture Transport
3.2. Initial and Boundary Conditions
3.3. Model Parameters
4. Results and Analysis
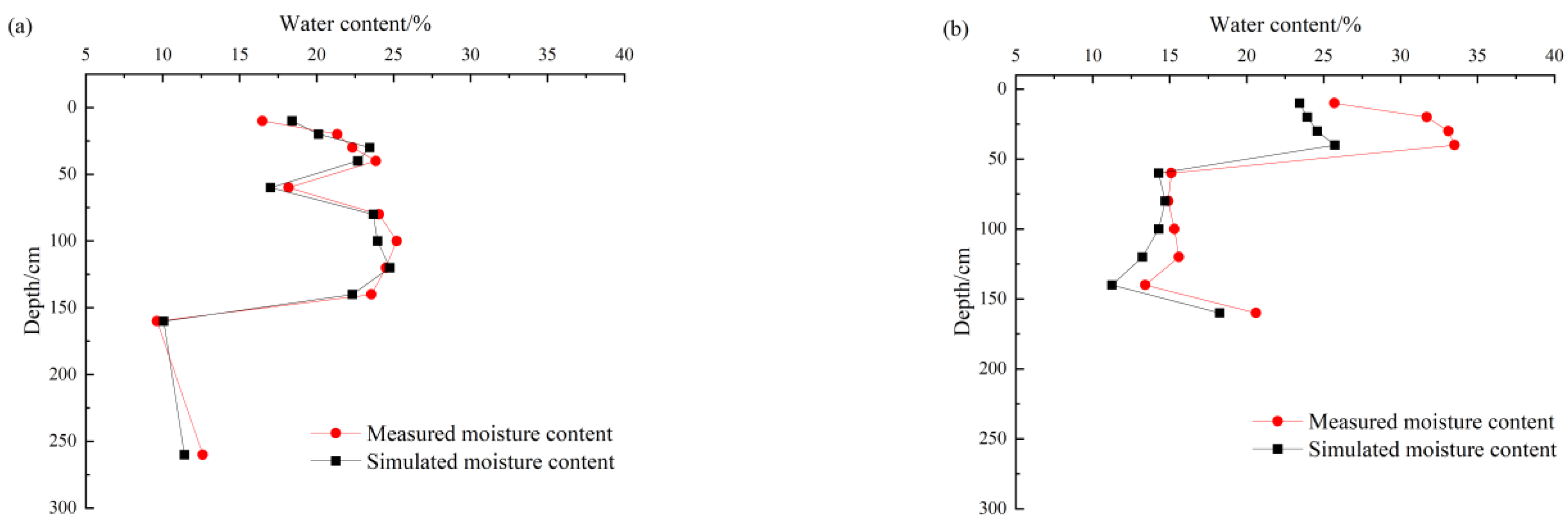
4.1. Model Validation
4.1.1. Model Result Validation
4.1.2. Model Accuracy Verification
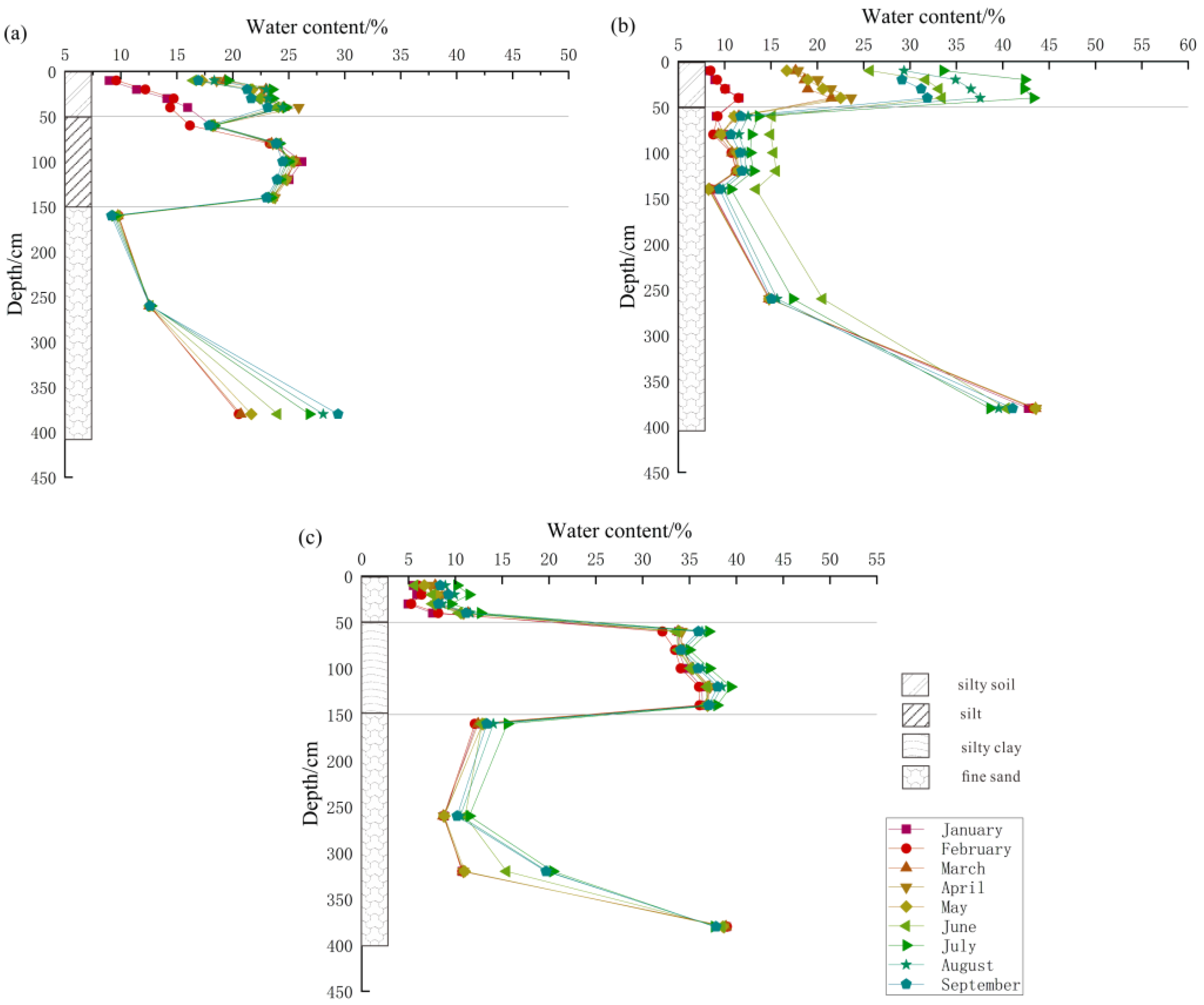
4.2. Influence of a Layered Heterogeneous Structure on Water Movement in the Vadose Zone
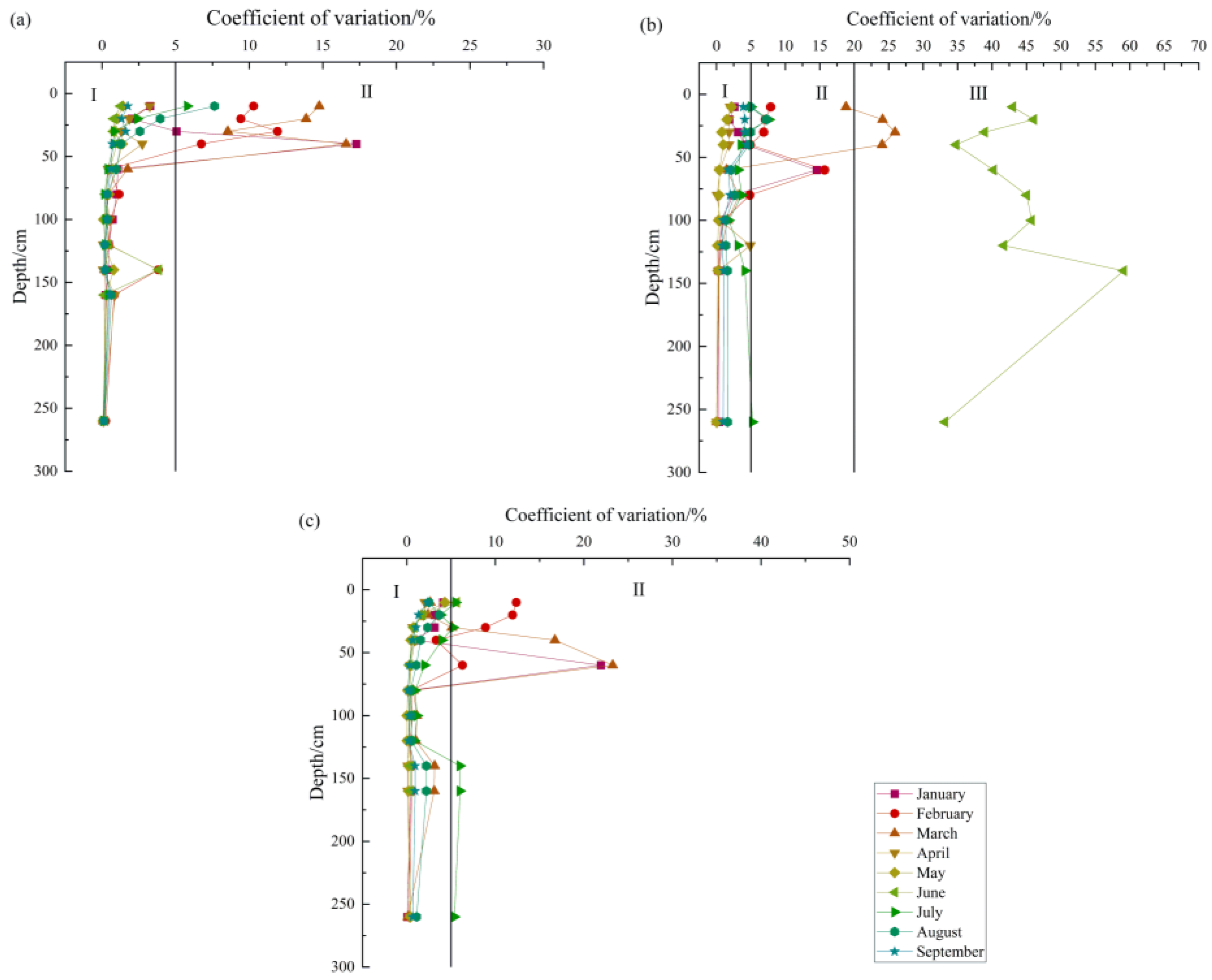
4.3. Profile Water Content Variability Characteristics
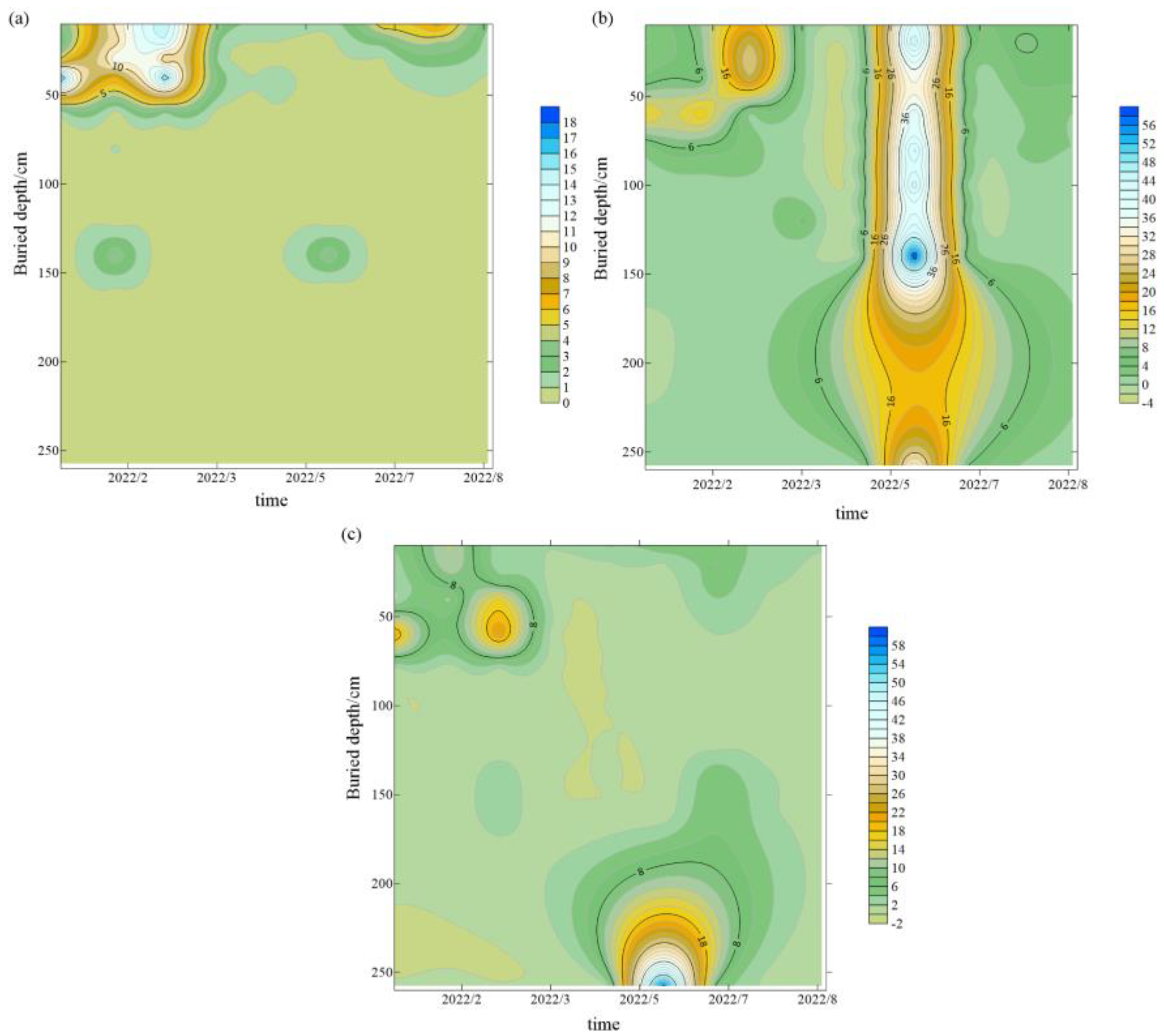
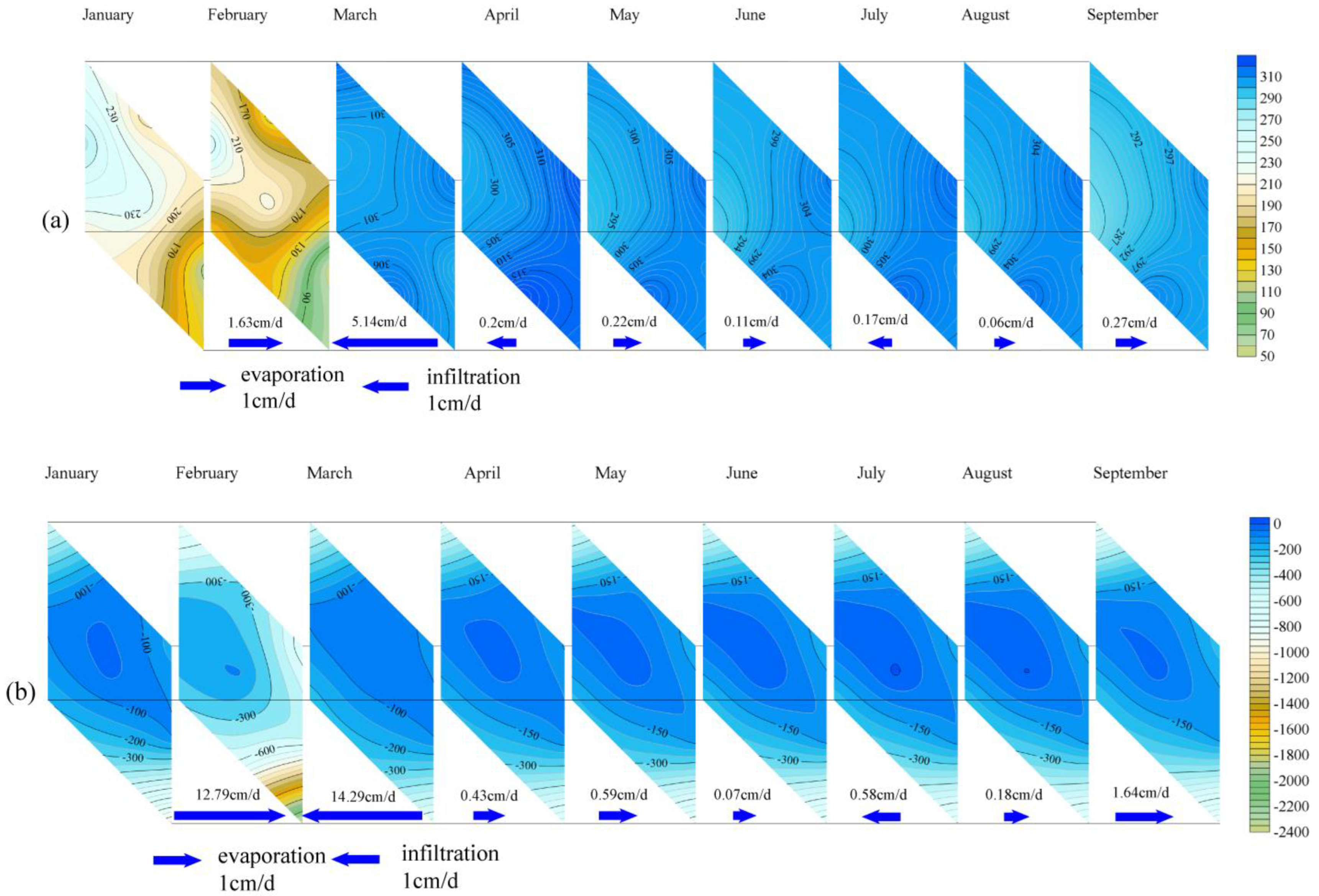
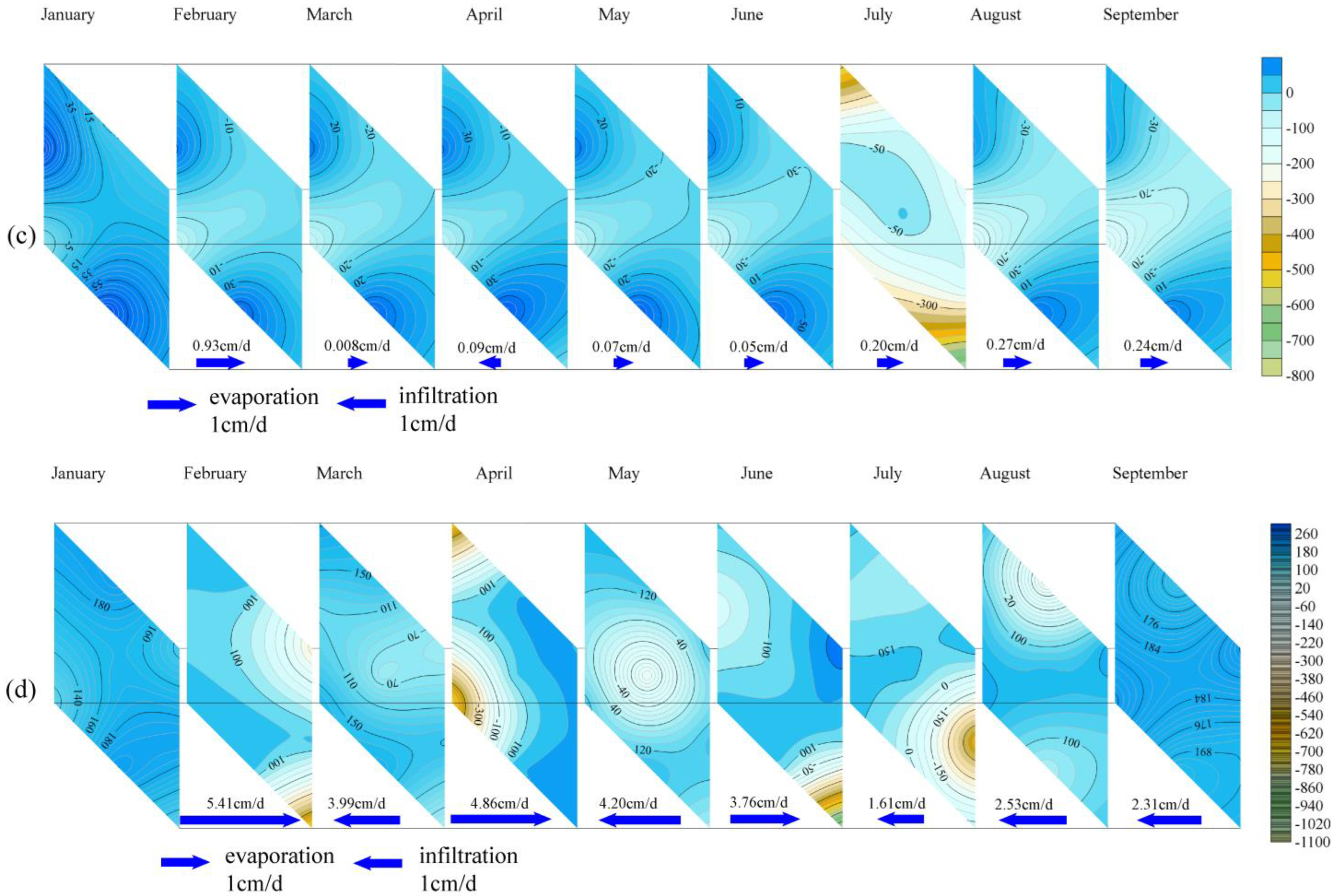
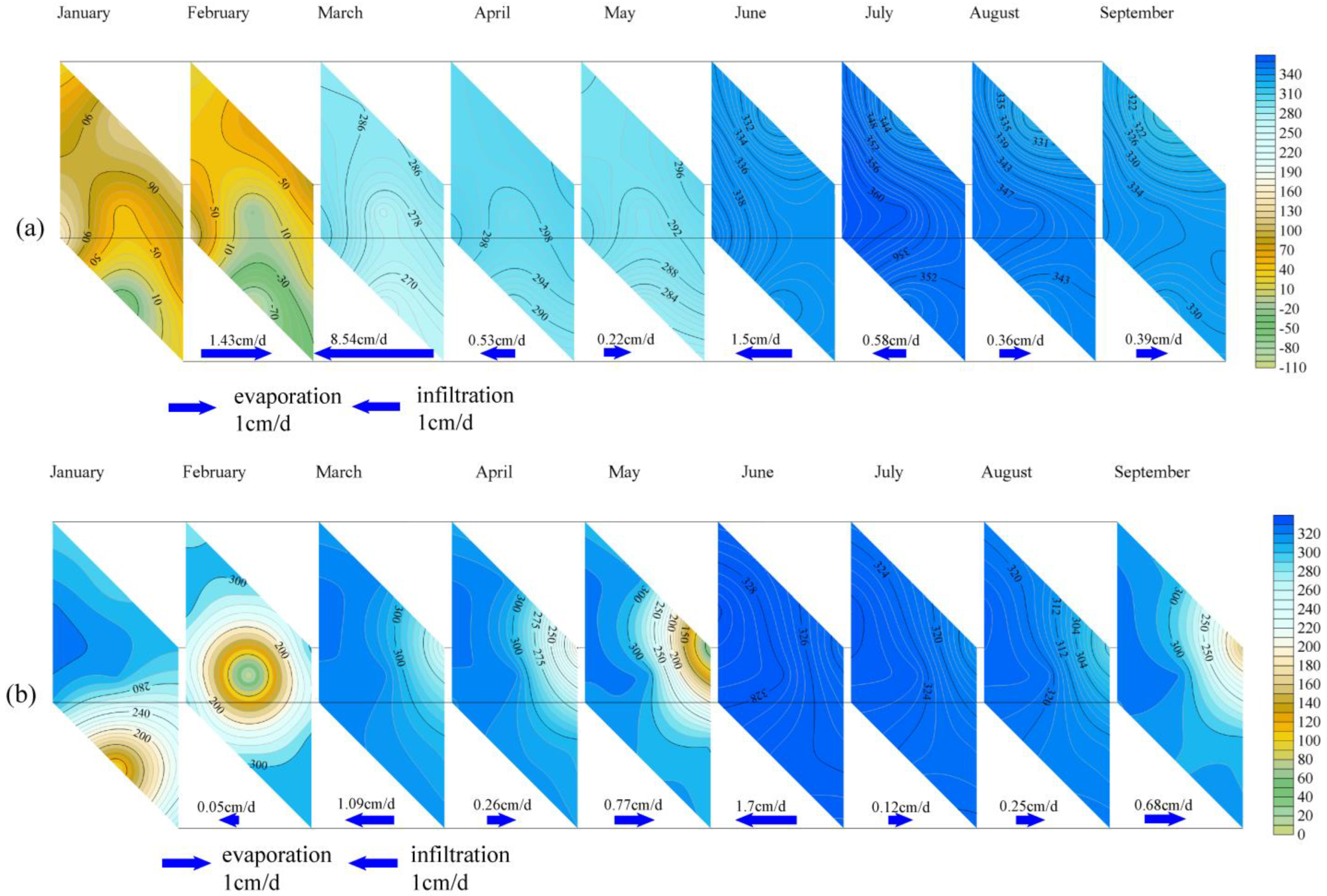
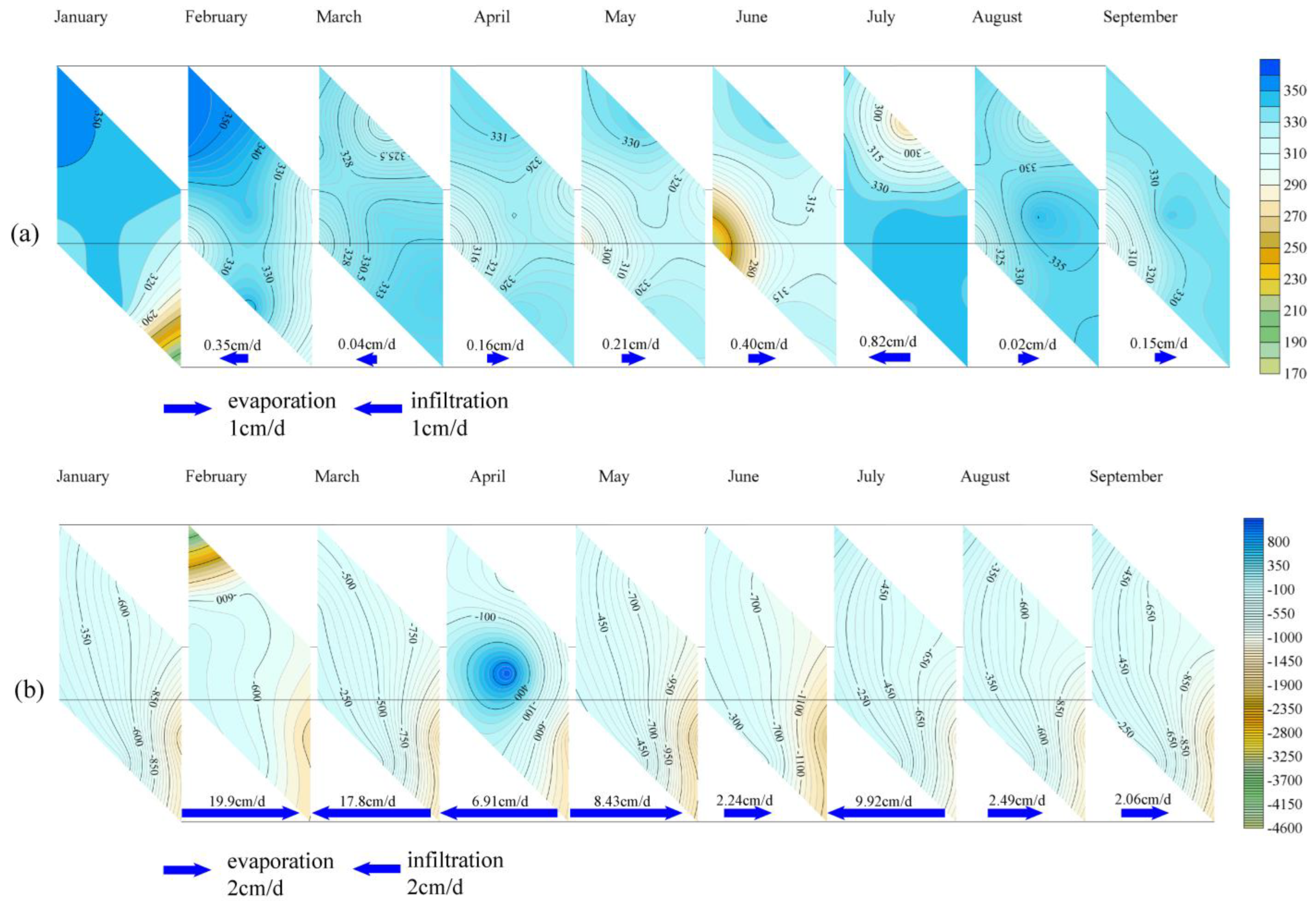
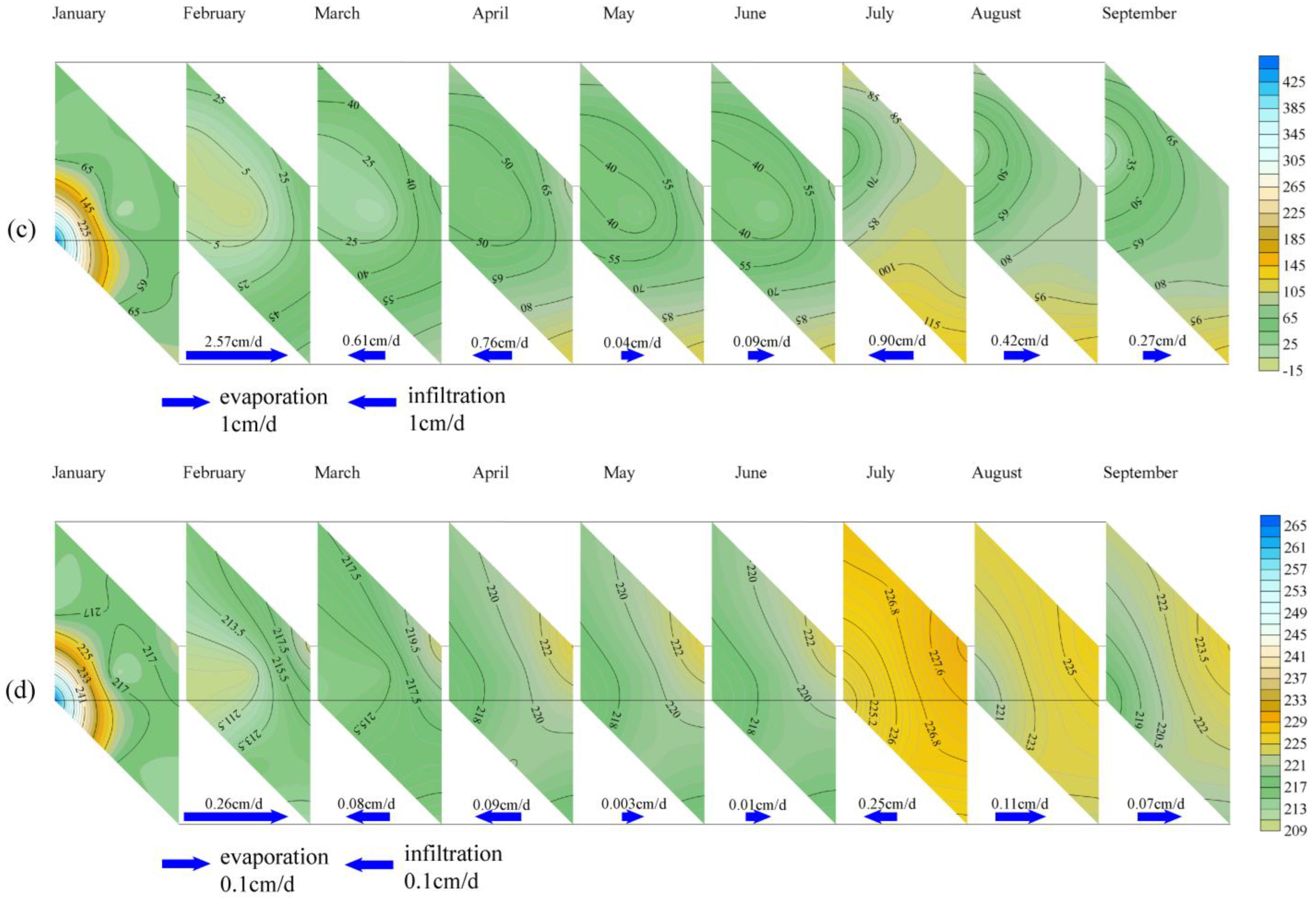
4.4. Spatial and Temporal Distribution Characteristics of the Water Movement in the Layered Heterogeneous Vadose Zone
5. Discussion
6. Conclusions
- (1)
- Comparing and analyzing the simulated and measured values in the HYDRAS-3D model, the two showed good consistency, verifying the accuracy and reliability of the model, indicating that the model can be applied well in experiments.
- (2)
- The water content at the interface of the soil layer will undergo a sudden change. Expressing the characteristics of water content variability more accurately in the test cylinder profiles, water movement in the vadose zone was divided into the following stages: (I) stable period, (II) slow change period, and (III) rainfall rapid change period. From April to May and July to September in the YC03 test cylinder, which was not significantly affected by rainfall, and from April to September in the YC02 and YC04 test cylinders, the CV of the soil moisture content was 5% or less, and water movement in the vadose zone was in the (I) stable period. The CV of the soil moisture content of the three test cylinders from January to March was mostly between 5 and 20%, with large fluctuations and frequent moisture exchanges in the vertical direction, particularly from 60 to 80 cm. In June, the YC03 test cylinder, which was significantly affected by rainfall, had a CV of water content in the entire profile of >30% and a maximum value of 59.11% when the water movement in the vadose zone was in the (III) rainfall rapid change period.
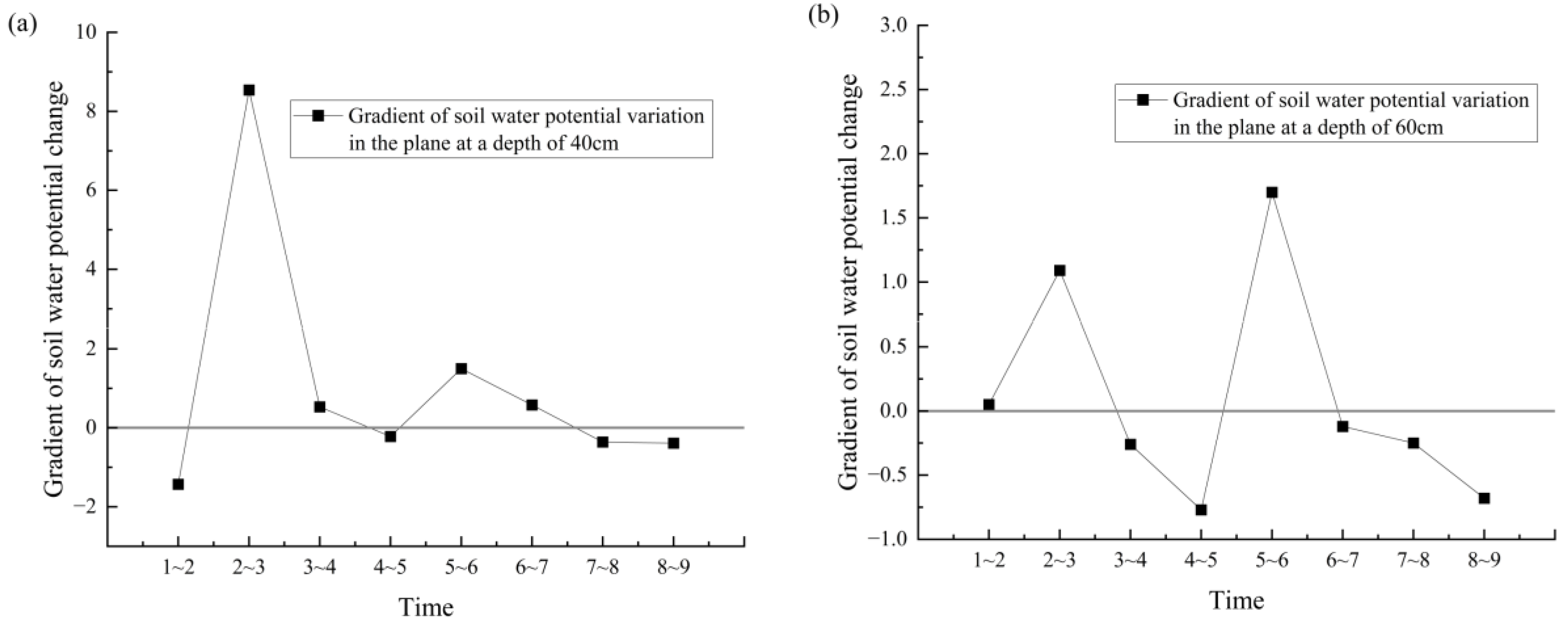
- (3)
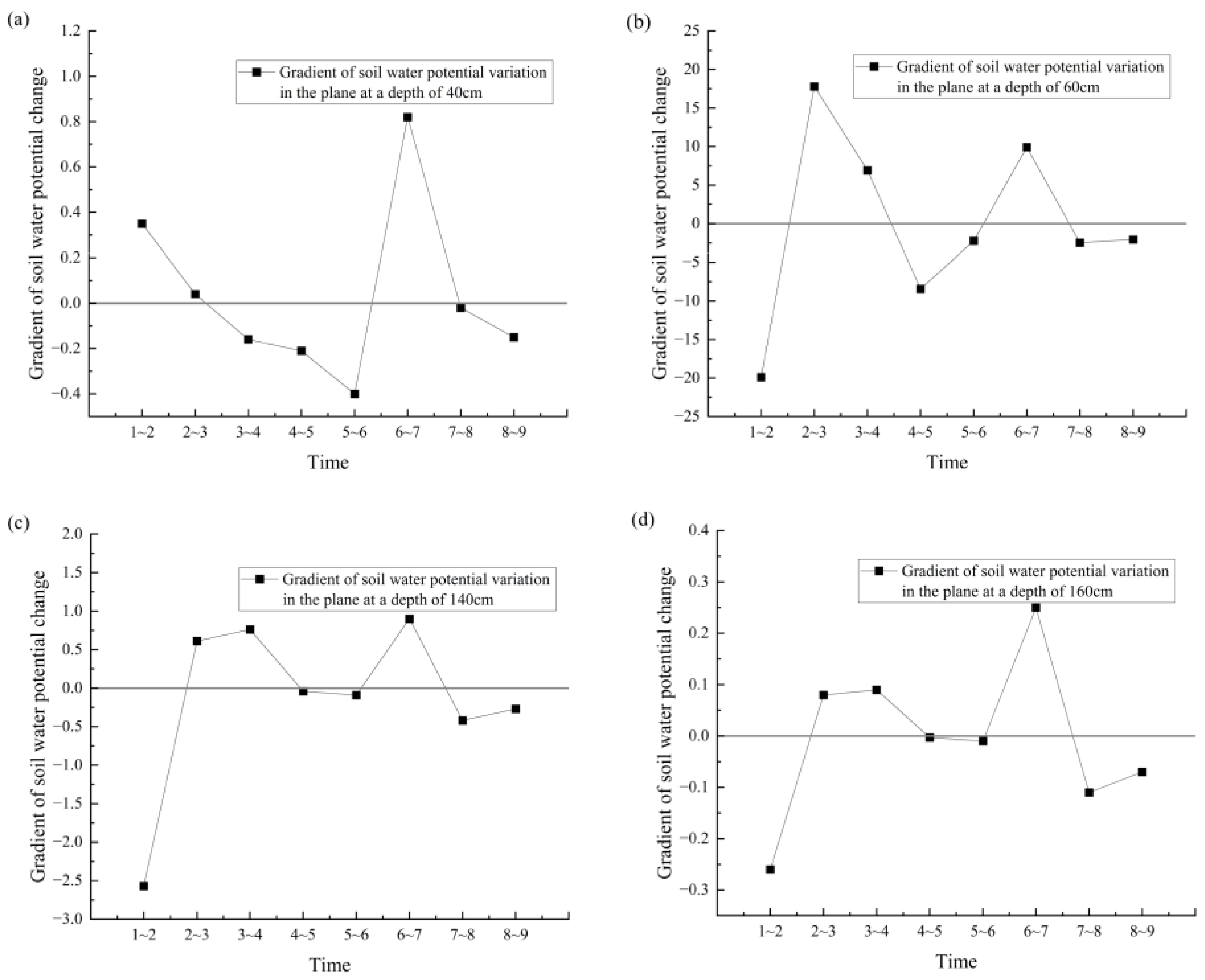
- The two largest values (19.9 and 17.8 cm/day) of the temporal change gradient of the soil water potential were observed in the silty clay layers of the YC04 test cylinder. The influence of the soil–layer interface on evaporation and infiltration in the silty clay layer was the most pronounced.
- (4)
- The lateral movement of soil moisture in the plane at the interface was also affected to some extent by the layered heterogeneous structure, with the degree and time affected by the differences in the soil layers above and below the interface. The fine sand layer was the most affected by the soil–layer interface, followed by the silty soil and silty clay layers. The silty sand layer was the least affected by the soil–layer interface.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Edmunds, W.M.; Tyler, S. Unsaturated zones as archives of past climates: Toward a new proxy for continental regions. Hydrogeol. J. 2002, 10, 216–228. [Google Scholar] [CrossRef]
- Gong, Z.N.; Gong, H.L.; Deng, W. An overview of water movement in groundwater -Soil-Plant-Atmosphere continuum with shallow water table. J. Agro-Environ. Sci. 2006, 25, 365–373. [Google Scholar]
- Ji, X.B.; Kang, E.S.; Zhao, W.Z. Simulation of heat and water transfer in a surface irrigated, cropped sandy soil. Agric. Water Manag. 2009, 96, 1010–1020. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Shangguan, W.; Li, L.; Yao, Y.; Yu, F. Improved daily SMAP satellite soil moisture prediction over China using deep learning model with transfer learning. J. Hydrol. 2021, 600, 126698. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Xu, F.; Li, C.; Xian, T. Validation of Four Satellite-Derived Soil Moisture Products Using Ground-Based In Situ Observations over Northern China. Remote Sens. 2022, 14, 1419. [Google Scholar] [CrossRef]
- Dabrowska-Zielinska, K.; Budzynska, M.; Tomaszewska, M.; Malinska, A.; Gatkowska, M.; Bartold, M.; Malek, I. Assessment of Carbon Flux and Soil Moisture in Wetlands Applying Sentinel-1 Data. Remote Sens. 2016, 8, 756. [Google Scholar] [CrossRef]
- Hutchinson, J.S.; Vought, T.J.; Hutchinson, S.L. Continuous soil moisture mapping using MODIS NDVI and LST products. Pap. Appl. Geogr. Conf. 2006, 29, 140–149. [Google Scholar]
- Dabrowska-Zielinska, K.; Budzynska, M.; Tomaszewska, M.; Bartold, M.; Gatkowska, M.; Malek, I.; Turlej, K.; Napiorkowska, M. Monitoring Wetlands Ecosystems Using ALOS PALSAR (L-Band, HV) Supplemented by Optical Data: A Case Study of Biebrza Wetlands in Northeast Poland. Remote Sens. 2014, 6, 1605–1633. [Google Scholar] [CrossRef]
- Zhao, G.Z. Study on Transgormation Mechanism of Vadose Zone Water-Groundwater in the Wind-Blown Sand Area of the Ordos Basin; Chang’an University: Xi’an, China, 2011. [Google Scholar]
- Xu, Y.Z.; Zhao, G.Z.; Mu, N.S. Review on factors affecting the process of water movement in vadose zone. J. N. China Univ. Water Resour. Electr. Power Nat. Sci. Ed. 2019, 40, 37–41. [Google Scholar]
- Li, Y.; Ren, X.; Robert, H. Influence of various soil textures and layer positions on infiltration characteristics of layered soils. J. Drain. Irrig. Mach. Eng. 2012, 30, 485–490. [Google Scholar]
- Miller, D.E.; Gardner, W.H. Water infiltration into stratified soil. Soil Sci. Soc. Am. J. 1962, 26, 115–119. [Google Scholar] [CrossRef]
- Hill, D.E.; Parlange, J.Y. Wetting front instability in layered soils. Soil Sci. Soc. Am. J. 1972, 36, 697–702. [Google Scholar] [CrossRef]
- Chen, J.; Huang, G.H.; Huang, Q.Z. Simulation of one-dimensional solute transport in homogeneous and heterogeneous soils with scale-dependent fractional advection-dispersion equation. Adv. Water Sci. 2006, 3, 299–304. [Google Scholar]
- Yu, S.P.; Yang, J.S. Effect of clay interlayers on soil water-sait movement in easily-salinized regions. Adv. Watter Sci. 2011, 22, 495–501. [Google Scholar]
- Wang, W.Y.; Wang, Q.J.; Shen, B.; Zhang, J.F. Infiltration characteristics of soil with double layer structure in Qinwangchuan area of Gansu Province. J. Soil Eros. Water Conserv. 1998, 2, 37–41. [Google Scholar]
- Li, J.S.; Yang, F.Y.; Li, Y.F. Water and nitrogen distribution under subsurface drip fertigation as affected by layered-textural soils. Trans. CSAE 2009, 25, 25–31. [Google Scholar]
- Wang, Q.J.; Wang, Z.R.; Zhang, J.F. Infiltration mechanism of layered soil and its simulation model. Shui Li Xue Bao 1998, S1, 77–80. [Google Scholar]
- Zettl, J.D.; Barbour, S.L.; Huang, M. Influence of textural laying on field capacity of coarse soils. Can. J. Soil Sci. 2011, 91, 133–147. [Google Scholar] [CrossRef]
- Li, Y.T.; Wang, W.K.; Xiao, J.Y.; Yang, X.T. Field test of moisture migration in vadose zone under heterogeneity. J. Saf. Environ. 2012, 12, 134–137. [Google Scholar]
- Cui, H.H.; Zhang, G.H.; Zhang, Y.Z.; Zhang, B.; Feng, X.; Lang, X.J. Soil water-holding properties of different soil body configuration. Agric. Res. Arid Areas 2020, 38, 1–5. [Google Scholar]
- Xu, Z.Q.; Mao, X.M.; Chen, S. Tank experiment on the influence of the sequence alignment on water movement in multi-layered soil. China Rural. Water Hydropower 2016, 8, 59–62. [Google Scholar]
- Shang, J. Water Dynamics of Vadose Zone in Badan Jaran Desert; China University of Geosciences: Beijing, China, 2014. [Google Scholar]
- Meng, L.Q.; Nie, Z.L. Simulation of Water Migration in Unsaturated Zone in Typical Area of Wuwei Basin. J. Agric. Catastrophol. 2021, 11, 146–149+151. [Google Scholar]
- Liu, Z.X. Study on the Law of Water Migration in the Aeration Zone of Minqin Basin; China University of Geosciences: Beijing, China, 2020. [Google Scholar]
- Dai, Z.G. Numerical simulation of soil water movement in free infiltration under surge-root irrigation in red soil region based on Hydrus-2D. Agric. Res. Arid Areas 2020, 38, 27–31. [Google Scholar]
- Xu, J.Z.; Liu, W.X. Simulation of Soil Moisture Movement under Negative Pressure Micro-irrigation Based on HYDRUS-2D. Trans. Chin. Soc. Agric. Mach. 2021, 52, 287–296. [Google Scholar]
- Li, C.Y.; Ren, L.; Li, B.G. Parametric Estimation of the Van Genuchten’s Equation by the Optimization Method. Adv. Water Sci. 2001, 12, 473–478. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Bartold, M.; Kluczek, M. A Machine Learning Approach for Mapping Chlorophyll Fluorescence at Inland Wetlands. Remote Sens. 2023, 15, 2392. [Google Scholar] [CrossRef]

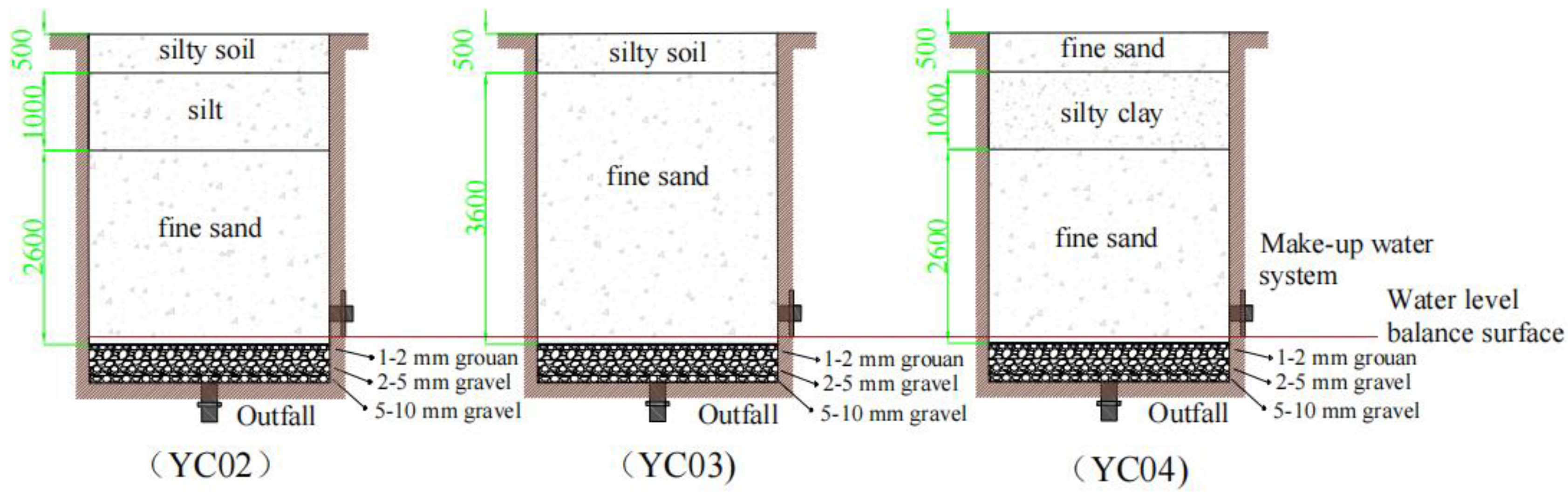

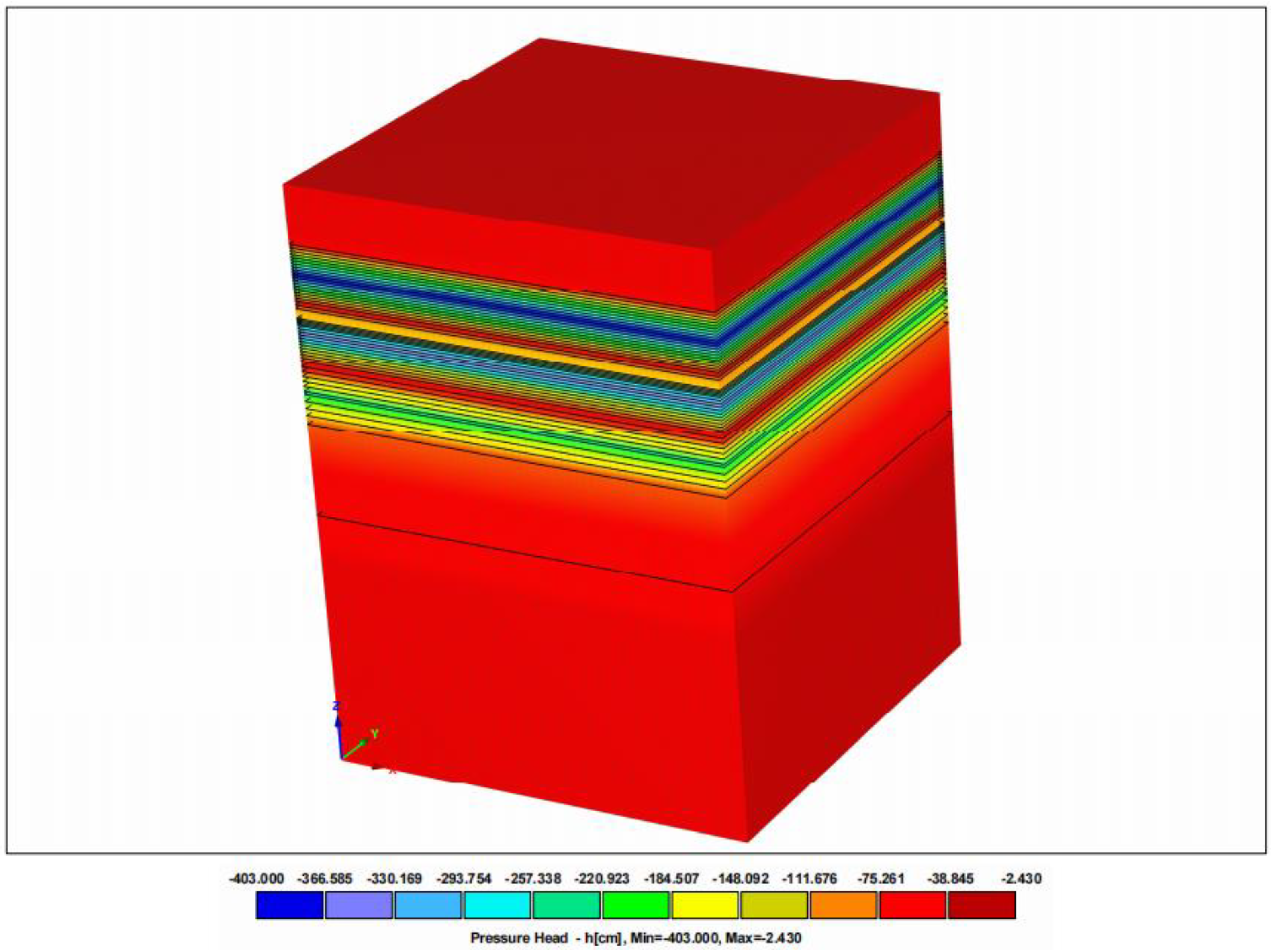
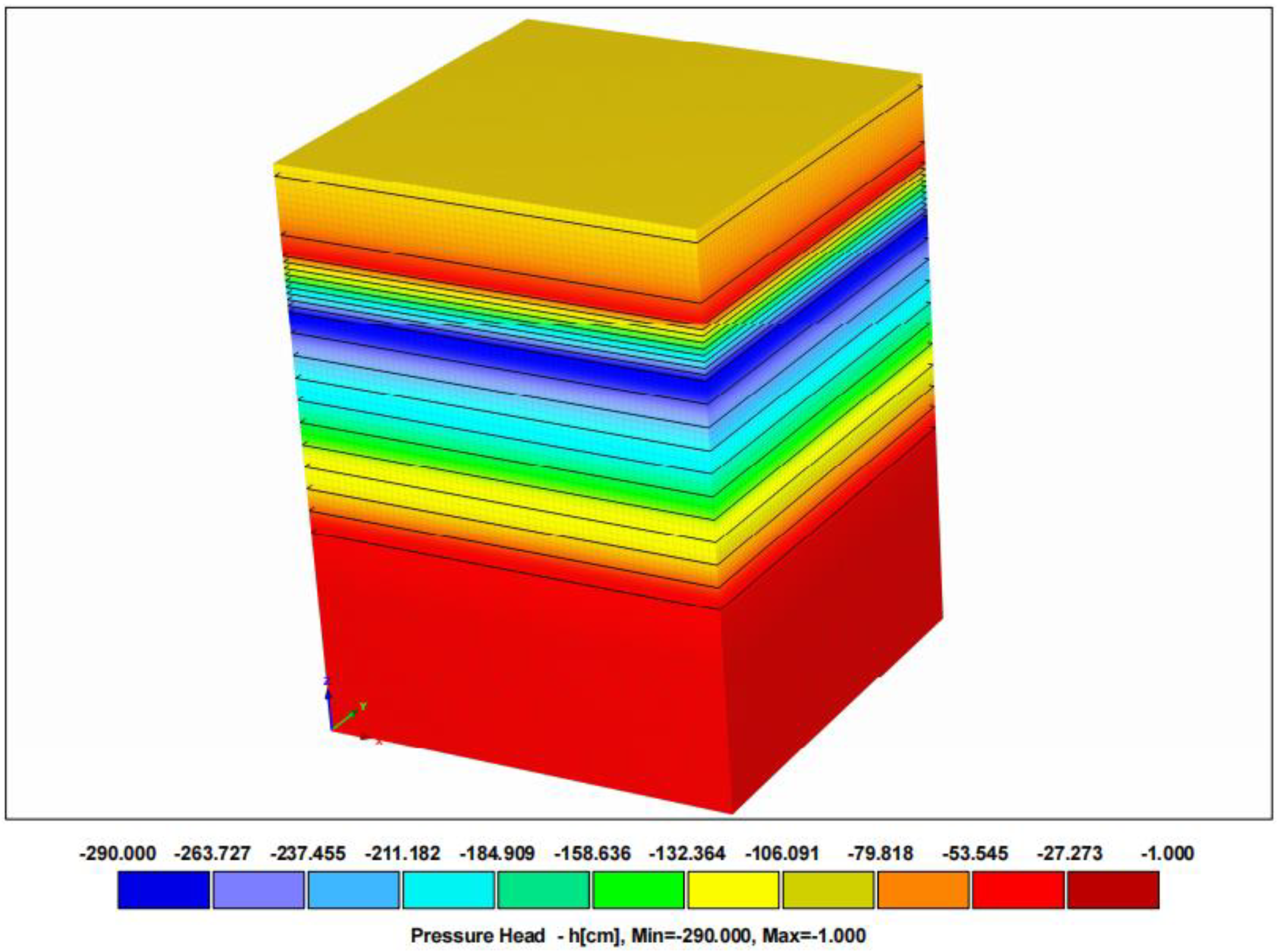
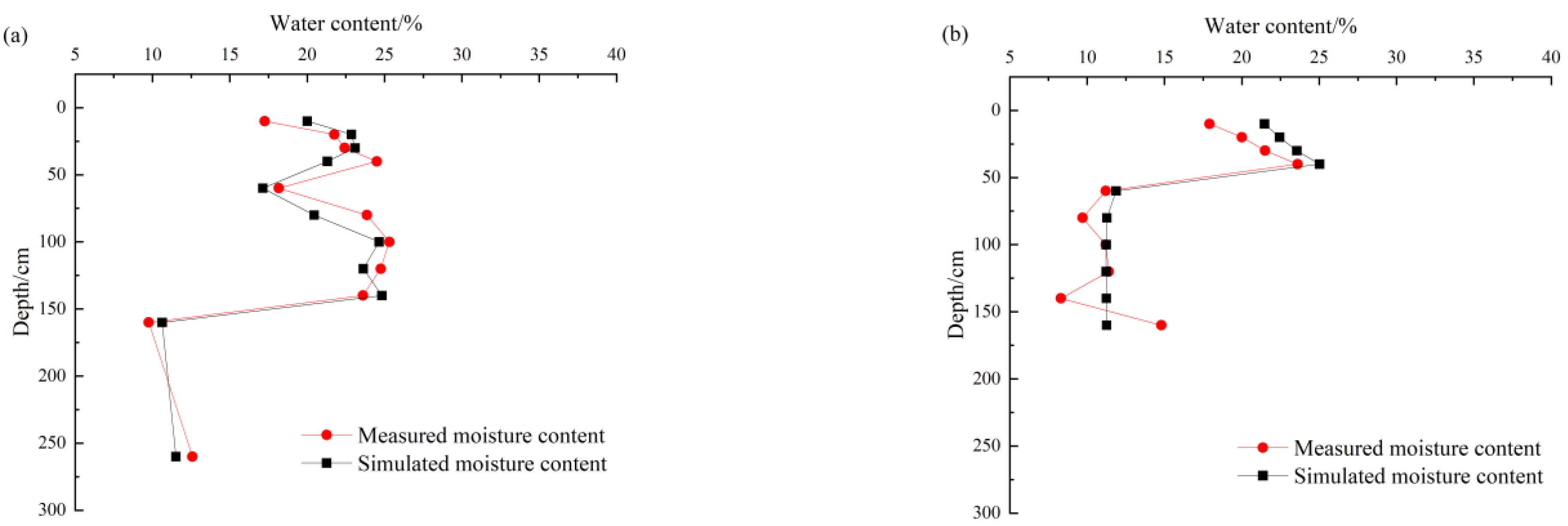


| Test Cylinder Number | Monitoring System Burial Depth (cm) |
|---|---|
| YC02 | −10/−20/−30/−40/−60/−80/−100/−120/−140/−160/−260/−380 |
| YC03 | −10/−20/−30/−40/−60/−80/−100/−120/−140/−160/−380 |
| YC04 | −10/−20/−30/−40/−60/−80/−100/−120/−140/−160/−260/−320/−380 |
| Test Medium | Fit Parameters | |||
|---|---|---|---|---|
| θr (cm3/cm−3) | θs (cm3/cm−3) | α (cm−1) | n | |
| Silty clay | 0.0857 | 0.4732 | 0.0079 | 1.4394 |
| Silty soil | 0.0541 | 0.4545 | 0.0485 | 1.6653 |
| silt | 0.0552 | 0.4790 | 0.0229 | 1.4717 |
| fine sand | 0.0969 | 0.3595 | 0.1986 | 2.4909 |
| Number | Buried Depth (cm) | Soil Physical Parameters | |||||
|---|---|---|---|---|---|---|---|
| θr (cm3/cm−3) | θs (cm3/cm−3) | α (cm−1) | n | Ks (cm/d) | l (-) | ||
| YC02 test tube | 0.064 0.057 0.0969 | 0.064 0.057 0.0969 | 0.46 0.48 0.3595 | 0.0985 0.03 0.1986 | 1.66 1.96 2.68 | 200 350.2 712.8 | 0.5 0.5 0.5 |
| YC03 test tube | 0.064 0.112 | 0.064 0.112 | 0.46 0.3595 | 0.0485 0.1986 | 1.66 2.68 | 200 712.8 | 0.5 0.5 |
| Number | Buried Depth (cm) | R2 | |RE| (%) | RMSE |
|---|---|---|---|---|
| YC02 test tube | 0~50 50~150 100~400 | 0.769 0.958 0.986 | 0.990 3.650 2.660 | 0.0221 0.0178 0.0097 |
| YC03 test tube | 0~50 50~400 | 0.629 0.859 | 10.46 2.170 | 0.0249 0.0200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, S.; Zhao, G. Study on Spatiotemporal Transport Characteristics of Soil Moisture in Layered Heterogeneous Vadose Zone Based on HYDRAS-3D. Water 2023, 15, 3550. https://doi.org/10.3390/w15203550
Xie S, Zhao G. Study on Spatiotemporal Transport Characteristics of Soil Moisture in Layered Heterogeneous Vadose Zone Based on HYDRAS-3D. Water. 2023; 15(20):3550. https://doi.org/10.3390/w15203550
Chicago/Turabian StyleXie, Simin, and Guizhang Zhao. 2023. "Study on Spatiotemporal Transport Characteristics of Soil Moisture in Layered Heterogeneous Vadose Zone Based on HYDRAS-3D" Water 15, no. 20: 3550. https://doi.org/10.3390/w15203550
APA StyleXie, S., & Zhao, G. (2023). Study on Spatiotemporal Transport Characteristics of Soil Moisture in Layered Heterogeneous Vadose Zone Based on HYDRAS-3D. Water, 15(20), 3550. https://doi.org/10.3390/w15203550





