Decision Support System for Sustainable Exploitation of the Eocene Aquifer in the West Bank, Palestine
Abstract
:1. Introduction
2. Materials and Methods
2.1. Methodological Framework
2.2. Study Area
2.3. Available Groundwater Flow Model and Additional Data
2.3.1. MODFLOW Model of the Eocene Aquifer
2.3.2. Additional Data Used for GDSS
2.4. Uncertainty Assessment
2.4.1. Identification of Uncertain Parameters
2.4.2. Experimental Setup for Uncertainty Analysis
2.5. Development of Abstraction Strategies Using Model-Based Optimization
2.5.1. Identification of Abstraction Strategies Based on Aquifer Saturated Thickness
2.5.2. Optimization Formulation
2.6. Sensitivity and Reliability of the Optimal Abstraction Strategies
- Change the hydraulic conductivity, hydraulic conductance, and recharge by a certain percentage (−20%, −10%, 0%, +10%, and +20%), one parameter at a time.
- Perform optimization for five different pumping strategies.
- Compare the objective function values of the optimal solutions for different parameters and different pumping strategies.
2.7. Assessing Nitrogen Pollution Potential for the Optimal Abstraction Strategies
2.8. Groundwater Decision Support System (GDSS) Design and Implementation
- Select and load optimal strategies (pumping wells, together with associated information) and visualize results as spatial data (groundwater heads) and water balance.
- Modify selected strategy (add, edit, or delete wells; change recharge or hydraulic conductivity), run the MODFLOW model, and present the modified results.
- Visualize well capture zones of the optimal strategies together with land use or on-ground nitrogen loading data.
3. Results
3.1. Model Results for Exiting Conditions
3.2. Uncertainty Assessment Results
3.2.1. Convergence of Monte Carlo Simulations (MCSs) for Uncertainty Analysis
3.2.2. Results from Uncertainty Analysis of Identified Parameters
3.3. Optimal Abstraction Strategies Results
3.3.1. Wells Distribution and Water Balance Results for the Five Optimal Strategies
3.3.2. Sensitivity and Reliability of the Five Identified Optimal Abstraction Strategies
3.4. GDSS Visualization Results
4. Discussion
- Average annual recharge of the aquifer was estimated at 75.6 Mm3 and it is the only inflow to the system. About 74% of this inflow is abstracted through pumping wells and the rest is outflow through the drains and general head boundary downstream.
- Groundwater head of the aquifer varies from 10 to 375 m above mean sea level. The general direction of the head gradient is from south to north. The saturated aquifer thickness is in the range 20–80% of pre-developed saturated thickness (PST).
- The mid-western part of the aquifer is already overused with the current aquifer thickness below 20–30% of PST. The southern and northern part are in better conditions with potential for further utilization.
- Simulated groundwater head was the primary model output for which uncertainty of parameters was tested. Out of the four parameters considered in the uncertainty analysis (recharge, hydraulic conductivity, hydraulic conductance at the boundaries and wells distribution within well fields), aquifer recharge brings the highest uncertainty and has the most impact on modelling results, followed by hydraulic conductivity. Groundwater head variations due to overall (combined) uncertainty were found to vary in the range of 40 to 95 m between the 5th percentile and 95th percentile, while in the inter-quartile range, they varied between 20 and 40 m throughout the aquifer.
- Five pumping strategies were developed based on the pre-developed saturated thickness (PST) of the aquifer. Allowable depletion up to 60, 50, 40, and 30% of PST was introduced for the places where the existing groundwater level is above that level for strategy 01, 02, 03, and 04, respectively. For the rest of the areas, the existing groundwater level was maintained. For strategy 05, restoration of the groundwater level was introduced, bringing it to the level of 30% of PST where it is below 30% PST.
- The objective function of optimization for all strategies was to maximize the weighted sum of well pumping rates, subject to hydraulic head constraints at 205 locations, withdrawal constraints for each managed well and linear summation constraints for each well field.
- Total optimal pumping rate from the aquifer was obtained as 52.6, 54.1, 56.7, 60.2, and 50.1 Mm3/year for strategy 01, 02, 03, 04, and 05, respectively, considering existing and potential well locations. Three new potential well field areas were identified, located in the north-west, the south-east, and at the middle-east region of the aquifer.
- Sensitivity analysis, performed by re-optimization of strategies 02 and 03 with varying parameter values, confirmed that the optimal abstraction is most sensitive to recharge, followed by hydraulic conductivity and hydraulic conductance.
- Example results from the sensitivity analysis of strategy 02 show that the total optimal abstraction increases by 7.5 to 7.8 Mm3/year for a 10% increase in recharge. For each 10% increase in hydraulic conductivity, the total optimal abstraction reduces by 2.7 to 3.5 Mm3/year. A change in hydraulic conductance at the model boundaries of 10% results in less than 0.5 Mm3/year variation of total optimal abstraction.
- The reliability of the pumping decreases with an increase in the abstraction rate.
- The reliability of strategy 01 was in the range of 40 to 60%. Strategy 04 was the worst in terms of reliability, where reliability dropped below 10% in the north-western part due to high abstraction from the new well field in that region.
- Strategy 05 performed best in terms of reliability as it was a restoration strategy. It had reliability above 60% for most of the areas, with some areas having reliability above 80%.
5. Conclusions
- There were no measured data on hydraulic conductivity, and this parameter has been assessed only by model calibration. Given its significance, revealed in the uncertainty analysis, further data on hydraulic conductivity (independent from the model) are needed.
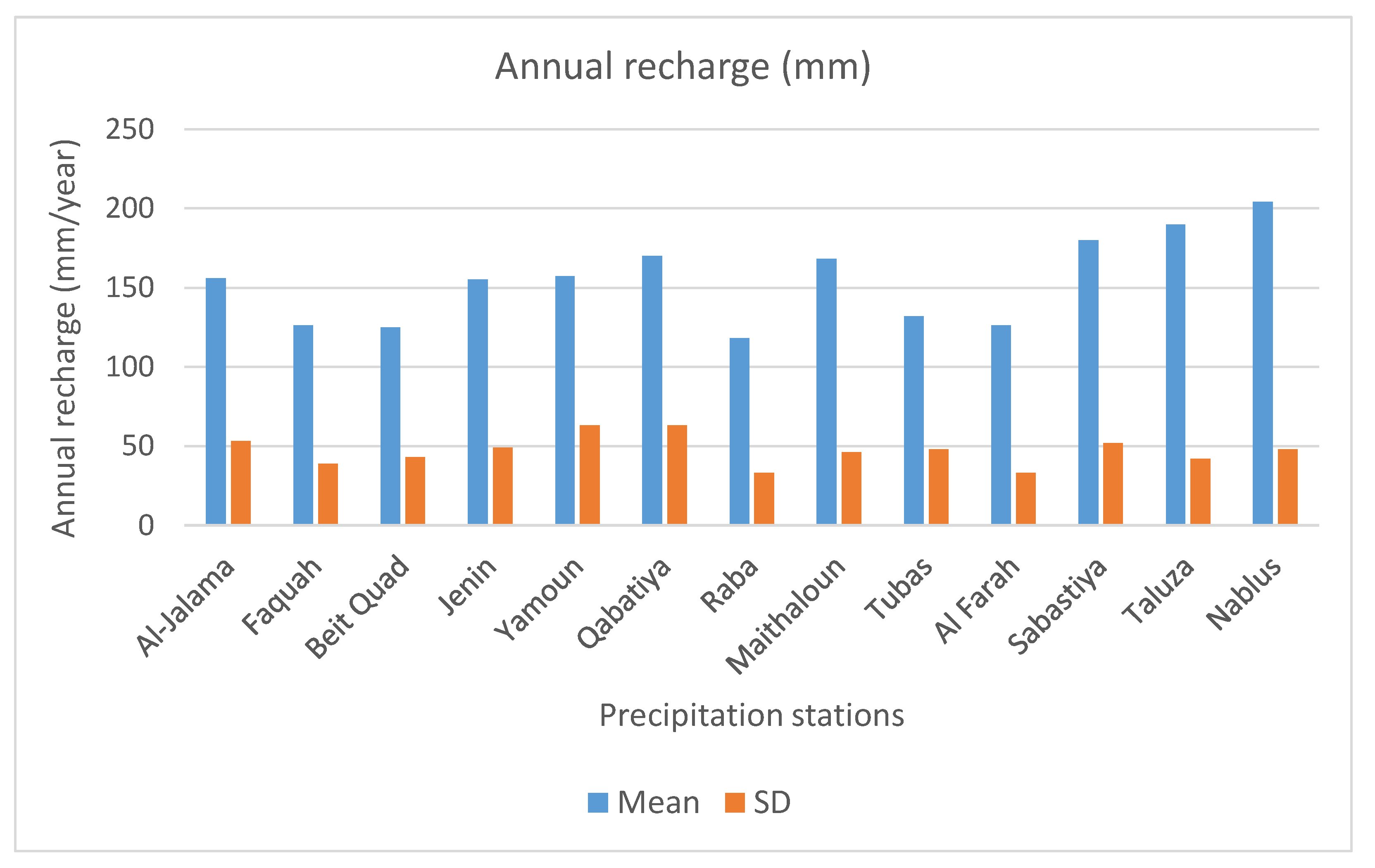
- Aquifer recharge has been calculated as a percentage of precipitation rates (from multiple stations), following the methodology that uses variation of groundwater levels and its relation to inflows and outflows [43]. As this is the most uncertain parameter, different methods for its assessment need to be considered, including distributed soil water balance models or direct measurements.
- The optimal abstraction strategies were obtained using successive linear programming optimization of GWM. As this is a non-linear system, future studies may consider coupling the simulation model with global optimization algorithms.
- The optimal strategies were designed using a steady state groundwater simulation model. Future studies should consider coupling of the transient simulation model with optimization algorithms that will include temporal storage changes.
- The optimization results depend critically on the groundwater simulation model. Collection of further accurate data regarding well abstractions and boundary conditions for model improvement are needed.
- This study considered only uncertainty of the model parameters. Uncertainty of the conceptual model should be considered in future studies.
- GDSS has been developed as a prototype application only. Further extensions are recommended towards a more comprehensive decision support system, with better comparative analysis of proposed management strategies, potentially including Multi-Criteria Analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahmoud, N.; Zayed, O.; Petrusevski, B. Groundwater Quality of Drinking Water Wells in the West Bank, Palestine. Water 2022, 14, 377. [Google Scholar] [CrossRef]
- PWA. Strategic Water Resources and Transmission Plan; Palestinian Water Authority: Ramallah, Palestine, 2014; Available online: http://www.pwa.ps/page.aspx?id=sTpd7oa2511676167asTpd7o (accessed on 1 November 2022).
- World Bank. Securing Water for Development in West Bank and Gaza; World Bank: Washington, DC, USA, 2018; Available online: https://openknowledge.worldbank.org/handle/10986/30252?show=full (accessed on 1 November 2022).
- UNEP. State of Environment and Outlook Report for the Occupied Palestinian Territory 2020; United Nations Environment Programme: Nairobi, Kenya, 2020; Available online: https://wedocs.unep.org/handle/20.500.11822/32268 (accessed on 1 November 2022).
- Rushton, K.R. Groundwater Hydrology: Conceptual and Computational Models; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Zhou, Y.; Li, W. A review of regional groundwater flow modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Baalousha, H.M.; Lowry, C.S. Applied Groundwater Modelling for Water Resource Management and Protection. Water 2022, 14, 1142. [Google Scholar] [CrossRef]
- McDonald, M.; Harbaugh, A.W. A Modular Three-Dimensional Finite Difference Ground-Water Flow Model. In Techniques of Water-Resources Investigations, Book 6; U.S. Geological Survey: Reston, VA, USA, 1988; p. 588. [Google Scholar]
- Harbaugh, A.W. U.S. Geological Survey Techniques and Methods 6-A16. In MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—the Ground-Water Flow Process; U.S. Geological Survey: Reston, VA, USA, 2005. [Google Scholar]
- SUSMAQ. Conceptual and Steady-State Models of the Eocene Aquifer in the North-Eastern Aquifer Basin; House of Water and Environment: Ramallah, Palestine, 2004. [Google Scholar]
- Tubeileh, H.; Shaheen, H.; Aliewi, A. Modeling the Eocene Aquifer in Northern West Bank. An-Najah Univ. J. Res. A 2006, 20, 41–62. [Google Scholar]
- Abdel-Ghafour, D.; Aliewi, A. Adopting numerical approach for groundwater management in Eocene Aquifer, West Bank-Palestine. In Groundwater Modeling and Management under Uncertainty; CRC Press: Boca Raton, FL, USA, 2012; p. 24. [Google Scholar]
- Deeb, A.A. Modelling of Groundwater Recharge in the Eocene Aquifer (Palestine) Using the USGS Soil Water Balance (SWB) Software. Master’s Thesis, Department of Water and Environmental Engineering, Faculty of Graduate Studies, Al-Najah National University, Nablus, Palestine, 2021. [Google Scholar]
- Wu, J.C.; Zeng, X.K. Review of the uncertainty analysis of groundwater numerical simulation. Chin. Sci. Bull. 2013, 58, 3044–3052. [Google Scholar] [CrossRef] [Green Version]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Rojas, R.; Kahunde, S.; Peeters, L.; Batelaan, O.; Feyen, L.; Dassargues, A. Application of a multimodel approach to account for conceptual model and scenario uncertainties in groundwater modelling. J. Hydrol. 2010, 394, 416–435. [Google Scholar] [CrossRef] [Green Version]
- Ballio, F.; Guadagnini, A. Convergence assessment of numerical Monte Carlo simulations in groundwater hydrology. Water Resour. Res. 2004, 40, W04603. [Google Scholar] [CrossRef]
- Hassan, A.E.; Bekhit, H.M.; Chapman, J.B. Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model. Environ. Model. Softw. 2009, 24, 749–763. [Google Scholar] [CrossRef]
- Guillaume, J.H.A.; Hunt, R.J.; Comunian, A.; Blakers, R.S.; Fu, B. Methods for exploring uncertainty in groundwater management predictions. In Integrated Groundwater Management: Concepts, Approaches and Challenges; Jakeman, A.J., Barreteau, O., Hunt, R.J., Rinaudo, J.-D., Ross, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 711–737. [Google Scholar] [CrossRef] [Green Version]
- Yeh, W.W.G. Review: Optimization methods for groundwater modeling and management. Hydrogeol. J. 2015, 23, 1051–1065. [Google Scholar] [CrossRef]
- Jonoski, A.; Zhou, Y.; Nonner, J.; Meijer, S. Model-aided design and optimization of artificial recharge-pumping systems. Hydrol. Sci. J. 1997, 42, 937–953. [Google Scholar] [CrossRef]
- Ahlfeld, D.P.; Mulligan, A.E. Optimal Management of Flow in Groundwater Systems; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Maskey, S.; Jonoski, A.; Solomatine, D.P. Groundwater remediation strategy using global optimization algorithms. J. Water Resour. Plan. Manag. 2002, 128, 431–440. [Google Scholar] [CrossRef] [Green Version]
- Sedki, A.; Ouazar, D. Simulation-Optimization Modeling for Sustainable Groundwater Development: A Moroccan Coastal Aquifer Case Study. Water Resour. Manag. 2011, 25, 2855–2875. [Google Scholar] [CrossRef]
- Ebrahim, G.Y.; Jonoski, A.; Maktoumi, A.A.; Ahmed, M.; Mynett, A. Simulation-Optimization Approach for Evaluating the Feasibility of Managed Aquifer Recharge in the Samail Lower Catchment, Oman. J. Water Resour. Plan. Manag. 2016, 142, 05015007. [Google Scholar] [CrossRef]
- Kamali, A.; Niksokhan, M.H. Multi-objective optimization for sustainable groundwater management by developing of coupled quantity-quality simulation-optimization model. J. Hydroinform. 2017, 19, 973–992. [Google Scholar] [CrossRef]
- Ashu, A.B.; Lee, S.-I. Simulation-Optimization Model for Conjunctive Management of Surface Water and Groundwater for Agricultural Use. Water 2021, 13, 3444. [Google Scholar] [CrossRef]
- Paul, S.; Waldron, B.; Jazaei, F.; Larsen, D.; Schoefernacker, S. Groundwater well optimization to minimize contaminant movement from a surficial shallow aquifer to a lower water supply aquifer using stochastic simulation-optimization modeling techniques: Strategy formulation. MethodsX 2022, 9, 101765. [Google Scholar] [CrossRef]
- Kharmah, R.N. Optimal Management of Groundwater Pumping the Case of the Eocene Aquifer, Palestine. Master’s Thesis, Department of Water and Environmental Engineering, Faculty of Graduate Studies, Al-Najah National University, Nablus, Palestine, 2007. [Google Scholar]
- Ahlfeld, D.P.; Barlow, P.M.; Mulligan, A.E. GWM—A Ground-Water Management Process for the U.S. Geological Survey Modular Ground-Water Model (MODFLOW-2000); Open-File Report 2005-1072; U.S. Geological Survey: Washington, DC, USA, 2005; p. 124. [Google Scholar]
- Andricevic, R.; Kitanidis, P.K. Optimization of the pumping schedule in aquifer remediation under uncertainty. Water Resour. Res. 1990, 26, 875–885. [Google Scholar] [CrossRef]
- Ndambuki, J.M.; Otieno, F.A.; Stroet, C.B.; Veling, E.J. Groundwater management under uncertainty: A multi-objective approach. WATER SA-PRETORIA- 2000, 26, 35–42. [Google Scholar]
- Wagner, J.M.; Shamir, U.; Nemati, H.R. Groundwater quality management under uncertainty: Stochastic programming approaches and the value of information. Water Resour. Res. 1992, 28, 1233–1246. [Google Scholar] [CrossRef]
- Kifanyi, G.E.; Ndambuki, J.M.; Odai, S.N.; Gyamfi, C. Quantitative management of groundwater resources in regional aquifers under uncertainty: A retrospective optimization approach. Groundw. Sustain. Dev. 2019, 8, 530–540. [Google Scholar] [CrossRef]
- Peralta, R.C.; Kalwij, I.M. Groundwater Optimization Handbook, Flow, Contaminant Transport, and Conjunctive Management; Routledge: England, UK, 2012; ISBN 978-1-4398-3806-8. [Google Scholar]
- Almasri, M.N.; Judeh, T.G.; Shadeed, S.M. Identification of the Nitrogen Sources in the Eocene Aquifer Area (Palestine). Water 2020, 12, 1121. [Google Scholar] [CrossRef]
- Almoradie, A.; Cortes, V.J.; Jonoski, A. Web-based stakeholder collaboration in flood risk management. J. Flood Risk Manag. 2015, 8, 19–38. [Google Scholar] [CrossRef]
- Kumar, S.; Godrej, A.N.; Grizzard, T.J. A web-based environmental decision support system for legacy models. J. Hydroinform. 2015, 17, 874–890. [Google Scholar] [CrossRef] [Green Version]
- Khelifi, O.; Lodolo, A.; Vranes, S.; Centi, G.; Miertus, S. A web-based decision support tool for groundwater remediation technologies selection. J. Hydroinform. 2006, 8, 91–100. [Google Scholar] [CrossRef]
- Glass, J.; Junghanns, R.; Schlick, R.; Stefan, C. The INOWAS platform: A web-based numerical groundwater modelling approach for groundwater management applications. Environ. Model. Softw. 2022, 155, 105452. [Google Scholar] [CrossRef]
- Aliyari, H.; Kholghi, M.; Zahedi, S.; Momeni, M. Providing decision support system in groundwater resources management for the purpose of sustainable development. J. Water Supply Res. Technol.-Aqua 2018, 67, 423–437. [Google Scholar] [CrossRef]
- Aquaveo. Groundwater Modelling System (GMS). 2022. Available online: https://www.aquaveo.com/software/gms-groundwater-modeling-system-introduction (accessed on 9 December 2022).
- Abusaada, M.; Sauter, M. Recharge Estimation in Karst Aquifers by Applying Water Level Fluctuation Approach. Int. J. Earth Sci. Geophys. 2017, 3, 10–35840. [Google Scholar]
- Bakker, M.; Post, V.; Langevin, C.D.; Hughes, J.D.; White, J.T.; Starn, J.J.; Fienen, M.N. Scripting MODFLOW Model Development Using Python and FloPy. Groundwater 2016, 54, 733–739. [Google Scholar] [CrossRef]
- Pollock, D.W. User Guide for MODPATH Version 7—A Particle-Tracking Model for MODFLOW; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2016; p. 35. [Google Scholar] [CrossRef] [Green Version]
- Rojas, R.; Feyen, L.; Dassargues, A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging. Water Resour. Res. 2008, 44, W12418. [Google Scholar] [CrossRef] [Green Version]
- Refsgaard, J.C.; van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P.A. Uncertainty in the environmental modelling process—A framework and guidance. Environ. Model. Softw. 2007, 22, 1543–1556. [Google Scholar] [CrossRef] [Green Version]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Uusitalo, L.; Lehikoinen, A.; Helle, I.; Myrberg, K. An overview of methods to evaluate uncertainty of deterministic models in decision support. Environ. Model. Softw. 2015, 63, 24–31. [Google Scholar] [CrossRef]































| Strategy: | Existing | 01 | 02 | 03 | 04 | 05 |
|---|---|---|---|---|---|---|
| Total abstraction (Mm3/year) | 49.4 | 52.6 | 54.1 | 56.7 | 60.2 | 50.1 |
| Percentage increase (%) | - | 6.7 | 9.5 | 14.8 | 21.9 | 1.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jonoski, A.; Ahmed, T.; Almasri, M.N.; Abu-Saadah, M. Decision Support System for Sustainable Exploitation of the Eocene Aquifer in the West Bank, Palestine. Water 2023, 15, 365. https://doi.org/10.3390/w15020365
Jonoski A, Ahmed T, Almasri MN, Abu-Saadah M. Decision Support System for Sustainable Exploitation of the Eocene Aquifer in the West Bank, Palestine. Water. 2023; 15(2):365. https://doi.org/10.3390/w15020365
Chicago/Turabian StyleJonoski, Andreja, Tanvir Ahmed, Mohammad N. Almasri, and Muath Abu-Saadah. 2023. "Decision Support System for Sustainable Exploitation of the Eocene Aquifer in the West Bank, Palestine" Water 15, no. 2: 365. https://doi.org/10.3390/w15020365









