Triggering of Rain-Induced Landslides, with Applications in Southern Italy
Abstract
:1. Introduction
2. Physical Models
3. Hydrological Models
4. Coupled Hydrological and Physical Models
5. Some Model Applications
5.1. Application of Physical Modelling
5.2. Application of Hydrological Modelling
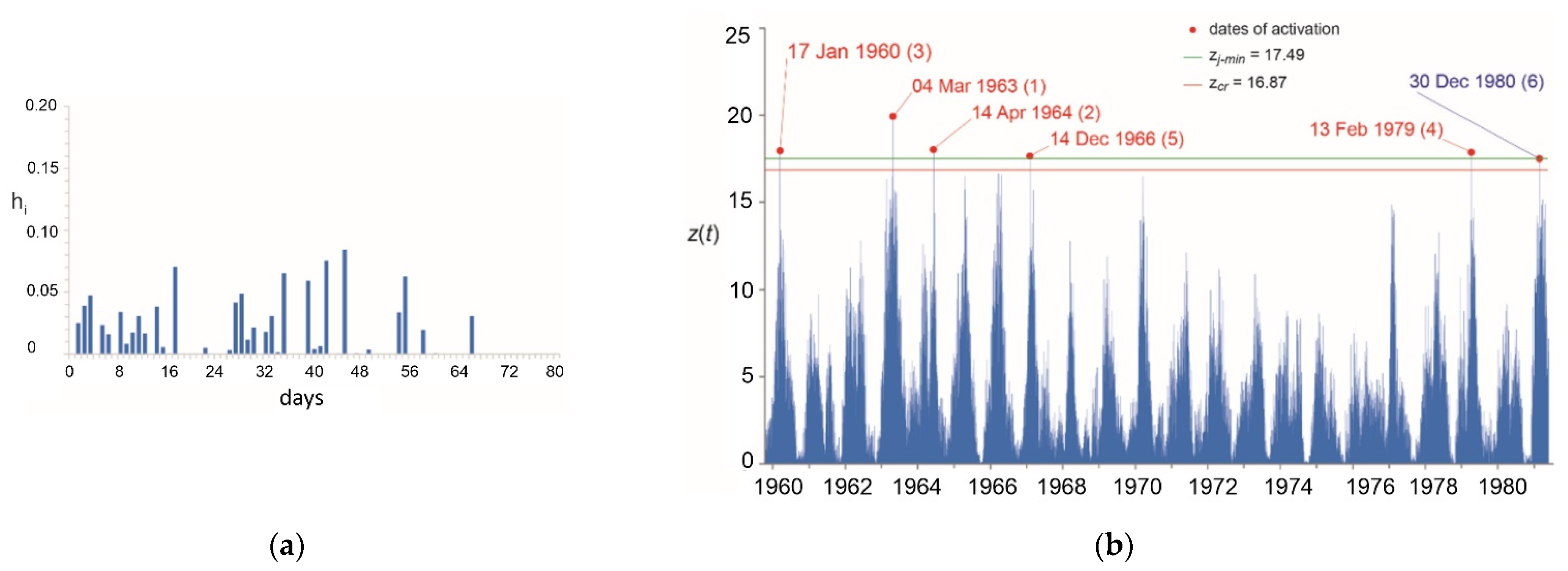
- For the Campanian shallow landslides of the Sorrento Peninsula, the obtained is quite short (28 days), about a half of those obtained for the Calabrian rock slides (ranging between 46 and 74 days), thus confirming the expected direct relationship between base time, on one side, and the extent of instability masses and groundwater paths on the other -cf. [9].
- The best performances were observed for the San Fili-Uncino (Figure 8) and for the San Benedetto Ullano-San Rocco case studies, with neither missing nor false alarms both in calibration and in validation (in fact, even for this latter case, the predicted activation anticipates “only few hours”, the alarm issued by the public authority of Civil Protection, hence Φv is actually 100%).
- Less satisfactory results were instead obtained for the Sorrento Peninsula study case. In general, concerning shallow landslides, worse modelling results are intrinsically expected due to a number of reasons: the differences in extent of the triggered landslides, heterogeneities in slope materials, inhomogeneous rainfall fields (especially in case of short-lasting, high-intensity storms) and poor quality of rain data due to low density of the rain-gauge network. Moreover, some dates of activation may even be missing, especially in remote areas. Anyhow, despite all such limitations, Φ greater than 80% and 73% were obtained for calibration and validation in the Sorrento Peninsula, respectively.
- For the Acri case study, the application of the model was evidently hampered by misleading geotechnical information (cf. e.g., [148]), reflecting in the unsatisfactory values of Φ obtained both in calibration (ca. 83%) and especially in validation (ca. 62%). For this case study, some of the available dates of activation apparently refer to secondary portions of the main rockslide; historical archives did not permit an accurate understanding of the mobilised volumes, and then secondary movements (or even activations of different nearby phenomena) may have been incorrectly attributed to the investigated slope movement.
6. Conclusions and Some Research Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Skill Score | Formula | Range | Optimal Value |
|---|---|---|---|
| Probability of Detection | [0, 1] | 1 | |
| Probability of False Detection | [0, 1] | 0 | |
| Probability of False Alarms | [0, 1] | 1 | |
| Hanssen and Kuipers | [−1, 1] | 1 |
References
- Popescu, M.E. Landslide causal factors and landslide remedial options. In Proceedings of the 3rd International Conference on Landslides, Slope Stability and Safety of Infrastructures, Singapore, 11–12 July 2002. [Google Scholar]
- Peranić, J.; Čeh, N.; Arbanas, Ž. The use of soil moisture and pore-water pressure sensors for the interpretation of landslide behaviour in small-scale physical models. Sensors 2022, 22, 7337. [Google Scholar] [CrossRef] [PubMed]
- Campbell, R.H. Debris flow originating from soil slip during rainstorm in southern California. Q. J. Eng. Geol. Hydrogeol. 1975, 7, 377–384. [Google Scholar] [CrossRef]
- De Vita, P.; Piscopo, V. Influences of hydrological and hydrogeological conditions on debris flows in peri-vesuvian hillslopes. Nat. Hazards Earth Syst. Sci. 2002, 2, 27–35. [Google Scholar] [CrossRef]
- Fiorillo, F.; Esposito, L.; Grelle, G.; Revellino, P.; Guadagno, F.M. Further hydrological analyses on landslide initiation in the Sarno area (Italy). Ital. J. Geosci. 2013, 132, 341–349. [Google Scholar] [CrossRef]
- Schilirò, L.; Poueme Djueyep, G.; Esposito, C.; Scarascia Mugnozza, G. The role of initial soil conditions in shallow landslide triggering: Insights from physically based approaches. Geofluids 2019, 2019, 2453786. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons, Inc.: New York, NY, USA, 1993; 544p. [Google Scholar]
- Brand, E.W. Landslides in Southeast Asia: A state-of-the-art report. In Proceedings of the IV International Symposium on Landslides, Canadian Geotechnical Society, Toronto, ON, Canada, 16–21 September 1984. [Google Scholar]
- Cascini, L.; Versace, P. Eventi pluviometrici e movimenti franosi. In Proceedings of the XVI Convegno Nazionale di Geotecnica, Bologna, Italy, 14–16 May 1986. (In Italian). [Google Scholar]
- Cascini, L.; Versace, P. Relationship between rainfall and landslide in a gneissic cover. In Proceedings of the Fifth International Symposium on Landslides, Lausanne, Switzerland, 10–15 July 1988. [Google Scholar]
- Wieczorek, G.F. Landslide Triggering Mechanisms. In Landslides: Investigation and Mitigation; Turner, A.K., Schuster, R.L., Eds.; National Academy Press: Washington, DC, USA, 1996; pp. 76–90. [Google Scholar]
- Van Asch, T.W.J.; Buma, J.; Van Beek, L.P.H. A view on some hydrological triggering systems in landslides. Geomorphology 1999, 30, 25–32. [Google Scholar] [CrossRef]
- Jakob, M.; Weatherly, H. A hydroclimatic threshold for landslide initiation on the North Shore Mountains of Vancouver, British Columbia. Geomorphology 2003, 54, 137–156. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Melillo, M. Rainfall and landslide initiation. In Rainfall—Modeling, Measurement and Applications, 1st ed.; Morbidelli, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 427–450. [Google Scholar]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Vennari, C.; Guzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Terranova, O.; Gariano, S.L.; Iaquinta, P.; Lupiano, V.; Rago, V.; Iovine, G. Example of application of GASAKe for predicting the occurrence of rainfall-induced landslides in Southern Italy. Geoscience 2018, 8, 78. [Google Scholar] [CrossRef]
- Zaruba, Q. Vliv klimatických poměrů na smršťování křídových slínů. Věda přír 1936, 17, 217–231. [Google Scholar]
- Capparelli, G.; Versace, P. FLaIR and SUSHI: Two mathematical models for early warning of landslides induced by rainfall. Landslides 2011, 8, 67–79. [Google Scholar] [CrossRef]
- Cauvin, S.; Cordier, M.O.; Dousson, C.; Laborie, P.; Lévy, F.; Montmain, J.; Porcheron, M.; Servet, I.; Travé-Massuyès, L. Monitoring and alarm interpretation in industrial environments. AI Commun. 1998, 11, 139–173. [Google Scholar]
- Iovine, G.; Iaquinta, P.; Terranova, O. Emergency management of landslide risk during autumn-winter 2008/2009 in Calabria (Italy), The example of San Benedetto Ullano. Proceedings of 18th World IMACS Congress and MODSIM09 International Congress on Modelling and Simulation, Cairns, Australia, 13–17 July 2009. [Google Scholar]
- Carter, J. The Notion of Threshold: An Investigation into Conceptual Accompaniment in Aristotle and Hegel, Conserveries Mémorielles 2010, 7. Available online: http://cm.revues.org/431 (accessed on 17 October 2022).
- White, I.D.; Mottershead, D.N.; Harrison, J.J. Environmental Systems, 2nd ed.; Chapman & Hall: London, UK, 1996; 616p. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: San Diego, CA, USA, 1995; 467p. [Google Scholar]
- Accadia, C.; Mariani, S.; Casaioli, M.; Lavagnini, A.; Speranza, A. Sensitivity of precipitation forecast skill scores to bilinear interpolation and a simple nearest-neighbor average method on high-resolution verification grids. Weather. Forecast. 2003, 18, 918–932. [Google Scholar] [CrossRef]
- Staley, D.M.; Kean, J.W.; Cannon, S.H.; Schmidt, K.M.; Laber, J.L. Objective definition of rainfall intensity–duration thresholds for the initiation of post-fire debris flows in southern California. Landslides 2013, 10, 547–562. [Google Scholar] [CrossRef]
- Mirus, B.B.; Morphew, M.D.; Smith, J.B. Developing hydro-meteorological thresholds for shallow landslide initiation and early warning. Water 2018, 10, 1274. [Google Scholar] [CrossRef] [Green Version]
- Keefer, D.K.; Wilson, R.C.; Mark, R.K.; Brabb, E.E.; Brown, W.M., III; Ellen, S.D.; Harp, E.L.; Wieczorek, G.F.; Alger, C.S.; Zatkin, R.S. Real-time Landslide Warning During Heavy Rainfall. Science 1987, 238, 921–925. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Piciullo, L.; Gariano, S.L.; Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Guzetti, F.; Calvello, M. Definition and performance of a threshold-based regional early warning model for rainfall-induced landslides. Landslides 2017, 14, 995–1008. [Google Scholar] [CrossRef]
- Rossi, M.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Luciani, S.; Ardizzone, F.; Balducci, V.; Bianchi, C.; Cardinali, M.; Fiorucci, F.; et al. SANF: National warning system for rainfall-induced landslides in Italy. Proceedings of 11th International and 2nd North American Symposium on Landslides and Engineered Slopes, Banff, AB, Canada, 3–8 June 2012. [Google Scholar]
- Chung, C.J.F.; Fabbri, A.G. Validation of spatial prediction models for landslide hazard mapping. Nat. Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Lee, G.; Kim, W.; Oh, H.; Youn, B.D.; Kim, N.H. Review of statistical model calibration and validation—From the perspective of uncertainty structures. Struct. Multidiscip. Optim. 2019, 60, 1619–1644. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Terzaghi, K. Stability of steep slopes on hard unweathered rock. Geotechnique 1962, 12, 251–270. [Google Scholar] [CrossRef]
- Johnson, A.M. Debris flow. In Slope Instability; Brunsden, D., Prior, D.B., Eds.; Wiley: Chichester, UK, 1984; pp. 257–361. [Google Scholar]
- Montgomery, D.R.; Dietrich, W.E. A physically-based model for the topographic control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
- Wilson, R.C.; Wieczorek, G.F. Rainfall thresholds for the initiation of debris flow at La Honda, California. Environ. Eng. Geosci. 1995, 1, 11–27. [Google Scholar] [CrossRef]
- Crosta, G.B. Regionalization of rainfall thresholds: An aid to landslide hazard evaluation. Environ. Geol. 1998, 35, 131–145. [Google Scholar] [CrossRef]
- Terlien, M.T.J. The determination of statistical and deterministic hydrological landslide-triggering thresholds. Environ. Geol. 1998, 35, 125–130. [Google Scholar] [CrossRef]
- Crosta, G.B.; Dal Negro, P.; Frattini, P. Soil slips and debris flows on terraced slopes. Nat. Hazards Earth Syst. Sci. 2003, 3, 31–42. [Google Scholar] [CrossRef] [Green Version]
- Pisani, G.; Castelli, M.; Scavia, C. Hydrogeological model and hydraulic behaviour of a large landslide in the Italian Western Alps. Nat. Hazards Earth Syst. Sci. 2010, 10, 2391–2406. [Google Scholar] [CrossRef] [Green Version]
- Van Asch, T.W.J.; Sukmantalya, I.N. The modelling of soil slip erosion in the upper Komering area, South Sumatra Province, Indonesia. Geogr. Fis. Din. Quat. 1993, 16, 81–86. [Google Scholar]
- Terlien, M.J.M. Modelling Spatial and Temporal Variations in Rainfall-Triggered Landslides; International Institute for Aerospace Survey and Earth Sciences (ITC): Enschede, The Netherlands, 1996; 254p. [Google Scholar]
- Chen, H.; Dadson, S.; Chi, Y. Recent rainfall-induced landslides and debris flow in northern Taiwan. Geomorphology 2006, 77, 112–125. [Google Scholar] [CrossRef]
- Jamaludin, S.; Ali, F. An overview of some empirical correlations between rainfall and shallow landslides and their applications in Malaysia. Electron. J. Geotech. Eng. 2011, 16, 1429–1440. [Google Scholar]
- Huang, Y.H. Slope Stability Analysis by the Limit Equilibrium Method: Fundamentals and Methods; ASCE Press: Reston, VA, USA, 2014; p. 363. [Google Scholar]
- Janbu, N. Application of composite slip surfaces for stability analysis. In Proceedings of the European Conference on Stability of Earth Slopes, Stockholm, Sweden, 20–25 September 1954. [Google Scholar]
- Bishop, A.W. The use of the slip circle in the stability analysis of slopes. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surfaces. Géotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Spencer, E. A method of analysis of the stability of embankments assuming parallel inter-slice forces. Géotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Sarma, S.K. Stability analysis of embankments and slopes. Géotechnique 1973, 23, 423–433. [Google Scholar] [CrossRef]
- Anagnosti, P. Three-dimensional stability of fill dams. In Proceedings of the 7th International Conference on soil Mechanics and Foundation Engineering, Mexico City, Mexico, 29 August 1969; Volume 2, pp. 275–280. [Google Scholar]
- Kumar, S.; Choudhary, S.S.; Burman, A. Recent advances in 3D slope stability analysis: A detailed review. Model. Earth Syst. Environ. 2022, 1–18. [Google Scholar] [CrossRef]
- Quecedo, M.; Pastor, M.; Herreros, M.I. Numerical modelling of impulse wave generated by fast landslides. Int. J. Numer. Methods Eng. 2004, 59, 1633–1656. [Google Scholar] [CrossRef]
- Baligh, M.M.; Azzouz, A.S. End Effects of Stability of Cohesive Slopes. J. Geotech. Eng. Div. 1975, 101, 1105–1117. [Google Scholar] [CrossRef]
- Chen, R.H. Three-Dimensional Slope Stability Analysis; Report JHRP-81-17; Purdue University: West Lafayette, IN, USA, 1981. [Google Scholar]
- Gens, A.; Hutchinson, J.N.; Cavounidis, S. Three-Dimensional Analysis of Slides in Cohesive Soils. Geotechnique 1988, 38, 1–23. [Google Scholar] [CrossRef]
- Stark, T.D.; Eid, H.T. Performance of Three-Dimensional Slope Stability Methods in Practice. J. Geotech. Geoenviron. Eng. 1998, 124, 1049–1060. [Google Scholar] [CrossRef]
- Arellano, D.; Stark, T.D. Importance of Three-Dimensional Slope Stability Analises in practice. In Proceedings of the Sessions of Geo-Denver 2000, Denver, CO, USA, 5–8 August 2000; ASCE: Reston, VA, USA, 2000; pp. 18–32. [Google Scholar]
- Shen, J.; Karakus, M. Three-dimensional numerical analysis for rock slope stability using shear strength reduction method. Can. Geotech. J. 2014, 51, 164–172. [Google Scholar] [CrossRef]
- Reid, M.E.; Christian, S.B.; Brien, D.L.; Henderson, S. Scoops3D—Software to Analyze Three-Dimensional Slope Stability throughout a Digital Landscape; US Geological Survey: Reston, VA, USA, 2015. [Google Scholar]
- Borselli, L. “SSAP 5.1—“Slope Stability Analysis Program”. Manuale di Riferimento del Codice SSAP Versione 5.1. 2022. Available online: https://doi.org/10.13140/RG.2.2.31522.91841 (accessed on 5 September 2022).
- Innocenti, A.; Pazzi, V.; Borselli, L.; Nocentini, M.; Lombardi, L.; Gigli, G.; Fanti, R. Reconstruction of the evolution phases of a landslide by using multi-layer back-analysis methods. Landslides 2023, 20, 189–207. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek–Brown failure criterion and GSI—2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Carranza-Torres, C. Elasto-plastic solution of tunnel problems using the generalized form of the Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2004, 41, 629–639. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.C. Review of predictive capability of JRC-JCS model in engineering practice. In Proceedings of the International Symposium on Rock Joints, Loen, Norway, 4–6 June 1990. [Google Scholar]
- Barton, N. Shear strength criteria for rock, rock joints, rockfill and rock masses: Problems and some solutions. J. Rock Mech. Geotech. Eng. 2013, 5, 249–261. [Google Scholar] [CrossRef] [Green Version]
- Olson, S.M.; Stark, T.D. Yield strength ratio and liquefaction analysis of slopes and embankments. J. Geotech. Geoenviron. Eng. 2003, 129, 727–737. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, W.E.; Wilson, C.J.; Montgomery, D.R.; McKean, J.; Bauer, R. Erosion thresholds and land surface morphology. Geology 1992, 20, 675–679. [Google Scholar] [CrossRef]
- Dietrich, W.E.; Wilson, C.J.; Montgomery, D.R.; McKean, J. Analysis of erosion thresholds, channel networks, and landscape morphology using a digital terrain model. J. Geol. 1993, 101, 259–278. [Google Scholar] [CrossRef] [Green Version]
- Borga, M.; Dalla Fontana, G.; Cazorzi, F. Analysis of topographic and climatic control on rainfall-triggered shallow landsliding using a quasi-dynamic wetness index. J. Hydrol. 2002, 268, 56–71. [Google Scholar] [CrossRef]
- Lanni, C.; Borga, M.; Rigon, R.; Tarolli, P. Modelling shallow landslide susceptibility by means of a subsurface flow path connectivity index and estimates of soil depth spatial distribution. Hydrol. Earth Syst. Sci. 2012, 16, 3959–3971. [Google Scholar] [CrossRef] [Green Version]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0; U.S. Geological Survey: Reston, VA, USA, 2009; 75p. [Google Scholar]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. F Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Liao, Z.; Hong, Y.; Kirschbaum, D.; Adler, R.F.; Gourley, J.J.; Wooten, R. Evaluation of TRIGRS (transient rainfall infiltration and grid-based regional slope-stability analysis)’s predictive skill for hurricane-triggered landslides: A case study in Macon County, North Carolina. Nat. Hazards 2011, 58, 325–339. [Google Scholar] [CrossRef]
- Park, D.W.; Nikhil, N.V.; Lee, S.R. Landslide and debris flow susceptibility zonation using TRIGRS for the 2011 Seoul landslide event. Nat. Hazards Earth Syst. Sci. 2013, 11, 2833–2849. [Google Scholar] [CrossRef] [Green Version]
- Grelle, G.; Soriano, M.; Revellino, P.; Guerriero, L.; Anderson, L.G.; Diambra, A.; Fiorillo, F.; Esposito, E.; Diodato, N.; Guadagno, F.M. Space–time prediction of rainfall-induced shallow landslides through a combined probabilistic/deterministic approach, optimized for initial water table conditions. Bull. Eng. Geol. Environ. 2014, 73, 877–890. [Google Scholar] [CrossRef]
- Salciarini, D.; Fanelli, G.; Tamagnini, C. A probabilistic model for rainfall—Induced shallow landslide prediction at the regional scale. Landslides 2017, 14, 1731–1746. [Google Scholar] [CrossRef]
- Ciurleo, M.; Mandaglio, M.C.; Moraci, N. A quantitative approach for debris flow inception and propagation analysis in the lead up to risk management. Landslides 2021, 18, 2073–2093. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Conte, E. Rainfall threshold for shallow landslide triggering due to rising water table. Water 2022, 14, 2966. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Conte, E. A simplified analytical method to predict shallow landslides induced by rainfall in unsaturated soils. Water 2022, 14, 3180. [Google Scholar] [CrossRef]
- Fenti, V.; Silvano, S.; Carampin, R. Quadro d’insieme sulla franosità e i dissesti nel bacino del T. Fiorentina (Belluno). Studi Trentini Sci. Nat. Acta Geol. 1984, 61, 3–31. [Google Scholar]
- Govi, M.; Mortara, G.; Sorzana, P.F. Eventi idrologici e frane. Geol. Appl. Idrogeol. 1985, 20, 359–375. [Google Scholar]
- Cannon, S.H.; Ellen, S.D. Rainfall conditions for abundant debris avalanches, San Francisco Bay region, California. Calif. Geol. 1985, 38, 267–272. [Google Scholar]
- Cancelli, A.; Nova, R. Landslides in Soil Debris Cover triggered by Rainstorms in Valtellina (Central Alps—Italy). In Proceedings of the IV International Conference and Field Workshop on Landslides, Tokyo, Japan, 23–31 August 1985; pp. 267–272. [Google Scholar]
- Sangrey, D.A.; Harrop-Williams, K.O.; Klaiber, J.A. Predicting ground-water response to precipitation. J. Geotech. Eng. 1984, 110, 957–975. [Google Scholar] [CrossRef]
- Crozier, M.J. Landslides: Causes, Consequences and Environment; Croom Helm: London, UK, 1986; 252p. [Google Scholar]
- Owen, R.C. Soil strength and microclimate in the distribution of shallow landslides. J. Hydrol. 1981, 20, 17–26. [Google Scholar]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flow: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Dolojan, N.L.J.; Moriguchi, S.; Hashimoto, M.; Terada, K. Mapping method of rainfall-induced landslide hazards by infiltration and slope stability analysis. Landslides 2021, 18, 2039–2057. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. Ser. A Phys. 1980, 62A, 23–27. [Google Scholar]
- Polloni, G.; Ceriani, M.; Lauzi, S.; Padovan, N.; Crosta, G. Rainfall and soil slipping events in Valtellina. In Proceedings of the Sixth International Symposium on Landslides, Christchurch, New Zealand, 10–14 February 1992. [Google Scholar]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Lumb, P. Slope failures in Hong Kong. Q. J. Eng. Geol. 1975, 8, 31–65. [Google Scholar] [CrossRef]
- Chun, K.W.; Kim, M.; Catani, F.; Choi, B.; Seo, J.I. Effect of antecedent rainfall conditions and their variations on shallow landslide-triggering rainfall thresholds in South Korea. Landslides 2021, 18, 569–582. [Google Scholar]
- Kim, S.K.; Hong, W.P.; Kim, Y.M. Prediction of rainfall triggered landslides in Korea. In Proceedings of the VI International Symposium on Landslides, Christchurch, New Zealand, 10–14 February 1992. [Google Scholar]
- Page, M.J.; Trustrum, N.A.; De Rose, R.C. A high-resolution record of storm-induced erosion from lake sediments, New Zealand. J. Paleolimnol. 1994, 11, 333–348. [Google Scholar] [CrossRef]
- Brunsden, D. Mudslides. In Slope Instability; Brunsden, D., Prior, D.B., Eds.; John Wiley & Sons: London, UK, 1984; pp. 363–418. [Google Scholar]
- Polemio, M.; Sdao, F. The role of rainfall in the landslide hazard: The case of the Avigliano urban area (southern Apennines, Italy). Eng. Geol. 1999, 53, 297–309. [Google Scholar] [CrossRef]
- Bonnard, C.; Noverraz, F. Influence of climate change on large landslides: Assessment of long-term movements and trends. In Proceedings of the International Conference on Landslides: Causes Impact and Countermeasures, Davos, Switzerland, 17–21 June 2001. [Google Scholar]
- Zêzere, J.L.; Rodrigues, M.L. Rainfall thresholds for landsliding in Lisbon area (Portugal). In Landslides; Rybář, J., Stemberk, J., Wagner, P., Eds.; A.A. Balkema: Lisse, The Netherlands, 2002; pp. 333–338. [Google Scholar]
- Trigo, R.M.; Zêzere, J.L.; Rodrigues, M.L.; Trigo, I.F. The influence of the North Atlantic Oscillation on rainfall triggering of Landslides near Lisbon. Nat. Hazards 2005, 36, 331–354. [Google Scholar] [CrossRef]
- Wieczorek, G.F. Effect of rainfall intensity and duration on debris flows in central Santa Cruz Mountains, California, In Debris Flows/Avalanches: Processes, Recognition and Mitigation; Costa, J.E., Wieczorek, G.F., Eds.; Geological Society of America: Boulder, CO, USA, 1987; Volume VII, pp. 93–104. [Google Scholar]
- Flentje, P.; Chowdhury, R. Slope instability, hazard and risk associated with a rainstorm event: A case study. In Proceedings of the 8th International Symposium on Landslides, Cardiff, UK, 23–26 June 2000. [Google Scholar]
- Dikau, R.; Schrott, L. The temporal stability and activity of landslides in Europe with respect to climatic change (TESLEC): Main objectives and results. Geomorphology 1999, 30, 1–12. [Google Scholar] [CrossRef]
- Corominas, J. Landslides and climate. Keynote lecture. In Proceedings of the 8th International Symposium on Landslides, Cardiff, UK, 26–30 June 2000. [Google Scholar]
- Marques, R.; Zêzere, J.; Trigo, R.; Gaspar, J.; Trigo, I. Rainfall patterns and critical values associated with landslides in Povoação County (São Miguel Island, Azores): Relationships with the North Atlantic Oscillation. Hydrol. Process. 2008, 22, 478–494. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Ferrari, E.; Iovino, F.; Nicolaci, A.; Veltri, A. Reforestation and land use change in a drainage basin of Southern Italy. iForest 2013, 6, 175–182. [Google Scholar] [CrossRef] [Green Version]
- D’Ippolito, A.; Calomino, F.; Alfonsi, G.; Lauria, A. Flow resistance in open channel due to vegetation at reach scale: A review. Water 2021, 13, 116. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Calomino, F.; Alfonsi, G.; Lauria, A. Drag coefficient of in-line emergent vegetation in open channel flow. Int. J. River Basin Manag. 2021, 15, 329–334. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Bed roughness effects on the turbulence characteristics of flows through emergent rigid vegetation. Water 2020, 12, 2401. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; D’Ippolito, A.; Gaudio, R. Effects of fluvial instability on the bed morphology in vegetated channels. Environ. Fluid Mech. 2022, 22, 619–644. [Google Scholar] [CrossRef]
- D’Ippolito, A.; Calomino, F.; Penna, N.; Dey, S.; Gaudio, R. Simulation of accelerated subcritical flow profiles in an open channel with emergent rigid vegetation. Appl. Sci. 2022, 12, 6960. [Google Scholar] [CrossRef]
- Capparelli, G.; Iaquinta, P.; Iovine, G.; Terranova, O.G.; Versace, P. Modelling the rainfall-induced mobilization of a large slope movement in northern Calabria. Nat. Hazards 2012, 61, 247–256. [Google Scholar] [CrossRef]
- Simoni, S.; Zanotti, F.; Bertoldi, G.; Rigon, R. Modelling the probability of occurrence of shallow landslides and channelized debris flows using GEOtop-FS. Hydrol. Process. 2008, 22, 532–545. [Google Scholar] [CrossRef]
- Crozier, M.J. The climate-landslide couple: A southern hemisphere perspective. In Rapid Mass Movement as a Source of Climatic Evidence for the Holocene; Matthews, J.A., Brunsden, D., Frenzel, B., Gläser, B., Weiß, M.M., Eds.; Gustav Fischer: Stuttgart, Germany, 1997; pp. 333–354. [Google Scholar]
- Sengupta, A.; Gupta, S.; Anbarasu, K. Rainfall thresholds for the initiation of landslide at Lanta Khola in north Sikkim, India. Nat. Hazards 2010, 52, 31–42. [Google Scholar] [CrossRef]
- Govi, M.; Sorzana, P.F. Landslide susceptibility as function of critical rainfall amount in Piedmont basin (North-Western Italy). Stud. Geomorphol. Carpatho-Balc. 1980, 14, 43–60. [Google Scholar]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control of rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139, 79–90. [Google Scholar] [CrossRef]
- Rahardjo, H.; Leong, E.C.; Rezaur, R.B. Assessment and instrumentation of slopes for stability against rainfall. In Proceedings of the Fourteenth Southeast Asian Geotechnical Conference, Hong Kong, 10−14 December 2001. [Google Scholar]
- Glade, T.; Crozier, M.; Smith, P. Applying probability determination to refine landslide-triggering rainfall thresholds using an empirical “Antecedent Daily Rainfall Model”. Pure Appl. Geophys. 2000, 157, 1059–1079. [Google Scholar] [CrossRef]
- Godt, J.W.; Baum, R.L.; Chleborad, A.F. Rainfall characteristics for shallow landsliding in Seattle, Washington, USA. Earth Surf. Process. Landf. 2006, 31, 97–110. [Google Scholar] [CrossRef]
- Napolitano, E.; Fusco, F.; Baum, R.L.; Godt, J.W.; De Vita, P. Effect of antecedent-hydrological conditions on rainfall triggering of debris flows in ash-fall pyroclastic mantled slopes of Campania (southern Italy). Landslides 2016, 13, 967–983. [Google Scholar] [CrossRef]
- Crozier, M.J. Prediction of rainfall-triggered landslides: A test of the antecedent water status model. Earth Surf. Process. Landforms 1999, 24, 825–833. [Google Scholar] [CrossRef]
- Brand, E.W. Keynote paper: Slope instability in tropical areas. In Proceedings of the Sixth International Symposium on Landslides, Christchurch, New Zealand, 10–14 February 1992. [Google Scholar]
- Brunetti, M.T.; Peruccacci, S.; Antronico, L.; Bartolini, D.; Deganutti, A.M.; Gariano, S.L.; Iovine, G.; Luciani, S.; Luino, F.; Melillo, M.; et al. Catalogue of Rainfall Events with Shallow Landslides and New Rainfall Thresholds in Italy. In Engineering Geology for Society and Territory; Lollino, G., Ed.; Springer International Publishing: Cham, Switzerland, 2015; Volume 2, pp. 1575–1579. [Google Scholar]
- Sirangelo, B.; Versace, P. A real time forecasting for landslides triggered by rainfall. Meccanica 1996, 31, 1–13. [Google Scholar] [CrossRef]
- Terranova, O.; Gariano, S.L.; Iaquinta, P.; Iovine, G. GASAKe: Forecasting landslide activations by a genetic-algorithms-based hydrological model. Geosci. Model Dev. 2015, 8, 1955–1978. [Google Scholar] [CrossRef] [Green Version]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- He, X.; Hong, Y.; Vergara, H.; Zhang, K.; Kirstetter, P.E.; Gourley, J.J.; Zhang, Y.; Qiao, G.; Liu, C. Development of a coupled hydrological-geotechnical framework for rainfall-induced landslides prediction. J. Hydrol. 2016, 543, 395–405. [Google Scholar] [CrossRef]
- Zhang, K.; Xue, X.; Hong, Y.; Gourley, J.J.; Lu, N.; Wan, Z.; Hong, Z.; Wooten, R. iCRESTRIGRS: A coupled modeling system for cascading Flood–Landslide disaster forecasting. Hydrol. Earth Syst. Sci. 2016, 20, 5035–5048. [Google Scholar] [CrossRef] [Green Version]
- Aristizábal, E.; Vélez, J.I.; Martínez, H.E.; Jaboyedoff, M. SHIA_Landslide: A distributed conceptual and physically based model to forecast the temporal and spatial occurrence of shallow landslides triggered by rainfall in tropical and mountainous basins. Landslides 2016, 13, 497–517. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, K.; van Beek, L.P.H.; Tian, X.; Bogaard, T.A. Physically-based landslide prediction over a large region: Scaling low-resolution hydrological model results for high-resolution slope stability assessment. Environ. Model. Softw. 2020, 124, 104607. [Google Scholar] [CrossRef]
- Tran, T.V.; Alvioli, M.; Lee, G.; An, H.U. Three-dimensional, time-dependent modeling of rainfall-induced landslides over a digital landscape: A case study. Landslides 2018, 15, 1071–1084. [Google Scholar] [CrossRef]
- Mergili, M.; Marchesini, I.; Alvioli, M.; Metz, M.; Schneider-Muntau, B.; Rossi, M.; Guzzetti, F. A strategy for GIS-based 3-D slope stability modelling over large areas. Geosci. Model Dev. 2014, 7, 2969–2982. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Zhang, K.; Wang, S.; Xia, Y.; Chao, L. iHydroSlide3D v1.0: An advanced hydrological-geotechnical model for hydrological simulation and three-dimensional landslide prediction. Geosci. Model Dev. Discuss. 2021. [Google Scholar] [CrossRef]
- Chen, C.-W.; Oguchi, T.; Hayakawa, Y.S.; Saito, H.; Chen, H. Relationship between landslide size and rainfall conditions in Taiwan. Landslides 2017, 14, 1235–1240. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Bordoni, M.; Corradini, B.; Lucchelli, L.; Valentino, R.; Bittelli, M.; Vivaldi, V.; Meisina, C. Empirical and physically based thresholds for the occurrence of shallow landslides in a prone area of Northern Italian Apennines. Water 2019, 11, 2653. [Google Scholar] [CrossRef] [Green Version]
- Melillo, M.; Brunetti, M.T.; Perruccacci, S.; Gariano, S.L.; Roccati, A.; Guzzetti, F. A tool for the automatic calculation of rainfall thresholds for landslide occurrence. Environ. Modell. Softw. 2018, 105, 230–243. [Google Scholar] [CrossRef]
- Lazzari, M.; Piccarreta, M.; Ray, R.L.; Manfreda, S. Modeling antecedent soil moisture to constrain rainfall thresholds for shallow landslides occurrence. In Landslides—Investigation and Monitoring; Ray, R., Lazzari, M., Eds.; IntechOpen Limited: London, UK, 2020; pp. 1–31. [Google Scholar]
- Manfreda, S.; Mita, L.; Dal Sasso, S.F.; Samela, C.; Mancusi, L. Exploiting the use of physical information for the calibration of a lumped hydrological model. Hydrol. Process. 2018, 32, 1–14. [Google Scholar] [CrossRef]
- Iovine, G.; Lollino, P.; Gariano, S.L.; Terranova, O. Coupling limit equilibrium analyses and real-time monitoring to refine a landslide surveillance system in Calabria (southern Italy). Nat. Hazards Earth Syst. Sci. 2010, 10, 2341–2354. [Google Scholar] [CrossRef] [Green Version]
- Vennari, C.; Gariano, S.L.; Antronico, L.; Brunetti, M.T.; Iovine, G.; Peruccacci, S.; Terranova, O.; Guzzetti, F. Rainfall thresholds for shallow landslide occurrence in Calabria, southern Italy. Nat. Hazards Earth Syst. Sci. 2014, 14, 317–330. [Google Scholar] [CrossRef] [Green Version]
- Terranova, O.; Antronico, L.; Gullà, G. Landslide triggering scenarios in homogeneous geological contexts: The area surrounding Acri (Calabria, Italy). Geomorphology 2007, 87, 250–267. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; Wiley: New York, NY, USA, 1989; 383p. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
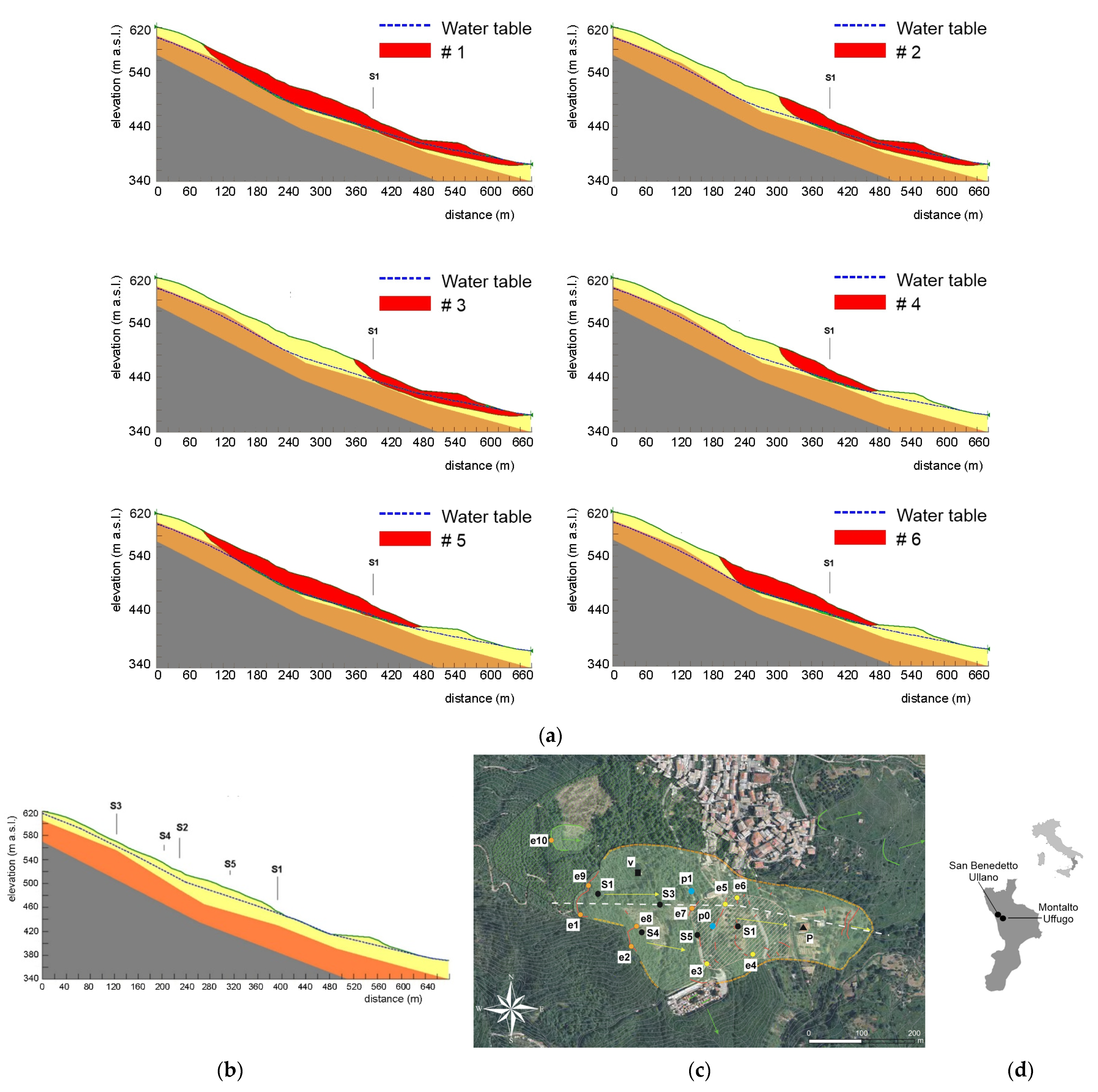
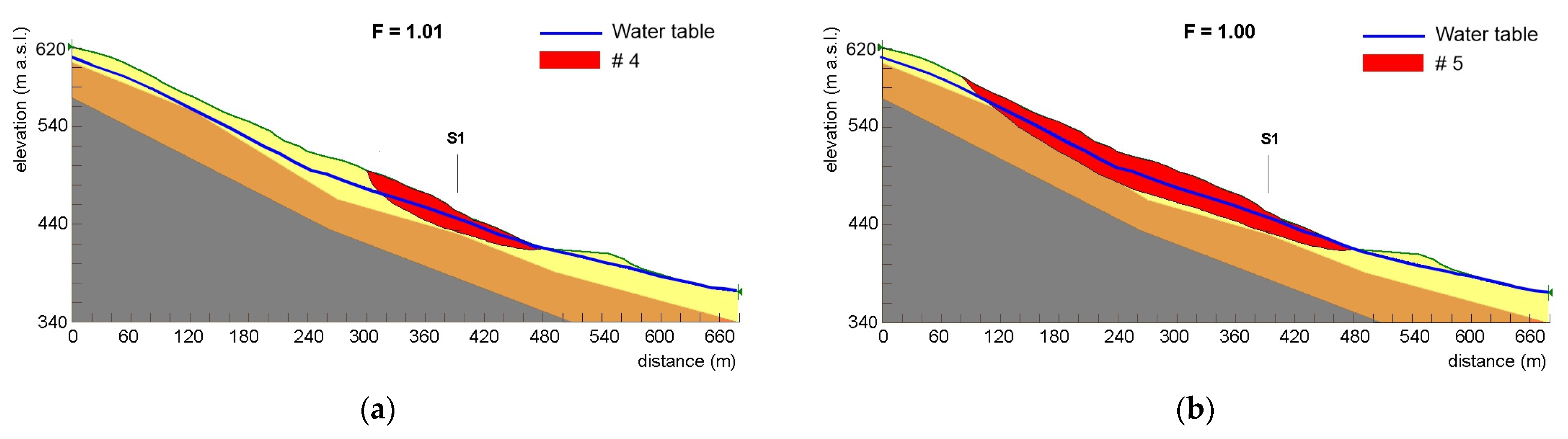




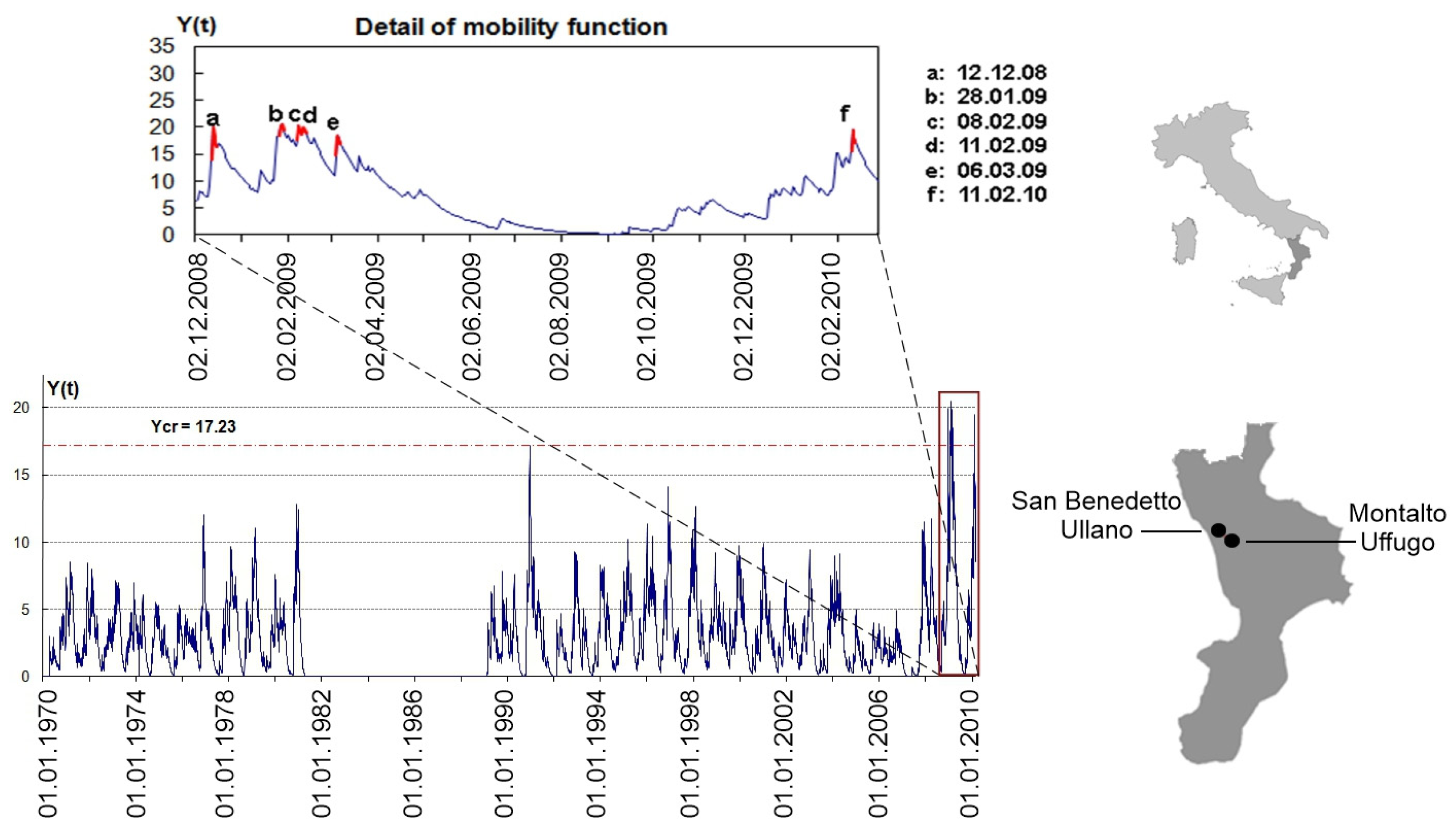
| Case Study | Landslide Type | Activation Date (Calibration + Validation) | tb (Days) | Φc (%) | Φv (%) |
|---|---|---|---|---|---|
| Acri-Serra di Buda | Rockslide | 5 + 1 | 74 | 82.8 | 62.2 |
| San Benedetto Ullano-San Rocco | Rockslide | 2 + 1 | 46 | 100 | 96.2 * |
| San Fili-Uncino | Rockslide | 5 + 1 | 66 | 100 | 100 |
| Sorrento Peninsula | Soil-slip | 10 + 1 | 28 | 80.6 | 73.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ippolito, A.; Lupiano, V.; Rago, V.; Terranova, O.G.; Iovine, G. Triggering of Rain-Induced Landslides, with Applications in Southern Italy. Water 2023, 15, 277. https://doi.org/10.3390/w15020277
D’Ippolito A, Lupiano V, Rago V, Terranova OG, Iovine G. Triggering of Rain-Induced Landslides, with Applications in Southern Italy. Water. 2023; 15(2):277. https://doi.org/10.3390/w15020277
Chicago/Turabian StyleD’Ippolito, Antonino, Valeria Lupiano, Valeria Rago, Oreste G. Terranova, and Giulio Iovine. 2023. "Triggering of Rain-Induced Landslides, with Applications in Southern Italy" Water 15, no. 2: 277. https://doi.org/10.3390/w15020277






