Groundwater Management and Allocation Models: A Review
Abstract
:1. Introduction
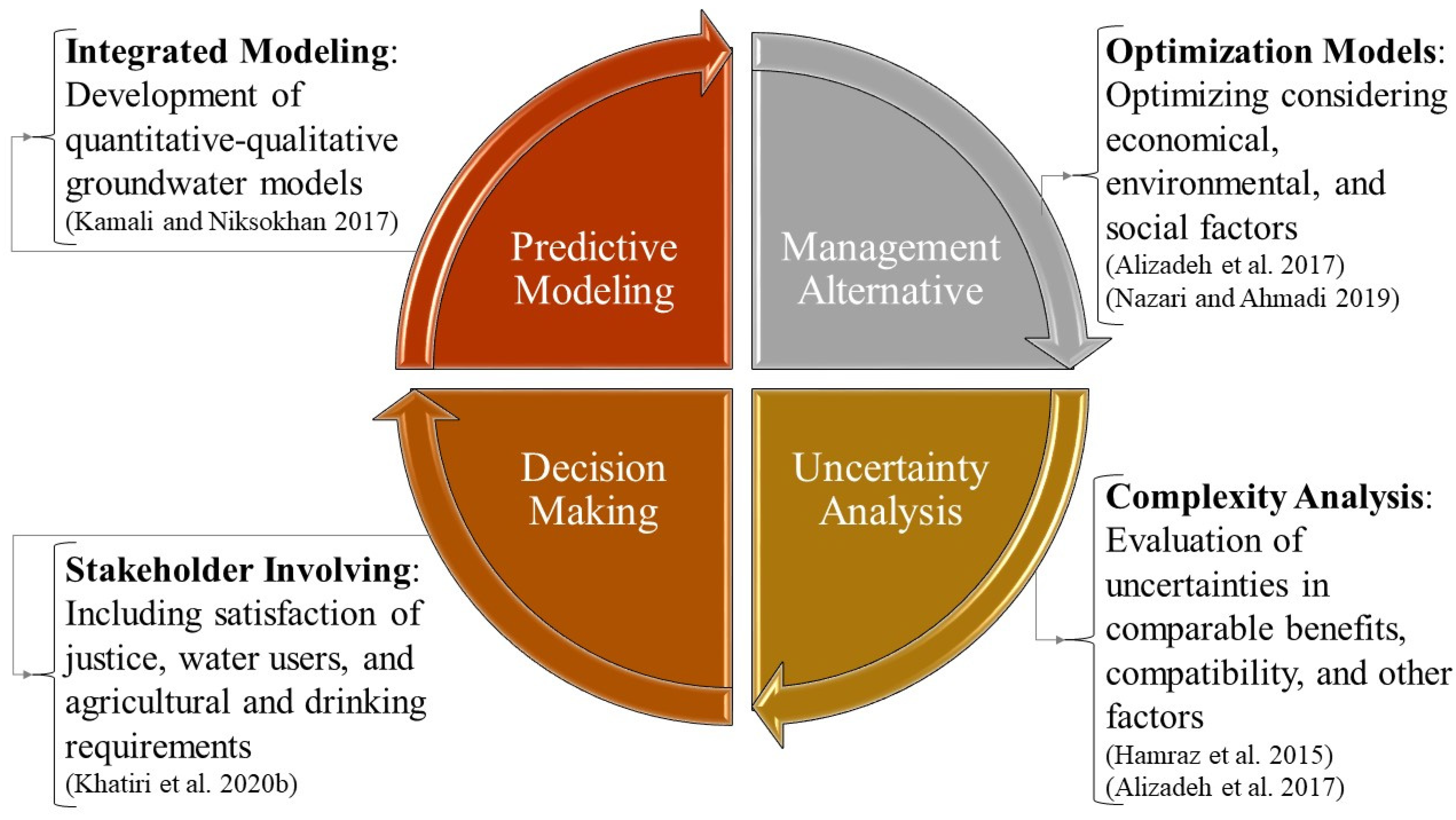
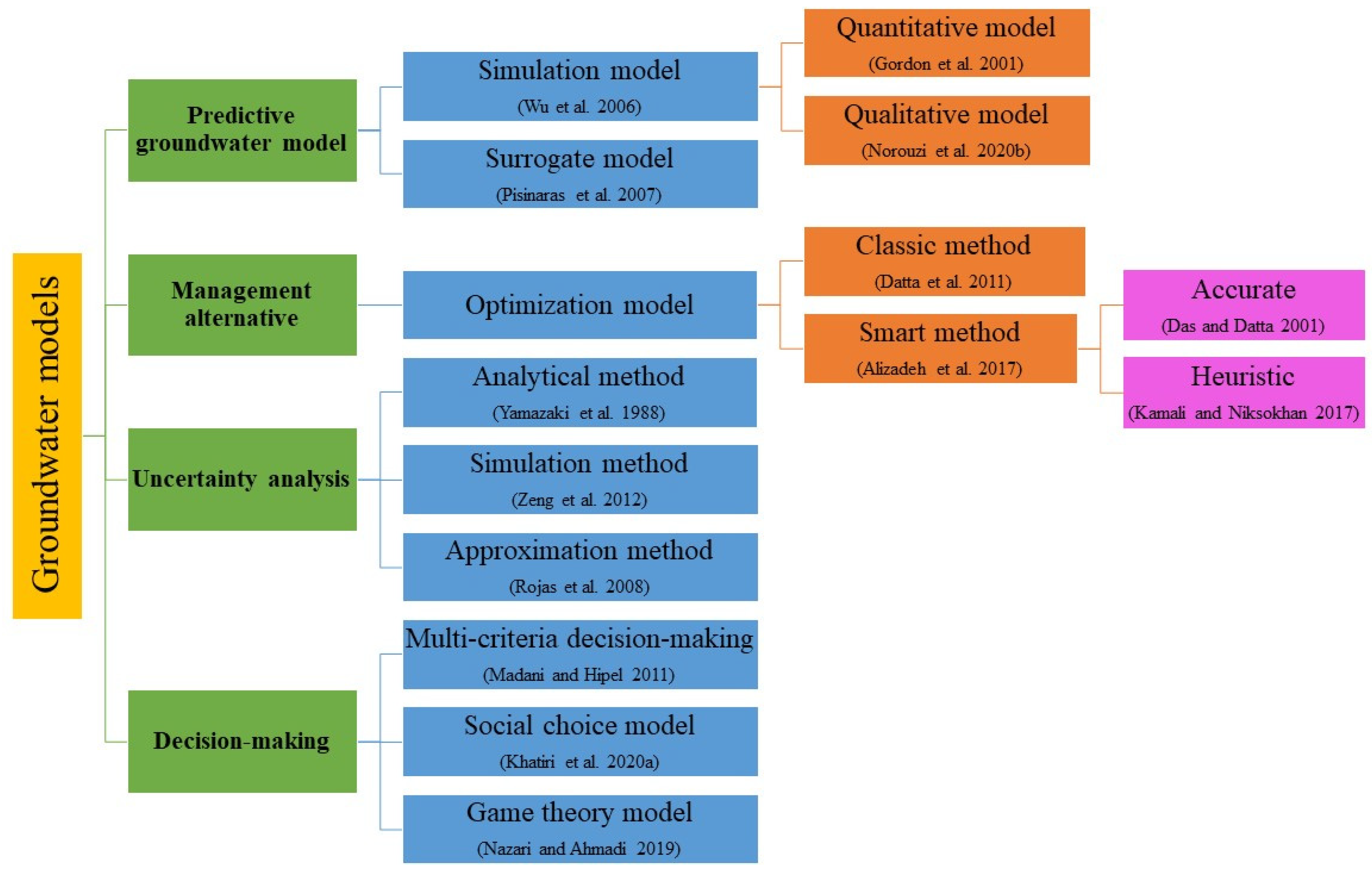
2. Predictive Modeling
- Predicting and forecasting natural and artificial changes in the aquifer; Forecasting is exclusive to deterministic models with high certainty. However, prediction is commonly utilized for probability models,
- Investigating the plan by elaborating the system based on different hypotheses about the nature and dynamics of descriptive groundwater models, which have not been intrinsically designed as a forecasting tool,
- Producing a hypothetical system to investigate groundwater flow principles with general or specific models for training as a part of a computer code advancement.
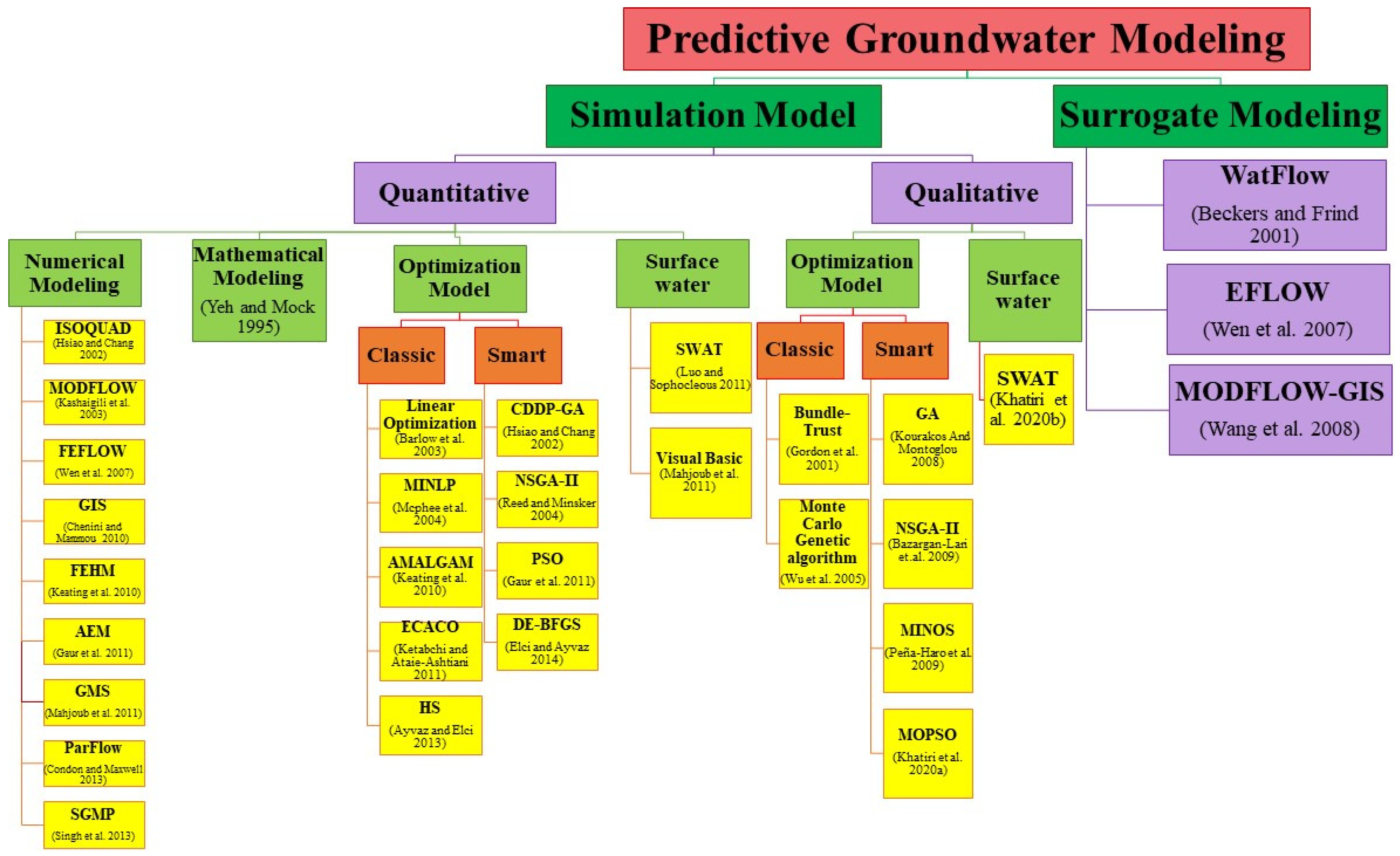
2.1. Simulation Model
2.1.1. Quantitative Modeling
- Investigating the full effects of developing groundwater using the existing and predicted water [76].
- The part related to groundwater flow,
- The part related to contamination and its relevant reactions.
Conjunctive with Mathematical and Numerical Models
Conjunctive with Surface Water Model
2.1.2. Groundwater Quality Simulation Model
2.2. Surrogate Model
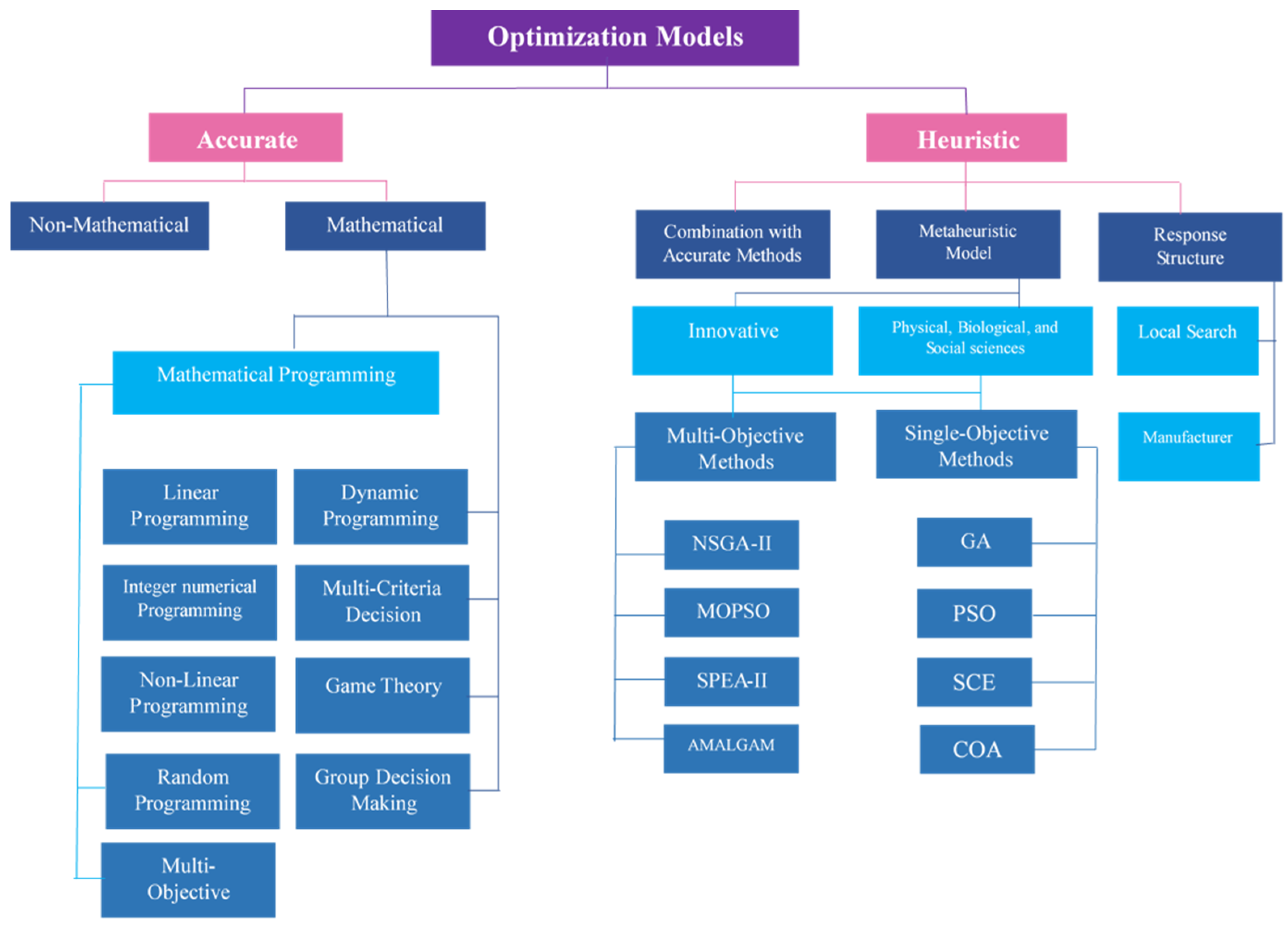
3. Management Alternative
3.1. Accurate Optimization
3.2. Heuristic Optimization
3.2.1. Combination with Accurate Methods
3.2.2. Metaheuristic Models
3.2.3. Response Structure Models
3.3. Optimization Techniques Coupled with Surrogate Modeling
4. Uncertainty Analysis
4.1. Analytical Methods
4.2. Approximation Methods
4.3. Simulation Methods
5. Decision Making
- Reduction of drawdown,
- Reduction of environmental pollution factors,
- Optimal increase in pumping,
- Decreasing water scarcity,
- A balance between water supply and water demand, and justice.
6. Summary and Conclusions
7. Prospects for Future Studies
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEM | Analytic Element Method |
| ANFIS | Adaptive-Network-Based Fuzzy Inference System |
| BMA | Bayesian Model Averaging |
| CDDP | Constrained Differential Dynamic Programming |
| DREAM | Differential Evolution Adaptive Metropolis |
| ECACO | Elitist Continuous Ant Colony Optimization |
| FB | Fallback Bargaining |
| FEHM | Finite Element Heat and Mass Transfer |
| FOK | Fuzzy Ordinary Kriging |
| FPDE | Fuzzy Partial Differential Equation |
| FPPA | Fuzzy Parameterized Probabilistic Analysis |
| FSPDE | Fuzzy-Stochastic Partial Differential Equation |
| GLUE | Generalized Likelihood Uncertainty Estimation |
| GS/RF | GeoSys/RockFlow |
| HS | Heuristic Harmony Search |
| LTM | Long-Term Monitoring |
| MCMC | Markov Chain Monte Carlo |
| MCS | Monte-Carlo Simulation |
| MINLP | Mixed Integer Non-Linear Programming |
| MPS | Multiple-Point Geostatistical method |
| NSMC | Null-Space Monte Carlo |
| PGREM3D | Parallel Groundwater Transport and Remediation Codes |
| PSO | Particle Swarm Optimization |
| RSBT | Rubinstein Sequential Bargaining Theory |
| SCR | Social Choice Rule |
| SGeMS | Stanford Geostatistical Modeling Software |
| SPDE | Stochastic Partial Differential Equation |
| SWAT | Soil and Water Assessment Tool |
| YCRT | Young Conflict–Resolution Theory |
References
- Howard, K.W.; Maier, H. Road de-icing salt as a potential constraint on urban growth in the Greater Toronto Area, Canada. J. Contam. Hydrol. 2007, 91, 146–170. [Google Scholar] [CrossRef] [PubMed]
- Michael, H.A.; Voss, C.I. Evaluation of the sustainability of deep groundwater as an arsenic-safe resource in the Bengal Basin. Proc. Natl. Acad. Sci. USA 2008, 105, 8531–8536. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harou, J.J.; Pulido-Velazquez, M.; Rosenberg, D.E.; Medellín-Azuara, J.; Lund, J.R.; Howitt, R.E. Hydro-economic models: Concepts, design, applications, and future prospects. J. Hydrol. 2009, 375, 627–643. [Google Scholar] [CrossRef] [Green Version]
- Chandio, A.; Lee, T.; Mirjat, M. The extent of waterlogging in the lower Indus Basin (Pakistan)—A modeling study of groundwater levels. J. Hydrol. 2012, 426–427, 103–111. [Google Scholar] [CrossRef]
- Meenal, M.; Eldho, T.I. Simulation–optimization model for groundwater contamination remediation using meshfree point collocation method and particle swarm optimization. Sadhana 2012, 37, 351–369. [Google Scholar] [CrossRef] [Green Version]
- Kazemzadeh-Parsi, M.J.; Daneshmand, F.; Ahmadfard, M.A.; Adamowski, J.; Martel, R. Optimal groundwater remediation design of pump and treat systems via a simulation–optimization approach and firefly algorithm. Eng. Optim. 2014, 47, 1–17. [Google Scholar] [CrossRef]
- Sreekanth, J.; Moore, C.; Wolf, L. Pareto-based efficient stochastic simulation–optimization for robust and reliable groundwater management. J. Hydrol. 2016, 533, 180–190. [Google Scholar] [CrossRef]
- Khatiri, K.N.; Niksokhan, M.H.; Sarang, A.; Kamali, A. Coupled Simulation-Optimization Model for the Management of Groundwater Resources by Considering Uncertainty and Conflict Resolution. Water Resour. Manag. 2020, 34, 3585–3608. [Google Scholar] [CrossRef]
- Hassan, A.E.; Bekhit, H.M.; Chapman, J.B. Uncertainty assessment of a stochastic groundwater flow model using GLUE analysis. J. Hydrol. 2008, 362, 89–109. [Google Scholar] [CrossRef]
- Hassan, A.E.; Bekhit, H.M.; Chapman, J.B. Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model. Environ. Model. Softw. 2009, 24, 749–763. [Google Scholar] [CrossRef]
- Kamali, A.; Niksokhan, M.H. Multi-objective optimization for sustainable groundwater management by developing of coupled quantity-quality simulation-optimization model. J. Hydroinform. 2017, 19, 973–992. [Google Scholar] [CrossRef]
- Alizadeh, M.R.; Nikoo, M.R.; Rakhshandehroo, G.R. Developing a Multi-Objective Conflict-Resolution Model for Optimal Groundwater Management Based on Fallback Bargaining Models and Social Choice Rules: A Case Study. Water Resour. Manag. 2017, 31, 1457–1472. [Google Scholar] [CrossRef]
- Nazari, S.; Ahmadi, A. Non-cooperative stability assessments of groundwater resources management based on the tradeoff between the economy and the environment. J. Hydrol. 2019, 578, 124075. [Google Scholar] [CrossRef]
- Hamraz, B.; Akbarpour, A.; Bilondi, M.P.; Tabas, S.S. On the assessment of ground water parameter uncertainty over an arid aquifer. Arab. J. Geosci. 2015, 8, 10759–10773. [Google Scholar] [CrossRef]
- Khatiri, K.N.; Niksokhan, M.H.; Sarang, A. Choosing various likelihood functions on uncertainty assessment in groundwater simulation-optimization model. Water Supply 2020, 20, 737–750. [Google Scholar] [CrossRef]
- Wu, J.; Zheng, C.; Chien, C.C.; Zheng, L. A comparative study of Monte Carlo simple genetic algorithm and noisy genetic algorithm for cost-effective sampling network design under uncertainty. Adv. Water Resour. 2006, 29, 899–911. [Google Scholar] [CrossRef]
- Pisinaras, V.; Petalas, C.; Tsihrintzis, V.A.; Zagana, E. A groundwater flow model for water resources management in the Ismarida plain, North Greece. Environ. Model. Assess. 2007, 12, 75–89. [Google Scholar] [CrossRef]
- Yamazaki, F.; Member, A.; Shinozuka, M.; Dasgupta, G. Neumann Expansion for Stochastic Finite Element Analysis. J. Eng. Mech. 1988, 114, 1335–1354. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, D.; Wu, J. Sensitivity analysis of the probability distribution of groundwater level series based on information entropy. Stoch. Hydrol. Hydraul. 2012, 26, 345–356. [Google Scholar] [CrossRef]
- Rojas, R.; Feyen, L.; Dassargues, A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Madani, K.; Hipel, K.W. Non-Cooperative Stability Definitions for Strategic Analysis of Generic Water Resources Conflicts. Water Resour. Manag. 2011, 25, 1949–1977. [Google Scholar] [CrossRef]
- Tyson, H.N.; Weber, E.M. Use of electronic computer in the simulation of dynamic behaviour of groundwater basin. In Proceedings of the ASCE Water Resources Engineering Conference, Milwaukee, WI, USA, 15 May 1963; Volume 15. [Google Scholar]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Wageningen Center for Agricultural and Documentation: Wageningen, The Netherlands, 1978. [Google Scholar]
- Belmans, C.; Wesseling, J.; Feddes, R. Simulation model of the water balance of a cropped soil: SWATRE. J. Hydrol. 1983, 63, 271–286. [Google Scholar] [CrossRef]
- Lerner, D.N.; Kumar, P.B. Defining the catchment of a borehole in an unconsolidated valley aquifer with limited data. Q. J. Eng. Geol. Hydrogeol. 1991, 24, 323–331. [Google Scholar] [CrossRef]
- Varni, M.; Carrera, J. Simulation of groundwater age distributions. Water Resour. Res. 1998, 34, 3271–3281. [Google Scholar] [CrossRef]
- Izbicki, J.; Stamos, C.; Nishikawa, T.; Martin, P. Comparison of ground-water flow model particle-tracking results and isotopic data in the Mojave River ground-water basin, southern California, USA. J. Hydrol. 2004, 292, 30–47. [Google Scholar] [CrossRef]
- Bester, M.; Frind, E.; Molson, J.; Rudolph, D. Numerical Investigation of Road Salt Impact on an Urban Wellfield. Groundwater 2006, 44, 165–175. [Google Scholar] [CrossRef]
- Hsiao, C.-T.; Chang, L.-C. Dynamic Optimal Groundwater Management with Inclusion of Fixed Costs. J. Water Resour. Plan. Manag. 2002, 128, 57–65. [Google Scholar] [CrossRef] [Green Version]
- Kashaigili, J.J.; Mashauri, D.A.; Abdo, G. Groundwater management by using mathematical modeling: Case of the Makutupora groundwater basin in dodoma Tanzania. Botsw. J. Technol. 2003, 12, 19–24. [Google Scholar] [CrossRef]
- Wen, X.H.; Wu, Y.Q.; Lee, L.J.E.; Su, J.P.; Wu, J. Groundwater flow modeling in the Zhangye Basin, Northwestern China. Environ. Earth Sci. 2007, 53, 77–84. [Google Scholar] [CrossRef]
- Chenini, I.; Mammou, A.B. Groundwater recharge study in arid region: An approach using GIS techniques and numerical modeling. Comput. Geosci. 2010, 36, 801–817. [Google Scholar] [CrossRef]
- Keating, E.H.; Doherty, J.; Vrugt, J.A.; Kang, Q. Optimization and uncertainty assessment of strongly nonlinear groundwater models with high parameter dimensionality. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Gaur, S.; Chahar, B.; Graillot, D. Analytic elements method and particle swarm optimization based simulation–optimization model for groundwater management. J. Hydrol. 2011, 402, 217–227. [Google Scholar] [CrossRef]
- Mahjoub, H.; Mohammadi, M.M.; Parsinejad, M. Conjunctive Use Modeling of Groundwater and Surface Water. J. Water Resour. Prot. 2011, 3, 726–734. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M.; Gangopadhyay, S. The impact of subsurface conceptualization on land energy fluxes. Adv. Water Resour. 2013, 60, 188–203. [Google Scholar] [CrossRef]
- Singh, A. Groundwater modelling for the assessment of water management alternatives. J. Hydrol. 2013, 481, 220–229. [Google Scholar] [CrossRef]
- Yeh, T.-C.J.; Mock, P.A. A Structured Approach for Calibrating Steady-State Ground-Water Flow Models. Groundwater 1996, 34, 444–450. [Google Scholar] [CrossRef]
- Barlow, P.M.; Ahlfeld, D.P.; Dickerman, D.C. Conjunctive-Management Models for Sustained Yield of Stream-Aquifer Systems. J. Water Resour. Plan. Manag. 2003, 129, 35–48. [Google Scholar] [CrossRef]
- McPhee, J.; Yeh, W.W.-G. Multiobjective Optimization for Sustainable Groundwater Management in Semiarid Regions. J. Water Resour. Plan. Manag. 2004, 130, 490–497. [Google Scholar] [CrossRef] [Green Version]
- Ketabchi, H.; Ataie-Ashtiani, B. Development of combined ant colony optimization algorithm and numerical simulation for optimal management of coastal aquifers. Iran-Water Resour. Res. 2010, 7, 1–12. [Google Scholar]
- Ayvaz, M.T.; Elçi, A. A groundwater management tool for solving the pumping cost minimization problem for the Tahtali watershed (Izmir-Turkey) using hybrid HS-Solver optimization algorithm. J. Hydrol. 2013, 478, 63–76. [Google Scholar] [CrossRef]
- Reed, P.M.; Minsker, B.S. Striking the Balance: Long-Term Groundwater Monitoring Design for Conflicting Objectives. J. Water Resour. Plan. Manag. 2004, 130, 140–149. [Google Scholar] [CrossRef]
- Elçi, A.; Ayvaz, M.T. Differential-Evolution algorithm based optimization for the site selection of groundwater production wells with the consideration of the vulnerability concept. J. Hydrol. 2014, 511, 736–749. [Google Scholar] [CrossRef]
- Luo, Y.; Sophocleous, M. Two-way coupling of unsaturated-saturated flow by integrating the SWAT and MODFLOW models with application in an irrigation district in arid region of West China. J. Arid. Land 2011, 3, 164–173. [Google Scholar] [CrossRef] [Green Version]
- Gordon, E.; Shamir, U.; Bensabat, J. Optimal Extraction of Water from Regional Aquiferunder Salinization. J. Water Resour. Plan. Manag. 2001, 127, 71–77. [Google Scholar] [CrossRef] [Green Version]
- Kourakos, G.; Mantoglou, A. Remediation of heterogeneous aquifers based on multiobjective optimization and adaptive determination of critical realizations. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Bazargan-Lari, M.R.; Kerachian, R.; Mansoori, A. A Conflict-Resolution Model for the Conjunctive Use of Surface and Groundwater Resources that Considers Water-Quality Issues: A Case Study. Environ. Manag. 2008, 43, 470–482. [Google Scholar] [CrossRef]
- Peña-Haro, S.; Pulido-Velazquez, M.; Sahuquillo, A. A hydro-economic modelling framework for optimal management of groundwater nitrate pollution from agriculture. J. Hydrol. 2009, 373, 193–203. [Google Scholar] [CrossRef]
- Beckers, J.; Frind, E. Simulating groundwater flow and runoff for the Oro Moraine aquifer system. Part II. Automated calibration and mass balance calculations. J. Hydrol. 2001, 243, 73–90. [Google Scholar] [CrossRef]
- Wang, L.; Fang, L.; Hipel, K.W. Basin-wide cooperative water resources allocation. Eur. J. Oper. Res. 2008, 190, 798–817. [Google Scholar] [CrossRef]
- Mugunthan, P.; Shoemaker, C.A.; Regis, R.G. Comparison of function approximation, heuristic, and derivative-based methods for automatic calibration of computationally expensive groundwater bioremediation models. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Achari, G.; Li, H. A comparison of numerical solutions of partial differential equations with probabilistic and possibilistic parameters for the quantification of uncertainty in subsurface solute transport. J. Contam. Hydrol. 2009, 110, 45–59. [Google Scholar] [CrossRef] [PubMed]
- Galbiati, L.; Bouraoui, F.; Elorza, F.J.; Bidoglio, G. Modeling diffuse pollution loading into a Mediterranean lagoon: Development and application of an integrated surface–subsurface model tool. Ecol. Model. 2006, 193, 4–18. [Google Scholar] [CrossRef]
- Feyen, L.; Caers, J. Quantifying geological uncertainty for flow and transport modeling in multi-modal heterogeneous formations. Adv. Water Resour. 2006, 29, 912–929. [Google Scholar] [CrossRef]
- Rejani, R.; Jha, M.K.; Panda, S.N.; Mull, R. Simulation Modeling for Efficient Groundwater Management in Balasore Coastal Basin, India. Water Resour. Manag. 2007, 22, 23–50. [Google Scholar] [CrossRef]
- Kerachian, R.; Fallahnia, M.; Bazargan-Lari, M.R.; Mansoori, A.; Sedghi, H. A fuzzy game theoretic approach for groundwater resources management: Application of Rubinstein Bargaining Theory. Resour. Conserv. Recycl. 2010, 54, 673–682. [Google Scholar] [CrossRef]
- Qin, X.S. Assessing environmental risks through fuzzy parameterized probabilistic analysis. Stoch. Hydrol. Hydraul. 2011, 26, 43–58. [Google Scholar] [CrossRef]
- Dhar, A.; Patil, R.S. Multiobjective Design of Groundwater Monitoring Network Under Epistemic Uncertainty. Water Resour. Manag. 2012, 26, 1809–1825. [Google Scholar] [CrossRef]
- Narula, K.K.; Gosain, A. Modeling hydrology, groundwater recharge and non-point nitrate loadings in the Himalayan Upper Yamuna basin. Sci. Total Environ. 2013, 468–469, S102–S116. [Google Scholar] [CrossRef]
- Pulido-Velazquez, M.; Peña-Haro, S.; García-Prats, A.; Mocholi-Almudever, A.F.; Henriquez-Dole, L.; Macian-Sorribes, H.; Lopez-Nicolas, A. Integrated assessment of the impact of climate and land use changes on groundwater quantity and quality in the Mancha Oriental system (Spain). Hydrol. Earth Syst. Sci. 2015, 19, 1677–1693. [Google Scholar] [CrossRef] [Green Version]
- Alizadeh, M.R.; Nikoo, M.R.; Rakhshandehroo, G.R. Developing an optimal groundwater allocation model considering stakeholder interactions; application of fallback bargaining models. Iran-Water Resources Research. 2016, 11, 43–56. [Google Scholar]
- Heydari, F.; Saghafian, B.; Delavar, M. Coupled Quantity-Quality Simulation-Optimization Model for Conjunctive Surface-Groundwater Use. Water Resour. Manag. 2016, 30, 4381–4397. [Google Scholar] [CrossRef]
- Eltarabily, M.G.; Negm, A.M.; Yoshimura, C.; Saavedra, O.C. Modeling the impact of nitrate fertilizers on groundwater quality in the southern part of the Nile Delta, Egypt. Water Supply 2016, 17, 561–570. [Google Scholar] [CrossRef]
- Singh, V.S.; Gupta, C.P. Groundwater in a coral island. Environ. Earth Sci. 1999, 37, 72–77. [Google Scholar] [CrossRef]
- Kresic, N. Hydrogeology and Groundwater Modeling, 2nd ed.; CRC Press: New York, NY, USA, 2007; ISBN 978-08-4933-348-4. [Google Scholar]
- Bowen, R. Groundwater; Springer Science & Business Media: New York, NY, USA, 1986. [Google Scholar]
- Bear, J. Fundamentals of Ground-Water Modeling; Superfund Technology Support Center for Ground Water, Robert S. Kerr Environmental Research Laboratory: Washington, DC, USA, 1992. [Google Scholar]
- Boulding, J.R.; Ginn, J.S. Practical Handbook of Soil, Vadose Zone, and Ground-Water Contamination: Assessment, Prevention, and Remediation; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Konikow, L.F.; Reilly, T.E.; Barlow, P.M.; Voss, C.I. Groundwater modeling. In The Handbook of Groundwater Engineering; CRC Press: Boca Raton, FL, USA, 2006; pp. 815–866. [Google Scholar]
- Thangarajan, M. Groundwater: Resource Evaluation, Augmentation, Contamination, Restoration, Modeling and Management; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Ghosh, N.C.; Sharma, K.D. Groundwater Modelling Management; Capital Publishing Company: New Delhi, India, 2006; p. 594. [Google Scholar]
- Karamouz, M.; Tabari, M.M.R.; Kerachian, R. Application of Genetic Algorithms and Artificial Neural Networks in Conjunctive Use of Surface and Groundwater Resources. Water Int. 2007, 32, 163–176. [Google Scholar] [CrossRef]
- Izady, A.; Davary, K.; Alizadeh, A.; Ziaei, A.N.; Akhavan, S.; Alipoor, A.; Joodavi, A.; Brusseau, M.L. Groundwater conceptualization and modeling using distributed SWAT-based recharge for the semi-arid agricultural Neishaboor plain, Iran. Hydrogeol. J. 2014, 23, 47–68. [Google Scholar] [CrossRef]
- Singh, A.; Panda, S.N. Integrated Salt and Water Balance Modeling for the Management of Waterlogging and Salinization. I: Validation of SAHYSMOD. J. Irrig. Drain. Eng. 2012, 138, 955–963. [Google Scholar] [CrossRef]
- Yihdego, Y.; Becht, R. Simulation of lake–aquifer interaction at Lake Naivasha, Kenya using a three-dimensional flow model with the high conductivity technique and a DEM with bathymetry. J. Hydrol. 2013, 503, 111–122. [Google Scholar] [CrossRef]
- Hill, M.C. Methods and guidelines for effective model calibration. U.S. Geol. Survey Water—Res. Invest. Rep. 1998, 98, 90. [Google Scholar]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and application of the integrated SWAT–MODFLOW model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Starks, P.J.; Arnold, J.G.; Srinivasan, R. A model integration framework for linking SWAT and MODFLOW. Environ. Model. Softw. 2015, 73, 103–116. [Google Scholar] [CrossRef]
- Sophocleous, M.; Perkins, S.P. Methodology and application of combined watershed and ground-water models in Kansas. J. Hydrol. 2000, 236, 185–201. [Google Scholar] [CrossRef]
- Chung, I.-M.; Kim, N.-W.; Lee, J.; Sophocleous, M. Assessing distributed groundwater recharge rate using integrated surface water-groundwater modelling: Application to Mihocheon watershed, South Korea. Hydrogeol. J. 2010, 18, 1253–1264. [Google Scholar] [CrossRef]
- Bailey, R.; Rathjens, H.; Bieger, K.; Chaubey, I.; Arnold, J. SWATMOD-Prep: Graphical user interface for preparing coupled SWAT-MODFLOW simulations. J. Am. Water Resour. Assoc. 2017, 53, 400–410. [Google Scholar] [CrossRef]
- Abbas, S.; Xuan, Y.; Bailey, R. Improving river flow simulation using a coupled surface-groundwater model for integrated water resources management. EPiC Ser. Eng. 2018, 3, 1–9. [Google Scholar]
- Deb, P.; Kiem, A.; Willgoose, G. Mechanisms influencing non-stationarity in rainfall-runoff relationships in southeast Australia. J. Hydrol. 2019, 571, 749–764. [Google Scholar] [CrossRef]
- Deb, P.; Kiem, A.S.; Willgoose, G. A linked surface water-groundwater modelling approach to more realistically simulate rainfall-runoff non-stationarity in semi-arid regions. J. Hydrol. 2019, 575, 273–291. [Google Scholar] [CrossRef]
- Chunn, D.; Faramarzi, M.; Smerdon, B.; Alessi, D.S. Application of an Integrated SWAT–MODFLOW Model to Evaluate Potential Impacts of Climate Change and Water Withdrawals on Groundwater–Surface Water Interactions in West-Central Alberta. Water 2019, 11, 110. [Google Scholar] [CrossRef] [Green Version]
- Molina-Navarro, E.; Bailey, R.T.; Andersen, H.E.; Thodsen, H.; Nielsen, A.; Park, S.; Jensen, J.S.; Jensen, J.B.; Trolle, D. Comparison of abstraction scenarios simulated by SWAT and SWAT-MODFLOW. Hydrol. Sci. J. 2019, 64, 434–454. [Google Scholar] [CrossRef]
- Sith, R.; Watanabe, A.; Nakamura, T.; Yamamoto, T.; Nadaoka, K. Assessment of water quality and evaluation of best management practices in a small agricultural watershed adjacent to Coral Reef area in Japan. Agric. Water Manag. 2018, 213, 659–673. [Google Scholar] [CrossRef]
- Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT-MODFLOW model for large-scale mixed agro-urban river basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
- Sophocleous, M.; Koelliker, J.; Govindaraju, R.; Birdie, T.; Ramireddygari, S.; Perkins, S. Integrated numerical modeling for basin-wide water management: The case of the Rattlesnake Creek basin in south-central Kansas. J. Hydrol. 1999, 214, 179–196. [Google Scholar] [CrossRef]
- Gao, F.; Feng, G.; Han, M.; Dash, P.; Jenkins, J.; Liu, C. Assessment of Surface Water Resources in the Big Sunflower River Watershed Using Coupled SWAT–MODFLOW Model. Water 2019, 11, 528. [Google Scholar] [CrossRef] [Green Version]
- Taie Semiromi, M.; Koch, M. Analysis of spatio-temporal variability of surface–groundwater interactions in the Gharehsoo river basin, Iran, using a coupled SWAT-MODFLOW model. Environ. Earth Sci. 2019, 78, 201. [Google Scholar] [CrossRef]
- Basagaoglu, H.; Marino, M.A. Joint Management of Surface and Ground Water Supplies. Groundwater 1999, 37, 214–222. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Niswonger, R.G.; Fogg, G.E. River-aquifer interactions, geologic heterogeneity, and low-flow management. Groundwater 2006, 44, 837–852. [Google Scholar] [CrossRef]
- He, X.; Sonnenborg, T.O.; Jørgensen, F.; Høyer, A.-S.; Møller, R.R.; Jensen, K.H. Analyzing the effects of geological and parameter uncertainty on prediction of groundwater head and travel time. Hydrol. Earth Syst. Sci. 2013, 17, 3245–3260. [Google Scholar] [CrossRef] [Green Version]
- Cao, G.; Zheng, C.; Scanlon, B.R.; Liu, J.; Li, W. Use of flow modeling to assess sustainability of groundwater resources in the North China Plain. Water Resour. Res. 2013, 49, 159–175. [Google Scholar] [CrossRef]
- El Alfy, M. Numerical groundwater modelling as an effective tool for management of water resources in arid areas. Hydrol. Sci. J. 2014, 59, 1259–1274. [Google Scholar] [CrossRef]
- Nakhaei, M.; Mohammadi, M.; Rezaei, M. Optimizing of Aquifer Withdrawal Numerical Model Using Genetic Algorithm (Case Study: Uromiyeh Coastal Aquifer). Iran-Water Resour. Res. 2014, 10, 94–97. [Google Scholar]
- Parsapour-Moghaddam, P.; Abed-Elmdoust, A.; Kerachian, R. A Heuristic Evolutionary Game Theoretic Methodology for Conjunctive Use of Surface and Groundwater Resources. Water Resour. Manag. 2015, 29, 3905–3918. [Google Scholar] [CrossRef]
- Zekri, S.; Triki, C.; Al-Maktoumi, A.; Bazargan-Lari, M.R. An Optimization-Simulation Approach for Groundwater Abstraction under Recharge Uncertainty. Water Resour. Manag. 2015, 29, 3681–3695. [Google Scholar] [CrossRef]
- Safavi, H.R.; Darzi, F.; Mariño, M.A. Simulation-Optimization Modeling of Conjunctive Use of Surface Water and Groundwater. Water Resour. Manag. 2009, 24, 1965–1988. [Google Scholar] [CrossRef]
- Harrar, W.G.; Sonnenborg, T.O. Capture zone, travel time, and solute-transport predictions using inverse modeling and different geological models. Appl. Hydrogeol. 2003, 11, 536–548. [Google Scholar] [CrossRef]
- Mace, R.E.; Chowdhury, A.H.; Anaya, R.; Way, S.C.T. A Numerical Groundwater Flow Model of the Upper and Middle Trinity Aquifer, Hill Country Area; Texas Water Development Board Open File Report 00-02; Texas Water Development Board: Austin, TX, USA, 2000. [Google Scholar]
- Simpson, T.; Toropov, V.; Balabanov, V.; Viana, F. Design and analysis of computer experiments in multidisciplinary design optimization: A review of how far we have come-or not. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008; p. 5802. [Google Scholar]
- Gorissen, D. Heterogeneous Evolution of Surrogate Models. Master’s Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2007. [Google Scholar]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Review of surrogate modeling in water resources. Water Resour. Res. 2012, 48, W07401. [Google Scholar] [CrossRef]
- Blanning, R.W. The construction and implementation of metamodels. Simulation 1975, 24, 177–184. [Google Scholar] [CrossRef]
- Khu, S.-T.; Werner, M. Reduction of Monte-Carlo simulation runs for uncertainty estimation in hydrological modelling. Hydrol. Earth Syst. Sci. 2003, 7, 680–692. [Google Scholar] [CrossRef] [Green Version]
- Mugunthan, P.; Shoemaker, C.A. Assessing the impacts of parameter uncertainty for computationally expensive groundwater models. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Bliznyuk, N.; Ruppert, D.; Shoemaker, C.; Regis, R.; Wild, S.; Mugunthan, P. Bayesian Calibration and Uncertainty Analysis for Computationally Expensive Models Using Optimization and Radial Basis Function Approximation. J. Comput. Graph. Stat. 2008, 17, 270–294. [Google Scholar] [CrossRef]
- Ndambuki, J.M. Multi-Objective Groundwater Quantity Management: A Stochastic Approach. Ph.D. Thesis, Technische Universiteit Delft, MG Delft, The Netherlands, 2002. [Google Scholar]
- Bhattacharjya, R.K.; Datta, B. Optimal Management of Coastal Aquifers Using Linked Simulation Optimization Approach. Water Resour. Manag. 2005, 19, 295–320. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Coupled simulation-optimization model for coastal aquifer management using genetic programming-based ensemble surrogate models and multiple-realization optimization. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Mategaonkar, M.; Eldho, T. Groundwater remediation optimization using a point collocation method and particle swarm optimization. Environ. Model. Softw. 2012, 32, 37–48. [Google Scholar] [CrossRef]
- Das, A.; Datta, B. Application of optimisation techniques in groundwater quantity and quality management. Sadhana 2001, 26, 293–316. [Google Scholar] [CrossRef] [Green Version]
- Zare, M.; Nikoo, M.R.; Nematollahi, B.; Gandomi, A.H.; Al-Wardy, M.; Al-Rawas, G.A. Progressive improvement of DRASTICA and SI models for groundwater vulnerability assessment based on evolutionary algorithms. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef]
- Wang, H.; Jin, X. Characterization of groundwater contaminant source using Bayesian method. Stoch. Environ. Res. Risk Assess. 2012, 27, 867–876. [Google Scholar] [CrossRef]
- El-Bihery, M.A. Groundwater flow modeling of quaternary aquifer Ras Sudr, Egypt. Environ. Geol. 2009, 58, 1095–1105. [Google Scholar] [CrossRef]
- Reichard, E.G. Groundwater-Surface Water Management With Stochastic Surface Water Supplies: A Simulation Optimization Approach. Water Resour. Res. 1995, 31, 2845–2865. [Google Scholar] [CrossRef]
- Vermeulen, P.; Heemink, A.; Stroet, C.T. Reduced models for linear groundwater flow models using empirical orthogonal functions. Adv. Water Resour. 2004, 27, 57–69. [Google Scholar] [CrossRef]
- Siade, A.J.; Putti, M.; Yeh, W.W.-G. Snapshot selection for groundwater model reduction using proper orthogonal decomposition. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Vermeulen, P.T.M.; Heemink, A.W.; Valstar, J.R. Inverse modeling of groundwater flow using model reduction. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef] [Green Version]
- Vermeulen, P.T.M.; Stroet, C.B.M.T.; Heemink, A.W. Model inversion of transient nonlinear groundwater flow models using model reduction. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef] [Green Version]
- Cheng, W.-C.; Putti, M.; Kendall, D.R.; Yeh, W.W.-G. A real-time groundwater management model using data assimilation. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. A Stochastic Radial Basis Function Method for the Global Optimization of Expensive Functions. INFORMS J. Comput. 2007, 19, 497–509. [Google Scholar] [CrossRef]
- Gutmann, H.-M. A Radial Basis Function Method for Global Optimization. J. Glob. Optim. 2001, 19, 201–227. [Google Scholar] [CrossRef]
- Jones, D.R. A Taxonomy of Global Optimization Methods Based on Response Surfaces. J. Glob. Optim. 2001, 21, 345–383. [Google Scholar] [CrossRef]
- Yan, S.; Minsker, B. Optimal groundwater remediation design using an Adaptive Neural Network Genetic Algorithm. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Regis, R.G.; Shoemaker, C.A. Parallel Stochastic Global Optimization Using Radial Basis Functions. INFORMS J. Comput. 2009, 21, 411–426. [Google Scholar] [CrossRef]
- Yan, S.; Minsker, B. Applying Dynamic Surrogate Models in Noisy Genetic Algorithms to Optimize Groundwater Remediation Designs. J. Water Resour. Plan. Manag. 2011, 137, 284–292. [Google Scholar] [CrossRef]
- Schultz, M.T.; Small, M.J.; Farrow, R.S.; Fischbeck, P.S. State Water Pollution Control Policy Insights from a Reduced-Form Model. J. Water Resour. Plan. Manag. 2004, 130, 150–159. [Google Scholar] [CrossRef]
- Schultz, M.T.; Small, M.J.; Fischbeck, P.S.; Farrow, R.S. Evaluating response surface designs for uncertainty analysis and prescriptive applications of a large-scale water quality model. Environ. Model. Assess. 2006, 11, 345–359. [Google Scholar] [CrossRef]
- Borgonovo, E.; Castaings, W.; Tarantola, S. Model emulation and moment-independent sensitivity analysis: An application to environmental modelling. Environ. Model. Softw. 2012, 34, 105–115. [Google Scholar] [CrossRef]
- Mondal, A.; Efendiev, Y.; Mallick, B.; Datta-Gupta, A. Bayesian uncertainty quantification for flows in heterogeneous porous media using reversible jump Markov chain Monte Carlo methods. Adv. Water Resour. 2010, 33, 241–256. [Google Scholar] [CrossRef]
- Singh, A.; Mishra, S.; Ruskauff, G. Model Averaging Techniques for Quantifying Conceptual Model Uncertainty. Groundwater 2010, 48, 701–715. [Google Scholar] [CrossRef]
- Prakash, O.; Datta, B. Characterization of Groundwater Pollution Sources with Unknown Release Time History. J. Water Resour. Prot. 2014, 6, 337–350. [Google Scholar] [CrossRef] [Green Version]
- Karamouz, M.; Tabari, M.M.R.; Kerachian, R.; Zahraie, B. Conjunctive Use of Surface and Groundwater Resources with Emphasis on Water Quality. In Impacts of Global Climate Change; U.S. Environmental Protection Agency: Washington, DC, USA, 2005; pp. 1–12. [Google Scholar] [CrossRef]
- Chadalavada, S.; Datta, B. Dynamic Optimal Monitoring Network Design for Transient Transport of Pollutants in Groundwater Aquifers. Water Resour. Manag. 2007, 22, 651–670. [Google Scholar] [CrossRef]
- Luo, Q.; Wu, J.; Yang, Y.; Qian, J.; Wu, J. Optimal design of groundwater remediation system using a probabilistic multi-objective fast harmony search algorithm under uncertainty. J. Hydrol. 2014, 519, 3305–3315. [Google Scholar] [CrossRef]
- Katsifarakis, K.L.; Mouti, M.; Ntrogkouli, K. Optimization of groundwater resources management in polluted aquifers. Glob. Nest 2009, 11, 283–290. [Google Scholar]
- Ayvaz, M.T. A linked simulation–optimization model for solving the unknown groundwater pollution source identification problems. J. Contam. Hydrol. 2010, 117, 46–59. [Google Scholar] [CrossRef]
- Bayer, P.; Finkel, M. Optimization of concentration control by evolution strategies: Formulation, application, and assessment of remedial solutions. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.-J.; Chang, L.-C. Application of Optimal Control and Fuzzy Theory for Dynamic Groundwater Remediation Design. Water Resour. Manag. 2008, 23, 647–660. [Google Scholar] [CrossRef]
- Luo, Q.; Wu, J.; Yang, Y.; Qian, J.; Wu, J. Multi-objective optimization of long-term groundwater monitoring network design using a probabilistic Pareto genetic algorithm under uncertainty. J. Hydrol. 2016, 534, 352–363. [Google Scholar] [CrossRef]
- Abebe, A.J.; Guinot, V.; Solomatine, D.P. Fuzzy alpha-cut vs. Monte Carlo techniques in assessing uncertainty in model parameters. In Proceedings of the 4th International Conference on Hydroinformatics, Cedar Rapids, Iowa City, IA, USA, 23–27 August 2000. [Google Scholar]
- Feyen, L.; Beven, K.J.; De Smedt, F.; Freer, J. Stochastic capture zone delineation within the generalized likelihood uncertainty estimation methodology: Conditioning on head observations. Water Resour. Res. 2001, 37, 625–638. [Google Scholar] [CrossRef]
- Ababou, R.; Al-Bitar, A. Salt water intrusion with heterogeneity and uncertainty: Mathematical modeling and analyses. In Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 2004; Volume 55, pp. 1559–1571. [Google Scholar]
- Kumar, V.; Schuhmacher, M. Fuzzy uncertainty analysis in system modelling. In Proceeding of the 38th European Symposium of the Working Party on Computer Aided Process Engineering, Barcelona, Spain, 29 May–1 June 2005. [Google Scholar]
- Faybishenko, B. Fuzzy-probabilistic calculations of water-balance uncertainty. Stoch. Hydrol. Hydraul. 2010, 24, 939–952. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, K. Development of a fuzzy-stochastic nonlinear model to incorporate aleatoric and epistemic uncertainty. J. Contam. Hydrol. 2010, 111, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.C.; Lu, L.; Tang, T. Bayesian analysis for uncertainty and risk in a groundwater numerical model’s predictions. Hum. Ecol. Risk Assess. Int. J. 2011, 17, 1310–1331. [Google Scholar] [CrossRef]
- Yoon, H.; Hart, D.B.; McKenna, S.A. Parameter estimation and predictive uncertainty in stochastic inverse modeling of groundwater flow: Comparing null-space Monte Carlo and multiple starting point methods. Water Resour. Res. 2013, 49, 536–553. [Google Scholar] [CrossRef]
- Juckem, P.F.; Fienen, M.N.; Hunt, R.J. Simulation of Groundwater Flow and Interaction of Groundwater and Surface Water on the Lac du Flambeau Reservation, Wisconsin; US Geological Survey: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- Neuman, S.P.; Wierenga, P.J. A Comprehensive Strategy of Hydrogeologic Modeling and Uncertainty Analysis for Nuclear Facilities And Sites; Report NUREG/CR-6805; The University of Arizona: Tucson, AZ, USA, 2003. [Google Scholar]
- Gómez-Hernández, J.J. Complexity. Groundwater 2006, 44, 782–785. [Google Scholar] [CrossRef]
- Hill, M.C. The Practical Use of Simplicity in Developing Ground Water Models. Groundwater 2006, 44, 775–781. [Google Scholar] [CrossRef]
- Hill, M.C.; Tiedeman, C.R. Effective Groundwater Model Calibration: With Analysis of Data, Sensitivities, Predictions, and Uncertainty; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Hunt, R.J.; Doherty, J.; Tonkin, M.J. Are Models Too Simple? Arguments for Increased Parameterization. Groundwater 2007, 45, 254–262. [Google Scholar] [CrossRef]
- Renard, P. Stochastic Hydrogeology: What Professionals Really Need? Groundwater 2007, 45, 531–541. [Google Scholar] [CrossRef] [Green Version]
- Walker, W.; Marchau, V. Dealing with Uncertainty in Policy Analysis and Policymaking. Integr. Assess. 2003, 4, 1–4. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Henriksen, H.J.; Harrar, W.G.; Scholten, H.; Kassahun, A. Quality assurance in model based water management—Review of existing practice and outline of new approaches. Environ. Model. Softw. 2005, 20, 1201–1215. [Google Scholar] [CrossRef]
- Van der Sluijs, J. Uncertainty as a monster in the science–policy interface: Four coping strategies. Water Sci. Technol. 2005, 52, 87–92. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.J. Ignorance is bliss: Or seven reasons not to use uncertainty analysis. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P.A. Uncertainty in the environmental modelling process—A framework and guidance. Environ. Model. Softw. 2007, 22, 1543–1556. [Google Scholar] [CrossRef] [Green Version]
- Meyer, P.D.; Ye, M.; Neuman, S.P.; Cantrell, K.J. Combined Estimation of Hydrogeologic Conceptual Model and Parameter Uncertainty; No. PNNL-14534; NUREG/CR-6843; Pacific Northwest National Lab (PNNL): Richland, WA, USA, 2004. [Google Scholar] [CrossRef] [Green Version]
- Højberg, A.; Refsgaard, J. Model uncertainty—parameter uncertainty versus conceptual models. Water Sci. Technol. 2005, 52, 177–186. [Google Scholar] [CrossRef]
- Troldborg, L.; Refsgaard, J.C.; Jensen, K.H.; Engesgaard, P. The importance of alternative conceptual models for simulation of concentrations in a multi-aquifer system. Appl. Hydrogeol. 2007, 15, 843–860. [Google Scholar] [CrossRef]
- Seifert, D.; Sonnenborg, T.O.; Scharling, P.; Hinsby, K. Use of alternative conceptual models to assess the impact of a buried valley on groundwater vulnerability. Appl. Hydrogeol. 2007, 16, 659–674. [Google Scholar] [CrossRef]
- Ijiri, Y.; Saegusa, H.; Sawada, A.; Ono, M.; Watanabe, K.; Karasaki, K.; Doughty, C.; Shimo, M.; Fumimura, K. Evaluation of uncertainties originating from the different modeling approaches applied to analyze regional groundwater flow in the Tono area of Japan. J. Contam. Hydrol. 2009, 103, 168–181. [Google Scholar] [CrossRef] [Green Version]
- Rojas, R.; Batelaan, O.; Feyen, L.; Dassargues, A. Assessment of conceptual model uncertainty for the regional aquifer Pampa del Tamarugal—North Chile. Hydrol. Earth Syst. Sci. 2010, 14, 171–192. [Google Scholar] [CrossRef] [Green Version]
- Refsgaard, J.C.; Christensen, S.; Sonnenborg, T.O.; Seifert, D.; Højberg, A.L.; Troldborg, L. Review of strategies for handling geological uncertainty in groundwater flow and transport modeling. Adv. Water Resour. 2012, 36, 36–50. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Xia, J.; Yang, H. Comparing uncertainty analysis techniques for a SWAT application to the Chaohe Basin in China. J. Hydrol. 2008, 358, 1–23. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Johnson, C.A.; Van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Vrugt, J.; Ter Braak, C.; Diks, C.; Robinson, B.; Hyman, J.; Higdon, D. Accelerating Markov Chain Monte Carlo simulation using self-adaptative differential evolution with randomized subspace sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Bates, B.C.; Campbell, E.P. A Markov Chain Monte Carlo Scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water Resour. Res. 2001, 37, 937–947. [Google Scholar] [CrossRef]
- Gao, W.; Wu, D.; Song, C.; Tin-Loi, F.; Li, X. Hybrid probabilistic interval analysis of bar structures with uncertainty using a mixed perturbation Monte-Carlo method. Finite Elem. Anal. Des. 2011, 47, 643–652. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Merigó, J.M.; Xu, Y. A coupled stochastic inverse/sharp interface seawater intrusion approach for coastal aquifers under groundwater parameter uncertainty. J. Hydrol. 2016, 540, 774–783. [Google Scholar] [CrossRef]
- Linde, N.; Ginsbourger, D.; Irving, J.; Nobile, F.; Doucet, A. On uncertainty quantification in hydrogeology and hydrogeophysics. Adv. Water Resour. 2017, 110, 166–181. [Google Scholar] [CrossRef]
- Van Geer, F.C.; Stroet, C.B.M.T.; Yangxiao, Z. Using Kalman Filtering to Improve and Quantify the Uncertainty of Numerical Groundwater Simulations: The Role of System Noise and Its Calibration. Water Resour. Res. 1991, 27, 1987–1994. [Google Scholar] [CrossRef]
- Porter, D.W.; Gibbs, B.P.; Jones, W.F.; Huyakorn, P.S.; Hamm, L.; Flach, G.P. Data fusion modeling for groundwater systems. J. Contam. Hydrol. 2000, 42, 303–335. [Google Scholar] [CrossRef]
- Panzeri, M.; Riva, M.; Guadagnini, A.; Neuman, S. EnKF coupled with groundwater flow moment equations applied to Lauswiesen aquifer, Germany. J. Hydrol. 2015, 521, 205–216. [Google Scholar] [CrossRef] [Green Version]
- Marchant, B.; Mackay, J.; Bloomfield, J. Quantifying uncertainty in predictions of groundwater levels using formal likelihood methods. J. Hydrol. 2016, 540, 699–711. [Google Scholar] [CrossRef]
- Han, F.; Zheng, Y. Joint analysis of input and parametric uncertainties in watershed water quality modeling: A formal Bayesian approach. Adv. Water Resour. 2018, 116, 77–94. [Google Scholar] [CrossRef]
- Chen, M.; Izady, A.; Abdalla, O.A.; Amerjeed, M. A surrogate-based sensitivity quantification and Bayesian inversion of a regional groundwater flow model. J. Hydrol. 2018, 557, 826–837. [Google Scholar] [CrossRef]
- Tang, Z.-C.; Lu, Z.; Wang, P.; Xia, Y.; Yang, P.; Wang, P. Efficient numerical simulation method for evaluations of global sensitivity analysis with parameter uncertainty. Appl. Math. Model. 2015, 40, 597–611. [Google Scholar] [CrossRef]
- Joodavi, A.; Zare, M.; Ziaei, A.N.; Ferré, T.P. Groundwater management under uncertainty using a stochastic multi-cell model. J. Hydrol. 2017, 551, 265–277. [Google Scholar] [CrossRef]
- Kifanyi, G.; Ndambuki, J.; Odai, S.; Gyamfi, C. Quantitative management of groundwater resources in regional aquifers under uncertainty: A retrospective optimization approach. Groundw. Sustain. Dev. 2019, 8, 530–540. [Google Scholar] [CrossRef]
- Sreekanth, J.; Moore, C. Novel patch modelling method for efficient simulation and prediction uncertainty analysis of multi-scale groundwater flow and transport processes. J. Hydrol. 2018, 559, 122–135. [Google Scholar] [CrossRef]
- Beven, K.J. A manifesto for the enquiringly thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef] [Green Version]
- Tolson, B.A.; Shoemaker, C.A. Efficient prediction uncertainty approximation in the calibration of environmental simulation models. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Ter Braak, C.J. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44, 9. [Google Scholar] [CrossRef]
- Laloy, E.; Vrugt, J.A. High-dimensional posterior exploration of hydrologic models using multiple-try DREAM(ZS) and high-performance computing. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Nakao, M.; Wichelns, D.; Montgomery, J.T. Game Theory Analysis of Competition for Groundwater Involving El Paso, Texas and Ciudad Juarez, Mexico; Agricultural and Applied Economics Association (AAEA): New Orleans, LA, USA, 2002. [Google Scholar]
- Loáiciga, H.A. Analytic game—Theoretic approach to ground-water extraction. J. Hydrol. 2004, 297, 22–33. [Google Scholar] [CrossRef]
- Salazar, R.; Szidarouszky, F.; Coppola, E.J.; Rojana, A. Application of game theory for groundwater conflict in Mexico. J. Environ. Manag. 2007, 84, 560–571. [Google Scholar]
- Saak, A.E.; Peterson, J.M. Groundwater use under incomplete information. J. Environ. Econ. Manag. 2007, 54, 214–228. [Google Scholar] [CrossRef] [Green Version]
- Martínez, Y.M.; Esteban, E. Social choice and groundwater management: Application of the uniform rule. Cienc. Investig. Agrar. 2014, 41, 3–4. [Google Scholar] [CrossRef] [Green Version]
- Madani, K. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Hui, E.C.M.; Bao, H. The logic behind conflicts in land acquisitions in contemporary China: A framework based upon game theory. Land Use Policy 2013, 30, 373–380. [Google Scholar] [CrossRef]
- Madani, K.; Dinar, A. Non-Cooperative Institutions for Sustainable Management of Common Pool Resources; Water Science and Policy Center, University of California: Riverside, CA, USA, 2010. [Google Scholar]
- Esteban, E.; Dinar, A. Cooperative Management of Groundwater Resources in the Presence of Environmental Externalities. Environ. Resour. Econ. 2012, 54, 443–469. [Google Scholar] [CrossRef]
| Model Type | Limitations |
|---|---|
| Analog model | |
| Analytical model |
|
| Porous media model |
| Simulation Model | |||
|---|---|---|---|
| Quantitative Model | Time Step | Reference | Case Study |
| Analytic Element Method | Annual | [34] | Dore-France |
| FEFLOW | Monthly | [31] | Zhangye, China |
| Finite Element Heat and Mass Transfer | Annual | [33] | Yucca Flat, USA |
| GMS | Annual | [35] | Maraghe plain, Iran |
| GMS-MODFLOW 2000 | Monthly | [76] | Nakuru district, Nairobi |
| ISOQUAD | 3 Months | [29] | Hypothetical |
| MODFLOW | Annual | [93] | Hypothetical |
| [39] | Island | ||
| [40] | Upper San Pedro River Basin, southeastern Arizona, Mexico | ||
| [94] | Cosumnes River in California | ||
| [73] | The southern part of Tehran, Iran | ||
| [17] | Ismarida plain, northeastern Greece | ||
| [78] | Musim-cheon Basin in Korea | ||
| [81] | Mihocheon watershed, south Korea | ||
| [45] | Yellow River Basin, Inner Mongolia, China | ||
| [95] | Ølgod, Jutland, Denmark | ||
| [42] | Izmir, Turkey | ||
| [96] | NCP, China | ||
| [97] | East Owienat, Egypt | ||
| [44] | Izmir, Turkey | ||
| [98] | Uromieh, Iran | ||
| [99] | Rafsanjan plain, Iran | ||
| [100] | aquifer-Muscat, Oman | ||
| MODFLOW and ANN | Monthly | [101] | Najafabad plain in westcentral, Iran |
| MODFLOW and UCODE | Annual | [102] | Glacial-till plain on the Jutland peninsula in western Denmark |
| MODFLOW-96 | Monthly | [103] | Hill Country, USA |
| ParFlow | Monthly | [36] | Klamath River, California, USA |
| WatFlow | Annual | [50] | Oro Moraine in Canada |
| Simulation Model | |||
|---|---|---|---|
| Groundwater Quality Simulation Model | Time Step | Reference | Case Study |
| MT3D | Annual | [59] | Hypothetical |
| Monthly | [46] | Na’aman Aquifer, Western Galilee, Israel | |
| [16] | Hypothetical | ||
| [56] | Balasore coastal basin, India | ||
| [48] | Tehran aquifer, Iran | ||
| [57] | Tehran aquifer, Iran | ||
| [58] | Hypothetical | ||
| [60] | Upper Yamuna watershed, India | ||
| [61] | Jucar river basin, Spain | ||
| [64] | Nile Delta, Egypt | ||
| MT3DMS | Annual | [49] | Hypothetical |
| Daily | [55] | Hypothetical | |
| Monthly | [54] | Bonello watershed, Italy | |
| [63] | Najaf Abad plain, Iran | ||
| [12] | Kavar-Maharloo aquifer, Iran | ||
| [11] | Isfehan-Barkhoar, Iran | ||
| [13] | Bad-Khaledabad, Iran | ||
| [8] | Isfehan-Barkhoar, Iran | ||
| [15] | Isfehan-Barkhoar, Iran | ||
| Parallel Groundwater Transport and Remediation Codes | Daily | [117] | Hypothetical |
| SAHYSMOD | Seasonal | [56] | Haryana State, India |
| SEAWAT | Annual | [118] | Ras Sudr, Egypt |
| Optimization Approach | Study | Optimization Approach | Study |
|---|---|---|---|
| Simulated Annealing | [137] | Artificial Neural Network (ANN) | [138] |
| Genetic Algorithm (GA) | [43] | Particle Swarm Optimization | [34] |
| [138] | [114] | ||
| [73] | [5] | ||
| [47] | [11] | ||
| [139] | [8] | ||
| [48] | Harmony Search Algorithm | [140] | |
| [141] | [142] | ||
| [57] | Firefly Algorithm | [6] | |
| [101] | GAMS | [93] | |
| [59] | Mixed Integer Non-linear Programming | [40] | |
| [98] | CMA-ES | [143] | |
| [99] | Constrained Differential Dynamic Programming-Adaptive-Network-based Fuzzy Inference System | [144] | |
| [100] | MINOS | [61] | |
| [63] | Elitist Continuous Ant Colony Optimization | [41] | |
| [7] | Heuristic Harmony Search | [42] | |
| [145] | Constrained Differential Dynamic Programming | [29] | |
| [12] |
| Reference | Simulation | Uncertainty Technique | Case Study | |
|---|---|---|---|---|
| Quantitative Modeling | Qualitative Modeling | |||
| [146] | No | No | Fuzzy α-cut | Vannetin basin, France |
| Monte-Carlo simulation | ||||
| [147] | MODFLOW | No | generalized likelihood uncertainty estimation | Hypothetical |
| [148] | BIGFLOW | No | Monte Carlo | Plain of Tadla, Morocco |
| [149] | No | No | Fuzzy α-cut | Hypothetical |
| Monte-Carlo simulation | ||||
| [55] | MODFLOW | MT3DMS | Spatial bootstrap | Hypothetical |
| [20] | MODFLOW | No | generalized likelihood uncertainty estimation | Hypothetical |
| Bayesian model averaging | ||||
| [47] | MODFLOW | MT3D | Monte Carlo | Hypothetical |
| [53] | No | No | Fuzzy-stochastic partial differential equation, Fuzzy partial differential equation, and Stochastic partial differential equation | Hypothetical |
| [33] | Finite element heat and mass transfer | Null-space Monte Carlo | Yucca Flat, USA | |
| Markov chain Monte Carlo (Differential Evolution Adaptive Metropolis) | ||||
| [150] | No | No | Fuzzy-probabilistic | Hanford site, Washington, USA |
| Monte Carlo simulation | ||||
| [151] | No | No | Hybrid propagation | No |
| [152] | MODFLOW | No | AM- Markov chain Monte Carlo | Hypothetical |
| [58] | MODFLOW | MT3D | Fuzzy parameterized probabilistic analysis | Hypothetical |
| [59] | MODFLOW | MT3D | Fuzzy ordinary Kriging | Hypothetical |
| [117] | No | Parallel groundwater transport and remediation codes | Markov chain Monte Carlo | Hypothetical |
| [95] | MODFLOW | No | Multiple-point geostatistical method | Ølgod, Jutland, Denmark |
| Stanford geostatistical modeling software | ||||
| [153] | MODFLOW | No | Null-space Monte Carlo | No |
| [154] | GFLOW | Monte Carlo | Wisconsin, USA | |
| [100] | MODFLOW | No | Monte-Carlo simulation | Muscat, Oman |
| [14] | MODFLOW | No | generalized likelihood uncertainty estimation | Birjand aquifer, Iran |
| [12] | MODFLOW | No | Monte Carlo | Tashk-Bakhtegan river basin, Iran |
| [8] | MODFLOW | MT3DMS | DREAMzs | Isfahan-Barkhoar, Iran |
| [15] | MODFLOW | MT3DMS | DREAMzs | Isfahan-Barkhoar, Iran |
| Reference | Simulation | Game Theory or Conflict Resolution | Case Study | |
|---|---|---|---|---|
| Quantitative Modeling | Qualitative Modeling | |||
| [196] | No | No | Nash bargaining scenario | El Paso, Texas and Ciudad Juarez, Mexico |
| Nash non-cooperative game | ||||
| [197] | No | No | Non-cooperative equilibrium | South-central Texas, US |
| [198] | No | No | Game theory | Guanajuato, Mexico |
| [199] | No | No | Game-theory model | Hypothetical |
| [48] | MODFLOW | MT3D | Young conflict–resolution theory | Tehran aquifer, Iran |
| [57] | MODFLOW | MT3D | Rubinstein’s sequential bargaining theory | Tehran aquifer, Iran |
| [200] | No | No | Social choice rule | Western La Mancha aquifer, Spain |
| [99] | MODFLOW | No | MCSGA | Rafsanjan plain, Iran |
| NGA | ||||
| [12] | MODFLOW | MT3DMS | Social choice rule-Fallback Bargaining | Kavar-Maharloo aquifer, Iran |
| [13] | MODFLOW | MT3DMS | Non-cooperative game theory | Khaledabad, Iran |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norouzi Khatiri, K.; Nematollahi, B.; Hafeziyeh, S.; Niksokhan, M.H.; Nikoo, M.R.; Al-Rawas, G. Groundwater Management and Allocation Models: A Review. Water 2023, 15, 253. https://doi.org/10.3390/w15020253
Norouzi Khatiri K, Nematollahi B, Hafeziyeh S, Niksokhan MH, Nikoo MR, Al-Rawas G. Groundwater Management and Allocation Models: A Review. Water. 2023; 15(2):253. https://doi.org/10.3390/w15020253
Chicago/Turabian StyleNorouzi Khatiri, Khadijeh, Banafsheh Nematollahi, Samira Hafeziyeh, Mohammad Hossein Niksokhan, Mohammad Reza Nikoo, and Ghazi Al-Rawas. 2023. "Groundwater Management and Allocation Models: A Review" Water 15, no. 2: 253. https://doi.org/10.3390/w15020253