Application of Machine Learning Coupled with Stochastic Numerical Analyses for Sizing Hybrid Surge Vessels on Low-Head Pumping Mains
Abstract
1. Introduction
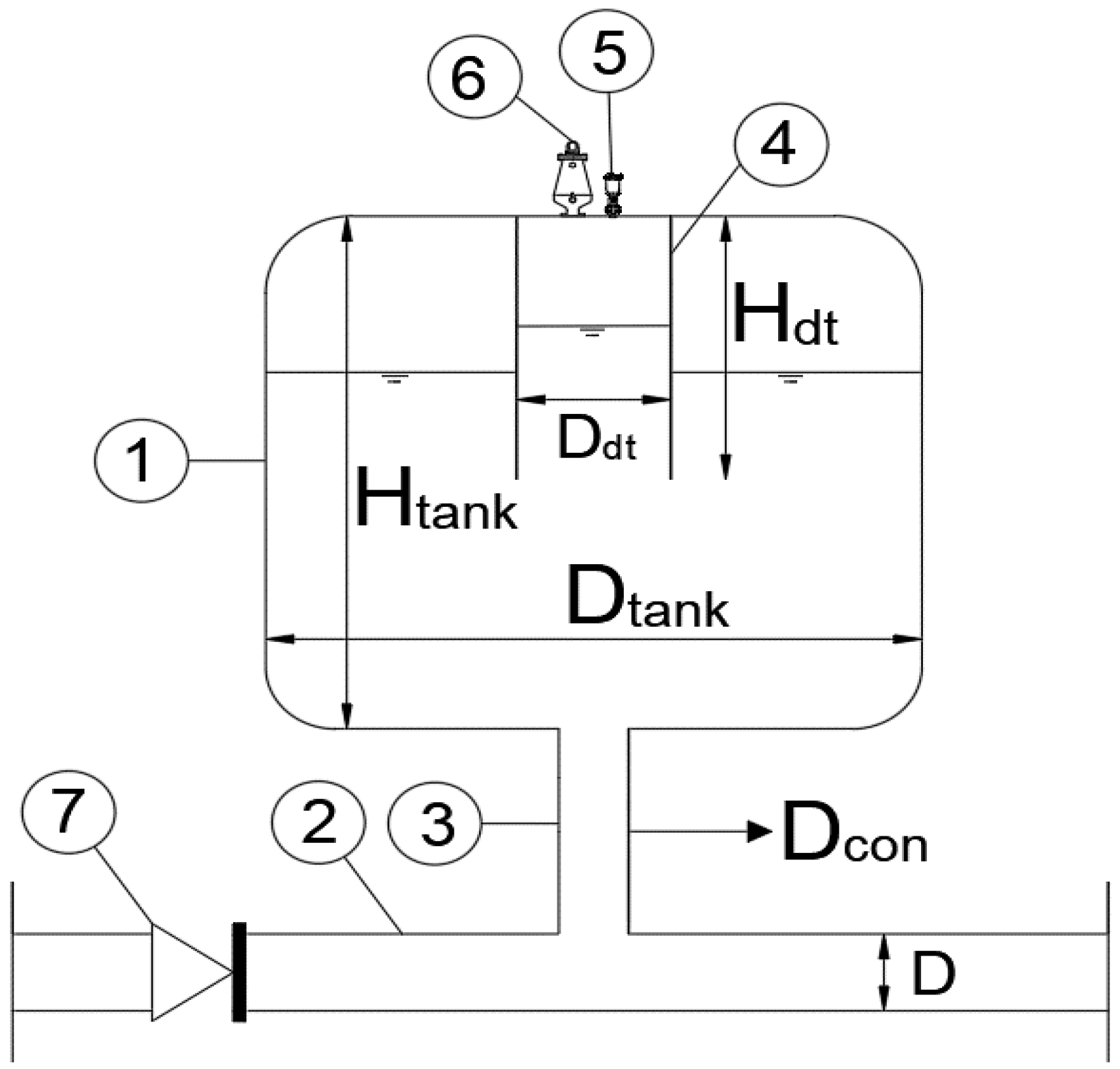
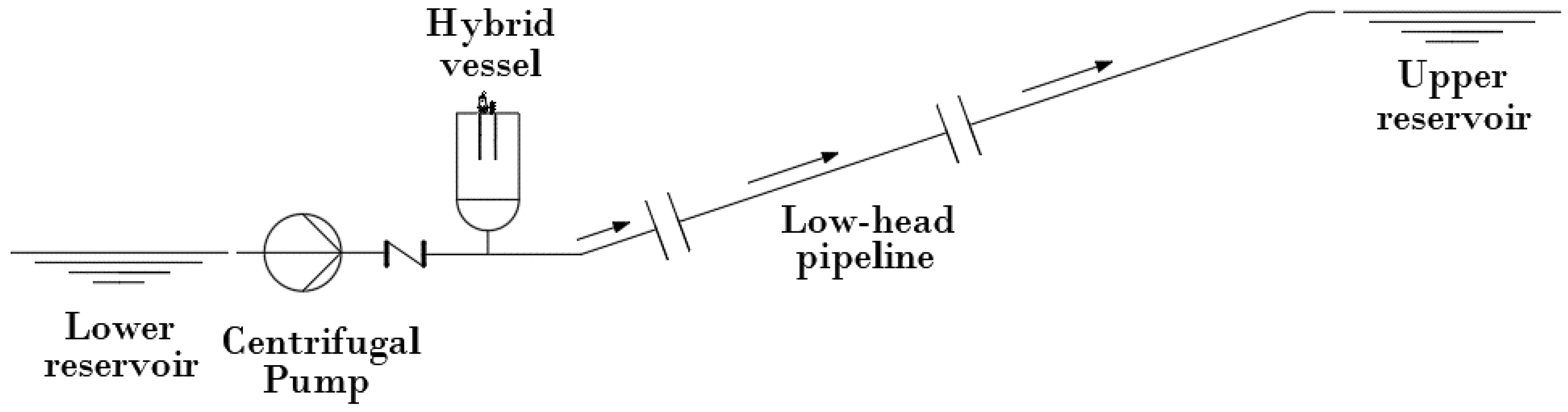
Hybrid Surge Vessels
2. Materials and Methods
2.1. Allowable Safe Pressure Limits
2.2. Numerical Modelling of Pressure Profile along the Pipeline
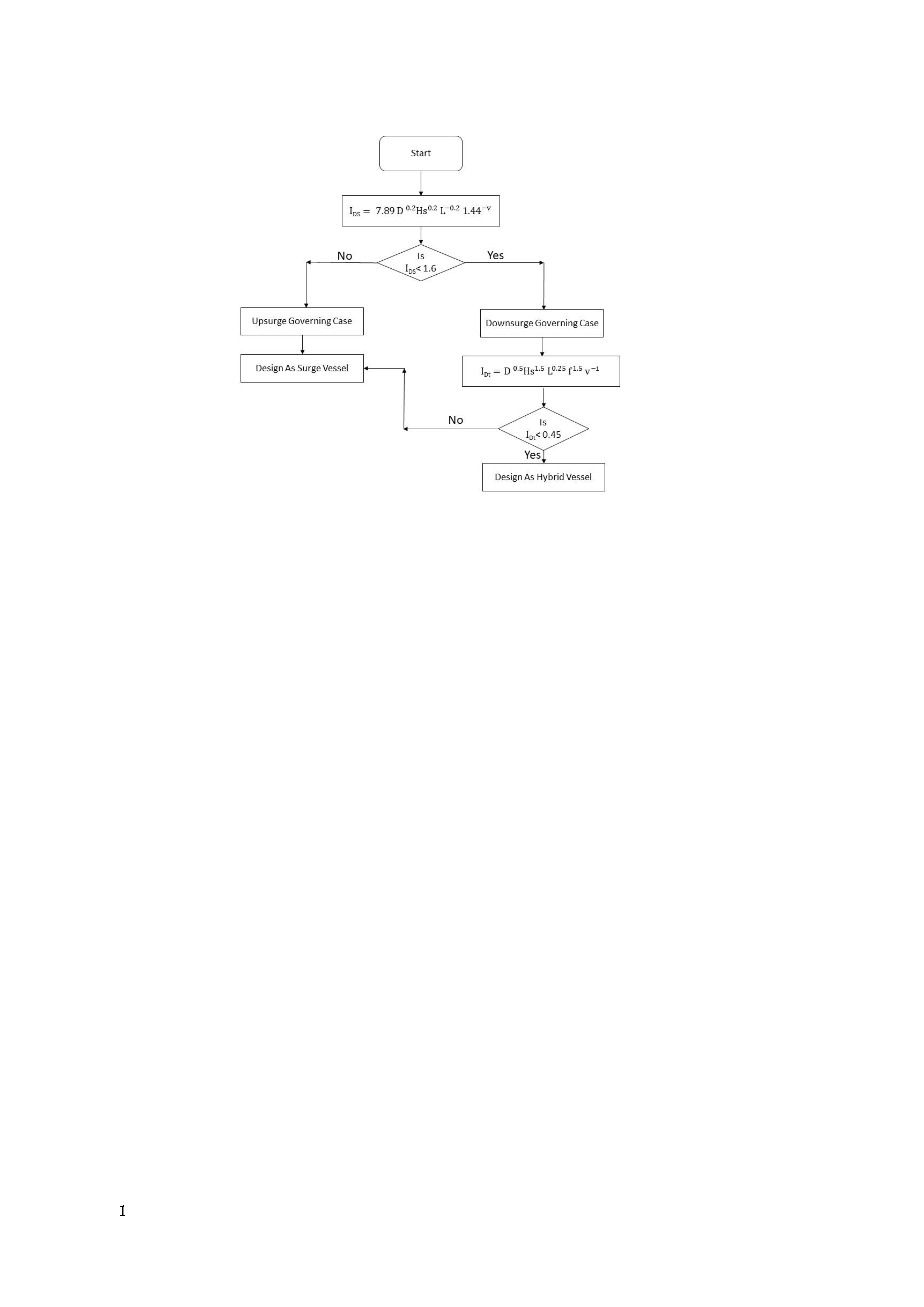
2.3. Hybrid Surge Vessel Optimum Sizing Approach
- A uniform probability distribution is allocated to input parameters for sampling within predetermined realistic ranges.
- According to a predetermined number of Monte Carlo Simulations, random samples are taken from input parameters’ distribution.
- For each stochastic run, which is a different pipeline profile and hydraulic situation, combinations of random variables are inserted into the numerical model, which is then solved deterministically for the pressure change throughout the pipeline. In order to optimize the volume of the hybrid surge vessel, each deterministic run is repeated through numerous iterations.
- The least-square linearization (LSL) method is used to determine the lowest influencing input parameters, which may be eliminated without affecting accuracy, using the result of the Method of Characteristic in the previous phase using the parameter coefficient of sensitivity, :where wi is the coefficient of regression, , difference between parameter and mean, and is the variance of .
- Then, an approximation relation can be generated using machine learning utilizing generated matrices with random parameters and the associated optimal vessel volume.
2.4. Sizing Predictive Model Development
3. Results and Discussions
3.1. Model Setup—Deterministic Run
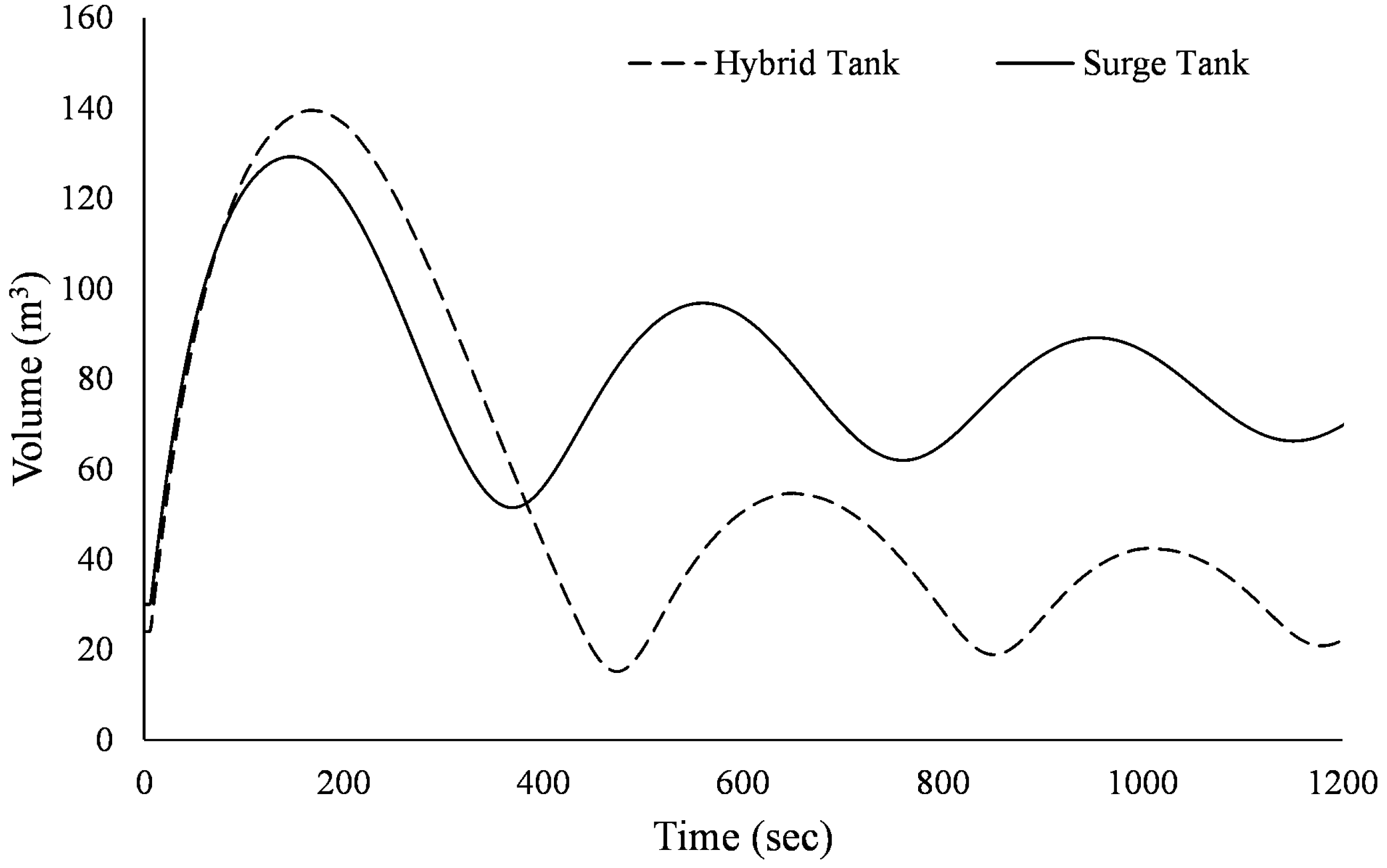
3.2. Hybrid Surge Vessel Sizing
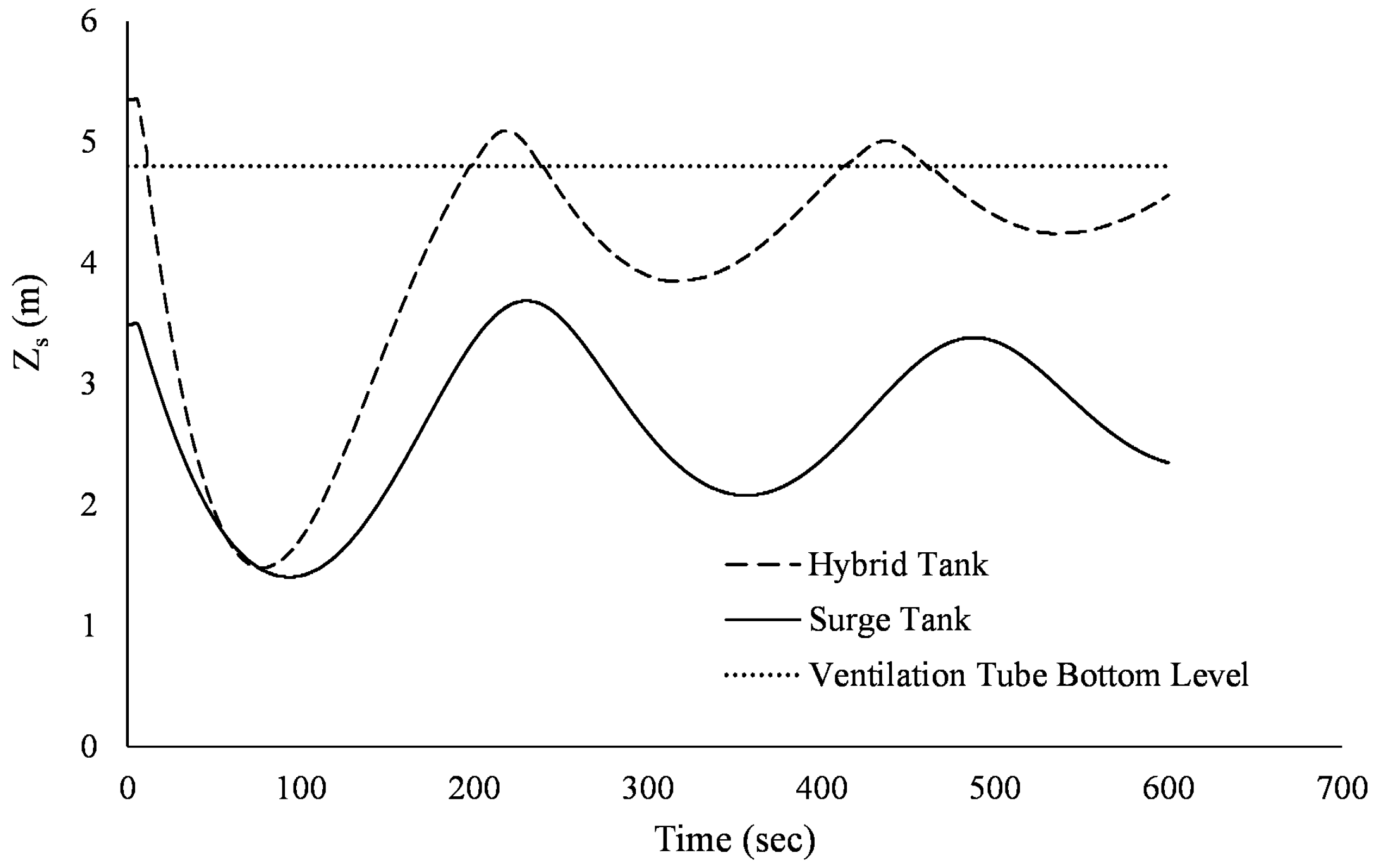
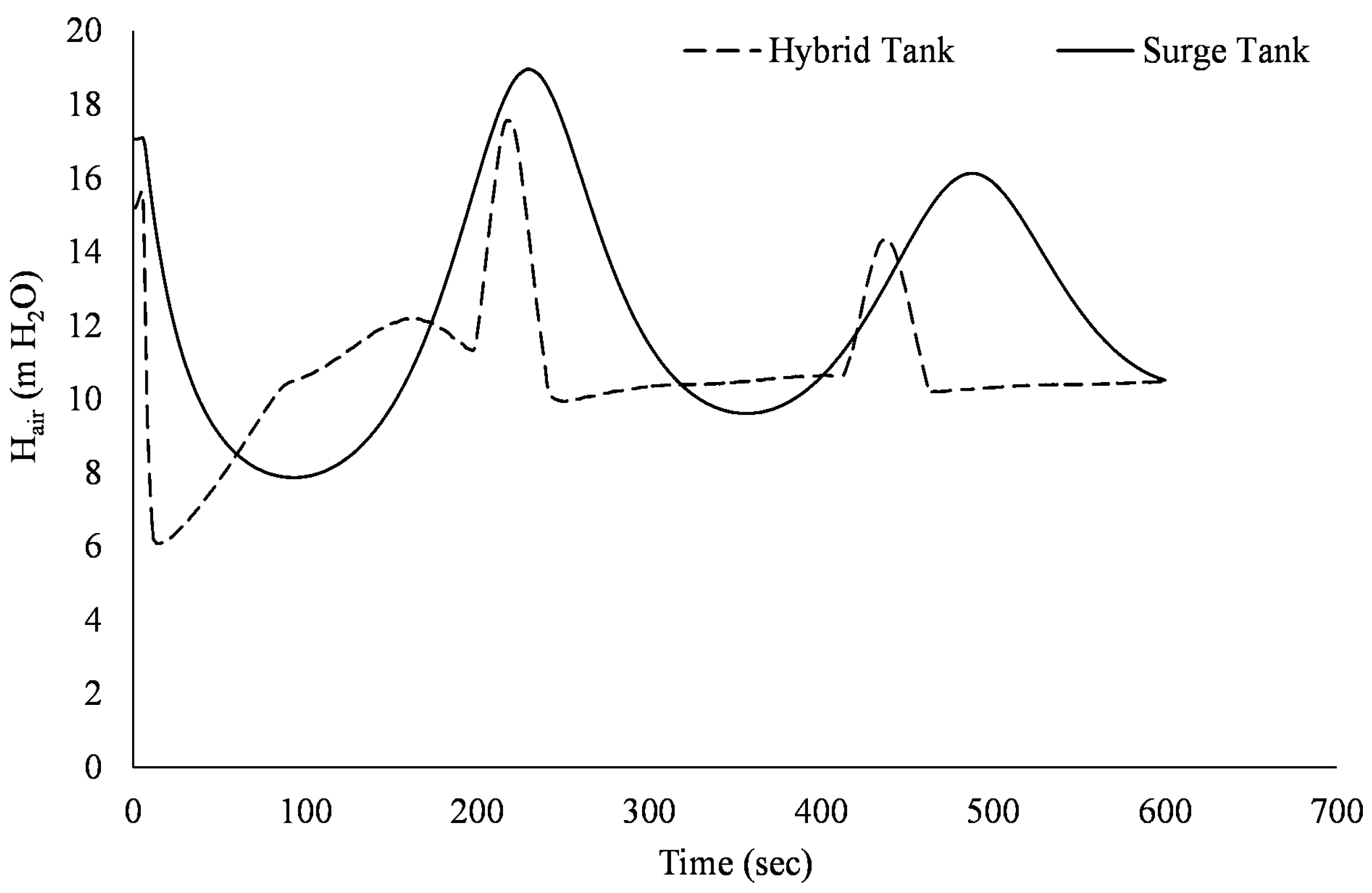
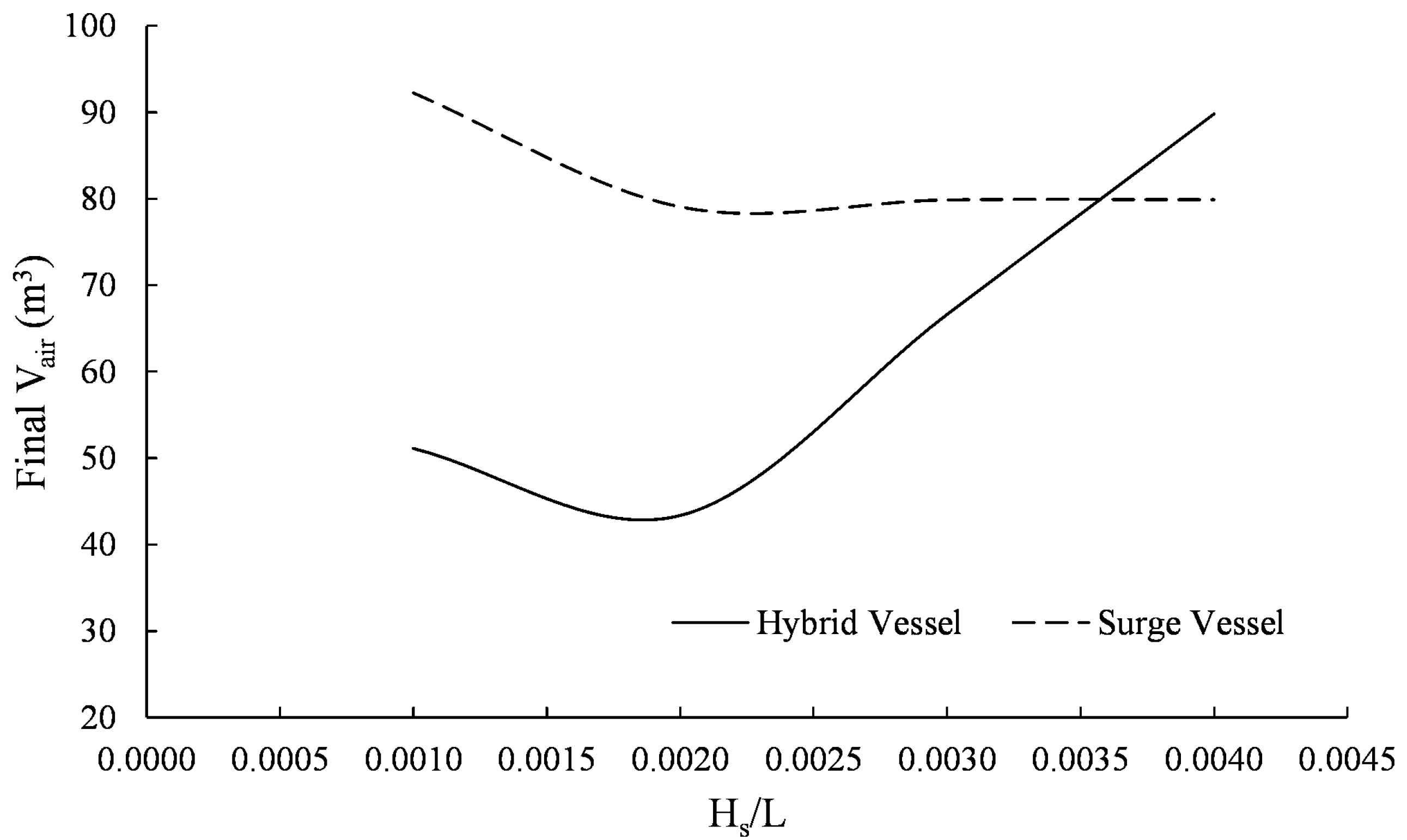
3.3. Hybrid Surge Vessel Versus Standard Surge Vessel
3.4. Model Setup—Stochastic Runs
3.5. Parameters Selection
3.6. Developed Genetic Programming Models
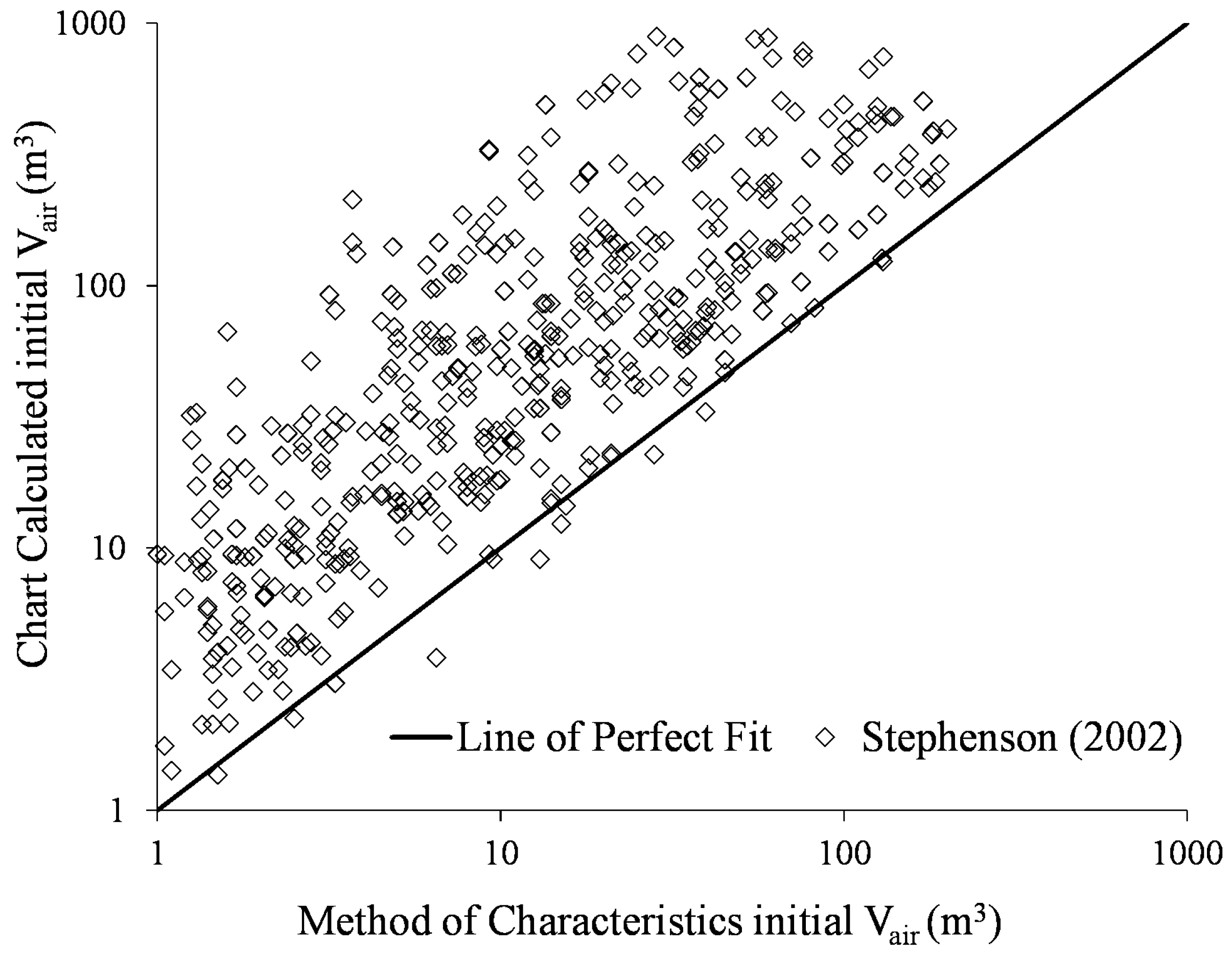
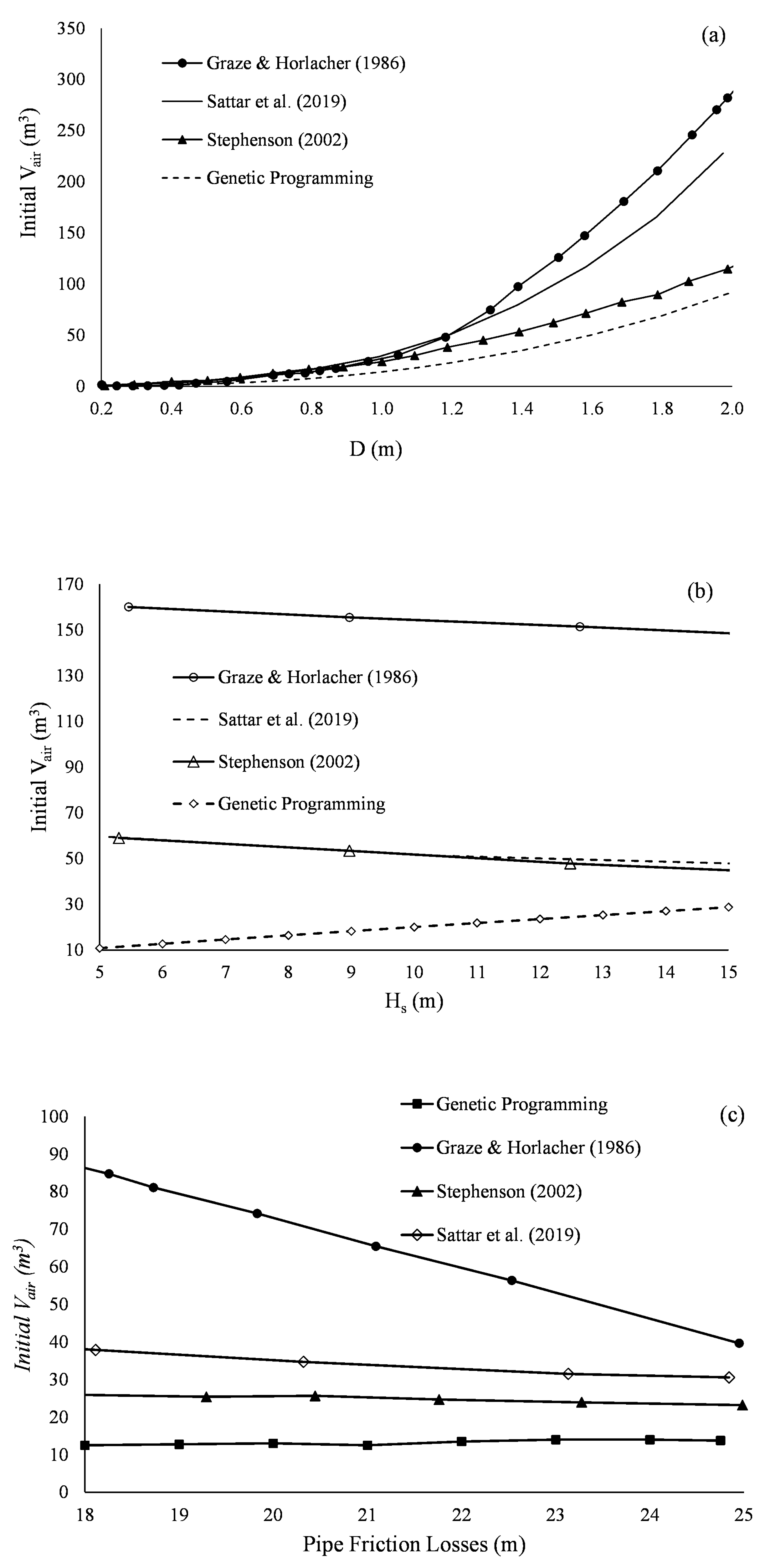
3.7. Comparison with Classical Design Charts
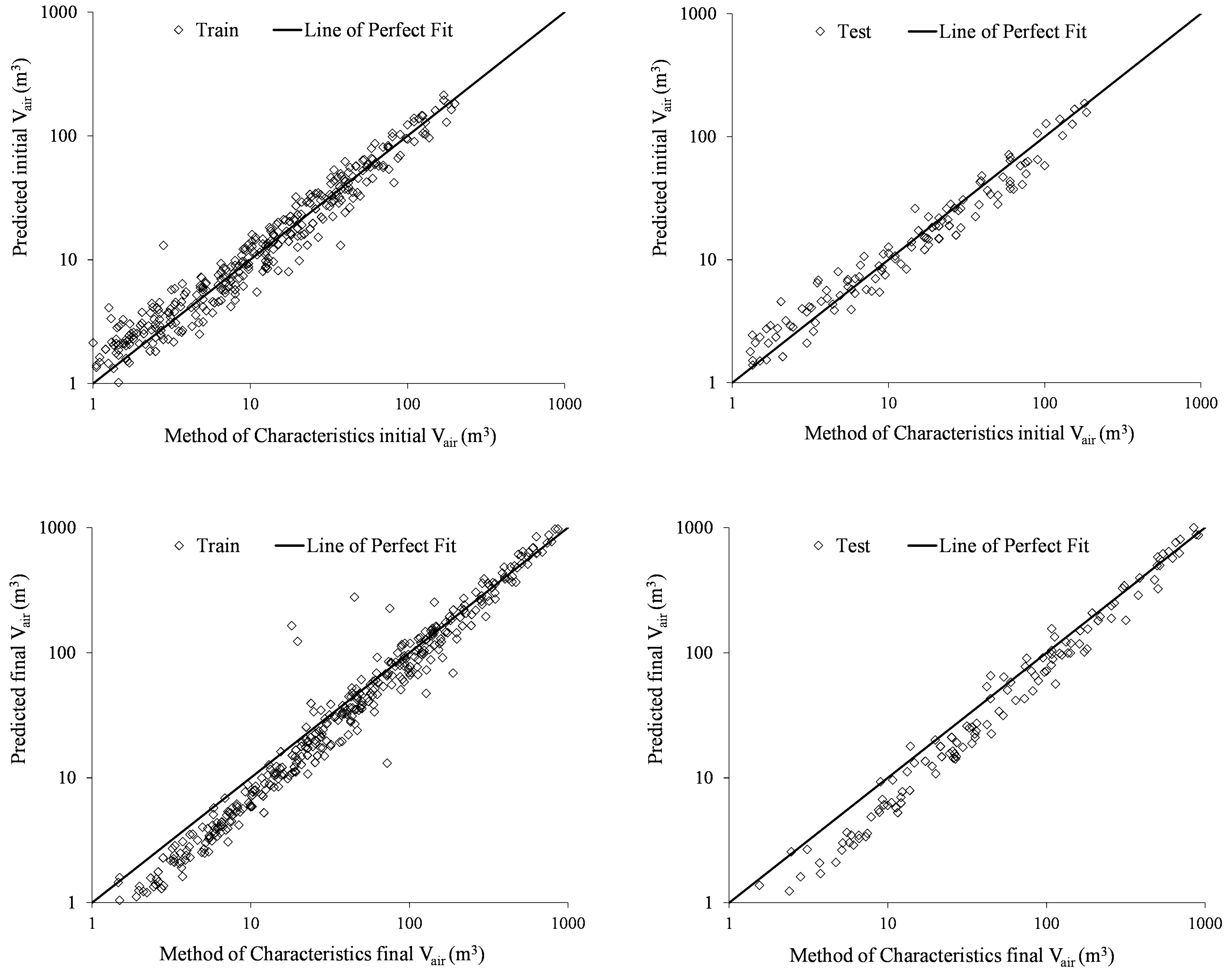
3.8. Testing and Validation of the Developed Models
3.9. Parametric Analysis of the Developed MODELS
3.10. Genetic Programming Models’ Application Range
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Laiq, S.J. Analyzing Transient Behavior and Cost Effectiveness of a TSE Transmission Line Considering Different Pipeline Materials. In Pipelines 2014: From Underground to the Forefront of Innovation and Sustainability; ASCE Library: Reston, VA, USA, 2014; pp. 2201–2210. [Google Scholar] [CrossRef]
- Triki, A.; Chaker, M.A. Compound technique-based inline design strategy for water-hammer control in steel pressurized-piping systems. Int. J. Press. Vessel. Pip. 2019, 169, 188–203. [Google Scholar] [CrossRef]
- Chaker, M.A.; Triki, A. Investigating the branching redesign strategy for surge control in pressurized steel piping systems. Int. J. Press. Vessel. Pip. 2020, 180, 104044. [Google Scholar] [CrossRef]
- Garg, R.K.; Kumar, A. Experimental and numerical investigations of water hammer analysis in pipeline with two different materials and their combined configuration. Int. J. Press. Vessel. Pip. 2020, 188, 104219. [Google Scholar] [CrossRef]
- Ostfeld, A. (Ed.) Water Supply System Analysis—Selected Topics [Internet]; InTech: London, UK, 2012. [Google Scholar] [CrossRef]
- Zhu, M.L.; Shen, B.; Zhang, Y.H.; Wang, T. Research on protection of water hammer in long-distance pressurized water transfer pipeline project. J. Xi’an Univ. Archit. Technol. (Nat. Sci. Ed.) 2007, 39, 40–43. [Google Scholar]
- Zhiyong, L. Comparative research on protective measures of pump-stopping water hammer in water intake pumping station along river. Trans. Chin. Soc. Agric. Mach. 2005, 7, 61–64. [Google Scholar]
- Feng, T.; Jia, Y.; Xie, R. Characteristics and protective measures of water hammer in cascade pumping station for long distance pressure water delivery. China Water Wastewater 2008, 14, 16. [Google Scholar]
- Calamak, M.; Bozkus, Z. Comparison of performance of two run-of-river plants during transient conditions. J. Perform. Constr. Facil. 2013, 27, 624–632. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, Y.; Wang, C. Research on air valve of water supply pipelines. Procedia Eng. 2015, 119, 884–891. [Google Scholar] [CrossRef]
- Arefi, M.H.; Ghaeini-Hessaroeyeh, M.; Memarzadeh, R. Numerical modeling of water hammer in long water transmission pipeline. Appl. Water Sci. 2021, 11, 140. [Google Scholar] [CrossRef]
- Li, G.; Wu, X.; Li, L.; Qiu, W.; Cui, W. Research on water hammer protection for a long-distance water supply system of a deep well pump group. IOP Conf. Ser. Earth Environ. Sci. 2021, 826, 012047. [Google Scholar] [CrossRef]
- Graze, H.R.; Horlacher, H.B. Air Chamber Design charts. In Proceedings of the 8th Australian Fluid Mechanics Conference, University of Newcastle, Newcastle, NSW, Australia, 28 November–2 December October 1982; Volume 28, pp. 14–18. [Google Scholar]
- Ruus, E.; Karney, B.W. Applied Hydraulic Transients; Ruus Consulting Ltd., Ken Fench: British Columbia, BC, Canada, 1997. [Google Scholar]
- Stephenson, D. Simple guide for design of air vessels for water hammer protection of pumping lines. J. Hydraul. Eng. 2002, 128, 792–797. [Google Scholar] [CrossRef]
- Izquierdo, J.; Lopez, P.A.; Lopez, G.; Martinez, F.J.; Perez, R. Encapsulation of air vessel design in a neural network. Appl. Math. Model. 2006, 30, 395–405. [Google Scholar] [CrossRef]
- De Martino, G.; Fontana, N. Simplified approach for the optimal sizing of throttled air chambers. J. Hydraul. Eng. 2012, 138, 1101–1109. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, Y.B.; Xu, Y.; Jang, T.U. Optimal sizing of an air vessel in a long-distance water-supply pumping system using the SQP method. J. Pipeline Syst. Eng. Pract. 2016, 7, 05016001. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, J.; Yu, X.; Chen, S. Water hammer protective performance of a spherical air vessel caused by a pump trip. Water Supply 2019, 19, 1862–1869. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Yu, X.; Shi, L.; Zhao, W.; Xu, H. Formula for selecting optimal location of air vessel in long-distance pumping systems. Int. J. Press. Vessel. Pip. 2019, 172, 127–133. [Google Scholar] [CrossRef]
- Miao, D.; Zhang, J.; Chen, S.; Li, D.Z. An approximate analytical method to size an air vessel in a water supply system. Water Sci. Technol. Water Supply 2017, 17, 1016–1021. [Google Scholar] [CrossRef]
- Sattar, A.M.; Soliman, M.; El-Ansary, A. Preliminary sizing of surge vessels on pumping mains. Urban Water J. 2019, 16, 738–748. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, J.; Yu, X.D.; Wang, X.T.; Chen, X.Y.; Zhang, Z.X. Optimal volume selection of air vessels in long-distance water supply systems. AQUA—Water Infrastruct. Ecosyst. Soc. 2021, 70, 1053–1065. [Google Scholar] [CrossRef]
- Wan, W.; Zhang, B. Investigation of water hammer protection in water supply pipeline systems using an intelligent self-controlled surge tank. Energies 2018, 11, 1450. [Google Scholar] [CrossRef]
- Charlatte FAYAT Group. A.R.A.A. Dipping Tube Surge Vessel. SPT 140-04-GB. 1978. Available online: https://www.charlattereservoirs.fayat.com (accessed on 17 September 2023).
- Verhoeven, R.; Van Poucke, L.; Huygens, M. Waterhammer Protection with Air Vessels A Comparative Study. WIT Trans. Eng. Sci. 1998, 18, 3–14. Available online: https://www.witpress.com/elibrary/wit-transactions-on-engineering-sciences/18/6215 (accessed on 17 September 2023).
- Ruus, E.; Karney, B.; El-Fitiany, F.A. Charts for water hammer in low head pump discharge lines resulting from water column separation and check valve closure. Can. J. Civ. Eng. 1984, 11, 717–742. [Google Scholar] [CrossRef][Green Version]
- Boulos, P.F.; Karney, B.W.; Wood, D.J.; Lingireddy, S. Hydraulic transient guidelines for protecting water distribution systems. J. Am. Water Work. Assoc. 2005, 97, 111–124. [Google Scholar] [CrossRef]
- Leruth, P.; Pothof, I. Innovative air vessel design for long distance water transmission pipelines. In Proceeding of the 11th International Conference on Pressure Surges, Lisbon, Portugal, 24–26 October 2012; BHR Group Ltd.: Lisbon, Portugal, 2012. [Google Scholar]
- Wang, R.; Li, P.; Wang, Z.; Zhang, F. Dipping Tube Hydropneumatic Tank Theory and Application in Water Distribution Systems. In Proceedings of the 2012 Second International Conference on Electric Technology and Civil Engineering, Washington, DC, USA, 18–20 May 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 958–961. Available online: https://dl.acm.org/doi/proceedings/10.5555/2373291 (accessed on 17 September 2023).
- Wang, R.H.; Wang, Z.X.; Zhang, F.; Sun, J.L.; Wang, X.X.; Luo, J.; Yang, H.B. Hydraulic transient prevention with dipping tube hydropneumatic tank. Appl. Mech. Mater. 2013, 316, 762–765. [Google Scholar] [CrossRef]
- Moghaddas, S.M.; Samani, H.M.; Haghighi, A. Transient protection optimization of pipelines using air-chamber and air-inlet valves. KSCE J. Civ. Eng. 2017, 21, 1991–1997. [Google Scholar] [CrossRef]
- Hu, J.; Zhai, X.; Hu, X.; Meng, Z.; Zhang, J.; Yang, G. Water Hammer Protection Characteristics and Hydraulic Performance of a Novel Air Chamber with an Adjustable Central Standpipe in a Pressurized Water Supply System. Sustainability 2023, 15, 29730. [Google Scholar] [CrossRef]
- Bentley Systems. Bentley HAMMER Connect. 2023. Available online: https://www.bentley.com (accessed on 17 September 2023).
- Zhang, Z. Hydraulic Transients and Computations, 1st ed.; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Radi, A.; Poli, R. Genetic programming discovers efficient learning rules for the hidden and output layers of feedforward neural networks. In Genetic Programming: Second European Workshop, EuroGP’99 Göteborg, Sweden, 26–27 May 1999 Proceedings 2; Springer Science & Business Media: New York, NY, USA, 1999; pp. 120–134. [Google Scholar] [CrossRef]
- Ruus, E. Charts for water-hammer in pipelines with air chambers. Can. J. Civ. Eng. 1977, 4, 293–313. [Google Scholar] [CrossRef]
- Sharif, F.; Siosemarde, M.; Merufinia, E.; Esmatsaatlo, M. Comparative hydraulic simulation of water hammer in transition pipe line systems with different diameter and types. J. Civ. Eng. Urban. 2014, 4, 282–286, pii: S225204301400043-4. [Google Scholar]








| Performance Indicator | Equation | Variables |
|---|---|---|
| Coefficient of determination | P(ij) is the value predicted by the program, Tj is the target value, and n is the number of samples, , | |
| Root mean square error | ||
| Coefficient of efficiency | Esn = 1 − | |
| Index of agreement | Dag = 1 − | |
| Gradients of the regression | ||
| Slope of regression line | and | |
| Cross testing coefficient | ||
| Standard deviation errors |
| Iteration Number | (m3) | (m) | (m) | (m3) | (m3) | (m3) | (m) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 35 | 5.00 | 3.00 | 1.00 | 7.00 | 21.36 | 1.64 | 1.03 | −5.21 |
| 2 | 2 | 35 | 5.00 | 3.00 | 1.50 | 7.00 | 21.76 | 1.60 | 1.05 | −4.51 |
| 3 | 2 | 35 | 5.00 | 3.00 | 2.00 | 7.00 | 22.68 | 1.55 | 1.04 | −3.70 |
| 4 | 2 | 35 | 5.00 | 3.00 | 2.50 | 7.00 | 23.51 | 1.48 | 1.04 | −3.00 |
| 5 | 2 | 26 | 5.35 | 2.50 | 1.50 | 5.25 | 21.00 | 1.23 | 1.05 | −3.34 |
| 6 | 2 | 26 | 5.35 | 2.50 | 2.00 | 5.25 | 21.72 | 1.20 | 1.04 | −2.51 |
| 7 | 2 | 24 | 4.95 | 2.50 | 1.50 | 4.75 | 20.39 | 1.17 | 1.15 | −3.59 |
| 8 | 2 | 24 | 4.95 | 2.50 | 1.75 | 4.75 | 20.74 | 1.15 | 1.14 | −3.12 |
| 9 | 2 | 24 | 4.95 | 2.50 | 1.80 | 4.75 | 20.90 | 1.14 | 1.15 | −2.91 |
| 10 | 2 | 23 | 4.75 | 2.50 | 1.80 | 4.62 | 20.50 | 1.11 | 1.21 | −3.00 |
| Case | (m) | (m) | (m3) | (m3) | (m3) | (m3) | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 4.3 | 60 | 7.2 | 53.96 | 53.96 |
| 2 | 2.95 | 30 | 3.6 | 27.23 | 54.46 | ||
| 3 | 2.45 | 20 | 2.5 | 18.46 | 55.38 | ||
| 2 | 1 | * 5.2 | 4.3 | 90 | 18 | 87.24 | 87.24 |
| 3 | 3 | 30 | 6 | 29.47 | 88.41 | ||
| 4 | 2.6 | 22.5 | 4.5 | 21.59 | 86.36 |
| Parameter | Range | |
|---|---|---|
| Lower Bound | Upper Bound | |
| f | 0.015 | 0.030 |
| L (m) | 2500 | 15,000 |
| v (m/s) | 0.5 | 2.5 |
| D (m) | 0.25 | 2.0 |
| Hs (m) | 5 | 40 |
| a (m/s) | 250 | 1400 |
| Volume (m3) | f | L (m) | v (m/s) | D (m) | Hs (m) | a (m/s) | (m3) |
|---|---|---|---|---|---|---|---|
| 3.38 | 0.001 | 0.05 | 94.23 | 2.32 | 0.01 | -- | |
| 0.001 | 0.20 | 0 | 2.80 | 0.38 | 1.75 | 95.11 | |
| 3.7 | 2.71 | 3.43 | 89.39 | 0.66 | 0.066 | -- |
| Model | Data Partitioning | R2 | RMSE | RAE | Esn | Dag |
|---|---|---|---|---|---|---|
| [13] | NA | 0.25 | 98 | 1.82 | −6.48 | −0.06 |
| [15] | NA | 0.17 | 339 | 4.92 | −89.35 | −0.67 |
| GP- | Train | 0.88 | 33 | 0.258 | 0.88 | 0.94 |
| Test | 0.81 | 44 | 0.334 | 0.78 | 0.89 | |
| GP- | Train | 0.94 | 8 | 0.19 | 0.94 | 0.97 |
| Test | 0.94 | 10 | 0.21 | 0.93 | 0.96 | |
| GP- | Train | 0.96 | 32 | 0.149 | 0.95 | 0.98 |
| Test | 0.97 | 40 | 0.144 | 0.97 | 0.98 |
| Parameter | [13] | Parameter | [15] | ||
|---|---|---|---|---|---|
| 0 to 160 | 0 to 18 | 0.5 to 8 | 0.02 to 4.2 | ||
| 0.1 to 1 | 0.03 to 2.6 | 1 to 2.2 | 1.2 to 17.8 | ||
| −0.8 to −0.1 | −0.74 to −0.03 | 0.2 to 0.7 | 0.15 to 0.48 |
| Model | R (R > 0.8) | K (0.85 < K < 1.15) | K′ (0.85 < K′ < 1.15) | m′ (m′ < 0.1) | n′ (n′ < 0.1) |
|---|---|---|---|---|---|
| GP- | 0.96 | 1.01 | 0.97 | −0.09 | −0.09 |
| GP- | 0.98 | 1.02 | 0.97 | −0.03 | −0.03 |
| GP- | 0.99 | 1.04 | 0.95 | −0.01 | 0.00 |
| Model | Mean Prediction Error | Deviation of Prediction Error | Width of Uncertainty Band | 95% Prediction Error Interval |
|---|---|---|---|---|
| [13]- | +0.31 | 0.51 | ±1.01 | +0.01 to +51 |
| [15]- | +0.66 | 0.40 | ±0.78 | +0.01 to +7.88 |
| GP- | −0.08 | 0.24 | ±0.47 | +0.14 to +10.59 |
| GP- | 0 | 0.13 | ±0.26 | +0.30 to +3.30 |
| GP- | −0.12 | 0.13 | ±0.25 | +0.43 to +4.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sattar, A.M.A.; Ghazal, A.N.; Elhakeem, M.; Elansary, A.S.; Gharabaghi, B. Application of Machine Learning Coupled with Stochastic Numerical Analyses for Sizing Hybrid Surge Vessels on Low-Head Pumping Mains. Water 2023, 15, 3525. https://doi.org/10.3390/w15193525
Sattar AMA, Ghazal AN, Elhakeem M, Elansary AS, Gharabaghi B. Application of Machine Learning Coupled with Stochastic Numerical Analyses for Sizing Hybrid Surge Vessels on Low-Head Pumping Mains. Water. 2023; 15(19):3525. https://doi.org/10.3390/w15193525
Chicago/Turabian StyleSattar, Ahmed M. A., Abedalkareem Nedal Ghazal, Mohamed Elhakeem, Amgad S. Elansary, and Bahram Gharabaghi. 2023. "Application of Machine Learning Coupled with Stochastic Numerical Analyses for Sizing Hybrid Surge Vessels on Low-Head Pumping Mains" Water 15, no. 19: 3525. https://doi.org/10.3390/w15193525
APA StyleSattar, A. M. A., Ghazal, A. N., Elhakeem, M., Elansary, A. S., & Gharabaghi, B. (2023). Application of Machine Learning Coupled with Stochastic Numerical Analyses for Sizing Hybrid Surge Vessels on Low-Head Pumping Mains. Water, 15(19), 3525. https://doi.org/10.3390/w15193525








