Abstract
The current study seeks to conduct time series forecasting of droughts by means of the state-of-the-art XGBoost algorithm. To explore the drought variability in one of the semi-arid regions of Turkey, i.e., Denizli, the self-calibrated Palmer Drought Severity Index (sc-PDSI) values were used and projections were made for different horizons, including short-term (1-month: t + 1), mid-term (3-months: t + 3 and 6-months: t + 6), and long-term (12-months: t + 12) periods. The original sc-PDSI time series was subjected to the partial autocorrelation function to identify the input configurations and, accordingly, one- (t − 1) and two-month (t − 2) lags were used to perform the forecast of the targeted outcomes. This research further incorporated the recently introduced variational mode decomposition (VMD) for signal processing into the predictive model to enhance the accuracy. The proposed model was not only benchmarked with the standalone XGBoost but also with the model generated by its hybridization with the discrete wavelet transform (DWT). The overall results revealed that the VMD-XGBoost model outperformed its counterparts in all lead-time forecasts with NSE values of 0.9778, 0.9405, 0.8476, and 0.6681 for t + 1, t + 3, t + 6, and t + 12, respectively. Transparency of the proposed hybrid model was further ensured by the Mann–Whitney U test, highlighting the results as statistically significant.
1. Introduction
The complexity of the processes involved in the global hydrological cycle makes pinpointing the root causes of the drought phenomenon quite challenging. Since droughts are typically slow-onset hazards forming gradually (except flash droughts that have drastic impacts on agricultural facilities), they are also called “misery in slow motion” [1]. Despite the general definition highlighting the precipitation deficit regarding droughts, they occur once the humidity is subpar, which results from the disruption of the balance between precipitation and evapotranspiration for many years in a particular region [2]. The drought phenomenon also poses significant threats to three main pillars of sustainability, i.e., economic (such as over-costing water supply due to the decrease in freshwater resources, disruptions in livestock, degradations in agricultural activities, interruptions in tourism, etc.) [3], environmental (water scarcity/stress-related diseases, degradations in water quantity and quality, etc.) [4], and social (social uncertainties, increase in irregular migration, etc.) pillars [5], across the globe. Given that 1.43 billion people on a global scale have been adversely affected by drought incidents over the last two decades [1], countries should essentially focus more on hydro-climatological risks and route their sources into activities embracing mitigation measures to combat droughts in a sustainable way. It is worth mentioning that the underlying reasons for the poor performance of the world are the inadequate global drought monitoring and impact assessment systems as well as a lack of systematic reporting of economic and social consequences, even in developed countries [6]. Here, some of the Sustainable Development Goals (SDGs) targeted under the 2030 agenda (i.e., SDGs 6, 11, 12, 13, and 15) are directly related to the drought phenomenon [7,8]. Therefore, there has been a recent and growing interest by the research community on sustainable solutions to combating drought [9,10,11].
The vast majority of the research carried out regarding the context of drought-resilient regions and reducing the potential adverse effects are generally grounded on the accurate estimation of droughts and determining the possible drought periods within future timeframes. To accomplish this aim, drought indices that quantify the corresponding phenomenon have widely been utilized. In this sense, drought indices were put forward based on drought types covering different dynamic processes and addressing corresponding targets. Among the drought indices, meteorological indices, i.e., China Z Index (CZI), Palmer Drought Severity Index (PDSI), Standardized Precipitation Index (SPI), Standardized Precipitation Evapotranspiration Index (SPEI), Effective Drought Index (EDI), etc., requiring relatively easy-to-obtain data (such as precipitation, temperature, evapotranspiration, etc.) account for a significant proportion [12]. In addition, hydrological drought indices such as the Streamflow Drought Index (SDI), Standardized Streamflow Index (SSFI), Standardized Reservoir Supply Index (SRSI), and remote-sensing-based drought indices such as the Normalized Difference Vegetation Index (NDVI), Enhanced Vegetation Index (EVI), and Evaporative Stress Index (ESI) have also commonly been used by researchers to assess the different forms of droughts.
Machine learning (ML) has revolutionized applications made in divergent fields, leveraging advancements in computer science to drive unprecedented progress [13,14]. Thus, scholars harness machine learning to process vast amounts of complex data and extract valuable insights for optimization, predictive modeling, etc. [15,16]. To substantiate the drought projections by means of these indices, the use of ML algorithms has become a rising trend in recent years, especially with the effect of the overarching technology empowering researchers to solve such intricate problems [17]. Associatively, the existing body of knowledge covers a wide range of ML applications for modeling different drought indices, such as SPI [18,19], SPEI [20,21], PDSI [2,22], and EDI [23], under various forecasting horizons, i.e., short-term, mid-term, and long-term periods.
Among the aforementioned indices, the SPI is a widely used index that characterizes meteorological droughts on different timescales, namely, SPI3, SPI6, SPI9, SPI12, SPI24, etc. For instance, Belayneh et al. [24] performed short-term drought forecasting based on SPI3 and SPI6 values in the Awash river basin with hybrid wavelet and ML methods. From a different facet, Ali et al. [25] explored the usability of the historical monthly rainfall, temperature, humidity, and Southern Oscillation Index (SOI) values to predict SPI values in different regions (i.e., Islamabad, Dera Ismail Khan, and Multan). Malik et al. [26] further evaluated the applicability of the ML algorithms in predicting SPI values for various lead times, i.e., 1, 3, 6, 9, 12, and 24 months. Moreover, to verify the practicality of the ML algorithms in SPI-based drought projections, several studies have been introduced with a plethora of ML methods, i.e., random forest (RF) [27,28], decision trees (DT) [29], M5 model tree [30], gradient boosting regression model (GBM) [31], reduced error pruning [18], k-nearest neighbor algorithm [32], etc., in the pertinent literature. Furthermore, considering the crucial role of temperature on meteorological processes and the fact that evapotranspiration can be computed depending on temperature (to exemplify, with Thornthwaite, Hargreaves–Samani, and FAO Penman–Monteith equations), the SPEI covering both precipitation and evapotranspiration can be used for quantifying drought phenomena. Hence, many researchers adopted a variety of ML algorithms, e.g., ANN [33], XGBoost [21], ELM [34], kNN [35], M5P tree [20], etc., to forecast the SPEI. The SPEI was adopted by Vicente-Serrano et al. [36] to enhance the representation ability of climate change alterations based on taking the temperature impact into account on drought intensity and multi-quantity characteristics compared to the SPI [37]. Recently, Fung et al. [38] adopted the improved support vector regression (SVR) for predicting SPEI-1, SPEI-3, and SPEI-6 at different timescales. Li et al. [39] explored the role of antecedent sea surface temperature in conjunction with the ML approaches (namely SVR, RF, and ELM) to determine drought patterns in different regions from North America, Asia, Europe, and Africa with regard to 1- and 3-month lead times of SPEI.
Although extensive research has been carried out on the prediction of SPI and SPEI, limited efforts have been devoted to model PDSI/sc-PDSI based on the utilization of ML algorithms in the pertinent literature. In fact, the PDSI demonstrates several strengths, for instance, allowing the simulation of soil moisture content month by month and ensuring the comparison of the severity of drought events in regions characterized by different climatic conditions [40]. The reason for the limited applications can be linked to the fact that it requires additional variables (such as soil data and a total water balance). Still, some studies addressed the applicability of data-driven techniques in both PDSI and sc-PDSI forecasting. For instance, Diodato et al. [41] focused on predicting the PDSI time series covering 1801–2014 in California by means of the Pacific Decadal Oscillation (PDO) and El Niño Southern Oscillation (ENSO) indices that were both used as input time series. Tufaner and Özbeyaz [42] proposed a straightforward prediction rationale for the PDSI using linear regression, ANN, SVM, and decision trees with the help of various hydro-meteorological variables. The authors concluded that the ANN showed the best performance with a slight accuracy difference. In addition, Özger et al. [2] focused on incorporating two different signal-processing techniques, namely, continuous wavelet transform (CWT) and empirical mode decomposition (EMD), and underlined the vitality of the selection of the most appropriate mother wavelet type in sc-PDSI predictions. For ML-based predictions, they not only used standalone ANFIS, SVM, and M5 Model Tree, but also combined them with the corresponding two pre-processing algorithms in order to perform comprehensive performance comparisons. As a result, the researchers found that the highest predictive accuracy was obtained with the hybrid WD-ANFIS framework. Likewise, Aghelpour et al. [22] predicted the PDSI using divergent ML techniques, i.e., autoregressive moving average (ARMA), radial basis function neural network (RBFNN), and SVM, using two fundamental meteorological parameters, temperature and precipitation. They further integrated the dragonfly algorithm (DA) into the utilized ML models for the purpose of hyper-parameter tuning and acquired the best predictive outcomes by means of the SVM model optimized with the DA.
Considering all the extrapolated outputs from the extant literature as a result of diligent investigations, the current research is mainly concentrated on the following objectives and corresponding contributions to fill the research gaps in the existing body of knowledge:
- The present study, rather than focalizing on the PDSI, is intended to forecast the time series of sc-PDSI as it provides more consistent and justifiable results with respect to any climate and location.
- Despite some studies that incorporated some of the signal-processing techniques, no single research examining the integration of the VMD technique to the ML algorithms exists in the drought forecasting literature.
- The past attempts accounted for a limited application of tree-based ensemble algorithms in PDSI/sc-PDSI time series modeling, whereas this research encapsulated the utilization of the XGBoost algorithm in forecasting various lead times, i.e., short-, mid-, and long-term horizons.
- The constructed VMD-XGBoost hybrid framework was benchmarked with not only the standalone XGBoost technique but also the DWT-XGBoost algorithm to accentuate its robustness.
- All the attained results were evaluated based on both divergent performance indicators and statistical significance tests (i.e., Kolmogorov–Smirnov, Shapiro–Wilk, and Mann–Whitney U tests). Such a transparent assessment has not been acknowledged in the drought forecasting literature.
Above all, this research provided insightful contributions to the body of drought modeling knowledge in terms of both methodological and conceptual manners as well as presenting important considerations regarding the determination of future dry and wet drought periods in semi-arid regions. Overall, the findings of this study are expected to minimize the harmful effects of climate change through timely and accurate identification of the periods most susceptible to climate variations in different timescales.
The remaining parts of the current research continue with the presentation of the research design and the details regarding the development of the predictive modeling scheme (Section 2). Section 3 covers the introduction of materials used in this study. In Section 3.1, the focalized study area is described, while the explanation of the concentrated drought index (i.e., sc-PDSI) is made in Section 3.2. Section 4 presents the working principles of the employed methodology and the performance evaluation indicators. In Section 4.1, this research elucidates signal-processing algorithms (discrete wavelet transform in Section 4.1.1 and variational mode decomposition in Section 4.1.2) used to divide the sc-PDSI time series into its sub-bands, while a description of XGBoost is made in Section 4.2. In addition, Section 4.3 exhibits the metrics considered to assess the performance of the predictive frameworks. Section 5 covers the presentation of the attained results. Section 6 focuses on the discussion of the obtained findings and the practical implications for the focused region. In this section, the outcomes of this research are evaluated based on the aspect of statistical significance (Section 6.1) and are benchmarked with the findings attained in the pertinent literature (Section 6.2). In addition, practical implications of the proposed predictive analysis and its potential benefits from several facets are presented in Section 6.3. Finally, a brief overview of the study is provided in the Conclusions section (Section 7).
2. Research Design and Model Development
The primary objective of this research is to perform drought forecasting in different horizons (called lead times) for a semi-arid region of Turkey, i.e., Denizli. To realize the corresponding aim, the current study is focalized on utilizing the self-calibrated Palmer Drought Severity Index due to its many advantages (presented in Section 3.2). In this regard, the time series of the drought values covering a hundred-year period (i.e., 1921–2020) were obtained from [43]. Given that one of the significant points of constructing an ML model is the identification of optimum model structure, the attained drought series were subjected to the partial autocorrelation function (PACF) tests for defining input variables (called lags). The PACF is a statistical tool offering valuable insights regarding temporal dependencies within the time series data and the underlying structure of the corresponding time series [44]. It helps identify the direct relationship between an observation and its lags, while removing the indirect effects of intermediate time points. Hence, the PACF guides the selection of lag terms that contribute to forecasting future values in ML models. The information from PACF is used to specify the lag structure of the autoregressive component of the forecasting model and, thereby, increase the accuracy of the predictions [45]. In addition, the PACF analysis aids in avoiding overfitting or underfitting of the model, as including too many and too few lags can result in overfitting leading to poor model performance on unseen data and underfitting leading to inadequate model performance, respectively. Therefore, a balance mechanism satisfied by the PACF is essential to achieve the stability of the constructed model in both short-term and long-term horizons. While the lag times were established through the PACF investigations, the drought forecasting was carried out for four different lead times, including short-term (1-month: t + 1 and 3-months: t + 3), mid-term (6-months: t + 6), and long-term (12-months: t + 12). It is worth mentioning that the train/test splitting ratio was set to 70/30 as it is one of the commonly embraced scenarios within the literature.
This study intended to illustrate the applicability of the state-of-the-art XGBoost algorithm in projecting drought incidents efficiently, and thereby not only employed the standalone XGBoost algorithm but also explored its utility with signal-processing techniques. Hence, the original time series were subjected to a recently pioneered variational mode decomposition (VMD) algorithm resulting in various sub-bands that have different time and frequency characteristics at first, and then the XGBoost was integrated into the prediction framework to model each sub-signal separately. This study further adopted the commonly embraced discrete wavelet transform (DWT) as another pre-processing algorithm in order to illustrate the enhanced forecasting capability of the proposed hybrid ML framework. In addition, to ensure the fairness of the comparisons, the same number of sub-signals (i.e., a total of seven) was extracted in both VMD and DWT algorithms. After attaining the forecasting results, the current study incorporated various performance evaluation indicators into the outcomes of the employed models to conduct comprehensive comparisons. Also, the illustrative graphs containing both scatter diagrams and comparative time series were presented in addition to the accuracy indicators and the most successful model was signified in this regard. Finally, the results obtained were assessed in terms of whether they produced statistically significant sc-PDSI values. The analysis steps followed in this research are represented in Figure 1.
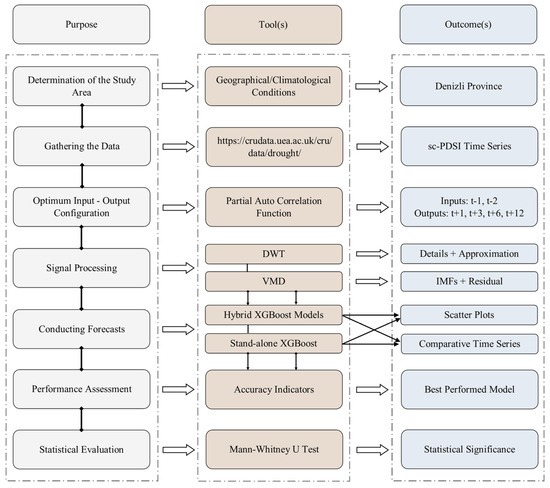
Figure 1.
Flow of the current research.
3. Materials
3.1. Study Area
The present research selected the province of Denizli, which is geographically located in the inner parts of the Aegean region and the southwest of the Anatolian peninsula (Figure 2). The city extends between 28°35′3.95” E–30°16′11.05” E and 38°27′44.88” W–36°52′2.79” W. The city covers 1.5% of the entirety of Turkey with a surface area of 12,134 km2. The maximum elevation of Denizli is 2532 m at Mount Honaz, which is also the highest mountain in the Aegean region. Along with the high mountains, the city is surrounded by plains and plateaus. Denizli, being the 23rd most populated city in Turkey, hosts more than 1 million residents [46].
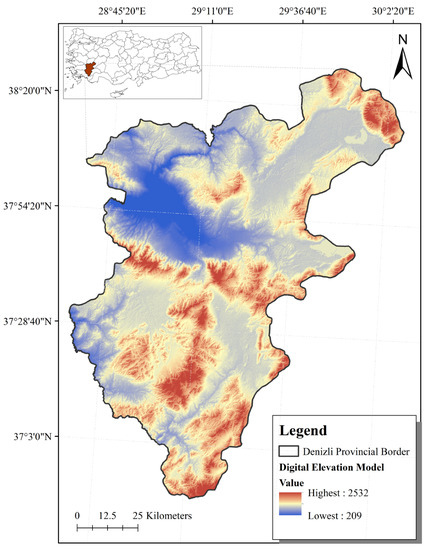
Figure 2.
Study area (Denizli Province).
The mean annual temperature in Denizli is 17.8 °C, with the lowest and highest mean temperatures of 10.5 °C and 34.4 °C in January and in August, respectively [47]. The average annual rainfall in Denizli is 566.1 mm while the highest and lowest precipitations are observed in December and August with 90.3 mm and 8.1 mm, respectively. The average annual humidity rates are below 50% in June, July, and August across the city and they increase in other months, reaching up to 70% in December and January [47].
3.2. Self-Calibrated Palmer Drought Severity Index (sc-PDSI)
The Palmer Drought Severity Index (PDSI) [48] is one of the most commonly utilized meteorological drought indices in the pertinent literature. Different from other meteorological drought indices (such as SPI, SPEI, etc.), the PDSI takes soil-water content into account along with the core meteorological variables, i.e., precipitation and temperature. Hence, the PDSI is mostly concentrated on the soil-water balance in a region of interest. A typical PDSI calculation rationale follows a set of steps, including the determination of humidity anomalies, computation of the amount of rainfall through the exclusion of different hydrological variables (i.e., potential evapotranspiration, potential recharge, potential runoff, and potential loss), and identification of moisture anomaly index reflecting the wetness and dryness conditions of a period.
In general, a monthly resolution is used for the computation of PDSI values, and as a cumulative index, a current PDSI value () is grounded on the previous values () representing the trend of climatic conditions. Hence, duration factors denoted by and are used as the weighting coefficients as expressed in Equation (1):
where is the moisture anomaly index. It is especially worth mentioning that the duration factors govern the sensitivity of the PDSI to sudden abrupt changes in precipitation and humidity. As a result, the monthly PDSI values dividing the wet and dry conditions are classified as presented in Table 1, in which the corresponding classification is also valid for the self-calibrated PDSI (sc-PDSI).

Table 1.
Classification of the PDSI and sc-PDSI.
Concerning the criticism of the originally developed PDSI due to the fact that it was calibrated based only on nine locations mainly located in the mid-west of the United States [49], the sc-PDSI was adopted by Wells et al. [50]. The sc-PDSI offers more consistent and justifiable results as it represents the conditions of any climate and location more realistically than the PDSI. The reason behind this fact is that it considers different duration factors which are identified by the least square method for wet and dry periods. Thus, one can conclude that the sc-PDSI has more certain statistical properties in a way that extreme droughts occur 2%, and extreme wet spells 2%, of the time of the calibration period at any location [49]. Furthermore, concerning the calculation procedure, the sc-PDSI values vary with respect to the calibration period, which necessitates the consideration of several decades.
4. Methods
This study employed two different signal-processing techniques (i.e., discrete wavelet transform and variational mode decomposition) by hybridizing them with the state-of-the-art XGBoost ML algorithm and compared the performance of each model based on several performance evaluation indicators. Therefore, this section includes a brief explanation of corresponding algorithms and the utilized performance metrics. Briefly, Section 4.1 introduces the details regarding the adopted signal-processing algorithms, Section 4.2 describes the XGBoost algorithm, and the explanations of the utilized metrics are presented in Section 4.3.
4.1. Signal-Processing Algorithms
4.1.1. Discrete Wavelet Transform
The wavelet transform was proposed as a rewarding alternative to the well-known Fourier transform by Grossmann and Morlet [51]. In this regard, wavelet transform is able to process non-stationary data with time-varying frequency in a more flexible manner [52,53]. The frequency variations leading to the non-stationary behavior are handled by extracting frequency components in a way that transforms the time-domain signals into both time-domain and frequency-domain signals [54]. The wavelet further ensures detection of the high- and low-frequency signals through its time-localized feature [55]. Unlike the Fourier transform having the potential of losing the basic ingredients of time series (e.g., trend, seasonality, cycling, etc.), the wavelet transform commits enhanced prediction power when it is hybridized with the ML algorithms as all local and regional characteristics of a time series are preserved [56].
One of the most important features of wavelet transform comes from its decomposition ability in various resolutions. Equation (2) explains the wavelets, which are produced by the scaled and shifted versions of the basis functions [57]:
where represents the wavelets. The selection of the mother wavelet is critical in wavelet transform. There are many mother wavelets in a set of wavelet families, such as Daubechies, Coiflet, Symlet, Morlet, Mexican hat, Meyer, and Haar wavelets [58]. In the selection of a suitable mother wavelet, the similarity between the signal and the mother wavelet is searched for. Hence, if the correlation between the waveform of the signal and the shape of any wavelet is high, then that particular wavelet can be used as a mother wavelet for the original signal.
The wavelet transform has two different types, i.e., continuous wavelet transform (CWT) and discrete wavelet transform (DWT). It is worth mentioning that the existing research recognizes the critical role played by the DWT in water-related (e.g., meteorological, hydrological, etc.) time series due to the discrete feature of the corresponding time series [59]. In addition, the DWT is more efficient compared to the CWT since it limits the production of excessively redundant data which is a consequence of computing all wavelet coefficients in any possible scale. DWT can be expressed in Equation (3) [60]:
where and are the dilation and time factors, respectively. is the real numbers domain, and and are integers. The dyadic grid arrangement illustrated in Equation (4) () is applied since it enables the most efficient case for practical purposes.
With , the characteristics of the original time series in the frequency domain and time domain are reflected simultaneously.
4.1.2. Variational Mode Decomposition
The variational mode decomposition (VMD) is one of the efficient signal-processing algorithms in processing non-linear and non-stationary signals. Dragomiretskiy and Zosso [61] fostered the VMD algorithm which, unlike other decomposition techniques, can prevent iterative computation by creating a cyclic scanning operation at different frequencies making the algorithm robust against noise in time series [62]. Hence, non-linear trends and harmonic patterns are removed from the complex time series through its non-recursive procedure [63]. The VMD is based on extracting k number of Intrinsic Mode Functions (IMFs), having a specific center frequency and bandwidth from the original signal. Each IMF represents a sub-signal comprising different amplitudes and frequencies as expressed in Equation (5):
where denotes the IMFs attained as a result of the decomposition, while is the frequency center of each sub-signal. Also, (*) and are the convolutional operator and Dirac distribution, respectively. denotes the partial derivative with respect to time and represents the imaginary unit.
In order to transform the above-presented constraint problem into the unconstrained variational problem, two different operators, i.e., representing the Lagrange multipliers and representing the quadratic penalty factors, are used as indicated in Equation (6):
Here, with regard to the alternative direction method of multipliers, the VMD iteratively updates and using Equations (7) and (8):
in which n denotes the number of iterations and () represent the Fourier transform of the corresponding variables. It is worth mentioning that the iterative process is terminated (Equation (9)) once the tolerance () is satisfied:
For more details regarding the VMD, one can follow the study of Dragomiretskiy and Zosso [61].
4.2. Machine Learning Algorithm
This study utilized the eXtreme Gradient Boosting (shortly XGBoost) algorithm which was pioneered by Chen and Guestrin [64]. This flexible and powerful algorithm [65], similar to several tree-based approaches (such as random forest, extremely randomized trees, etc.), utilizes the Classical and Regression Trees (CART) to generate base classifiers. However, different from its counterparts, decision trees are trained sequentially in the XGBoost algorithm by means of the previously separated and introduced training set, whereby newly generated decision trees are adjoined iteratively to the weak learners to enhance the predictive success of the algorithm in accordance with the objective function [66]. It is especially worth mentioning that the objective function comprises two different terms, i.e., the loss function () and regularization term (), in which the accuracy and the complexity of the configured model are controlled with the former and the latter, respectively. The loss function is expressed in Equation (10):
in which denotes the value of the loss function at iteration . In addition, and represent the actual and predicted class labels of sample , respectively. is the decision tree function, whereas is the number of instances in the training set. Also, the regularization term is defined in Equation (11):
Here, and are the regularization weights. and represent the number of trees in the final node and the weights of the leaves in the trees, respectively. To approximate the loss function, 2nd order Taylor expansion is applied within the XGBoost operational procedures [67] as indicated by Equation (12).
where and represent the first- and second-order gradients of the loss function as introduced in Equations (13) and (14), respectively.
With the adoption of the Taylor expansion, the XGBoost algorithm provides significant advances in terms of computational efficiency, and due to its robust structure, more reliable results can be achieved [68].
In addition, the XGBoost was preferred in this research as it can efficiently deal with large datasets with its parallel processing and distributed computing feature [65]. Apart from the comparison between other neural-network-based and/or kernel-based approaches, compared to the other tree-based ensemble learning algorithms, XGBoost contains several additional advantages. For instance, although decision trees offer simple implementation, they may not be effective in solving complex and multi-dimensional non-linear problems [69]. Random Forest is an ensemble learning algorithm with significant advances such as robustness to outliers and resistance to overfitting phenomena once the predictions of multiple trees are aggregated. Still, concerning the large number of trees required to solve complex problems, the Random Forest algorithm results in computationally expensive outcomes [70]. Moreover, there are other ensemble learning methods embracing the gradient boosting rationale, such as gradient boosting and stochastic gradient boosting methods. Gradient boosting was initially introduced to accommodate various differentiable loss functions. Although Gradient Boosting Decision Trees (GBDT) exhibit greater robustness than other boosting models (e.g., Adaptive boosting, shortly Adaboost) in identifying outliers, their effective regularization of the iterative additive process constrains GBDT’s overall generalization [68]. This regularization is contingent on the model’s complexity. Consequently, the XGBoost algorithm was devised to enhance GBDT’s performance. In contrast to GBDT, XGBoost can potentially achieve superior accuracy through the utilization of diverse regularization techniques and by managing tree complexity [71]. By leveraging its advanced framework, which encompasses parallel tree boosting, XGBoost can effectively address both regression and classification challenges through the utilization of the boosted trees it constructs. Furthermore, another factor contributing to the superiority of the XGBoost lies in the objective function (comprising two major components, i.e., the loss function enhancing the predictive power and regularization terms controlling the overfitting phenomenon) employed during the learning process [72].
The XGBoost algorithm encompasses several hyper-parameters that need to be diligently determined to better mimic the nature of the interested problem. The existing literature recognized the critical role played by several hyper-parameter tuning processes including traditional search algorithms and state-of-the-art metaheuristics. However, the current research employed the traditional trial–error approach in order to limit the model complexity and reduce the computational burden. Also, concerning the fact that this study also incorporated the signal-processing techniques into the predictions resulting in individual prediction of each sub-signal, adopting an optimization technique for all predictions could not only be challenging but also less practical since each optimization scenario would yield different hyper-parameter sets. Overall, the definitions of the hyper-parameters of the XGBoost algorithm can be found in [73]. It is worth mentioning that, as a result of the trial–error approach, “booster” is selected as dart, “learning rate” is determined as 0.1, “number of estimators” is identified as 250, “maximum depth tree” is found as 11, and “subsampling columns by tree” is obtained as 0.9, whereas the remaining hyper-parameters are used as default. All the predictions made through the XGBoost algorithm contained the abovementioned parameter set in order to remain consistent and constitute a fair comparison datum line among the forecasting attempts.
4.3. Performance Evaluation Indicators
In the current research, the performance of the predictive models was assessed with respect to several statistical evaluation metrics, including the root mean square error (RMSE), performance index (PI), Nash–Sutcliffe Efficiency (NSE) index [74], Wilmott’s refined (WI) index [75], and the determination coefficient (R2). Here, the smaller the RMSE varying between 0 and ∞, the higher the accuracy of the model. In a similar vein, the PI can also take values between 0 and ∞, in which the computed PI values close to 0 illustrate the high predictive power of the constructed ML algorithms [76]. This study further considered the NSE as it is the most widely embraced performance evaluation indicator in hydrology-related studies [77,78,79]. The lowest value of the NSE can take -∞, while the maximum NSE can be 1. Here, Moriasi et al. [80] concluded that the values above 0.7 for the NSE indicate that the predictions have acceptable accuracy. Regarding the WI, −1 and 1 refer to the lowest possible and highest possible prediction success, respectively. In the current research, one of the commonly applied performance metrics in almost all study domains, R2, was also investigated to assess how well the adopted techniques simulate the prediction outcome. The lowest value R2 can take is 0 (indicating poor performance), while the maximum is 1 (indicating excellent performance). The equations for the calculation of the utilized performance evaluation indicators are presented in Table 2.

Table 2.
Calculation rationale of the performance evaluation indicators utilized in the current research.
5. Results
This study examined the fluctuations of sc-PDSI values for a hundred-year period between 1921 and 2021 in Denizli, Turkey as depicted in Figure 3. Aside from the temporal resolution, the utilized data is on a resolution of 0.5° longitude by 0.5° latitude. Regarding the descriptive statistics of the dataset utilized, the maximum and minimum values of sc-PDSI values are 5.14 and −5.50, respectively. This illustrates that the focalized region can reflect the characteristics of extreme wet and extreme drought conditions in different parts of the considered period. In addition, the average sc-PDSI value is found as −0.43 and the standard deviation of the sc-PDSI values is 1.95, while the skewness and the kurtosis of the hundred-year sc-PDSI dataset for Denizli are 0.06 and −0.23, respectively.
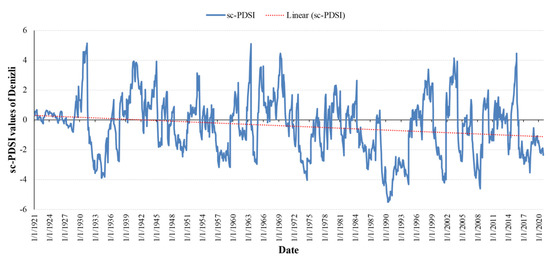
Figure 3.
Original sc−PDSI time series of Denizli.
The current research further hybridized the state-of-the-art XGBoost algorithm with two different signal decomposition techniques, namely, DTW and VMD, to forecast the sc-PDSI time series for four different horizons, i.e., 1-month, 3-month, 6-month, and 12-month lead times. The major aim of the present research is to exhibit the predictive power of the VMD-XGBoost framework, and the proposed prediction scheme was not only benchmarked with the standalone XGBoost implementation but also with the DWT-XGBoost model since the DWT has long been embraced as a commonly adopted and well-performing signal pre-processing technique by the literature. In order to identify the input–output combinations regarding the configuration of the prediction models, the original sc-PDSI time series was subjected to the PACF test and the input variables that can be used were determined (Figure 4). As can be seen from the figure, 1- and 2-month lagging of the time series is correlated with the original series. Hence, this study regarded “t − 1” and “t − 2” as the inputs for the prediction tasks. It is worth mentioning that determining the number of past observations through the corresponding lag orders helps significantly improve the model’s accuracy in capturing the time series patterns. It is therefore that one can conclude the more accurate the representation of temporal dependencies with relevant lags, the more accurate the forecasting attempts. Furthermore, the spectral bands of the original sc-PDSI time series were extracted by means of the DWT and VMD in order to enhance the drought forecasting ability of the XGBoost algorithm. In both models, a total of seven sub-bands were obtained to satisfy the fair comparison datum line, and for DWT and VMD, the approximation and residual were acquired as additional sub-bands, respectively (Figure 5). Figure 5a reveals that the DWT produced different sub-bands, each capturing different frequency ranges and details of the original signal. Accordingly, seven different sub-bands representing the high-frequency components or details of the signal at different levels of decomposition were attained. One can see from the figure that, from Band 1 (i.e., finest detail) to Band 7 (i.e., coarsest detail), the frequency content captured increases whereas the time resolution decreases. In addition, DWT represented the low-frequency components of the signal at the coarsest level of the decomposition process by the Approximation band. Hence, this band also ensures the performing of a multi-resolution analysis of the signal, facilitating a deeper understanding of its frequency content and structure as it captures the overall trends and relatively slower variations in the original time series. Furthermore, Figure 5b contains a set of sub-signals generated by the VMD technique. It is worth mentioning that, in the VMD application, sub-bands/sub-signals are also referred to as “modes”. The modes with distinct frequency components pertaining to the different spectrums and the residual band containing the components that are not captured by the extracted modes are provided in the figure. Similar to the DWT technique, the VMD produced divergent sub-bands each capturing different levels of frequency components (i.e., from Band 1 to Band 7). Each mode provides a unique view of the signal’s frequency content, allowing for a detailed analysis of the signal across various frequency bands. On the other hand, the residual band encompasses noise, artifacts, or any high-frequency components that might be disregarded by the extracted sub-signal, called modes.
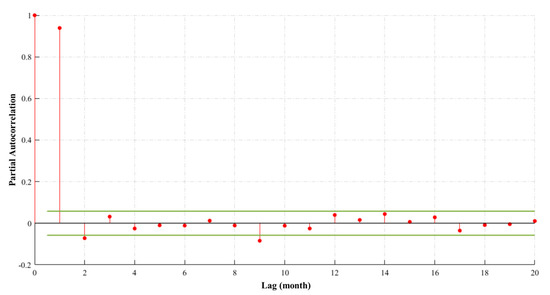
Figure 4.
Partial autocorrelation function of the original sc−PDSI time series.
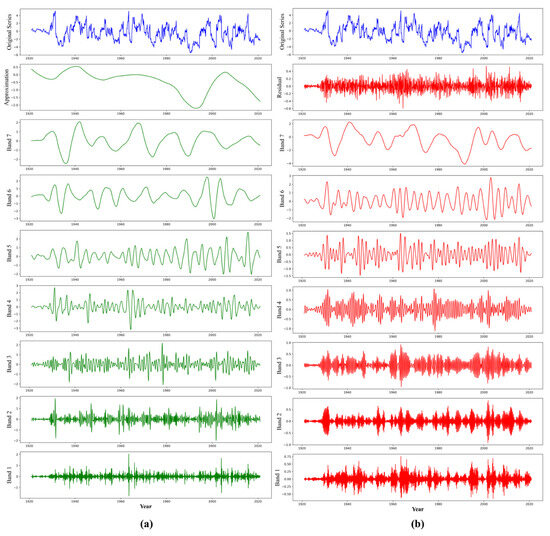
Figure 5.
Spectral bands produced with (a) DWT and (b) VMD.
The accuracies of the proposed prediction scheme and the benchmarking models were comprehensively evaluated based on several performance indicators, such as RMSE, PI, NSE, WI, and R2. Table 3 illustrates the results attained through the standalone XGBoost as well as hybrid VMD-XGBoost and DWT-XGBoost models for different horizons with respect to the testing set. The results are quite revealing of the fact that the standalone XGBoost model performed well (NSE: 0.8688) in the short-term drought forecast (i.e., “t + 1”) even without subjecting the sc-PDSI dataset to any decomposition method, whereas the performance of the corresponding model significantly decreased as for the mid-term and long-term forecasts, such that the standalone XGBoost model yielded an NSE of 0.6394 which is lower than the acceptable model efficiency threshold (i.e., NSE > 0.7) proposed by Moriasi et al. [80] for 3-month lead times. In addition, for 6-month and 12-month lead times, NSE values of 0.3572 and −0.0330 were achieved, respectively. Likewise, the RMSE values increased and the values of PI, WI, and R2 decreased, which also shows that the standalone model efficiencies were not satisfactory for extended lead times (Table 3). The table further demonstrates that, once the VMD was incorporated into the pre-processing stage to explore the spectral bands of the original sc-PDSI dataset, the predictive power of the model significantly increased. Associatively, the hybrid VMD-XGBoost model acquired an NSE of 0.9778 and an R2 of 0.9786 for short-term forecasts. Concerning the mid-term forecasts (i.e., 3-month and 6-month lead times), a considerable enhancement was achieved compared to the standalone model’s forecasts with an NSE of 0.9405 and an R2 of 0.9421 and an NSE of 0.8476 and an R2 of 0.8503 for “t + 3” and “t + 6”, respectively. In a similar vein, in the long-term forecast conducted to approximate the 12-months-ahead sc-PDSI values, the VMD-XGBoost model yielded an NSE of 0.6681 and an R2 of 0.6704 which underlines the superiority of the proposed hybrid model over the standalone prediction scheme.

Table 3.
Model performances with regard to the performance indicators concerning the testing set.
The performance of the adopted VMD-XGBoost predictive framework was also benchmarked by hybridizing the XGBoost model with a widely applied DWT signal-processing technique. The performance assessments regarding the DWT-XGBoost showed that, although the accuracies for each lead time have been remarkably augmented compared to the standalone XGBoost model, the DWT-XGBoost was still not able to outperform the proposed hybrid VMD-XGBoost prediction rationale. Accordingly, one can focalize on the NSE values computed (0.9778 for “t + 1”, 0.8457 for “t + 3”, 0.7345 for “t + 6”, and 0.5785 for “t + 12”) through the DWT-XGBoost and other performance indicators, revealing the superiority of the VMD-XGBoost (Table 3). What is important regarding the results is that the two hybrid models provided satisfactory modeling success for short-term drought forecasts based on all performance indicators. On the other hand, the outcomes of the current research illustrated the fact that utilizing the VMD-XGBoost model provides the most promising drought modeling performance for the remaining lead times.
In addition, the scatter plots and time series achieved with respect to the testing set are presented in Figure 6, Figure 7 and Figure 8 according to the adopted standalone, VMD-XGBoost, and DWT-XGBoost models, respectively. The scatter plots extracted as a result of the standalone XGBoost and the corresponding comparative time series reveal that the short-term forecasting results are well-scattered against the observed sc-PDSI series. On the other hand, for the mid-term and long-term predictions, the standalone XGBoost was not only incapable of catching the extreme drought events but also overestimated the dry periods and underestimated the wet periods (Figure 6). Regardless of this, the fluctuation patterns were barely recognized with the standalone XGBoost, leading to the attainment of considerably low R2 values for 6-month and 12-month lead times with 0.3692 and 0.0617, respectively.
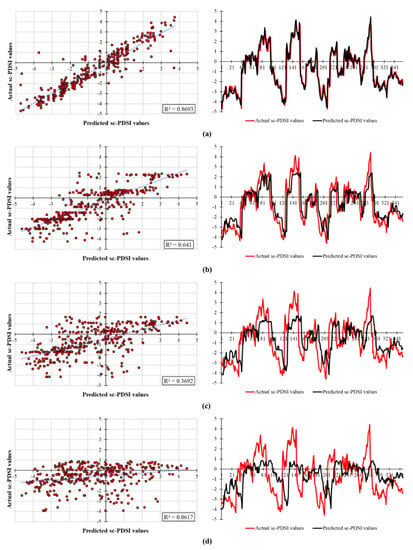
Figure 6.
Standalone model results with regard to the testing set (a) t + 1 (b) t + 3 (c) t + 6 (d) t + 12.
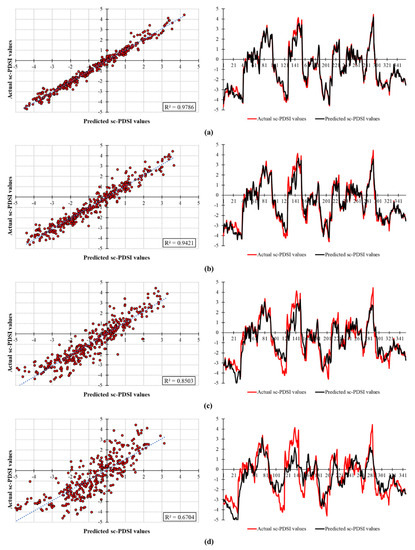
Figure 7.
VMD−based model results with regard to the testing set (a) t + 1 (b) t + 3 (c) t + 6 (d) t + 12.
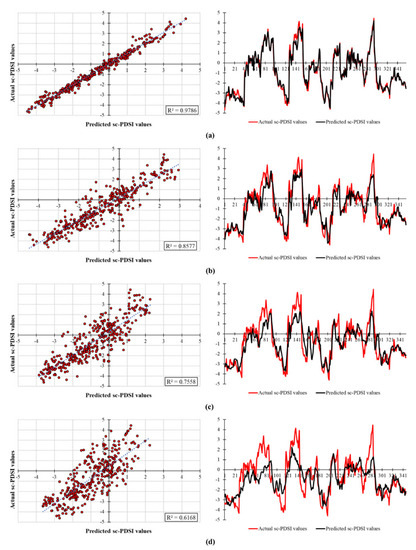
Figure 8.
DWT−based model results with regard to the testing set (a) t + 1 (b) t + 3 (c) t + 6 (d) t + 12.
Concerning the scatter plots and actual/predicted sc-PDSI time series generated by the testing results of the hybrid VMD-XGBoost, one can conclude that the corresponding model forecasted drought events for 1-month and 3-month lead times accurately. When it comes to 6-month forecasts, the VMD-XGBoost clearly followed the pattern, while the proposed model missed only some of the dry and wet periods (Figure 7). Also, for the results obtained with respect to the 12-month lead time, despite the moderate events being well-represented, the VMD-XGBoost model underestimated or overestimated some extreme periods; this fact results in relatively lower R2 values (i.e., 0.6704). In a similar vein, the hybrid benchmarking model (namely, DWT-XGBoost) was capable of forecasting droughts in short-term and mid-term horizons, whereas the performance of the corresponding model was significantly reduced once the long-term forecasts were attempted. Hence, almost none of the extreme periods were able to be modeled with DWT-XGBoost, resulting in statistically disputed accuracies (Figure 8).
6. Discussion
6.1. Investigating the Statistical Significance of the Obtained Results
In the literature, there are many hypothesis-testing techniques that can mainly be divided into two groups: parametric and non-parametric tests. These tests are used for anatomizing the population structures from which the data are obtained in terms of the distribution where focalized sample groups come from. Recent attempts in the relevant literature also take the same concern into account for examining the statistical differences between the targeted and estimated outcomes [81]. For instance, Başakın et al. [79] employed several ML algorithms to forecast monthly wind speed time series, and after attaining the predictive results, they subjected the ML forecasts and measured wind speed series to the Kruskal–Wallis test to ensure that the models not only provide accurate predictions but are also statistically significant. In a similar vein, Özbayrak et al. [82] performed a statistical significance assessment using the Kruskal–Wallis test of the regression estimations and numerical model results, and as a result, they concluded that the null hypothesis was rejected in the corresponding test, meaning that the actual and predicted values had the same distribution. This study subjected the obtained results to additional tests in order to verify whether the configured models provide statistically significant outcomes. The pertinent literature widely employs the t-test to compare the means of two sample groups to determine whether there is a statistically significant difference between the obtained and predicted instances. However, the t-test is a parametric test that can be used only if the sample groups are normally distributed and their variances are homogeneous [83]. Table 4 presents the normal distribution results regarding the pre-defined testing set. The table illustrates that, according to Kolmogorov–Smirnov and Shapiro–Wilk normality tests, p values for the testing set were found as 0.000, resulting in the rejection of the null hypothesis (: data follows a normal distribution). Levene’s test, which is another pre-requisite of the t-test, was also performed to test the variance homogeneity among the sample groups (i.e., actual and predicted sc-PDSI series). Table 5 demonstrates that the null hypothesis (called homogeneity of variance) was rejected based on the p values attained by Levene’s test (p: 0.000 < 0.05).

Table 4.
Test of normality results.

Table 5.
Test of homogeneity of variances.
The existing literature recognizes the utility of the non-parametric tests (i.e., Mann–Whitney U test) once the means between sample groups cannot be statistically assessed by parametric tests [84]. Hence, the current research adopted the Mann–Whitney U test to evaluate the forecasting results in terms of statistical significance. In this respect, the test hypotheses were determined as and reflecting the non-existence and existence of statistically significant differences between the results of sample groups (i.e., actual and predicted sc-PDSI series), respectively. According to Table 6, which highlights the Mann–Whitney U test results, it can be seen that hypothesis was accepted for all of the employed models (i.e., standalone XGBoost, VMD-XGBoost, and DWT-XGBoost) with a 95% confidence interval. Therefore, there are no significant differences between the medians of actual and forecasted drought series in any of the adopted predictive models. Finally, considering the presented p values, the XGBoost model reinforced with the VMD algorithm outperformed its counterparts as being the model with the highest probability of accepting hypothesis for each lead time.

Table 6.
P-values of Mann–Whitney U test at 95% significance level.
6.2. Evaluating the Proposed Framework Compared to the Existing Literature
The existing body of knowledge regarding drought forecasting is mostly concentrated on index-based modeling attempts due to their practicality. Despite several indices having been proposed by researchers, this study focalized on the sc-PDSI forecasts, and thereby, Table 7 which is composed of the details of the recent studies serving similar purposes is presented in order to comprehensively evaluate the current research. According to the table, various researchers have modeled droughts based on both PDSI and sc-PDSI with respect to the monthly time series covering long-term periods, e.g., at least 32 years by Tufaner and Özbeyaz [42] and at most 214 years by Diodato et al. [41]. In addition, the vast majority of the attempts focused on using the previous records (i.e., lags) of the original PDSI/sc-PDSI series in order to perform forecasts, whereas some of the researchers configured their models based on climate variabilities [41] as well as hydro-meteorological [42] and meteorological [22] variables. Although some authors conducted forecasting with respect to short-term horizons, most attempts were devoted to additionally exploring mid-term and long-term projections,. Likewise, the current research aimed to investigate the short-, mid-, and long-term variability of the sc-PDSI series.
Furthermore, there is a growing body of literature that recognizes the crucial impact of signal-processing techniques to achieve enhanced accuracies in drought modeling. For example, different forms of wavelet transform, i.e., CWT [2], DWT [85], and EMD [2,86] algorithms, were frequently used in the pertinent literature. However, none of the studies considered the recently pioneered and efficient VMD technique in past attempts. Thus, this research compared the impact of the VMD technique with the widely adopted and robust DWT on the enhancements that can be acquired in the predictive outcomes. Therefore, the implementation of the VMD is shown as an initial attempt in the drought forecasting literature. Table 7 further highlights the employed ML algorithms in PDSI/sc-PDSI forecasting attempts. As can be seen from the table, a great deal of methods were used, including regression-based (LR and ARMA), neural-network-based (ANN and RBFNN), distance-based (kNN), and tree-based (M5) techniques. It is apparent from this table that only Özger et al. [2] incorporated the M5 model tree algorithm as a tree-based approach into drought predictions. Accordingly, this research aimed to use the state-of-the-art XGBoost algorithm for the first time to conduct sc-PDSI forecasts.
From other facets, limited studies have assessed their results in terms of statistical significance which should be diligently investigated. For instance, Özger et al. [2] and Başakın et al. [86] considered the Kolmogorov–Smirnov tests in a way that compares the observed and predicted time series in order to signify whether the attained predictions are statistically acceptable. This research underpinned the same purpose in discussing the key outcomes; however, we employed the Mann–Whitney U test due to the fact that the sc-PDSI series does not satisfy the normality test in accordance with the Kolmogorov–Smirnov or Shapiro–Wilk tests. Hence, this work also generates fresh insights regarding the efforts devoted to statistical significance assessments. Still, there is a crucial point that has neither been acknowledged in this study nor in any of the past research, except the study of Aghelpour et al. [22] who used the DA method (Table 7). Several theories on the origin of ML utilization showed that ML techniques contain several hyper-parameters that need to be carefully determined to help the adopted algorithm mimic the nature of the problem entirely [87]. To accomplish this aim, many optimization algorithms have been proposed in the relevant literature including for drought forecasting attempts, such as traditional grid search and random search [88] as well as meta-heuristic optimization techniques [89,90]. The corresponding point constitutes one of the limitations of the current research, and therefore, integrating the hyper-parameter tuning processes into the ML implementation would be a valuable research direction. Despite their computational burden, the utilization of recently fostered advanced meta-heuristics, especially, in conjunction with the XGBoost algorithm for sc-PDSI forecasting would not only enhance the robustness of the models but also augment the accuracy of the predictions. In addition, the existing attempts lack the implementation of advanced deep learning techniques in the PDSI/sc-PDSI forecasts (Table 7). This fact further highlights another possible future research direction, in which exploring the hybridization of deep learning algorithms (such as recurrent neural networks, convolutional neural networks, deep belief networks, etc.) with the VMD in follow-up attempts could make insightful contributions to the body of knowledge.

Table 7.
Benchmarking the current study with the existing literature.
Table 7.
Benchmarking the current study with the existing literature.
| I | II | III | IV | V | VI | VII | VIII | IX | X |
|---|---|---|---|---|---|---|---|---|---|
| Diodato et al. [41] | PDSI | 1801–2014 | PDO, ENSO | PDSI | N/A | N/A | ES | N/A | ES |
| Tufaner and Özbeyaz [42] | PDSI | 1980–2011 | Hydro-meteorological variables * | PDSI | N/A | N/A | LR, ANN, SVM, and DT | N/A | ANN |
| Özger et al. [2] | sc-PDSI | 1901–2016 | sc-PDSI (t − 2, t − 1, t) | sc-PDSI (t + 1, t + 3, t + 6) | EMD and CWT | N/A | ANFIS, SVM, M5 | Kolmogorov–Smirnov | WD-ANFIS |
| Aghelpour et al. [22] | PDSI | 1960–2018 | Temperature, precipitation | PDSI | N/A | DA | ARMA, RBFNN, SVM | N/A | SVM-DA |
| Başakın et al. [86] | sc-PDSI | 1901–2016 | sc-PDSI (t − 1, t) | sc-PDSI (t + 1, t + 3, t + 6) | EMD | N/A | ANFIS | Kolmogorov–Smirnov | EMD-ANFIS |
| This study | sc-PDSI | 1921–2020 | sc-PDSI (t − 2, t − 1) | sc-PDSI (t + 1, t + 3, t + 6, t + 12) | DWT & VMD | N/A | XGBoost | Mann–Whitney U | VMD-XGBoost |
Titles—I: Reference, II: Index, III: Focalized Period, IV: Inputs/lag times, V: Outputs/Lead-times, VI: Signal-processing technique(s), VII: Hyper-parameter optimization algorithm(s), VIII: Adopted ML method(s), IX: Statistical significance investigation rationale, X: Best-performing model. * refers to hydro-meteorological variables including average temperature, monthly average actual pressure, monthly average wind speed, monthly average relative humidity, monthly total rainfall, potential evapotranspiration, available water capacity, and runoff. Abbreviations for: IV—ENSO: El Niño Southern Oscillation, PDO: Pacific Decadal Oscillation, VI—CWT: Continuous Wavelet Transform, DWT: Discrete Wavelet Transform, EMD: Empirical Mode Decomposition, VMD: Variational Mode Decomposition, VII—DA: Dragonfly Optimization, VIII—ANFIS: Adaptive-Network-Based Fuzzy Inference System, ANN: Artificial Neural Network, ARMA: Autoregressive Moving Average, DT: Decision Trees, ES: Ensemble Simulation, FL: Fuzzy Logic, kNN: k Nearest Neighbor, LR: Linear Regression, M5: M5 Model Tree, RBFNN: Radial Basis Function Neural Network, SVM: Support Vector Machine, XGBoost: eXtreme Gradient Boosting.
6.3. Practical Implications of the Drought Forecasting for Denizli
Given the vital impacts of climate change across the globe, recently, researchers accelerated their attempts regarding the projection of drought incidents in the pertinent literature. Hence, various paradigms covering the adoption of not only statistical approaches but also ML techniques have been offered for forecasting droughts. This research considered the application of ML models for forecasting the drought conditions of Denizli, Turkey. There are several reasons for choosing the corresponding region. For instance, the sustainability of the city is under heightened risk in terms of water resources, particularly since it is characterized by a semi-arid and Mediterranean climate. In addition, the findings of the current research offer significant advances in terms of agricultural activities, as the city plays a crucial role in agricultural production, especially in areas such as cotton, grapes, olives, and vegetable farming. Forecasting drought conditions for different horizons is also important for the city, as it encompasses a variety of habitats and exhibits a level of biodiversity due to its divergent landscape, such as fertile plains, rugged mountains, plateaus, and valleys, each supporting different types of habitats and species. Modeling future droughts is not only vital from an environmental facet but is also significant in terms of the economy. The city holds significant economic importance within the country with its several key sectors (e.g., agribusiness, textile, tourism, etc.) contributing to its overall economic activity and growth. Hence, understanding future drought conditions helps decision makers and policy makers to guide farmers to adopt drought-resistant crops and efficient irrigation methods and implement water management strategies to mitigate agricultural losses. In addition, as the textile industry heavily relies on the availability/accessibility of water, preparedness for water scarcity through drought analysis is essential for sustainable textile production. Similar strategies can also be considered for other water-dependent sectors, such as mining, manufacturing, etc. In a similar vein, since the city covers many thermal springs attracting tourists from all around the world, determining drought conditions of the city further ensures the sustainable utilization of such natural sources aiding the economic resilience of the city.
7. Conclusions
The primary purpose of the present study is to conduct drought forecasting for different horizons by means of hybrid ML techniques. To accomplish the overarching aim of this study, the sc-PDSI time series of Denizli, which is one of the cities characterized by a semi-arid climate in Turkey, was used. In addition, this research utilized the XGBoost algorithm to predict droughts for 1-month, 3-month, 6-month, and 12-month lead times. Through the partial autocorrelation function of the original time series, the 1-month and 2-month lags are determined as inputs in order to forecast the targeted horizons. It is especially worth mentioning that this study not only employed the standalone XGBoost algorithm but also incorporated the VMD technique subjecting the original dataset to pre-processing into the XGBoost algorithm to achieve more enhanced forecasting accuracies. Likewise, the hybrid VMD-XGBoost framework was benchmarked with the model formed by the integration of the XGBoost and the DWT algorithms. The reason for selecting the VMD is that this is the initial attempt in the literature regarding its implementation in drought forecasting, while the DWT was selected as a baseline algorithm due to its widespread adhibition.
The results attained clearly revealed the practicality of the XGBoost algorithm in drought time series modeling, in which this conclusion is of vital importance since this study utilized the XGBoost algorithm to forecast PDSI/sc-PDSI series for the first time. Still, although the standalone XGBoost model performed well in short-term drought forecasts, the accuracy declined from the 1-month lead time to those computed for the 12-month lead time. Furthermore, the hybrid VMD-XGBoost model outperformed its counterparts, i.e., standalone XGBoost and DWT-XGBoost, for all the attempted lead time forecasts. Along with the several performance evaluation metrics considered within the scope of the study, this research further examined the statistical significance of the attained predictive outcomes. Hence, actual and forecasted time series were subjected to the normality tests at first, and then the Mann–Whitney U test was implemented to the corresponding time series as the original data was not characterized by the normal distribution. Associate results also highlighted that the VMD-XGBoost predictive model is not only a practical and efficient tool to model drought series with high accuracies but also yields statistically significant time series.
Furthermore, the attempts made in this study offer a wide range of practical implications that can significantly enhance real-world applications. For instance, utilizing such techniques can conduce toward the adaption of early warning systems enabling timely preparedness and response actions. Also, integration of both in situ and remote-sensing-based measurements regarding hydro-environmental variables into ML applications can become widespread with such applications. Forecasting drought severities helps not only plan agricultural activities and resource allocation but also streamline actions regarding policy-making in the management of crop yield, water demand, land-use, and socio-economic developments.
Despite the efforts shown for comprehensively assessing the utility of the proposed hybrid model, this study still lacks some points in terms of both methodological and conceptual facets. Accordingly, the present research employed two different signal-processing techniques, namely, DWT and VMD, and compared the performance of them both in conjunction with the XGBoost algorithm. In future attempts, utilization of different decomposition techniques (e.g., EMD, seasonal algorithm, etc.) for dividing the original time series into sub-bands would be a promising research direction. In addition, as a predictive model, the present research adopted one ML algorithm, namely XGBoost. However, implementation of other advanced (such as deep learning techniques) algorithms to increase the accuracy of predictions can be fruitful for further studies. From another methodological aspect, a conventional trial–error approach was used to identify the hyper-parameters of the XGBoost algorithm, whereas incorporation of optimization techniques (such as meta-heuristics) into hyper-parameter tuning processes could yield promising outcomes to automate the entire predictive framework.
Concerning the conceptual aspect, there are still some issues allowing for the enhancement of such modeling attempts. For instance, this research concentrated on forecasting drought conditions of Denizli, Turkey, with regard to the sc-PDSI. In this sense, future studies may involve the prediction of other drought indices (such as SPI, SPEI, etc.) using the proposed model in order to increase the generalizability of the hybrid VMD-XGBoost. In addition, Denizli was selected as a focalized region within the scope of this study, while inspecting divergent domains having different climatic characteristics can also be considered to prove the global application of this work. On the one hand, this study performed the predictions up to 12 months, reflecting long-term drought conditions. On the other hand, future attempts can cover longer lead times (e.g., 24-, 36-, 48-month leads, etc.) to ensure several enhancements, including early preparedness, mitigation strategies, and sustainable water management. Overall, the current research is expected to contribute to the body of knowledge with both the illustration of yielding high accuracy and the transparent structure containing comprehensive statistical performance evaluation with respect to various indicators and statistical significance tests. The key outcomes of this study provide important considerations regarding the determination of future dry and wet drought periods in the semi-arid regions of Turkey, which, thus, allows decision makers and policy makers to allocate necessary resources to combat the corresponding jeopardous periods.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://crudata.uea.ac.uk/cru/data/drought/ (accessed on 4 April 2023).
Conflicts of Interest
The author declares no conflict of interest.
References
- Browder, G.; Sanchez, A.N.; Jongman, B.; Engle, N. An EPIC Response: Innovative Governance for Flood and Drought Risk Management. Rep. Exec. Summ. 2021, 23. [Google Scholar]
- Özger, M.; Başakın, E.E.; Ekmekcioğlu, Ö.; Hacısüleyman, V. Comparison of Wavelet and Empirical Mode Decomposition Hybrid Models in Drought Prediction. Comput. Electron. Agric. 2020, 179, 105851. [Google Scholar] [CrossRef]
- Harou, J.J.; Medellín-Azuara, J.; Zhu, T.; Tanaka, S.K.; Lund, J.R.; Stine, S.; Olivares, M.A.; Jenkins, M.W. Economic Consequences of Optimized Water Management for a Prolonged, Severe Drought in California. Water Resour. Res. 2010, 46, W05522. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Quiring, S.M.; Peña-Gallardo, M.; Yuan, S.; Domínguez-Castro, F. A Review of Environmental Droughts: Increased Risk under Global Warming? Earth-Sci. Rev. 2020, 201, 102953. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Svoboda, M.D.; Hayes, M.J. Understanding the Complex Impacts of Drought: A Key to Enhancing Drought Mitigation and Preparedness. Water Resour. Manag. 2007, 21, 763–774. [Google Scholar] [CrossRef]
- Mapedza, E.; McLeman, R. Drought Risks in Developing Regions: Challenges and Opportunities. In Current Directions in Water Scarcity Research; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–14. [Google Scholar]
- Zhang, X.; Chen, N.; Sheng, H.; Ip, C.; Yang, L.; Chen, Y.; Sang, Z.; Tadesse, T.; Lim, T.P.Y.; Rajabifard, A.; et al. Urban Drought Challenge to 2030 Sustainable Development Goals. Sci. Total Environ. 2019, 693, 133536. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, M.; Griggs, D.; Visbeck, M. Policy: Map the Interactions between Sustainable Development Goals. Nature 2016, 534, 320–322. [Google Scholar] [CrossRef]
- Belete, Y.; Shimelis, H.; Laing, M. Wheat Production in Drought-Prone Agro-Ecologies in Ethiopia: Diagnostic Assessment of Farmers’ Practices and Sustainable Coping Mechanisms and the Role of Improved Cultivars. Sustainability 2022, 14, 7579. [Google Scholar] [CrossRef]
- Bahrami, N.; Reza Nikoo, M.; Al-Rawas, G.; Al-Wardy, M.; Gandomi, A.H. Reservoir Optimal Operation with an Integrated Approach for Managing Floods and Droughts Using NSGA-III and Prospect Behavioral Theory. J. Hydrol. 2022, 610, 127961. [Google Scholar] [CrossRef]
- Kumar, P.; Debele, S.E.; Sahani, J.; Rawat, N.; Marti-Cardona, B.; Alfieri, S.M.; Basu, B.; Basu, A.S.; Bowyer, P.; Charizopoulos, N.; et al. Nature-Based Solutions Efficiency Evaluation against Natural Hazards: Modelling Methods, Advantages and Limitations. Sci. Total Environ. 2021, 784, 147058. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, M.; Fuchs, B. Handbook of Drought Indicators and Indices; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Başakın, E.E.; Ekmekcioğlu, Ö.; Stoy, P.C.; Özger, M. Estimation of Daily Reference Evapotranspiration by Hybrid Singular Spectrum Analysis-Based Stochastic Gradient Boosting. MethodsX 2023, 10, 102163. [Google Scholar] [CrossRef]
- Peng, F.; Wang, Y.; Xuan, H.; Nguyen, T.V.T. Efficient Road Traffic Anti-Collision Warning System Based on Fuzzy Nonlinear Programming. Int. J. Syst. Assur. Eng. Manag. 2022, 13, 456–461. [Google Scholar] [CrossRef]
- Koc, K. Role of National Conditions in Occupational Fatal Accidents in the Construction Industry Using Interpretable Machine Learning Approach. J. Manag. Eng. 2023, 39, 04023037. [Google Scholar] [CrossRef]
- Başakın, E.E.; Ekmekcioğlu, Ö.; Mohammadi, B. Letter to the Editor “Comparing Artificial Intelligence Techniques for Chlorophyll-a Prediction in US Lakes”. Environ. Sci. Pollut. Res. 2020, 27, 22131–22134. [Google Scholar] [CrossRef]
- Shahdad, M.; Saber, B. Drought Forecasting Using New Advanced Ensemble-Based Models of Reduced Error Pruning Tree. Acta Geophys. 2022, 70, 697–712. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B. Interpretable and Explainable AI (XAI) Model for Spatial Drought Prediction. Sci. Total Environ. 2021, 801, 149797. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Althobiani, F.; Kamruzzaman, M.; Shaid, S.; Roy, D.K.; Deb, L.; Islam, M.M.; Kundu, P.K.; Rahman, M.M. Estimating the Standardized Precipitation Evapotranspiration Index Using Data-Driven Techniques: A Regional Study of Bangladesh. Water 2022, 14, 1764. [Google Scholar] [CrossRef]
- Mokhtar, A.; Jalali, M.; He, H.; Al-Ansari, N.; Elbeltagi, A.; Alsafadi, K.; Abdo, H.G.; Sammen, S.S.; Gyasi-Agyei, Y.; Rodrigo-Comino, J. Estimation of SPEI Meteorological Drought Using Machine Learning Algorithms. IEEE Access 2021, 9, 65503–65523. [Google Scholar] [CrossRef]
- Aghelpour, P.; Mohammadi, B.; Mehdizadeh, S.; Bahrami-Pichaghchi, H.; Duan, Z. A Novel Hybrid Dragonfly Optimization Algorithm for Agricultural Drought Prediction. Stoch. Environ. Res. Risk Assess. 2021, 35, 2459–2477. [Google Scholar] [CrossRef]
- Anshuka, A.; Chandra, R.; Buzacott, A.J.V.; Sanderson, D.; van Ogtrop, F.F. Spatio Temporal Hydrological Extreme Forecasting Framework Using LSTM Deep Learning Model. Stoch. Environ. Res. Risk Assess. 2022, 36, 3467–3485. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B. Short-Term SPI Drought Forecasting in the Awash River Basin in Ethiopia Using Wavelet Transforms and Machine Learning Methods. Sustain. Water Resour. Manag. 2016, 2, 87–101. [Google Scholar] [CrossRef]
- Ali, M.; Deo, R.C.; Downs, N.J.; Maraseni, T. Multi-Stage Committee Based Extreme Learning Machine Model Incorporating the Influence of Climate Parameters and Seasonality on Drought Forecasting. Comput. Electron. Agric. 2018, 152, 149–165. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Salih, S.Q.; Kim, S.; Kim, N.W.; Yaseen, Z.M.; Singh, V.P. Drought Index Prediction Using Advanced Fuzzy Logic Model: Regional Case Study over Kumaon in India. PLoS ONE 2020, 15, e0233280. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, Z.; Zhang, L. Improving Regional Wheat Drought Risk Assessment for Insurance Application by Integrating Scenario-Driven Crop Model, Machine Learning, and Satellite Data. Agric. Syst. 2021, 191, 103141. [Google Scholar] [CrossRef]
- Lotfirad, M.; Esmaeili-Gisavandani, H.; Adib, A. Drought Monitoring and Prediction Using SPI, SPEI, and Random Forest Model in Various Climates of Iran. J. Water Clim. Chang. 2022, 13, 383–406. [Google Scholar] [CrossRef]
- Danandeh Mehr, A. Drought Classification Using Gradient Boosting Decision Tree. Acta Geophys. 2021, 69, 909–918. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ali, M.; Sharafati, A.; Al-Ansari, N.; Shahid, S. Forecasting Standardized Precipitation Index Using Data Intelligence Models: Regional Investigation of Bangladesh. Sci. Rep. 2021, 11, 3435. [Google Scholar] [CrossRef]
- Rose, M.A.J.; Chithra, N.R. Tree-Based Ensemble Model Prediction for Hydrological Drought in a Tropical River Basin of India. Int. J. Environ. Sci. Technol. 2022, 20, 4973–4990. [Google Scholar] [CrossRef]
- Citakoglu, H.; Coşkun, Ö. Comparison of Hybrid Machine Learning Methods for the Prediction of Short-Term Meteorological Droughts of Sakarya Meteorological Station in Turkey. Environ. Sci. Pollut. Res. 2022, 29, 75487–75511. [Google Scholar] [CrossRef]
- Gholizadeh, R.; Yılmaz, H.; Danandeh Mehr, A. Multitemporal Meteorological Drought Forecasting Using Bat-ELM. Acta Geophys. 2022, 70, 917–927. [Google Scholar] [CrossRef]
- Jamei, M.; Ahmadianfar, I.; Karbasi, M.; Malik, A.; Kisi, O.; Yaseen, Z.M. Development of Wavelet-Based Kalman Online Sequential Extreme Learning Machine Optimized with Boruta-Random Forest for Drought Index Forecasting. Eng. Appl. Artif. Intell. 2023, 117, 105545. [Google Scholar] [CrossRef]
- Raja, A.; Gopikrishnan, T. Drought Prediction and Validation for Desert Region Using Machine Learning Methods. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 47–53. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Ghasemi, P.; Karbasi, M.; Zamani Nouri, A.; Sarai Tabrizi, M.; Azamathulla, H.M. Application of Gaussian Process Regression to Forecast Multi-Step Ahead SPEI Drought Index. Alex. Eng. J. 2021, 60, 5375–5392. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Mirzaei, M. Improved Svr Machine Learning Models for Agricultural Drought Prediction at Downstream of Langat River Basin, Malaysia. J. Water Clim. Chang. 2020, 11, 1383–1398. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wu, X.; Xu, C.Y.; Guo, S.; Chen, X.; Zhang, Z. Robust Meteorological Drought Prediction Using Antecedent SST Fluctuations and Machine Learning. Water Resour. Res. 2021, 57, e2020WR029413. [Google Scholar] [CrossRef]
- Szép, I.J.; Mika, J.; Dunkel, Z. Palmer Drought Severity Index as Soil Moisture Indicator: Physical Interpretation, Statistical Behaviour and Relation to Global Climate. Phys. Chem. Earth Parts A/B/C 2005, 30, 231–243. [Google Scholar] [CrossRef]
- Diodato, N.; de Guenni, L.B.; Garcia, M.; Bellocchi, G. Decadal Oscillation in the Predictability of Palmer Drought Severity Index in California. Climate 2019, 7, 6. [Google Scholar] [CrossRef]
- Tufaner, F.; Özbeyaz, A. Estimation and Easy Calculation of the Palmer Drought Severity Index from the Meteorological Data by Using the Advanced Machine Learning Algorithms. Environ. Monit. Assess. 2020, 192, 576. [Google Scholar] [CrossRef]
- Self-Calibrating Palmer Drought Severity Index (ScPDSI). Available online: https://crudata.uea.ac.uk/cru/data/drought/ (accessed on 4 April 2023).
- Alsharif, M.; Younes, M.; Kim, J. Time Series ARIMA Model for Prediction of Daily and Monthly Average Global Solar Radiation: The Case Study of Seoul, South Korea. Symmetry 2019, 11, 240. [Google Scholar] [CrossRef]
- Khan, F.M.; Gupta, R. ARIMA and NAR Based Prediction Model for Time Series Analysis of COVID-19 Cases in India. J. Saf. Sci. Resil. 2020, 1, 12–18. [Google Scholar] [CrossRef]
- TUIK Geographic Statistics Portal. Available online: https://cip.tuik.gov.tr/# (accessed on 18 September 2021).
- MGM State Meteorological Service Statistics. Available online: https://www.mgm.gov.tr/eng/about.aspx (accessed on 18 September 2021).
- Palmer, W.C. Meteorological Drought; Research Paper No. 45; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965.
- Maule, C.F.; Thejll, P.; Christensen, J.H.; Svendsen, S.H.; Hannaford, J. Improved Confidence in Regional Climate Model Simulations of Precipitation Evaluated Using Drought Statistics from the ENSEMBLES Models. Clim. Dyn. 2013, 40, 155–173. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A Self-Calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Estévez, J.; Bellido-Jiménez, J.A.; Liu, X.; García-Marín, A.P. Monthly Precipitation Forecasts Using Wavelet Neural Networks Models in a Semiarid Environment. Water 2020, 12, 1909. [Google Scholar] [CrossRef]
- Wei, M.; You, X. yi Monthly Rainfall Forecasting by a Hybrid Neural Network of Discrete Wavelet Transformation and Deep Learning. Water Resour. Manag. 2022, 36, 4003–4018. [Google Scholar] [CrossRef]
- Saraiva, S.V.; de Carvalho, F.O.; Santos, C.A.G.; Barreto, L.C.; Freire, P.K. de M.M. Daily Streamflow Forecasting in Sobradinho Reservoir Using Machine Learning Models Coupled with Wavelet Transform and Bootstrapping. Appl. Soft Comput. 2021, 102, 107081. [Google Scholar] [CrossRef]
- Al-Qazzaz, N.K.; Mohd Ali, S.H.; Bin; Ahmad, S.A.; Islam, M.S.; Escudero, J. Selection of Mother Wavelet Functions for Multi-Channel EEG Signal Analysis during a Working Memory Task. Sensors 2015, 15, 29015–29035. [Google Scholar] [CrossRef]
- Koc, K.; Ekmekcioğlu, Ö.; Gurgun, A.P. Accident Prediction in Construction Using Hybrid Wavelet-Machine Learning. Autom. Constr. 2022, 133, 103987. [Google Scholar] [CrossRef]
- Merchant, F.A.; Castleman, K.R. Computer-Assisted Microscopy. In The Essential Guide to Image Processing; Elsevier: Amsterdam, The Netherlands, 2009; pp. 777–831. ISBN 9780123744579. [Google Scholar]
- Kambalimath, S.S.; Deka, P.C. Performance Enhancement of SVM Model Using Discrete Wavelet Transform for Daily Streamflow Forecasting. Environ. Earth Sci. 2021, 80, 101. [Google Scholar] [CrossRef]
- Kadkhodazadeh, M.; Farzin, S. A Novel Hybrid Framework Based on the ANFIS, Discrete Wavelet Transform, and Optimization Algorithm for the Estimation of Water Quality Parameters. J. Water Clim. Chang. 2022, 13, 2940–2961. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Melville, B.W. Comparative Study of Different Wavelet Based Neural Network Models for Rainfall-Runoff Modeling. J. Hydrol. 2014, 515, 47–58. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.H.; Yang, L.B.; Liu, X.M. Drought Prediction Based on an Improved VMD-OS-QR-ELM Model. PLoS ONE 2022, 17, e0262329. [Google Scholar] [CrossRef]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Ribeiro, G.T.; Mariani, V.C.; dos Coelho, L.S. Cooperative Ensemble Learning Model Improves Electric Short-Term Load Forecasting. Chaos Solitons Fractals 2023, 166, 112982. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-Based Method for Flash Flood Risk Assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Ekmekcioğlu, Ö.; Koc, K.; Özger, M.; Işık, Z. Exploring the Additional Value of Class Imbalance Distributions on Interpretable Flash Flood Susceptibility Prediction in the Black Warrior River Basin, Alabama, United States. J. Hydrol. 2022, 610, 127877. [Google Scholar] [CrossRef]
- Özger, M.; Serencam, U.; Ekmekcioğlu, Ö.; Başakın, E.E. Determining the Water Level Fluctuations of Lake Van through the Integrated Machine Learning Methods. Int. J. Glob. Warm. 2022, 27, 123. [Google Scholar] [CrossRef]
- Koc, K.; Ekmekcioğlu, Ö.; Gurgun, A.P. Integrating Feature Engineering, Genetic Algorithm and Tree-Based Machine Learning Methods to Predict the Post-Accident Disability Status of Construction Workers. Autom. Constr. 2021, 131, 103896. [Google Scholar] [CrossRef]
- Humbird, K.D.; Peterson, J.L.; Mcclarren, R.G. Deep Neural Network Initialization With Decision Trees. IEEE Trans. Neural Networks Learn. Syst. 2019, 30, 1286–1295. [Google Scholar] [CrossRef] [PubMed]
- Probst, P.; Wright, M.N.; Boulesteix, A. Hyperparameters and Tuning Strategies for Random Forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Lv, F.; Wang, J.; Cui, B.; Yu, J.; Sun, J.; Zhang, J. An Improved Extreme Gradient Boosting Approach to Vehicle Speed Prediction for Construction Simulation of Earthwork. Autom. Constr. 2020, 119, 103351. [Google Scholar] [CrossRef]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost Algorithm-Based Prediction of Concrete Electrical Resistivity for Structural Health Monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- XGBoost Parameters. Available online: https://xgboost.readthedocs.io/en/stable/parameter.html (accessed on 28 August 2023).
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models. Part 1: A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A Refined Index of Model Performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Assessment of Artificial Neural Network and Genetic Programming as Predictive Tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least Square Support Vector Machine and Multivariate Adaptive Regression Splines for Streamflow Prediction in Mountainous Basin Using Hydro-Meteorological Data as Inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Umar, I.K.; Nourani, V.; Gökçekuş, H. A Novel Multi-Model Data-Driven Ensemble Approach for the Prediction of Particulate Matter Concentration. Environ. Sci. Pollut. Res. 2021, 28, 49663–49677. [Google Scholar] [CrossRef]
- Başakın, E.E.; Ekmekcioğlu, Ö.; Çıtakoğlu, H.; Özger, M. A New Insight to the Wind Speed Forecasting: Robust Multi-Stage Ensemble Soft Computing Approach Based on Pre-Processing Uncertainty Assessment. Neural Comput. Appl. 2022, 34, 783–812. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Bayram, S.; Çıtakoğlu, H. Modeling Monthly Reference Evapotranspiration Process in Turkey: Application of Machine Learning Methods. Environ. Monit. Assess. 2023, 195, 67. [Google Scholar] [CrossRef]
- Özbayrak, A.; Ali, M.K.; Çıtakoğlu, H. Buckling Load Estimation Using Multiple Linear Regression Analysis and Multigene Genetic Programming Method in Cantilever Beams with Transverse Stiffeners. Arab. J. Sci. Eng. 2022, 48, 5347–5370. [Google Scholar] [CrossRef]
- Sullivan, L.M.; D’Agostino, R.B. Robustness of the t Test Applied to Data Distorted from Normality by Floor Effects. J. Dent. Res. 1992, 71, 1938–1943. [Google Scholar] [CrossRef]
- McKnight, P.E.; Najab, J. Mann-Whitney U Test. In The Corsini Encyclopedia of Psychology; Wiley: Hoboken, NY, USA, 2010; pp. 1–10. [Google Scholar]
- Achite, M.; Katipoğlu, O.M.; Jehanzaib, M.; Elshaboury, N.; Kartal, V.; Ali, S. Hydrological Drought Prediction Based on Hybrid Extreme Learning Machine: Wadi Mina Basin Case Study, Algeria. Atmosphere 2023, 14, 1447. [Google Scholar] [CrossRef]
- Başakın, E.E.; Ekmekcioğlu, Ö.; Özger, M. Drought Prediction Using Hybrid Soft-Computing Methods for Semi-Arid Region. Model. Earth Syst. Environ. 2021, 7, 2363–2371. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On Hyperparameter Optimization of Machine Learning Algorithms: Theory and Practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Alamri, A.M. Short-Term Spatio-Temporal Drought Forecasting Using Random Forests Model at New South Wales, Australia. Appl. Sci. 2020, 10, 4254. [Google Scholar] [CrossRef]
- Malik, A.; Tikhamarine, Y.; Souag-Gamane, D.; Rai, P.; Sammen, S.S.; Kisi, O. Support Vector Regression Integrated with Novel Meta-Heuristic Algorithms for Meteorological Drought Prediction. Meteorol. Atmos. Phys. 2021, 133, 891–909. [Google Scholar] [CrossRef]
- Kisi, O.; Docheshmeh Gorgij, A.; Zounemat-Kermani, M.; Mahdavi-Meymand, A.; Kim, S. Drought Forecasting Using Novel Heuristic Methods in a Semi-Arid Environment. J. Hydrol. 2019, 578, 124053. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).