Mapping Mean Velocity Field over Bed Forms Using Simplified Empirical-Moment Concept Approach

Abstract

The log-wake law was successful in mapping velocity fields for uniform flow over flat surfaces, even in cases of wake effects (velocity dips, wall effects, and secondary currents). However, natural riverbeds with undulations and bedforms challenge these models. This study introduces a moment-based empirical method for rough estimation of the velocity fields over stationary 2D bedforms. It proposes three polynomial velocity profile templates (first, fifth, and eighth orders) with coefficients deduced analytically while taking into account an array of flow conditions and assumptions, including slip velocity at the bed, mass and moment of momentum conservations, imposing inviscid potential flow near the water surface, and incorporation of near-bed shear stress utilizing a moment-based Chezy formula. Remarkably, the coefficients of these polynomials are primarily reliant on two crucial velocity scales, the depth-averaged velocity (u_o) and the moment-derived integral velocity (u₁), along with the dimensionless reattachment coefficient (K_r). Validation of the proposed approach comes from ten lab experiments, spanning Froude numbers from 0.1 to 0.32, offering empirical data to validate the obtained velocity profiles and to establish the relationship of the spatial variation in the normalized u₁ velocity along bedforms. This study reveals that the assumption of a slip boundary condition at the bed generally enhances the accuracy of predicted velocity profiles. The eighth-order polynomial profile excels within the eddy zone and close to reattachment points, while the fifth-order profile performs better downstream, approaching the crest. Importantly, the efficacy of this approach extends beyond water flow to encompass airflow scenarios, such as airflow over a negative step. The research findings highlight that linear velocity, as employed in Vertically Averaged and Moment models (VAM), exhibits approximately 70% less velocity mismatch compared to constant Vertically Averaged (VA) models. Moreover, the utilization of the fifth-order and eighth-order velocity profiles results in substantial improvements, reducing velocity mismatch by approximately 86% and 90%, respectively, in comparison to VA models. The insights gained from this study hold significant implications for advancing vertically averaged and moment-based models, enabling the generation of approximate yet more realistic velocity fields in scenarios involving flow over bedforms. These findings directly impact applications related to sediment transport and mixing phenomena.

1. Introduction

The velocity profile formulation for fully developed boundary layers in the context of uniform flow over flat surfaces has relied upon the logarithmic relation since 1938, commonly referred to as the law of the wall and the log law [1,2]. Subsequent refinements have introduced the wake function, resulting in the log-wake law, which provides a more accurate velocity profile. This improved profile accommodates existing phenomena such as velocity dip, accounts for wall effects, and incorporates secondary currents within water streams over flat surfaces [3,4,5].

Natural river systems, however, diverge from the ideal flat surfaces. Riverbeds are typically characterized by ripples and dunes, which introduce periodic complexities. Of these bed features, bedforms stand out as the primary sources of flow structure intricacies within alluvial channels. The flow pattern above bedforms exhibits considerable complexity. The substantial gradient on the leeward side of the bedforms prompts flow separation downstream of the crest, leading to the formation of an eddy region and a high-shear layer. This divergence from the logarithmic shape generates velocity profiles with pronounced deviations, particularly noticeable in the steep vertical gradient of the longitudinal velocity within the mixing zone.

Efforts have been dedicated to predicting velocity distributions over uneven boundaries. Notable early attempts in the hydrodynamic literature have approximated bedforms as sinusoidal profiles and considered inviscid flow scenarios. M. Thomson’s analytical solution for velocity variations over sinusoidal bed boundaries within the framework of stream and velocity potential functions is an illustrative example [6]. However, such approaches fall short when addressing the asymmetry of low-stage bedforms, especially in the presence of downstream separation zones.

In 1987, Nakagawa and Nezu [7] compared the longitudinal velocity profiles downstream of a negative step with a Gaussian distribution. They employed local maximum and minimum velocities, along with the minimum velocity’s vertical location and the half-width parameter (b50), as characteristic velocity and length scales. A tendency toward Gaussian distribution emerged as the flow approached the reattachment point downstream.

The separation zone extends approximately four times the height of bedforms, succeeded by an internal boundary layer [8,9]. Above it lies a wake-like region originating from the separation point and growing vertically as it moves downstream [10]. Above the wake region, there is an outer flow region where the potential flow assumption might hold [9,10,11].

Numerical research endeavors aimed at modeling the flow over 2D idealized bedforms with fixed boundaries have proliferated in the literature. These efforts categorically fall into simplified models (SM) and fully computational models (FCM). Simplified models generally adopt simplified assumptions and utilize turbulence closures for well-defined flow regions, which are coupled with suitable matching conditions and integral constraints. While computationally less intensive than FCM models, SM models offer insights into flow mechanics not easily attainable through other models [9]. Examples of SM models encompass the rotational-inviscid model [12], employing finite-element methods to solve the equation for inviscid rotational flow outside an assumed eddy, and the three-layer viscous flow model [11], accommodating boundary layer, internal viscous layer, and quasi-inviscid layer dynamics. Over the past decades, numerous FCM models have emerged involving solutions of Reynolds-averaged Navier–Stokes equations with relevant turbulence closure models like k, k–epsilon, or k–w [13,14,15]. Large eddy simulation-based approaches have also emerged, capturing more flow structure details over bedforms [16,17,18,19,20]. More recently, advances in computational resources have facilitated direct numerical simulations (DNS) of Navier–Stokes equations for studying sediment patterns with fully resolved flow fields [21,22].

Despite the data richness afforded by DNS simulations, their computational demands are substantial. One strategy to curtail the huge computational resource requirements involve the utilization of vertically averaged and moment models (VAM models), as will be described in the next sections.

This study aims to introduce a simplified approach for approximating mean velocity fields over stationary bedforms under fully developed turbulent low-regime flow conditions. The proposed approach hinges on the moment concept, employing polynomial velocity profiles as the velocity template for the flow field. The polynomial coefficients depend notably on two velocity scales—the depth-averaged velocity and moment-based integral velocity—alongside the dimensionless Chezy coefficient. The moment concept facilitates the recovery of vital velocity profile details overlooked by conventional depth-averaged models, all while avoiding the computational complexity of 2D vertical models [23,24,25,26,27,28].

The subsequent section provides a succinct introduction to the moment concept and outlines the new approach. The paper’s remaining structure is organized as follows. Section 2 delineates the methodologies, presenting the moment concept and detailing the selection of pertinent experiments from the existing literature. Section 3 addresses the identification of velocity and length scales, the results of dimensional analysis, and the conditions governing the selected velocity functions. Section 4 delves into the results, contrasting empirical velocity profiles with measured values from laboratory experiments in the literature. Section 5 presents this study’s findings, while Section 6 discusses its challenges, limitations, and prospects for the future.

2. Methodology

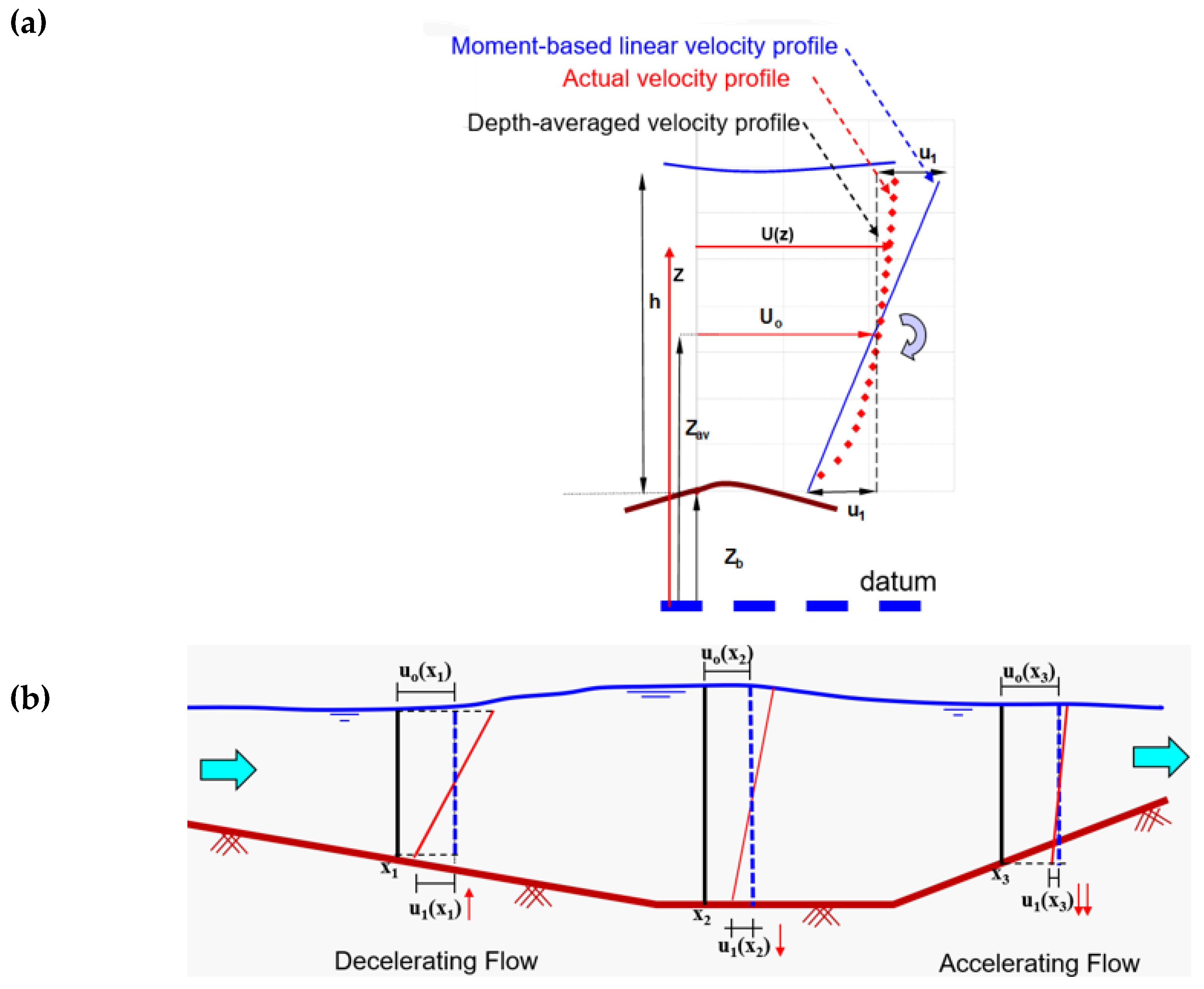
2.1. Moment of Momentum Concept

In situations involving flow separation in a vertical plane, conventional depth-averaged flow models exhibit limitations. An alternative approach, the moment of momentum concept, offers a potential solution to enhance the predictive capabilities of these models. By solving the moment of momentum equations in conjunction with the fundamental momentum and continuity equations, it becomes possible to achieve improved velocity predictions without elevating the computational complexity to the level of 2D vertical models. For a comprehensive understanding of this technique, interested readers can refer to the research by Steffler and Jin [23].

Adhering to this concept, a novel integral velocity scale denoted as u₁ can be determined by virtually transforming each velocity profile into an equivalent linear velocity profile that shares the same moment of momentum around the mid-water depth. Figure 1a illustrates the concept of the moment-based linear velocity profile, maintaining an equivalent moment of momentum as the actual velocity profile around the mid-depth.

Figure 1b presents a comparative analysis between conventional depth-averaged (vertically averaged) (VA) flow models and vertically averaged and moment models (VAM) in the context of simulating subcritical flow over variable bed topography featuring accelerating and decelerating zones. In the case of VA models, the velocity profile is described using a single velocity scale, namely, the depth-averaged velocity (u_o), which simplifies the representation of flow behavior. Conversely, VAM models employ two velocity scales, u_o and u₁, derived from the application of the moment concept.

In essence, the moment concept introduces an additional degree of freedom to the velocity distribution, replacing the constant velocity distribution assumed in VA models with a linear velocity distribution characterized by an additional velocity scale referred to as the new integral moment-based velocity scale (u₁). This augmentation of the velocity representation offers numerous advantages that enhance the capabilities of depth-averaged models. Notably, the average slope of the velocity profile can be computed using the u₁ scale as (2u₁/h), a feature that significantly improves the ability of VAM models to accurately address scenarios such as turbulence over bedforms and mixing, surpassing the performance of VA models.

Figure 1 elucidates the spatial variation in the "assumed linear velocity" based on the moment concept, depicting its behavior across both accelerating and decelerating flow conditions. In the case of decelerating flow, the velocity profile exhibits reduced uniformity, resulting in an increase in u₁ and a corresponding inclination in the linear velocity profile. Conversely, during accelerating flow, the velocity profile becomes more uniform, leading to a reduction in u₁.

Figure 2 depicts a prototypical spatial distribution of u₁ over one bedform wavelength. Notably, u₁ exhibits apparent continuity, with its value progressively rising downstream of the crest until it attains a peak value within the separation zone. Beyond this point, u₁ decreases downstream, reaching a minimum in proximity to or atop the crest. Figure 2 also contrasts the spatial distribution of u₁ as a function of distance x, with the corresponding value of u₁ for uniform flow over a flatbed (u_1log). The value of u₁ serves as an indicator of the degree of non-uniformity of the velocity profile shape.

An intriguing investigation lies in assessing the similarity of the spatial profile of u₁ for fully developed turbulent flow over bedforms. The subsequent sub-section details the experiments extracted from the literature that have been employed for this investigation.

2.2. Selected Lab Experiments from the Literature

The domain of flow mechanics over bedforms boasts a plethora of experiments where Laser Doppler Anemometry (LDA) has been employed to measure instantaneous velocity profiles over fixed dune and ripple configurations. These studies have reported longitudinal and vertical time-averaged velocities, along with turbulence intensities both parallel and normal to the flow direction.

Criteria of Selection

Within this study, a total of 10 experiments have been carefully chosen, encompassing ripples and dunes, as outlined in

Table 1. Summary of the geometric and flow parameters for laboratory experiments.

	T5 (1)	T6 (1)	Raudkivi (2)	Nezu (3)	RUN2 (4)	RUN3 (4)	RUN4 (4)	RUN5 (4)	RUN6 (4)	RUN7 (4)
h (m)	0.252	0.334	0.135	0.08	0.158	0.546	0.159	0.159	0.3	0.56
q (m2/s)	0.1	0.18	0.035	0.023	0.06	0.153	0.058	0.032	0.16	0.133
λ (m)	1.6	1.6	0.386	0.42	0.807	0.807	0.408	0.408	0.408	0.408
Δ (m)	0.08	0.08	0.0225	0.02	0.04	0.04	0.04	0.04	0.04	0.04
Rn	73,370	117,338	8000	16,429	44,408	69,127	42,857	23,645	96,000	59,257
ks (mm)	2.4	2.4	0.6	0.1	0.75	0.75	0.75	0.75	0.75	0.75
C*	17.02	17.53	15.34	19.15	18.33	19.99	18.32	17.99	19.51	19.92
u* (m/s)	0.0222	0.0284	0.0169	0.0150	0.0207	0.0140	0.0199	0.0112	0.0273	0.0119
λ/Δ	20	20	15.4	21	20.2	20.2	10.2	10.2	10.2	10.2
Δ/h	0.3	0.23	0.19	0.25	0.25	0.07	0.25	0.25	0.13	0.07
Fn	0.24	0.27	0.23	0.32	0.31	0.12	0.29	0.16	0.31	0.1
b (m)	1.5	1.5	0.08	0.4	0.9	0.9	0.9	0.9	0.9	0.9
Flume Length (m)	>53	>53	2.45	10	8	8	8	8	8	8
Velocity Device	LDA	LDA	Pitot Tube	LDA	LDA	LDA	LDA	LDA	LDA	LDA

⁽¹⁾: Van Mierlo et al. [29]. ⁽²⁾: Raudkivi [30,31]. ⁽³⁾: Nezu et al. [32]. ⁽⁴⁾: McLean et al. [33,34].

. The examined bedforms exhibit steepness ratios spanning from 1/10 to 1/20, crest height to water depth ratios ranging from 0.07 to 0.3, and Froude Numbers varying between 0.1 and 0.31.

Most of the lab experiments with good quality instruments for measuring water velocities (such as Laser Doppler Anemometry, LDA, or PIV) were conducted for the Froude number of 0.1 to 0.32. This chosen Froude number range, characterized by F_n² << 1 or F_n < 0.33, is typically associated with what is known as a “rigid lid” condition. This condition is imposed to mitigate surface wave perturbations, thereby facilitating precise measurements via laser techniques. By avoiding the challenges posed by specular reflections from surface wave-induced bubbles and droplets, researchers can attain more accurate and reliable data. Moreover, setting a minimum F_n value of 0.1 is particularly relevant as it ensures that the experimental scenarios involve rippled bed conditions rather than flatbed cases, adding a valuable dimension to the research context.

2.3. Main Assumptions

The following principal assumptions were considered in this study:

All experiments used for this study are over fixed bed boundaries;

Water is Newtonian, and the flow is fully developed shallow turbulent flow over a train of bedforms;

This study focuses on the low-regime flow applications, where F_n² << 1 (F_n < 1/3);

Bedforms are simplified as 1D ripples or dunes with constant bed width.

3. Analysis Using an Empirical Approach

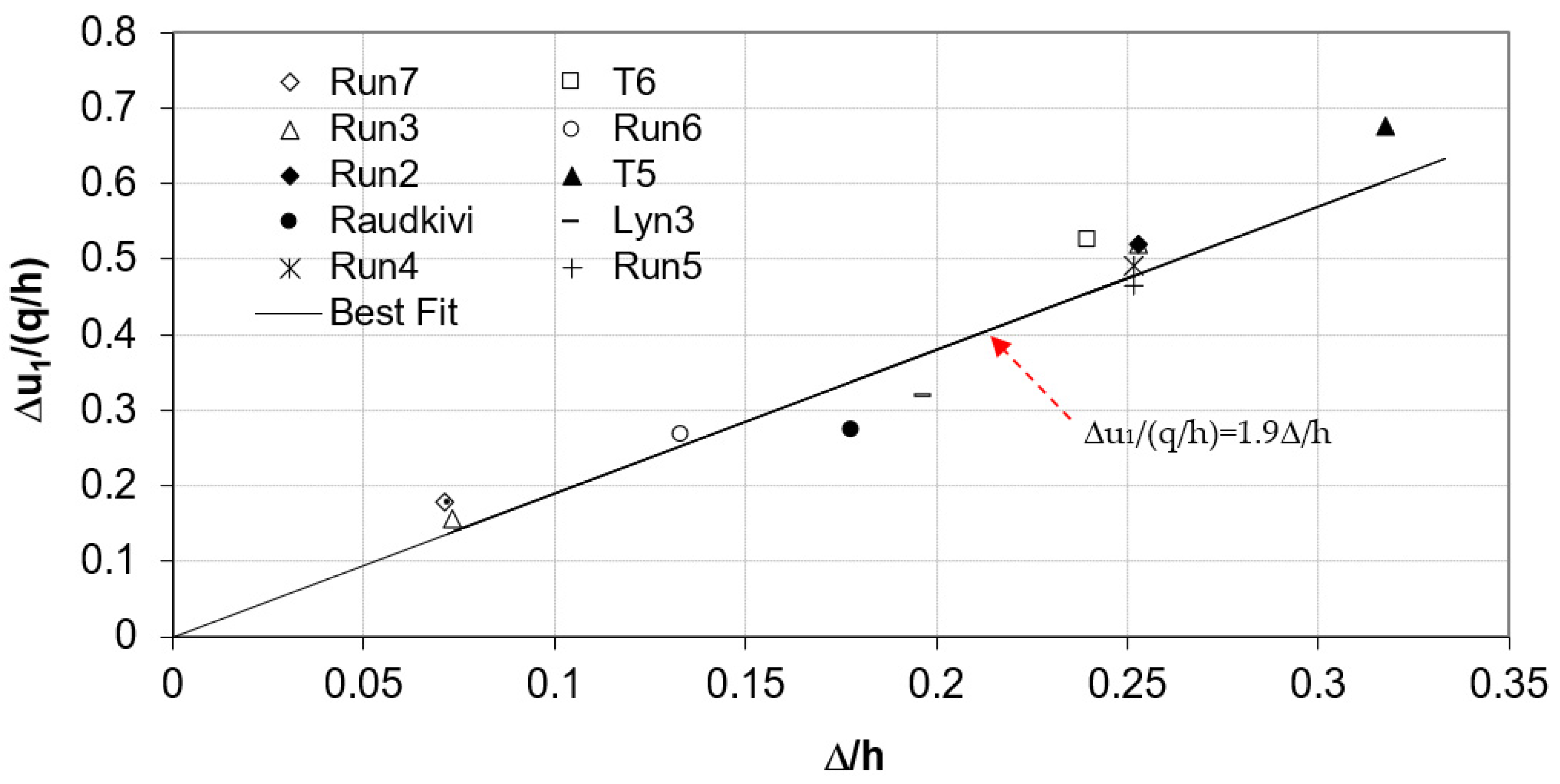
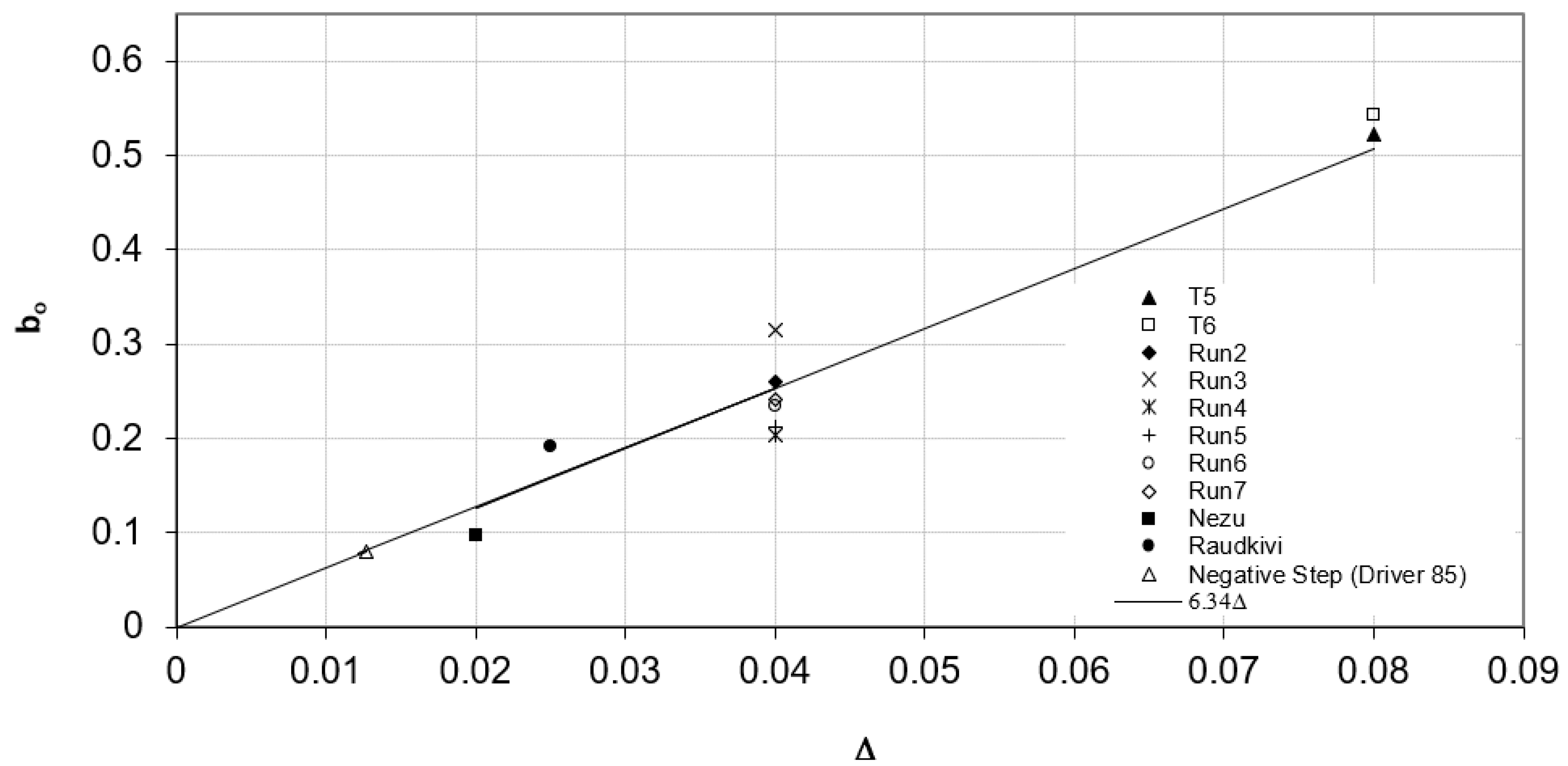
3.1. Selection of Velocity and Length Scales

The “bedform wavelength” encompasses several distinct definitions, as documented in the relevant literature. According to [35], bedform length can be delineated through four different definitions:

• Mean Bed Level Up Crossings: Defined as the distance between two consecutive crossings of the mean bed level when ascending;
• Mean Bed Level Down Crossings: Signifying the distance between two successive crossings of the mean bed level when descending;
• Crest-to-Crest: Describing the distance between two consecutive crests;
• Trough-to-Trough: Denoting the distance between two successive troughs.

In the context of our study, we have opted to adhere to the definition that characterizes bedform wavelength as the distance between two successive crests measured in the direction of the flow, as illustrated in Figure 2.

The selection of appropriate velocity and length scales plays a pivotal role in assessing the empirical approach.

Figure 3a illustrates the spatial distribution of u₁ across a single bedform wavelength for different experiments, with x coordinates normalized by the bedform wavelength. To explore the similarity of these distributions, the maximum net increase in integral velocity, denoted as Δu₁, was adopted as a velocity scale. To establish a length scale, bo, the x-coordinate corresponding to the point with a net increase in integral velocity equaling Δu₁/2, was selected, as shown in Figure 2. Normalized spatial distributions of u₁ profiles are depicted in Figure 3b.

Notably, these profiles exhibit similar trends and can be approximated by Equation (1).

$$u_1^{*}=\frac{\sqrt{x^{*}}}{c^2}{e}^{-\left(\frac{{x^{*}}^2}{2d^2}\right)}$$

(1)

where

$$u_1^{*}=\frac{u_1-u_{10}}{\Delta u_1}, x^{*}=x/b_o, \mathrm{c}=0.72, \mathrm{d}=0.64$$

(2)

Given the similarity in the spatial profiles of u₁, the subsequent step involves examining how velocity and length scales change with variations in flow and geometric parameters.

3.2. Dimensional Analysis

From a dimensional analysis point of view, the velocity scale, Δu₁, could be written as

Δu₁ = f₁[Δ, λ, h, q, C*, g, ν]

(3)

where Δ and λ are the bedform height and wavelength, respectively; h is the average water depth; q is the specific discharge per unit width [m²/s]; C* is the dimensionless Chezy coefficient based on the skin friction; g is the acceleration of gravity, and ν is the kinematic viscosity.

Since F_n² << 1 and we are interested in the low-stage bedforms only, the effect of water surface waves and, hence, the gravity effect can be neglected. Also, for large values of Reynolds number, viscous effects can be eliminated, and consequently, Equation (3) could be reduced to

$$\frac{\Delta u_1}{q/h}=f_2[\mathsf{\Delta }/\mathrm{h},\mathsf{\Delta }/\mathsf{\lambda },{\mathrm{C}}^{*}]$$

(4)

From the available experimental data, it was found that the steepness ratio, Δ/λ, has a minor effect, and thus, it was dropped from the relation. Also, the effect of the boundary roughness, which is represented in this relation via the dimensionless Chezy coefficient, is not large. Finally, Equation (4) was reduced to the following Equation (5) (Figure 4).

$$\frac{\Delta u_1}{q/h}\approx 1.9 [\mathsf{\Delta }/\mathrm{h}]$$

(5)

The previous relation shows that Δu₁ vanishes when the height of the bedform is reduced to zero, which is the case of the uniform flow over a flatbed. As the height of the bedform increases, a stronger shear layer zone exists downstream of the crest, causing large non-uniformity in the shape of the velocity profile, and, thus, Δu₁ increases.

The length scale, bo, is also found to be strongly dependent on the height of the bedform, Figure 5. The best-fit curve of the data seems to slightly under-predict bo for the experiments of long wavelengths such as T5, T6, and Run2, and it also over-predicts the length scale for the experiments of short wavelengths such as Run4 and Run5. Nevertheless, an average value of bo ≈ 6.34Δ could be assumed and was found to give reasonable results, as will be shown later on. After determining the length and the velocity scales, Equation (1) could be used to give the spatial distribution of u₁.

3.3. Velocity Functions and Flow/Boundary Conditions

3.3.1. Velocity Distribution Functions

To apply the empirical approach effectively, a suitable velocity distribution function is necessary. Initially, a linear velocity profile is assumed, as expressed in Equation (9). While it is anticipated that the linear profile may not accurately capture the behavior within the separation zone or near the point of reattachment, where the velocity profile is notably non-uniform, it represents an improvement over the traditional assumption of uniform velocity in depth-averaged models. As the downstream crest is approached, where the flow accelerates, the linear profile is expected to provide more accurate results.

For continuity and the moment of momentum conditions to be fulfilled while utilizing the linear profile, a slip velocity (u_o – u₁) must be accommodated at the bed, as indicated in Equation (6).

$$u\left(\eta \right)=u_o+u_1(2\eta -1)$$

(6)

where $\eta =\frac{z-z_b\left(x\right)}{h\left(x\right)}$, z_b(x) is the local elevation of the bed profile, and h(x) is the local water depth.

One way to achieve a better agreement is to change the template linear profile by using, for example, higher-order polynomials. A general form for the nth-order polynomial velocity profile can be written as

$$u(\eta )=u_o+\sum _{i=0}^{i=n}{a}_i{\eta }^i$$

(7)

where $a_i$ values are the (n + 1) coefficients of the n-polynomial.

3.3.2. Flow and Boundary Conditions

In order to use the higher-order polynomial distribution, more conditions and flow assumptions need to be set.

The first condition that should be specified is continuity, which could be given as

$${\int }_0^{1}u\left(\eta \right)d\eta ={\int }_0^1{(u}_o+\sum _{i=0}^{i=n}{a}_i{\eta }^i)d\eta {=u}_o$$

(8)

For the second condition, the integral moment of momentum of the velocity profile around its mid-depth is set equal to the corresponding value of the linear profile. This reduces to

$$\mathrm{h}{\int }_0^1(\eta -\frac{1}{2})u\left(\eta \right)d\eta =\mathrm{h}{\int }_0^1(\eta -\frac{1}{2}){(u}_o+{\sum }_{i=0}^{i=n}{a}_i{\eta }^i)d\eta = \mathrm{h}\frac{u_1}{6}$$

(9)

The application of a slip condition at the bed facilitates better agreement, particularly in comparison to the no-slip assumption, which poorly matches the near-bed velocity field, as shown in Figure 6.

Figure 6 presents a comparative analysis of the fifth-order polynomial velocity profiles under two distinct boundary conditions—one accounting for the no-slip condition at the bottom boundary and the other disregarding it. While the inclusion of the no-slip boundary condition aligns with physical principles, it mandates a zero-velocity profile at the bed. This condition indeed enhances the accuracy of estimating velocity profile gradients in the vicinity of the bed. However, it introduces challenges related to mass and moment of momentum conservation. Specifically, the no-slip condition causes the velocity distribution to exceed the measurements within the mid-depth zone while falling short near the surface. This discrepancy is essential to maintain the same trapped area under the velocity curve, ensuring mass conservation. Consequently, the velocity profile, when based on the no-slip condition, exhibits a misleading shear layer that does not exist.

In light of these considerations, it becomes evident that the fifth-order no-slip velocity profile yields higher average square errors or, in simpler terms, greater deviations from the measurements when compared to the fifth-order slip condition. Consequently, we have opted for the slip boundary condition in this study. Accordingly, a velocity gradient at the boundary, originally proposed by Engelund [35], is specified, allowing for a slip velocity. This approach implies that the actual boundary is conceptually elevated by a minute distance. Though this technique introduces a slip condition at the bed, close agreement with the very near-bed velocity field is not anticipated.

An approximation for the near-bed velocity gradient can be estimated at the boundary if the local bed shear stress is known. Elgamal [27] introduced a modified version of the Chezy resistance formula based on the moment concept to predict the spatial distribution of bed shear velocity over low-regime bedforms. This moment resistance formula is expressed as

$$u_{*}^2=\frac{U_o}{C_2^2}(U_o-K_{r }{u}_1)$$

(10)

where C₂ and K_r. are the revised Chezy dimensionless coefficient and point of reattachment coefficient, respectively. C₂ can be determined using Equation (11), which maintains the capability of the revised Chezy formula to be reduced to the original Chezy formula in the case of uniform flow.

$$C_2=C_{*}\sqrt{1-K_r \alpha }$$

(11)

The velocity gradient at the boundary can be approximated using Equation (10) and based on a simple eddy viscosity concept as

$${\left.\frac{\partial u}{\partial \eta }\right|}_{\eta =0}\approx q_{*}(U_o-K_r{u}_1)$$

(12)

$$q_{*}=\frac{C_{*}}{C_2^2{F}_{\nu t}}$$

(13)

where $F_{\nu t}$ is the eddy viscosity coefficient and is assumed to be constant for simplicity.

Another condition could be obtained by setting the velocity gradient at the surface to zero, which means zero shear stress at the surface. The same assumption has been adopted by previous researchers [37].

$${\left.\frac{\partial u}{\partial \eta }\right|}_{\eta =1}\approx 0$$

(14)

More conditions can be obtained by specifying the average variance or the higher-order statistics of the velocity relative to the mean values (for example: $\overline{{u^{\prime }}^2}$). Another condition can be obtained by specifying the moment of energy, $\overline{{u^{\prime }}^2 z^{\prime }}$, of the velocity profile. Unfortunately, using these higher-order relations leads to very lengthy and implicit polynomial coefficients. Therefore, they will not be presented in this work.

Additional conditions can be simply attained by specifying the higher-order velocity derivatives at the free surface. When the flow passes over bedforms, the outer layer seems to look like a potential flow region. This is what motivated [10] to assume a semi-inviscid-potential flow assumption within this region. A simpler but crude approximation could be used here via assuming a potential inviscid flow assumption in the outer layer near the water surface. This means that the outer flow velocity near the water surface does not vary vertically, and the air effects on the free surface are neglected. The outer potential flow assumption has been used before by different researchers [10,11]. The potential inviscid assumption near the water surface could be achieved by setting the higher velocity derivatives (at the water surface) to zeros. This crude assumption requires a relatively thick outer layer, which comes true when Δ/h << 1.

The application of the outer potential flow assumption near the water surface yields additional conditions:

$${\left.\frac{{\partial }^{i}U\left(\eta \right)}{\partial {\eta }^i}\right|}_{\eta =1}=0, i=2\to 3 \mathrm{for} \mathrm{the} \mathrm{fifth} \mathrm{polynomial}$$

(15)

$${\left.\frac{{\partial }^{i}U\left(\eta \right)}{\partial {\eta }^i}\right|}_{\eta =1}=0, i=2\to 6 \mathrm{for} \mathrm{the} \mathrm{eighth} \mathrm{polynomial}$$

(16)

In order to check the sensitivity of the results to the Δ/h ratio, various experiments with Δ/h ratios spanning from 0.07 to 0.3 were tested using linear, fifth-order, and eighth-order polynomial distributions. The analytical coefficients for the polynomial functions were symbolically derived using the Mathematica package, as detailed in Appendix A. Subsequent sections will encompass comparisons and discussions of these outcomes.

4. Results and Discussion

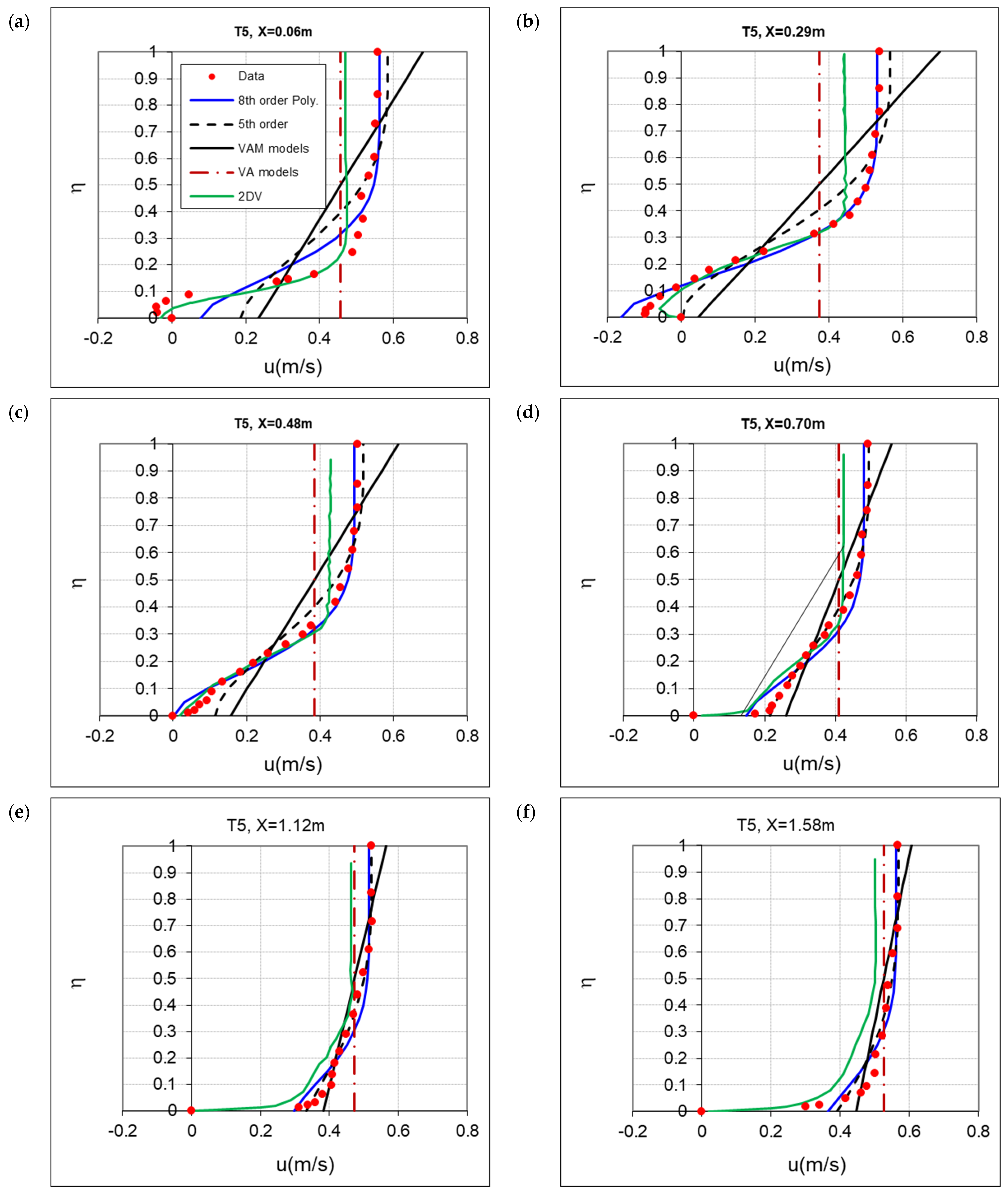
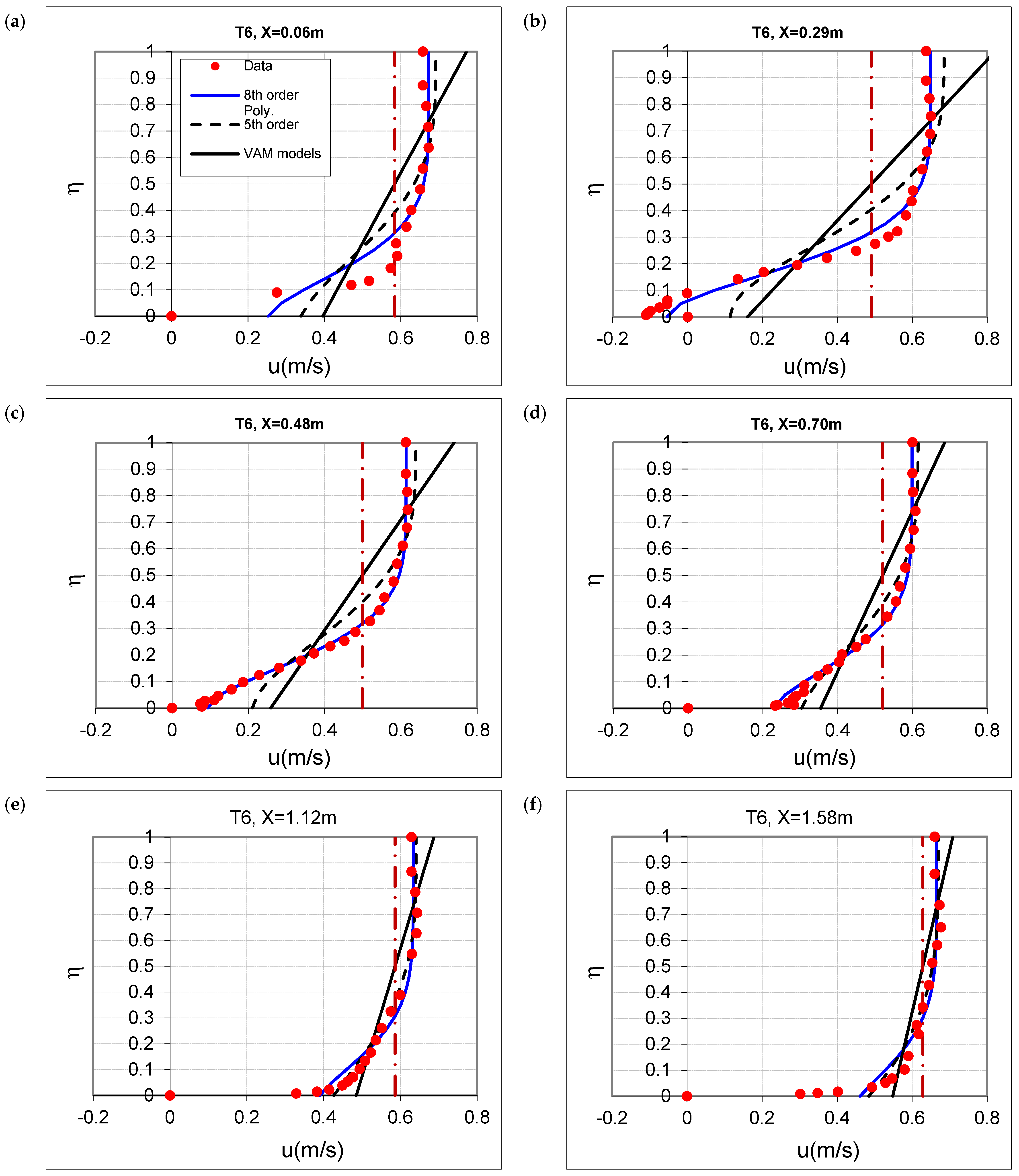
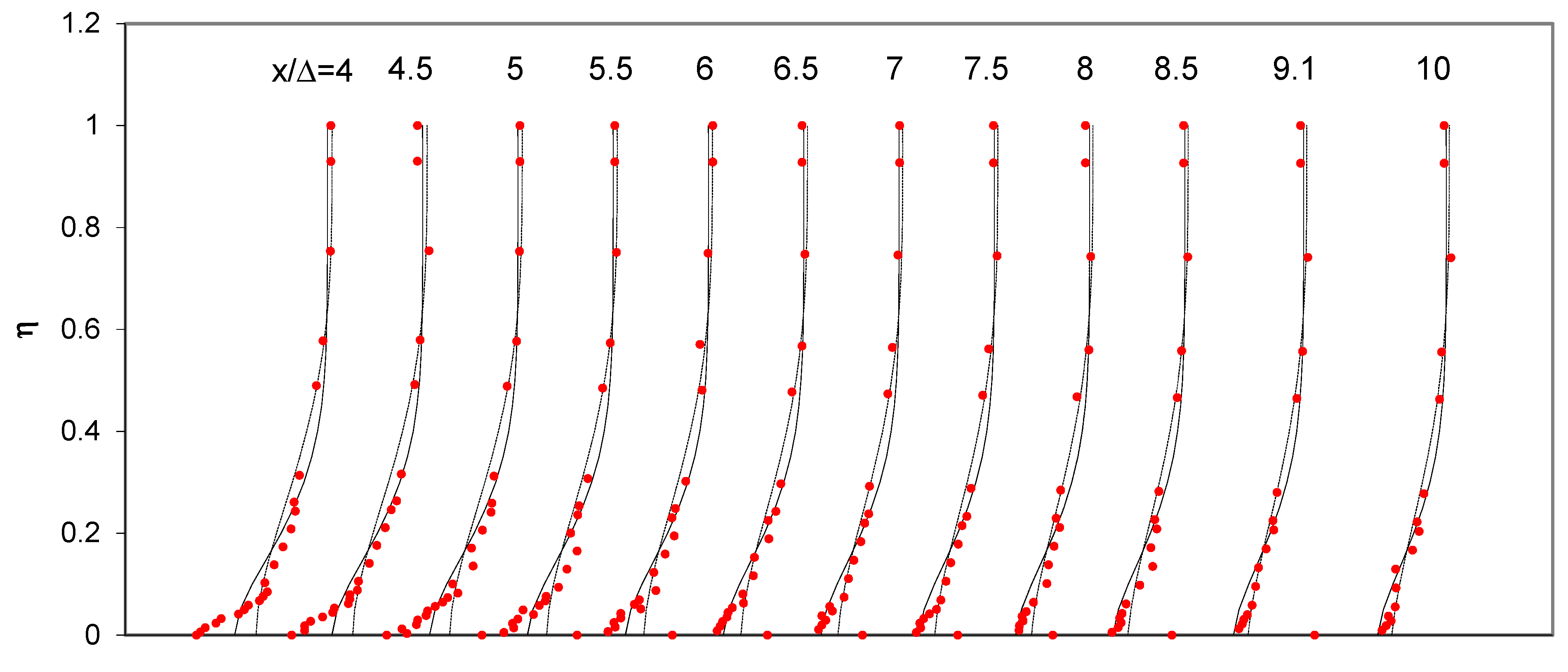
4.1. Verification of Flow over Bedforms

To apply the novel methodology, it is necessary to determine the local water depth. In scenarios characterized by low Froude numbers, a simplified rigid lid approximation can be employed as a preliminary estimate. The velocity scale is deduced from Equation (5), while the length scale is universally assumed to be 6.34 times the characteristic wavelength (Δ) across all examined cases.

The velocity profiles obtained from experiment T5 are illustrated in Figure 7. This experiment pertains to bedforms with the greatest wavelength within the dataset, yielding a length-to-height ratio approximating 20, indicative of dune formations. The ratio of dune height (Δ) to local water depth (h) was measured as 0.3.

Figure 7 also compares the results of the simplified mapping approach (via first, fifth, and eighth-order polynomial profiles) with the results of a 2D vertical model, as delineated in reference [38]. It is worth noting that our findings indicate that the mapping approach introduced in our current study appears to enhance the performance of the (VAM) model to a degree that results in improved outcomes in comparison to the 2DV model, specifically for the T5 experiment. It is important to clarify that the intent is not to assert the superiority of the VAM model over the 2DV models. Instead, the assertion is that the elucidated simplified mapping approach offers a substantial enhancement in velocity mapping within the context of depth-averaged models.

The classic log law is often considered unsuitable for accurately mapping flow characteristics within certain regions, particularly those involving reverse flow and negative velocity values associated with separation zones. To assess its performance, we selected Experiment T5 and applied the classic log law formula (Equation (1)) at two specific positions: the first at X = 0.06 m, situated within the separation zone; and the second at X = 1.58 m, positioned upstream of the crest over the stoss slope.

The classic log law equation is as follows:

$$\frac{u\left(z\right)}{u*}=c_1\mathrm{l}\mathrm{o}\mathrm{g}\left(\frac{z}{zo}\right)+c_2$$

(17)

This equation can be rewritten in terms of the normalized depth, h, as shown in Equation (18):

$$u\left(\eta \right)=\frac{uo}{C*}\left(c_1\mathrm{l}\mathrm{o}\mathrm{g}10\left(\frac{\eta .\mathrm{h}}{zo}\right)+c_2\right)$$

(18)

where,

$$zo=\left(0.11\left(\frac{\upsilon .C*}{uo}\right)+\frac{ks}{30}\right)$$

(19)

The universal coefficients, $c_1$ and $c_2$, typically equal 5.75 and 8.5, respectively, for turbulent flow over a flat rough surface.

Figure 8a,b present the comparison of the log law with measurements when utilizing the universal constants of 5.75 and 8.5. Notably, Figure 8c,d illustrate a significant overestimation of velocity profiles at both positions when employing the conventional log law with these universal coefficients. It becomes evident that achieving a more accurate match necessitates fine-tuning the coefficients $c_1$ and $c_2$. However, it is essential to highlight that the optimal values of these coefficients vary according to the specific position, as demonstrated in Figure 8c,d.

Our analysis of the log law’s application has revealed several limitations when mapping velocity fields over bedforms, which can be summarized as follows:

• The optimal constants for the log law vary based on the bedform’s location;
• As expected, the log law cannot accurately predict reverse flow and exhibits significant discrepancies within separation zones;
• A reasonable match with measurements near the crest can be achieved by optimizing the constants;
• Currently, no known formula exists for predicting the values of $c_1$ and $c_2$ over bedforms.

These findings underscore the challenges associated with using the log law to characterize flow patterns in complex topographical environments.

To quantify the disparity in velocity between various velocity templates and the measurements conducted during the T5 experiment, we introduce the Average Summation of Velocity Difference Square (ASVDS) as defined below:

$$ASVDS=\left(1/L\right){\int }_0^L\left({\int }_0^1{\left({\mathrm{u}}_{calc}\left(\eta ,x\right)-{\mathrm{u}}_{mes}\left(\eta ,x\right)\right)}^{2}d\eta \right)dx$$

(20)

Here, ASVDS represents the aggregate square differences between the calculated velocity, denoted as ${\mathrm{u}}_{calc}\left(\eta ,x\right)$, and the measured velocity, denoted as ${\mathrm{u}}_{mes}\left(\eta ,x\right)$.

Furthermore, we define the relative error of velocity mismatch (REVM) as the ratio of the ASVDS obtained with a particular velocity template to the corresponding value when utilizing the constant depth-averaged velocity model. The REVM is calculated as follows:

$$REVM=\frac{ASVDS (velocity template)}{ASVDS (VA model)}$$

(21)

It is important to note that a favorable velocity match is indicated by smaller values of ASVDS and REVM.

Figure 9 illustrates the computed velocity mismatch based on various velocity formulas. In Figure 9a, we present the ASVDS variations, while Figure 9b provides the variations in REVM for the different velocity templates in the context of the T5 experiment. Our findings reveal that linear velocity used in (VAM) models generally exhibits approximately 70% less velocity mismatch compared to the constant Velocity-Averaged (VA) models. Furthermore, the fifth-order and eighth-order velocity profiles demonstrate substantial improvements, with reductions in velocity mismatch of approximately 86% and 90%, respectively, compared to the VA models.

The velocity profiles obtained from experiment T6 are illustrated in Figure 10. This experiment pertains to bedforms with the greatest wavelength within the dataset, yielding a length-to-height ratio approximating 20, indicative of dune formations. The ratio of dune height (Δ) to local water depth (h) was measured as 0.23.

It is notable that the slope of the linear profile provides an overall assessment of the velocity distribution’s average inclination. However, a pronounced deviation between measurements and predictions is evident, particularly within the separation zone and in proximity to the reattachment point. Notably, improved agreement is observed over the stoss slope and as the flow accelerates approaching the crest (due to the existing favorable pressure gradient).

Comparing the calculated profiles of the eighth-order polynomial with the empirical data, a general congruence is identified within the separation zone and near the point of reattachment. Additionally, it is observed that the eighth-order profile successfully captures negative near-bed velocities within the eddy zone. Conversely, the fifth-order profile demonstrates a more favorable fit to the data as the flow accelerates toward the downstream crest.

Figure 11, Figure 12 and Figure 13 depict the velocity profiles for Run4, Run6, and Run7, respectively. These cases exhibit the shortest wavelength within the experimental range, resulting in a length-to-height ratio of approximately 10. These instances correspond to ripple formations [39]. In the context of Run4, the Δ/h ratio amounts to 0.25. Notably, the eighth-order profile yields favorable alignment within the eddy zone, while the fifth-order profile offers superior results downstream of the reattachment point.

For both Run6 and Run7, the water depth (h) is relatively greater, resulting in Δ/h ratios of 0.13 and 0.07, respectively. It is generally observed that when h/Δ exceeds 7, the eighth-order polynomial fails to predict negative near-bed velocities within the eddy zone. Nonetheless, the eighth-order profile continues to yield accurate predictions near the point of reattachment, whereas the fifth-order profile excels near the crest where flow acceleration is prominent.

Once again, the central objective of the proposed empirical approach is to provide a streamlined and expedient means of quantifying the flow field. The preceding findings demonstrate the efficacy of the new approach for both ripple and dune bed formations.

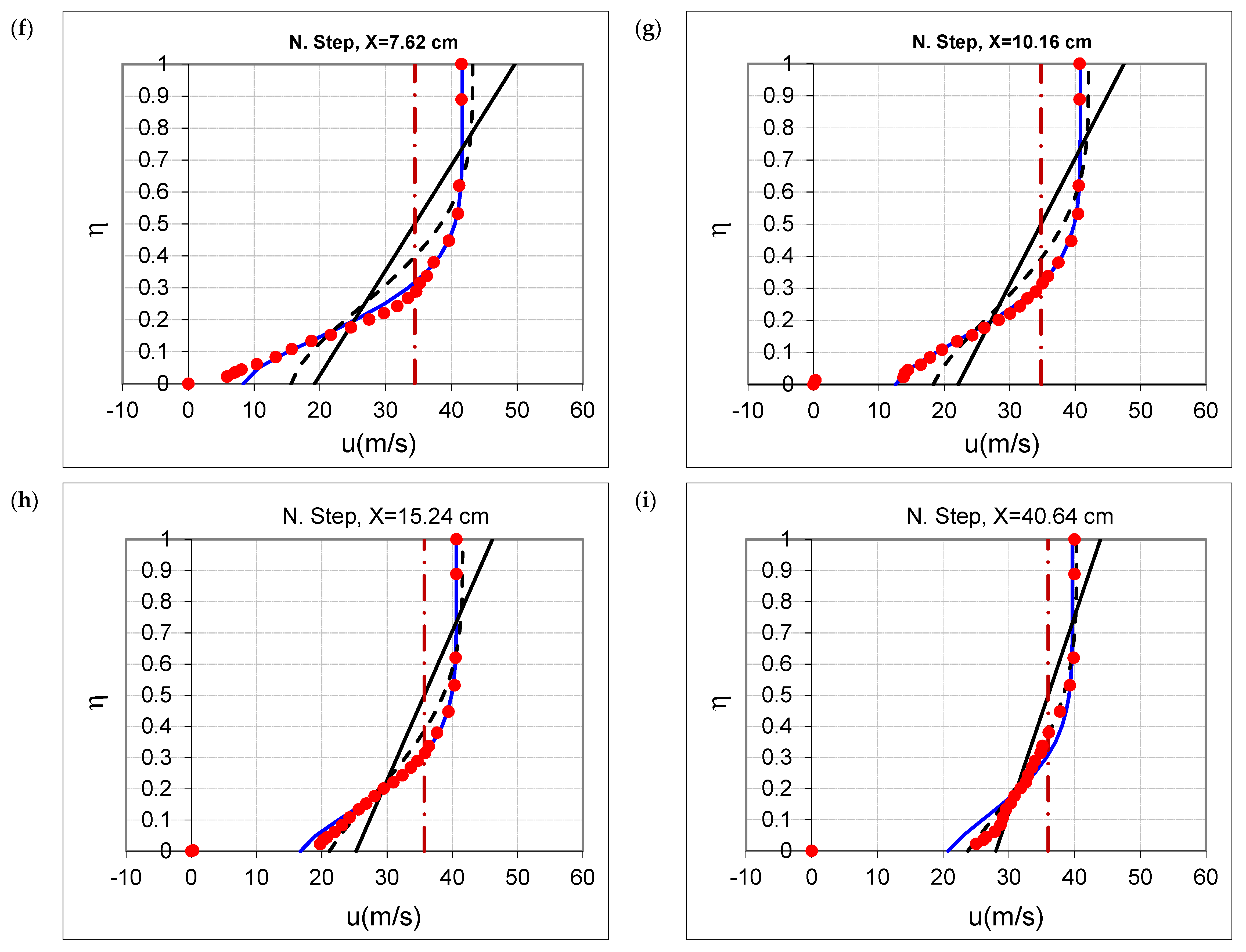
4.2. Evaluation in the Context of Negative Step Case

The presented methodology exhibits certain limitations. It assumes a state of periodic steadiness and a fully developed turbulent flow. Furthermore, the interplay between the length scale (bo) and the bedform height (Δ) implicitly indicates that the method should not be employed for bed formations with steepness ratios (Δ/λ) greater than 1/6.34 ≈ 0.16. This limitation is generally not problematic, as the upper threshold for steepness ratios in hydraulic rough beds, especially with natural low-stage bedforms, is well-documented to be around 0.06 [40].

Intriguingly, it is worthwhile to assess the methodology’s performance in a unique scenario—the negative step problem.

While the extension of this approach to address airflow over a negative step may appear unconventional at first glance, it is pertinent to note that the negative step problem can be viewed as a specialized instance of a bedform with an infinitely long wavelength, as demonstrated by Engel [8]. Additionally, Raudkivi [30] has identified compelling similarities between the flow characteristics downstream of a ripple crest and those associated with a negative step.

Furthermore, it is essential to recognize that the negative step problem holds practical significance. This is evident in situations where backward-facing steps are encountered downstream of hydraulic structures, such as hydraulic gates and weirs, as highlighted by Nakagawa and Nezu [7].

This case represents a special instance of flow over bedforms with a flat steepness ratio. To this end, an experiment involving airflow over a negative step conducted in a wind tunnel was undertaken, as outlined in Driver and Seegmiller [39]. Here, the velocity scale is again determined via Equation (5), and the length scale aligns with the proposed relationship, depicted in Figure 5.

Figure 14 provides a comparative visualization of the empirical data and the method’s predictions. Remarkable agreement is observed, particularly with the eighth-order profile near the point of reattachment. Additionally, the fifth-order profile exhibits strong agreement downstream of the reattachment point (x/Δ > 6). This finding signifies the viability of the proposed approach in the context of backward-step problems.

5. Conclusions

This study presents an empirical approach designed to estimate the longitudinal velocity field across bedforms under steady, fully developed turbulent flow conditions, particularly within the context of low-flow regime scenarios. The method proposed is straightforward and pragmatic, circumventing the need for complex iterations or the resolution of differential equations. This technique draws upon the concept of moments, establishing two distinct velocity scales: the depth-averaged longitudinal velocity (u_o) and the moment-derived integral velocity (u₁).

To validate and verify the proposed empirical methodology, measurements from 10 distinct laboratory experiments involving water flow over bedforms were selected from the existing literature. This selection encompassed both ripple and dune cases. The range of Froude Numbers spanned from 0.1 to 0.32, indicating a low-flow regime (F_n² << 1). Bedform characteristics, such as the ratio of bedform height to wavelength (Δ/λ) ranging from 0.1 to 0.2 and the ratio of bedform height to water depth (Δ/h) ranging from 0.07 to 0.3, were considered.

Based on the compiled experimental data, a dimensionless spatial relationship for u₁ was derived empirically. This relationship is contingent on velocity and length scales, as determined through dimensional analysis and regression techniques using the selected experimental dataset. Notably, both scales exhibited strong correlations with the bed feature’s height (Δ).

In order to approximately map the velocity field over bedforms, this study introduced three vertical polynomial velocity distribution functions: namely, first-order, fifth-order, and eighth-order polynomials. The coefficients of these polynomial functions were deduced analytically through the Mathematica package, guided by assumptions and conditions that encompassed slip velocity at the bed, conservation of mass, near-inviscid potential flow at the water surface, moment conservation around mid-water depth, and adherence to the moment-based Chezy formula for bed shear stress. It is important to emphasize that the polynomial coefficients primarily depended on the two velocity scales (u_o and u₁), as well as the dimensionless Chezy coefficient (C*) and other constant parameters.

The predictive capacity of the proposed empirical method’s velocity profiles was tested against experimental data concerning water flow over ripples and dunes, as well as airflow over a negative step. Several key insights emerged from this comparison:

• The adoption of a slip boundary condition at the bed yielded improved agreement between the empirical velocity profiles and measurements, as opposed to the accuracy achieved by considering the more realistic no-velocity slip conditions;
• While the linear profile exhibited limited agreement within the separation zone or near the point of reattachment where the velocity profile’s shape became notably non-uniform, it still represents an improvement over the uniform velocity assumption commonly employed in traditional depth-averaged flow models. As the downstream crest is approached, the acceleration of flow suggests better alignment with the linear profile;
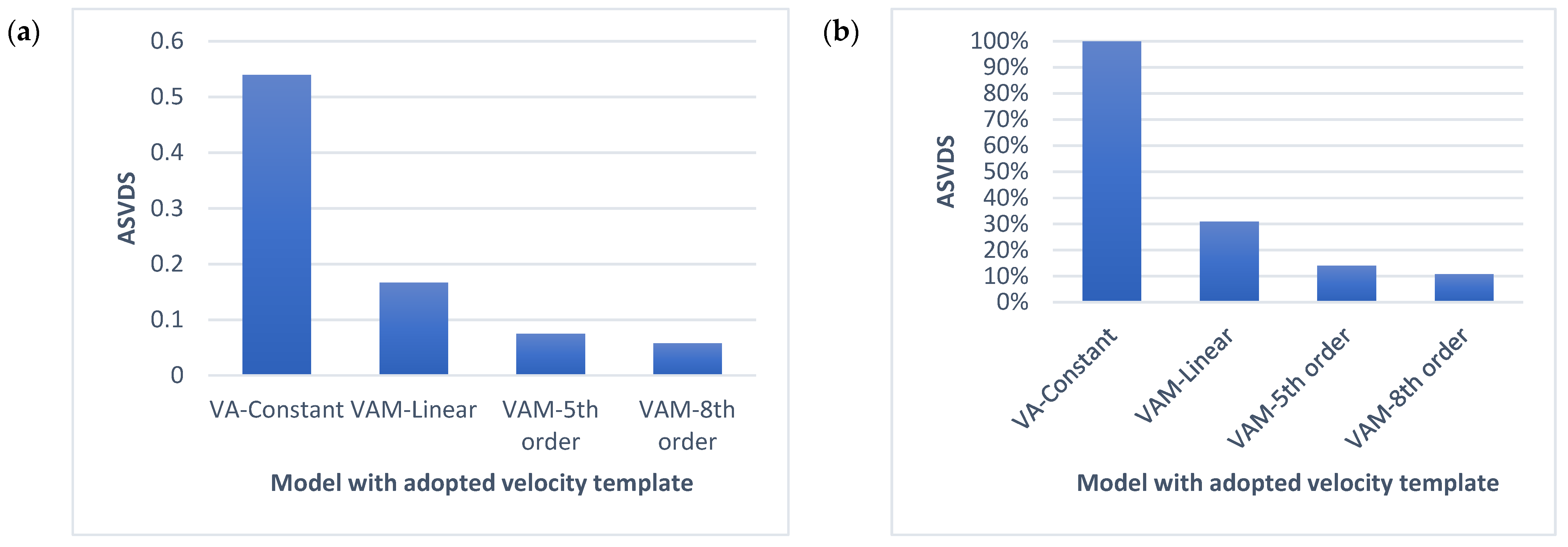
• Our findings reveal that linear velocity used in (VAM) models generally exhibits approximately 70% less velocity mismatch compared to the constant Vertically-Averaged (VA) models. Furthermore, the fifth-order and eighth-order velocity profiles demonstrate substantial improvements, with reductions in velocity mismatch of approximately 86% and 90%, respectively, compared to the VA models;
• The eighth-order polynomial profile generally yielded superior results within the eddy zone and proximity to the point of reattachment. Conversely, the fifth-order profile demonstrated better alignment downstream of the point of reattachment, particularly as the flow accelerated toward the crest.
• This novel approach was also successfully applied to the problem of airflow over a negative step within a wind tunnel, yielding satisfactory agreement with measured velocity data.

In summary, this study has introduced a straightforward empirical approach built primarily upon two velocity scales, u_o and u₁, offering a practical tool for approximating the longitudinal velocity field over fully developed 1D bedforms. The outcomes of this research provide a convenient means for analytical investigations seeking to estimate flow fields over bedforms. Moreover, these results enhance and extend the capabilities of the (VAM) models, enabling the production of approximate yet more realistic flow fields for scenarios involving flow over bedforms, as well as their effective utilization in applications concerning sediment transport and mixing.

6. Limitations and Outlook

The outcomes of this investigation have offered invaluable insights into the means of empirically mapping the velocity distributions over bedforms and negative steps. However, it is imperative to acknowledge specific constraints that should be taken into account during the application of these findings:

• The study in hand focuses on low-stage bedforms related to sand-bedded rivers and channels. Future work is required to assess the proposed approach for gravel-bedded bedforms;
• The analyses conducted in this study were centered on bedforms within the low-flow regime, specifically ripples and dunes, characterized by a low Froude number (F_n² << 1). As a result, this study’s conclusions cannot be readily extrapolated to encompass high-flow regime scenarios involving antidunes and other bedform configurations. Exploring the behavior of high-flow regime bedforms presents a promising avenue for future research endeavors;
• Another notable limitation pertains to the assumption of one-dimensional (1D) bedforms with a uniform bed width. To expand the applicability of the analyses, future work could focus on extending the methodology to encompass two-dimensional (2D) bedforms, which presents a distinct set of challenges and considerations;
• Furthermore, this study primarily delved into fully developed turbulent flow over a non-erodible train of bedforms. Temporal aspects concerning the evolution of bedforms were excluded from the scope of this investigation, warranting potential exploration in forthcoming studies.

It is essential to recognize that previous research has indeed leveraged 2D vertical models and even 3D numerical models to effectively tackle many of the challenges detailed above as limitations of our study. These models have exhibited commendable success in handling such problems, albeit within certain constraints. It is important to note that the applicability of 2D vertical and 3D numerical models is contingent upon specific circumstances. While these models demonstrate efficacy in managing particular scenarios, their utility is often limited by the computational demands and runtime requirements associated with their deployment. Consequently, when addressing large-scale problems, depth-averaged models emerge as a practical choice. This preference is primarily attributed to the advantages they offer in terms of simplicity, reduced data input prerequisites, and more manageable computational resources. Nevertheless, it is crucial to acknowledge that conventional depth-averaged models have their inherent limitations and inaccuracy. They are well-suited for idealized scenarios featuring simplified geometric and hydrostatic pressure assumptions. However, they tend to falter when tasked with simulating non-hydrostatic pressure flow and sediment interactions over dynamic bed topographies, particularly in cases involving flow separation. Notably, existing depth-averaged models have yet to effectively capture the evolution of bedforms originating from a flatbed. In our study, we propose a constructive middle ground by enhancing depth-averaged models through the integration of the moment approach and the implementation of the approximate velocity mapping procedure, as discussed in our work. This approach serves as a pragmatic response to address the limitations posed by depth-averaged models in complex scenarios.

In summary, the limitations delineated above pertain primarily to the depth-averaged models and do not reflect the capabilities of 2D vertical or 3D models. Our study endeavors to bridge this gap by advancing depth-averaged models and offering a viable solution to the challenges they encounter in simulating flow dynamics over variable bed topographies.

Considering these limitations, it is essential to emphasize that this study represents a pivotal stride toward approximating flow fields over bedforms and negative steps. The insights gained here serve as a solid foundation for subsequent inquiries, not only within the realm of analytical analysis but also for the expansion of the capabilities of depth-averaged and moment models. These extensions could substantially enhance their utility in addressing the complexities associated with non-uniform flows, encompassing various bed topographies and the dynamic evolution of bedforms.