1. Introduction
Changes in climate have altered the characteristics of water cycle components [
1,
2]. Notably, regional water availability has significantly changed, especially in snow-dominant regions [
3,
4]. These changes have mainly stemmed from shifts in precipitation characteristics such as the snow-to-rain ratio and alterations in the magnitude and timing of glacier- and snowmelt, causing variations in streamflow volume and peak timing [
5,
6,
7]. For instance, in certain regions in Canada, more frequent and intense floods in early spring and reduced water availability during summer have been observed [
8,
9,
10]. Such changes in hydroclimatic conditions can affect water management strategies, including the timing and volume of stored and released water from reservoirs to meet water demand [
11]. Therefore, gaining a better understanding of future water availability conditions is crucial to updating regional water management plans.
Global circulation models (GCMs) serve as the most credible tools for projecting future climates, as they mathematically represent geophysical processes in each sphere and their interactions [
12]. However, their projections are subject to uncertainties stemming from diverse sources, such as processe simplification, scenario definitions, and climate noise [
13,
14,
15]. Furthermore, downscaling their outputs for regional interpretability, especially for watershed management purposes, amplifies the inherent uncertainty in their projections [
16,
17]. Therefore, it is recommended to employ an ensemble of climate projections instead of relying on a single climate model [
18,
19]. The outputs of climate models can be utilized in hydrological models to estimate future streamflow conditions [
20].
The choice of employed hydrological models can, however, influence the estimated changes in a streamflow regime, including peak flow magnitude [
21,
22,
23]. Even within the same hydrological model, alternative representations of a process, such as evapotranspiration, can impact the flow estimation [
24,
25,
26]. Furthermore, different catchment discretization, such as lumped vs. semi-distributed approaches, can potentially lead to diverging results [
27,
28,
29]. Another source of difference can arise from the resolution of the climate data used for model calibration [
30]. For instance, the usage of ground data in the form of point or grid-based data can cause discrepancies between simulated flows [
31]. Despite the significance of the uncertainty arising from hydrologic process representation, catchment discretization, and utilized input data resolution, their combined impact on the analysis of water resource management in a changing climate remains understudied. Moreover, it is unclear how sensitive assessments are to each individual factor and their combinations. For example, in snow-dominant regions, it remains unclear whether it is more effective to employ multiple hydrological models, all using the same method for snowmelt representation (as commonly done in the literature), or to utilize the same hydrological model with multiple snow routines.
The objective of this study was to understand the sensitivity of water allocation analysis to the choice of hydrological modeling configuration, with the overarching goal of evaluating the impact of climate change on the snow-dominant Oldman River Basin in Canada. For this purpose, 16 hydrological modeling configurations were considered that involve the combination of two hydrological models, coupled with two snow routine modules, the consideration of two distinct catchment discretization approaches, and the incorporation of ground-based climate data at two different resolutions. These hydrological models were integrated with a water allocation model and supplied with climate model projections to estimate future changes in the study area. It is important to note that this research builds upon the work of Sharifinejad et al. [
31]. The prior study focused on impact assessment within the same basin, albeit limited to only four configurations relevant to catchment discretization and climate data resolution. In contrast, the current study significantly broadens this scope by encompassing a more extensive array of modeling configurations to achieve a more comprehensive understanding of the potential impacts of climate change on this water system. This type of analysis is critical to water management and has not been conducted before in cold region basins. The following sections introduce the Oldman River Basin and the employed impact assessment framework. Moreover, the performance of hydrological models and projected water system behavior are discussed, and concluding remarks are provided.
2. Case Study
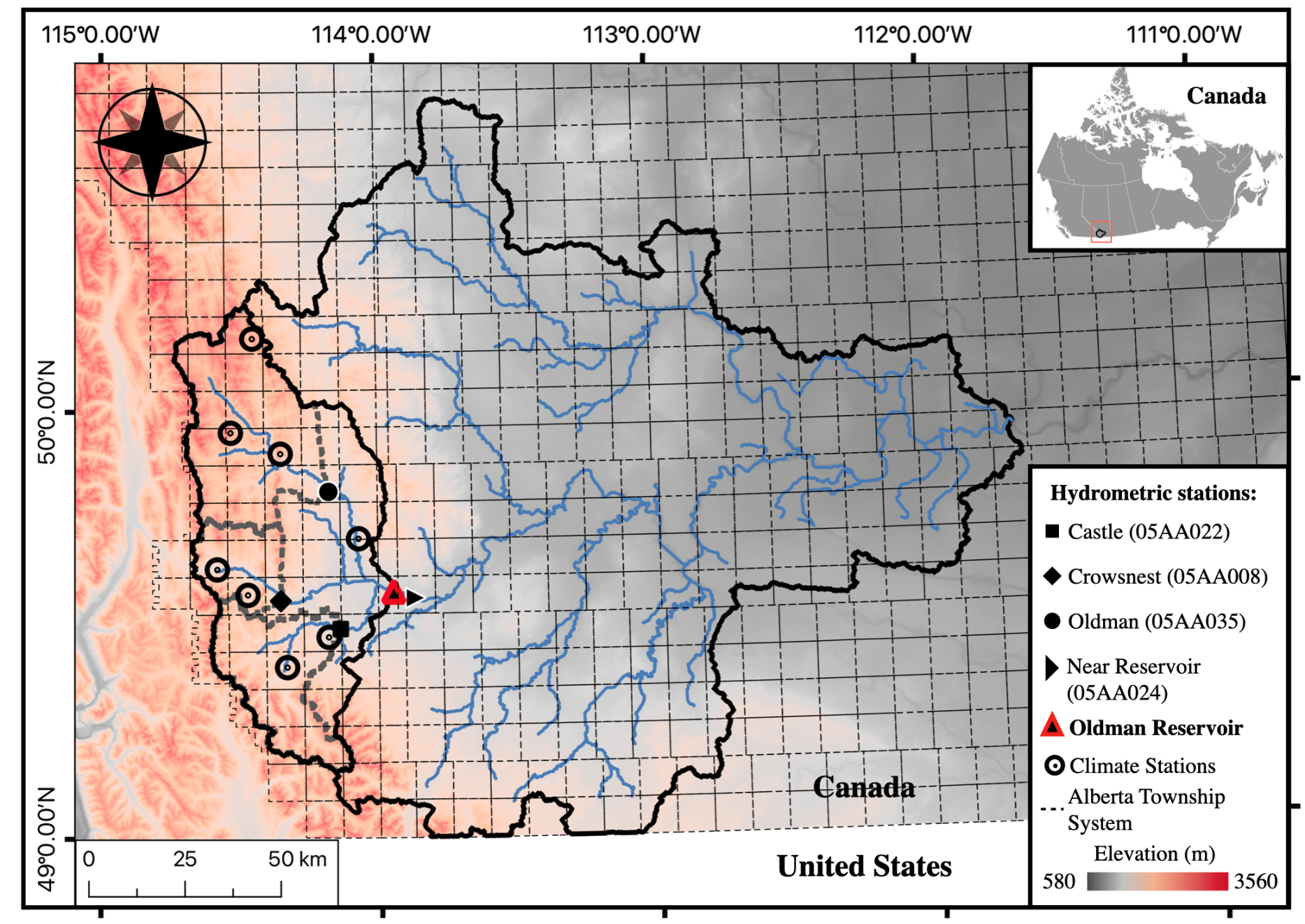
The Oldman River Basin covers approximately 27,500 km
2 in Alberta, Canada, as shown in
Figure 1. The multi-purpose Oldman Reservoir, with a capacity of 490 million m
3, is the largest dam in this region. It supports water for municipal uses, hydropower generation, and agricultural production, and plays a crucial role in flood management in the Prairies [
32]. The Oldman Reservoir is primarily fed by three major river inflows: the Castle, Crowsnest, and Oldman Rivers, originating from the Rocky Mountains. Their approximate long-term annual mean discharge during 1961–1990 is respectively 472, 153, and 383 million m
3. The drainage area at the reservoir closure is about 4380 km
2. In this study, the reservoir drainage area is split into four sub-watersheds (tributaries): the regions upstream of the hydrometric stations on the noted three main inflows, and an area below these stations reaching the Oldman Reservoir, hereafter referred to as Near Reservoir sub-watershed (NR), shown in
Figure 1. The drainage areas and streamflow discharge in each sub-watershed are presented in
Table A1 in
Appendix A.
Since a large number of users in the Prairies rely on the water released from the Oldman Reservoir, any changes in this dam’s water availability can put unprecedented pressure on the socioeconomic activities within the entire water system [
33]. Over the 20th century, an increase of 2–4 °C in the mean annual temperature and no significant trend in mean annual precipitation in the region have been observed [
34,
35,
36]. The rising temperature has led to alterations in the snow-over-rain ratio and an increased rate of snowmelt processes, thereby impacting the streamflow characteristics and posing water management challenges, particularly in flood control [
37,
38,
39,
40]. Moreover, in addition to climate variability and change, increased human activities, such as the expansion of agricultural areas, have altered the historical water availability in this region [
41,
42].
Regarding future projections, Tanzeeba and Gan [
43] estimated flows with about two weeks earlier peak timing and lower intensities during the summer in the outlet of the Oldman River Basin using a physically based hydrological model. In the Crowsnest River sub-watershed, significant increases in flow during winter by a maximum of 200% and a decrease in flow during summer by a maximum of 63% have been projected for the future, compared to the period from 1965 to 1997 [
44]. These changes in flow volume and peak timing pose challenges for reservoir operations to control flooding and meet water demand, particularly in satisfying irrigation water demand [
45,
46,
47]. Sharifinejad et al. [
31] used the HBV-MTL hydrological model to simulate the flow reaching the Oldman Reservoir and found that the estimated streamflow regime is sensitive to the choice of catchment discretization and input data resolution. Moreover, they projected increased flow intensity, along with an earlier peak timing, leading to severe water shortages during the summer in the basin. As previously noted, in our study, we extend this work by considering GR4J, another hydrological model, and two different snowmelt representations as well, increasing the number of model configurations from four to sixteen, as explained in the following section. This is to investigate different sources of uncertainty in the assessment of climate change impacts.
3. Materials and Methods
The historical and future periods considered in this study were 1961–1990 and 2021–2099, respectively. In the following sections, the previously noted hydrological configurations are explained. Moreover, the utilized objective function and calibration methods are described. In addition, the employed reservoir water allocation model, future climate projections, and measures used for impact assessment are elaborated upon.
3.1. Catchment Discretization
Under the semi-distributed approach, individual hydrological models were developed for the Castle, Crowsnest, Oldman River, and NR sub-watersheds, and their results were aggregated to estimate the inflow reaching the Oldman Reservoir. Streamflow data for these sub-watersheds were collected for 1961–1990 and are freely available from the Government of Canada [
48]. In contrast, the lumped approach treated the entire upstream area of the Oldman Reservoir as one entity, and a single hydrological model was developed for this region.
3.2. Observed Climate Data
Observed-station-based temperature and precipitation data, or point-based data corresponding to the previously mentioned sub-watersheds, were collected from Environment Canada and Climate Change Canada [
49] for the 1961–1990 period (see
Table A2). The locations of these stations are shown in
Figure 1. Moreover, a grid-based climate dataset for this region was collected from the Alberta Climate Information Service [
50] for each watershed, as shown in
Figure 1. These data were based on the Alberta Township System with a grid size of 9.7 × 9.7 km
2. This database was developed via transferring the climate station data into the centers of the grids using an inverse distance weighting method. The recorded average long-term precipitation and minimum and maximum temperatures based on these grid-based data during 1961–1990 are provided in
Table A2. For the semi-distributed approach, the point- and grid-based climate data corresponding to each sub-watershed were used for model development. In the lumped approach, the entire dataset was used. When point-scale climate data were utilized, the target area was divided into the zones of Thiessen polygons, with each climate station at the center of a polygon, and then weighted average climate data were found. Similarly, if the grid-based data were utilized, the target area was discretized into zones corresponding to the grids of the Alberta Township System, and weighted average climate data were used for modeling purposes.
3.3. Hydrological Models
HBV is a commonly used conceptual hydrological model known for its simplicity, ease of application, and good performance in estimating streamflow [
51,
52,
53]. In this study, a modified version of the HBV model, called HBV-MTL and developed by Sharifinejad et al. [
31], was used. This model requires daily precipitation and potential evapotranspiration as inputs, with the latter being estimated using temperature data. Based on the daily temperature values, precipitation is classified as rainfall, snowfall, or a mixture of rain and snow. Snowfall contributes to the snowpack state variable, which eventually melts when the temperature rises. Liquid water, whether from rainfall or snowmelt, infiltrates the soil or turns into runoff, depending on the soil moisture and temperature. In this model, infiltration into the frozen and thaw soil is estimated based on the modified SCS method used in the SWAT model [
54]. A portion of infiltrated water is retained by soil particles to form the soil moisture state variable. Some of the soil moisture is consumed through evapotranspiration processes, estimated using the method of Hargreaves and Samani [
55] and minimum and maximum temperature data. The remaining infiltrated water contributes to groundwater. In this model, groundwater is conceptualized with two state variables, representing shallow and deep soil layers’ water content. The shallow groundwater slowly seeps into the deeper reservoir. Meanwhile, the accumulated water in both these groundwater reservoirs is released progressively to form intermediate flow and baseflow. The combined flows, along with runoff, are routed through a triangle delay function to calculate the flow at the basin’s outlet. For more information on the equations, parameters, and their range used, please refer to [
31].
GR4J is a conceptual hydrological model that requires precipitation and potential evapotranspiration as input data to estimate flow [
56]. Evapotranspiration is estimated using temperature data. Its simplicity and limited data requirements make GR4J a suitable option for examining the impacts of climate change on streamflow [
57,
58]. In this model, net precipitation (obtained through subtracting potential evapotranspiration from precipitation) is partitioned into two segments through a parabolic equation. A portion of the net precipitation is stored in “production storage”, where the stored water gradually percolates. Furthermore, vegetation utilizes the stored water in production storage for evapotranspiration. The remaining portion of the net precipitation joins with the percolated water from production storage, and together, they enter the routing phase. In the routing phase, 10% of the available water is directed to the outlet using a two-sided unit hydrograph, while the remaining 90% of water is routed using a one-sided unit hydrograph and subsequently retained in routing storage, where it is released gradually over time. This routing storage is similar to the groundwater buckets in the HBV-MTL model. However, there is a difference in how GR4J manages the inflow to the routing storage, while HBV-MTL assumes instant inflow to the groundwater reservoirs and routes their outflow. For a more comprehensive understanding of the GR4J model’s structure and equations, please refer to Perrin et al. [
59].
3.4. Snow Process Representations
The Degree-Day or temperature index method [
52] is commonly used to estimate snowmelt due to its simplicity and minimum data requirement [
60,
61]. In this module, it is supposed that the snow accumulates homogenously over the basin or target zones. The Snowpack melt (
) occurs when the daily average temperature (
) is higher than the snowmelt threshold temperature (
), as shown in Equation (1), where the Degree-Day coefficient (
) represents the linear relationship between air temperature and available energy for snowmelt and often depends on the altitude and geographical characteristics of the basin [
62]. Consequently, the Snowpack state variable (
) at time
can be found considering the difference between the Snowfall (
) and Snowmelt (
) and initial Snowpack value
, see Equation (2). Despite its popularity, it is acknowledged that this module may not properly represent the snowmelt variability caused by elevation variations in the basin [
52].
CemaNeige [
63] is a modified Degree-Day approach that provides a way to represent snow processes within a watershed across different elevation ranges. In this approach, the basin is divided into five elevation zones, each with equal areas. This division has demonstrated a reasonable performance and was adopted in this study [
64]. To implement this approach, the observed precipitation and temperature values in the basin are adjusted to each band’s elevation. This adjustment is proportional to the difference between the average elevation of the bands and that of the entire basin via the employment of an elevation gradient factor [
65]. As a result, snow processes are simulated independently for each elevation band. This means that CemaNeige needs information about how elevation varies across the entire basin.
CemaNeige not only monitors the accumulation of snow particles but also keeps track of the temperature within the snowpack. To achieve this, it estimates the snowpack’s temperature in each timestep (
), as shown in Equation (3). This estimation is based on a weighted average of the air temperature in that specific timestep (
and the snowpack’s temperature in the previous timestep (
. The weighting is determined via a calibration parameter (
. If the snowpack’s temperature is below zero degrees Celsius, any positive ambient temperature does not lead to the melting of the snow. In other words, snowmelt does not occur as long as the temperature within the snowpack remains below freezing. When the snow temperature reaches zero degrees Celsius and the mean temperature (
) is positive, the “potential” snowmelt (
is calculated using a Degree-Day coefficient (
, as shown in Equation (4). Accordingly, the actual snowmelt is determined via adjusting the potential snowmelt value based on the snow coverage factor, see Equation (5). This factor is the ratio of accumulated snow
and snowfall (
) over the long-term mean annual snowfall (
.
In the final step of the process, the snowpack accumulation is updated via accounting for snowfall and estimated snowmelt (as described in Equation (2)). For more comprehensive information regarding the CemaNeige module, please refer to [
63].
3.5. Hydrological Model Calibration
In the context of this study, the historical data from 1961–1990 were divided into burn-out (warm-up), calibration, and control (validation) periods. The first six years of data were used in the warm-up period to reach acceptable initial conditions [
66]. Two-thirds of the remaining data were used for model calibration, and one-third was used for model evaluation. Moreover, we utilized Kling–Gupta efficiency (KGE) in the objective function for model calibration due to its effectiveness and ability to capture different aspects of model performance, including variability, bias, and correlation [
67]. In brief, KGE, as shown in Equation (6), has three components: notably, the ratio of simulated over observed standard deviations (
); the ratio of simulated over observed mean values (
); and the Pearson correlation (
), which investigates the linear relationship between simulated and observed values. In Equations (7)–(9),
and
are the standard deviations of simulated and observed flows,
and
are the long-term average simulated and observed flows, and
and
are simulated and observed flows, respectively.
The objective function used to find calibration parameters integrated KGE values derived from both daily and annual streamflow data, as both temporal resolutions are critical for water management applications. The Euclidean distance between the pair of annual and daily KGE measures and the point (1, 1) was used to compute the objective function, as demonstrated in Equation (10).
The Shuffled Complex Evolution algorithm [
68] was utilized in this study to find the best or “optimal parameter set” based on the provided objective function. This algorithm works by randomly generating 50 parameter sets, which are then divided into five batches. Each batch is locally evolved via generating new parameter sets using parents within the same batch. After a few iterations, the superior parameter sets in all batches are transferred into a new batch, while the rest of the parameter sets are replaced with newly generated random parameters. This process of local evolution and batch transfer is repeated for 100 iterations. Finally, the parameter set that yields the minimum value of the objective function and the best match between simulated and observed flows is identified as the optimal parameter set.
As part of our investigation, we aimed to tackle the uncertainties linked with the process of parameter selection in each hydrological model configuration. Consequently, our goal was not only to find the noted optimal parameter values but also to identify an ensemble of parameter sets that we called the “acceptable parameter set”, which can simulate streamflow with a performance of KGE > 0.5 at both daily and annual scales, derived from a uniform probability function. For this, we employed the Generalized Likelihood Uncertainty Estimation (GLUE) method [
69] to find acceptable parameters. Each hydrological model configuration generated multiple streamflow series corresponding to these acceptable parameter sets.
3.6. Water Allocation Model
An existing water allocation model, known as the Water Resources Management Model (WRMM), was utilized to simulate the Oldman Reservoir operation. This model was initially developed by Alberta Environment [
70] and later emulated by Sharifinejad et al. [
31]. The WRMM requires several input data, including weekly upstream inflow, precipitation, evaporation, reservoir physical properties such as maximum and minimum storage levels, weekly water demand values for different sectors, and water allocation priorities and rule curves. To optimize the allocation of water to various competing demands, the model divides each system component, including reservoir and water sectors, into multiple zones based on rule curves. Each zone is assigned specific cost values, and the model employs linear programming to allocate water, minimizing the cost or deviation from the ideal zone/level. The WRMM follows the Alberta Water Act to prioritize water demand and optimize the balance between social, economic, and environmental benefits [
71]. The water demand in the model is categorized into local and regional demand, similar to [
72]. The water balance in the reservoir is presented in Equation (11).
In this equation,
is the time between
and
,
is reservoir storage,
is the inflows to the reservoir,
is precipitation,
is evaporation, and
is the spill from the reservoir spillway.
and
represent local and regional withdrawals, respectively. The regional demand encompasses water needs for various inter- and intra-provincial activities, especially irrigating 216 km
2 of agricultural fields. The local water demand mainly includes support for local irrigated agriculture covering an area of 67 km
2. For more detailed information about the water allocation model, please refer to [
31]. The performance of the WRMM model has been verified in other studies as well [
73]. Here, we used local water demand as an indicator of a water deficit in the area, while regional water allocation primarily controlled reservoir volume dynamics.
3.7. Climate Projections
Precipitation and temperature data from 19 climate models, based on the NASA Earth Exchange Global Daily Downscaled Projections under Coupled Model Intercomparison Project 5 (CMIP5), were utilized to represent the future climate [
74]. This dataset was bias-corrected and spatially downscaled using bias-correction spatial disaggregation [
75]. The data with a spatial grid resolution of 25 × 25 km
2 were obtained for 1961–1990 and from 2021 to 2099. The projections are available under two representative concentration pathways (RCPs), 4.5 and 8.5, representing the intermediate and high radiative forcing scenarios by the end of the 21st century, respectively. These data have been successfully used in Canada [
76,
77,
78]. For this study area, a more in-depth analysis of the projections, as discussed by Sharifinejad et al. [
31], revealed that there will be an increase in temperature of up to 200% and an increase in precipitation of up to 72% in the future when compared to the reference period of 1961–1990.
3.8. Measures to Assess Water System Behavior
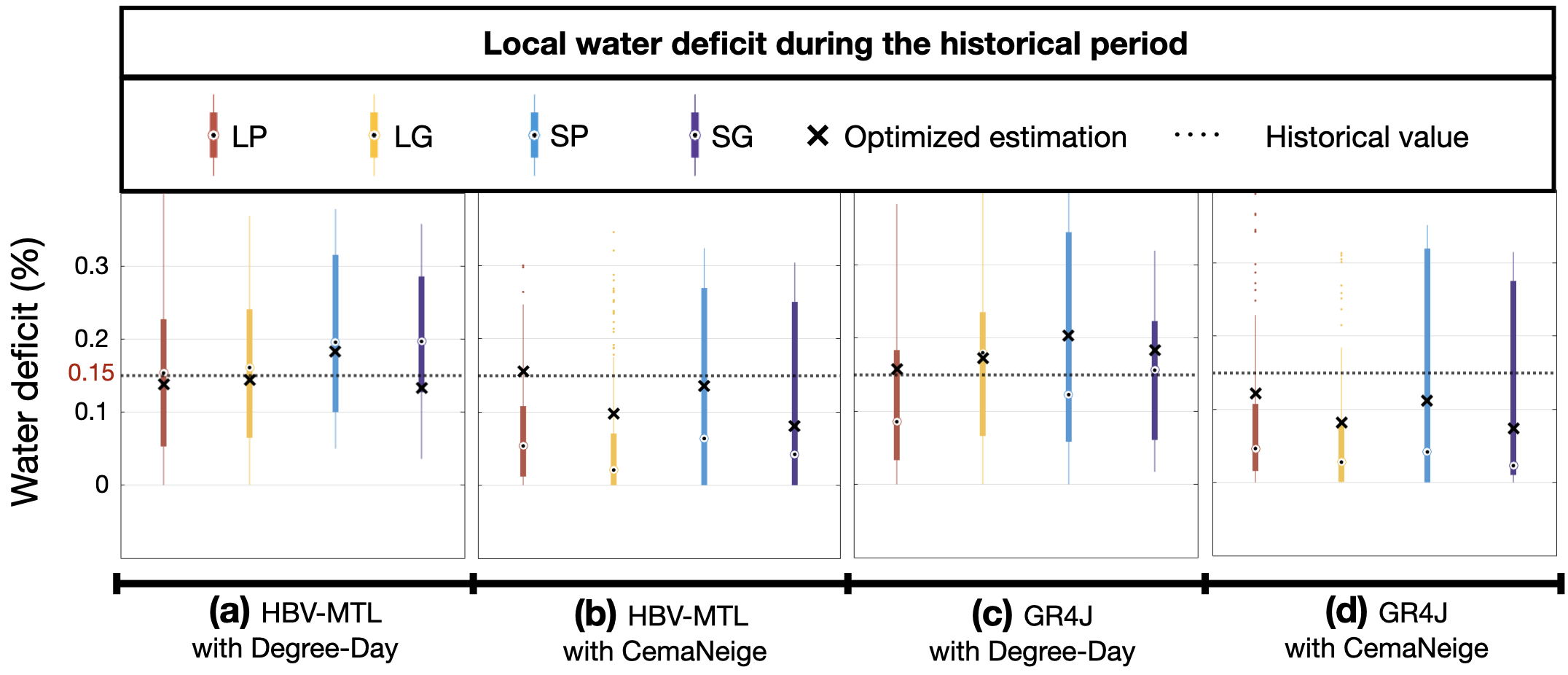
We compared the projected and observed expected hydrographs for the inflow reaching the Oldman Reservoir in the future with a focus on peak flow magnitude, timing, and average flow volume, as these characteristics are critical for reservoir operation. Moreover, we quantified various flow statistics during both historical and future periods that are relevant to water management. In brief, we determined quantiles for low (Q10), median (Q50), and extreme high flow (Q99), as well as the timing of the peak flow reaching the Oldman Reservoir. To obtain these flow statistics, we used flow–duration curves. Furthermore, we estimated changes in the Oldman Reservoir water storage and local water deficit during both historical and future periods. The annual water deficit was calculated as the relative difference between the total local water demand and supplied water each year. It should be noted that the long-term value of the annual water deficit (averaged over 30 years) during 1961–1990 was 15%, indicating that local demand was not fully met even during this period.
4. Results
4.1. Inflow Reaching the Oldman Reservoir during the Historical Period
As previously noted, the HBV-MTL and GR4J models, coupled with the Degree-Day and CemaNeige modules, were calibrated based on lumped and semi-distributed catchment discretization and using lumped and grid-based climate data. The optimal parameter sets for these models were found using the Shuffled Complex Evolution algorithm and are shown in
Table A3,
Table A4,
Table A5 and
Table A6. Here, the performance of these models during the calibration and control periods, based on the KGE measure, is presented in
Table 1. The KGE values during the calibration period ranged from 0.87 to 0.93, indicating that all models exhibited strong statistical agreement between the simulated and observed daily inflow values. Furthermore, the divergence in their KGE values was minimal. During the control period, the KGE values were smaller than in the calibration period, ranging from 0.64 to 0.84. Despite the slight decrease, these KGE values were still relatively high, demonstrating the overall good performance of the models. Hence, we retained all 16 hydrological model configurations for further assessments.
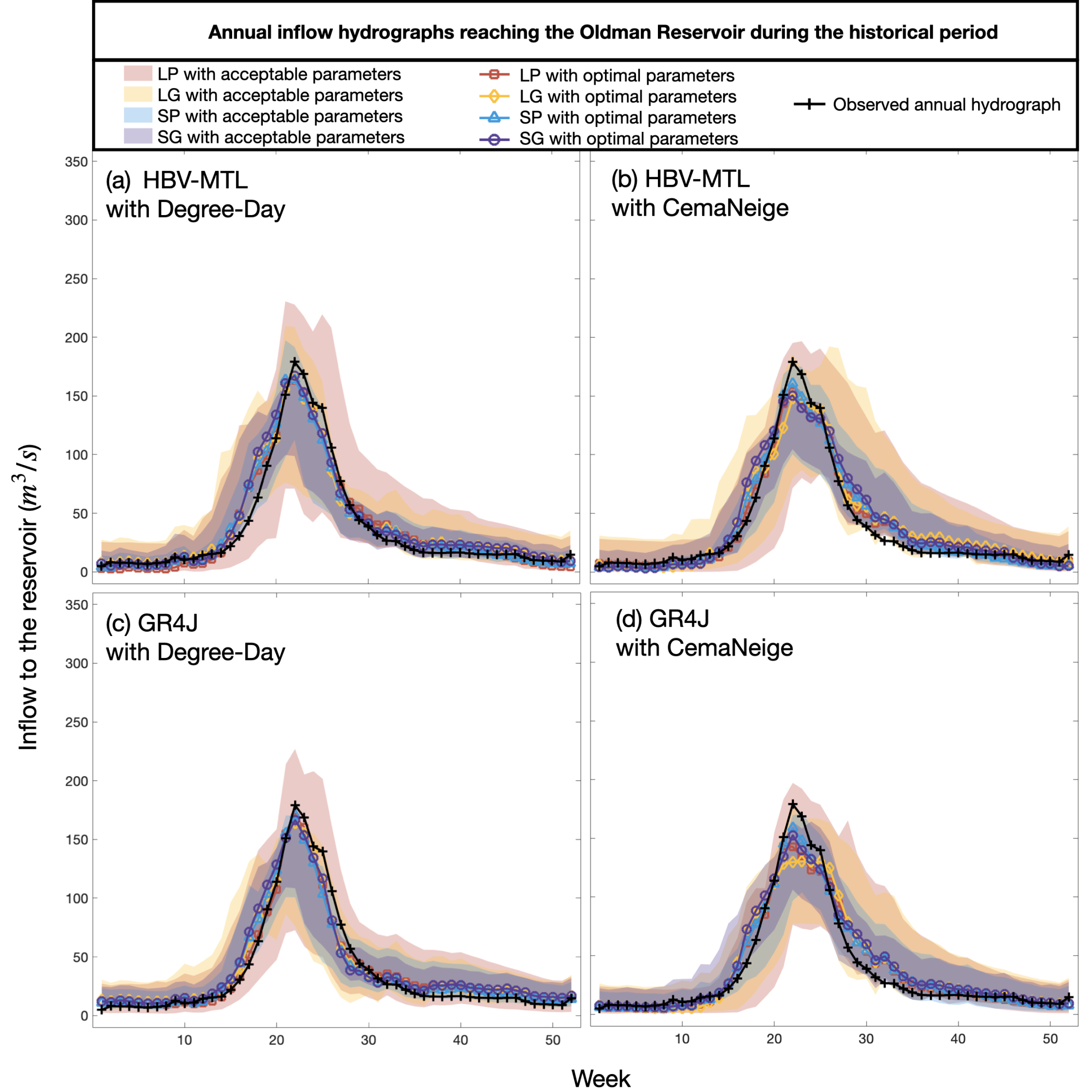
In addition to considering the KGE values, we also compared the simulated and observed inflow hydrographs for the entire historical period from 1961 to 1990 to examine how well the models reproduced the shape of the observed hydrograph. To achieve this, we calculated the expected (average) annual hydrographs for all 16 models over the 30-year period using the optimal and acceptable parameter sets identified using the GLUE method. The comparison results are visualized in
Figure 2, where the
x-axis represents the 52 weeks in a year. The top and bottom rows of
Figure 2 display the hydrographs based on the HBV-MTL and GR4J models, respectively. The left and right columns display the results of these models, coupled with the Degree-Day and CemaNeige modules, respectively. Each panel shows the inflow hydrographs for the models, calibrated using the lumped approach and point-based (LP) and grid-based (LG) data, as well as the semi-distributed approach with point-based (SP) and grid-based (SG) data. The solid lines and shades represent the inflow based on the models with optimal and acceptable parameter sets, respectively.
The analyses based on the optimal parameter sets revealed that all models adequately simulated the peak flow timing, with a maximum two-week difference between the simulated and observed peak flows. However, there were variations in the simulated peak flow intensity among the models. The GR4J models with the Degree-Day snow module demonstrated a better match with the observed peak flow, with differences ranging from 2% to 6%. Among these, the semi-distributed configurations calibrated with point-based data showed the smallest error in peak flow simulation. Analyzing the shape of the hydrographs on the falling limb slope showed that the models with CemaNeige performed better in capturing the second peak flow compared to the Degree-Day approach. This improvement was attributed to CemaNeige’s ability to preserve snow in high-elevation areas for longer durations than the Degree-Day module. Furthermore, the analysis highlighted that the choice of snow routing module had a more significant impact on the simulated flow compared to the other configurations, such as the type of hydrological model.
4.2. Inflow Reaching the Oldman Reservoir during the Future Period
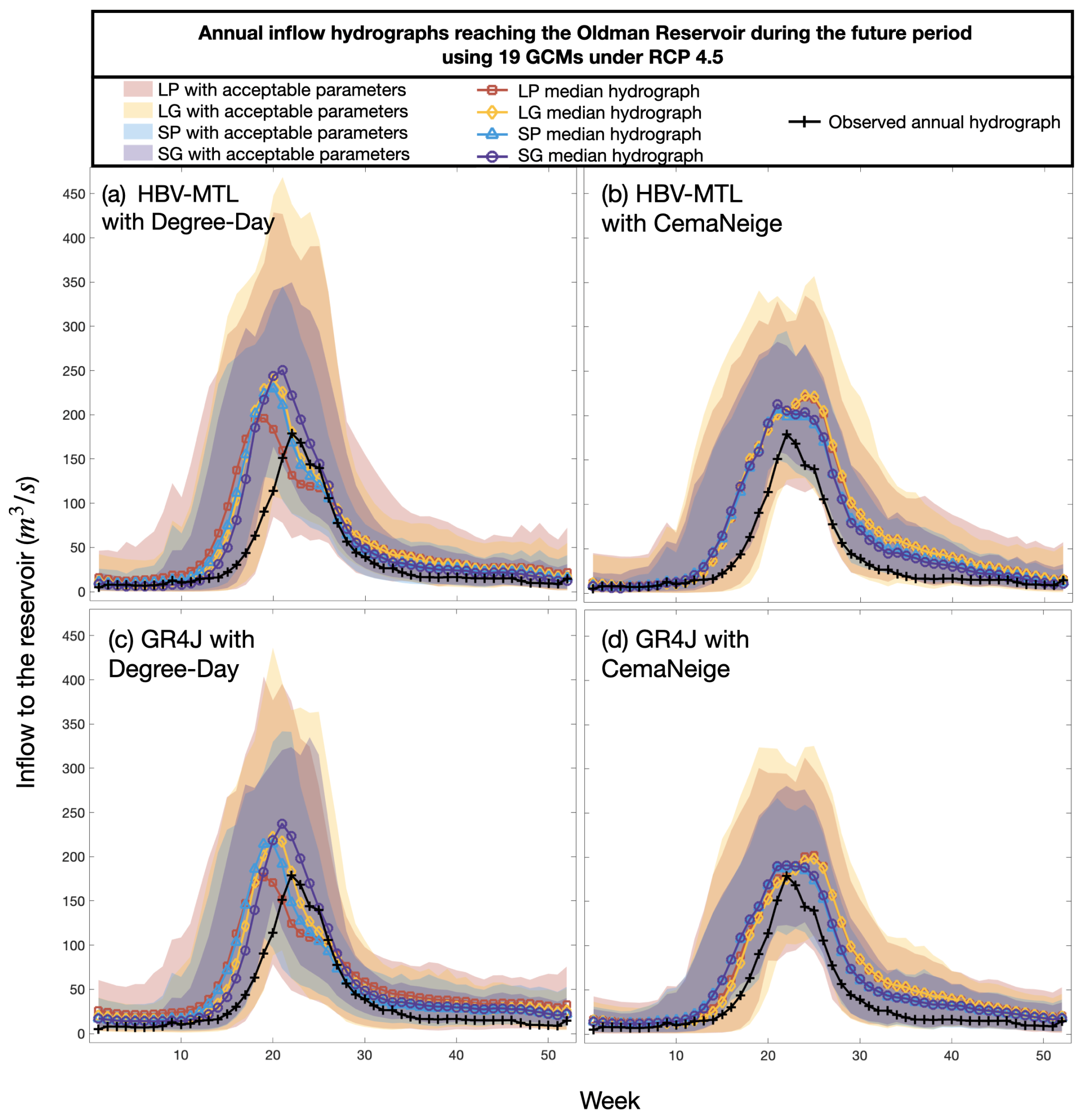
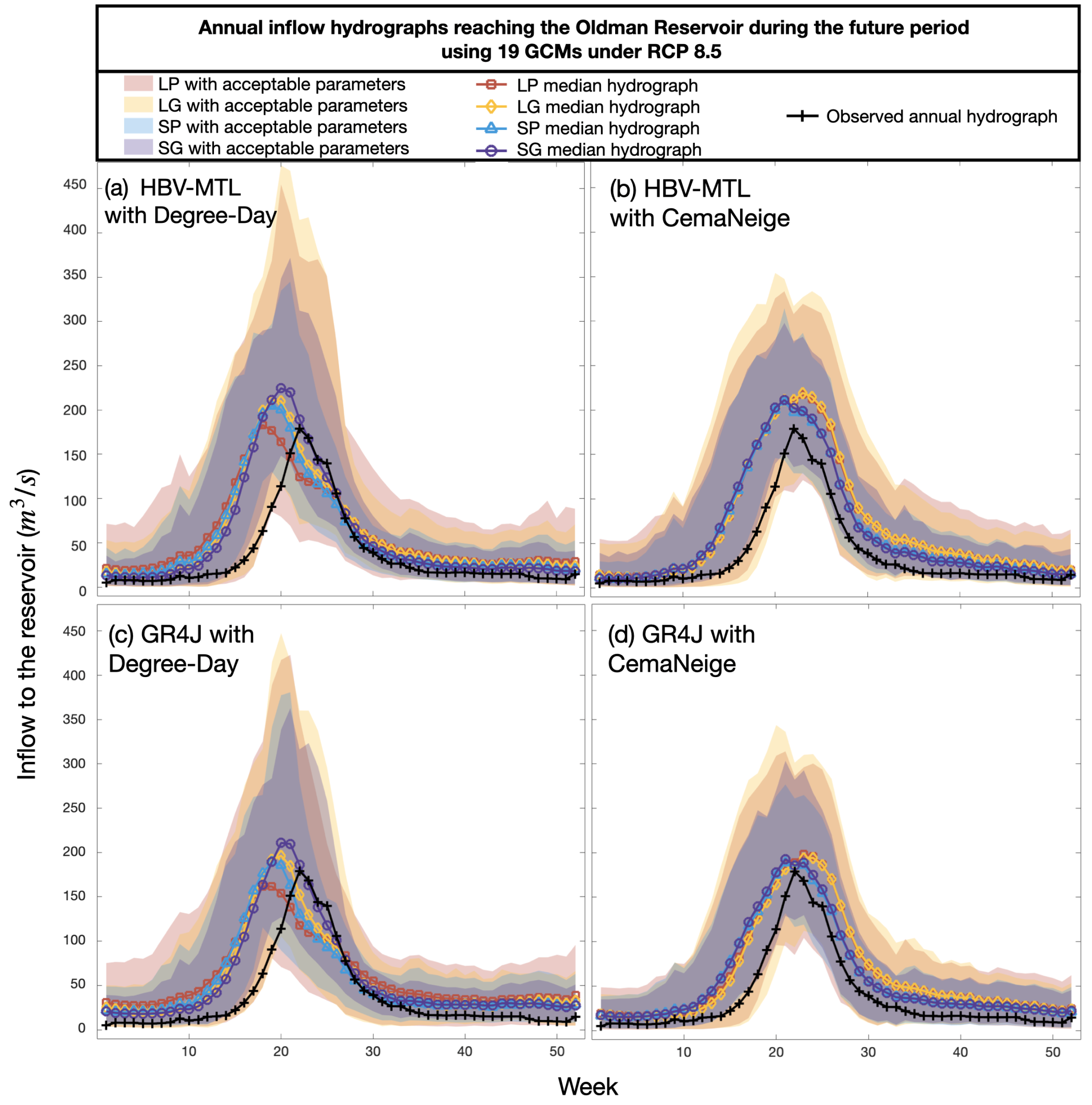
Since the performance of the hydrological models was reasonable and our strategy was to study uncertainties in water allocation stemming from modeling choices, all 16 models were used to project the streamflow reaching the Oldman Reservoir during 2021 and 2099. The annual inflow hydrographs in the future under RCPs 4.5 and 8.5 are shown in
Figure 3 and
Figure 4, respectively. In each figure, while the top and bottom rows present the flow for the HBV-MTL and GR4J models, the left and right columns show the results of these models using the Degree-Day and CemaNeige snow modules, respectively. In each panel, the envelopes of future inflow hydrographs are shown, considering the hydrological models with acceptable parameter sets for the lumped approach with point-based (LP) and grid-based (LG) data and the semi-distributed models with point-based (SP) and grid-based (SG) data. The medians of the envelopes are shown with solid lines. Under both future scenarios, all models unanimously projected more intense peak flows reaching the Oldman Reservoir in the future relative to the historical period. This could be due to projected increases in precipitation in the future, as noted previously. Overall, the snow module played a more prominent role than the other configurations in estimating future streamflow conditions, especially the peak flow timing and magnitude. While the hydrological models with the Degree-Day module projected intense and earlier peak flow timing, the CemaNeige module projected either similar or later peak flow timing, which could be due to the different modules’ formulated snowmelt processes. Moreover, it seems that the influence of catchment discretization and data resolution became more important using the Degree-Day module than the CemaNeige module. Indeed, the difference between the median projections using HBV-MTL and GR4J was relatively small; e.g., the difference for their peak projection was between 4–13%. The difference between the median peak flow projections of all 16 configurations could be as large as 42%. This illustrated the importance of using a multi-model approach for impact assessment.
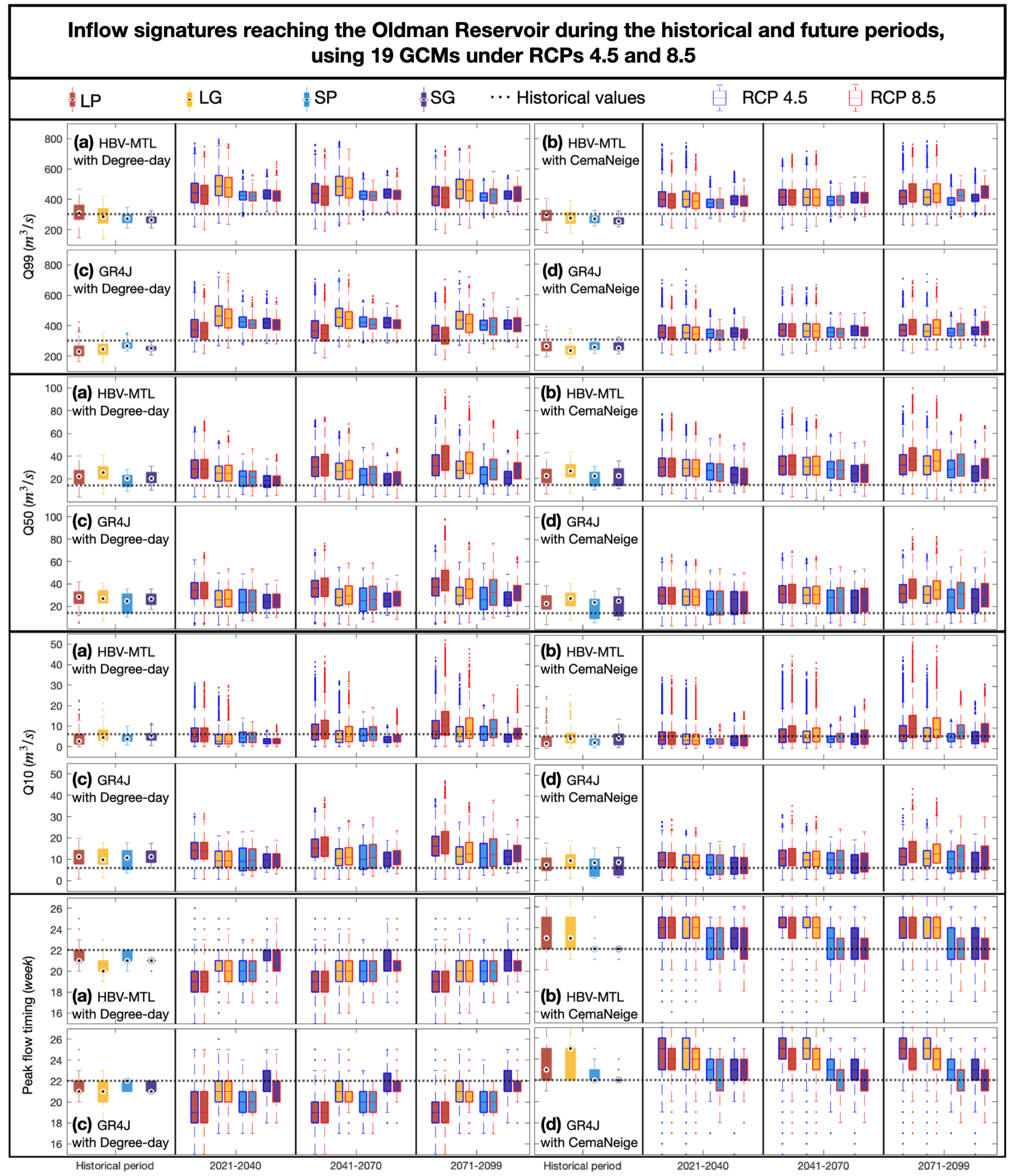
Here, we compare the historical and future Q99, Q50, Q10, and peak flow timing reaching the Oldman Reservoir in
Figure 5. For each flow signature, the observed values are displayed with a dashed line. The simulated (and future) values are shown using the models with acceptable parameter sets: HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules and GR4J with the (c) Degree-Day and (d) CemaNeige modules. The models were calibrated using a lumped approach with point-based (LP; red) and grid-based data (LG; yellow) and a semi-distributed approach with point-based (SP; blue) and grid-based data (SG; violet). The projections based on RCPs 4.5 and 8.5 are shown with blue and red box outlines, respectively. During the historical period, while the smallest difference among the models was for Q50, the largest divergence was more evident for the estimation of peak flow timing, in particular between the CemaNeige and Degree-Day modules. This was somewhat obvious due to these modules’ differences in snowmelt representation, e.g., with and without considering snowpack temperature, as discussed in
Section 3.4. Another important difference among the models was related to the estimation of low flows, for which the impact of HBV-MLT versus GR4J was more dominant than the other factors.
During 2021–2099, all hydrological models projected a rise in extremely high flow. Similar to the historical period, HBV-MTL presented slightly higher Q99 values than GR4J. Furthermore, the models with the Degree-Day module projected generally higher Q99 values in comparison to the CemaNeige module. For a given snow module, the role of catchment discretization in Q99 projection was larger than the data resolution. Considering the median values for Q50, the differences among the models were small, and all model configurations projected an increase in Q50 intensity in the future. Regarding the Q10 values, the projections became more sensitive to the choice of hydrological model than the choice of snow routine, followed by the choice of catchment discretization. Moreover, Q10 was larger under RCP 8.5 than under 4.5.
4.3. Reservoir Water Allocation during the Historical Period
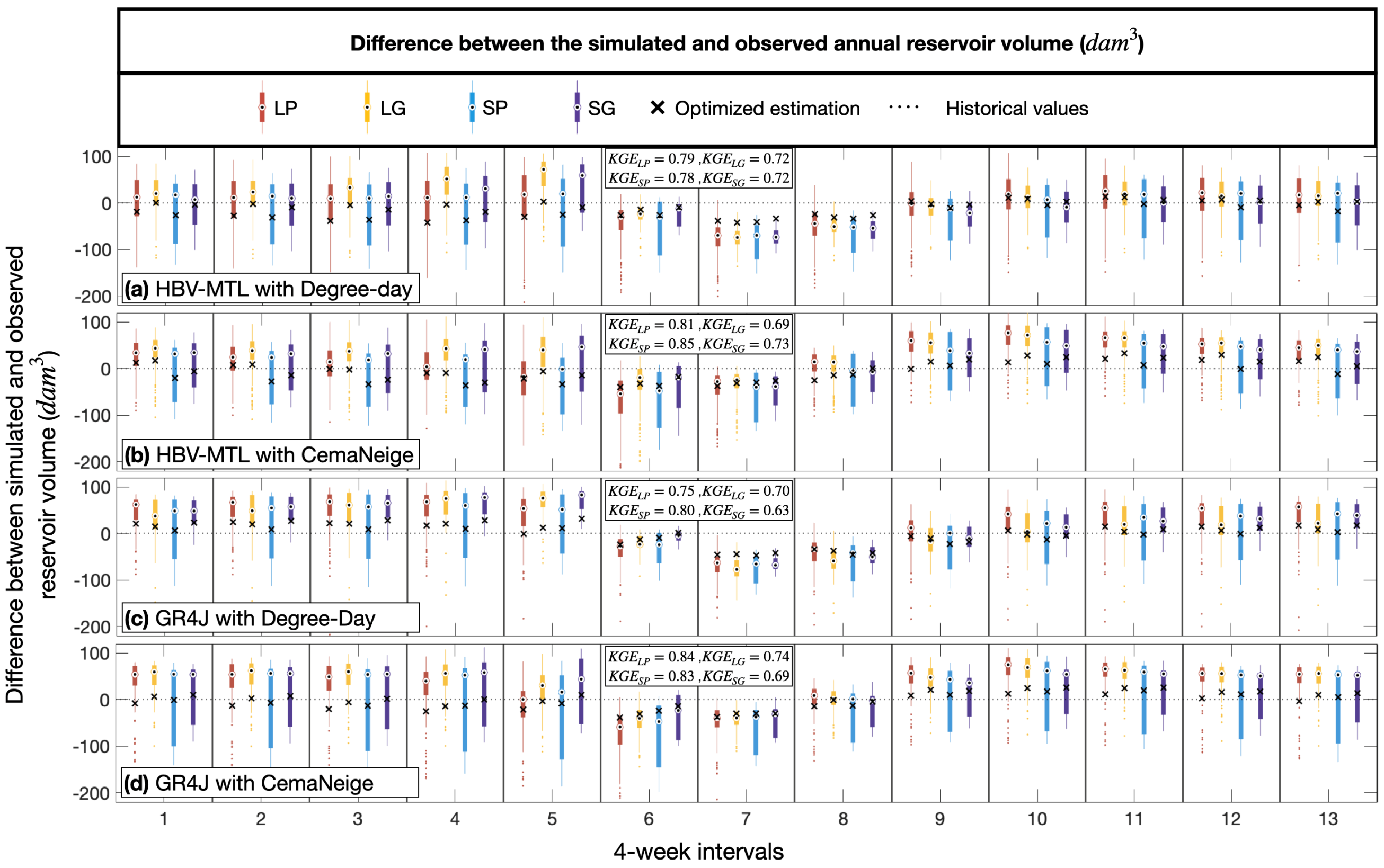
Here, we first examined the disparity between the observed and simulated water volume in the Oldman Reservoir during 1961–1990, which was obtained via feeding the estimated inflow based on the 16 hydrological model configurations into the Oldman water allocation model. The KGE values for this comparison are shown in
Figure 6, and they ranged between 0.69 and 0.85, demonstrating a good performance from the models. Moreover, although the difference between KGE values among the models was small, it seems that the models with the CemaNeige module, when using semi-distributed discretization and when calibrated with point-base data, outperformed the other configurations in estimating reservoir volume. To gain a better insight into the intra-annual performance of the models, the mean difference (dam
3) between the observed and simulated reservoir volume, averaged over a 30-year period for all models, based on optimal and acceptable parameter sets, is shown in
Figure 6. As can be seen, the performance of the models depended on the season. For instance, the HBV-MTL models better represented the historical values during the winter. Meanwhile, during early summer, when the water level is relatively high, the models with the CemaNeige module better reproduced the historical reservoir volume, and the models with the Degree-Day module performed slightly better during late summer.
Figure 7 compares the observed and simulated local water deficits of the 16 hydrological models using the acceptable and optimal parameter sets. While the influence of a snowmelt routine in estimating the water deficit was the most important factor, the choice of hydrological model was the least important one among the 16 configurations. The uncertainty boundaries of the simulations revealed that the models coupled with the Degree-Day module captured the historical conditions between the 25th and 75th percentiles. Considering the values found using the optimal parameter set, the HBV-MTL with Degree-Day module could capture the historical deficit well, and the difference between the considered catchment discretization and data conditions was small, as shown in the left panel.
4.4. Reservoir Water Allocation during the Future Period
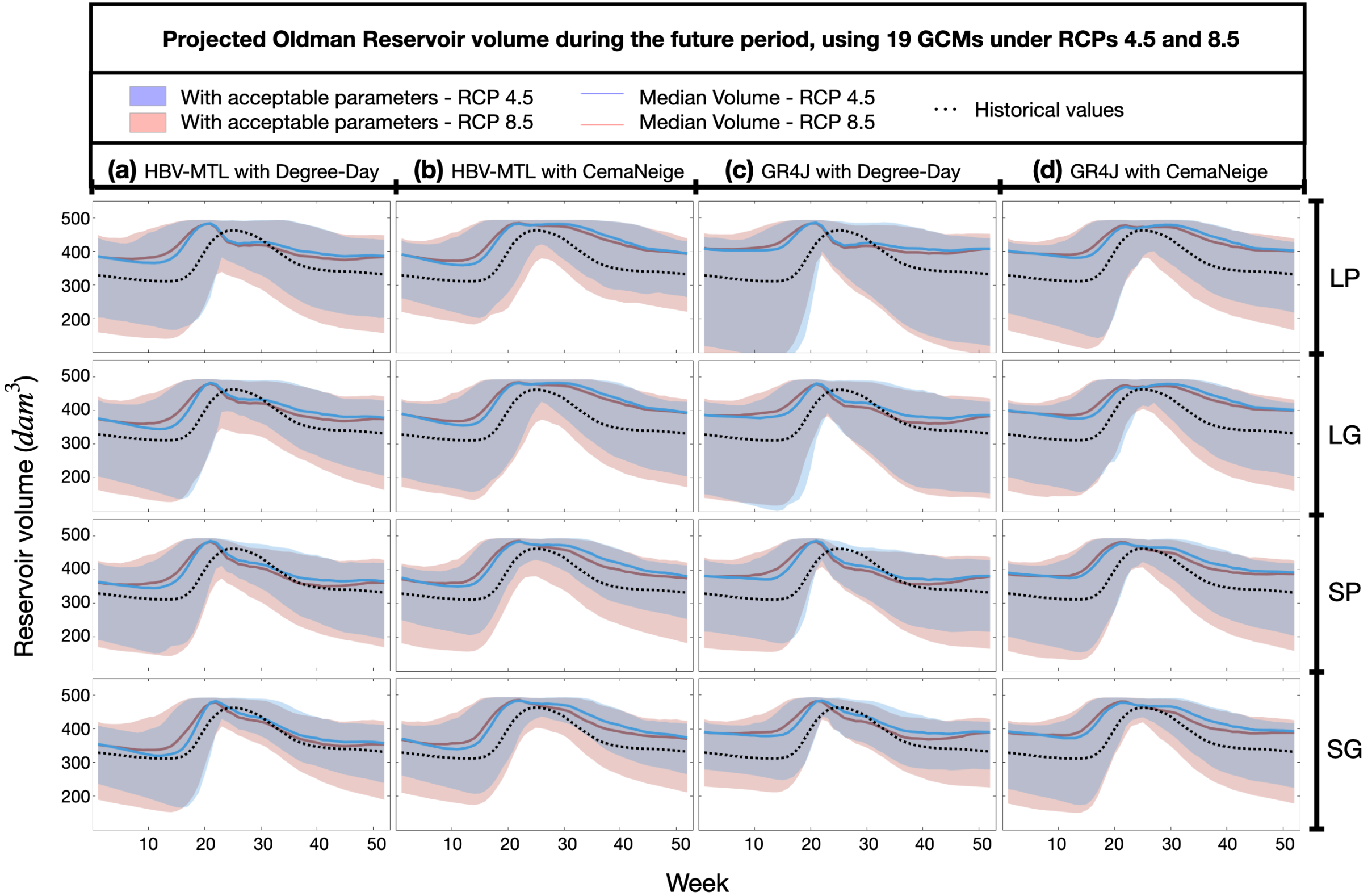
The volume of the Oldman reservoir in the future was estimated using the projections of 19 GCMs under RCPs 4.5 and 8.5, which were fed into the considered 16 hydrological models. The projected and historical reservoir storage was compared in
Figure 8. Similar to the previous observations, the role of snowmelt representation stood out among all configurations in projecting this storage; compare the median maximum storage values and their timing in the figure. Despite the divergences among the models, all of them unanimously projected increases with earlier shifts in the timing of the maximum volume in the future. Such changes were more obvious in the models with the Degree-Day snow module. These alterations in reservoir volume are important, indicating that business-as-usual operations should be revised to avoid dam overtopping a few weeks earlier than before in spring. These challenges for reservoir water management were more obvious under RCP 8.5, as larger water volume earlier in spring and lower values in summer were projected when a large irrigation supply was needed.
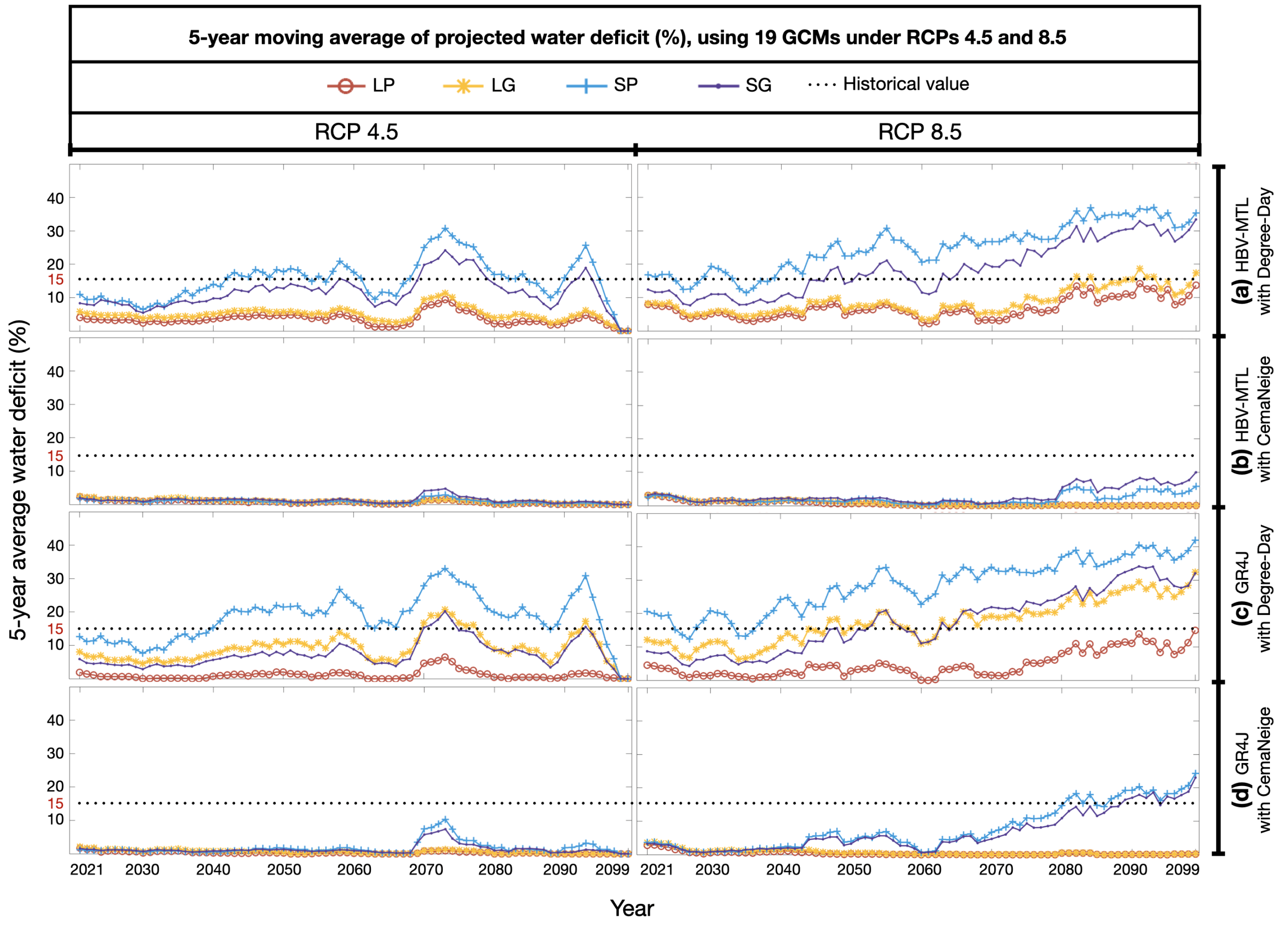
Here, we analyzed the evolution of the annual water deficit in the future and compared it with the average historical deficit of 15%.
Figure 9 presents the five-year moving average of the projected water deficit using the coupled models under RCPs 4.5 and 8.5. The models with the Degree-Day module project considerably larger water deficits throughout the century than those with the CemaNeige module, which was consistent with their behavior during the historical period. Moreover, the GR4J models suggested a slightly greater water deficit in the future than the HBV-MTL models. Using the same hydrological model and snow routine, the impact of catchment discretization was more significant than data conditions. The difference between projections was evident in the forcing scenario. While most models projected an increasing positive trend (
p-values < 0.05) in the water deficit by a maximum of 40% under RCP 8.5, the estimations under RCP 4 were are smaller and could be below the historical level by the end of the century. This is because, under RCP 8.5, the area’s temperature is expected to rise twice as much as under RCP 4.5 [
31]. Hence, meeting the local water demand could be challenging under the high concentration scenario.
5. Discussion
Our analysis demonstrated the importance of hydrological model configurations when examining water allocation under changing climate conditions. Moreover, it was found that the models employing semi-distributed catchment discretization and point-based data outperformed the lumped models calibrated with grid-based data, as noted by Sharifinejad et al. [
31]. Moreover, based on KGE values the performance of the HBV-MTL and GR4J models was almost similar, and the models with CemaNeige exhibited slightly superior performance than the Degree-Day snow module during the validation period. Nonetheless, considering other flow statistics, such as extremely low or high values or peak flow timing, the divergence between the models could become large. For instance, the models equipped with the CemaNeige module excelled at simulating peak flow timing, whereas those utilizing the Degree-Day module showed better performance in estimating the peak flow volume. Thus, we employed all models in climate change impact assessment due to the comprehensive nature of this study, in which all mentioned flow characteristics are vital for water management. Similarly, we showed how alternative hydrological configurations can influence the estimation of water system behavior in the future; especially the critical role of snowmelt representation was highlighted. Despite the differences between the models, all consistently projected higher peak flows during the snowmelt season and lower water availability during the summer, similar to Tanzeeba and Gan [
43] and Mahat and Anderson [
44].
There were a series of limitations in this study that should be improved upon in future works. For instance, we calibrated hydrological models based on historical observations and used them for impact assessment. However, it is important to acknowledge that these models may respond differently when forced by future climate projections [
79] and may not represent extreme flow values in the future [
80,
81]. Moreover, in addition to the considered hydrological configurations, it is crucial to account for the accurate representation of initial conditions, including the state of the snowpack at the beginning of the melt season and antecedent soil moisture conditions. These factors can significantly influence both the volume and timing of streamflow, potentially impacting the modeling of flood conditions [
82]. In addition to snowmelt, it is important to understand the sensitivity of assessments to represent other processes as well, such as evapotranspiration or infiltration. Moreover, we utilized CMIP5 projections under RCPs 4.5 and 8.5 for impact assessment. However, a recent study by Bourdeau-Goulet and Hassanzadeh [
8] has revealed a more significant increase in temperature and extreme precipitation under Shared Socioeconomic Pathways 2 and 5 for this region. Therefore, it is suggested to extend these analyses using these recently available CMIP6 projections for a more comprehensive assessment, similar to [
83]. Moreover, our analysis assumed no change in regional water demand during the 2021–2099 period compared to the historical period. Future studies should incorporate potential changes in water demand, in particular for irrigated agriculture, by taking into account changes in temperature and precipitation. This will enable a more reasonable evaluation of reservoir water management under changing water availability and demand conditions [
84].
6. Conclusions
The changing climate is placing unprecedented pressure on water resources. The impact of climate change on water systems can be assessed utilizing climate model projections and incorporating them into hydrological and water allocation models. This study aimed to understand the roles of various hydrological model configurations in estimating water system behavior under a changing climate. For this purpose, we considered 16 hydrological model configurations. Two distinct hydrological models, HBV-MTL and GR4J, were utilized, each with two snowmelt estimation modules: Degree-Day and CemaNeige. These models were calibrated using both lumped and semi-distributed catchment discretization approaches, incorporating point- and grid-based climate data. The models were employed to evaluate water allocation in the headwater Oldman River Basin in Alberta, Canada.
While all hydrological models exhibited relatively high KGE values during both the calibration and control periods, the differences between them become apparent when focusing on specific streamflow characteristics. Among all configurations, the snowmelt routine was found to play a crucial role, followed by the type of hydrological model, catchment discretization, and data resolution in most cases. This pattern consistently emerged in estimating reservoir storage, outflow, and the annual water deficit. However, the divergence between the models was more pronounced when estimating low and peak flow intensity and timing. The integrated models were then fed with the outputs of 19 climate models under RCPs 4.5 and 8.5 for impact assessment. While all models unanimously projected a significant increase in the intensity of inflow to the Oldman Reservoir, the magnitude of this increase depended on the chosen hydrological configuration. In particular, the projected shifts in peak flow timing were greatly influenced by the choice of snow models. In contrast, the projected intensity of low flow in the future was mainly controlled using the choice of hydrological model, as HBV-MTL provided lower values than GR4J.
Similar to the historical period, snowmelt modules exerted the primary influence on the simulated future reservoir dynamics. For instance, the models with the Degree-Day module projected a smaller reservoir water volume than those with the CemaNeige snow routine. This transition in the reservoir volume was clearly reflected in an estimated water deficit in which the models with the Degree-Day module suggested a considerably larger water shortage than those with the CemaNeige module. Moreover, an ascending trend in the water deficit was found, based on most models under RCP 8.5. Considering the alterations in inflow conditions, particularly the timing and magnitude of peak flow, and the challenges of meeting water demand, it becomes imperative to update the Oldman Reservoir operational plans to effectively mitigate the adverse impacts of climate change.
Overall, our study reveals that alternative configurations in hydrological modeling can significantly influence the projected climate change impacts on water systems. In our study area, the representation of snowmelt was found to be more crucial than other factors, such as the choice of hydrological model, catchment discretization, or data resolution. This highlights the importance of not only using a multi-model approach, as suggested in the literature, but also carefully considering multiple process representations for individual processes. The choice should be based on their significance in the context of the hydroclimatic conditions of watersheds. The study’s findings can be further validated and generalized via applying the same modeling approach in other study areas.
Author Contributions
Conceptualization, A.S. and E.H.; methodology, A.S. and E.H.; validation, A.S. and E.H.; formal analysis, A.S. and E.H.; investigation, A.S. and E.H.; resources, A.S. and E.H.; data curation, A.S.; writing—original draft preparation, A.S. and E.H.; writing—review and editing, A.S. and E.H.; visualization, A.S.; supervision, E.H.; project administration, E.H.; funding acquisition, E.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by an Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant, RGPIN-2020-05563, awarded to the corresponding author.
Data Availability Statement
Acknowledgments
The authors are thankful to Ali Nazemi for providing the operational data on the Oldman Reservoir used in this study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Table A1.
Hydrometric stations and average annual flow during 1961–1990 in each sub-watershed of the headwater Oldman River Basin.
Table A1.
Hydrometric stations and average annual flow during 1961–1990 in each sub-watershed of the headwater Oldman River Basin.
| Sub-Watershed | Station | Average Annual Flow (106 m3) | Drainage Area (km2) |
|---|
| Castle | 05AA022 | 472 | 821 |
| Crowsnest | 05AA008 | 153 | 403 |
| Oldman | 05AA035 | 383 | 1450 |
| NR | 05AA024 | 1200 | 1706 |
Table A2.
Average precipitation and temperature data during 1961–1990 in each sub-watershed of the headwater Oldman River Basin, obtained from point-based (climate stations) and grid-based data of the Alberta Township System.
Table A2.
Average precipitation and temperature data during 1961–1990 in each sub-watershed of the headwater Oldman River Basin, obtained from point-based (climate stations) and grid-based data of the Alberta Township System.
Sub-
Watershed | Point-Based Data | Grid-Based Data |
|---|
| Station | Mean
Annual
Precipitation (mm) | ) | ) | Number
of
Townships | Mean
Annual
Precipitation (mm) | ) | )
|
|---|
| Castle | Ironstone
Castle | 721 | −3 | 8 | 9 | 742 | −2 | 9.5 |
| Crowsnest | Coleman | 544 | −2.5 | 9 | 5 | 570 | −2.5 | 9 |
| Oldman | Sugarloaf Lo
Livingstone Lo
Hailstone Butte Lo | 536 | −5 | 4 | 19 | 605 | −3.5 | 8 |
| NR | Beaver Mines
Cowley Olin Creek | 380 | −1 | 6.5 | 22 | 537 | −2 | 10 |
Table A3.
Optimal calibration parameters obtained for HBV-MLT model with Degree-Day snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
Table A3.
Optimal calibration parameters obtained for HBV-MLT model with Degree-Day snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
|
Parameters
|
LP
|
LG
|
SP-Castle
|
SP-Crowsnest
|
SP-Oldman
|
SP-NR
|
SG-Castle
|
SG-Crowsnest
|
SG-Oldman
|
SG-NR
|
|---|
HBV-MTL
Degree-Day | Degree-day coefficient | 2.06 | 1.03 | 1.43 | 1.03 | 1.78 | 1.60 | 1.20 | 1.71 | 1.27 | 1.67 |
| Potential ET coefficient | 0.99 | 1.00 | 0.66 | 0.30 | 0.59 | 1.00 | 0.46 | 0.46 | 0.81 | 1.00 |
| Low soil moisture coefficient | 0.50 | 0.30 | 0.20 | 0.33 | 0.24 | 0.20 | 0.20 | 0.50 | 0.20 | 0.20 |
| Snow capacity to retain water | 0.00 | 0.00 | 0.00 | 0.16 | 0.00 | 0.00 | 0.20 | 0.17 | 0.20 | 0.13 |
| Topmost outlet’s coefficient | 0.01 | 0.14 | 0.15 | 0.09 | 0.04 | 0.23 | 0.19 | 0.03 | 0.06 | 0.30 |
| Intermediate outlet’s coefficient | 0.05 | 0.05 | 0.05 | 0.04 | 0.05 | 0.03 | 0.05 | 0.02 | 0.05 | 0.05 |
| Bottom outlet’s coefficient | 0.05 | 0.03 | 0.04 | 0.05 | 0.03 | 0.02 | 0.05 | 0.05 | 0.05 | 0.04 |
| Percolation coefficient | 0.04 | 0.05 | 0.05 | 0.04 | 0.01 | 0.04 | 0.05 | 0.05 | 0.05 | 0.02 |
| Topmost outlet’s trigger | 4.95 | 16.32 | 37.35 | 35.35 | 0.02 | 0.05 | 49.69 | 43.69 | 12.27 | 29.20 |
| Soil moisture capacity | 192 | 106 | 78 | 138 | 191 | 193 | 51 | 260 | 80 | 195 |
| Base of triangle delay function | 3.37 | 1.03 | 2.33 | 1.02 | 1.01 | 1.02 | 2.58 | 3.57 | 1.04 | 1.04 |
| Soil’s water absorption coefficient | 1.28 | 1.21 | 4.53 | 1.95 | 3.81 | 4.99 | 3.17 | 3.68 | 1.14 | 4.96 |
| Soil’s curve number | 85.1 | 54.5 | 67.3 | 31.0 | 33.5 | 32.0 | 69.7 | 72.5 | 47.3 | 50.1 |
| Frozen soil coefficient | 3.29 | 3.54 | 4.98 | 4.93 | 3.82 | 4.97 | 3.63 | 4.46 | 3.32 | 2.20 |
| Soil frost temperature threshold | 0.28 | −0.77 | −1.96 | −0.92 | 0.28 | −0.03 | −1.85 | −0.12 | 0.32 | −0.63 |
| Melting temperature threshold | 1.56 | 1.85 | 0.55 | 2.00 | −0.26 | 2.00 | 2.00 | 1.99 | 2.00 | 2.00 |
| Snow correction factor | 1.00 | 1.05 | 1.20 | 1.20 | 0.69 | 0.82 | 1.20 | 1.20 | 0.77 | 0.89 |
| Unit hydrograph delay time for Castle inflow | N/A | N/A | N/A | N/A | N/A | 2.76 | N/A | N/A | N/A | 2.41 |
| Unit hydrograph delay time for Crowsnest inflow | N/A | N/A | N/A | N/A | N/A | 1.83 | N/A | N/A | N/A | 2.99 |
| Unit hydrograph delay time for Oldman inflow | N/A | N/A | N/A | N/A | N/A | 2.19 | N/A | N/A | N/A | 2.54 |
Table A4.
Optimal calibration parameters obtained for HBV-MLT model with CemaNeige snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
Table A4.
Optimal calibration parameters obtained for HBV-MLT model with CemaNeige snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
|
Parameters
|
LP
|
LG
|
SP-Castle
|
SP-Crowsnest
|
SP-Oldman
|
SP-NR
|
SG-Castle
|
SG-Crowsnest
|
SG-Oldman
|
SG-NR
|
|---|
HBV-
MTL
CemaNeige | Degree-day coefficient | 6.00 | 5.98 | 3.83 | 2.72 | 5.98 | 5.94 | 3.37 | 4.02 | 4.95 | 5.74 |
| Potential ET coefficient | 1.00 | 1.00 | 1.00 | 0.45 | 0.99 | 1.00 | 0.75 | 0.65 | 1.00 | 1.00 |
| Low soil moisture coefficient | 0.27 | 0.27 | 0.22 | 0.50 | 0.26 | 0.20 | 0.21 | 0.40 | 0.40 | 0.20 |
| Snow capacity to retain water | 0.10 | 0.14 | 0.04 | 0.06 | 0.04 | 0.18 | 0.04 | 0.00 | 0.08 | 0.20 |
| Topmost outlet’s coefficient | 0.14 | 0.18 | 0.14 | 0.10 | 0.07 | 0.22 | 0.18 | 0.09 | 0.11 | 0.24 |
| Intermediate outlet’s coefficient | 0.02 | 0.02 | 0.03 | 0.02 | 0.05 | 0.04 | 0.02 | 0.03 | 0.04 | 0.03 |
| Bottom outlet’s coefficient | 0.00 | 0.05 | 0.05 | 0.05 | 0.00 | 0.04 | 0.04 | 0.05 | 0.05 | 0.04 |
| Percolation coefficient | 0.00 | 0.00 | 0.01 | 0.00 | 0.01 | 0.03 | 0.00 | 0.00 | 0.00 | 0.03 |
| Topmost outlet’s trigger | 35 | 39 | 30 | 48 | 13 | 0.2 | 0.9 | 48 | 27 | 5.2 |
| Soil moisture capacity | 87 | 124 | 71 | 61 | 67 | 228 | 67 | 396 | 108 | 196 |
| Base of triangle delay function | 1.01 | 1.12 | 2.27 | 1.07 | 1.06 | 1.08 | 2.59 | 1.05 | 1.02 | 1.03 |
| Soil’s water absorption coefficient | 1.04 | 1.00 | 2.20 | 1.01 | 1.02 | 2.82 | 1.40 | 2.77 | 1.08 | 2.82 |
| Soil’s curve number | 58.4 | 62.5 | 79.6 | 54.2 | 37.1 | 49.5 | 85.6 | 38.4 | 50.6 | 52.7 |
| Frozen soil coefficient | 4.96 | 1.97 | 4.98 | 4.25 | 3.33 | 3.39 | 2.67 | 4.23 | 4.90 | 3.50 |
| Soil frost temperature threshold | −1.46 | −0.55 | −1.86 | −1.45 | −1.51 | −0.89 | −1.33 | −1.68 | −1.90 | 0.14 |
| Thermal inertia factor | 0.47 | 0.88 | 0.66 | 0.94 | 0.14 | 0.62 | 0.96 | 0.92 | 0.93 | 0.74 |
| Snow correction factor | 0.77 | 0.79 | 1.18 | 1.12 | 0.77 | 0.60 | 1.20 | 1.18 | 0.73 | 0.60 |
| Unit hydrograph delay time for Castle inflow | N/A | N/A | N/A | N/A | N/A | 1.30 | N/A | N/A | N/A | 3.35 |
| Unit hydrograph delay time for Crowsnest inflow | N/A | N/A | N/A | N/A | N/A | 3.78 | N/A | N/A | N/A | 2.16 |
| Unit hydrograph delay time for Oldman inflow | N/A | N/A | N/A | N/A | N/A | 3.68 | N/A | N/A | N/A | 2.50 |
Table A5.
Optimal calibration parameters obtained for GR4J model with Degree-Day snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
Table A5.
Optimal calibration parameters obtained for GR4J model with Degree-Day snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
|
Parameters
|
LP
|
LG
|
SP-Castle
|
SP-Crowsnest
|
SP-Oldman
|
SP-NR
|
SG-Castle
|
SG-Crowsnest
|
SG-Oldman
|
SG-NR
|
|---|
GR4J-
Degree-Day | Degree-day coefficient | 1.47 | 1.19 | 1.07 | 1.33 | 1.95 | 1.66 | 1.09 | 1.49 | 1.26 | 1.67 |
| Melting temperature threshold | 0.50 | 1.65 | -0.35 | 2.00 | −0.90 | 2.00 | 2.00 | 1.82 | 1.42 | 2.00 |
| Snow capacity to retain water | 0.00 | 0.00 | 0.00 | 0.20 | 0.03 | 0.00 | 0.11 | 0.12 | 0.03 | 0.03 |
| Potential ET coefficient | 0.99 | 1.00 | 1.00 | 0.54 | 1.00 | 1.00 | 1.00 | 1.00 | 0.95 | 1.00 |
| Maximum production storage | 54 | 73 | 103 | 45 | 24 | 285 | 20 | 28 | 44 | 291 |
| Water exchange coefficient | −4.5 | −3.6 | 1.6 | 2.6 | −3.1 | −1.6 | 2.4 | 3.7 | −4.4 | −1.2 |
| Routing storage capacity | 442 | 353 | 155 | 399 | 406 | 2 | 225 | 478 | 327 | 1 |
| Unit hydrograph delay time | 0.51 | 0.50 | 0.75 | 1.07 | 0.54 | 0.92 | 0.56 | 0.87 | 0.50 | 0.88 |
| Snow correction factor | 1.12 | 1.20 | 1.20 | 1.17 | 0.92 | 1.20 | 1.20 | 1.20 | 1.03 | 1.20 |
| Unit hydrograph delay time for Castle inflow | N/A | N/A | N/A | N/A | N/A | 2.59 | N/A | N/A | N/A | 2.17 |
| Unit hydrograph delay time for Crowsnest inflow | N/A | N/A | N/A | N/A | N/A | 1.56 | N/A | N/A | N/A | 2.16 |
| Unit hydrograph delay time for Oldman inflow | N/A | N/A | N/A | N/A | N/A | 0.63 | N/A | N/A | N/A | 0.67 |
Table A6.
Optimal calibration parameters obtained for GR4J model with CemaNeige snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
Table A6.
Optimal calibration parameters obtained for GR4J model with CemaNeige snow routine during the historical period. The values are presented for (1) lumped models, calibrated using point- (LP) and grid-based data (LG), as well as (2) semi-distributed models with point- (SP) and grid-based (SG) data, for each sub-watershed.
|
Parameters
|
LP
|
LG
|
SP-Castle
|
SP-Crowsnest
|
SP-Oldman
|
SP-NR
|
SG-Castle
|
SG-Crowsnest
|
SG-Oldman
|
SG-NR
|
|---|
| GR4J-CemaNeige | Degree-day coefficient | 5.99 | 6.00 | 3.94 | 2.48 | 6.00 | 6.00 | 3.74 | 3.60 | 2.94 | 6.0 |
| Melting temperature threshold | 0.43 | 0.92 | 0.58 | 0.93 | 0.14 | 0.76 | 0.95 | 0.91 | 0.95 | 0.8 |
| Snow capacity to retain water | 0.09 | 0.00 | 0.05 | 0.07 | 0.00 | 1 × 10−1 | 0.05 | 0.04 | 0.02 | 0.1 |
| Potential ET coefficient | 0.87 | 0.88 | 1.00 | 0.43 | 0.87 | 1.00 | 0.98 | 0.66 | 1.00 | 1.0 |
| Maximum production storage | 61.1 | 68.1 | 73.6 | 10.0 | 10.0 | 216.6 | 42.5 | 16.5 | 10.0 | 218 |
| Water exchange coefficient | −9.9 | −9.6 | −0.35 | −1.50 | −9.98 | −8.98 | 1.09 | −1.84 | −10.00 | −7.9 |
| Routing storage capacity | 310 | 331 | 194 | 284 | 331 | 65 | 191 | 379 | 280 | 46 |
| Unit hydrograph delay time | 0.5 | 0.52 | 0.74 | 1.10 | 0.70 | 0.50 | 0.56 | 1.11 | 0.80 | 0.5 |
| Snow correction factor | 1.08 | 1.09 | 1.20 | 1.20 | 1.00 | 1.13 | 1.20 | 1.20 | 1.12 | 1.2 |
| Unit hydrograph delay time for Castle inflow | N/A | N/A | N/A | N/A | N/A | 1.54 | N/A | N/A | N/A | 1.96 |
| Unit hydrograph delay time for Crowsnest inflow | N/A | N/A | N/A | N/A | N/A | 3.98 | N/A | N/A | N/A | 1.29 |
| Unit hydrograph delay time for Oldman inflow | N/A | N/A | N/A | N/A | N/A | 2.68 | N/A | N/A | N/A | 2.11 |
References
- Grillakis, M.G. Increase in severe and extreme soil moisture droughts for Europe under climate change. Sci. Total Environ. 2019, 660, 1245–1255. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate change will affect global water availability through compounding changes in seasonal precipitation and evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef] [PubMed]
- Curry, C.L.; Islam, S.U.; Zwiers, F.W.; Déry, S.J. Atmospheric Rivers Increase Future Flood Risk in Western Canada’s Largest Pacific River. Geophys. Res. Lett. 2019, 46, 1651–1661. [Google Scholar] [CrossRef]
- Islam, S.U.; Déry, S.J.; Werner, A.T. Future Climate Change Impacts on Snow and Water Resources of the Fraser River Basin, British Columbia. J. Hydrometeorol. 2017, 18, 473–496. [Google Scholar] [CrossRef]
- Krasting, J.P.; Broccoli, A.J.; Dixon, K.W.; Lanzante, J.R. Future Changes in Northern Hemisphere Snowfall. J. Clim. 2013, 26, 7813–7828. [Google Scholar] [CrossRef]
- Pierce, D.W.; Cayan, D.R. The Uneven Response of Different Snow Measures to Human-Induced Climate Warming. J. Clim. 2013, 26, 4148–4167. [Google Scholar] [CrossRef]
- Crévolin, V.; Hassanzadeh, E.; Bourdeau-Goulet, S.C. Updating the Intensity-Duration-Frequency Curves in Major Canadian Cities under Changing Climate Using CMIP5 and CMIP6 Model Projections. Sustain. Cities Soc. 2023, 92, 104473. [Google Scholar] [CrossRef]
- Bourdeau-Goulet, S.C.; Hassanzadeh, E. Comparisons between CMIP5 and CMIP6 Models: Simulations of Climate Indices Influencing Food Security, Infrastructure Resilience, and Human Health in Canada. Earth’s Future 2021, 9, e2021EF001995. [Google Scholar] [CrossRef]
- Mohanty, M.P.; Simonovic, S.P. Changes in Floodplain Regimes over Canada Due to Climate Change Impacts: Observations from CMIP6 Models. Sci. Total Environ. 2021, 792, 148323. [Google Scholar] [CrossRef]
- Nazemi, A.; Zaerpour, M.; Hassanzadeh, E. Uncertainty in Bottom-Up Vulnerability Assessments of Water Supply Systems Due to Regional Streamflow Generation under Changing Conditions. J. Water Resour. Plann. Manag. 2020, 146, 04019071. [Google Scholar] [CrossRef]
- Kurkute, S.; Li, Z.; Li, Y.; Huo, F. Assessment and Projection of the Water Budget over Western Canada Using Convection-Permitting Weather Research and Forecasting Simulations. Hydrol. Earth Syst. Sci. 2020, 24, 3677–3697. [Google Scholar] [CrossRef]
- IPCC. 2023: Summary for Policymakers. In Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 1–34. [Google Scholar] [CrossRef]
- Hingray, B.; Saïd, M. Partitioning Internal Variability and Model Uncertainty Components in a Multimember Multimodel Ensemble of Climate Projections. J. Clim. 2014, 27, 6779–6798. [Google Scholar] [CrossRef]
- Giuntoli, I.; Villarini, G.; Prudhomme, C.; Hannah, D.M. Uncertainties in Projected Runoff over the Conterminous United States. Clim. Chang. 2018, 150, 149–162. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The Potential to Narrow Uncertainty in Regional Climate Predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
- Anaraki, M.V.; Farzin, S.; Mousavi, S.F.; Karami, H. Uncertainty Analysis of Climate Change Impacts on Flood Frequency by Using Hybrid Machine Learning Methods. Water Resour. Manag. 2021, 35, 199–223. [Google Scholar] [CrossRef]
- Karamouz, M.; Goharian, E.; Nazif, S. Reliability Assessment of the Water Supply Systems under Uncertain Future Extreme Climate Conditions. Earth Interact. 2013, 17, 1–27. [Google Scholar] [CrossRef]
- Dong, F.; Javed, A.; Saber, A.; Neumann, A.; Alberto Arnillas, C.; Kaltenecker, G.; Arhonditsis, G. A Flow-Weighted Ensemble Strategy to Assess the Impacts of Climate Change on Watershed Hydrology. J. Hydrol. 2021, 594, 125898. [Google Scholar] [CrossRef]
- Her, Y.; Yoo, S.H.; Cho, J.; Hwang, S.; Jeong, J.; Seong, C. Uncertainty in Hydrological Analysis of Climate Change: Multi-Parameter vs. Multi-GCM Ensemble Predictions. Sci. Rep. 2019, 9, 4974. [Google Scholar] [CrossRef]
- Hattermann, F.F.; Vetter, T.; Breuer, L.; Su, B.; Daggupati, P.; Donnelly, C.; Fekete, B.; Flörke, F.; Gosling, S.N.; Hoffmann, P.; et al. Sources of Uncertainty in Hydrological Climate Impact Assessment: A Cross-Scale Study. Environ. Res. Lett. 2018, 13, 015006. [Google Scholar] [CrossRef]
- Huang, S.; Shah, H.; Naz, B.S.; Shrestha, N.; Mishra, V.; Daggupati, P.; Ghimire, U.; Vetter, T. Impacts of Hydrological Model Calibration on Projected Hydrological Changes under Climate Change—A Multi-Model Assessment in Three Large River Basins. Clim. Chang. 2020, 163, 1143–1164. [Google Scholar] [CrossRef]
- Saavedra, D.; Mendoza, P.A.; Addor, N.; Llauca, H.; Vargas, X. A Multi-Objective Approach to Select Hydrological Models and Constrain Structural Uncertainties for Climate Impact Assessments. Hydrol. Process. 2022, 36, e14446. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Breuer, L.; Chamorro, A.; Flörke, M.; Pechlivanidis, I.G.; Schäfer, D.; Shah, H.; Vetter, T.; Wortmann, M.; et al. Propagation of Forcing and Model Uncertainties onto Hydrological Drought Characteristics in a Multi-Model Century-Long Experiment in Large River Basins. Clim. Chang. 2017, 141, 435–449. [Google Scholar] [CrossRef]
- Shi, L.; Feng, P.; Wang, B.; Liu, D.L.; Zhang, H.; Liu, J.; Yu, Q. Assessing Future Runoff Changes with Different Potential Evapotranspiration Inputs Based on Multi-Model Ensemble of CMIP5 Projections. J. Hydrol. 2022, 612, 128042. [Google Scholar] [CrossRef]
- Alvarado-Montero, R.; Uysal, G.; Collados-Lara, A.-J.; Arda Şorman, A.; Pulido-Velazquez, D.; Şensoy, A. Comparison of Sequential and Variational Assimilation Methods to Improve Hydrological Predictions in Snow Dominated Mountainous Catchments. J. Hydrol. 2022, 612, 127981. [Google Scholar] [CrossRef]
- Günther, D.; Marke, T.; Essery, R.; Strasser, U. Uncertainties in Snowpack Simulations—Assessing the Impact of Model Structure, Parameter Choice, and Forcing Data Error on Point-Scale Energy Balance Snow Model Performance. Water Resour. Res. 2019, 55, 2779–2800. [Google Scholar] [CrossRef]
- Nemri, S.; Kinnard, C. Comparing Calibration Strategies of a Conceptual Snow Hydrology Model and Their Impact on Model Performance and Parameter Identifiability. J. Hydrol. 2020, 582, 124474. [Google Scholar] [CrossRef]
- Ekmekcioğlu, Ö.; Demirel, M.C.; Booij, M.J. Effect of Data Length, Spin-Up Period, and Spatial Model Resolution on Fully Distributed Hydrological Model Calibration in the Moselle Basin. Hydrol. Sci. J. 2022, 67, 759–772. [Google Scholar] [CrossRef]
- Munoth, P.; Goyal, R. Effects of DEM Source, Spatial Resolution, and Drainage Area Threshold Values on Hydrological Modeling. Water Resour. Manag. 2019, 33, 3303–3319. [Google Scholar] [CrossRef]
- Uysal, G.; Şorman, A.Ü. Evaluation of PERSIANN Family Remote Sensing Precipitation Products for Snowmelt Runoff Estimation in a Mountainous Basin. Hydrol. Sci. J. 2021, 66, 1790–1807. [Google Scholar] [CrossRef]
- Sharifinejad, A.; Hassanzadeh, E.; Zaerpour, M. Assessing Water System Vulnerabilities under Changing Climate Conditions Using Different Representations of a Hydrological System. Hydrol. Sci. J. 2022, 67, 287–303. [Google Scholar] [CrossRef]
- Martz, L.; Bruneau, J.; Rolfe, J. Climate Change and Water: SSRB (South Saskatchewan River Basin) Final Technical Report. 2007. Available online: https://www.parc.ca/wp-content/uploads/2019/05/SSRB-2007-Climate_change_and_water.pdf (accessed on 7 August 2023).
- Nazemi, A.; Wheater, H.S.; Chun, K.P.; Bonsal, B.; Mekonnen, M. Forms and Drivers of Annual Streamflow Variability in the Headwaters of Canadian Prairies during the 20th Century. Hydrol. Process. 2017, 31, 221–239. [Google Scholar] [CrossRef]
- Harder, P.; Pomeroy, J.W.; Westbrook, C.J. Hydrological Resilience of a Canadian Rockies Headwaters Basin Subject to Changing Climate, Extreme Weather, and Forest Management. Hydrol. Process. 2015, 29, 3905–3924. [Google Scholar] [CrossRef]
- Whitfield, P.H.; Pomeroy, J.W. Changes to Flood Peaks of a Mountain River: Implications for Analysis of the 2013 Flood in the Upper Bow River, Canada. Hydrol. Process. 2016, 30, 4657–4673. [Google Scholar] [CrossRef]
- Zhang, X.; Flato, G.; Kirchmeier-Young, M.; Vincent, L.A.; Wan, H.; Wang, X.; Rong, R.; Fyfe, J.; Li, G.; Kharin, V.V. Changes in Temperature and Precipitation across Canada. Canada’s Changing Climate Report 2019. Available online: https://natural-resources.canada.ca/sites/www.nrcan.gc.ca/files/energy/Climate-change/pdf/CCCR-Chapter4-TemperatureAndPrecipitationAcrossCanada.pdf (accessed on 7 August 2023).
- Musselman, K.N.; Addor, N.; Vano, J.A.; Molotch, N.P. Winter Melt Trends Portend Widespread Declines in Snow Water Resources. Nat. Clim. Chang. 2021, 11, 418–424. [Google Scholar] [CrossRef]
- Newton, B.W.; Farjad, B.; Orwin, J.F. Spatial and Temporal Shifts in Historic and Future Temperature and Precipitation Patterns Related to Snow Accumulation and Melt Regimes in Alberta, Canada. Water 2021, 13, 1013. [Google Scholar] [CrossRef]
- Zaremehrjardy, M.; Victor, J.; Park, S.; Smerdon, B.; Alessi, D.S.; Faramarzi, M. Assessment of Snowmelt and Groundwater-Surface Water Dynamics in Mountains, Foothills, and Plains Regions in Northern Latitudes. J. Hydrol. 2022, 606, 127449. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, Y.; Li, Z.; Chang, J.; Guo, A. Quantifying the Uncertainty Interaction between the Model Input and Structure on Hydrological Processes. Water Resour. Manag. 2021, 35, 3915–3935. [Google Scholar] [CrossRef]
- ESTR Secretariat. Prairies Exozone Evidence for Key Findings Summary. In Canadian Biodiversity: Ecosystem Status and Trends 2010. Evidence for Key Findings Summary Report No. 4; Canadian Councils of Resource Ministers: Ottawa, ON, Canada, 2014; Available online: https://publications.gc.ca/collections/collection_2015/ec/En14-43-0-4-2014-eng.pdf (accessed on 7 August 2023).
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Tanzeeba, S.; Gan, T.Y. Potential Impact of Climate Change on the Water Availability of South Saskatchewan River Basin. Clim. Chang. 2012, 112, 355–386. [Google Scholar] [CrossRef]
- Mahat, V.; Anderson, A. Impacts of Climate and Catastrophic Forest Changes on Streamflow and Water Balance in a Mountainous Headwater Stream in Southern Alberta. Hydrol. Earth Syst. Sci. 2013, 17, 4941–4956. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Elshorbagy, A.; Wheater, H.; Gober, P.; Nazemi, A. Integrating Supply Uncertainties from Stochastic Modeling into Integrated Water Resource Management: Case Study of the Saskatchewan River Basin. J. Water Resour. Plan. Manag. 2016, 142, 05015006. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Elshorbagy, A.; Wheater, H.; Gober, P. A Risk-Based Framework for Water Resource Management under Changing Water Availability, Policy Options, and Irrigation Expansion. Adv. Water Resour. 2016, 94, 291–306. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Elshorbagy, A.; Nazemi, A.; Jardine, T.D.; Wheater, H.; Lindenschmidt, K.E. The Ecohydrological Vulnerability of a Large Inland Delta to Changing Regional Streamflows and Upstream Irrigation Expansion. Ecohydrology 2017, 10, e1824. [Google Scholar] [CrossRef]
- Government of Canada. Historical Climate Data. 2023. Available online: https://climate.weather.gc.ca/historical_data/search_historic_data_e.html (accessed on 7 August 2023).
- Environment and Climate Change Canada. Historical Hydrometric Data Search. 2023. Available online: https://wateroffice.ec.gc.ca/search/historical_e.html (accessed on 7 August 2023).
- Alberta Climate Information Service. Methodology and Data Sources for Agriculture and Forestry’s Interpolated Data (1961–2018). 2019. Available online: https://agriculture.alberta.ca/acis/docs/Methodology-and-data-sources-for-interpolated-data-y2019_m03_d27.pdf (accessed on 7 August 2023).
- Bergström, S. The Development of a Snow Routine for the HBV-2 Model. Nord. Hydrol. 1975, 6, 73–92. [Google Scholar] [CrossRef]
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and Test of the Distributed HBV-96 Hydrological Model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Seibert, J.; Bergström, S. A Retrospective on Hydrological Catchment Modelling Based on Half a Century with the HBV Model. Hydrol. Earth Syst. Sci. 2022, 26, 1371–1388. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Chen, J.; Arsenault, R.; Brissette, F.P.; Zhang, S. Climate Change Impact Studies: Should We Bias Correct Climate Model Outputs or Post-Process Impact Model Outputs? Water Resour. Res. 2021, 57, e2020WR028638. [Google Scholar] [CrossRef]
- Dallaire, G.; Poulin, A.; Arsenault, R.; Brissette, F. Uncertainty of Potential Evapotranspiration Modeling in Climate Change Impact Studies on Low Flows in North America. Hydrol. Sci. J. 2021, 66, 689–702. [Google Scholar] [CrossRef]
- Martel, J.-L.; Brissette, F.; Troin, M.; Arsenault, R.; Chen, J.; Su, T.; Lucas-Picher, P. CMIP5 and CMIP6 Model Projection Comparison for Hydrological Impacts over North America. Geophys. Res. Lett. 2022, 49, e2022GL098364. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Habib, E. Application of a Conceptual Hydrologic Model in Teaching Hydrologic Processes. Int. J. Eng. Educ. 2010, 26, 963–973. [Google Scholar]
- Seibert, J.; Vis, M.J.P. Teaching Hydrological Modeling with a User-Friendly Catchment-Runoff-Model Software Package. Hydrol. Earth Syst. Sci. 2012, 16, 3315–3325. [Google Scholar] [CrossRef]
- Wang, X.; Melesse, A.M. Evaluation of the SWAT Model’s Snowmelt Hydrology in a Northwestern Minnesota Watershed. Trans. Am. Soc. Agric. Biol. Eng. 2005, 48, 1359–1376. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. “As Simple as Possible but Not Simpler”: What Is Useful in a Temperature-Based Snow Accounting Routine? Part 2—Sensitivity Analysis of the Cemaneige Snow Accounting Routine on 380 Catchments. J. Hydrol. 2014, 517, 1176–1187. [Google Scholar] [CrossRef]
- Yang, X.; Magnusson, J.; Huang, S.; Beldring, S.; Xu, C.-Y. Dependence of Regionalization Methods on the Complexity of Hydrological Models in Multiple Climatic Regions. J. Hydrol. 2020, 582, 124357. [Google Scholar] [CrossRef]
- Guo, Q.; Chen, J.; Zhang, X.J.; Xu, C.; Chen, H. Impacts of Using State-of-the-Art Multivariate Bias Correction Methods on Hydrological Modeling over North America. Water Resour. Res. 2020, 56, e2019WR026659. [Google Scholar] [CrossRef]
- KlemeŠ, V. Operational Testing of Hydrological Simulation Models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modeling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Yarpiz. Shuffled Complex Evolution (SCE-UA). MATLAB Central File. 2020. Available online: https://www.mathworks.com/matlabcentral/fileexchange/52862-shuffled-complex-evolution-sce-ua (accessed on 7 August 2023).
- Beven, K.; Freer, J. Equifinality, Data Assimilation, and Uncertainty Estimation in Mechanistic Modelling of Complex Environmental Systems Using the GLUE Methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Alberta Environment. Water Resources Management Model Computer Program Description. Southern Region Resource Management Branch, Alberta Environment. 2002. Available online: https://open.alberta.ca/dataset/9c89dc9e-9469-4031-8b0d-a0a4bb691023/resource/946179ec-bb86-4e0f-9fa4-3e68c8ec99c8/download/waterresourcesmanagement-ssrb-infosheet.pdf (accessed on 7 August 2023).
- Akhtar, M.K.; de la Chevrotière, C.; Tanzeeba, S.; Tang, T.; Grover, P. A Serious Gaming Tool: Bow River Sim for Communicating Integrated Water Resources Management. J. Hydroinform. 2020, 22, 491–509. [Google Scholar] [CrossRef]
- Zandmoghaddam, S.; Nazemi, A.; Hassanzadeh, E.; Hatami, S. Representing Local Dynamics of Water Resource Systems through a Data-Driven Emulation Approach. Water Resour. Manag. 2019, 33, 3579–3594. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Elshorbagy, A.; Wheater, H.; Gober, P. Managing Water in Complex Systems: An Integrated Water Resources Model for Saskatchewan, Canada. Environ. Model. Softw. 2014, 58, 12–26. [Google Scholar] [CrossRef]
- NCCS. NASA Earth Exchange Global Daily Downscaled Projections (NEX-GDDP). Available online: https://www.nccs.nasa.gov/services/data-collections/land-based-products/nex-gddp (accessed on 2 November 2020).
- Thrasher, B.; Maurer, E.P.; McKellar, C.; Duffy, P.B. Technical Note: Bias Correcting Climate Model Simulated Daily Temperature Extremes with Quantile Mapping. Hydrol. Earth Syst. Sci. 2012, 16, 3309–3314. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Nazemi, A.; Adamowski, J.; Nguyen, T.H.; Van-Nguyen, V.T. Quantile-Based Downscaling of Rainfall Extremes: Notes on Methodological Functionality, Associated Uncertainty and Application in Practice. Adv. Water Resour. 2019, 131, 103371. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Nazemi, A.; Adamowski, J. Comparison of Continuous and Quantile-Based Downscaling Approaches to Evaluate the Climate Change Impacts on Characteristics of Extreme Rainfall. In Geo-Extreme 2021; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 343–351. [Google Scholar]
- Jaramillo, P.; Nazemi, A. Assessing Urban Water Security under Changing Climate: Challenges and Ways Forward. Sustain. Cities Soc. 2018, 41, 907–918. [Google Scholar] [CrossRef]
- Bérubé, S.; Brissette, F.; Arsenault, R. Optimal Hydrological Model Calibration Strategy for Climate Change Impact Studies. J. Hydrol. Eng. 2022, 27, 04021053. [Google Scholar] [CrossRef]
- Oubeidillah, A.A.; Kao, S.C.; Ashfaq, M.; Naz, B.S.; Tootle, G. A Large-Scale, High-Resolution Hydrological Model Parameter Data Set for Climate Change Impact Assessment for the Conterminous US. Hydrol. Earth Syst. Sci. 2014, 18, 67–84. [Google Scholar] [CrossRef]
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of high streamflow extremes in climate change studies: How do we calibrate hydrological models? Hydrol. Earth Syst. Sci. 2022, 26, 3863–3883. [Google Scholar] [CrossRef]
- Stergiadi, M.; Di Marco, N.; Avesani, D.; Righetti, M.; Borga, M. Impact of Geology on Seasonal Hydrological Predictability in Alpine Regions by a Sensitivity Analysis Framework. Water 2020, 12, 2255. [Google Scholar] [CrossRef]
- Ali, Z.; Iqbal, M.; Khan, I.U.; Masood, M.U.; Umer, M.; Lodhi, M.U.K.; Tariq, M.A.U.R. Hydrological Response under CMIP6 Climate Projection in Astore River Basin, Pakistan. J. Mt. Sci. 2023, 20, 2263–2281. [Google Scholar] [CrossRef]
- Iqbal, M.; Wen, J.; Masood, M.; Masood, M.U.; Adnan, M. Impacts of Climate and Land-Use Changes on Hydrological Processes of the Source Region of Yellow River, China. Sustainability 2022, 14, 14908. [Google Scholar] [CrossRef]
Figure 1.
The Oldman River Basin in Alberta, Canada, with the Castle (bottom-left), Crowsnest (middle-left), Oldman (top-left), and Near Reservoir sub-watersheds upstream of the Oldman Reservoir. Climate and hydrometric stations in each sub-watershed, as well as the grids of the Alberta Township system, are presented.
Figure 1.
The Oldman River Basin in Alberta, Canada, with the Castle (bottom-left), Crowsnest (middle-left), Oldman (top-left), and Near Reservoir sub-watersheds upstream of the Oldman Reservoir. Climate and hydrometric stations in each sub-watershed, as well as the grids of the Alberta Township system, are presented.
Figure 2.
Observed and simulated inflow hydrographs during 1961–1990 using HBV-MTL with (a) Degree-Day and (b) CemaNeige modules and GR4J with (c) Degree-Day and (d) CemaNeige modules, each calibrated using a lumped approach with point-based data (LP) and grid-based data (LG) and a semi-distributed approach with point-based (SP) and grid-based data (SG). The results are shown for the models with optimal and acceptable calibration parameter sets.
Figure 2.
Observed and simulated inflow hydrographs during 1961–1990 using HBV-MTL with (a) Degree-Day and (b) CemaNeige modules and GR4J with (c) Degree-Day and (d) CemaNeige modules, each calibrated using a lumped approach with point-based data (LP) and grid-based data (LG) and a semi-distributed approach with point-based (SP) and grid-based data (SG). The results are shown for the models with optimal and acceptable calibration parameter sets.
Figure 3.
Observed and future inflow hydrographs under RCP 4.5 during 2021–2099 using HBV-MTL with (a) Degree-Day and (b) CemaNeige modules and GR4J with (c) Degree-Day and (d) CemaNeige modules, each calibrated using a lumped approach with point-based (LP) and grid-based data (LG) and using a semi-distributed approach with point-based (SP) and grid-based data (SG).
Figure 3.
Observed and future inflow hydrographs under RCP 4.5 during 2021–2099 using HBV-MTL with (a) Degree-Day and (b) CemaNeige modules and GR4J with (c) Degree-Day and (d) CemaNeige modules, each calibrated using a lumped approach with point-based (LP) and grid-based data (LG) and using a semi-distributed approach with point-based (SP) and grid-based data (SG).
Figure 4.
Observed and future inflow hydrographs under RCP 8.5 during 2021–2099 using HBV-MTL with (a) Degree-Day and (b) CemaNeige modules and GR4J with (c) Degree-Day and (d) CemaNeige modules, each calibrated using a lumped approach with point-based (LP) and grid-based data (LG) and using semi-distributed approach with point-based (SP) and grid-based data (SG).
Figure 4.
Observed and future inflow hydrographs under RCP 8.5 during 2021–2099 using HBV-MTL with (a) Degree-Day and (b) CemaNeige modules and GR4J with (c) Degree-Day and (d) CemaNeige modules, each calibrated using a lumped approach with point-based (LP) and grid-based data (LG) and using semi-distributed approach with point-based (SP) and grid-based data (SG).
Figure 5.
Inflow signatures during the historical and future periods. Observed values are shown with a dashed line. Simulated values are shown using the models with acceptable parameter sets: HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules and GR4J with the (c) Degree-Day and (d) CemaNeige modules, calibrated using a lumped approach with point-based (LP; red) and grid-based data (LG; yellow) and a semi-distributed approach with point-based (SP; blue) and grid-based data (SG; violet). Projections based on RCPs 4.5 and 8.5 are shown with blue and red box outlines.
Figure 5.
Inflow signatures during the historical and future periods. Observed values are shown with a dashed line. Simulated values are shown using the models with acceptable parameter sets: HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules and GR4J with the (c) Degree-Day and (d) CemaNeige modules, calibrated using a lumped approach with point-based (LP; red) and grid-based data (LG; yellow) and a semi-distributed approach with point-based (SP; blue) and grid-based data (SG; violet). Projections based on RCPs 4.5 and 8.5 are shown with blue and red box outlines.
Figure 6.
Difference between the observed and simulated reservoir volume during 1961–1990 for models with acceptable and optimal parameter sets: HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J with the (c) Degree-Day and (d) CemaNeige modules. The models were calibrated using lumped point (LP) and grid-based (LG) data and semi-distributed with point- (SP) and grid-based (SG) data. The KGE values for each configuration are shown in boxes.
Figure 6.
Difference between the observed and simulated reservoir volume during 1961–1990 for models with acceptable and optimal parameter sets: HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J with the (c) Degree-Day and (d) CemaNeige modules. The models were calibrated using lumped point (LP) and grid-based (LG) data and semi-distributed with point- (SP) and grid-based (SG) data. The KGE values for each configuration are shown in boxes.
Figure 7.
Simulated versus observed water deficit in meeting local water demand during the historical period using HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J (c) with the Degree-Day and (d) CemaNeige modules, calibrated considering a lumped approach with point- (LP) and grid-based (LG) data and semi-distributed with point- (SP) and grid-based (SG) data using acceptable and optimal parameter sets.
Figure 7.
Simulated versus observed water deficit in meeting local water demand during the historical period using HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J (c) with the Degree-Day and (d) CemaNeige modules, calibrated considering a lumped approach with point- (LP) and grid-based (LG) data and semi-distributed with point- (SP) and grid-based (SG) data using acceptable and optimal parameter sets.
Figure 8.
Observed, as well as median and ensemble of, projected reservoir volume under RCPs 4.5 and 8.5 using HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J with the (c) Degree-Day and (d) CemaNeige modules, calibrated via lumping with point- (LP) and grid-based (LG) data and semi-distributed with point- (SP) and grid-based (SG) data.
Figure 8.
Observed, as well as median and ensemble of, projected reservoir volume under RCPs 4.5 and 8.5 using HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J with the (c) Degree-Day and (d) CemaNeige modules, calibrated via lumping with point- (LP) and grid-based (LG) data and semi-distributed with point- (SP) and grid-based (SG) data.
Figure 9.
Five-year moving average of projected water deficit (%) under RCPs 4.5 and 8.5 using the outputs of 19 GCMs fed into HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J with the (c) Degree-Day and (d) CemaNeige modules, developed based on a lumped approach with point- (LP) and grid-based data (LG) and a semi-distributed approach with point-(LP) and grid-based (LG) data.
Figure 9.
Five-year moving average of projected water deficit (%) under RCPs 4.5 and 8.5 using the outputs of 19 GCMs fed into HBV-MTL with the (a) Degree-Day and (b) CemaNeige modules, as well as GR4J with the (c) Degree-Day and (d) CemaNeige modules, developed based on a lumped approach with point- (LP) and grid-based data (LG) and a semi-distributed approach with point-(LP) and grid-based (LG) data.
Table 1.
Performance of 16 hydrological model configurations in estimating the daily inflow to the Oldman Reservoir, evaluated based on the KGE measure.
Table 1.
Performance of 16 hydrological model configurations in estimating the daily inflow to the Oldman Reservoir, evaluated based on the KGE measure.
| Configurations | Degree-Day | CemaNeige |
|---|
| Calibration | Control | Calibration | Control |
|---|
| HBV-MTL | Lumped-point data (LP) | 0.90 | 0.76 | 0.89 | 0.84 |
| Lumped-grid data (LG) | 0.89 | 0.65 | 0.87 | 0.64 |
| Semi-distributed-point data (SP) | 0.93 | 0.81 | 0.91 | 0.83 |
| Semi-distributed-grid data (SG) | 0.92 | 0.67 | 0.90 | 0.66 |
| GR4J | Lumped-point data (LP) | 0.88 | 0.82 | 0.88 | 0.86 |
| Lumped-grid data (LG) | 0.88 | 0.72 | 0.87 | 0.72 |
| Semi-distributed-point data (SP) | 0.92 | 0.83 | 0.90 | 0.84 |
| Semi-distributed-grid data (SG) | 0.89 | 0.65 | 0.89 | 0.68 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).