Improved Representation of Groundwater–Surface Water Interactions Using SWAT+gwflow and Modifications to the gwflow Module
Abstract
:1. Introduction
2. Materials and Methods
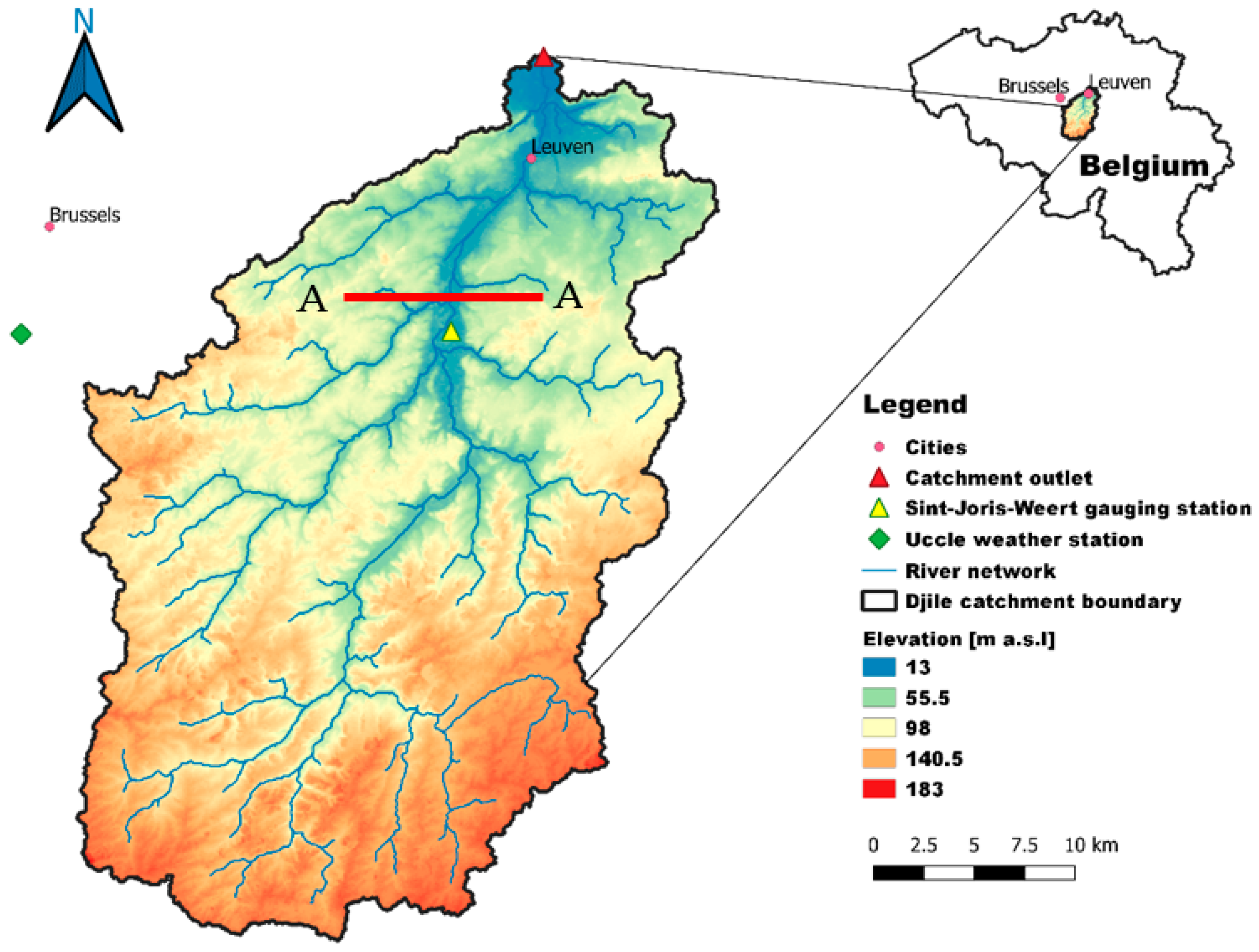
2.1. Study Area
2.2. Methodology
2.2.1. SWAT+ Model Setup
2.2.2. SWAT+ Model with the gwflow Module Setup
2.2.3. Modification to the gwflow Module
2.2.4. Sensitivity, Calibration, and Water Balance Analysis
3. Results
3.1. Sensitivity Analysis
3.2. Calibration, Validation, and Water Balance
3.3. Groundwater Model Outputs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siad, S.M.; Iacobellis, V.; Zdruli, P.; Gioia, A.; Stavi, I.; Hoogenboom, G. A Review of Coupled Hydrologic and Crop Growth Models. Agric. Water Manag. 2019, 224, 105746. [Google Scholar] [CrossRef]
- Larocque, M.; Broda, S. Groundwater–Surface Water Interactions in Canada; Taylor & Francis: Abingdon, UK, 2016; Volume 41, pp. 451–454. ISBN 0701-1784. [Google Scholar]
- Alley, W.M.; Reilly, T.E.; Franke, O.L. Sustainability of Ground-Water Resources; US Department of the Interior, US Geological Survey: Reston, VA, USA, 1999; Volume 1186, ISBN 0-607-93040-3. [Google Scholar]
- Moore, W.S. The Effect of Submarine Groundwater Discharge on the Ocean. Annu. Rev. Mar. Sci. 2010, 2, 59–88. [Google Scholar] [CrossRef] [PubMed]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An Introduction to the European Hydrological System—Systeme Hydrologique Europeen,“SHE”, 1: History and Philosophy of a Physically-Based, Distributed Modelling System. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G.; O’Connell, P.E. SHETRAN: Distributed River Basin Flow and Transport Modeling System. J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef]
- Maré, H.G.; Rademeyer, J.I.; Sami, K. Application on Groundwater/Surface Water Interaction Modeling in the Schoonspruit Catchment; Pretoria, South Africa. 2007. Available online: https://www.miya-water.com/fotos/artigos/02_application_on_groundwater_surface_water_interaction_modeling_in_the_schoonspruit_catchment_19810471915a326afa23030.pdf (accessed on 21 September 2022).
- Scibek, J.; Allen, D.M.; Cannon, A.J.; Whitfield, P.H. Groundwater–Surface Water Interaction under Scenarios of Climate Change Using a High-Resolution Transient Groundwater Model. J. Hydrol. 2007, 333, 165–181. [Google Scholar] [CrossRef]
- Stefania, G.A.; Rotiroti, M.; Fumagalli, L.; Simonetto, F.; Capodaglio, P.; Zanotti, C.; Bonomi, T. Modeling Groundwater/Surface-Water Interactions in an Alpine Valley (the Aosta Plain, NW Italy): The Effect of Groundwater Abstraction on Surface-Water Resources. Hydrogeol. J. 2018, 26, 147–162. [Google Scholar] [CrossRef]
- Chapman, S.W.; Parker, B.L.; Cherry, J.A.; Aravena, R.; Hunkeler, D. Groundwater–Surface Water Interaction and Its Role on TCE Groundwater Plume Attenuation. J. Contam. Hydrol. 2007, 91, 203–232. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-Surface Water Interactions: New Methods and Models to Improve Understanding of Processes and Dynamics. Adv. Water Resour. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Kalbus, E.; Reinstorf, F.; Schirmer, M. Measuring Methods for Groundwater–Surface Water Interactions: A Review. Hydrol. Earth Syst. Sci. 2006, 10, 873–887. [Google Scholar] [CrossRef]
- Levy, J.; Xu, Y. Groundwater Management and Groundwater/Surface-Water Interaction in the Context of South African Water Policy. 2011. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=c8a92cf8fb123f9f165ddd2f604ee3b1aa55edcf (accessed on 20 July 2023).
- Oxtobee, J.P.; Novakowski, K. A Field Investigation of Groundwater/Surface Water Interaction in a Fractured Bedrock Environment. J. Hydrol. 2002, 269, 169–193. [Google Scholar] [CrossRef]
- Woessner, W.W. Stream and Fluvial Plain Ground Water Interactions: Rescaling Hydrogeologic Thought. Groundwater 2000, 38, 423–429. [Google Scholar] [CrossRef]
- Yimer, E.A.; Van Schaeybroeck, B.; Van de Vyver, H.; Van Griensven, A. Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia. Atmosphere 2022, 13, 364. [Google Scholar] [CrossRef]
- Perkins, S.P.; Sophocleous, M. Development of a Comprehensive Watershed Model Applied to Study Stream Yield under Drought Conditions. Groundwater 1999, 37, 418–426. [Google Scholar] [CrossRef]
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing Regional-scale Spatio-temporal Patterns of Groundwater–Surface Water Interactions Using a Coupled SWAT–MODFLOW Model. Hydrol. Process. 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
- Markstrom, S.L.; Niswonger, R.G.; Regan, R.S.; Prudic, D.E.; Barlow, P.M. GSFLOW-Coupled Ground-Water and Surface-Water FLOW Model Based on the Integration of the Precipitation-Runoff Modeling System (PRMS) and the Modular Ground-Water Flow Model (MODFLOW-2005). US Geol. Surv. Tech. Methods 2008, 6, 240. [Google Scholar]
- Bailey, R.T.; Bieger, K.; Arnold, J.G.; Bosch, D.D. A New Physically-Based Spatially-Distributed Groundwater Flow Module for SWAT+. Hydrology 2020, 7, 75. [Google Scholar] [CrossRef]
- Kim, N.W.; Chung, I.M.; Won, Y.S.; Arnold, J.G. Development and Application of the Integrated SWAT–MODFLOW Model. J. Hydrol. 2008, 356, 1–16. [Google Scholar] [CrossRef]
- Putthividhya, A.; Laonamsai, J. SWAT and MODFLOW Modeling of Spatio-Temporal Runoff and Groundwater Recharge Distribution. In Proceedings of the World Environmental and Water Resources Congress 2017, Sacramento, CA, USA, 21–25 May 2017; pp. 51–65. [Google Scholar]
- Deb, P.; Kiem, A.S.; Willgoose, G. A Linked Surface Water-Groundwater Modelling Approach to More Realistically Simulate Rainfall-Runoff Non-Stationarity in Semi-Arid Regions. J. Hydrol. 2019, 575, 273–291. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Peterson, J.R.; Hamlett, J.M. Hydrologic Calibration of The Swat Model in A Watershed Containing Fragipan Soils. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 531–544. [Google Scholar] [CrossRef]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of Daily and Monthly Stream Discharge from Small Watersheds Using the SWAT Model. Trans. ASAE 2000, 43, 1431. [Google Scholar] [CrossRef]
- Srivastava, P.; McNair, J.N.; Johnson, T.E. Comparison of process-based and artificial neural network approaches for streamflow modeling in an agricultural watershed. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 545–563. [Google Scholar] [CrossRef]
- Galbiati, L.; Bouraoui, F.; Elorza, F.J.; Bidoglio, G. Modeling Diffuse Pollution Loading into a Mediterranean Lagoon: Development and Application of an Integrated Surface–Subsurface Model Tool. Ecol. Model. 2006, 193, 4–18. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Starks, P.J.; Arnold, J.G.; Srinivasan, R. A Model Integration Framework for Linking SWAT and MODFLOW. Environ. Model. Softw. 2015, 73, 103–116. [Google Scholar] [CrossRef]
- Sophocleous, M.; Perkins, S.P. Methodology and Application of Combined Watershed and Ground-Water Models in Kansas. J. Hydrol. 2000, 236, 185–201. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, The US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005; Volume 6. [Google Scholar]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M.; Volk, M.; Srinivasan, R. Introduction to SWAT+, a Completely Restructured Version of the Soil and Water Assessment Tool. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 115–130. [Google Scholar] [CrossRef]
- Van Oost, K.; Verstraeten, G.; Doetterl, S.; Notebaert, B.; Wiaux, F.; Broothaerts, N.; Six, J. Legacy of Human-Induced C Erosion and Burial on Soil–Atmosphere C Exchange. Proc. Natl. Acad. Sci. USA 2012, 109, 19492–19497. [Google Scholar] [CrossRef]
- Batelaan, O.; De Smedt, F. GIS-Based Recharge Estimation by Coupling Surface–Subsurface Water Balances. J. Hydrol. 2007, 337, 337–355. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M. Representing the Connectivity of Upland Areas to Floodplains and Streams in SWAT+. JAWRA J. Am. Water Resour. Assoc. 2019, 55, 578–590. [Google Scholar] [CrossRef]
- Alitane, A.; Essahlaoui, A.; Van Griensven, A.; Yimer, E.A.; Essahlaoui, N.; Mohajane, M.; Chawanda, C.J.; Van Rompaey, A. Towards a Decision-Making Approach of Sustainable Water Resources Management Based on Hydrological Modeling: A Case Study in Central Morocco. Sustainability 2022, 14, 10848. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Shangguan, W.; Hengl, T.; Mendes de Jesus, J.; Yuan, H.; Dai, Y. Mapping the Global Depth to Bedrock for Land Surface Modeling. J. Adv. Model. Earth Syst. 2017, 9, 65–88. [Google Scholar] [CrossRef]
- Wossenyeleh, B.K.; Worku, K.A.; Verbeiren, B.; Huysmans, M. Drought Propagation and Its Impact on Groundwater Hydrology of Wetlands: A Case Study on the Doode Bemde Nature Reserve (Belgium). Nat. Hazards Earth Syst. Sci. 2021, 21, 39–51. [Google Scholar] [CrossRef]
- Huscroft, J.; Gleeson, T.; Hartmann, J.; Börker, J. Compiling and Mapping Global Permeability of the Unconsolidated and Consolidated Earth: GLobal HYdrogeology MaPS 2.0 (GLHYMPS 2.0). Geophys. Res. Lett. 2018, 45, 1897–1904. [Google Scholar] [CrossRef]
- Wossenyeleh, B.K. Groundwater Drought Propagation and Distribution in Temperate and Semi-Arid Climates. 2021. Available online: https://lirias.kuleuven.be/3487237?limo=0 (accessed on 20 July 2023).
- Atkinson, S.E.; Woods, R.A.; Sivapalan, M. Climate and Landscape Controls on Water Balance Model Complexity over Changing Timescales. Water Resour. Res. 2002, 38, 50-1–50-17. [Google Scholar] [CrossRef]
- Basu, N.B.; Rao, P.S.C.; Winzeler, H.E.; Kumar, S.; Owens, P.; Merwade, V. Parsimonious Modeling of Hydrologic Responses in Engineered Watersheds: Structural Heterogeneity versus Functional Homogeneity. Water Resour. Res. 2010, 46, W04501. [Google Scholar] [CrossRef]
- Sivapalan, M. Process Complexity at Hillslope Scale, Process Simplicity at Watershed Scale: Is There a Connection? In Proceedings of the EGS-AGU-EUG Joint Assembly, Nice, France, 6–11 April 2003; p. 7973. [Google Scholar]
- Wagener, T.; Sivapalan, M.; Troch, P.; Woods, R. Catchment Classification and Hydrologic Similarity. Geogr. Compass 2007, 1, 901–931. [Google Scholar] [CrossRef]
- Yimer, E.A.; Yadollahi, S.; Riakhi, F.-E.; Alitane, A.; Weerasinghe, I.; Wirion, C.; Nossent, J.; van Griensven, A. A Groundwater Level-Based Filtering to Improve the Accuracy of Locating Agricultural Tile Drain and Ditch Networks. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103423. [Google Scholar] [CrossRef]
- Yimer, E.A.; Riakhi, F.-E.; Bailey, R.T.; Nossent, J.; van Griensven, A. The Impact of Extensive Agricultural Water Drainage on the Hydrology of the Kleine Nete Watershed, Belgium. Sci. Total Environ. 2023, 885, 163903. [Google Scholar] [CrossRef]
- Doherty, J. PEST User-Manual: Model-Independent Parameter Estimation; Watermark Numerical Computing: Brisbane, Australia, 2010. [Google Scholar]
- Saltelli, A.; Annoni, P. How to Avoid a Perfunctory Sensitivity Analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Possemiers, M.; Huysmans, M.; Peeters, L.; Batelaan, O.; Dassargues, A. Relationship between Sedimentary Features and Permeability at Different Scales in the Brussels Sands. Geol. Belg. 2012, 15, 156–164. [Google Scholar]
- Vandersteen, K.; Gedeon, M.; Beerten, K. A Synthesis of Hydraulic Conductivity Measurements of the Subsurface in Northeastern Belgium. Geol. Belg. 2014, 17, 196–210. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972; 764p. [Google Scholar]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability Distributions of Soil Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Loheide, S.P., II; Gorelick, S.M. A Local-Scale, High-Resolution Evapotranspiration Mapping Algorithm (ETMA) with Hydroecological Applications at Riparian Meadow Restoration Sites. Remote Sens. Environ. 2005, 98, 182–200. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Bailey, R.T.; Bieger, K.; Flores, L.; Tomer, M. Evaluating the Contribution of Subsurface Drainage to Watershed Water Yield Using SWAT+ with Groundwater Modeling. Sci. Total Environ. 2022, 802, 149962. [Google Scholar] [CrossRef]
- Kampf, S.K.; Burges, S.J. A Framework for Classifying and Comparing Distributed Hillslope and Catchment Hydrologic Models. Water Resour. Res. 2007, 43, W05423. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward Improved Calibration of Hydrologic Models: Multiple and Noncommensurable Measures of Information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Montanari, A.; Toth, E. Calibration of Hydrological Models in the Spectral Domain: An Opportunity for Scarcely Gauged Basins? Water Resour. Res. 2007, 43, W05434. [Google Scholar] [CrossRef]




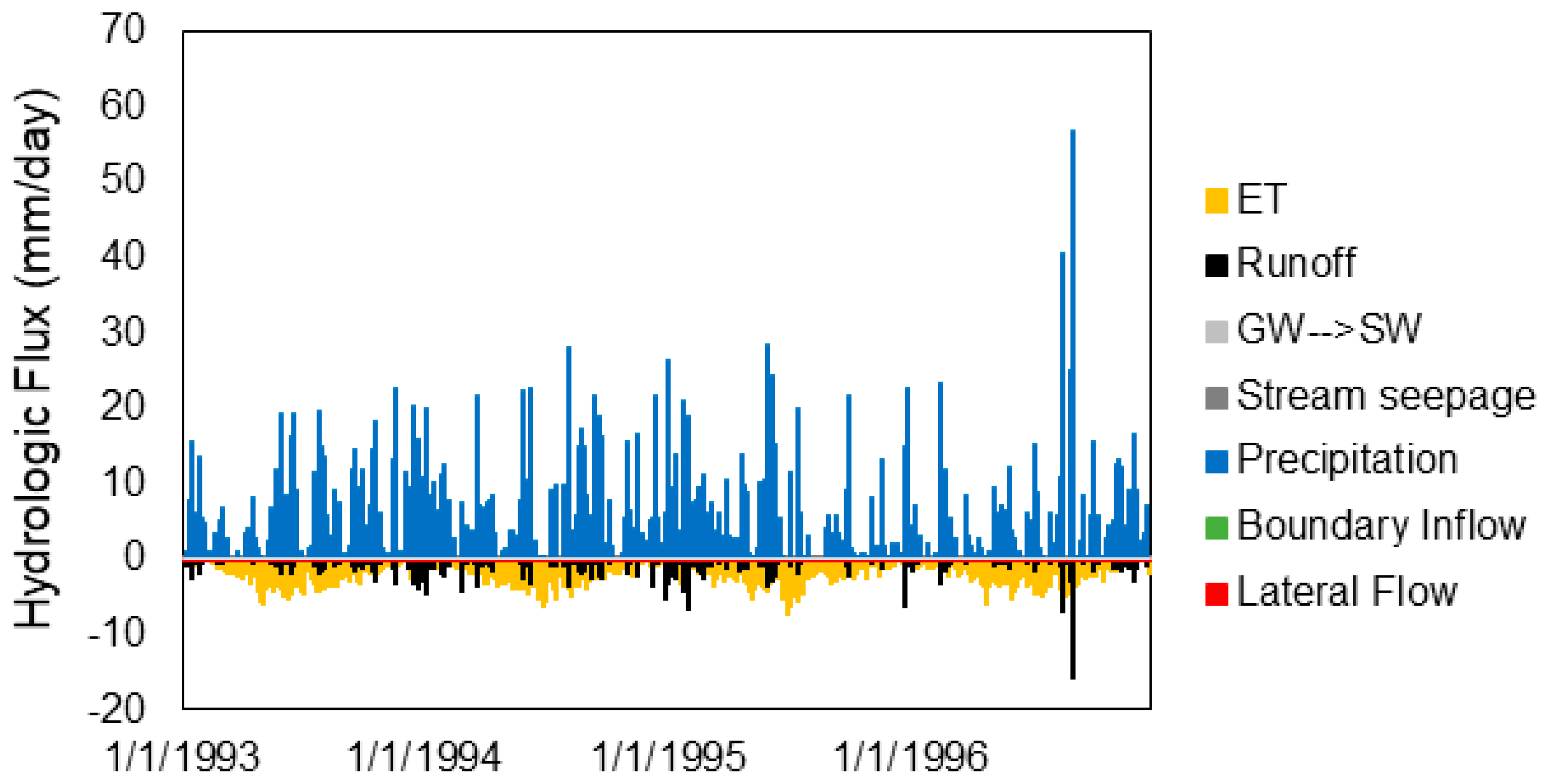



| Time Step | NSE | PBIAS (%) | Watershed Soil Water Balance | Groundwater Balance Error (mm) | ||||
|---|---|---|---|---|---|---|---|---|
| SWAT+ | SWAT+ gwflow | SWAT+ | SWAT+ gwflow | SWAT+ | SWAT+ gwflow | SWAT+ gwflow | ||
| Calibration (1983 to 1996) | Daily | −0.1 | 0.5 | 1.7 | −0.9 | 21.94 − 5.32 = 16.62 mm | 4.73 − 4.04 = 0.69 mm | −2 − (−3.12) = 1.12 mm |
| Monthly | 0.4 | 0.6 | 1.6 | −1.0 | ||||
| Validation 1 (1975 to 1982) | Daily | 0.1 | 0.5 | −5.6 | −11.0 | 25.4 − (−102.6) = 127.92 mm | 5.42 − 11.95 = −6.53 mm | 78.3 − 80 = −1.7 mm |
| Monthly | 0.6 | 0.7 | −5.6 | −10.9 | ||||
| Validation 2 (1997 to 2002) | Daily | −0.3 | 0.4 | 11.0 | 6.4 | 104.7 − 93.02 = 11.68 mm | 4.56 − 6.54 = 1.98 mm | 36.8 − 38 = −1.2 mm |
| Monthly | 0.1 | 0.5 | 11.0 | 4.9 | ||||
| Inputs to Watershed | ||||
|---|---|---|---|---|
| Without gwsoil | With gwsoil | |||
| Precipitation | 838.9 | 838.9 | ||
| Boundary Inflow | −5.5 | −26.5 | ||
| Lake seepage to groundwater | 0.4 | 0.3 | ||
| Outputs from Watershed | Percentage of Precipitation (%) | |||
| Without gwsoil | With gwsoil | |||
| Surface ET | 544.4 | 559 | 65 | 67 |
| Surface runoff | 66.4 | 83.6 | 8 | 10 |
| Soil lateral flow | 10.6 | 43.2 | 1 | 5 |
| Stream seepage to groundwater | −4.5 | −4.4 | - | - |
| Saturation excess flow | 164.2 | 0 | 20 | 0 |
| Groundwater ET | 0.2 | 0 | - | - |
| Internal Flow | Percentage of Precipitation (%) | |||
| Without gwsoil | With gwsoil | |||
| Recharge to the water table | 204.8 | 837.2 | - | - |
| Groundwater transfer to soil | 0 | 733.9 | 0 | 87 |
| Net recharge | 204.8 | 103.3 | 24 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yimer, E.A.; Bailey, R.T.; Piepers, L.L.; Nossent, J.; Van Griensven, A. Improved Representation of Groundwater–Surface Water Interactions Using SWAT+gwflow and Modifications to the gwflow Module. Water 2023, 15, 3249. https://doi.org/10.3390/w15183249
Yimer EA, Bailey RT, Piepers LL, Nossent J, Van Griensven A. Improved Representation of Groundwater–Surface Water Interactions Using SWAT+gwflow and Modifications to the gwflow Module. Water. 2023; 15(18):3249. https://doi.org/10.3390/w15183249
Chicago/Turabian StyleYimer, Estifanos Addisu, Ryan T. Bailey, Lise Leda Piepers, Jiri Nossent, and Ann Van Griensven. 2023. "Improved Representation of Groundwater–Surface Water Interactions Using SWAT+gwflow and Modifications to the gwflow Module" Water 15, no. 18: 3249. https://doi.org/10.3390/w15183249
APA StyleYimer, E. A., Bailey, R. T., Piepers, L. L., Nossent, J., & Van Griensven, A. (2023). Improved Representation of Groundwater–Surface Water Interactions Using SWAT+gwflow and Modifications to the gwflow Module. Water, 15(18), 3249. https://doi.org/10.3390/w15183249








